2015年辽宁省数据整理高级
- 格式:docx
- 大小:19.99 KB
- 文档页数:3

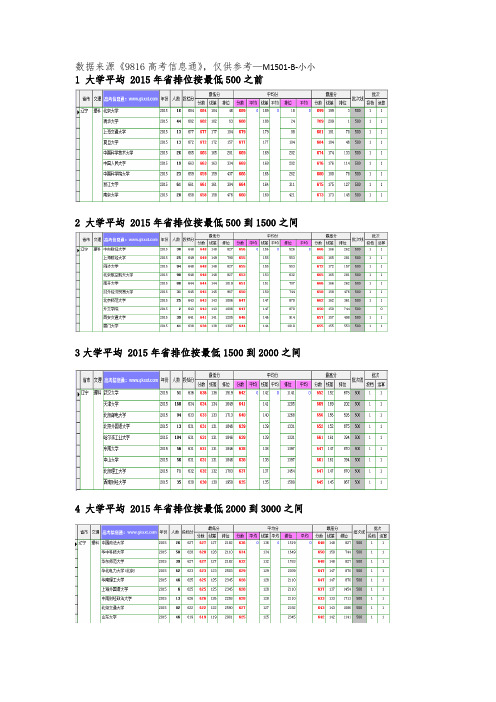
数据来源《9816高考信息通》,仅供参考—M1501-B-小小1 大学平均 2015年省排位按最低500之前
2 大学平均 2015年省排位按最低500到1500之间
3大学平均 2015年省排位按最低1500到2000之间
4 大学平均 2015年省排位按最低2000到3000之间
6大学平均 2015年省排位按最低5000到7000之间
7 大学平均 2015年省排位按最低7000到8000之间
8 大学平均 2015年省排位按最低8000到9000之间
10 大学平均 2015年省排位按最低10000到12000之间
11 大学平均 2015年省排位按最低12000到13000之间
12 大学平均 2015年省排位按最低13000到14000之间
14 大学平均 2015年省排位按最低15000到17000之间
15 大学平均 2015年省排位按最低17000到20000之间
17 大学平均 2015年省排位按最低22000到25000之间
上分数,不含自主、提前批、港澳等特殊类型招生数据。


辽宁省私家车保有量增长r及影响因素分析王翠【摘要】近年来,辽宁省的经济稳步发展,私家车保有量在快速上升.私家车保有量的变化趋势与辽宁省的基础设施建设、城市发展、交通以及环保等政策的制定有着密切联系,因此,准确的预测未来辽宁省私家车保有量有重要意义.本文以辽宁省1996~2015年私家车发展情况为研究对象,运用统计学及计量经济学相关知识,建立多元线性回归模型来分析私家车保有量的影响因素,经过模型检验和修正,进而分析各因素与保有量的影响关系.最后,根据得到的研究结果,对未来几年辽宁省私家车保有量进行预测并针对辽宁特殊的社会经济状况,为改善建成环境中潜藏着的复杂问题提出相关政策和建议.【期刊名称】《经济数学》【年(卷),期】2017(034)004【总页数】5页(P43-47)【关键词】私家车保有量;增长率;影响因素;多元回归【作者】王翠【作者单位】辽宁师范大学数学学院,辽宁大连 116029【正文语种】中文【中图分类】F426近年来,我国经济快速发展,社会的购买力逐渐增强.以作为高档耐用品的汽车行业为例,随着人们对出行的要求越来越高,私家车保有量也在逐年增加.私家车的普及不仅带来交通的便捷性,还带来了出行的舒适性.但在带来便利的同时,随之而来的问题也在困扰人民的生活.比如空气污染、拥挤的交通环境、驾驶的安全问题等.以辽宁省为例,城乡面貌和生活条件不断改善提高的同时,也伴随着诸多的失落和无助.因此,研究辽宁省私家车保有量的影响因素,准确的预测未来辽宁省私家车保有量,进而合理控制引导私家车保有量增长速度,使辽宁省汽车产业实现可持续发展变得尤为重要.本文主要研究辽宁省1996~2015年私家车保有量,运用统计学及计量经济学相关知识,得到辽宁省私家车保有量的现状.通过建立多元线性回归模型,利用Eviews及R统计软件,找到包括居民消费水平、工业总产值等因素对私家车保有量的影响.最后,尝试通过这些影响因素找到控制私家车保有量的方法,为相关部门应对辽宁特殊的社会经济状况,解决私家车带来的问题而制定政策提供思路与经济定量参考.为了研究可能存在的影响因素对辽宁省私家车保有量的直接影响程度,进而找到解决私家车增多带来的负面效应的方法,选择多元线性回归模型.众所周知,私家车的保有量和很多因素有关,在不同的经济发展水平区域,影响私家车保有量的因素也不同.受制于宏观经济大环境影响,以及自身体制、机制、结构等矛盾制约的辽宁经济的新常态之路略显艰难.基于辽宁经济的实际情况,选取辽宁省每万人私人汽车拥有量作为被解释变量Y,解释变量包括:1)居民消费水平(单位:元).随着经济的快速发展,人民生活水平越来越高,居民消费水平逐渐提高,证明人们的购买力逐渐增强.可见,作为奢侈消费品的汽车,与居民消费水平有密切联系.2)公路营运汽车拥有量(单位:万辆).根据经济学基本原理,公路营运汽车与私家车是互为替代品的关系.公交等公路营运汽车具有比私家车更大的载客量,因此,当以公交为代表的公路营运汽车数量增加时,私家车的需求量会减少.3)燃料类商品零售价格指数.燃料类商品零售价格指数指的是居民消费车用燃料及零配件价格指数和车辆使用及维修价格指数.根据经济学原理,燃料类商品零售价格指数是私家车保有量的互补品.一般情况下,当互补品的价格升高时,对私家车的需求量就会减少.因此,燃料类商品零售价格指数是影响私家车保有量的原因之一,同时也构成居民购买私家车的成本.国家政策.自1980年中央已推进汽车行业发展,但本文主要讨论与私家车相关的政策,“十五”计划明确“鼓励轿车进入家庭”.入世后,根据协议,中国将在汽车的生产、销售等领域放宽对国内外汽车公司的限制.中国政府削减进口关税,取消进口定额配制、国产化需求和技术转让政策.2007年以来,政策转向促进研发节能环保的汽车产业,带动国民经济的增长.因此国家推出政策在一定程度上有助于私家车的消费.本文的数据来源中国统计年鉴,选取1996~2015年共20年辽宁省的相关数据[1],并对其进行了处理,如表1所示.采用的计量经济学模型为:Yt=Q0+Q1X1t+Q2X2t+Q3X3t+Q4Dt+ut.其中,Yt表示私人汽车拥有量(万辆);X1t表示居民消费水平(元);X2t表示公路营运汽车拥有量(万辆);X3t表示燃料类商品零售价格指数;Dt表示国家政策,即当第t年有国家政策鼓励汽车消费时,Dt=1,否则,Dt=0;ut为随机扰动项. 通过对表1的数据进行统计,根据时间序列数据,采用普通最小二乘法(OLS),利用数学软件Eviews对设定的模型进行计量分析[2],结果如表2所示.将上述将上述回归结果整理为:Yt=-142.874 3+0.012 2X1t+0.071 2X2t-0.000 1X3t+0.010 6Dt,R2=0.995 9,f=926.321 2,D.W=1.202 5.从结果中可以看出,模型的拟合优度非常好,模型整体也非常显著,但是有几个自变量的t值检验没有通过,说明该模型可能存在多重共线性.综合来看,需要对上述模型进行计量经济学检验,并进行修正,使得模型的方程能够得到改进.首先,运用R统计软件,采用相关系数计算方法进行指标间的相关性分析,可以发现X1与X2的相关系数比较高,大于0.9.因此可以断定该模型必然存在多重共线性.采用Frisch综合分析法[3-5]对其进行逐步回归消除.首先写出以Y为因变量,以X1,X2,X3,D分别为自变量建立一元线性回归模型,可以获得以下4个方程:Yt=-75.600 6+0.02 X1t,R2=0.991 2,Yt=-76.951 2+5.201 2X2t,R2=0.823 9,Yt=1 124.455-9.382 1X3t,R2=0.208 8,Yt=18.447 5+147.813 8X4t,R2=0.169 8.综上所述,通过比较R2的大小选择以X1为自变量的一元线性回归模型,再利用逐步回归的法则,如表3所示.根据表3可以看出D1的R2值没有增加,而且t值的显著性检验也没有通过,所以最终只保留X1:居民消费水平(单位:元);X2:公路营运汽车拥有量(单位:万辆);X3:燃料类商品零售价格指数;这几个影响因素.得出消除多重共线性之后的最终模型为R2=0.995 9,F=1 316.640,D.W=1.188 0接下来,进行自相关性检验.由于该数据是时间序列数据,因此就要对其自相关性进行检验.根据回归结果可以得出,D.W=1.188 0,其中n=20;k=3在显著性水平为5%的情况下,DL=1;Du=1.68;可以得出DL<D.W<4-Du.因此在此区域不存在自相关性,所以不需要消除自相关性,模型保留.4.2.1 经济意义检验从回归得出的结果来看,X1的系数为0.02,X2的系数为-0.61,X3的系数为-0.93,各变量符号与预期的相一致,并且其大小在经济理论上解释的通.对于X1,当公路营运汽车拥有量和燃料类商品零售价格指数不变时,居民消费水平增加增加1元,辽宁省私家车保有量就会增加0.02万辆,就是说,在1996~2015年间,在对于X2,当居民消费水平和燃料类商品零售价格指数不变时,公路营运汽车拥有量每增加1万辆,辽宁省私家车保有量就会减少0.61万辆;对于X3,当居民消费水平和公路营运汽车拥有量不变时,燃料类商品零售价格指数每增加1%,辽宁省私家车保有量就会减少0.93万辆.综上所述,该模型通过经济意义检验.4.2.2 回归系数的显著性检验(t检验)从回归结果看,回归系数的t值[6,7]分别为:t1=20.247 66,t2=-2.130 310,t3=-2.323 627,查t分布表,在自由度为16,在95%的置信系数下,有t0.025(16)=2.12,由于各解释变量系数t值均大于临界值,因此拒绝H0,所以此模型中的变量和参数的t值统计值均显著.即居民消费水平、公路营运汽车拥有量和燃料类商品零售价格指数都对辽宁省私家车保有量具有显著影响.根据经济理论,居民消费水平的增加,意味着居民拥有充裕的资金用于汽车的消费.一般认为,公共交通工具是私家车的替代品.所以当公路营运汽车拥有量增加时,居民的汽车购买量也会相应降低.然而,燃料类商品零售价格指数的增加意味着居民的燃油费用将会增多,人们将会减少对车辆的购买,或倾向于选择其他交通工具出行.4.2.3 回归方程的总体显著性检验(F检验)F==1 316.640.得出的F值1 316.640大于在5%的显著水平上,自由度为3和16的F临界值是3.24,因此F=1 316.640是显著的,拒绝H0,即可认为,在95%的置信系数下,辽宁省的私家车保有量与居民消费水平、公路营运汽车拥有量、燃料类商品零售价格指数存在着显著的线性关系.4.2.4 拟合优度及模型估计效果检验从输出结果看,可绝系数R2=0.995 966,说明该模型的解释变量解释了1996~2015年间的辽宁省私家车保有量变化的99.60%,而R2最大值为1,因此样本回归方程对数据拟合效果较好.根据中国统计年鉴,得到辽宁省1996~2015年私家车保有量的数据见表5,其曲线图如图1所示.由1996~2015年辽宁省私家车保有量曲线图可知辽宁省私家车保有量指数增长趋势,因此利用Excel对曲线进行拟合[8-10],结果如图2所示,可以看到拟合效果是非常理想的,且可以得到预测模型为:Y=1E-169e0.196x.利用该模型对未来几年辽宁省私家车保有量进行预测就可以先实现.辽宁省的私家车保有量和辽宁省居民消费水平正相关.随着国民经济的快速发展,人们收入和消费水平不断提高直接地刺激和拉动私家车消费;辽宁省私家车保有量和公路营运汽车数量负相关,私家车和公交车之间存在着对道路、汽油等资源的争夺.此外,辽宁省私家车保有量和燃料类商品零售价格指数负相关,油价的上涨会抑制私家车的数量.相关部门在制定未来交通规划方案时,应该侧重考虑上述三个因素的作用.通过预测模型可以看出,未来辽宁省私家车会大幅度增长,一方面极大地满足人们的消费欲望,改善和提升人们的生活质量,另一方面也可以推动和促进我国汽车产业的快速发展,在一定程度上也加快了交通基础设施建设的步伐,提高了城市交通管理和综合管理的水平.但是需要理性看待社会现象,私家车增长引起的负面影响也应纳入省政建设的考虑范围.短期预测作为制定近期决策的依据,需要结合长裙预测运用于实际工作中.短期预测方法既要保障近期决策在短期战略与规划的指导下进行,也要为远期规划的实施赢得时间.【相关文献】[1] 中华人民共和国国家统计局.2016年中国统计年鉴[M].北京:中国统计出版社,2016.[2] 宗刚,张广利.基于计量经济学模型选取与汽车保有量相关的因素[J].汽车工业研究,2008(7):2-6.[3] 刘恺.北京市私家车保有量的计量经济学分析.山西财经大学学报,2012(S2):3-4.[4] 达摩达尔·N.古扎拉蒂.计量经济学[M].北京:中国人民大学出版社, 2004.[5] 李阳.影响我国私家车拥有量的因素分析[J].消费导刊, 2008(8):8-9.[6] 梁海澄.私家车发展的问题及对策[J].交通与运输, 2006,32(1):32-34.[7] 王建平,王建丽.私家车发展状况的国际比较与借鉴[J]. 山西财经大学学报, 2004,26(5):77-79.[8] 梁慧玲,林玉蕊.我国私家车保有量的模型分析.产业与科技论坛, 2014(22):78-79.[9] 罗中德,赖美艳.中国社会消费品零售总额的预测分析[J]. 统计与决策, 2013(2):143-145.[10] 杨德平,刘喜华,孙海涛.经济预测方法及MATLAB实现[M].北京:机械工业出版社, 2012.。


辽宁省教育厅关于成立2013―2015年辽宁省普通高等学校机械类等专业教学指导委员会的通知文章属性•【制定机关】辽宁省教育厅•【公布日期】2013.04.08•【字号】辽教发[2013]77号•【施行日期】2013.04.08•【效力等级】地方规范性文件•【时效性】现行有效•【主题分类】中等教育正文辽宁省教育厅关于成立2013-2015年辽宁省普通高等学校机械类等专业教学指导委员会的通知(辽教发[2013]77号)省内各普通本科高等学校:为贯彻落实国家和省中长期教育改革和发展规划纲要以及《教育部关于全面提高高等教育质量的若干意见》精神,强化专业内涵建设,进一步提高专业建设水平,提升人才培养质量,充分发挥专家学者对高等教育教学改革的研究、咨询、指导作用,结合我省经济社会发展需要,根据我省高校本科专业设置情况,经研究,决定成立辽宁省普通高等学校机械类、仪器类、材料类、电气类、电子信息类、自动化类、计算机类、土木类、化工与制药类、环境科学与工程类、食品科学与工程类、建筑学类、生物工程类、法学类等专业教学指导委员会(以下简称“教指委”)。
现就有关事项通知如下:一、教指委性质教指委是辽宁省教育厅聘请并领导的专家组织,具有非常设学术机构的性质,接受辽宁省教育厅的委托,开展普通高等学校本科教学的研究、咨询、指导、评估、服务等工作。
二、选聘原则教指委的选聘原则是思想政治素质过硬,熟悉本科教育教学规律,热心人才培养工作,具有丰富的教育教学或教学管理等相关工作经验,在相关专业领域有较高的学术造诣,学风端正,思想活跃,具有较强的工作能力和组织协调能力,作风正派。
各教指委在省内有关学校推荐并广泛征求意见的基础上,考虑老中青相结合等原则进行选聘。
委员包括辽宁省普通高等学校从事本科教学工作和教学管理工作、企事业单位热心人才培养工作、行业主管部门关心人才培养工作等三方面专家。
三、组建形式及委员任期各教指委设主任委员1人,副主任委员若干人,设秘书长1人,教指委的工作由主任委员主持、副主任委员协助,秘书长协助主任和副主任委员处理日常工作。
2015年辽宁普通高考网上报名系统操作手册(考生版)目录辽宁省2015年普通高校招生考试网上报名考生须知 (4)需要做什么? (7)登录系统前 (7)具体报名流程 (7)具体怎么做? (9)1.选择报名类型 (9)1.1 怎么操作 (9)1.2 要注意什么 (10)2.注册系统 (10)2.1怎么操作 (10)2.2要注意什么 (10)3.登录系统 (10)3.1 怎么操作 (10)3.2 遇到问题怎么办 (11)4.阅读考生须知 (11)4.1 怎么操作 (11)4.2 要注意什么 (11)5.修改密码 (12)5.1 怎么操作 (12)5.2 要注意什么 (12)5.3 遇到问题怎么办 (12)6.进入主界面 (13)6.1 要注意什么 (13)7.填报修改报名信息 (14)7.1 怎么操作 (14)7.2 要注意什么 (14)7.3 遇到问题怎么办 (15)8.查看或再次修改报名信息 (16)8.1 怎么操作 (16)8.2 要注意什么 (16)9.下载当前报名信息 (16)9.1 怎么操作 (16)9.2 要注意什么 (17)9.3 遇到问题怎么办 (18)10.报名费用支付 (18)10.1 怎么操作 (18)10.2 要注意什么 (21)10.3 遇到问题怎么办 (22)辽宁省2015年普通高校招生考试网上报名考生须知辽宁省2015年普通高等学校招生考试(以下简称普通高考)采用网上报名方式,包括考生网上填报基本信息、现场资格审查和身份验证信息采集、网上缴费等环节,为顺利完成报名信息网上填报,考生须认真阅读相关报名文件、了解相关政策,并按照有关要求和规定程序完成高考网上报名。
一、填报时间艺术类考生网上填报基本信息的时间为2014年11月18日至20日,现场资格审查和身份验证信息采集、网上缴费的时间为2014年11月21日至24日。
各市须于2014年11月28日16:00前完成艺术类考生的报名最终确认工作。
人口重心和经济重心时空演变研究——以辽宁省为例刘桂春;张昊;刘志晨【摘要】运用重心分析模型计算得到辽宁省2000—2015年人口重心与经济重心的地理坐标,并分析其动态演变轨迹,在此基础上计算两者的空间重叠性与变动一致性,分析其耦合态势.结果表明:辽宁省人口重心主要位于鞍山市的海城,经济重心主要介于海城和营口的大石桥之间;人口重心位于几何中心的西南部,经济重心则位于其东南部,两者的分离意味着辽宁省产出较高GDP的地区未能吸引较多的人口流入;人口重心与经济重心的移动轨迹都为东北-西南走向,且人口重心移动速度慢于经济重心,原因在于人口移动是一个长期且缓慢的过程,滞后性特征显著;人口重心与经济重心整体上耦合协调程度不高,呈现出减弱—增强—减弱的明显波动态势.【期刊名称】《哈尔滨商业大学学报(社会科学版)》【年(卷),期】2017(000)005【总页数】10页(P58-67)【关键词】人口重心;经济重心;时空演变;辽宁省【作者】刘桂春;张昊;刘志晨【作者单位】辽宁师范大学海洋经济与可持续发展研究中心,辽宁大连116029;辽宁师范大学海洋经济与可持续发展研究中心,辽宁大连116029;辽宁师范大学城市与环境学院,辽宁大连116029【正文语种】中文【中图分类】C91人口流动会对区域经济均衡发展产生重要影响,而地区间的经济发展不平衡会促进人口流动[1]。
人口集聚可以促进区域经济的发展,区域经济的发展反过来又可以影响人口的集聚。
人口与经济活动分布的空间变化能够反映发展的区域差异,是区域差异研究的重要组成部分。
人口重心、经济重心的动态演变轨迹能清楚地反映出区域的经济发展及其均衡程度,揭示区域发展差异的变化。
国外学者最先在经济学中运用了重心方法,美国学者F.Walker在1874年对美国西部大开发和南部阳光地带的快速发展所导致的美国人口重心变化进行了研究,但当时重心的计算方法并不完善。
后来Bellone F和Cunningham R[2]两位学者改进了重心计算方法,即以人们方便到达各地的中心位置距离作为标准来计算。
中国人口数量2015全国总人口13亿6千万(中国人口最多的省份排名) 2015年中国人口数量及各省人口排名省区市 人口数量 人口排名GDP GDP( 亿元) 人均G(元)人均排名排名1 河南省9613万人 5 14234 15056 162 山东省9082万人 2 25326 27148 73 四川省8673万人 9 9657 11708 254 广东省7859万人 1 29863 32142 65 江苏省7381万人 3 24738 32985 56 河北省6735万人 6 13387 19363 117 湖南省6629万人 13 8366 13123 208 安徽省6338万人 15 6906 11180 289 湖北省5988万人 11 8451 14733 1710 广西省4822万人 18 5386 11417 2711 浙江省4647万人 4 17633 35730 412 云南省4333万人 23 4260 9459 3013 江西省4222万人 19 5323 12204 2414 辽宁省4203万人 8 10418 24645 915 贵州省3837万人 26 2543 6742 3116 黑龙江省3813万人 14 7081 18463 1217 陕西省3674万人 21 4806 12843 2118 福建省3466万人 12 8440 23663 1019 山西省3294万人 17 5465 16143 1520 重庆市3107万人 24 3938 14011 1821 吉林省2699万人 22 4693 17211 1322 甘肃省2593万人 27 2494 9527 2923 内蒙古2379万人 16 6140 25558 824 新疆区1905万人 25 3305 16164 1425 上海市1625万人 7 11658 65473 126 北京市1423万人 10 8879 57431 227 天津市1007万人 20 5014 7972 328 海南省803万人 28 1121 13361 1929 宁夏区572万人 29 769 12695 2330 青海省529万人 30 706 12809 2231 西藏区267万人 31 326 11567 26原文标题:中国人口数量2015 全国总人口136072万人(各省人口排名)。
1、因为后序遍历栈中保留当前结点的祖先的信息,用一变量保存栈的最高栈顶指针,每当退栈时,栈顶指针高于保存最高栈顶指针的值时,则将该栈倒入辅助栈中,辅助栈始终保存最长路径长度上的结点,直至后序遍历完毕,则辅助栈中内容即为所求。
void LongestPath(BiTree bt)//求二叉树中的第一条最长路径长度{BiTree p=bt,l[],s[]; //l, s是栈,元素是二叉树结点指针,l中保留当前最长路径中的结点int i,top=0,tag[],longest=0;while(p || top>0){ while(p) {s[++top]=p;tag[top]=0; p=p->Lc;} //沿左分枝向下if(tag[top]==1) //当前结点的右分枝已遍历{if(!s[top]->Lc && !s[top]->Rc) //只有到叶子结点时,才查看路径长度if(top>longest) {for(i=1;i<=top;i++) l[i]=s[i]; longest=top; top--;}//保留当前最长路径到l栈,记住最高栈顶指针,退栈}else if(top>0) {tag[top]=1; p=s[top].Rc;} //沿右子分枝向下}//while(p!=null||top>0)}//结束LongestPath2、给定n个村庄之间的交通图,若村庄i和j之间有道路,则将顶点i和j用边连接,边上的Wij表示这条道路的长度,现在要从这n个村庄中选择一个村庄建一所医院,问这所医院应建在哪个村庄,才能使离医院最远的村庄到医院的路程最短?试设计一个解答上述问题的算法,并应用该算法解答如图所示的实例。
(20分)3、二叉树的层次遍历序列的第一个结点是二叉树的根。
实际上,层次遍历序列中的每个结点都是“局部根”。
确定根后,到二叉树的中序序列中,查到该结点,该结点将二叉树分为“左根右”三部分。
若左、右子树均有,则层次序列根结点的后面应是左右子树的根;若中序序列中只有左子树或只有右子树,则在层次序列的根结点后也只有左子树的根或右子树的根。
这样,定义一个全局变量指针R,指向层次序列待处理元素。
算法中先处理根结点,将根结点和左右子女的信息入队列。
然后,在队列不空的条件下,循环处理二叉树的结点。
队列中元素的数据结构定义如下:typedef struct{ int lvl; //层次序列指针,总是指向当前“根结点”在层次序列中的位置int l,h; //中序序列的下上界int f; //层次序列中当前“根结点”的双亲结点的指针int lr; // 1—双亲的左子树 2—双亲的右子树}qnode;BiTree Creat(datatype in[],level[],int n)//由二叉树的层次序列level[n]和中序序列in[n]生成二叉树。
n是二叉树的结点数{if (n<1) {printf(“参数错误\n”); exit(0);}qnode s,Q[]; //Q是元素为qnode类型的队列,容量足够大init(Q); int R=0; //R是层次序列指针,指向当前待处理的结点BiTree p=(BiTree)malloc(sizeof(BiNode)); //生成根结点p->data=level[0]; p->lchild=null; p->rchild=null; //填写该结点数据for (i=0; i<n; i++) //在中序序列中查找根结点,然后,左右子女信息入队列if (in[i]==level[0]) break;if (i==0) //根结点无左子树,遍历序列的1—n-1是右子树{p->lchild=null;s.lvl=++R; s.l=i+1; s.h=n-1; s.f=p; s.lr=2; enqueue(Q,s);}else if (i==n-1) //根结点无右子树,遍历序列的1—n-1是左子树{p->rchild=null;s.lvl=++R; s.l=1; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);}else //根结点有左子树和右子树{s.lvl=++R; s.l=0; s.h=i-1; s.f=p; s.lr=1;enqueue(Q,s);//左子树有关信息入队列s.lvl=++R; s.l=i+1;s.h=n-1;s.f=p; s.lr=2;enqueue(Q,s);//右子树有关信息入队列}while (!empty(Q)) //当队列不空,进行循环,构造二叉树的左右子树{ s=delqueue(Q); father=s.f;for (i=s.l; i<=s.h; i++)if (in[i]==level[s.lvl]) break;p=(bitreptr)malloc(sizeof(binode)); //申请结点空间p->data=level[s.lvl]; p->lchild=null; p->rchild=null; //填写该结点数据if (s.lr==1) father->lchild=p;else father->rchild=p; //让双亲的子女指针指向该结点if (i==s.l){p->lchild=null; //处理无左子女s.lvl=++R; s.l=i+1; s.f=p; s.lr=2; enqueue(Q,s);}else if (i==s.h){p->rchild=null; //处理无右子女s.lvl=++R; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);}else{s.lvl=++R; s.h=i-1; s.f=p; s.lr=1; enqueue(Q,s);//左子树有关信息入队列s.lvl=++R; s.l=i+1; s.f=p; s.lr=2; enqueue(Q,s); //右子树有关信息入队列}}//结束while (!empty(Q))return(p);}//算法结束4、已知有向图G=(V,E),其中V={V1,V2,V3,V4,V5,V6,V7},E={<V1,V2>,<V1,V3>,<V1,V4>,<V2,V5>,<V3,V5>,<V3,V6>,<V4,V6>,<V5,V7>,<V6,V7>}写出G的拓扑排序的结果。
G拓扑排序的结果是:V1、V2、V4、V3、V5、V6、V75、#define maxsize 栈空间容量void InOutS(int s[maxsize])//s是元素为整数的栈,本算法进行入栈和退栈操作。
{int top=0; //top为栈顶指针,定义top=0时为栈空。
for(i=1; i<=n; i++) //n个整数序列作处理。
{scanf(“%d”,&x); //从键盘读入整数序列。
if(x!=-1) //读入的整数不等于-1时入栈。
if(top==maxsize-1){printf(“栈满\n”);exit(0);}else s[++top]=x; //x入栈。
else //读入的整数等于-1时退栈。
{if(top==0){printf(“栈空\n”);exit(0);}else printf(“出栈元素是%d\n”,s[top--]);}}}//算法结6、给定n个村庄之间的交通图,若村庄i和j之间有道路,则将顶点i和j用边连接,边上的Wij表示这条道路的长度,现在要从这n个村庄中选择一个村庄建一所医院,问这所医院应建在哪个村庄,才能使离医院最远的村庄到医院的路程最短?试设计一个解答上述问题的算法,并应用该算法解答如图所示的实例。
(20分)7、对二叉树的某层上的结点进行运算,采用队列结构按层次遍历最适宜。
int LeafKlevel(BiTree bt, int k) //求二叉树bt 的第k(k>1) 层上叶子结点个数{if(bt==null || k<1) return(0);BiTree p=bt,Q[]; //Q是队列,元素是二叉树结点指针,容量足够大int front=0,rear=1,leaf=0; //front 和rear是队头和队尾指针, leaf是叶子结点数int last=1,level=1; Q[1]=p; //last是二叉树同层最右结点的指针,level 是二叉树的层数while(front<=rear){p=Q[++front];if(level==k && !p->lchild && !p->rchild) leaf++; //叶子结点if(p->lchild) Q[++rear]=p->lchild; //左子女入队if(p->rchild) Q[++rear]=p->rchild; //右子女入队if(front==last) {level++; //二叉树同层最右结点已处理,层数增1last=rear; } //last移到指向下层最右一元素if(level>k) return (leaf); //层数大于k 后退出运行}//while }//结束LeafKLevel。