安徽省合肥市2020届高三高考数学(文科)三模试卷及答案解析

第 1 页 共 18 页 2021年高考数学模拟试卷汇编：三角函数及解三角形 1．（2020届安徽省“江南十校”高三综合素质检测）已知2π()12cos ()(0)3f x x ωω=-+>.给出下列判断：
①若12()1,()1f x f x ==-，且12min πx x -=，则2ω=；
②存在(0,2)ω∈使得()f x 的图象向右平移
6π个单位长度后得到的图象关于y 轴对称； ③若()f x 在[]0,2π上恰有7个零点，则ω的取值范围为4147,2424⎡⎫⎪⎢⎭⎣
； ④若()f x 在ππ,64⎡⎤-⎢⎥⎣⎦
上单调递增，则ω的取值范围为20,3⎛⎤ ⎥⎝⎦. 其中，判断正确的个数为（ ）
A ．1
B ．2
C ．3
D ．4 2．（2020届百校联考高考考前冲刺）已知O 为坐标原点，角α的终边经过点(3,)(0)P m m <且10sin m α=
，则sin 2α=( ) A ．45 B ．35 C ．35- D ．45- 3．（2020届百校联考高考考前冲刺）已知函数()2tan()(0)f x x ωω=>的图象与直线2y =的相邻交点间的距离为π，若定义{},max ,,a a b a b b a b
⎧=⎨<⎩…，则函数()max{()h x f x =，()cos }f x x 在区间3,22ππ⎛⎫ ⎪⎝⎭
内的图象是( ) A ． B ．。

专题03 命题形式变化及真假判定【热点聚焦与扩展】（一）命题结构变换1、四类命题间的互化：设原命题为“若，则”的形式，则 （1）否命题：“若，则” （2）逆命题：“若，则” （3）逆否命题：“若，则”2、，（1）用“或”字连接的两个命题（或条件），表示两个命题（或条件）中至少有一个成立即可，记为 （2）用“且”字连接的两个命题（或条件），表示两个命题（或条件）要同时成立，记为3、命题的否定：命题的否定并不是简单地在某个地方加一个“不”字，对于不同形式的命题也有不同的方法（1）一些常用词的“否定”：是→不是 全是→不全是 至少一个→都没有 至多个→至少个 小于→大于等于 （2）含有逻辑联结词的否定：逻辑联接词对应改变，同时均变为：或→且 且→或（3）全称命题与存在性命题的否定全称命题： 存在性命题： 规律为：两变一不变① 两变：量词对应发生变化（），条件要进行否定 ② 一不变：所属的原集合的不变化（二）命题真假的判断：判断命题真假需要借助所学过的数学知识，但在一组有关系的命题中，真假性也存在一定的关联.1、四类命题：原命题与逆否命题真假性相同，同理，逆命题与否命题互为逆否命题，所以真假性也相同.而原命题与逆命题，原命题与否命题真假没有关联p q p ⌝q ⌝q p q ⌝p ⌝p q ∨p q ∧p q ∨p q ∧p ⌝n 1n +,p q ,p q ⌝⌝p q p ⌝q ⌝p q p ⌝q ⌝():,:,()p x M p x p x M p x ∀∈→⌝∃∈⌝():,:,()p x M p x p x M p x ∃∈→⌝∀∈⌝∀⇔∃()p x ()p x ⇒⌝x M2、，，如下列真值表所示：简而言之“一真则真” 简而言之“一假则假” 3、：与命题真假相反. 4、全称命题：真：要证明每一个中的元素均可使命题成立 假：只需举出一个反例即可 5、存在性命题：真：只需在举出一个使命题成立的元素即可 假：要证明中所有的元素均不能使命题成立【经典例题】例1、【2020年高考全国Ⅱ卷文理16】设有下列四个命题： 1p ：两两相交且不过同一点的三条直线必在同一平面内．2p ：过空间中任意三点有且仅有一个平面． 3p ：若空间两条直线不相交，则这两条直线平行． 4p ：若直线⊂l 平面α，直线⊥m 平面α，则l m ⊥．则下述命题中所有真命题的序号是 ． ①41p p ∧②21p p ∧③32p p ∨⌝④ 43p p ⌝∨⌝ 【答案】①③④【思路导引】利用两交线直线确定一个平面可判断命题1p 的真假；利用三点共线可判断命题2p 的真假；利用异面直线可判断命题3p 的真假，利用线面垂直的定义可判断命题4p 的真假．再利用复合命题的真假可得出结论． 【解析】对于命题1p ，可设1l 与2l 相交，这两条直线确定的平面为α；若3l 与1l 相交，则交点A 在平面α内，p q ∨p q ∧p ⌝p M M M同理3l 与2l 的交点B 也在平面α内，∴AB α⊂，即3l α⊂，命题1p 为真命题；对于命题2p ，若三点共线，则过这三个点的平面有无数个，命题2p 为假命题；对于命题3p ，空间中两条直线相交、平行或异面，命题3p 为假命题；对于命题4p ，若直线m ⊥平面α，则m 垂直于平面α内所有直线，直线l ⊂平面α，∴直线m ⊥直线l ，命题4p 为真命题．综上可知，14p p ∧为真命题，12p p ∧为假命题，23p p ⌝∨为真命题，34p p ⌝∨⌝为真命题．故答案为：①③④．【专家解读】本题的特点是注重知识的灵活应用，本题考查了空间点、线、面位置关系的判断，考查复合命题真假的判断，考查数学运算、直观想象、逻辑推理等学科素养．解题关键是正确理解空间点线面的位置关系，理解或命题、且命题、非命题的含义及其真值表．例2．【四川省宜宾市2020届高三三模】下列命题是假命题的是（ ）A ．000sin cos x R x x ∃∈-，B ．00cos 1x R x ∃∈≥，C ．()01ln x x x ∀∈+∞-≥，，D ．(0)tan 2x x x π∀∈>，，【答案】A【解析】因为sin cos )4x x x π-=-，其值域为[，所以A 项错误；因为cos [1,1]x ∈-，所以B 项正确；令()1ln =--f x x x ，11'()1x f x x x-=-=， 当01x <<时，'()0f x <，当1x >时，'()0f x >，所以函数()1ln =--f x x x 在(0,1)上单调减，在(1,)+∞上单调增， 所以()1ln =--f x x x 在1x =处取得最小值，且(1)0f =， 所以()0f x ≥在(0,)+∞上恒成立，所以C 项正确；借助于三角函数线，可知(0)tan 2x x x π∀∈>，，，所以D 项正确；故选：A.【专家解读】该题考查的是有关命题真假的判断，涉及到的知识点有三角函数的值域，导数的应用，属于简单题目.例3．【2020届陕西省西安中学高三四模】已知命题p ：x R ∃∈，20x ->；命题q ：0x ∀≥x <，则下列说法中正确的是 A ．p q ∨是假命题 B ．p q ∧是真命题 C ．()p q ∧⌝是真命题 D ．()p q ∨⌝是假命题【答案】C【解析】命题p ，003,20x x ∃=->，即命题p 为真，对命题q ，去111424x x ==>= ，所以命题q 为假，p ⌝为真 所以()p q ∧⌝是真命题，故选：C.【专家解读】(1)对于一些简单命题，判断为真，许推理证明，若判断为假，只需找出一个反例即可； (2)对于复合命题的真假判断应利用真值表；(3)也可以利用“互为逆否命题”的等价性，通过判断其逆否命题的真假来判断原命题的真假.例4．【湖南省长沙市长郡中学2020届高三三模】已知命题:p x R ∃∈，2230x x ++<，则命题p 的否定是（ ）A ．x R ∃∈，2230x x ++>B ．x R ∀∈，2230x x ++≤C ．x R ∀∈，2230x x ++≥D ．x R ∀∈，2230x x ++>【答案】C【解析】命题p 为特称命题，其否定为:p x R ⌝∀∈，2230x x ++≥. 故选：C.【专家解读】本题考查特称命题的否定的改写，要注意量词和结论的变化，属于基础题. 例5．【河北省鸡泽县第一中学2020年高三三模】下列命题是真命题的为( ) A ．若＝，则x ＝y B ．若x 2＝1，则x ＝1 C ．若x ＝y ，则＝D ．若x <y ，则x 2<y 2【答案】A 【解析】由得x=y ，而由x 2=1得x=±1，由x=y ，不一定有意义，而x ＜y 得不到x 2＜y 2，故选A ．例6．【河南省名校联盟2020年高三三模】下列命题为真命题的个数是（ ） ①{x x x ∀∈是无理数}，2x 是无理数； ②若0a b ⋅=，则0a =或0b =；③命题“若220x y +=，x ∈R ，y ∈R ，则0x y ==”的逆否命题为真命题；④函数()x xe ef x x--=是偶函数.A ．1B ．2C ．3D ．4【答案】B【解析】对于①中，当x =22x =为有理数，故①错误；对于②中，若0a b ⋅=，可以有a b ⊥，不一定要0a =或0b =，故②错误；对于③中，命题“若220x y +=，x ∈R ，y ∈R ，则0x y ==”为真命题，其逆否命题为真命题，故③正确；对于④中，()()x x x xe e e ef x f x x x-----===-，且函数的定义域是(,0)(0,)-∞+∞，定义域关于原点对称，所以函数()x xe ef x x--=是偶函数，故④正确.综上，真命题的个数是2.故选：B.【专家解读】本题考查命题真假的判断，涉及全称命题的真假的判断、逆否命题真假的判断、向量垂直等价条件的应用以及函数奇偶性的判断，考查推理能力.例7．【安徽省六安市第一中学2020届高三三模】下列命题错误的是( )A ．命题“若0xy =，则x ，y 中至少有一个为零”的否定是：“若0xy ≠，则x ，y 都不为零”B ．对于命题0:p x R ∃∈，使得20010x x ++<，则:p x R ⌝∀∈，均有210x x ++≥C ．命题“若0m >，则方程20x x m +-=有实根”的逆否命题为“若方程20x x m +-=无实根，则0m ≤”D ．“1x =”是“2320x x -+=”的充分不必要条件 【答案】A【解析】A 选项中命题的否定是：若0xy =，则x ，y 都不为零，故A 不正确；B 选项是一个特称命题的否定，变化正确；C 选项是写一个命题的逆否命题，需要原来的命题条件和结论都否定再交换位置，C 正确；D 选项由前者可以推出后者，而反过来不是只推出1x =，故D 正确， 故选：A.【专家解读】本题考查了命题的否定，逆否命题，充分不必要条件，意在考查学生的推断能力.【精选精练】1．【2020届湖南长沙市第一中学高三三模】已知命题p ：x R ∀∈，23x x <；命题q ：x R ∃∈，321x x =-，则下列命题中为真命题的是：（ ） A ．p q ∧ B ．p q ⌝∧ C ．p q ∧⌝ D ．p q ⌝∧⌝【答案】B【解析】0x =可知: 命题p ：x R ∀∈，23x x <为假命题，由函数图象可知命题32:,1q x R x x ∃∈=-为真命题，所以p q ⌝∧为真命题．2．【河南省开封市2020届高三二模】已知:0p x ∀>，10x x-≥，则p ⌝为（ ） A ．00x ∃>，0010x x -< B ．00x ∃≤，0010x x -< C ．0x ∀>，10x x -< D ．00x ∀≤，10x x-≥ 【答案】A【解析】因为1:0,0p x x x∀>-，是全称命题， 故p ⌝为：00x ∃>，0010x x -<；故选：A ． 【专家解读】本题考查含量词命题的否定，属于基础题．3．【黑龙江省大庆实验中学2020届高三三模】下列说法错误的是（ ）A ．命题“若2320x x -+=，则1x =”的逆否命题为：“若1x ≠，则2320x x -+≠”B ．“1x >”是“||1x >”的充分而不必要条件C ．若p 且q 为假命题，则p 、q 均为假命题D ．命题:p “存在x ∈R ，使得210x x ++<”，则非:p “任意x ∈R ，均有210x x ++≥”【答案】C【解析】对于选项A ，命题“若2320x x -+=，则1x =”的逆否命题为：“若1x ≠，则2320x x -+≠”，即原命题为真命题；对于选项B ，当1x >时，||1x >，当||1x >，1x >或1x <，即原命题为真命题； 对于选项C ，若p 且q 为假命题，则p 、q 中至少有一个为假命题，即原命题为假命题；对于选项D ，命题:p “存在x ∈R ，使得210x x ++<”，则非:p “任意x ∈R ，均有210x x ++≥”， 即原命题为真命题；故选C.【专家解读】本题考查了命题的逆否命题的真假、充分必要条件、复合命题的真假及特称命题的否定，重点考查了逻辑推理能力，属中档题.4．【吉林省长春市2020届高考数学二模】命题p ：存在实数0x ，对任意实数x ，使得()0sin sin x x x +=-恒成立；q ：0a ∀>，()ln a xf x a x+=-为奇函数，则下列命题是真命题的是（ ） A ．p q ∧ B ．()()p q ⌝∨⌝ C ．()p q ∧⌝ D ．()p q ⌝∧【答案】A【解析】对于命题p ，由于()sin sin x x π+=-，所以命题p 为真命题.对于命题q ，由于0a >，由0a xa x+>-解得a x a -<<，且()()1ln ln ln a x a x a x f x f x a x a x a x --++⎛⎫-===-=- ⎪+--⎝⎭，所以()f x 是奇函数，故q 为真命题.所以p q ∧为真命题. ()()p q ⌝∨⌝、()p q ∧⌝、()p q ⌝∧都是假命题.故选：A【专家解读】本小题主要考查诱导公式，考查函数的奇偶性，考查含有逻辑联结词命题真假性的判断，属于基础题.5．【四川省绵阳南山中学2020届高三高考仿真模拟】已知α、β是两个不同的平面，m 、n 是两条不重合的直线，命题p ：“若m α⊥，m n ⊥，则//n α”；命题q ：“若αβ⊥，n αβ=，m n ⊥，则m β⊥”，则下列命题为真命题的是（ ） A ．p q ∧ B ．p q ∨C ．()p q ∨⌝D ．()p q ⌝∧【答案】C【解析】命题p 中，若m α⊥，m n ⊥，则n 与α可能平行，也可能n ⊂α，故命题p 为假命题； 命题q 中，若αβ⊥，n αβ=，m n ⊥，m 与β的位置关系可能是m β⊂，//m β，也可能m 与β相交，故命题q 为假命题.因此p q ∧，p q ∨，()p q ⌝∧都是假命题，()p q ∨⌝为真命题.故选：C.【专家解读】本题主要考查判断复合命题的真假，涉及线面位置关系，属于基础题型. 6．【辽宁省沈阳二中2020届高三五模试题】已知命题“x R ∃∈，使212(1)02x a x +-+≤”是假命题，则实数a 的取值范围是( ) A ．(,1)-∞- B ．(1,3)- C ．(3,)-+∞ D ．(3,1)-【答案】B【解析】因为命题“x R ∃∈，使212(1)02x a x +-+≤”是假命题，所以212(1)02x a x +-+>恒成立，所以2()114202a ∆=--⨯⨯<，解得13a -<<，故实数a 的取值范围是(1,3)-．故选B ． 【专家解读】对于函数恒成立或者有解求参的问题，常用方法有：变量分离，参变分离，转化为函数最值问题；或者直接求函数最值，使得函数最值大于或者小于0；或者分离成两个函数，使得一个函数恒大于或小于另一个函数．而二次函数的恒成立问题，也可以采取以上方法，当二次不等式在R 上大于或者小于0恒成立时，可以直接采用判别式法.7．【2020届重庆市南开中学高三三模】已知,x y R ∈，命题“若220x y +=，则0x =或0y =”的原命题，逆命题，否命题和逆否命题这四个命题中，真命题个数为（ ） A ．0B ．2C ．3D ．4【答案】B【解析】由于220x y +=，则0x y ==，所以原命题为真命题，其逆否命题也是真命题.否命题为“若220x y +≠，则0x ≠且0y ≠”，如220,1,0x y x y ==+≠，所以否命题为假命题，故逆命题也是假命题.所以真命题的个数为2.故选：B【专家解读】本小题主要考查四种命题的真假性的判断，属于基础题. 8．【黑龙江省哈尔滨三中2020届四模试题】下列命题错误的是（ ） A ．若“p q ∧”为真命题，则p 与q 均为真命题 B ．命题“p q ∧为真”是“p q ∨为真”的必要不充分条件C ．若0:p x R ∃∈，2210x x +->，则:p x R ⌝∀∈，2210x x +-≤D ．“1x =”是“1x ≥”的充分不必要条件 【答案】B【解析】若“p q ∧”为真命题，则p 与q 均为真命题，故A 正确；若“p q ∧为真，则p 真，q 真，此时“p q ∨为真成立，若“p q ∨为真，则有可能,p q 一真一假，此时“p q ∧为假，所以命题“p q ∧为真”是“p q ∨为真”的充分不必要条件，故B 错误；由特称命题的否定为全称命题可得若0:p x R ∃∈，2210x x +->，则:p x R ⌝∀∈，2210x x +-≤，故C 正确；若“1x =”，则“1x ≥”成立，反之不成立，所以“1x =”是“1x ≥”的充分不必要条件，故D 正确； 故选：B.【专家解读】本小题主要考查复合命题的真假、全称命题与特称命题的相互转化以及充分条件，必要条件等基础知识，属于基础题.9．【黑龙江省哈尔滨市第一中学2020届高三三模】下列关于命题的说法错误的是（ ） A ．命题“若2320x x -+=，则2x =”的逆否命题为“若2x ≠，则2320x x -+≠” B ．“2a =”是“函数()log a f x x =在区间()0,∞+上为增函数”的充分不必要条件 C ．“若0x 为()y f x =的极值点，则()00f x '=”的逆命题为真 D ．命题p ：2x ∀>，230x ->的否定是02x ∃>，0230x -≤ 【答案】C【解析】对于A ，由逆否命题的概念可得命题“若2320x x -+=，则2x =”的逆否命题为“若2x ≠，则2320x x -+≠”，故A 正确；对于B ，若2a =，则函数()log a f x x =在区间()0,∞+上为增函数；若函数()log a f x x =在区间()0,∞+上为增函数，则只需满足1a >；所以“2a =”是“函数()log a f x x =在区间()0,∞+上为增函数”的充分不必要条件，故B 正确；对于C ，“若0x 为()y f x =的极值点，则()00f x '=” 的逆命题为“若()00f x '=，则0x 为()y f x =的极值点”，对函数()3f x x =，()00f '=，但0x =不是函数()f x 的极值点，所以原命题的逆命题为假命题，故C 错误；对于D ，由全称命题的否定可知命题p ：2x ∀>，230x ->的否定是02x ∃>，0230x -≤，故D 正确. 故选：C.【专家解读】本题考查了逆否命题、逆命题的改写、全称命题的否定，考查了充分条件、必要条件的判断及对数函数性质、极值点的概念，属于基础题.10．【黑龙江省哈尔滨市第一中学2020届高三6月模拟】已知命题p ：棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥；命题q ：棱柱的所有的侧面都是长方形或正方形，下列命题为真命题的是（ ） A ．p q ∧ B ．p q ⌝∧C ．p q ∧⌝D ．p q ⌝∧⌝【答案】D【解析】对于命题p ，因为棱锥的侧棱长与底面多边形的边长相等，故棱锥的侧面为等边三角形， 如果该棱锥是六棱锥，则六个侧面顶角的和为360︒，但六棱锥的侧面的顶角和小于360︒，矛盾，故p 为假命题.对于命题q ，斜棱柱有侧面不是长方形，故命题q 为假命题. 故p q ⌝∧⌝为真命题.故选：D.【专家解读】复合命题p q ∨的真假判断为“一真必真，全假才假”，p q ∧的真假判断为“全真才真，一假必假”，p ⌝的真假判断是“真假相反”．11．【广东省肇庆市2020届高中毕业班第三次统一检测】如图，正方体1111ABCD A B C D -的棱长为1，P 为1AA 的中点，M 在侧面11AA B B 上，有下列四个命题：①若1D M CP ⊥，则BCM ∆ ②平面1A BD 内存在与11D C 平行的直线；③过A 作平面α，使得棱AD ，1AA ，11D C 在平面α的正投影的长度相等，则这样的平面α有4个；④过A 作面β与面1A BD 平行，则正方体1111ABCD A B C D -在面β． 则上述四个命题中，真命题的个数为（ ）A ．1B ．2C ．3D ．4【答案】C 【解析】对于①，以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，建立空间直角坐标系，如图1所示；过M 作MG ⊥平面ABCD ，G 是垂足，过G 作GH BC ⊥，交BC 于H ，连结MH ，则(0,0,0)D ，(0,1,0)C ，(1,0,0)A ，1(1,0,)2P ，(0,1,0)C ，1(0,0,1)D ，(1,1,0)B ，设(1,,)M a b ，则1(1,,1)D M a b =-，1(1,1,)2CP =-，∵1D M CP ⊥， ∴1111022D M CP a b ⋅=-+-=，解得21a b -=， ∴1CH a =-，21MG b a ==-，MH ==，∴11122BCM S BC MH ∆=⨯⨯=⋅112210=≥=，当35a =时，min ()BCM S ∆=，①正确； 对于11//D C DC ，DC平面1A BD D =，所以11D C 也与平面1A BD 相交．故②错； ③过A 作平面α，使得棱AD ，1AA ，11D C 在平面α的正投影的长度相等，因为11//D C AB ，且11D C AB =，故11D C 在平面α的正投影的长度等于AB 在平面α的正投影的长度，使得棱AD ，1AA ，11D C 在平面α的正投影的长度相等，即使得使得棱AD ，1AA ，AB 面α的正投影的长度相等，若棱AD ，1AA ，AB 面α的同侧，则α为过A 且与平面1A BD 平行的平面，若棱AD ，1AA ，AB 中有一条棱和另外两条棱分别在平面α的异侧，则这样的平面α有3个，故满足使得棱AD ，1AA ，11D C 在平面α的正投影的长度相等的平面α有4个；③正确．④过A 作面β与面1A BD 平行，则正方体1111ABCD A B C D -在面β的正投影为一个正六边形，其中1AC ⊥平面β，而1AC 分别垂直于正三角形1A BD 和11CB D ，所以根据对称性，正方体的8个顶点中，1AC 在平面β内的投影点重合与正六边形的中心，其它六个顶点投影恰是正六边形的六个顶点，且正六边形的边长等于正三角形1A BD 的外接圆半径（投影线与正三角形1A BD 、11CB D 垂直），所以正六边形的边长为sin 6023a =÷︒=，所以投影的面积为2266a ==⎝⎭．④对．故选C ． 【专家解读】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查空间想象能力与思维能力，考查运算求解能力．12．【黑龙江省哈尔滨市第三中学校2020届高三三模】已知a R ∈，命题“存在x ∈R ，使230x ax a --≤”为假命题，则a 的取值范围为______.【答案】()12,0-【解析】命题：“存在x ∈R ，使230x ax a --≤”为假命题即230x ax a -->恒成立，则∆<0，即：2120a a ∆=+<，解得120a -<<，故实数a 的取值范围为()12,0-故答案为：()12,0-【专家解读】本题考查由命题的真假求参数的范围，考查一元二次不等式的应用，体现了等价转化的思想，属于中等题.13．【2020届湖南省永州市祁阳县高三二模】已知：()2:,21p x R x m x ∀∈>+，0:,q x R ∃∈200210x x m +--=， （1）若q 是真命题，求实数m 的取值范围；（2）若()p q ∧⌝为真命题，求实数m 的取值范围.【答案】（1）2m ≥-；（2）2m <-.【解析】（1）因为0:R,q x ∃∈200210x x m +--=为真命题，所以方程2210x x m +--=有实根，所以判别式()4410m ∆=++≥，所以实数m 的取值范围为2m ≥-.（2）()221x m x >+可化为220mx x m -+<，若:R,p x ∀∈()221x m x >+为真命题， 则220mx x m -+<对任意的x ∈R 恒成立，当0m =时，不等式可化为20x -<，显然不恒成立；当0m ≠时，有20440m m <⎧⎨-<⎩，1m ∴<-， 由（1）知，若q ⌝为真命题，则2m <-，又()p q ∧⌝为真，故p 、q ⌝均为真命题，所以实数m 需满足12m m <-⎧⎨<-⎩，解得2m <-， 所以实数m 的取值范围为2m <-.【专家解读】本题考查利用复合命题的真假求参数的取值范围；考查运算求解能力和逻辑思维能力；熟练掌握复合命题的真假判断是求解本题的关键；属于中档题.。

安徽省临泉第一中学2023届高三下学期模拟考试（三模）数学试题学校:___________姓名：___________班级：___________考号：___________二、多选题四、解答题(1)求A ∠的大小；(2)22AB =，点D 在BC(1)求证：平面PAE ⊥平面PBC (2)判断在线段AP 上是否存在点在，求出AQ 的长；若不存在，请说明理由21．已知双曲线C ：(22221y x a b -=参考答案：故选：C.6．A【分析】画出图分析，将可.取BC ，BD 中点E 取BE 的中点O ，则故AB AD +的最大值为故选：A.【详解】2与球O 的截面图如图所示，设球，则母线长为3r ，由已知得228πr =，22π4S r =+244则(1)(2)(3)f f f ++++ 20221()(1)(2)(3)i f i f f f ==++∑2022()(2)(3)g i f f =+++∑【详解】如图所示，设PQ 的中点为B ，过P 、Q 、B 分别作由题意可知，抛物线C ：24x y =的焦点为4PM PF PM PA +=+≥，即最小值为点共线时等号成立，故A 正确；11对于B ，四面体11ABB C 的外接球，即为正三棱台设外接球半径为r ， 由1263OO =2211113=+==OC OO O C OC ，可知球心即为故3r OC ==，所以外接球表面积对于C ，如图2，1OO ⊥平面ABCα截棱台所得截面为长方形1MNC B 对于D ，棱台111ABC A B C -体积V =1113262432AMN A B C V -=⨯=，AMN V -故选：ABC.12．ABD所以a 的取值范围是10,2e ⎛⎫⎪⎝⎭.故答案为：10,2e ⎛⎫⎪⎝⎭.16．332/332【分析】作圆M 关于y 轴对称的圆，根据对称性，把问题转化为转化为在半径为则NF OB ⊥，又NB NO =，所以由对称性可得OE OA =，1sin 2ABO S OA OB AOB =⨯⨯∠ 所以2ABO EBO EFO S S S == ，（2）选①：由上可知，在πsin sin 6AB BDADB =∠，所以sin（2）取BE的中点O，连接OP.由（1）知PE⊥平面PBC，故PE22．(1)答案见解析；(2)①()e 1,++∞；②证明见解析【分析】（1）先求()f x '，设()g x 数的单调性的关系求其单调区间；。

课时规范练A组基础对点练1．抛掷两枚质地均匀的骰子，向上的点数之差的绝对值为3的概率是()A.19 B.16C.118 D.112解析：抛掷两枚质地均匀的骰子，向上的点数之差的绝对值为3的情况有：1,4；4,1；2,5；5,2；3,6；6,3共6种，而抛掷两枚质地均匀的骰子的情况有36种，所以所求概率P＝636＝16，故选B.答案：B2．某同学先后投掷一枚质地均匀的骰子两次，第一次向上的点数记为x，第二次向上的点数记为y，在直角坐标系xOy中，以(x，y)为坐标的点落在直线2x －y＝1上的概率为()A.112 B.19C.536 D.16解析：先后投掷两次骰子的结果共有6×6＝36种，而以(x，y)为坐标的点落在直线2x－y＝1上的结果有(1,1)，(2,3)，(3,5)，共3种，故所求概率为336＝1 12.答案：A3．若某公司从五位大学毕业生甲、乙、丙、丁、戊中录用三人，这五人被录用的机会均等，则甲或乙被录用的概率为()A.23 B.25C.35 D.910解析：由题意知，从五位大学毕业生中录用三人，所有不同的可能结果有(甲，乙，丙)，(甲，乙，丁)，(甲，乙，戊)，(甲，丙，丁)，(甲，丙，戊)，(甲，丁，戊)，(乙，丙，丁)，(乙，丙，戊)，(乙，丁，戊)，(丙，丁，戊)，共10种，其中“甲与乙均未被录用”的所有不同的可能结果只有(丙，丁，戌)这1种，故其对立事件“甲或乙被录用”的可能结果有9种，所求概率P＝910.答案：D4．从1,2,3,4中任取2个不同的数，则取出的2个数之差的绝对值为2的概率是()A.12 B.13C.14 D.16解析：从1,2,3,4中任取2个不同的数有以下六种情况：(1,2)，(1,3)，(1,4)，(2,3)，(2,4)，(3,4)，满足取出的2个数之差的绝对值为2的有(1,3)，(2,4)，故所求概率是26＝1 3.答案：B5．从正方形四个顶点及其中心这5个点中，任取2个点，则这2个点的距离小于该正方形边长的概率为()A.15 B.25C.35 D.45解析：取两个点的所有情况有10种，两个点的距离小于正方形边长的情况有4种，所以所求概率为410＝25.答案：B6．从字母a，b，c，d，e中任取两个不同字母，则取到字母a的概率为________．解析：总的取法有：ab，ac，ad，ae，bc，bd，be，cd，ce，de共10种，其中含有a的有ab，ac，ad，ae共4种，故所求概率为410＝2 5.答案：2 57．如图的茎叶图是甲、乙两人在4次模拟测试中的成绩，其中一个数字被污损，则甲的平均成绩不超过乙的平均成绩的概率为________.解析：依题意，记题中的被污损数字为x，若甲的平均成绩不超过乙的平均成绩，则有(8＋9＋2＋1)－(5＋3＋x＋5)≤0，x≥7，即此时x的可能取值是7,8,9，因此甲的平均成绩不超过乙的平均成绩的概率P＝310＝0.3.答案：0.38．设连续掷两次骰子得到的点数分别为m，n，令平面向量a＝(m，n)，b＝(1，－3)．(1)求使得事件“a⊥b”发生的概率；(2)求使得事件“|a|≤|b|”发生的概率．解析：(1)由题意知，m∈{1,2,3,4,5,6}，n∈{1,2,3,4,5,6}，故(m，n)所有可能的取法共36种．a⊥b，即m－3n＝0，即m＝3n，共有2种：(3,1)、(6,2)，所以事件a⊥b的概率为236＝1 18.(2)|a|≤|b|，即m2＋n2≤10，共有(1,1)、(1,2)、(1,3)、(2,1)、(2,2)、(3,1)6种，其概率为636＝1 6.9．某校高三学生体检后，为了解高三学生的视力情况，该校从高三六个班的300名学生中以班为单位(每班学生50人)，每班按随机抽样方法抽取了8名学生的视力数据．其中高三(1)班抽取的8名学生的视力数据与人数见下表：视力数据4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.95.0 5.1 5.2 5.3人数2221 1(1)用上述样本数据估计高三(1)班学生视力的平均值；(2)已知其余五个班学生视力的平均值分别为4.3、4.4、4.5、4.6、4.8.若从这六个班中任意抽取两个班学生视力的平均值作比较，求抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率．解析：(1)高三(1)班学生视力的平均值为4.4×2＋4.6×2＋4.8×2＋4.9＋5.18＝4.7，故估计高三(1)班学生视力的平均值为4.7.(2)从这六个班中任意抽取两个班学生视力的平均值作比较，所有的取法共有15种，而满足抽取的两个班学生视力的平均值之差的绝对值不小于0.2的取法有：(4.3,4.5)，(4.3,4.6)，(4.3,4.7)，(4.3,4.8)，(4.4,4.6)，(4.4,4.7)，(4.4,4.8)，(4.5,4.7)，(4.5,4.8)，(4.6,4.8)，共有10种，故抽取的两个班学生视力的平均值之差的绝对值不小于0.2的概率为P＝1015＝2 3.B组能力提升练10．(2019·河北三市联考)袋子中装有大小相同的5个小球，分别有2个红球、3个白球．现从中随机抽取2个小球，则这2个小球中既有红球也有白球的概率为()A.34 B.710C.45 D.35解析：设2个红球分别为a、b,3个白球分别为A、B、C，从中随机抽取2个，则有(a，b)，(a，A)，(a，B)，(a，C)，(b，A)，(b，B)，(b，C)，(A，B)，(A，C)，(B，C)，共10个基本事件，其中既有红球也有白球的基本事件有6个，则所求概率为P＝610＝3 5.答案：D11．在2,0,1,5这组数据中，随机取出三个不同的数，则数字2是取出的三个不同数的中位数的概率为()A.34 B.58C.12 D.14解析：分析题意可知，共有(0,1,2)，(0,2,5)，(1,2,5)，(0,1,5)4种取法，符合题意的取法有2种，故所求概率P＝12.答案：C12．(2018·商丘模拟)已知函数f(x)＝13x3＋ax2＋b2x＋1，若a是从1,2,3三个数中任取的一个数，b是从0,1,2三个数中任取的一个数，则该函数有两个极值点的概率为()A.79 B.13C.59 D.23解析：f′(x)＝x2＋2ax＋b2，要使函数f(x)有两个极值点，则有Δ＝(2a)2－4b2>0，即a2>b2.由题意知所有的基本事件有9个，即(1,0)，(1,1)，(1,2)，(2,0)，(2,1)，(2,2)，(3,0)，(3,1)，(3,2)，其中第一个数表示a的取值，第二个数表示b的取值．满足a2>b2的共有6个，P＝69＝2 3.答案：D13．将一颗骰子投掷两次分别得到点数a，b，则直线ax－by＝0与圆(x－2)2＋y2＝2相交的概率为________．解析：圆心(2,0)到直线ax－by＝0的距离d＝|2a|a2＋b2，当d<2时，直线与圆相交，则有d＝|2a|a2＋b2<2，得b>a，满足b>a的共有15种情况，因此直线ax－by＝0与圆(x－2)2＋y2＝2相交的概率为1536＝5 12.答案：5 1214．(2019·长沙长郡中学检测)在所有的两位数10～99中，任取一个数，则这个数能被2或3整除的概率是________．解析：所有两位数共有90个，其中2的倍数有45个，3的倍数有30个，6的倍数有15个，所以能被2或3整除的共有45＋30－15＝60(个)，所以所求概率是6090＝2 3.答案：2 315．设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18.现采用分层抽样的方法从这三个协会中抽取6名运动员组队参加比赛．(1)求应从这三个协会中分别抽取的运动员的人数；(2)将抽取的6名运动员进行编号，编号分别为A1，A2，A3，A4，A5，A6，现从这6名运动员中随机抽取2人参加双打比赛．①用所给编号列出所有可能的结果；②设A为事件“编号为A5和A6的两名运动员中至少有1人被抽到”，求事件A发生的概率．解析：(1)应从甲、乙、丙三个协会中抽取的运动员人数分别为3,1,2.(2)①从6名运动员中随机抽取2人参加双打比赛的所有可能结果为{A1，A2}，{A1，A3}，{A1，A4}，{A1，A5}，{A1，A6}，{A2，A3}，{A2，A4}，{A2，A5}，{A2，A6}，{A3，A4}，{A3，A5}，{A3，A6}，{A4，A5}，{A4，A6}，{A5，A6}，共15种．②编号为A5和A6的两名运动员中至少有1人被抽到的所有可能结果为{A1，A5}，{A1，A6}，{A2，A5}，{A2，A6}，{A3，A5}，{A3，A6}，{A4，A5}，{A4，A6}，{A5，A6}，共9种．因此，事件A发生的概率P(A)＝915＝3 5.。

热点02 数学传统文化和实际民生为载体的创新题【命题形式】1、考查题型主要是选择题和填空题，计算题和证明题比较少，涉及到的知识点主要集中在函数、数列、立体几何证明与计算、复数、组合、三角函数、概率、推理、圆锥曲线。

2、数学文化考查背景总结如下:①以数学名著为考查背景，以中国数学典籍史料中优秀成果为背景。

②以数学猜想和定理为命题背景。

③以数学名家的故事为命题背景，以数学家的故事，为考查背景，正是对创新精神数学精神的一种传承。

④以数学的应用为命题背景。

⑤历史名人。

⑥历史发展。

3、文化背景的考查在突出所要考查的数学知识的同时，培养学生的数学素养，不仅可以让学生理解数学文化形成数学素养，同时也让学生感受我们古代数学的伟大成就，增强爱国情怀，引导学生了解数学文化体现数学文化以数化人的本质内涵。

这是新高考考察的目的，从而这类问题也是新高考必考题型。

4、数学高考题渗透了大量的数学文化，尤其是渗透到中国古代独特的数学题目。

但这些题目考查的知识点有限，很多内容并未涉及到。

我们现在的社会在飞速发展，无论是科技还是人的思想都不断地变化。

为了让学生能够更好地适应未来社会的发展，我们的教育需要及时更新，不仅仅要反映在教材，考试也应该与时俱进，而不再是摸小球，投骰子，算水费这些老古董的模型背景，更应该与时俱进。

比如以科技为背景文化材料都可以作为激发学生学习兴趣的新材料。

像2020年12月2日嫦娥五号成功降落在月球上，它里面所涉及的轨道、运动都能成为很好的考查背景材料，而这些发射卫星的基地名称也可以作为命题背景的一大亮眼之处。

除次以外，同样可以结合其他学科知识和实际民生，比如新冠肺炎这些热点问题也可以成为出题的背景，进入数学高考题。

【满分技巧】1、多掌握数学文化知识通过对数学文化知识了解使学生对文化素养的提升，做题时能够做到有的放矢，减少对这类问题的恐惧心理。

2、注意数学文化的译文很多数学文化的题型都是选用的是中国传统数学文化，题目前面都是以文言文的形式出现，而后面都会对给出译文，译文才是本题的关键题意，所以这类题的关键地方是在译文上理解。

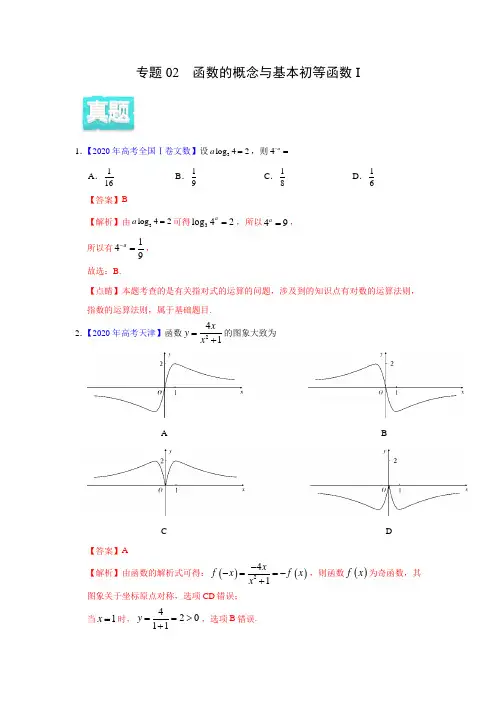
专题02 函数的概念与基本初等函数I1．【2020年高考全国Ⅰ卷文数】设3log 42a =，则4a -= A ．116B ．19C ．18D ．16【答案】B【解析】由3log 42a =可得3log 42a=，所以49a =，所以有149a-=， 故选：B.【点睛】本题考查的是有关指对式的运算的问题，涉及到的知识点有对数的运算法则，指数的运算法则，属于基础题目. 2．【2020年高考天津】函数241xy x =+的图象大致为A BC D【答案】A【解析】由函数的解析式可得：()()241xf x f x x --==-+，则函数()f x 为奇函数，其图象关于坐标原点对称，选项CD 错误； 当1x =时，42011y ==>+，选项B 错误.故选：A.【点睛】函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项．3．【2020年高考全国Ⅱ卷文数】在新冠肺炎疫情防控期间，某超市开通网上销售业务，每天能完成1200份订单的配货，由于订单量大幅增加，导致订单积压．为解决困难，许多志愿者踊跃报名参加配货工作．已知该超市某日积压500份订单未配货，预计第二天的新订单超过1600份的概率为0.05．志愿者每人每天能完成50份订单的配货，为使第二天完成积压订单及当日订单的配货的概率不小于0.95，则至少需要志愿者 A ．10名 B ．18名C ．24名D ．32名【答案】B【解析】由题意，第二天新增订单数为50016001200900+-=，设需要志愿者x 名，500.95900x≥，17.1x ≥,故需要志愿者18名. 故选：B【点晴】本题主要考查函数模型的简单应用，属于基础题.4．【2020年高考全国Ⅲ卷文数】Logistic 模型是常用数学模型之一，可应用于流行病学领城．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位：天)的Logistic 模型：0.23(53)()=1et I K t --+，其中K 为最大确诊病例数．当I (*t )=0.95K 时，标志着已初步遏制疫情，则*t 约为（ln19≈3） A ．60B ．63C ．66D ．69【答案】C 【解析】()()0.23531t K I t e--=+，所以()()0.23530.951t K I t K e**--==+，则()0.235319t e*-=，所以，()0.2353ln193t *-=≈，解得353660.23t *≈+≈. 故选：C.【点睛】本题考查对数的运算，考查指数与对数的互化，考查计算能力，属于中等题.5．【2020年高考全国Ⅲ卷文数】设a =log 32，b =log 53，c =23，则 A ．a <c <bB ．a <b <cC ．b <c <aD ．c <a <b【答案】A 【解析】因为333112log 2log 9333a c =<==，355112log 3log 25333b c =>==， 所以a c b <<. 故选A .【点晴】本题考查对数式大小的比较，考查学生转化与化归的思想，是一道中档题. 6．【2020年高考全国Ⅱ卷文数】设函数f (x )=x 3－31x ，则f (x ) A ．是奇函数，且在(0,+∞)单调递增 B ．是奇函数，且在(0,+∞)单调递减 C ．是偶函数，且在(0,+∞)单调递增D ．是偶函数，且在(0,+∞)单调递减【答案】A【解析】因为函数()331f x x x =-定义域为{}0x x ≠，其关于原点对称，而()()f x f x -=-，所以函数()f x 为奇函数．又因为函数3y x =在0,上单调递增，在,0上单调递增， 而331y x x-==在0,上单调递减，在,0上单调递减，所以函数()331f x x x=-在0,上单调递增，在,0上单调递增．故选：A ．【点睛】本题主要考查利用函数的解析式研究函数的性质，属于基础题． 7．【2020年高考全国Ⅱ卷文数】若2x −2y <3−x −3−y ，则A ．ln(y −x +1)>0B ．ln(y −x +1)<0C ．ln|x −y |>0D ．ln|x −y |<0【答案】A【解析】由2233x y x y ---<-得：2323x x y y ---<-，令()23ttf t -=-，2x y =为R 上的增函数，3x y -=为R 上的减函数，()f t ∴为R 上的增函数，x y ∴<，0y x ->，11y x ∴-+>，()ln 10y x ∴-+>，则A 正确，B 错误；x y -与1的大小不确定，故CD 无法确定.故选：A.【点睛】本题考查对数式的大小的判断问题，解题关键是能够通过构造函数的方式，利用函数的单调性得到,x y 的大小关系，考查了转化与化归的数学思想. 8．【2020年高考天津】设0.70.80.713,(),log 0.83a b c -===，则,,a b c 的大小关系为A ．a b c <<B ．b a c <<C ．b c a <<D ．c a b <<【答案】D【解析】因为0.731a =>，0.80.80.71333b a -⎛⎫==>= ⎪⎝⎭，0.70.7log 0.8log 0.71c =<=，所以1c a b <<<. 故选：D.【点睛】本题考查的是有关指数幂和对数值的比较大小问题，在解题的过程中，注意应用指数函数和对数函数的单调性，确定其对应值的范围. 比较指对幂形式的数的大小关系，常用方法：（1）利用指数函数的单调性：xy a =，当1a >时，函数递增；当01a <<时，函数递减；（2）利用对数函数的单调性：log a y x =，当1a >时，函数递增；当01a <<时，函数递减；（3）借助于中间值，例如：0或1等.9．【2020年新高考全国Ⅰ卷】基本再生数R 0与世代间隔T 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段，可以用指数模型：(e )rtI t =描述累计感染病例数I (t )随时间t (单位:天)的变化规律，指数增长率r 与R 0，T 近似满足R 0 =1+rT .有学者基于已有数据估计出R 0=3.28，T =6.据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为(ln2≈0.69) A ．1.2天 B ．1.8天 C ．2.5天 D ．3.5天【答案】B【解析】因为0 3.28R =，6T =，01R rT =+，所以 3.2810.386r -==，所以()0.38rt t I t e e ==，设在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间为1t 天， 则10.38()0.382t t t e e +=，所以10.382t e =，所以10.38ln 2t =， 所以1ln 20.691.80.380.38t =≈≈天. 故选：B.【点睛】本题考查了指数型函数模型的应用，考查了指数式化对数式，属于基础题. 10．【2020年新高考全国Ⅰ卷】若定义在R 的奇函数f (x )在(0),-∞单调递减，且f (2)=0，则满足(10)xf x -≥的x 的取值范围是 A ．[)1,1][3,-+∞ B ．3,1][,[01]-- C ．[)1,0][1,-+∞ ．1,0]3][[1,-【答案】D【解析】因为定义在R 上的奇函数()f x 在(,0)-∞上单调递减，且(2)0f =， 所以()f x 在(0,)+∞上也是单调递减，且(2)0f -=，(0)0f =， 所以当(,2)(0,2)x ∈-∞-⋃时，()0f x >，当(2,0)(2,)x ∈-+∞时，()0f x <，所以由(10)xf x -≥可得：021012x x x <⎧⎨-≤-≤-≥⎩或或001212x x x >⎧⎨≤-≤-≤-⎩或或0x =解得10x -≤≤或13x ≤≤，所以满足(10)xf x -≥的x 的取值范围是[1,0][1,3]-⋃， 故选：D.【点睛】本题考查利用函数奇偶性与单调性解抽象函数不等式，考查分类讨论思想方法，属中档题.11．【2020年新高考全国Ⅰ卷】信息熵是信息论中的一个重要概念.设随机变量X 所有可能的取值为1,2,,n ，且1()0(1,2,,),1ni i i P X i p i n p ===>==∑，定义X 的信息熵21()log ni i i H X p p ==-∑.A ．若n =1，则H (X )=0B ．若n =2，则H (X )随着1p 的增大而增大C ．若1(1,2,,)i p i n n==，则H (X )随着n 的增大而增大D ．若n =2m ，随机变量Y 所有可能的取值为1,2,,m ，且21()(1,2,,)j m j P Y j p p j m +-==+=，则H (X )≤H (Y )【答案】AC【解析】对于A 选项，若1n =，则11,1i p ==，所以()()21log 10H X =-⨯=，所以A 选项正确.对于B 选项，若2n =，则1,2i =，211p p =-， 所以()()()121121X log 1log 1H p p p p =-⋅+-⋅-⎡⎤⎣⎦， 当114p =时，()221133log log 4444H X ⎛⎫=-⋅+⋅ ⎪⎝⎭， 当13p 4=时，()223311log log 4444H X ⎛⎫=-⋅+⋅ ⎪⎝⎭，两者相等，所以B 选项错误. 对于C 选项，若()11,2,,i p i n n==，则()222111log log log H X n n nn n ⎛⎫=-⋅⨯=-= ⎪⎝⎭，则()H X 随着n 的增大而增大，所以C 选项正确.对于D 选项，若2n m =，随机变量Y 的所有可能的取值为1,2,,m ，且()21j m j P Y j p p +-==+（1,2,,j m =）.()2222111log log mmi i i i i iH X p p p p ===-⋅=⋅∑∑ 122221222122121111log log log log m m m mp p p p p p p p --=⋅+⋅++⋅+⋅. ()H Y =()()()122221212122211111log log log m m m m m m m m p p p p p p p p p p p p -+-++⋅++⋅+++⋅+++12222122212221221121111log log log log m m m m m mp p p p p p p p p p p p ---=⋅+⋅++⋅+⋅++++.由于()01,2,,2i p i m >=，所以2111i i m ip p p +->+， 所以222111log log i i m ip p p +->+， 所以222111log log i i i i m ip p p p p +-⋅>⋅+， 所以()()H X H Y >，所以D 选项错误. 故选：AC【点睛】本小题主要考查对新定义“信息熵”的理解和运用，考查分析、思考和解决问题的能力，涉及对数运算和对数函数及不等式的基本性质的运用，属于难题.12．【2020年高考天津】已知函数3,0,(),0.x x f x x x ⎧≥=⎨-<⎩若函数2()()2()g x f x kx x k =--∈R 恰有4个零点，则k 的取值范围是 A ．1(,)(22,)2-∞-+∞B ．1(,)(0,22)2-∞-C ．(,0)(0,22)-∞D ．(,0)(22,)-∞+∞【答案】D【解析】注意到(0)0g =，所以要使()g x 恰有4个零点，只需方程()|2|||f x kx x -=恰有3个实根 即可， 令()h x =()||f x x ，即|2|y kx =-与()()||f x h x x =的图象有3个不同交点.因为2,0()()1,0x x f x h x x x ⎧>==⎨<⎩， 当0k =时，此时2y =，如图1，2y =与()()||f x h x x =有2个不同交点，不满足题意； 当k 0<时，如图2，此时|2|y kx =-与()()||f x h x x =恒有3个不同交点，满足题意； 当0k >时，如图3，当2y kx =-与2yx 相切时，联立方程得220x kx -+=，令0∆=得280k -=，解得22k =（负值舍去），所以22k >. 综上，k 的取值范围为(,0)(22,)-∞+∞.故选：D.【点晴】本题主要考查函数与方程的应用，考查数形结合思想，转化与化归思想，是一道中档题.13．【2020年高考北京】已知函数()21xf x x =--，则不等式()0f x >的解集是A. (1,1)-B. (,1)(1,)-∞-+∞C. (0,1)D. (,0)(1,)-∞⋃+∞【答案】D【解析】因为()21xf x x =--，所以()0f x >等价于21x x >+，在同一直角坐标系中作出2xy =和1y x =+的图象如图：两函数图象的交点坐标为(0,1),(1,2)， 不等式21x x >+的解为0x <或1x >.所以不等式()0f x >的解集为：()(),01,-∞⋃+∞. 故选：D.【点睛】本题考查了图象法解不等式，属于基础题.14．【2020年高考浙江】函数y =x cos x +sin x 在区间[–π，π]上的图象可能是【答案】A【解析】因为()cos sin f x x x x =+，则()()cos sin f x x x x f x -=--=-， 即题中所给的函数为奇函数，函数图象关于坐标原点对称， 据此可知选项CD 错误；且x π=时，cos sin 0y ππππ=+=-<，据此可知选项B 错误. 故选：A.【点睛】函数图象的识辨可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置．(2)从函数的单调性，判断图象的变化趋势．(3)从函数的奇偶性，判断图象的对称性．(4)从函数的特征点，排除不合要求的图象．利用上述方法排除、筛选选项．15．【2020年高考浙江】已知a ，b ∈R 且ab ≠0，对于任意x ≥0均有(x –a )(x –b )(x –2a –b )≥0，则 A ．a <0 B ．a >0 C ．b <0 D ．b >0【答案】C【解析】因为0ab ≠，所以0a ≠且0b ≠，设()()()(2)f x x a x b x a b =----，则()f x 零点为123,,2x a x b x a b ===+ 当0a >时，则23x x <，1>0x ，要使()0f x ≥，必有2a b a +=，且0b <， 即=-b a ，且0b <，所以0b <；当0a <时，则23x x >，10x <，要使()0f x ≥，必有0b <.综上一定有0b <. 故选：C【点晴】本题主要考查三次函数在给定区间上恒成立问题，考查学生分类讨论思想，是一道中档题.16．【2020年高考江苏】已知y =f (x )是奇函数，当x ≥0时，()23f x x =，则()8f -的值是 ▲ ． 【答案】4-【解析】23(8)84f ==，因为()f x 为奇函数，所以(8)(8)4f f -=-=- 故答案为：4-【点睛】本题考查根据奇函数性质求函数值，考查基本分析求解能力，属基础题. 17．【2020年高考北京】函数1()ln 1f x x x =++的定义域是____________． 【答案】(0,)+∞【解析】由题意得010x x >⎧⎨+≠⎩，0x ∴>故答案为：(0,)+∞【点睛】本题考查函数定义域，考查基本分析求解能力，属基础题.1．【2020·北京高三月考】已知函数()y f x =满足(1)2()f x f x +=，且(5)3(3)4f f =+，则(4)f = A ．16 B ．8C ．4D ．2【答案】B【解析】因为(1)2()f x f x +=,且(5)3(3)4f f =+,故()()324442f f =+,解得()48f =.故选B.【点睛】本题主要考查了根据函数性质求解函数值的问题,属于基础题.2．【2020·宜宾市叙州区第二中学校高三一模（文）】已知函数()32,0log ,0x x f x x x ⎧≤=⎨>⎩，则=3f f ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭A．2B ．12C ．3log 2-D ．3log 2【答案】A【解析】依题意12331log log 32f -===-⎝⎭，12122f f f -⎛⎫⎛⎫=-== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故选A.【点睛】本小题主要考查根据分段函数解析式求函数值，属于基础题.3．【安徽省2020届高三名校高考冲刺模拟卷数学（文科）试题】已知10.23121log 3,(),23a b c ===，则A ．a <b <cB ．c <b <aC ．c <a <bD ．b <a <c【答案】A【解析】∵1122log 3log 10a =<=，0.20110()()133b <=<=，1131222c <=<=，∴a <b <c ，故选A ．4．【2020·重庆巴蜀中学高三月考（文）】已知定义在R 上的函数()f x 满足()12f =，对任意的实数1x ，2x 且12x x <，()()1212f x f x x x -<-，则不等式()1f x x ->的解集为A ．(),2-∞-B ．2,C ．()(),11,-∞-⋃+∞D ．()(),22,-∞-⋃+∞【答案】B【解析】设()()1F x f x x =--，则()()11F x f x x -=--，()()11110F f =--=，对任意的1x ，2x 且12x x <，()()1212f x f x x x -<-， 得()()112211f x x f x x --<--， 即()()12F x F x <， 所以()F x 在R 上是增函数，不等式()1f x x ->即为()()11F x F ->， 所以11x ->，2x >. 故选B.【点睛】本题考查函数的单调性解不等式，属于中档题．5．【2020届广东省惠州市高三6月模拟数学（文）试题】已知函数||()e ||x f x x =+，则满足1(21)3f x f ⎛⎫-< ⎪⎝⎭的x 取值范围是A ．12,33⎛⎫⎪⎝⎭B ．12,33⎡⎫⎪⎢⎣⎭C ．12,23⎛⎫⎪⎝⎭D ．12,23⎡⎫⎪⎢⎣⎭【答案】A【解析】由||()e ||()x f x x f x --=+-=，知()f x 是偶函数，∴不等式1(21)3f x f ⎛⎫-< ⎪⎝⎭等价为1(|21|)()3f x f -<，当0x >时，()e xf x x =+，()f x 在区间[0,)+∞上单调递增，1|21|,3x ∴-<解得1233x <<.故选A.【点睛】本题考查根据函数的奇偶性和单调性求解函数不等式的问题，关键是能够利用单调性将不等式转化为自变量大小关系，从而解出不等式，属于中档题. 6．【2020届广东省惠州市高三6月模拟数学（文）试题】函数πx x y x=的图象大致形状是A ．B ．C ．D ．【答案】B【解析】当0x <时，ππx xx y x -==-；当0x >时，ππx x x y x ==，πx y =为R 上的增函数，πx x y x∴=在(),0-∞上单调递减，在()0,+∞上单调递增，可知B 正确.故选B. 【点睛】本题考查函数图象的识别，解题关键是能够通过分类讨论的方式得到函数在不同区间内的解析式，进而根据指数函数单调性判断出结果.7．【2020·重庆市育才中学高三开学考试（文）】若函数()23,121,1x ax a x f x ax x ⎧--≥=⎨-<⎩是R 上的增函数，则实数a 的取值范围是A ．103⎡⎫-⎪⎢⎣⎭，B ．103⎛⎤ ⎥⎝⎦，C ．1,3⎛⎤-∞- ⎥⎝⎦D ．13⎡⎫+∞⎪⎢⎣⎭，【答案】B【解析】由函数()23,121,1x ax a x f x ax x ⎧--≥=⎨-<⎩是R 上的增函数，则1202113a a a a a⎧≤⎪⎪>⎨⎪-≤--⎪⎩，解得103a <≤，即实数a 的取值范围是103⎛⎤ ⎥⎝⎦，. 故选B.【点睛】本题考查了分段函数的性质，重点考查了运算能力，属基础题.8．【贵州省黔东南州2019-2020学年高三高考模拟考试卷数学（文科)试题】已知函数()f x 的图象关于点()1,0对称，当1x >时，2()5f x x mx =-+，且()f x 在(,0)-∞上单调递增，则m 的取值范围为 A ．[4,)+∞ B ．[2,)+∞C ．(,4]-∞D ．(,2]-∞【答案】C【解析】函数()f x 的图象关于点()1,0对称且在(,0)-∞上单调递增，所以()f x 在(2,)+∞上单调递增，所以对称轴22m≤，即4m ≤. 故选C.【点睛】本题考查函数的性质，涉及到单调性、对称性等知识，考查学生数形结合的思想，是一道容易题.9．【2020·北京市八一中学高三月考】函数()()213f x ax a x =---在区间[)1,-+∞上是增函数，则实数a 的取值范围是 A ．1,3⎛⎤-∞ ⎥⎝⎦B ．(],0-∞C ．10,3⎛⎤ ⎥⎝⎦D ．10,3⎡⎤⎢⎥⎣⎦【答案】D【解析】若0a =，则()3f x x =-，()f x 在区间[)1,-+∞上是增函数，符合.若0a ≠，因为()f x 在区间[)1,-+∞上是增函数，故0112a a a>⎧⎪-⎨≤-⎪⎩，解得103a <≤.综上，1 03a≤≤.故选D.【点睛】本题考查含参数的函数的单调性，注意根据解析式的特点合理分类，比如解析式是二次三项式，则需讨论二次项系数的正负以及对称轴的位置，本题属于基础题.10．【2020·四川省成都外国语学校高三月考（文）】若函数,1()42,12xa xf x ax x⎧>⎪=⎨⎛⎫-+≤⎪⎪⎝⎭⎩是R上的单调递增函数，则实数a的取值范围是A．()1,+∞B．（1,8）C．（4,8）D．[4,8)【答案】D【解析】因为函数,1()42,12xa xf x ax x⎧>⎪=⎨⎛⎫-+≤⎪⎪⎝⎭⎩是R上的单调递增函数，所以140482422aaaaa⎧⎪>⎪⎪->∴≤<⎨⎪⎪-+≤⎪⎩故选D.【点睛】本题考查根据分段函数单调性求参数，考查基本分析判断能力，属中档题.11．【2020届山西省太原五中高三3月模拟数学（文）试题】函数ln||cos ()sinx xf xx x⋅=+在[π,0)(0,π]-的图像大致为A．B．C．D．【答案】D【解析】因为ln ||cos ()()sin x xf x f x x x⋅-=-=-+，所以()f x 为奇函数，关于原点对称，故排除A ，又因为()10f ±=，π()02f ±=，π()03f >，()0f π<，故排除B ，C.故选D.【点睛】本题考查函数图象的识别，根据函数的性质以及特殊值法灵活判断，属于基础题.12．【2020·宜宾市叙州区第二中学校高三一模（文）】已知()f x 是定义在R 上的偶函数，在区间[0,)+∞上为增函数，且1()03f =，则不等式18(log )0f x >的解集为A ．1(,2)2B ．(2,)+∞C ．1(0,)(2,)2+∞ D ．1(,1)(2,)2+∞【答案】C【解析】∵118811(log )0()(log )()33f x f f x f >=⇔>，又()f x 在区间[0,)+∞上为增函数，∴181log 3x >，∴118811log log 33x x 或><-，∴1022x x <或，∴不等式18(log )0f x >的解集为1(0,)(2,)2+∞，故选C.13．【2020·宜宾市叙州区第一中学校高三一模（文）】已知函数()()()1f x x ax b =-+为偶函数，且在0,上单调递减，则()30f x -<的解集为A ．()2,4 B ．()(),24,-∞+∞C ．()1,1-D ．()(),11,-∞-⋃+∞【答案】B【解析】因为()()2f x ax b a x b =+--为偶函数，所以0b a -=，即b a =， ∴()2f x ax a =-，因为()f x 在()0,∞+上单调递减， 所以0a <，∴()()2330f x a x a -=--<，可化为()2310x -->， 即2680x x -+>，解得2x <或4x >. 故选B .【点睛】本题主要考查奇偶性与单调性的应用以及一元二次不等式的解法，还考查了运算求解的能力，属于中档题.14．【天津市十二区县重点学校2020届高三下学期毕业班联考（一）数学试题】已知函数(2)y f x =-的图象关于直线2x =对称，在(0,)x ∈+∞时，()f x 单调递增．若()ln34a f =，e (2)b f -=，1ln πc f ⎛⎫= ⎪⎝⎭（其中e 为自然对数的底数，π为圆周率），则,,a b c 的大小关系为 A ．a c b >> B ．a b c >> C ．c a b >> D ．c b a >>【答案】A【解析】因为函数(2)y f x =-的图象关于直线2x =对称，所以()f x 的图象关于y 轴对称，因为(0,)x ∈+∞时，()f x 单调递增，所以(,0)x ∈-∞时，()f x 单调递减； 因为ln3ln e e 01444,0221,lnln ln e 1->=<<==π>=π，所以a c b >>. 故选A.【点睛】本题主要考查函数的性质，根据条件判断出函数的单调性和奇偶性是求解的关键，侧重考查数学抽象的核心素养.15．【2020·山东省高三期末】函数()y f x =是R 上的奇函数，当0x <时，()2xf x =，则当0x >时，()f x =A ．2x -B ．2x -C ．2x --D ．2x【答案】C 【解析】0x <时，()2xf x =.当0x >时，0x -<，()2xf x --=，由于函数()y f x =是奇函数，()()2xf x f x -∴=--=-，因此，当0x >时，()2xf x -=-，故选C.【点睛】本题考查奇偶函数解析式的求解，一般利用对称转移法求解，即先求出()f x -的表达式，再利用奇偶性得出()f x 的表达式，考查分析问题和运算求解能力，属于中等题.16．【2020·山东省高三期末】函数()y f x =与()y g x =的图象如图所示，则()()y f x g x =⋅的部分图象可能是A ．B ．C ．D ．【答案】A【解析】由图象可知()y f x =的图象关于y 轴对称，是偶函数，()y g x =的图象关于原点对称，是奇函数，并且定义域{}0x x ≠，()()y f x g x ∴=⋅的定义域是{}0x x ≠，并且是奇函数，排除B ，又π0,2x ⎛⎫∈ ⎪⎝⎭时，()0f x >，()0g x <，()()0f x g x ∴⋅<，排除C,D. 满足条件的只有A. 故选A.【点睛】本题考查函数图象的识别，意在考查函数的基本性质，属于基础题型. 17．【2020届广东省化州市高三第四次模拟数学（文）试题】已知函数()()2,0,ln 1,0,x x f x x x ⎧⎪=⎨+>⎪⎩若不等式()10f x kx k -++<的解集为空集，则实数k 的取值范围为A ．(222,0⎤-⎦B ．(232,0⎤-⎦C ．222,0⎡⎤-⎣⎦D ．[]1,0-【答案】C【解析】因为不等式()10f x kx k -++<的解集为空集， 所以不等式()10f x kx k -++恒成立.()10f x kx k -++可变形为()(1)1f x k x --.在同一坐标系中作出函数(),(1)1y f x y k x ==--的图象，如图：直线(1)1y k x =--过定点(1,1)A -，当直线(1)1y k x =--与2(0)y x x =相切时，方程()10f x kx k -++=有一个实数解，可得2(1)1x k x =--，即210x kx k -++=，由24(1)0k k ∆=-+=，可得2k =-2k =+（舍去）， 故由函数图象可知使不等式恒成立的实数k的取值范围为2⎡⎤-⎣⎦.故选C.【点睛】本题考查了函数图象、根据函数的图象求参数的取值范围，考查了数形结合思想，属于中档题.18．【2020·山东省青岛第五十八中学高三一模】已知函数229,1()4,1x ax x f x x a x x ⎧-+≤⎪=⎨++>⎪⎩，若()f x 的最小值为(1)f ，则实数a 的值可以是A ．1B ．2C ．3D ．4【答案】BCD 【解析】当1x >,4()4f x x a a x=++≥+, 当且仅当2x =时,等号成立；当1x ≤时,2()29f x x ax =-+为二次函数,要想在1x =处取最小,则对称轴要满足1x a =≥,且(1)4f a ≤+,即1294a a -+≤+,解得2a ≥,故选BCD.【点睛】本题考查分段函数的最值问题,处理时应对每段函数进行分类讨论,找到每段的最小值.19．【2020·山东省高三零模】已知定义在R 上的函数()y f x =满足条件()()2f x f x +=-，且函数()1y f x =-为奇函数，则A ．函数()y f x =是周期函数B ．函数()y f x =的图象关于点()1,0-对称C ．函数()y f x =为R 上的偶函数D ．函数()y f x =为R 上的单调函数 【答案】ABC【解析】因为()()2f x f x +=-，所以()()()42f x f x f x +=-+=，即4T=，故A 正确；因为函数()1y f x =-为奇函数，所以函数()1y f x =-的图像关于原点成中心对称，所以B 正确；又函数()1y f x =-为奇函数，所以()()11f x f x --=--，根据()()2f x f x +=-，令1x -代x 有()()11f x f x +=--，所以()()11f x f x +=--，令1x -代x 有()()f x f x -=，即函数()f x 为R 上的偶函数，C 正确；因为函数()1y f x =-为奇函数，所以()10f -=，又函数()f x 为R 上的偶函数，()10f =，所以函数不单调，D 不正确.故选ABC.【点睛】本题考查了函数的周期性和奇偶性以及对称性，属于基础题.20．【2020届上海市高三高考压轴卷数学试题】已知函数()223f x x ax =-++在区间(),4-∞上是增函数，则实数a 的取值范围是______.【答案】[)4,+∞【解析】()223f x x ax =-++对称轴方程为x a =， ()f x 在区间(),4-∞上是增函数，所以4a ≥.故答案为[)4,+∞.【点睛】本题考查函数的单调性求参数，熟练掌握初等简单函数的性质是解题的关键，属于基础题.21．【福建省厦门外国语学校2020届高三下学期高考最后一次模拟数学（文）试题】已知函数2,0()(2),0x x f x f x x ⎧>=⎨+≤⎩，则(1)f -=_____________【答案】2【解析】函数2,0()(2),0x x f x f x x ⎧>=⎨+≤⎩，则()1(1)122f f -===. 故答案为：2【点睛】本题考查了分段函数求值，考查了基本运算求解能力，属于基础题.22．【2020·陕西省交大附中高三三模（文）】设函数23(0)()(2)(0)x x x f x f x x ⎧+≥=⎨+<⎩，则()–3f =_____【答案】4【解析】函数23(0)()(2)(0)x x x f x f x x ⎧+≥=⎨+<⎩，2(3)(1)(1)1314f f f -=-==+⨯=．【点睛】本题考查的知识点是分段函数的应用，函数求值，难度不大，属于基础题． 23．【2020·宜宾市叙州区第二中学校高三一模（文）】奇函数()f x 满足()()11f x f x +=-，当01x <≤时，()()2log 4f x x a =+，若1522f ⎛⎫=-⎪⎝⎭，则()a f a +=___________. 【答案】2【解析】由于函数()y f x =为奇函数，且()()()111f x f x f x +=-=--，即()()2f x f x +=-，()()()42f x f x f x ∴+=-+=，所以，函数()y f x =是以4为周期的奇函数，()21511log 22222f f f a ⎛⎫⎛⎫⎛⎫∴=-=-=-+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 解得2a =. ()()()222f f f =-=-，()20f ∴=.因此，()()222a f a f +=+=.故答案为2.【点睛】本题考查函数值的计算，推导出函数的周期性是解答的关键，考查推理能力与计算能力，属于中等题.24．【2020届上海市高三高考压轴卷数学试题】函数()lg 2cos 21y x =-的定义域是______. 【答案】5πππ5π3,,,36666⎡⎫⎛⎫⎛⎤---⎪ ⎪ ⎢⎥⎣⎭⎝⎭⎝⎦【解析】因为()lg 2cos 21y x =-，所以2902cos 210x x ⎧-≥⎨->⎩，所以331cos 22x x -≤≤⎧⎪⎨>⎪⎩， 所以33ππππ,66x k x k k -≤≤⎧⎪⎨-<<+∈⎪⎩Z ， 解得5π36x -≤<-或ππ66x -<<或5π36x <≤. 故答案为5πππ5π3,,,36666⎡⎫⎛⎫⎛⎤---⎪ ⎪ ⎢⎥⎣⎭⎝⎭⎝⎦. 【点睛】本题主要考查函数定义域的求法以及一元二次不等式，三角不等式的解法，还考查了运算求解的能力，属于中档题.25．【江苏省南京市金陵中学、南通市海安高级中学、南京市外国语学校2020届高三下学期第四次模拟数学试题】已知函数()02,2,2x f x f x x ≤<=-≥⎪⎩若对于正数()*n k n ∈N ，直线n y k x =与函数()y f x =的图象恰有21n 个不同的交点，则数列{}2nk 的前n 项和为________. 【答案】()41n n + 【解析】当02x ≤<时，()y f x ==()2211x y -+=，0y ≥； 当2x ≥时()()2f x f x =-，函数周期为2，画出函数图象，如图所示：n y k x =与函数恰有21n 个不同的交点，根据图象知，直线n y k x =与第1n +个半圆相切，故()2244211n k n n n ==++-，故2211114441n k n n n n ⎛⎫==- ⎪++⎝⎭， 数列{}2n k 的前n 项和为()11111114223141n n n n ⎛⎫-+-+⋅⋅⋅+-= ⎪++⎝⎭. 故答案为：()41n n +. 【点睛】本题考查了数列求和，直线和圆的位置关系，意在考查学生的计算能力和转化能力，综合应用能力，画出图象是解题的关键.。

压轴题型03 函数与导数经典常考压轴小题命题预测有关函数与导数常见经典压轴小题的高考试题，考查重点是零点、不等式、恒成立等问题，通常与函数性质、解析式、图像等均相关，需要考生具有逻辑推理、直观想象和数学运算核心素养. 同时，对于实际问题，需要考生具有数据分析、数学建模核心素养.预计预测2024年高考，多以小题形式出现，也有可能会将其渗透在解答题的表达之中，相对独立．具体估计为：（1）导数的计算和几何意义是高考命题的热点，多以选择题、填空题形式考查，难度较小．（2）应用导数研究函数的单调性、极值、最值多在选择题、填空题靠后的位置考查，难度中等偏上，属综合性问题． 高频考法（1）函数嵌套、零点嵌套问题 （2）零点问题（3）导数的同构思想 （4）双重最值问题 （5）构造函数解不等式01函数嵌套、零点嵌套问题解决嵌套函数零点个数的一般步骤(1)换元解套,转化为()t g x =与()y f t =的零点.(2)依次解方程,令()0f t =,求t ,代入()t g x =求出x 的值或判断图象交点个数.【典例1-1】（上海市浦东新区上海市实验学校2024届高三学期第三次月考数学试题）已知函数()f x 是2024届高考数学专项练习定义在R 的偶函数，当0x ≥时，()()3πcos 1,012211,12xx x f x x ⎧⎡⎤−≤≤⎪⎢⎥⎣⎦⎪=⎨⎛⎫⎪+> ⎪⎪⎝⎭⎩，若函数()()()()()25566g x f x a f x a a ⎡⎤=−++∈⎣⎦R 有且仅有6个不同的零点，则实数a 取值范围 .【答案】(]30,12⎧⎫⎨⎬⎩⎭【解析】因为()()()()()()25566560g x f x a f x a f x f x a =−++=−⋅−=⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦， 由()0g x =，可得()65f x =或()f x a =， 由函数()f x 是定义在R 上的偶函数，当0x ≥时，()3πsin ,012211,12xx x f x x ⎧≤≤⎪⎪=⎨⎛⎫⎪+> ⎪⎪⎝⎭⎩， 当01x ≤≤时，ππ022x ≤≤，如下图所示：因为1112x⎛⎫+> ⎪⎝⎭，由图可知，直线65y =与函数()f x 的图象有4个交点，所以，直线y a =与函数()f x 的图象有2个交点，由图可得(]30,12a ⎧⎫∈⋃⎨⎬⎩⎭.综上所述，实数a 的取值范围是(]30,12⎧⎫⎨⎬⎩⎭.故答案为：(]30,12⎧⎫⎨⎬⎩⎭.【典例1-2】（安徽省合肥市六校联盟2023-2024学年高三学期期中联考数学试题）已知函数()42,13,1x x f x x x ⎧−<⎪=⎨−≥⎪⎩，()22g x x ax =++，若函数()()y g f x =有6个零点，则实数a 的取值范围为 .【答案】(3,2−−【解析】画出()42,13,1x x f x x x ⎧−<⎪=⎨−≥⎪⎩的图象如下：因为()22g x x ax =++最多两个零点，即当280a ∆=−>，2a >22a <−时，()22g x x ax =++有两个不等零点12,t t ，要想()()y g f x =有六个零点，结合函数图象，要()1f x t =和()2f x t =分别有3个零点， 则()12,0,2t t ∈且12t t ≠，即()22g x x ax =++的两个不等零点()12,0,2t t ∈，则要满足()()2Δ800222000a a g g ⎧=−>⎪⎪<−<⎪⎨⎪>⎪>⎪⎩，解得322a −<<− 故实数a 的取值范围为(3,2−− 故答案为：(3,22−−【变式1-1】（海南省琼中黎族苗族自治县琼中中学2024届高三高考全真模拟卷（二）数学试题）已知函数()23,369,3x x f x x x x ⎧−≤=⎨−+−>⎩，若函数()()()22g x f x af x ⎡⎤=−+⎣⎦有6个零点，则a 的值可能为（ ） A ．1− B ．2−C ．3−D ．4−【答案】C【解析】由题可得，()()330f f =−=，()f x 在()(),0,3,−∞+∞上单调递减，在()0,3上单调递增，则据此可作出函数()f x 大致图象如图所示，令()f x t =，则由题意可得220t at −+=有2个不同的实数解1t ，2t ，且()12,3,0t t ∈−，则()()2121212Δ80601122203331130a t t a a t t t t a ⎧=−>⎪−<+=<⎪⇒−<<−⎨=>⎪⎪++=+>⎩3a =−满足题意. 故选：C ．【变式1-2】（河南省部分重点高中2023-2024学年高三阶段性考试（四）数学试题）已知函数()2ln ,0,43,0,x x f x x x x ⎧>=⎨++≤⎩若函数()()()241g x f x f x m =−++⎡⎤⎣⎦恰有8个零点，则m 的最小值是（ ） A ．1 B ．2 C ．3 D ．4【答案】B【解析】设()f x t =，因为()g x 有8个零点，所以方程()f x t =有4个不同的实根，结合()f x 的图像可得2410t t m −++=在(]0,3内有4个不同的实根，即214m t t +=−+在(]0,3内有2个不同的实根，可知314m ≤+<，即可求得结果．画出函数()2ln ,043,0x x f x x x x ⎧>=⎨++≤⎩，，的图像如图所示，设()f x t =，由()()()2410g x f x f x m =−++=⎡⎤⎣⎦，得2410t t m −++=.因为()g x 有8个零点，所以方程()f x t =有4个不同的实根，结合()f x 的图像可得在(]03t ∈,内有4个不同的实根.所以方程2410t t m −++=必有两个不等的实数根，即214m t t +=−+在(]03t ∈,内有2个不同的实根，结合图像由图可知，314m ≤+<，故23m ≤<，即m 的最小值是2. 故选：B02 零点问题（1）直接法：直接根据题设条件构造关于参数的不等式，再通过解不等式确定参数范围； （2）分离参数法：先将参数分离，转化成球函数值域的问题加以解决；（3）数形结合法：先将解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解． 【典例2-1】（2024·海南省直辖县级单位·模拟预测）已知函数()()()lg ,011,022,2x x f x x x f x x ⎧−<⎪=−−≤<⎨⎪−≥⎩的图象在区间(),(0)t t t −>内恰好有5对关于y 轴对称的点，则t 的值可以是（ ）A ．4B ．5C ．6D ．7【答案】C【解析】令()()11,022,2x x g x g x x ⎧−−≤<⎪=⎨−≥⎪⎩，()lg m x x =，因为()lg m x x =与()lg y x =−的图象关于y 轴对称，因为函数()()()lg ,011,022,2x x f x x x f x x ⎧−<⎪=−−≤<⎨⎪−≥⎩的图象在区间(),(0)t t t −>内恰好有5对关于y 轴对称的点，所以问题转化为()lg m x x =与()()11,022,2x x g x g x x ⎧−−≤<⎪=⎨−≥⎪⎩的图象在()0,(0)t t >内有5个不同的交点，在同一平面直角坐标系中画出()lg m x x =与()()11,022,2x x g x g x x ⎧−−≤<⎪=⎨−≥⎪⎩的图象如下所示：因为()10lg101m ==，当10x >时()1m x >，()()()()()()13579111g g g g g g ======， 结合图象及选项可得t 的值可以是6，其他值均不符合要求,. 故选：C【典例2-2】（2024·四川成都·三模）若函数()2e xf x kx =−大于0的零点有且只有一个，则实数k 的值为（ ） A ．4 B ．2e C ．e 2D ．2e 4【答案】D【解析】函数()f x 有且仅有一个正零点，即方程2ex k x=有且仅有一个正根，令()2e xg x x =，则()()3e 2x x g x x ='−，当0x <时，()0g x '>，当02x <<时，()0g x '<，当2x >时，()0g x '>，即函数()g x 在(),0∞−和()2,∞+上单调递增，在()0,2上单调递减，且()2e24g =，0x →时，()g x ∞→+，x →−∞时，()0g x →，x →+∞时，()g x ∞→+，可作出图象如下，方程2e x k x =有且仅有一个正根，所以2e 4k =.故选：D.【变式2-1】（2024·北京海淀·一模）已知()()3,0lg 1,0x x f x x x ⎧≤⎪=⎨+>⎪⎩，函数()f x 的零点个数为m ，过点(0,2)与曲线()y f x =相切的直线的条数为n ，则,m n 的值分别为（ ） A ．1,1 B ．1,2 C ．2,1 D ．2,2【答案】B【解析】令()0f x =，即0x ≤时，30x =，解得0x =， 0x >时，()lg 10x +=，无解，故1m =，设过点(0,2)与曲线()y f x =相切的直线的切点为()00,x y ，当0x <时，()23f x x '=，则有()320003y x x x x −=−，有()3200023x x x −=−，整理可得301x =−，即01x =−，即当00x <时，有一条切线，当0x >时，()lg e1f x x '=+，则有()()000lg 1e lg 1y x x x x −=−++， 有()()000l 2g elg 11x x x −+=−+，整理可得()()()000221lg 10lg e x x x ++−++=， 令()()()()()2l 0g 2l 1e 1g g x x x x x =++−++>， 则()()2lg 1g x x '=−+， 令()0g x '=，可得99x =，故当()0,99x ∈时，()0g x '>，即()g x 在()0,99上单调递增， 当()99,x ∈+∞时，()0g x '<，即()g x 在()99,∞+上单调递减， 由()()992lg e 99220099lg e 0g =+⨯+−=>，()02020g =−=>，故()g x 在()0,99x ∈上没有零点， 又()()9992lg e 999210003999lg e 10000g =+⨯+−⨯=−<， 故()g x 在()99,999上必有唯一零点， 即当00x >时，亦可有一条切线符合要求， 故2n =.故选：B.【变式2-2】（2024·甘肃武威·模拟预测）已知函数()4ln 12f x ax a x ⎛⎫=−−+ ⎪⎝⎭有3个零点，则实数a 的取值范围是（ ）A ．()1,+∞B ．()2,+∞C ．(),1−∞−D ．(),2−∞−【答案】C【解析】将()y f x =的图象向左平移2个单位长度，可得函数()()22ln 2xg x f x ax x−=+=−+的图象， 所以原题转化为“函数()2ln2xg x ax x−=−+有3个零点”， 即研究直线y ax =与函数()2ln2xh x x−=+图象交点的个数问题． 因为()h x 的定义域为()2,2−，且()()22ln ln ln1022x xh x h x x x+−−+=+==−+， 所以()h x 为奇函数．因为()22222440222(2)4x x x h x x x x x x '+−+−⎛⎫=⋅=⨯=< ⎪−+−+−⎝⎭'， 所以()h x 在区间()2,2−上为减函数，且曲线()y h x =在点()0,0处的切线方程为y x =−． 当0x =时，2112xx x−+⨯=−+； 当02x <<时，2ln2xx x−<−+； 当20x −<<的，2ln2xx x−>−+， 作出()h x 的图象．如图：由图知：当1a <−时，直线y ax =与函数()2ln2xh x x−=+的图象有3个交点．故实数a 的取值范围是(),1∞−−． 故选：C.03 导数的同构思想同构式的应用：（1）在方程中的应用：如果方程()0f a =和()0f b =呈现同构特征，则,a b 可视为方程()0f x =的两个根（2）在不等式中的应用：如果不等式的两侧呈现同构特征，则可将相同的结构构造为一个函数，进而和函数的单调性找到联系。

专题6.2 等差数列及其前n 项和1．（江西师范大学附属中学2019届高三三模）已知数列{}n a 为等差数列，n S 为其前n 项和，5632a a a +=+，则7S =（ ）A ．2B ．7C ．14D ．28【答案】C 【解析】5632a a a +=+ 44422a d a d a d ∴++=++-，解得：42a =()177477142a a S a +∴===，本题选C 。

2．（安徽省1号卷A10联盟2019届模拟）等差数列{}n a 的前n 项和为n S ，若2163S =，则31119a a a ++=（ ）A ．12B ．9C ．6D ．3【答案】B【解析】由等差数列性质可知：21112163S a ==，解得：113a =311191139a a a a ∴++==本题选B 。

3．（贵州省贵阳市2019届高三模拟）已知{a n }为递增的等差数列，a 4+a 7=2，a 5•a 6=-8，则公差d=（ ） A ．6 B ．6-C ．2-D ．4【答案】A【解析】∵{a n }为递增的等差数列，且a 4+a 7=2，a 5•a 6=-8， ∴a 5+a 6=2，∴a 5，a 6是方程22x 80x --=的两个根，且a 5＜a 6， ∴a 5=-2，a 6=4， ∴d=a 6-a 5=6， 故选A 。

4．（河北衡水中学2019届高三调研）已知等比数列{}n a 中，若12a =，且1324,,2a a a 成等差数列，则5a =（ ）A ．2B ．2或32C ．2或-32D ．-1【答案】B【解析】设等比数列{}n a 的公比为q （q 0≠），1324,,2a a a 成等差数列， 321224a a a ∴=+，10a ≠， 220q q ∴--=，解得：q=2q=-1或，451a =a q ∴，5a =232或，故选B.5．（浙江省金华十校2019届高三模拟）等差数列{}n a ，等比数列{}n b ，满足111a b ==，53a b =，则9a 能取到的最小整数是（ ）A ．1-B ．0C ．2D ．3【答案】B【解析】等差数列{}n a 的公差设为d ，等比数列{}n b 的公比设为q ，0q ≠，由111a b ==，53a b =，可得214d q +=，则2291812(1)211a d q q =+=+-=->-，可得9a 能取到的最小整数是0，故选B 。

§6.2等差数列及其前n项和【考点集训】考点一等差数列的定义及通项公式1.(2018陕西咸阳12月模拟,7)《张丘建算经》卷上一题大意为今有女善织,日益功疾,且从第二天起,每天比前一天多织相同量的布,现在一月(按30天计)共织布390尺,最后一天织布21尺,则该女第一天共织多少布?()A.3尺B.4尺C.5尺D.6尺答案C2.(2017安徽淮南一模,15)已知数列{a n}满足递推关系式a n+1=2a n+2n-1(n∈N*),且为等差数列,则λ的值是.答案-13.(2018河南开封定位考试,17)已知数列{a n}满足a1=,且a n+1=.(1)求证:数列是等差数列;(2)若b n=a n a n+1,求数列{b n}的前n项和S n.解析(1)证明:∵a=,∴=,n+1∴-=.∴数列是以2为首项,为公差的等差数列.(2)由(1)知a n=,∴b n==4-,∴S n=4--…-=4-=.考点二等差数列的性质(2019届湖北宜昌模拟,6)已知数列{a}满足=25·,且a2+a4+a6=9,则lo(a5+a7+a9)=()nA.-3B.3C.-D.答案A考点三等差数列的前n项和1.(2018安徽安庆调研,5)等差数列{a n}中,已知S15=90,那么a8=()A.12B.4C.3D.6答案D2.(2017河南部分重点中学二联,6)设S n是公差不为零的等差数列{a n}的前n项和,且a1>0,若S5=S9,则当S n最大时,n=()A.6B.7C.10D.9答案B3.(2019届福建龙岩永定区模拟,10)已知等差数列{a n},{b n}的前n项和分别为S n和T n,且=,则=()A.B.C.D.答案 D炼技法 【方法集训】方法1 等差数列的判定与证明的方法(2019届福建三明模拟,17)已知数列{a n }中,a n =2n-1. (1)证明:数列{a n }是等差数列;(2)若数列{a n }的前n 项和S n =25,求n.解析 (1)证明:∵a n+1-a n =2(n+1)-1-(2n-1)=2,a 1=1, ∴数列{a n }是等差数列,首项为1,公差为2. (2)由(1)得数列{a n }的前n 项和S n =n+ -×2=n 2,由S n =25得n 2=25,又n>0,解得n=5.方法2 等差数列前n 项和的最值问题的解决方法1.(2019届江西高安模拟,11)已知数列{a n }是等差数列,其前n 项和为S n ,满足a 1+3a 2=S 6,给出下列结论:(1)a 7=0;(2)S 13=0;(3)S 7最小;(4)S 5=S 8.其中正确结论的个数是( )A.1B.2C.3D.4答案 C2.(2019届福建龙岩新罗区模拟,12)已知等差数列{a n }的公差为-2,前n 项和为S n ,a 3,a 4,a 5为某三角形的三边长,且该三角形有一个内角为120°,若S n ≤S m 对任意的n ∈N *恒成立,则实数m=( ) A.7 B.6 C.5D.4答案 B3.(2019届福建龙岩新罗区模拟,16)等差数列{a n }中,S n 是它的前n 项和,且S 6<S 7,S 6>S 8,给出下列结论: ①数列{a n }的公差d<0;②S 9<S 6;③S 14<0;④S 7一定是S n 中的最大值. 其中正确的是 (填序号). 答案 ①②③④过专题【五年高考】A 组 统一命题·课标卷题组考点一 等差数列的定义及通项公式(2016课标全国Ⅱ,17,12分)等差数列{a n }中,a 3+a 4=4,a 5+a 7=6.(1)求{a n }的通项公式;(2)设b n =[a n ],求数列{b n }的前10项和,其中[x]表示不超过x 的最大整数,如[0.9]=0,[2.6]=2. 解析 (1)设数列{a n }的公差为d,由题意有2a 1+5d=4,a 1+5d=3. 解得a 1=1,d=.(3分) 所以{a n }的通项公式为a n =.(5分) (2)由(1)知,b n =.(6分) 当n=1,2,3时,1≤<2,b n =1; 当n=4,5时,2<<3,b n =2;当n=6,7,8时,3≤<4,bn=3;当n=9,10时,4<<5,bn=4.(10分)所以数列{bn}的前10项和为1×3+2×2+3×3+4×2=24.(12分)考点二等差数列的性质(2015课标Ⅱ,5,5分)设Sn 是等差数列{an}的前n项和.若a1+a3+a5=3,则S5=()A.5B.7C.9D.11答案A考点三等差数列的前n项和1.(2015课标Ⅰ,7,5分)已知{a n}是公差为1的等差数列,S n为{a n}的前n项和.若S8=4S4,则a10=()A. B. C.10 D.12答案B2.(2014课标Ⅱ,5,5分)等差数列{a n}的公差为2,若a2,a4,a8成等比数列,则{a n}的前n项和S n=()A.n(n+1)B.n(n-1)C. D.-答案A3.(2018课标全国Ⅱ,17,12分)记S n为等差数列{a n}的前n项和,已知a1=-7,S3=-15.(1)求{a n}的通项公式;(2)求S n,并求S n的最小值.解析(1)设{an}的公差为d,由题意得3a1+3d=-15.由a1=-7得d=2.所以{an}的通项公式为a n=2n-9.(2)由(1)得S n=n2-8n=(n-4)2-16.所以当n=4时,Sn取得最小值,最小值为-16.B组自主命题·省(区、市)卷题组考点一等差数列的定义及通项公式1.(2016浙江,8,5分)如图,点列{A n},{B n}分别在某锐角的两边上,且|A n A n+1|=|A n+1A n+2|,A n≠A n+2,n∈N*,|B n B n+1|=|B n+1B n+2|,B n≠B n+2,n∈N*.(P≠Q表示点P与Q不重合)若d n=|A n B n|,S n为△A n B n B n+1的面积,则()A.{S n}是等差数列B.{}是等差数列C.{d n}是等差数列D.{}是等差数列答案A2.(2014辽宁,9,5分)设等差数列{a n}的公差为d.若数列{}为递减数列,则()A.d>0B.d<0C.a1d>0D.a1d<0答案D3.(2015北京,16,13分)已知等差数列{a n}满足a1+a2=10,a4-a3=2.(1)求{a n}的通项公式;(2)设等比数列{b n}满足b2=a3,b3=a7.问:b6与数列{a n}的第几项相等?解析(1)设等差数列{an}的公差为d.因为a4-a3=2,所以d=2.又因为a1+a2=10,所以2a1+d=10,故a1=4.所以an=4+2(n-1)=2n+2(n=1,2,…).(2)设等比数列{b n}的公比为q.因为b2=a3=8,b3=a7=16,所以q=2,b1=4.所以b6=4×26-1=128.由128=2n+2得n=63.所以b6与数列{an}的第63项相等.4.(2014浙江,19,14分)已知等差数列{a n}的公差d>0.设{a n}的前n项和为S n,a1=1,S2·S3=36.(1)求d及S n;(2)求m,k(m,k∈N*)的值,使得a m+a m+1+a m+2+…+a m+k=65.解析(1)由题意知(2a1+d)(3a1+3d)=36,将a1=1代入上式解得d=2或d=-5.因为d>0,所以d=2.从而an=2n-1,S n=n2(n∈N*).(2)由(1)得a m+a m+1+a m+2+…+a m+k=(2m+k-1)(k+1),所以(2m+k-1)(k+1)=65.由m,k∈N*知2m+k-1≥k+1>1,故-所以考点二等差数列的性质1.(2014重庆,2,5分)在等差数列{a n}中,a1=2,a3+a5=10,则a7=()A.5B.8C.10D.14答案B2.(2015陕西,13,5分)中位数为1010的一组数构成等差数列,其末项为2015,则该数列的首项为. 答案5考点三等差数列的前n项和1.(2017浙江,6,4分)已知等差数列{a n}的公差为d,前n项和为S n,则“d>0”是“S4+S6>2S5”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件答案C2.(2015安徽,13,5分)已知数列{a n}中,a1=1,a n=a n-1+(n≥2),则数列{a n}的前9项和等于.答案27C组教师专用题组考点一等差数列的定义及通项公式1.(2013安徽,7,5分)设S n为等差数列{a n}的前n项和,S8=4a3,a7=-2,则a9=()A.-6B.-4C.-2D.2答案A2.(2014陕西,14,5分)已知f(x)=,x≥0,若f1(x)=f(x),f n+1(x)=f(f n(x)),n∈N+,则f2014(x)的表达式为.答案f2014(x)=3.(2015福建,17,12分)等差数列{a n}中,a2=4,a4+a7=15.(1)求数列{a n}的通项公式;(2)设b n=-+n,求b1+b2+b3+…+b10的值.解析(1)设等差数列{an}的公差为d.由已知得解得所以an=a1+(n-1)d=n+2.(2)由(1)可得b n=2n+n.所以b1+b2+b3+…+b10=(2+1)+(22+2)+(23+3)+…+(210+10)=(2+22+23+...+210)+(1+2+3+ (10)=--+=(211-2)+55=211+53=2101.4.(2013课标Ⅰ,17,12分)已知等差数列{a n}的前n项和S n满足S3=0,S5=-5.(1)求{a n}的通项公式;(2)求数列-的前n项和.解析(1)设{an}的公差为d,则S n=na1+- d.由已知可得-解得a1=1,d=-1.故{an}的通项公式为a n=2-n.(2)由(1)知-=--=---,从而数列-的前n项和为--+-+…+---=-.5.(2013江西,17,12分)在△ABC中,角A,B,C的对边分别为a,b,c,已知sin Asin B+sin Bsin C+cos2B=1.(1)求证:a,b,c成等差数列;(2)若C=,求的值.解析(1)证明:由已知得sin Asin B+sin Bsin C=2sin2B,因为sin B≠0,所以sin A+sin C=2sin B,由正弦定理,有a+c=2b,即a,b,c成等差数列.(2)由C=,c=2b-a及余弦定理得(2b-a)2=a2+b2+ab,即有5ab-3b2=0,所以=.考点二 等差数列的性质(2013辽宁,4,5分)下面是关于公差d>0的等差数列{a n }的四个命题: p 1:数列{a n }是递增数列; p 2:数列{na n }是递增数列; p 3:数列是递增数列; p 4:数列{a n +3nd}是递增数列.其中的真命题为( ) A.p 1,p 2 B.p 3,p 4 C.p 2,p 3 D.p 1,p 4 答案 D考点三 等差数列的前n 项和1.(2014天津,5,5分)设{a n }是首项为a 1,公差为-1的等差数列,S n 为其前n 项和.若S 1,S 2,S 4成等比数列,则a 1=( ) A.2B.-2C.D.-答案 D2.(2014重庆,16,13分)已知{a n }是首项为1,公差为2的等差数列,S n 表示{a n }的前n 项和.(1)求a n 及S n ;(2)设{b n }是首项为2的等比数列,公比q 满足q 2-(a 4+1)q+S 4=0.求{b n }的通项公式及其前n 项和T n . 解析 (1)因为{a n }是首项a 1=1,公差d=2的等差数列,所以a n =a 1+(n-1)d=2n-1. 故S n =1+3+…+(2n-1)== -=n 2. (2)由(1)得a 4=7,S 4=16.因为q 2-(a 4+1)q+S 4=0,即q 2-8q+16=0,所以(q-4)2=0,从而q=4. 又因为b 1=2,{b n }是公比q=4的等比数列,所以b n =b 1q n-1=2×4n-1=22n-1. 从而{b n }的前n 项和T n =- -= (4n-1). 3.(2013浙江,19,14分)在公差为d 的等差数列{a n }中,已知a 1=10,且a 1,2a 2+2,5a 3成等比数列.(1)求d,a n ;(2)若d<0,求|a 1|+|a 2|+|a 3|+…+|a n |.解析 (1)由题意得5a 3·a 1=(2a 2+2)2,即d 2-3d-4=0.故d=-1或d=4.所以a n =-n+11,n ∈N *或a n =4n+6,n ∈N *.(2)设数列{a n }的前n 项和为S n .因为d<0,由(1)得d=-1,a n =-n+11,所以当n ≤11时, |a 1|+|a 2|+|a 3|+…+|a n |=S n =-n 2+n.当n ≥12时,|a 1|+|a 2|+|a 3|+…+|a n |=-S n +2S 11=n 2-n+110. 综上所述,|a 1|+|a 2|+|a 3|+…+|a n | = --【三年模拟】时间:45分钟 分值:60分一、选择题(每小题5分,共35分)1.(2018河南开封定位考试,5)等差数列{a n }的前n 项和为S n ,且a 1+a 5=10,S 4=16,则数列{a n }的公差为( ) A.1 B.2 C.3 D.4 答案 B2.(2017辽宁六校协作体期中,8)已知等差数列{a n},{b n}的前n项和分别为S n,T n,若对于任意的正整数n,都有=-,则-+=()A. B. C. D.答案A3.(2018云南玉溪模拟,9)若{a n}是等差数列,公差d<0,a1>0,且a2013(a2012+a2013)<0,则使数列{a n}的前n项和S n>0成立的最大正整数n是()A.4027B.4026C.4025D.4024答案D4.(2017广东惠州二调,7)设S n是等差数列{a n}的前n项和,若=,则=()A.1B.-1C.2D.答案A5.(2019届河北唐山模拟,8)已知数列{a n}的前n项和S n=2+λa n,且a1=1,则S5=()A.27B.C.D.31答案C6.(2019届浙江温州模拟,9)已知{a n},{b n}均为等差数列,且a2=4,a4=6,b3=3,b7=9,由{a n},{b n}的公共项组成新数列{c n},则c10=()A.18B.24C.30D.36答案C7.(2019届河北唐山模拟,6)设{a n}是任意等差数列,它的前n项和、前2n项和与前4n项和分别为X,Y,Z,则下列等式中恒成立的是()A.2X+Z=3YB.4X+Z=4YC.2X+3Z=7YD.8X+Z=6Y答案D二、填空题(共5分)8.(2018四川德阳一模,7)我国古代数学名著《张邱建算经》中有“分钱问题”:今有与人钱,初一人与三钱,次一人与四钱,次一人与五钱,以次与之,转多一钱,与讫,还敛聚与均分之,人得一百钱,问人几何?意思是:将钱分给若干人,第一人给3钱,第二人给4钱,第三人给5钱,以此类推,每人比前一人多给1钱,分完后,再把钱收回平均分给各人,结果每人分得100钱,问有多少人?则题中的人数是.答案195三、解答题(共20分)9.(2018广东惠州一调,17)已知等差数列{a n}的公差不为0,前n项和为S n(n∈N*),S5=25,且S1,S2,S4成等比数列.(1)求a n与S n;(2)设b n=,求证:b1+b2+b3+…+b n<1.解析(1)设等差数列{a}的公差为d(d≠0),n则由S=25可得a3=5,即a1+2d=5①,5又S,S2,S4成等比数列,且S1=a1,S2=2a1+d,S4=4a1+6d,1所以(2a+d)2=a1(4a1+6d),整理得2a1d=d2,1因为d≠0,所以d=2a②,1联立①②,解得a=1,d=2,1所以a=1+2(n-1)=2n-1,S n=-=n2.n(2)证明:由(1)得b n==-,所以b1+b2+b3+…+b n=-+-+…+-=1-.又∵n∈N*,∴1-<1.∴b1+b2+b3+…+b n<1.10.(2019届河北曲周模拟,17)等差数列{a n}中,公差d<0,a2+a6=-8,a3a5=7.(1)求{a n}的通项公式;(2)记T n为数列{b n}前n项的和,其中b n=|a n|,n∈N*,若T n≥1464,求n的最小值.解析(1)∵等差数列{an}中,公差d<0,a2+a6=-8,∴a2+a6=a3+a5=-8,又∵a3a5=7,∴a3,a5是一元二次方程x2+8x+7=0的两个根,且a3>a5,解方程x2+8x+7=0,得a3=-1,a5=-7,∴--解得a1=5,d=-3.∴a n=5+(n-1)×(-3)=-3n+8.(2)由(1)知{a n}的前n项和S n=5n+-×(-3)=-n2+n.∵b n=|a n|,∴b1=5,b2=2,b3=|-1|=1,b4=|-4|=4,当n≥3时,bn=|a n|=3n-8.当n<3时,T1=5,T2=7;当n≥3时,Tn=-S n+2S2=-+14.∵T n≥1464,∴T n=-+14≥1464,即(3n-100)(n+29)≥0,解得n≥,∴n的最小值为34.。

课时规范练A组基础对点练1．已知A，B两地间的距离为10 km，B，C两地间的距离为20 km ，现测得∠AB＝120°，则A，C两地间的距离为()A．10 km B．10 3 kmC．10 5 km D．107 km解析：如图所示，由余弦定理可得：AC2＝100＋400－2×10×20×cos 120°＝700，∴AC＝107(km)．答案：D2.(2019·银川一中月考)如图，设A，B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离为50 m，∠ACB＝45°，∠CAB＝105°后，就可以计算出A，B两点的距离为()A．50 2 m B．50 3 mC．25 2 m D.2522m解析：由正弦定理得ABsin∠ACB＝ACsin B，∴AB＝AC·sin∠ACBsin B＝50×2212＝502，故A，B两点的距离为50 2 m.答案：A3．某位居民站在离地20 m高的阳台上观测到对面小高层房顶的仰角为60°，小高层底部的俯角为45°，那么这栋小高层的高度为()A．20(1＋33)m B．20(1＋3)mC．10(2＋6)m D．20(2＋6)m解析：如图，设AB 为阳台的高度，CD 为小高层的高度，AE 为水平线．由题意知AB ＝20 m ，∠DAE ＝45°，∠CAE ＝60°，故DE ＝20 m ，CE ＝20 3 m ．所以CD ＝20(1＋3)m.故选B. 答案：B4．某船开始看见灯塔在南偏东30°方向，后来船沿南偏东60°的方向航行15 km 后，看见灯塔在正西方向，则这时船与灯塔的距离是( ) A ．5 km B ．10 km C ．5 3 kmD ．5 2 km解析：作出示意图(如图)，点A 为该船开始的位置，点B 为灯塔的位置，点C 为该船后来的位置，所以在△ABC 中， 有∠BAC ＝60°－30°＝30°，B ＝120°，AC ＝15， 由正弦定理，得15sin 120°＝BC sin 30°， 即BC ＝15×1232＝53，即这时船与灯塔的距离是5 3km. 答案：C5．为绘制海底地貌图，测量海底两点C ，D 之间的距离， 海底探测仪沿水平方向在A ，B 两点进行测量，A ，B ， C ，D 在同一个铅垂平面内，海底探测仪测得∠BAC ＝30°，∠DAC ＝45°，∠ABD ＝45°，∠DBC ＝75°， A ，B 两点的距离为 3 海里，则C ，D 之间的距 离为( ) A. 5 海里 B ．2 海里 C.⎝⎛⎭⎪⎫6＋22 海里 D ．(2＋1) 海里解析：∠ADB ＝180°－30°－45°－45°＝60°，在△ABD 中，由正弦定理，得BD ＝ 3 sin 75°sin 60°＝6＋22， 在△ABC 中，∠ACB ＝180°－30°－45°－75°＝30°， 所以BC ＝BA ＝3，在△BCD 中，由余弦定理，得CD 2＝BC 2＋BD 2－2BC ·BD cos ∠ DBC ＝3＋⎝ ⎛⎭⎪⎫6＋222－2×3×6＋22×6－24＝5，所以CD ＝ 5.答案：A6．台风中心从A 地以每小时20千米的速度向东北方向移动，离台风中心30千米内的地区为危险区，城市B 在A 的正东40千米处，B 城市处于危险区内的 持续时间为( ) A ．0.5小时 B ．1小时 C ．1.5小时D ．2小时解析：根据题意画出相应的图形，如图所示．BE ＝BF ＝30 km ，△ABD 为等腰直角三角形且AB ＝40 km ，由勾股定理得AD ＝BD ＝20 2 km ，由BD ⊥AD ， 可得ED ＝DF ，在Rt △BED 中，由勾股定理得ED ＝BE 2－BD 2＝10 km ，所以EF ＝2ED ＝20 km ，因此B 市处于危险区内的时间为20÷20＝1(h)． 答案：B7．如图，一艘船上午9：30在A 处测得灯塔S 在它的北偏东30°处，之后它继续沿正北方向匀速航行，上午10：00到达B 处，此时又测得灯塔S 在它的北偏东75°处，且与它相距8 2 n mile.此船的航速是________ n mile/h. 解析：设航速为v n mile/h ，在△ABS 中，AB ＝12v ，BS ＝8 2 n mile ，∠BSA ＝45°，由正弦定理，得82sin 30°＝12v sin 45°，所以v ＝32. 答案：328.(2019·西安模拟)游客从某旅游景区的景点A 处至景点C 处有两条线路．线路1是从A 沿直线步行到C ，线路2是先从A 沿直线步行到景点B 处，然后从B 沿直线步行到C .现有甲、乙两位游客从A 处同时出发匀速步行，甲的速度是乙的速度的119倍，甲走线路2，乙走线路1，最后他们同时到达C 处．经测量，AB ＝1 040 m ，BC ＝500 m ，则sin ∠BAC 等于__________． 解析：依题意，设乙的速度为x m/s ， 则甲的速度为119x m/s ， 因为AB ＝1 040，BC ＝500，所以AC x ＝1 040＋500119x ，解得：AC ＝1 260，在△ABC 中由余弦定理可知 cos ∠BAC ＝AB 2＋AC 2－BC 22AB ·AC＝1 0402＋1 2602－50022×1 040×1 260＝8491＝1213，所以sin ∠BAC ＝1－cos 2∠BAC ＝1－⎝ ⎛⎭⎪⎫12132＝513. 答案：5139.如图，在△ABC 中，∠ABC ＝90°，AB ＝3，BC ＝1，P 为△ABC 内一点，∠BPC ＝90°.(1)若PB ＝12，求P A ；(2)若∠APB ＝150°，求tan ∠PBA .解析：(1)由已知得∠PBC ＝60°，所以∠PBA ＝30°.在△PBA 中，由余弦定理得P A 2＝3＋14－2×3×12cos 30°＝74.故P A ＝72.(2)设∠PBA ＝α，由已知得PB ＝sin α. 在△PBA 中，由正弦定理得，3sin 150°＝sin αsin (30°－α)，化简得3cos α＝4sin α. 所以tan α＝34，即tan ∠PBA ＝34.10．(2019·宜宾模拟)一艘海轮从A 出发，沿北偏东75°的方向航行(23－2)n mil到达海岛B ，然后从B 出发，沿北偏东15°的方向航行4 n mile 到达海岛C .(1)求AC 的长；(2)如果下次航行直接从A 出发到达C ，求∠CAB 的大小． 解析：(1)由题意，在△ABC 中，∠ABC ＝180°－75°＋15°＝120°，AB ＝23－2，BC ＝4， 根据余弦定理得AC 2＝AB 2＋BC 2－2AB ×BC ×cos ∠ABC ＝(23－2)2＋42＋(23－2)×4＝24， 所以AC ＝2 6. (2)根据正弦定理得， sin ∠BAC ＝4×3226＝22，所以∠CAB＝45°.B组能力提升练11．如图，某海上缉私小分队驾驶缉私艇以40 km/h的速度由A处出发，沿北偏东60°方向进行海上巡逻，当航行半小时到达B处时，发现北偏西45°方向有一艘船C，若船C位于A的北偏东30°方向上，则缉私艇所在的B处与船C的距离是()A．5(6＋2) km B．5(6－2) kmC．10(6－2) km D．10(6＋2) km解析：由题意知∠BAC＝60°－30°＝30°，∠CBA＝30°＋45°＝75°，所以∠ACB＝180°－30°－75°＝75°，故AC＝AB，因为AB＝40×12＝20，所以AC＝AB＝20.在△ABC中，由余弦定理得：BC2＝AC2＋AB2－2AC·AB cos∠CAB＝400＋400－2×20×20cos 30°＝400(2－3)，故BC＝400(2－3)＝200(3－1)2＝10(6－2)．答案：C12．(2019·广州模拟)如图，在海岸线上相距26千米的A，C两地分别测得小岛B在A的北偏西α方向，在C的北偏西π2－α方向，且cos α＝63，则B，C之间的距离是()A．303千米B．30千米C．123千米D．12千米解析：依题意得，AC ＝26，sin ∠BAC ＝sin ⎝ ⎛⎭⎪⎫π2＋α＝cos α＝63， sin B ＝sin ⎝ ⎛⎭⎪⎫π2－2α＝cos 2α＝2cos 2α－1＝13，在△ABC 中，由正弦定理得，BC ＝AC sin ∠BAC sin B ＝26×6313＝12，则B 与C 之间的距离是12千米． 答案：D13．(2019·长沙模拟)地面上有两座塔AB ，CD ，相距120米，一人分别在两塔底测得一塔顶的仰角是另一塔顶仰角的2倍，在两 塔底连线的中点O 处测得塔顶的仰角互为余角，则两塔的高 度分别为( ) A ．50米，100米 B ．40米，90米 C ．40米，50米D ．30米，40米解析：设高塔高H ，矮塔高h ，在矮塔下望高塔仰角为α，在 O 点望高塔仰角为β.分别在两塔底部测得一塔顶仰角是另一塔顶仰角的两倍，所以在高塔下望矮塔仰角为α2，即tan α＝H 120，tan α2＝h120， 根据倍角公式有H120＝2×h 1201－⎝ ⎛⎭⎪⎫h 1202①， 在塔底连线的中点O 测得两塔顶的仰角互为余角，所以在O 点望矮塔仰角为π2－β，即tan β＝H 60，tan ⎝ ⎛⎭⎪⎫π2－β＝h60，根据诱导公式有H 60＝60h ②， 联立①②得H ＝90，h ＝40. 即两座塔的高度为40米，90米．答案：B14.(2019·衡水模拟)如图，为了测量河对岸电视塔CD的高度，小王在点A处测得塔顶D的仰角为30°，塔底C与A的连线同河岸成15°角，小王向前走了1 200 m到达M处，测得塔底C与M的连线同河岸成60°角，则电视塔CD的高度为__________．解析：在△ACM中，∠MCA＝60°－15°＝45°，∠AMC＝180°－60°＝120°，由正弦定理得AMsin∠MCA ＝ACsin∠AMC，即1 20022＝AC32，解得AC＝600 6.在Rt△ACD中，因为tan∠DAC＝DCAC ＝33，所以DC＝AC tan∠DAC＝6006×33＝6002(m)．答案：600 2 m15．(2019·遂宁模拟)海轮“和谐号”从A处以每小时21海里的速度出发，海轮“奋斗号”在A处北偏东45°的方向，且与A 相距10海里的C处，沿北偏东105°的方向以每小时9海里的速度行驶，则海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为__________小时．解析：设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x小时，如图，则由已知得△ABC中，AC＝10，AB＝21x，BC＝9x，∠ACB＝120°，由余弦定理得：(21x)2＝100＋(9x)2－2×10×9x×cos 120°，整理，得36x2－9x－10＝0，解得x＝23或x＝－512(舍)．所以海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为23小时．答案：2 316．如图，现要在一块半径为1 m ，圆心角为π3的扇形白铁片AOB 上剪出一个平行四边形MNPQ ，使点P 在弧AB 上，点Q 在OA 上，点M ，N 在OB 上，设∠BOP ＝θ，平行四边形MNPQ 的面积为S .(1)求S 关于θ的函数关系式． (2)求S 的最大值及相应的θ角．解析：(1)分别过P ，Q 作PD ⊥OB 于点D ，QE ⊥OB 于点E ，则四边形QEDP 为矩形．由扇形半径为1 m ， 得PD ＝sin θ，OD ＝cos θ. 在Rt △OEQ 中， OE ＝33QE ＝33PD ，MN ＝QP ＝DE ＝OD －OE ＝cos θ－33sin θ，S ＝MN ·PD ＝⎝ ⎛⎭⎪⎫cos θ－33sin θ·sin θ＝sin θcos θ－33sin 2θ，θ∈⎝ ⎛⎭⎪⎫0，π3.(2)S ＝12sin 2θ－36(1－cos 2θ)＝12sin 2θ＋36cos 2θ－36＝33sin ⎝ ⎛⎭⎪⎫2θ＋π6－36，因为θ∈⎝ ⎛⎭⎪⎫0，π3，所以2θ＋π6∈⎝ ⎛⎭⎪⎫π6，5π6，sin ⎝ ⎛⎭⎪⎫2θ＋π6∈⎝ ⎛⎦⎥⎤12，1. 当θ＝π6时，S max ＝36(m 2)．。