二叉树课程设计毕业设计(论文)

算法与数据结构课程设计报告设计题目：二叉排序树与平衡二叉树专业通信工程班级学生学号指导教师起止时间2015.12.28-2015.12.31湖北师范学院2015-2016年上学期一、需求分析1、设计任务用顺序存储结构实现二叉排序树的有关操作。

2、要求用顺序表（一维数组）作存储结构(1) 以回车（“\n”）为输入结束标志，输入数列L，生成一棵二叉树序列T；(2) 对二叉排序树T作中序遍历，输出结果；(3)计算二叉排序树T查找成功的平均查找长度，输出结果；(4)输入元素X，查找二叉排序树T，若存在含X的结点，则删除该结点，并作中序遍历（执行操作2）；否则输出信息“无X”；3、分析(1) 建立二叉排序树，首先用一个一维数组记录下读入的数据，然后再用边查找边插入的方式将数据一一对应放在完全二叉树相应的位置，为空的树结点用“0” 补齐。

(2) 中序遍历二叉树也采用递归函数的方式，先访问左子树2i,然后访问根结点i,最后访问右子树2i+1.先向左走到底再层层返回，直至所有的结点都被访问完毕。

(3) 计算二叉排序树的平均查找长度时，采用类似中序遍历的递归方式，用s记录总查找长度，j记录每个结点的查找长度，s置初值为0，采用累加的方式最终得到总查找长度s。

平均查找长度就等于s/i(i为树中结点的总个数)。

(4) 删除二叉排序树中某个结点，采用边查找边插入的方式，类似重新建立一个一维数组作为存储新树的空间。

将原数组中的数据一个一个的插入树中，若遇到需要删除的结点则不执行插入操作。

(5) 分别编写功能函数和主测试函数，随机输入二叉树序列进行验证。

二、概要设计1、数据结构程序中的数据采用“树形结构”作为其数据结构。

本题采用的是“二叉排序树”。

2、数据类型定义顺序表是用一组地址连续的存储单元依次自上而下、自左而右存储完全二插树上的结点元素，即将完全二叉树上编号为i的结点元素存储在如上定义的一维数组中下标为i-1的分量中。

二叉树后序非递归遍历多核程序设计摘要：遍历二叉树是二叉树一种重要的运算，遍历的方法也有很多种，这里我主要采用的遍历方式是二叉树后序非递归遍历，在遍历的过程中先遍历左子树在遍历右子树，最后遍历根结点。

与单核环境下串行的速度相比，在多核中并行运行程序所花费的时间有所缩减，速度也有所提高。

所以在我完成的串行程序中添加了循环并行化指导语句，实现了程序的并行化。

这样有利于提高二叉树后序非递归遍历的运行速度，达到让程序运行花费更短时间的目的。

除此之外，还提高了CPU的利用率，缩短了循环所需要的时间。

关键词多核，循环并行化，OpenMP，二叉树后序遍历，加速比。

引言：OpenMP的规范由SGI发起，它是一种面向共享内存以及分布式共享内存的多处理器多线程并行编程语言。

OpenMP是一种共享内存并行的应用程序编程接口。

所有的处理器都被连接到一个共享的内存单元上，处理器在访问内存的时候使用的是相同的内存编址空间。

由于内存是共享的，因此，某一处理器写入内存的数据会立刻被其它处理器访问到。

OpenMP的重要性在于，它能够为编写多线程程序提供一种简单的方法，而无需程序员进行复杂的线程创建、同步、负载平衡和销毁工作。

循环并行化是使用OpenMP并行化程序的最重要部分。

由于大量科学计算程序将很大一部分的的时间用在处理循环计算上，而对于循环并行化处理来说，这一部分的应用非常关键，因此循环并行化在OpenMP应用程序中是一个相对独立且非常重要的组成部分。

本文中通过实现二叉树非递归后序遍历的循环并行化，与并行之前的串行程序进行比较，分别求出串并行时间，并得出加速比。

理论分析后序遍历是二叉树遍历的一种。

后序遍历指在访问根结点、遍历左子树与遍历右子树三者中，首先遍历左子树，然后遍历右子树，最后遍历访问根结点，在遍历左、右子树时，仍然先遍历左子树，然后遍历右子树，最后遍历根结点。

后序遍历有递归算法和非递归算法两种。

而在本文中我采用的是二叉树后序的非递归方法。

长春建筑学院《数据结构》课程设计（论文）基于二叉树遍历系统设计与实现Binary tree traversal System Design and Implementation年级:学号:姓名:专业:指导老师:二零一三年十二月摘要针对现实世界中许多关系复杂的数据，如人类社会的家谱，各种社会组织机构,博弈交通等复杂事物或过程以及客观世界中广泛存在的具有分支关系或层次特性的对象．如操作系统的文件构成、人工智能和算法分析的模型表示以及数据库系统的信息组织形式等，用线性结构难以把其中的逻辑关系表达出来，必须借助于数和图这样的非线性结构，因此在以模拟客观世界问题，解决客观世界问题为主要任务的计算机领域中树型结构是信息的一种重要组织形式，树有着广泛应用。

在树型结构的应用中又以二叉树最为常用。

二叉树是一种非常重要的非线性结构，所描述的数据有明显的层次关系，其中的每个元素只有一个前驱，二叉树是最为常用的数据结构，它的实际应用非常广泛，二叉树的遍历方式有三种，前序遍历，中序遍历，后序遍历，先序遍历的顺序为：NLR 先根结点，然后左子树，右子树；中序遍历顺序为；LNR先左子树，然后根结点，右子树；后序遍历顺序为：LRN先左子树，然后右子树，根结点。

由前序和中序遍历，有中序和后序遍历序列可以唯一确定一棵二叉树。

对于给几个数据的排序或在已知的几个数据中进行查找，二叉树均能提供一种十分有效的方法，比如在查找问题上，任何借助于比较法查找长度为Ⅳ的一个序表的算法，都可以表示成一株二叉树。

反之，任何二叉树都对应一个查找有序表的有效方法根据树的数学理论，对于算法分析的某些最有启发性的应用，是与给出用于计算各种类型中不同树的数目的公式有关的。

本文对二叉树以及二叉树的各种功能做介绍以及写出一些基本的程序，让读者对二叉树的理解有更好的效果。

关键词：二叉树；左子树；右子树AbstractIn many real world of complex data, such as the human society family, social organization, widespread game traffic complex thing or process and the objective world with a branch or level characteristics of the object. If the operating system file analysis, artificial intelligence and algorithm model representation and database information system the form of organization, with a linear structure to express the logic relationship among them, must depend on the number and the diagram of such nonlinear structure, so in order to simulate the objective world, solve problems as the main task of the computer field in the tree structure is an important organization form of information, the tree has a broad application. In the application of tree structure in which the two fork tree is the most commonly used.Two binary tree is a kind of very important nonlinear structure, hiberarchy description of the data, where each element is only a precursor, two fork tree is the most commonly used data structure, its application is very extensive, there are three kinds of two binary tree traversal, preorder traversal, in the traversal, postorder traversal, preorder traversal sequence: NLR to the root node, and then the left subtree, right subtree; in order traversal sequence; LNR before the left sub tree, then the root node, the right subtree; after the traversal order: LRN first and then the left subtree, right subtree, root node. By preorder traversal and traversal, with the order and post order traversal sequence can be uniquely identified a two binary tree.For several data sorting or searching in several data known, two fork tree can provide a very effective method, such as search problems, any by the comparison method to find the length of a sequential algorithm of Table IV, can be expressed as a two fork tree. Conversely, any two fork tree corresponds to an effective method to find the ordered list according to the mathematical theory of tree, for some algorithm analysis of the application of heuristic, is given for the number and different types of tree calculation formula.Various functions of two binary tree and binary tree in this paper two introduces and write some of the basic procedures, to allow readers to understand the two fork tree has a better effect.Keywords:Two tree; the left subtree; right subtree目录摘要 (I)ABSTRACT (Ⅱ)第1章绪论 ................................................................................................................ - 1 -1.1设计目的 (1)1.2设计内容 (1)1.3设计要求 (1)1.4设计思想 (2)1.5系统模块划分 (2)1.6主要功能模块设计 (2)第2章系统总体设计 (3)2.1基本理论 (3)2.2概要设计 (3)第3章详细设计 (4)3.1建立二叉树 (4)3.2二叉树的层次遍历和中序遍历 (4)3.3求二叉树的深度 (7)3.4将二叉树中所有结点的左右子树相互交换 (7)3.5求二叉树中叶子结点的数目 (9)第4章流程分析图 (11)4.1流程图 (11)4.2主要功能模块设计 (11)4.3模块设计 (12)4.4函数主要调用关系图 (13)第5章系统测试 (14)5.1调试分析 (14)5.2实验结果 (15)结论 (17)致谢 (18)参考文献 (18)第1章绪论引言：树型结构是一类重要的非线性数据结构，其中一树和二叉树最重要。

目录1 问题描述 (1)2 需求分析 (1)3 概要设计 (1)3．1模块划分……………………………………………………….错误!未定义书签。

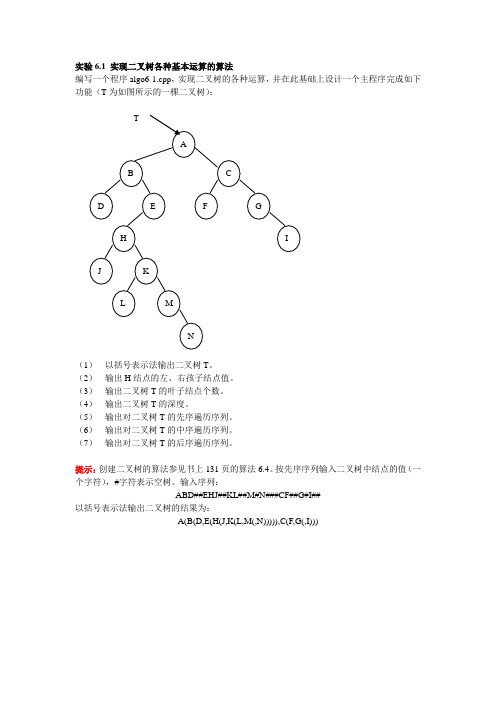
4 详细设计.................................................................................... (6)4．1主要模块流程图 (7)4．2 数据类型的定义 (8)4．3 主要模块的算法描述 (8)5 测试分析 (14)6 课程设计总结 (17)参考文献 (18)附录（源程序清单） (19)1 问题描述建立一棵二叉树；再以广义表表示法输出这棵二叉树；然后对该树进行先序、中序、后序遍历及层次遍历。

要求：（1）采用二叉链表存储二叉树；（2）先序、中序、后序遍历设计非递归算法。

2 需求分析二叉树一种数据结构，用于保存和处理树状的数据，比如家谱。

他的应用极为广泛，因为根据数据结构的理论，任何复杂的树够可以转换为二叉中并进行处理，二叉树在排序、查找、大规模数据索引方面有很多很多应用。

而且二叉树排序是简单算法排序中速度最快的。

在二叉树的一些应用中，常常要求在树中查找具有某种特征的节点，或者对树中全部节点逐一进行某种处理。

这就提出了遍历二叉树。

根据遍历的方向的选择，就有了前序遍历，中序遍历和后序遍历以及层次遍历二叉树。

因此掌握二叉树的各种遍历二叉树算法非常重要，而且高效的遍历算法能够节省很多成本。

3 概要设计3．1模块划分本程序包括七个模块：（1）主程序模块void main(){初始化；以广义表表示法输出；建立二叉树；非递归先序遍历二叉树并输出；非递归中序遍历二叉树并输出；非递归后序遍历二叉树并输出；层次遍历二叉树并输出；}（2）以广义表表示法输出——实现对二叉树的输出（3）二叉树建立模块——建立一个二叉树并对二叉树进行初始化（4）非递归先序遍历模块——实现对二叉树的递归先序遍历并输出（5）非递归中序遍历模块——实现对二叉树的递归中序遍历并输出（6）非递归后序遍历模块——实现对二叉树的递归后序遍历并输出（7）层次遍历模块——实现对二叉树的层次遍历并输出4 详细设计4．1主要模块流程图主流程图建立一棵二叉树以广义表表示法输出一棵二叉树非递归先序遍历非递归中序遍历非递归后序遍历层次遍历4．2数据类型的定义（1）二叉树的二叉链表存储类型typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;} BiTNode,*BiTree;（2）栈类型的定义typedef struct SqStack/*定义一个顺序栈*/{BiTNode *base;BiTNode *top;int stacksize;}SqStack;void InitStack(SqStack *S)/*栈的初始化*/{S->base=(BiTNode*)malloc(STACK_INIT_SIZE*sizeof(BiTNode));S->top=S->base;S->stacksize=STACK_INIT_SIZE;}void Push(SqStack *S,BiTNode e)/*入栈算法*/{if(S->top-S->base>=S->stacksize){S->base=(BiTNode*)realloc(S->base,(S->stacksize+STACKINCREMENT)*sizeof(BiTNode));S->top=S->base+S->stacksize;S->stacksize+=STACKINCREMENT;}*(S->top)=e;S->top++;}BiTNode Pop(SqStack *S)/*出栈算法*/{S->top --;return *S->top;}int StackEmpty(SqStack *S)/*判栈空*/{if(S->top == S->base )return 1;elsereturn 0;}4．3主要模块的算法描述（1）主函数void main(){BiTree Ta;int a=1;printf("请创建树\n");Ta=CreateBiTree();printf("广义表表示法输出二叉树\n");printfBTree(Ta);printf("\n");printf(" 请选择：\n");printf(" （1）先序遍历\n");printf(" （2）中序遍历\n");printf(" （3）后序遍历\n");printf(" （4）层次遍历\n");printf(" （0）结束程序\n");while(a){scanf("%d",&a);if(a==1){（2）建立二叉树BiTree CreateBiTree()/*以二叉链表的存储方式建立一棵二叉树*/ {char p;BiTree T;scanf("%c",&p);if(p=='#')T=NULL;else{T=(BiTNode *)malloc(sizeof(BiTNode));T->data=p;T->lchild=CreateBiTree();T->rchild=CreateBiTree();}return (T);}（3）用广义表表示法输出二叉树void printfbitree(t)/*用广义表表示法输出二叉树*/{if(t!=NULL){printf("%c",t->data);if(t->lchild!=NULL||t->rchild!=NULL){printf("(");printfbitree(t->lchild);if(t->rchild!=NULL)printf(",");printfbirree(t->rchild);printf(")");}}}（4）非递归先序遍历二叉树void PreOrder(BiTree T)/*非递归先序遍历二叉树*/ {SqStack S;BiTree p=T;InitStack(&S);if(p)Push(&S,*p);while(!StackEmpty(&S)){p=(BiTNode *)malloc(sizeof(BiTNode));*p=Pop(&S);printf("%c",p->data);if(p->rchild)Push(&S,*p->rchild);if(p->lchild)Push(&S,*p->lchild);}}（5）非递归中序遍历二叉树void InOrder(BiTree T)/* 非递归中序遍历二叉树*/ {SqStack S;BiTree p=T;InitStack(&S);while(p||!StackEmpty(&S)){if(p){Push(&S,*p);p=p->lchild;}else{p=(BiTNode *)malloc(sizeof(BiTNode));*p=Pop(&S);printf("%c",p->data);p=p->rchild;}}}（6）非递归后序遍历二叉树void PostOrder(BiTree T)/ *非递归后序遍历二叉树*/ SqStack S;BiTNode p, *l, *r;InitStack(&S);Push(&S, *T);while(!StackEmpty(&S)){p = Pop(&S);l = p.lchild;r = p.rchild;if (l == NULL && r == NULL){printf("%c", p.data);}else{p.lchild = NULL;p.rchild = NULL;Push(&S, p);if (r != NULL) Push(&S, *r);if (l != NULL) Push(&S, *l);}}}（7）层次遍历void LevelOrderTraverse(BiTree T) /*层序遍历*/ {BiTree Q[STACK_INIT_SIZE];int front=0,rear=0;BiTree p;if(T){ //根结点入队Q[rear]=T;rear=(rear+1)%STACK_INIT_SIZE;}while(front!=rear){p=Q[front]; //队头元素出队front=(front+1)%STACK_INIT_SIZE;printf("%c",p->data);if(p->lchild){ //左孩子不为空，入队Q[rear]=p->lchild;rear=(rear+1)%STACK_INIT_SIZE;}if(p->rchild){ //右孩子不为空，入队Q[rear]=p->rchild;rear=(rear+1)%STACK_INIT_SIZE;}}}5 测试分析6 课程设计总结通过这次课程设计使我充分的理解了从建立二叉树到输出二叉树再遍历二叉树的基本原理与算法，尤其是深刻的学习了二叉树遍历的非递归实现的算法。

数据结构课程设计课程名称：平衡二叉树的生成院系：信息工程学院年级专业：10级计科学号：学生姓名：指导教师：开题时间： 2010 年 12 月 01 日完成时间： 2010 年 12 月 31 日信息工程学院X X X X X X X数据结构课程设计成绩评定表院系：信息工程学院年级专业：学号：姓名：摘要本篇论文系计科专业10年末课程设计论文，按照相应要求写作而成。

主要讨论的是平衡二叉树的生成问题，借助本程序可以由用户输入数值，并生成平衡二叉树，并可以对数据进行方便的修改和删除添加，任意插入或删除一个结点后仍然要求任然构成平衡二叉树，并按中序遍历输出这棵平衡二叉树。

·本论文共由五个章构成，每个内容独立成章，各章下设相应子章节。

各个章节逐渐递进，分别是：第一章：需求分析第二章系统设计第三章编码第四章测试第五章维护本论文特点：1.论述清楚，目录详尽，可以方便的查询相应章节，方便使用。

2.图文结合，几乎没一个子程序模块都有相应的流程图与之对应，有利于读者理解每个子程序的设计思路。

3.模块分化清晰，每个模块独立成节，又彼此联系，深化了C语言模块化编程的特点。

4.测试模块配合对应的运行截图，真实可信，对读者理解程序的运行情况起到了很大作用。

5.程序清单完整详细，解释详细。

目录第一章需求分析 (1)1.1功能描述­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­11.2数据词典­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­1第二章系统设计 (3)2.1 基本概念介绍­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­3 2.2 总体设计­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­8 2.3 插入结点­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­10 2.4 删除结点­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­11 2.5 中序遍历­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­11 第三章编码 (12)3.1 总体编码­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­123.2 总流程图­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­153.3 以指针T所指结点为根的二叉树作右平衡旋转处理­­­­­­­­­­­­16 第四章测试 (17)4.1 创建二叉树测试­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­174.2 插入结点测试­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­194.3 删除结点测试­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­204.4中序遍历结点测试­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­214.5 先序遍历测试­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­21 第五章维护 (22)5.1维护­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­22第一章需求分析1.1功能描述平衡二叉树是数据结构中一个非常重要的概念。

关于二叉树CAI的论文1、需求分析软件要求能动态的演示二叉树的各种操作，使客户能够真正的理解二叉树的原理，并且能用二叉树解决实际问题。

使用者需要学习的二叉树的功能有遍历（包括前序遍历，中序遍历和后序遍历），线索化（包括前序线索化，中序线索化和后序线索化），查看叶子节点，查找任意节点，插入节点，删除节点，计算树高。

这样，就把对于二叉树的基本操作包含了进去，客户通过这些操作就能准确的把握住二叉树的中心，学会使用二叉树。

综上所述，本软件的需求有一下几点：（1）创建二叉树<1>二叉树使用读入自定义数据文件方式创建二叉树<2>二叉树的节点要有明确的组织方式<3>程序使用先序方式创建二叉树<4>二叉树创建过程要有严格的异常处理措施（2）遍历（先序、中序、后序）遍历过程要有清晰的算法和形象的图形展示，图形展示必须基于真实的二叉树结构（3）线索化（先序、中序、后序）遍历过程要有清晰的算法和形象的图形展示，图形展示必须基于真实的二叉树结构。

（4）查看叶子节点<1>能够清晰的展现叶子节点<2>查找过程要求有动态演示过程（5）查找任意节点<1>查找要有清晰和统一的方式<2>查找过程要有严格的异常处理措施<3>查找过程要求有动态演示过程（6）插入节点<1>插入要有清晰和统一的方式<2>可以向已创建的二叉树中的任意节点插入新节点<3>插入节点过程要求有动态演示（7）删除子树<1>删除要有清晰和统一的方式<2>可以删除已创建的二叉树中的任意子树<3>删除子树过程要求有动态演示过程（8）树的高度<1>求树高过程要求有动态演示过程<2>树的高度能够自适应屏幕（9）异常处理<1>按键不能混乱<2>显示不能混乱<3>运行正常，没有运行错误2、术语定义（1）二叉树：每个节点最多有两个子树的有序树。

二叉排序树课程设计一、课程目标知识目标：1. 学生能够理解二叉排序树的基本概念和性质，掌握其结构特点和应用场景。

2. 学生能够掌握二叉排序树的插入、删除和查找操作，并了解其时间复杂度。

3. 学生能够理解二叉排序树与其他排序算法的关系，了解其在排序中的应用。

技能目标：1. 学生能够运用所学知识，独立构建二叉排序树，并实现插入、删除和查找功能。

2. 学生能够分析二叉排序树的性能，对其进行优化，提高排序效率。

3. 学生能够运用二叉排序树解决实际问题，如数据排序、查找等。

情感态度价值观目标：1. 学生通过学习二叉排序树，培养对数据结构和算法的兴趣，提高解决问题的能力。

2. 学生在学习过程中，学会合作、交流，培养团队精神和共享意识。

3. 学生能够认识到二叉排序树在实际应用中的价值，激发对计算机科学的热爱。

本课程针对高中年级学生，课程性质为理论与实践相结合。

在教学过程中，注重启发式教学，引导学生主动探究、实践。

根据学生特点和教学要求，课程目标具体、可衡量，以便学生和教师能够清晰地了解课程的预期成果。

课程目标的分解为具体的学习成果，为后续的教学设计和评估提供依据。

二、教学内容1. 引入二叉排序树的概念，讲解其定义、性质和基本操作。

- 理解二叉树的基础知识，回顾二叉树的遍历方法。

- 介绍二叉排序树的定义，阐述其特点及应用场景。

- 分析二叉排序树的性质，如二叉排序树的中序遍历结果为有序序列。

2. 探讨二叉排序树的构建、插入、删除和查找操作。

- 讲解二叉排序树的构建方法，学会从无序数据建立二叉排序树。

- 分析插入、删除和查找操作的步骤，理解它们的时间复杂度。

- 举例说明如何利用二叉排序树实现数据排序和查找。

3. 分析二叉排序树的性能及优化方法。

- 探讨二叉排序树的高度、平衡因子等性能指标。

- 介绍常见的优化方法，如平衡二叉树（AVL树）和红黑树。

4. 实践环节：二叉排序树的应用。

- 设计实践题目，让学生动手实现二叉排序树的基本操作。

二叉排序树课程设计一、课程目标知识目标：1. 理解二叉排序树的概念和特点；2. 掌握二叉排序树的插入、删除和查找操作；3. 能够分析二叉排序树的时间复杂度；4. 了解二叉排序树在实际应用中的优势。

技能目标：1. 能够手动构建二叉排序树并进行基本操作；2. 能够运用编程语言实现二叉排序树的基本功能；3. 能够分析并解决二叉排序树相关的问题；4. 能够运用二叉排序树解决实际排序和查找问题。

情感态度价值观目标：1. 培养学生对数据结构和算法的兴趣，激发学习热情；2. 培养学生的逻辑思维能力和问题解决能力；3. 培养学生的团队协作意识，学会与他人共同分析、解决问题；4. 培养学生严谨的科学态度，注重算法的正确性和效率。

课程性质：本课程为计算机科学领域的数据结构与算法课程，旨在让学生掌握二叉排序树的基本概念和操作，提高学生的编程能力和逻辑思维能力。

学生特点：学生具备基本的计算机知识和编程基础，对数据结构有一定了解，但对二叉排序树的认识可能较浅。

教学要求：结合学生特点，采用讲解、实践和讨论相结合的教学方法，使学生在理解二叉排序树理论知识的基础上，能够动手实践并解决实际问题。

在教学过程中，注重培养学生的自主学习能力和团队合作精神，提高学生的综合素质。

通过本课程的学习，使学生能够达到上述课程目标，为后续相关课程打下坚实基础。

二、教学内容1. 引入二叉排序树的概念，阐述其定义、性质和应用场景；- 教材章节：第三章第一节“二叉排序树的定义和性质”2. 讲解二叉排序树的插入、删除、查找操作及其实现方法；- 教材章节：第三章第二节“二叉排序树的操作”3. 分析二叉排序树的性能特点，包括时间复杂度和空间复杂度；- 教材章节：第三章第三节“二叉排序树的性能分析”4. 介绍二叉排序树在实际应用中的优势，如排序、查找等；- 教材章节：第三章第四节“二叉排序树的应用”5. 结合实例，让学生动手实践二叉排序树的构建和操作；- 教材章节：第三章实例分析与编程练习6. 总结二叉排序树的特点和适用场景，与其他排序方法进行对比；- 教材章节：第三章总结与拓展教学进度安排：1. 第1课时：引入二叉排序树的概念、性质和应用场景；2. 第2课时：讲解二叉排序树的插入、删除、查找操作；3. 第3课时：分析二叉排序树的性能特点；4. 第4课时：介绍二叉排序树在实际应用中的优势；5. 第5课时：结合实例，学生动手实践二叉排序树的构建和操作；6. 第6课时：总结二叉排序树，与其他排序方法进行对比。

上机报告班级：070921姓名：张丽娜学号：07092029报告名称：设计一棵二叉树上机时间：2010年10月14号报告时间：2010年10月20号摘要1 实验目的:深入理解二叉树的链式存储结构，灵活运用二叉树的基本函数，掌握二叉树的遍历过程，能够针对递归结构的二叉树进行查询、修 改、删除等操作.2 实验方法：先自行拟定所要设计的二叉树，通过递归函数、字符串比较函数、 指针以及结构体型变量的使用对树中的各个节点进行存储，遍历， 交换，删除等操作。

3 实验结果:先序序列: 1 2 4 8 9 5 3 6 10 7中序序列: 2 4 8 9 5 1 3 6 10 7后序序列: 2 4 8 9 5 3 6 10 7 1层序遍历序列: 1 2 3 4 5 6 7 8 9 10所设计的二叉树二 问题重述：1 2 104 9 8 7 65 3用word绘出所要进行操作的二叉树，编写程序采用凹入法打印该二叉树，编程输出该二叉树的先序、中序、后序以及层次遍历序列。

交换该树的左右子树，同时采用凹入法打印。

最后删除该树的某个节点，以及以该节点为根的子树，并打印删除后的二叉树。

三内容：1 算法描述：①先序遍历:按照先访问根节点，再访问左子树，最后访问右子树的顺序访问二叉树中的所有节点.②中序遍历:按照先访问左子树，再访问根节点，最后访问右子树的顺序访问二叉树中的所有节点.③后序遍历:按照先访问左子树，再访问右子树，最后访问根节点的顺序访问二叉树中的所有节点.三种遍历方法类似于栈的表述。

④删除某个节点:该程序中主要使用了字符串比较函数，判断该节点是否存在于该树，若存在则删除该节点以及它的子树。

⑤层序遍历：层序遍历主要是按照从上到下，从左到右的次序进行访问二叉树的各个节点。

⑥凹入法打印：主要要弄清分层后各节点的关系，调用递归函数即可实现。

⑦交换左右子树:在后序遍历一个树的时候每访问一个节点后加上一个语句——调换这个节点的左右子树。