期末复习之分式

八下期末复习讲义——分式的基本性质及运算一、知识梳理1、一般地，如果A 、B 表示两个整式，并且B 中含有字母，那么代数式A B叫做 。

2、分式的 时，分式有意义；分式的 时，分式的值为0。

3、用具体的数值代替分式中的字母，按照分式的运算关系计算，所得的结果就是 。

4、分式的基本性质：分式的分子和分母都乘（或除以） 的整式，分式的值 。

5、根据分式的基本性质，把一个分式的分子和分母分别除以它们的 ，叫做分式的约分。

6、根据分式的基本性质，把几个异分母的分式化成同分母的分式，叫做分式的 。

7、同分母的分式相加减，分母 ，把分子 ；异分母的分式相加减，先 ， 再 。

8、分式乘分式,用 的积做积的分子，用 的积做积的分母；分式除以分式，把除式的分子、分母颠倒位置后，与被除式相 。

9、分式的加、减、乘、除混合运算的顺序是：先 ，后 ，如果有括号，先进行括号内的运算。

二、基础练习1、下列各式中，24,2),(31,23,2,312---+-x x b a y x m x π，分式有 。

2、当x 时，分式31-+x x 有意义；当x 时，分式32-x x 无意义； 当x 时，分式392--x x 的值为零。

3、填空：（1）b a ab b a 2)( =+； （2）21()a a a c ++= ； （3）()()222x y x y x y+=≠-； 4、若分式1232-a a 的值为负数，则a 的取值范围为 。

5、请你写一个关于x 的分式，使此分式当3=x 时，它的值为2。

6、当2a =-时，求分式43a a +的值；7、约分：12122++-a a a8、计算：（3、4两小题写出最简公分母）（1）4233m m +-- （2）1122a a -+-（3）22222x x xx x +-⋅- （4）2222222x y x xy y x y x y -++⋅+-三、课后练习基础部分A ：1、填空：()b ab a =； 231()3xy x y =；2、化简112---a a ，其结果为（ ） A ．1+a B. 1-a C .a -1 D.1--a 3、化简1xx y x ÷⋅，其结果为（ ） A. 1 B.xy C.x y D.yx4、通分：)2)(1(++a a a ，31a +；5、计算：（1）22494n m nm --－2294m n m n +-； （2）2211x x x +÷-6、化简求值：22121-÷--a a a ，其中1a =。

【典型例题】例1.例2.分析：先化简，再代入求值，化简通分时，把提出“－”号后，看作一个整体。

解：当时，原式例3.分析：本题若通过通分化简是不可能的，利用的方法来解决较好。

解：注：本题创新之处是打破了传统做法，利用总结出的规律拆项的方法使问题有规律又简洁。

例4.化简原式，由，得或，当x＝2时，原式无意义，故舍去。

时，原式例5.解：∵∴∴原式例6.【思考与分析】已知实数a、b满足：ab＝1，要求＋的值，还真有点麻烦，不过若考虑运用分式的基本性质对分式的分子、分母同乘以b，对分式的分子、分母同乘以a，再利用ab＝1代换即可得到同分母的两个分式相加．解：因为ab＝1，所以【小结】有关分式的这种求值，一定要根据分式的结构特点，巧妙地运用分式的基本性质进行恒等变换，使之靠近已知条件，以便充分运用条件.另外，本题还可以设a＝b＝1，使问题快速、准确地获解.例7.【思考与分析】首先看题目给的条件似乎没有必然的联系，但是经过化简含有，可以利用，建立联系解答.【精选易错题】1、且；或；2、解：（1）（2）3、解：原式小结：公式、性质混合应用4、5、【思考与分析】在计算时会感觉要求的式子很长，不知如何下手，仔细观察各个式子的特点巧妙运用平方差公式逐步通分，会得到想要的结果.解：原式＝反思】本题若用常规方法太繁琐，根据题目特点巧用平方差公式，采用分步通分法，从而使运算简便.6、错解：∵，∴当x＋3≠0即x≠－3时，原分式有意义.错解剖析：约去分式的分子、分母的公因式，造成字母的取值范围扩大，因而发生错误.正解：分母x2＋x－6＝（x＋3）（x－2）≠0，即x≠2且x≠－3时，原分式有意义.。

《分式》期末复习题一、填空。

1、在ma y x xy x x 1,3,3,21,21,12+++π中，分式的个数是 个。

2、使分式2xx +有意义的x 的取值范围是 。

3、如果分式2xx-的值为0，那么x 为 。

4、要使分式231x x +-有意义，则x 需满足的条件为．5、．若关于x 的分式方程222-=--x m x x 有增根，则m 的值为__________.6、若分式242--x x 的值为0，则x 的值为 ．7、 分式28,9,12zyx xy z x x z y -+-的最简公分母是 。

8、用科学记数法表示-0.0000064记为 。

9、计算：=-321)(b a ；=+-23π ；－3－2= ；10、 计算：3)32(x y -= ()()23323a b ab ----⨯＝11、化简分式2b ab b+的结果为 。

12、分式,21xxyy51,212-的最简公分母为 ；13、约分：=-2264xyy x ；932--x x = ；14、如果2a b=，则2222a ab b a b-++= 。

15、计算a b a b b a a +⎛⎫-÷ ⎪⎝⎭的结果为 。

计算：222a a b b b a ⎛⎫-÷= ⎪⎝⎭．16、计算：2933aa a -=-- ．ab b ba a -+-＝ ；17、如果把分式yx x232-中的x,y 都扩大3倍，那么分式的值（ ）A 扩大3倍B 不变C 缩小3倍D 扩大2倍 18、已知113x y-=,则代数式21422x xy y x xy y----的值为 。

二、计算。

（1）222x y xy x yx y+--- （2）⎪⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛-y x x y 11（3）()dcdb a cab 234322222-∙-÷（4）111122----÷-a a a a a a⑷2222x yxy y x xx ⎛⎫--÷- ⎪⎝⎭102006)21()23()1(-+---（5）、化简求值：23331111x x x x x -÷-+--，其中x=2。

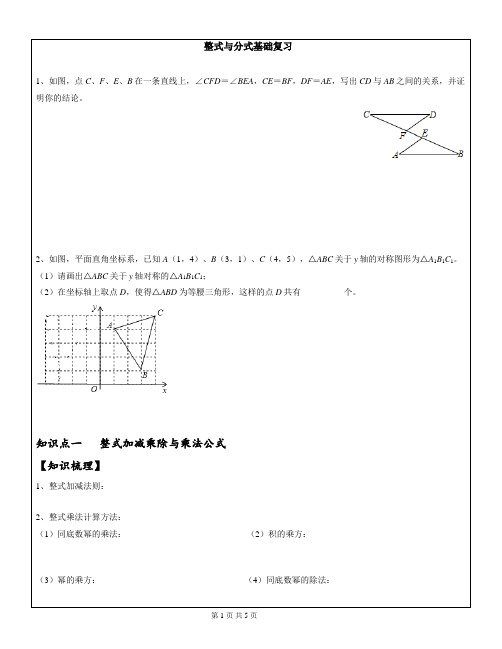
《分式》期末复习班级 姓名课前练习1.在(3)5,,,214a b x x x a b a π-++++中，是分式的有（ ）A 、2 个 B 、3个 C 、4个 D 、5个2. 计算22()ab a b-的结果是（ ） A ．a B ．b C ．1 D ．－b 3.如果把分式2a b ab+中的x 和y 都扩大2倍，即分式的值（ ） A 、扩大4倍； B 、扩大2倍； C 、不变； D 缩小2倍4.能使分式2244x x x --+的值为零的所有x 的值是（ ） A.2x = B.2x =- C.2x = 或2x =- D.2=x 或1=x 5.当x = 时，分式12x -无意义． 6..①())0(10 53≠=a axy xy a ②() 1422=-+a a 。

７．计算 x y x y 2211-+- 22224421yxy x y x y x y x ++-÷+--８．解方程3131=---x x x 625+-=-x x x x24.某工程队承接了3000米的修路任务，在修好600米后，引进了新设备，工作效率是原来的2倍，一共用30天完成了任务，求引进新设备前平均每天修路多少米？课堂练习：1. 下列各式是最简分式的是（ ） A.a 84 B.a b a 2 Ｃ.yx -1 D.22a b a b -- 2. 化简aba b a +-222的结果为（ ） A.a b a 2- B.a b a - C.a b a + D.b a b a +- 3. 下列各式与y x y x +-相等的是（ ） A.5)(5)(+++-y x y x B.y x y x +-22 Ｃ.222)(y x y x -- D.2222yx y x +- 4.一份工作，甲单独做需a 天完成，乙单独做需b 天完成，则甲乙两人合作一天的工作量是（ ）A.a +b;B.b a +1；C.2b a +；D.ba 11+ 5. 若023=-y x ，则1+yx 等于（ ） A.32 B.23 C.35 D.-35 6. 当x 时，分式32-x x 无意义. 7. 分式bx ax 1,1的最简公分母为 . 8. 化简=-32224m n m . 9. 在括号内填入适当的单项式,使等式成立:22)(1xy xy =. 10.当x= 时，分式372--x x 的值为1. 11计算. b a a b a b --- 12.)1(1a a a a -÷- 13. )(22a b b a a ab a -÷-14.13)181(++÷+--x x x x 其中32=x 15.解方程：xx x 1512=-+31. 甲商品每件价格比乙商品贵6元，用90元买得甲商品的件数与用60元买得乙商品的件数相等，求甲、乙两种商品每件价格各是多少元？. 甲班与乙班同学到离校15千米的公园秋游，两班同时出发，甲班的速度是乙班同学速度的1.2倍，结果比乙班同学早到半小时，求两个班同学的速度各是多少？课后练习1、下列约分结果正确的是（ ）A 、yz z y x yz x 1281282222=B 、y x y x y x -=--22C 、11122+-=--+-m m m m D 、b a m b m a =++ 2、若分式112+-x x 的值为0，则x 的取值为（ ）A 、1=x B 、1-=x C 、1±=x D 、无法确定 3、若xy y x =+，则yx 11+的值为（ ） A 、0 B 、1 C 、-1 D 、2 4、计算：xy y y x x 222-+-，结果为（ ） A 、1 B 、-1 C 、y x +2 D 、y x + 5、某农场开挖一条480米的渠道，开工后，每天比原计划多挖20米，结果提前4天完成任务，若设原计划每天挖x 米，那么求x 时所列方程正确的是（ ）A 、448020480=--x xB 、204480480=+-x xC 、420480480=+-x xD 、204804480=--xx 6、当x 时，分式31-+x x 有意义. 7..若关于x 的分式方程311x a x x --=-无解，则a = ． 8、xyzx y xy 61,4,13-的最简公分母是 。

期末复习： 分式一、选择题1.下列各式中，分式的个数为（ ）3x y -，21a x -，错误！未找到引用源。

，3a b -，12x y +，12x y +，2123x x =-+. A.5 B.4 C.3 D.2 ▓下列各式：π8,11,5,21,7,322x x y x b a a -++中，分式有 A 、1个 B 、2个 C 、3个 D 、4个 2. 若分式112+-x x 的值为零，那么错误！未找到引用源。

的值为( ) A.错误！未找到引用源。

或错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.错误！未找到引用源。

3.下列分式是最简分式的是（ ） A.11m m -- B.3xy y xy - C.22x y x y -+ D.6132m m - ▓下列分式是最简分式的（ ） A ．223a a b B ．23a a a - C ．22 a b a b ++ D ．222a ab a b -- 4. 若分式21a +有意义，则a 的取值范围是（ ） A ．a =0 B ．a =1 C ．a ≠-1 D ．a ≠0 5．下列各式正确的是（ ） A.c c a b a b =---- B.c c a b a b=---+ C.c c a b a b =--++ D.c c a b a b-=---- 6. 下列计算，正确的是（ ） A ．1221-=÷- B ．x x x 214243=÷-- C.6326)2(x x =--- D.222743x x x =+-- ▓.下列各式运算正确的是（ ） A.()()22 1a b b a -=- B.221a b a b a b +=++ C.111a b a b+=+ D.2 2x x ÷= ▓下列约分正确的是（ ）A.133m m m =++ B.122x y y x +=-- C.936321b b a a =++ D.()()x a b x y b a y -=- ▓下列各式变形正确的是（ ） A.x y x y x y x y -++=--- B.22a b a b c d c d--=++ C.0.20.03230.40.0545a b a b c d c d --=++ D.a b b a b c c b --=-- 7. 将分式2x x y +中的x 、y 的值同时扩大2倍，则分式的值（ ） A.扩大为原来的2倍 B.缩小到原来的21 C.保持不变 D.无法确定 ▓如果把的x 与y 都扩大10倍，那么这个代数式的值（ ） A ．不变 B ． 扩大50倍C ．扩大10倍D ．缩小到原来的8.化简211x x x x+-- 的结果是（ ） A ．x +1 B ．x -1 C ．-x D ．x9.计算 的结果是（ ）A ．-3B ．3C ．-12D ．12 10.运动会上，初二（3）班啦啦队买了两种价格的雪糕，其中甲种雪糕共花费40元，乙种雪糕共花费30元，甲种雪糕比乙种雪糕多20根.乙种雪糕价格是甲种雪糕价格的 1.5倍，若设甲种雪糕的价格为错误！未找到引用源。

人教版八年级上册数学期末专题复习---《分式方程实际问题》1. 端午节前后，张阿姨两次到超市购买同一种粽子．节前，按标价购买，用了96元；节后，按标价的6折购买，用了72元，两次一共购买了27个．这种粽子的标价是多少？2. 在我市某一城市美化工程招标时，有甲、乙两个工程队投标，经测算：甲队单独完成这项工程需要60天，若由甲队先做20天，剩下的工程由甲、乙合作24天可完成.（1）乙队单独完成这项工程需要多少天？（2）甲队施工一天，需付工程款3.5万元，乙队施工一天需付工程款2万元.若该工程计划在70天内完成，在不超过计划天数的前提下，是由甲队或乙队单独完成工程省钱？还是由甲乙两队全程合作完成该工程省钱？3. 甲、乙两个工程队共同承担一项筑路任务，甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天，且甲队单独施工45天和乙队单独施工30天的工作量相同.(1)甲、乙两队单独完成此项任务各需多少天？(2)若甲、乙两队共同工作了3天后，乙队因设备检修停止施工，由甲队单独继续施工，为了不影响工程进度，甲队的工作效率提高到原来的2倍，要使甲队总的工作量不少于乙队的工作量的2倍，那么甲队至少再单独施工多少天？4.京广高速铁路工程指挥部，要对某路段工程进行招标，接到了甲、乙两个工程队的投标书.从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的；若由甲队先做10天，剩下的工程再由甲、乙两队合作30天完成.（1）求甲、乙两队单独完成这项工程各需多少天？（2）已知甲队每天的施工费用为8.4万元，乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程，拟安排预算的施工费用是否够用？若不够用，需追加预算多少万元？请给出你的判断并说明理由.5. 从甲地到乙地有两条公路，一条是全长600km的普通公路，另一条是全长480km的高速公路，某客车在高速公路上行驶的平均速度比在普通公路上快45km/h，由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半，求该客车由高速公路从甲地到乙地所需的时间．6. “母亲节”前夕,某商店根据市场调查,用3 000元购进第一批盒装花,上市后很快售完,接着又用5 000元购进第二批这种盒装花.已知第二批所购花的盒数是第一批所购花的盒数的2倍，且每盒花的进价比第一批的进价少5元.求第一批盒装花每盒的进价.7.现有甲、乙两个空调安装队分别为A、B两个公司安装空调,甲安装队为A公司安装66台空调，乙安装队为B公司安装80台空调,乙安装队提前一天开工,最后与甲安装队恰好同时完成安装任务,已知甲队比乙队平均每天多安装2台空调,求甲、乙两个安装队平均每天各安装多少台空调?8.某商厦预测一种应季衬衫能畅销市场，于是用8000元购进了这种衬衫，衬衫面市后，果然供不应求，商厦又用17600元购进了第二批这种衬衫，第二批所购数量是第一批购进数量的2倍，但单价贵了4元．（1）求这两批衬衫的进价分别是多少元？（2）商厦销售这两批衬衫时都是统一售价，这两批衬衫全部售出后，商店获利不少22400元，求售价至少每件多少元？9. 元旦晚会上，王老师要为她的学生及班级的六位科任老师送上贺年卡，网上购买贺年卡的优惠条件是：购买50或50张以上享受团购价.王老师发现：零售价与团购价的比是5：4，王老师计算了一下，按计划购买贺年卡只能享受零售价，如果比原计划多购买6张贺年卡就能享受团购价，这样她正好花了100元，而且比原计划还节约10元钱；（1）贺年卡的零售价是多少？（2）班里有多少学生？10. 某商家预测一种衬衫能畅销市场，就用12000元购进了一批这种衬衫，上市后果然供不应求，商家又用了26400元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但每件进价贵了10元．（1）该商家购进的第一批衬衫是多少件？（2）若两批衬衫都按每件150元价格销售，则两批衬衫全部售完后的利润是多少元？11.列方程解应用题.豆腐文化节前夕，我市对观光路工程招标时，接到甲、乙两个工程队的投标书，甲、乙施工一天的工程费用分别为1.5万元和1.1万元，市政局根据甲乙两队的投标书测算，应有三种施工方案：(1)甲队单独做这项工程刚好如期完成.(2)乙队单独做这项工程，要比规定日期多5天.(3)若甲、乙两队合作4天后，余下的工程由乙队单独做，也正好如期完成.在确保如期完成的情况下，你认为哪种方案最节省工程款，通过计算说明理由.12.马拉松爱好者张老师作为业余组选手也参与了此次马拉松全程比赛.专业组选手上午8点准时出发，30分钟后张老师出发；在冠军选手到达终点一个半小时后，张老师抵达终点.已知马拉松全程约为42千米，张老师的平均速度是冠军选手的.（1）求冠军选手和张老师的平均速度分别为多少？（2）若明年张老师参加马拉松比赛的起跑时间不变，他计划不超过中午十一点抵达终点，则张老师今年必须加强跑步锻炼，使明年参加比赛时的平均速度至少比今年的平均速度提高百分之多少才能完成计划？。

期末专题复习 分式知识点1 分式的定义我们将 的式子叫做分式。

练习 下列各式是分式的打√，不是分式的打╳.①23-x ② a 21 ③222n m - ④x 1 ⑤π1 ⑥222yx x- ⑦)(1y x x + ⑧1-xy 知识点2 分式有意义的条件当分式的 时，分式有意义。

练习 x 取何值时，下列分式有意义？ ①21+x ②x y x 3- ③)3)(1(2-+-x x x ④422-+x x⑤x x x 312+- ⑥112+x ⑦yx y x +- 知识点3 分式的值为零的条件 当分式的分子 ，分母 时，分式的值为零。

练习 x 取何值时，下列分式的值为零？①31-+a a ②3)2)(1(+++a a a ③112--a a ④xx x 3922-- 知识点4 分式的基本性质分式的分子、分母同时 ，分式的值不变。

练习 1. 利用分式的基本性质填空：①x x x x 3322+=+ ②123692-=-x x x xy ③2)(b a b a b a -=+- ④244422+=+--x x x x 2. 约分：（1）acab1510-（2）y x y x 322.36.1- （3）112--m m（4）y x x xy y -+-24422（5）322)(27)(12b a a b a --（7）22164mmm -- （8）2442-+-x x x知识点5 分式的乘除运算乘法法则：分式乘以分式，把它们的分子、分母 .除法法则：分式除以分式，将除式中的分子、分母 .用符号表示为：bd ac d c b a =⨯ bcadc d b a d c b a =⨯=÷练习 1.填空：①=-⋅)29(283x yy x __ ____． ②=+-÷-xy x x xy x 33322__ ____． ③=+÷+)(1b a b a ___ ___． ④=--⨯++⋅+aba b a b ab a b ab 2222222 . 2. 计算： ①232285xy yx y ⨯ ② n m m n m m n m n m --÷--242222③11.11)1(122+-÷--x x x x④ 2229425523ab a b a a --⨯++⑤a b bab a b ab a b a a 222222242⨯+÷+-- ⑥x x x x x x --⨯-÷+--32)3(44622知识点6 分式的加减运算法则 同分母分式相加减，分母不变，分子相加减.异分母分式相加减，先通分，变成同分母分式后再加减.用符号表示为：b c a b c b a ±=± bdbcad bd bc bd ad d c b a ±=±=±练习 计算：①x x x x x -+--+224222 ② xx x x x x x x +---+--+++35223634222 ③b a aa b b b a b a ---+-+22 ④xyy x xy x y -+-22 ⑤412234272--+--x x x ⑥941522333222-++-++a a a a知识点7 分式的混合运算分式的混合运算，先乘方，再乘除，最后算加减，有括号的先算括号里面的. 练习 ① yy y y y yy y 4)44122(22-÷+--+-+ ② )()(nm mnm n m mn m +-÷-+③111212+-÷⎪⎭⎫ ⎝⎛+-x x x ④2211yx xy y x y x -÷⎪⎪⎭⎫ ⎝⎛++-⑤（x －x 1-x 2）÷（1－x 1） ⑥221()a ba b a b b a-÷-+-⑦ 111121122+-÷⎪⎪⎭⎫ ⎝⎛-+-++x x x x x x ⑧先化简，再求值：⎝⎛⎭⎫1＋ 1x －2÷ x 2－2x ＋1 x 2－4，其中x ＝－5．知识点8 整数指数幂 公式 ：n nx x1=- . 如：9131322==- ； 3232321yx y x y x =⋅=-. 练习 填空：3)(--a ＝___ ___ ； =-2)3(__ ____ ；=--3)51(____ __．=-+-01)π()21(__ ____ ； －1＋（3.14）0＋2－1＝___ ___．计算：．．．①)()(32232b a b a ---⋅ ② xy z y x ⋅--2325)( ③22332)()5(-----⋅mn n m知识点9 科学记数法通常将一个很大 (或很小)的数表示成n a 10⨯（a ≤1<10）的形式. 练习．．用科学记数法表示： （1）0.000 16 （2）－0.000 031 02 （3）104 000 000 （4）—0.000 003知识点10 分式方程① 解分式方程时，方程各项都乘以最简公分母（没有分母的项也要乘）. ② 解分式方程，必须检验.凡是使最简公分母为0的根，必须舍去. 练习 确定下列方程中的最简公分母： ①1712112-=-++x x x ②625--=-x x x x ③1275723=-+-xx x ④y y y y 2434216252--=+-+解下列分式方程： ①34231--=+-x xx ②3625+=-x x③ 45411--=--x xx ④1211422+=+--x x x x x ⑤ 1412112-=-++x x x ⑥27x x ++23x x -＝261x -知识点11 分式方程应用题步骤: 审-----设----列----解----验-----答 可以借助自画的表格列方程. 练习 根据题意列方程：1. 某农场挖一条480米的渠道，开工后，每天比原计划多挖20米，结果提前4天完成任务，求原计划每天挖多少米.设原计划每天挖x 米.2. 一辆汽车先以一定速度行驶120千米，后因临时有任务，每小时加5千米，又行驶135千米，结果行驶这两段路程所用时间相等，求汽车先后行驶的速度. 设汽车之前行驶的速度为x 千米/时.3. 一个车间加工720个零件，预计每天做48个，就能如期完成，现在要提前5天完成，每天应该做多少个？设每天应该做x 多少个. 4. 甲、乙两同学学习电脑打字，甲打一篇3000字的文章与乙打一篇2400字的文章所用的时间相同，已知甲每分钟比乙多打12个字，问甲、乙两人每分钟各打字多少个？ 设甲每分钟打字x 个.列方程解应用题：某校招生录取时，为了防止数据输入出错，2640名学生的成绩数据分别由两位程序操作员各向计算机输入一遍，然后让计算机比较两人的输入是否一致.已知甲的输入速度是乙的2倍，结果甲比乙少用2小时输完.问这两个操作员每分钟各能输入多少名学生的成绩？。