四川省成都市铁路中学2012-2013学年八年级上学期入学检测数学试题

第 1 页 共 1 页ba cED A C 2013年数学参考答案11．21；12．61；13．－2；14．－2＜x ＜0或x ＞3；15．13；16．8；17．32π；18．51 三、解答题(每小题15分，共60分)19．解：(1)设甲材料每千克x 元，乙材料每千克y 元，则4023105x y x y +=⎧⎨+=⎩，解得1525x y =⎧⎨=⎩，所以甲材料每千克15元，乙材料每千克25元；(2)设生产A 产品m 件，生产B 产品(50－m)件，则生产这50件产品的材料费为 15×30m ＋25×10m ＋15×20(50－m)＋25×20(50－m)＝－100m ＋40000，由题意：－100m ＋40000≤38000，解得m ≥20，又∵50－m ≥28，解得m ≤22，∴20≤m ≤22， ∴m 的值为20，21，22，共有三种方案，如下表：(3)设总生产成本为W 元，加工费为：200m ＋300(50－m)，则W ＝－100m ＋40000＋200m ＋300(50－m)＝－200m ＋55000， ∵W 随m 的增大而减小，而m ＝20，21，22，∴当m ＝22时，总成本最低，此时W ＝－200×22＋55000＝50600元．20．解：(1)过点C 作线段CD ⊥AB 于D ，过点B 作线段BE ⊥AC 于E ；在Rt △ACD 中，b CD ＝sinA ，在Rt △BCD 中，a CD ＝sinB ∴CD ＝asinB ＝bsinA ，则B bA a sin sin =， 又 sin(π－C)＝sinC ，∴sinC ＝sin ∠BCE ，则在Rt △BCE 中，sin ∠BCE ＝a BE ＝sinC ，又 在Rt △ABE 中sinA ＝c BE，∴BE ＝cSinA ＝aSinC ，则C c A a sin sin =．综上所述CcB b A a sin sin sin ==； (2)由(1)知B b A a sin sin =，则31a ＝︒45sin 5，∴a ＝325．21．解：(1)连接OB ，∵PB 是⊙O 的切线，∴∠PBO ＝90°，∵OA ＝OB ，BA ⊥PO 于D ，∴AD ＝BD ，∠POA ＝∠POB ，又∵PO ＝PO ，∴△PAO ≌△PBO(SAS)，∴∠PAO ＝∠PBO ＝90°，∴直线PA 为⊙O 的切线．(2)EF 2＝4OD•OP． 证明：∵∠PAO ＝∠PDA ＝90° ∴∠OAD ＋∠AOD ＝90°，∠OPA ＋∠AOP＝90°，∴∠OAD ＝∠OPA ，∴△OAD ∽△OPA ，∴OP OA OA OD =，即OA 2＝OD•OP，又∵EF ＝2OA ，∴EF 2＝4OD•OP．(3)∵OA ＝OC ，AD ＝BD ，BC ＝18，∴OD ＝21BC ＝9(三角形中位线定理)，设AD ＝x ，∵tan∠F ＝21，∴FD ＝2x ，OA ＝OF ＝2x －9，在Rt△AOD 中，由勾股定理，得(2x －9)2＝x 2＋92，解之得，x 1＝12，x 2＝0(不合题意，舍去)，∴AD ＝12，OA ＝2x －9＝15，∵AC 是⊙O 直径，∴∠ABC ＝90°，又∵AC ＝2OA ＝30，BC ＝18，∴cos ∠ACB ＝3018＝53．∵OA 2＝OD•OP，∴9(PE ＋15)＝225，∴PE ＝10． 22．解：(1)令y ＝0，即－x 2＋335x ＋2＝0；解得 x 1＝－33，x 2＝23．∴C(－33，0)、A(23，0)．令x ＝0，即y ＝2，∴B(0，2)．综上，A(23，0)、B(0，2)．(2)令AB 方程为y ＝k 1x ＋2因为点A(23，0)在直线上，∴0＝23k 1＋2，∴k 1＝－33， ∴直线AB 的解析式为y ＝－33x ＋2． (3)由A(23，0)、B(0，2)得：OA ＝23，OB ＝2，AB ＝4，∠BAO＝30°，∠DOA＝60°； OD 与O 点关于AB 对称，∴OD＝OA ＝23，∴D 点的横坐标为3，纵坐标为3，即D(3，3)． 因为y ＝x k 过点D ，∴3＝3k，∴k＝33． (4)AP ＝t ，AQ ＝21t ，P 到x 轴的距离：AP•sin30°＝21t ，OQ ＝OA －AQ ＝23－21t ； ∴S △OPQ ＝21•(23－21t)•21t ＝－81(t －23)2＋23；依题意，得0＜t≤4，∴当t ＝23时，S 有最大值为23．。

某某省某某铁中2011-2012学年八年级数学下学期期中考试试题（满分150分，考试时间120分钟）A 卷（共100分）一、选择题（每小题3分，共30分）1．下列多项式分解因式，结果正确的是（ ）A ．()22244-=+-a a a B ．()2221441a a a -=-+C ．()222141x x +=+ D ．()222y x y xy x +=++2．分式22111,,a b a b a b+--的最简公分母是（ ） A ．()()22a b a b+-B ．()222a b-C ．22a b -D ．()()22a b a b--3．不等式⎪⎩⎪⎨⎧≥<212x x 的解集在数轴上应表示为（）4．如果把分式yx x+2中的x 和y 都扩大3倍，那么分式的值（ ） A ．扩大3倍 B ．不变 C ．缩小3倍 D ．缩小6倍5．已知线段AB ，点C 是它的黄金分割点（AC>BC ）。

设以AC 为边的正方形的面积为S 1，，以AB 、CB 分别为长和宽的矩形的面积为S 2，则（ ）A ．S 1>S 2B ．S 1=S 2C ．S 1<S 2D ．不能确定6．在比例尺是1∶8000的临江市城区地图上，某某路的长度约为25cm ，它的实际长度约为（ ） A ．320mB ．320cmC ．2000cmD ．2000m7．如图所示，若321∠=∠=∠，则图中相似的三角形有（ ） A ．2对 B ．3对 C ．4对 D ．5对2 2A 22B 22C 22DA21F E D 38．若分式2242x x x ---的值为零，则x 的值为（ ）A ．2或－2B ．2C ．－2D ．49．甲、乙两名工人加工某种零件，已知甲每天比乙多加工5个零件，甲加工80个零件和乙加工70个零件所用的天数相同．设甲每天加工x 个零件，则根据题意列出方程是( )． A.57080+=x x B.x x 70580=- C.x x 70580=+ D.57080-=x x ()44)2(144232+-⎥⎦⎤⎢⎣⎡--+-x x x x x x 的积为整数．．．．的整数．．x 的个数为（ ） A. 2个 B. 3个 C. 4个 D. 5个二、填空题：（每小题4分，共16分） 11．不等式3x –10≤0的正整数解是．12．在Rt△ABC 中，AB =3，AC =4，∠A =90°，AD ⊥BC ，那么AD ∶BC =． 13．如果关于x 的分式方程342(2)m m x x x x =+--有增根，那么m 的值是．14．若多项式23x x a -+可分为(5)()x x b --，则a =，b =．三、解答题（共30分）15．计算：（每小题6分，共12分） （1）分解因式：222(1)4a a +- ．（2）已知33=a ，求aa aa a a ----+-221121的值.16．解不等式（组）（每小题6分，共12分） （1）求不等式111326x x x +---≥的正整数解． （2）解不等式组()⎪⎩⎪⎨⎧-≤-+>-x x x x 2371211325并把解集在数轴上表示出来.17．（6分）解方程：114112=---+x x x四、解答题 (每小题6分，共12分)18．如图，小明欲测量一古塔的高度，他站在该塔的影子的顶端C 处，并使自己的影子与古塔的影子在一条直线上，此时，他距离该塔20m. 已知小明的身高是1.6m , 他的影子长2m ， 求古塔的高度.19．在争创全国综合治理先进城市的活动中，某县“文明突击队”决定清运一堆重达100吨的垃圾．开工后，附近居某某动参加到劳动中，使清运垃圾的速度比原计划提高了一倍，结果提前4小时完成任务，问“文明突击队”原计划每小时清运多少吨垃圾？五、解答题（12分）20．如图所示，Rt △ABC 中，∠ACB =90°，CD ⊥AB于D ，P 为CD 的中点，直线AP 交BC 于E ，EF ⊥AB 于F ．（1）求证：DB AD BCAC =22；（2）若CE =1，BE =4，求EF 及AC 的长．B 卷（共50分）一、填空题：（每小题4分，共20分） 21．若n m n m +=+811，则nmm n +=． 22．不等式⎩⎨⎧<->+5242b x a x 的解是32<<x ，那么a +b 的值等于．BD FAE C23．如图,点E 是□ABCD 的AD 边延长线上一点， BE 与CD 交于点F ，若点D 是AE 的黄金分割点， 且AD>DE ，AB=15+， 则CF 的长是．24．已知02=-+b a ，则代数式)(8)(22222b a b a +--=.25．在日常生活中,取款、上网等都需要密码，有一种用“分解因式”法产生的密码， 方便记忆，密码产生原理是：对于多项式44y x -，其分解因式的结果是))()((22y x y x y x ++-，若取x=8，y=8，则各个因式的值是128)(,16)(,0)(22=+=+=-y x y x y x , 于是可以把“016128”作为一个六位数的密码。

第2题图第4题图第6题图第9题图第8题图第11题图第14题图第15题图2013年数 学(考试时间一、单项选择题：(每小题5分，共50分1．关于x 的不等式组⎩⎨⎧>->-010x k x 只有3个整数解，则k 的取值范围是( )A. －3≤k ≤－2B. －3≤k ＜－2C. －3＜k ≤－2D. －3＜k ＜－2 2．如图，在等腰三角形ABC 中，∠ABC ＝120º，点P 是底边AC 上一个动点，M 、N 分别是AB 、BC 的中点，若PM ＋PN 的最小值为2，则△ABC 的周长是( ) A ．2B ．2+C ．4D ．4+3．已知sin α＋cos α＝y ，sin α•cos α＝x ，则x 、y 的关系是( ) A. y ＝x B. y ＝2x ＋1 C. y 2＝2x ＋1 D. y 2＝1－2x 4．如图，点A 在双曲线y ＝x 4上，点B 在双曲线y ＝xk(k ≠0)上，AB ∥x 轴，分别过点A 、B 向x 轴作垂线，垂足分别为D 、C ，若矩形ABCD 的面积是8，则k 的值为( )A. 6B. 8C. 10D. 12 5．当－1≤x≤2时，函数y ＝ax ＋6满足y≤10，则a 满足( )A ．a≤2B ．a ≥－4C ．－4≤a≤2D ．－4≤a≤2且a ≠0 6．如图，用邻边长分别为a 、b(a ﹤b)的矩形硬纸板裁出以a 为直径的两个半圆，再裁出与矩形的较长边、两个半圆均相切的两个小圆．把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽(拼接处材料忽略不计)，则a 与b 满足的关系式是( ) A. b ＝3a B. b ＝215+ a C. b ＝25a D.b ＝2a 7．设a ＝6－1，则3a 3＋12a 2－3a －10＝( )A. 20B. 22C. 46＋10D. 46＋128．如图，已知⊙O 的弦AB 、CD 相交于点P ，PA ＝4cm ，PB ＝3cm ，PC ＝6cm ，EA 切⊙O 于点A ，AE 与CD 的延长线交于点E ，若AE ＝25cm ，则PE 的长为( )A. 2cmB. 3cmC. 4cmD. 5cm 9．如图，△ABC 中，D 、E 是BC 边上的点，BD ︰DE ︰EC ＝3︰2︰1，M 在AC 边上，CM ︰MA ＝1︰2，BM 交AD ，AE 于H ，G ，则BH ︰HG ︰GM 等于( )A. 3︰2︰1B. 5︰3︰1C. 25︰12︰5D. 51︰24︰1010．如果方程(x －1)(x ²－2x ＋m)＝0的三根可以作为一个三角形的三边之长，那么实数m 的取值范围是( )A. 0≤m ≤1B. m ≥43C. 43＜m ≤1D. 43≤m ≤1 二、填空题：(每小题5分，共40分)11．已知平面上四点A(0，0)，B(10，0)，C(10，6)，D(0，6)，直线y ＝mx －3m ＋2将四边形ABCD 分成面积相等的两部分，则m 的值为 ．12．已知a 、b 、c 为实数，且31=+b a ab ，41=+c b bc ，51=+a c ca ．则cabc ab abc++＝ ．13．已知方程2x ２－4x ＋1＝0的两根为α、β，则ββαα4141-+-＝ ．14．如图所示是一次函数y 1＝kx ＋b 和反比例函数y 2＝xm的图象，kx ＋b －xm＞0时，则x 的取值范围为 ． 15．如图，已知△ABC ≌△DCE ≌△HEF ，三条对应边BC 、CE 、EF 在同一条直线上，连接BH ，分别交AC 、DC 、DE于点P、Q 、K ，其中S △PCQ ＝1，则图中三个阴影部分的面积和为 ．ABCP MN18题图17题图16．函数y ＝|x －1|＋2|x －2|＋3|x －3|＋4|x －4|的最小值是 ．17．如图1，直线l 上放置了一个边长为3的等边三角形，当等边三角形沿着直线翻转一次到达图2的位置．如果等边三角形翻转24次，则顶点A 移动的路径总长是 (用π表示)．18．将正整数按下表的规律排列，把行与列交叉处的一个数称为某行某列的数，记作a ij ，如第2行第4列的数是15，记作a 24＝15；又如第3行第2列的数是8，记作a 32＝8，则数a 82＝ ． 三、解答题：(每小题15分，共60分)19．某工厂计划生产A 、B 两种产品共50件，需购买甲、乙两种材料．生产一件A 产品需甲种材料30千克、乙种材料10千克；生产一件B 产品需甲、乙两种材料各20千克．经测算，购买甲、乙两种材料各1千克共需资金40元，购买甲种材料2千克和乙种材料3千克共需资金105元． (1)甲、乙两种材料每千克分别是多少元？(2)现工厂用于购买甲、乙两种材料的资金不超过38000元，且生产B 产品不少于28件，问符合条件的生产方案有哪几种？(3)在(2)的条件下，若生产一件A 产品需加工费200元，生产一件B 产品需加工费300元，应选择哪种生产方案，使生产这50件产品的成本最低？(成本＝材料费＋加工费)20．在Rt △ABC 中，设BC ＝a ，AC ＝b ，AB ＝c ， 根据正弦函数的定义，有c a ＝sinA ，c b ＝sinB ，又sinC ＝1＝cc，则c CcB b A a ===sin sin sin ，从而在直角三角形ABC 中，CcB b A a sin sin sin ==． 思考：那么对于任意的三角形，以上关系式是否仍然成立？ 探究：可分为锐角三角形和钝角三角形两种情况：如图，当△ABC 是锐角三角形时，作AB 边上的高是CD ，根据任意角三角函数的定义，有a CD ＝sinB ，bCD＝sinA ，即 CD ＝asinB＝bsinA ，则B bA a sin sin =， 同理可得B bC c sin sin =，从而CcB b A a sin sin sin ==． (1)根据材料所提示，请证明若△ABC 是钝角三角形时，以上关系式仍然成立．(补充：sin(180º－C)＝sinC)(2)在△ABC 中，若b ＝5，∠B ＝45º，sinA ＝31，求a 边长．21．如图，PB 为⊙O 的切线，B 为切点，直线PO 交⊙于点E 、F ，过点B 作PO 的垂线BA ，垂足为点D ，交⊙O 于点A ，延长AO 与⊙O 交于点C ，连接BC ，AF ． (1)求证：直线PA 为⊙O 的切线；(2)试探究线段EF 、OD 、OP 之间的等量关系，并加以证明； (3)若BC ＝18，tan ∠F ＝21，求cos ∠ACB 的值和线段PE 的长．22．如图，抛物线y ＝－x 2＋335x ＋2与x 轴交于C ．A 两点，与y 轴交于点B ．点O 关于直线AB 的对称点为D ，E 为线段AB 的中点． (1)分别求出点A 、点B 的坐标； (2)求直线AB 的解析式；(3)若反比例函数y ＝xk的图象过点D ，求k 值； (4)两动点P 、Q 同时从点A 出发，分别沿AB 、AO 方向向B 、O 移动，点P 每秒移动1个单位，点Q 每秒移动21个单位，设△POQ 的面积为S ，移动时间为t ，问：S 是否存在最大值？若存在，求出这个最大值，并求出此时的t 值；若不存在，请说明理由．cbaCBAc baDCBAA BC。

（时间：120分钟 满分150分）一 选择题(每小题有且仅有一个选项是正确的，选对得5分，共60分) 1．0300tan 的值为（ ）A ．33 B ．3- C ．3 D ．33-2．设集合{}b a A ,=，则满足{}c b a B A ,,= 的集合B 的个数为（ ） A.8 B. 4 C. 3 D. 1 3已知α为第四象限角，且3tan 4α=-，则sin α等于（ ）A.35 B. 45 C.35- D.45- 4．如果1sin()2πα+=-，那么cos()2πα+的值为 （ ）A. 12-B.12C.5. 将函数)32sin()(π-=x x f 的图像左移3π，再将图像上各点横坐标压缩到原来的21，则所得到的图象的解析式为（ ） A x y sin = B )34sin(π+=x yC )324sin(π-=x y D )3sin(π+=x y6．已知函数)1(+=x f y 定义域是[]-23，，则y f x =-()21的定义域是（ ）A ．[]052， B. []-14， C. ]73[，- D. ]37[，-7．函数33)(3--=x x x f 有零点的区间是（ ）A ．()0,1-B ．()1,0C ．()2,1D ．()3,28． 函数xxa y x=(01)a <<的图象的大致形状是( )9．设11,1,,32α⎧⎫∈-⎨⎬⎩⎭，则使函数y x α=的定义域为R ，且为奇函数的所有α的值为（ ）A. 1，3B.12，1 C. -1，3 D. -1，1，3 10 ．已知ω是正实数，函数)sin(2x y ⋅=ω在]4,3[ππ-是增函数，那么( )A 230≤<ω B 20≤<ω C 7240≤<ω D 2≥ω 11．已知函数x x f x2log )31()(-=，若实数0x 是方程0)(=x f 的解，且010x x <<，则)(1x f 的值 （ ）A 等于0B 不大于0C 恒为正值D 恒为负值 12．若函数)(x f 满足)(1)1(x f x f =+，且当]1,1(-∈x 时，||)(x x f =,则函数)(x f y =的图象与函数 ||log 3x y =的图象的交点的个数为 ( )A 3B 4C 6D 8二 填空题：13．角α的顶点在原点，始边在x 轴的非负半轴上，终边过点P , y ）, 若21cos =α，则y 的值为______ 14．已知)(x f 是定义在实数集上的函数，且)()1(x f x f -=+，若4)1(=f ,则=)2010(f ___________.15．函数)62sin(2π+-=x y的单调增区间为_______________16．对于任意实数x ,符号[x ]表示不超过x 的最大整数,例如[-1.5]=-2,[2.5]=2,定义函数{}[]x x x =-,则给出下列四个命题：①函数{}x 的定义域是R,值域为[0,1];②方程{}12x =有无数个解；③函数{}x 是周期函数；④函数{}x 是增函数.其中正确的序号是___________ 三 解答题：17．（本小题满分12分） 化简或求值： （I ）245lg 8lg 344932lg21+-（II ）︒+︒-︒︒+126cos )324cos(54sin 216sin 2118．（本小题满分12分）已知θ)43,21(ππ∈，且2512cos sin -=⋅θθ（1） 求θθcos sin -的值; (2) 求θtan 之值19. （本小题满分12分） 已知函数x x f 2log 1)(-=的定义域为A ，函数m x x x g +-=sin cos )(2的值域为B ，若A B A =⋂，求实数m 的取值范围。

O DC AB D CBA 某某省某某铁中2012-2013学年八年级12月检测数学试题A 卷（满分100分）一、选择题（每小题3分，共30分） 1.0.81的平方根是（ ）A 、0.9B 、±0.9C 、0.09D 、±2．以下列各组数据为边长作三角形，其中能组成直角三角形的是 （ ） A 、3、5、3 B 、4、6、8 C 、7、24、25 D 、6、12、133.下列数中，0.4583，.7.3，3.14，2，38-，2π… 是无理数的有（ ）A 、 2个B 、 3个C 、 4个D 、 5个 4．下列说法正确的是（ ） A.064.0-3± C. 16的立方根是3165．点(35)p ，关于y 轴对称的点的坐标为（ ）A ． (3,5)B ． (5,3)C ．(3,5)D ． (3,5) 6．下列图形中，既是轴对称图形，又是中心对称图形的是（ ） A ．等腰梯形B ．矩形C ．正三角形D ．平行四边形7． 如图，矩形ABCD 的两条对角线相交于点O ，602AOB AB ∠==°，，则矩形的边长BC 的长是（ ） A ．2B ．4C．． （7题图）8．如果点P (m ，1+2m )在第二象限，那么m 的取值X 围是 （ ）A ．210<<m B ．021<<-m C ．0<m D ．21>m 9．如图，下列条件不能使四边形ABCD 一定是平行四边形的是（ ） A ．//AB CD AB =CD B ．//AD BC //AB CDC ．//AD BC B D ∠=∠ D.//AD BC AB =CD10．如图,在正方形ABCD 中，E 为DC 边上的点，连接BE ，将ΔBCE 绕点C 顺时针方向旋转90°得到ΔDCF ，连接EF ，若∠BEC=60°，则∠ EFD 的度数为 （ ）A 、10°B 、15°C 、20°D 、25° 二、填空题（每小题3分，共15分） 11．不等式532x x <+的解集是． 12.己知函数32-+=x y ，则自变量x 的取值X 围是.13．化简：(1)、()=-22；（2）、3125=。

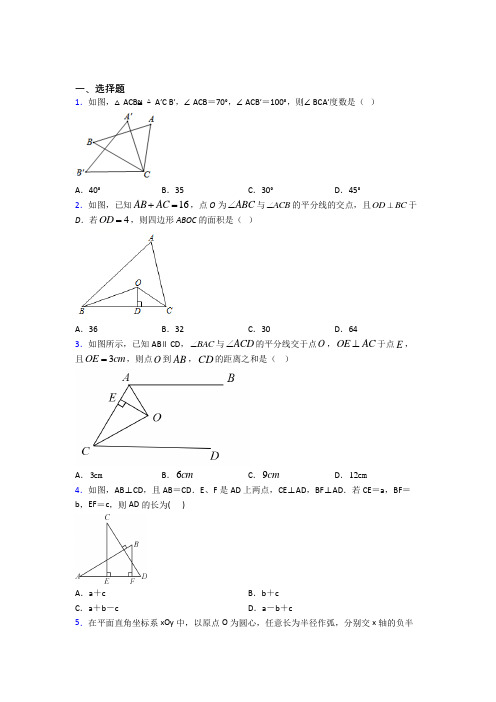
一、选择题1．如图，△ACB ≌△A′C B′，∠ACB ＝70°，∠ACB′＝100°，则∠BCA′度数是（ ）A ．40°B ．35C ．30°D ．45°2．如图，已知16AB AC +=，点O 为ABC ∠与ACB ∠的平分线的交点，且OD BC 于D ．若4OD =，则四边形ABOC 的面积是（ ）A ．36B ．32C ．30D ．643．如图所示，已知AB ∥CD ，BAC ∠与ACD ∠的平分线交于点O ，OE AC ⊥于点E ，且3OE cm =，则点O 到AB ，CD 的距离之和是（ ）A ．3cmB ．6cmC ．9cmD ．12cm 4．如图，AB ⊥CD ，且AB ＝CD ．E 、F 是AD 上两点，CE ⊥AD ，BF ⊥AD ．若CE ＝a ，BF ＝b ，EF ＝c ，则AD 的长为( )A ．a ＋cB ．b ＋cC ．a ＋b －cD ．a －b ＋c5．在平面直角坐标系xOy 中，以原点O 为圆心，任意长为半径作弧，分别交x 轴的负半轴和y轴的正半轴于A点，B点，分别以点A，点B为圆心，AB的长为半径作弧，两弧交于P点，若点P的坐标为(m，n)，则下列结论正确的是（）A．m＝2n B．2m＝n C．m＝n D．m＝－n6．工人师傅常用直角尺平分一个角，做法如下：如图所示，在∠AOB的边OA，OB上分别取OM＝ON，移动直角尺，使直角尺两边相同的刻度分别与M，N重合（即CM＝CN）．此时过直角尺顶点C的射线OC即是∠AOB的平分线．这种做法的道理是（）A．HL B．SAS C．SSS D．ASA7．如图，AB＝AC，AD＝AE，∠A＝105°，∠D＝25°，则∠ABE等于（）A．65°B．60°C．55°D．50°，还需增加的8．如图，ABC和DEF中，∠A=∠D，∠C=∠F，要使ABC DEF条件是（）A．AB=EF B．AC=DF C．∠B=∠E D．CB=DE9．如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别是点D、E，AD=3，BE=1，则DE的长是（）A．1.5 B．2 C．22D1010．点Р在AOB ∠的角平分线上，点Р到OA 边的距离等于5，点Q 是OB 边上的任意一点，则下列选项正确的是（ ）A ．5PQ >B ．5PO ≥C ． 5PQ <D ．5PO ≤ 11．如图，AB 与CD 相交于点E ，AD=CB ，要使△ADE ≌△CBE ，需添加一个条件，则添加的条件以及相应的判定定理正确的是（ ）A ．AE=CE ；SASB ．DE=BE ；SASC ．∠D=∠B ；AASD ．∠A=∠C ；ASA 12．如图，AD 是ABC 的角平分线，:4:3AB AC = ，则ABD △与ACD △的面积比为（ ）．A ．4:3B ．16:9C ．3:4D ．9:1613．如图，已知∠A=∠D ， AM=DN ，根据下列条件不能够判定△ABN ≅△DCN 的是（ ）A ．BM ∥CNB ．∠M=∠NC ．BM=CND ．AB=CD 14．如图，OB 平分∠MON ，A 为OB 的中点，AE ⊥ON ，EA=3，D 为OM 上的一个动点，C 是DA 延长线与BC 的交点，BC //OM ，则CD 的最小值是（ ）A ．6B ．8C ．10D ．1215．如图，在△ABC 中，点E 和F 分别是AC ，BC 上一点，EF ∥AB ，∠BCA 的平分线交AB 于点D ，∠MAC 是△ABC 的外角，若∠MAC ＝α，∠EFC ＝β，∠ADC ＝γ，则α、β、γ三者间的数量关系是（ ）A ．β＝α+γB ．β＝2γ﹣αC ．β＝α+2γD ．β＝2α﹣2γ二、填空题16．如图所示的是一张直角ABC 纸片（90C ∠=︒），其中30BAC ∠=︒，如果用两张完全相同的这种纸片恰好能拼成如图2所示的ABD △，若2BC =，则ABD △的周长为______．17．如图，AOP BOP ∠=∠，PD OA ⊥，C 是OB 上的动点，连接PC ，若4PD =，则PC 的最小值为_________．18．如图，AC AE =，AD AB =，90ACB DAB ∠=∠=︒，33BAE ∠=︒，//CB AE ，AC 与DE 相交于点F ．（1）DAC ∠=______．（2）当1AF =时，BC 的长为______．19．如图，已知ABC 的周长是8，OB ，OC 分别平分ABC ∠和ACB ∠，OD BC 于D ，且3OD =，ABC 的面积是______．20．如图，AC//BD ，OA ，OB 分别平分BAC ∠和ABD ∠，OE AB ⊥，垂足为E ，如果OE 5=，那么AC 与BD 的距离是________21．如图所示，在ABC 中，AB AC =，AD 是ABC 的角平分线，DE AB ⊥，DF AC ⊥，垂足分别是E ，F ．则下面结论中（1）DA 平分EDF ∠；（2）AE AF =，DE DF =；（3）AD 上的点到B ，C 两点的距离相等；（4）图中共有3对全等三角形．正确的有________ ．22．如图，在ABC 中，AD 平分BAC ∠，P 为线段AD 上的一个动点，PE AD ⊥交直线BC 于点E ．若35B ∠=︒，85ACB ∠=︒，则E ∠的度数为______．23．如图，已知AB AC =，D 为BAC ∠的角平分线上面一点，连接BD ，CD ；如图，已知AB AC =，D 、E 为BAC ∠的角平分线上面两点，连接BD ，CD ，BE ，CE ；如图，已知AB AC =，D 、E 、F 为BAC ∠的角平分线上面三点，连接BD ，CD ，BE ，CE ，BF ，CF ；…，依此规律，第n 个图形中有全等三角形的对数是______．24．如图，已知ABC DCB ∠=∠，则需添加的一个条件是______可使ACB DBC ≌．（只写一个即可，不添加辅助线）．25．如图，已知点(44)A -，，一个以A 为顶点的45︒角绕点A 旋转，角的两边分别交x 轴正半轴，y 轴负半轴于E 、F ，连接EF ．当△AEF 直角三角形时，点E 的坐标是________．26．如图，在△ABC 和△DBC 中，∠ACB=∠DBC=90°，E 是BC 的中点，DE ⊥AB ，垂足为F ，AB=DE ．若BD=8cm ，则AC 的长为_________．三、解答题27．如图，点E ，F 在线段BD 上，已知AF BD ⊥，CE BD ⊥，//AD CB ，DE BF =，求证：AF CE =．28．如图，,AD BF 相交于点,//,O AB DF AB DF =，点E 与点C 在BF 上，且BE CF =．（1）求证：ABC DFE ∆≅∆；（2）求证：点О为BF 的中点．29．如图，A 、D 、F 、B 在同一直线上，EF ∥CD ，AE ∥BC ，且AD ＝BF ．求证：AE ＝BC30．如图，在△ABD 中，∠ABD ＝90°，AB=BD ，点E 在线段BD 上，延长AB 使BC=BE ，连接AE 、CE 、CD ，点M 在线段AE 上，点N 在线段CD 上，BM ⊥BN ，易证△ABE ≌△DBC ；仔细观察，请逐一找出图中其他的全等三角形，并说明理由．。

2012年数 学(考试时间一、单项选择题：(每小题5分，共50分1．在平面直角坐标系xOy 中，已知点P(2，2)，点Q 在y 轴上，△PQO 是等腰三角形，则满足条件的点Q 共有( )A. 5个B. 4个C.3个D. 2个2．⊙O 内有一定点G ，OG ＝5cm ，⊙O 的半径为13cm ，则过G 点的所有弦中，长度为整数的弦共有( )条．A. 2B. 3C. 4D. 无数 3．如图所示，四边形ABCD 中，DC ∥AB ，BC ＝1，AB ＝AC ＝AD ＝2.则BD 的长为( )A. 14B. 15C. 32D. 234．口袋中有20个球，其中白球9个，红球5个，黑球6个．现从中任取10个球，使得白球不少于2个，但不多于8个，红球不少于2个，黑球不多于3个，那么上述取法的种数是( ) A. 20 B. 18 C. 16 D. 145．如图，矩形ABCD 的对角线BD 经过坐标原点，矩形的边分别平行于坐标轴，点C 在反比例函数y ＝xk k 122++的图象上．若点A 的坐标为(－2，－2)，则k 的值为( ) A ．1B ．－3C ．4D ．1或－36．已知四条直线y ＝kx －3，y ＝－1，y ＝3和x ＝1所围成的四边形的面积是12，则k 的值为( ) A. 1或－2 B. 2或－1 C. 3 D. 4 7．如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm 2，则该半圆的半径为( )A. (4＋5)cmB. 9cmC. 45cmD. 62cm8．已知sin α•cos α＝81，且0º＜α＜45º，则cos α－sin α的值为( )A.23 B. －23 C. 43 D. －439．如图，已知扇形AOB 的半径为12，OA ⊥OB ，C 为OB 上一点，以OA 为直径的半圆O 1；和以BC 为直径的半圆O 2相切于点D ，则图中阴影部分的面积是( )A. 6πB. 10πC. 12πD. 20π10．如果a 和b 为正数，并且方程x ２＋ax ＋2b ＝0和x ２＋2bx ＋a ＝0都有实数根，那么a ＋b 的最小值是( )A. 4B. 5C. 6D. 7 二、填空题：(每小题5分，共40分) 11．若不等式组⎩⎨⎧>->-022x b a x 的解集是－1＜x ＜1，则(a ＋b)2012＝ ．12．如图，已知A 、B 两点的坐标分别为(23，0)、(0，2)，P 是△AOB 外接圆上的一点，且∠AOP ＝45º，则点P 的坐标为 ．13．已知一个半圆形工件，未搬动前如图所示，直径平行于地面放置，搬动时为了保护圆弧部分不受损伤，先将半圆作如图所示的无滑动翻转，使它的直径紧贴地面，再将它沿地面平移50米，半圆的直径为8米，则圆心O 所经过的路线长是 米．14．若对图1中星形截去一个角，如图2，再对图2中的角进一步截去，如图3，则图中的∠A ＋∠B ＋∠C＋∠D＋∠E ＋∠F ＋∠G ＋∠H ＋∠M ＋∠N ＝ 度．15．函数y 1＝|x|，y 1＝31x ＋34，当y 1＞y 2时，x 的范围是 ． 16．若实数a 是方程x ２－2012x ＋1＝0的一个解，则代数式a 2－2011a ＋120122 a 的值为 ．17．已知三个非负实数a 、b 、c 满足：3a ＋2b ＋c ＝5和2a ＋b －3c ＝1，若m ＝3a ＋b －7c ，则m 的最小值为 ．18．如图，在平面直角坐标系中，有若干个整数点，其顺序按图中“→”方向排列，如(1，0)，(2，0)，(2，1)，(3，2)，(3，1)，(3，0)，(4，0)，…，根据这个规律探索可得，第100个点的坐标为 ．三、解答题：(每小题15分，共60分)19．某生姜种植基地计划种植A 、B 两种生姜30亩．已知A 、B 两种生姜的年产量分别为2000千克/亩、2500千克/亩，收购单价分别是8元/千克、7元/千克． (1)若该基地收获两种生姜的年总产量为68000千克，求A 、B 两种生姜各种多少亩？(2)若要求种植A 种生姜的亩数不少于B 种的一半，那么种植A 、B 两种生姜各多少亩时，全部收购该基地生姜的年总收入最多？最多是多少元？20．由直角三角形边角关系，可将三角形面积公式变形，得S △ABC ＝21bc •sin ∠A ①，即三角形的面积等于两边之长与夹角正弦之积的一半．如图，在△ABC 中，CD ⊥AB 于D ，∠ACD ＝α，∠DCB ＝β．∵S △ABC ＝S △ADC ＋S △BDC ，由公式①，得21AC •BC •sin(α＋β)＝21AC •CD •sin α＋21BC •CD •sin β，即AC •BC •sin(α＋β)＝AC •CD •sin α＋BC •CD •sin β②．你能利用直角三角形边角关系，消去②中的AC 、BC 、CD 吗？不能，说明理由；能，写出解决过程．21．如图1，在△ABC 中，AB ＝AC ，∠A ＝90º，O 为BC 的中点，动点E 、F 分别在边AB 、AC 上，且∠EOF ＝45º． (1)猜想线段AE 、EF 、CF 之间的数量关系，并证明你的猜想；(2)如图2，若以O 为圆心的圆与AB 相切，试探究直线EF 与⊙O 的位置关系，并证明你的结论．22．如图，抛物线y ＝ax 2＋bx ＋c 与x 轴交于A 、B 两点(点A 在点B 左侧)，与y 轴交于点C ，且当x ＝0和x ＝2时，y 的值相等．直线y ＝3x －7与这条抛物线相交于两点，其中一点的横坐标是4，另一点是这条抛物线的顶点M ． (1)求这条抛物线的解析式；(2)P 为线段BM 上一点，过点P 向x 轴引垂线，垂足为Q ．若点P 在线段BM 上运动(点P 不与点B 、M 重合)，设OQ 的长为t ，四边形PQAC 的面积为S ．求S 与t 之间的函数关系式及自变量t 的取值范围；(3)在线段BM 上是否存在点N ，使△NMC 为等腰三角形？若存在，请求出点N 的坐标；若不存在，请说明理由．。

CDEB OA注意事项：1. 全卷分A 卷和B 卷，A 卷满分100分，B 卷满分50分；考试时间120分钟．2. 在作答前，考生务必将自己的姓名、准考证号涂写在答题卡(机读卡加答题卷)上。

A 卷（共100分） 第Ⅰ卷（选择题，共30分）一、选择题：（每小题3分，共3 0分)每小题均有四个选项，其中只有一项符合题目要求。

1. 已知b a >则下列不等式中正确的是（ ）A .b a 33->-B . 33ba ->-C .b a ->-33D .33->-b a 2、使不等式15xx +<成立的最小整数是（ ） A. 0 B. 1 C. 2 D. 33. 如图3，在△ABC 中，DE ∥BC ，且AD ：DB ＝1：2，那么DE ：BC 的等于（ ） A.1：3 B.1：2 C.2：3 D.3：24.若函数b kx y +=(b k ,为常数)的图象如图4所示，那么当0>y 时，x 的取值范围是( ) A.1>xB.2>xC.1<xD.2<x5.如图，在△AOB 中，∠B=30°.将△AOB 绕点O 顺时针旋转52°得到△DOE ，边DE 与OB 交于点C (D 不在OB 上)，则∠DCO 的度数为（ ） A.22° B.52° C.60° D.82°6. 甲、乙两人同时从A 地出发，骑自行车行30千米到B 地，甲比乙每小时少走3千米，结果乙先到40分钟，若设乙每小时走x 千米，则可列方程（ ） A.3030233x x -=- B.3030233x x -=+ C.3030233x x -=+ D.3030233x x -=- 7.若关于x 方程1011m xx x --=--有增根,那么m 的值 为( )A.3B. 2C.1D.-1 8. 函数xx21y -=中自变量的取值范围是（ ） A. x ≤21且x ≠0 B.x ＞21-且x ≠0 C.x ≠0 D.x ＜21且x ≠09.如图5，已知DE ∥BC ，EF ∥AB ， 则下列比例式中错误的是（ ） A.AC AE AB AD = B. FB EACF CE =C. BD ADBC DE =D. CB CF AB EF =10.若三角形的三边长分别为a 、b 、c ，满足03222=-+-b c b c a b a ，则这个三角形是（ ） A 、等腰三角形 B 、直角三角形 C 、等边三角形 D 、三角形的形状不确定第Ⅱ卷(非选择题，共7()分)二、填空题：(每小题4分，共l 6分) 11. 如果2925x y x y +=-，那么x ：y= 。

2012～2013学年度第一学期八年级数学试卷姓名--------------分数-------------一．选择题（每小题3分，共30分）1. 化简22x yx y--的结果…………………………………………………………… ……【 】 A.x ＋y B.x －y C.y － x D.－x －y2.从∠A 、∠B 、∠C 、∠D 的度数之比中，能判定四边形ABCD 是平行四边形的是…………【 】A.1∶2∶3∶4B.2∶2∶3∶3C.2∶3∶2∶3D.1∶2∶2∶33.下面的性质中,平行四边形不一定具有的是……………………………………… 【 】Ａ.对角互补 Ｂ.邻角互补 Ｃ.对角相等 Ｄ.对边相等4. 平行四边形一边长12cm ，那么它的两条对角线的长度可能是……………………【 】A.8cm 和16cmB.10cm 和16cmC.8cm 和14cmD.8cm 和12cm5．下列命题中正确的是……………………………………………………………………【 】 A.对角线互相平分的四边形是菱形 B.对角线互相平分且相等的四边形是菱形 C.对角线互相垂直的四边形是菱形 D.对角线互相垂直平分的四边形是菱形 6. 如图，D 是△ABC 内一点，BD ⊥CD ，BD=4，CD=3，E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点，且四边形EFGH 的周长是14，则AD 的长是……………………【 】 A.5 B.7 C.8 D.9 7. 给出四个特征：(1)两条对角线相等；(2)任一组对角互补；(3)任一组邻角互补； (4)是轴对称图形但不是中心对称图形.其中属于矩形和等腰梯形共同具有的特征的共有…………………………………………【 】 A.1个 B.2个 C.3个 D.4个8．下列说法中错误的是……………………………………………………………… ……【 】A ．两条对角线互相平分的四边形是平行四边形；B ．两条对角线互相垂直的矩形是正方形；C ．两条对角线相等的四边形是矩形；D ．两条对角线相等的菱形是正方形．9．如图，将一边长为12的正方形纸片ABCD 的顶点A 折叠至DC 边上的点E ，使DE ＝5，折痕为PQ ，则PQ 的长为……………………………………………………………【 】A.12B.13C.14D.1510. 在□ABCD 中，点A 1、A 2、A 3、A 4和C 1、C 2、C 3、C 4分别是AB 和CD 的五等分点，点B 1、B 2、和D 1、D 2分别是BC 和DA 的三等分点，已知四边形A 4B 2C 4D 2的面积为1，则□ABCD 的面积为……………【 】 A.2 B.53 C.35D.15二、填空题（每小题4分，共16分）11. 在□ABCD 中，若∠A －∠B ＝40°，则∠A ＝______，∠B ＝______． 12. 菱形两对角线长分别为24cm 和10cm,则菱形的高为__________13. 如图，梯形ABCD 中，AD ∥BC ，AB ＝CD ＝AD ＝1，∠B ＝60°，直线MN 为梯形ABCD 的对称轴，P 为MN 上一点，那么PC ＋PD 的最小值为______．14．已知：四边形ABCD 中,AD ∥BC.分别添加下列条件∶①AB ∥CD ；②AB=DC ；③AD=BC ；④∠A=∠C ⑤∠B=∠C.能使四边形成为平行四边形的条件的序号有____________.（把你认为正确的序号都填在横线上）三. 解答题（共54分）15. (本小题满分6分) 在等腰梯形ABCD 中，AD ∥BC ，E 是AD 的中点，求证：BE=CE.第6题图第9题图第13题图第15题图第10题图16．(本小题满分8分) 如图,平行四边形ABCD 中,AE ⊥BD,CF ⊥BD,垂足分别为E 、F,求证：四边形AECF 是平行四边形. 【证明】17. (本小题满分8分) 如图所示，折叠矩形的一边AD ，使点D 落在BC 边上的点F 处，已知AB=8cm ，BC=10cm ，求EC 的长. 【解】18. (本小题满分10分) 已知：如图，在□ABCD 中，E 、F 分别为边AB 、CD 的中点，BD 是对角线，AG ∥DB交CB 的延长线于G. (1)求证∶△ADE ≌△CBF ；(2)若四边形 BEDF 是菱形，则四边形AGBD 是什么特殊四边形？并证明你的结论. 【证明】19. (本小题满分10分) 如图，四边形ABCD 、AEFG 均为正方形连接DE 、BG ，试判断DE 与BG 的关系，并加以证明． 【证明】20. (本小题满分12分) 如图，在直角坐标系中，矩形OABC 的顶点O 与坐标原点重合，顶点A ，C 分别在坐标轴上，顶点B 的坐标为（4，2）．过点D （0，3）和E （6，0）的直线分别与AB ，BC 交于点M ，N ．（1）求直线DE 的解析式和点M 的坐标； （2）若反比例函数xmy =（x ＞0）的图象经过点M ，求该反比例函数的解析式，并通过计算判断点N 是否在该函数的图象上； （3）若反比例函数xmy =（x ＞0）的图象与△MNB 有公共点，请直接．．写出m 的取值范围____________； （4）试写出：过MB 中点且把矩形OABC 的面积平均分成两部分的直线的解析式是________________.【解】参考答案一、1A 2C 3A 4B 5D 6D 7B 8C 9B 10C 二、11.110° 70° 12.12013①③④ 三、15.∵ABCD 是等腰梯形，AD ∥BC ，∴AB=DC ，∠A=∠D …………2分 又∵E 是AD 中点，∴AE=DE ，∴△ABE ≌△DCE(SAS)…………4分 ∴BE=CE …………6分16.∵AE ⊥BD,CF ⊥BD ，∴∠AEB=∠CFD=90°，AE ∥CF ，………3分 又∵ABCD 是平行四边形，∴ AB=CD ，AB ∥CD ，∠ABE=∠CDF ， ∴△ABE ≌△DCF(AAS)…………6分 ∴AE=CF …………7分，∴AECF 是平行四边形.…………………8分17.由题意：AF=AD=10，AB=8，由勾股定理得：BF=6， ∴FC=4，……4分设CE=x ，则EF=DE=8－x ，……6分第19题图 第18题图第16题图第17题图 第20题图第16题图再由勾股定理得：()22284x x -=+，解得x=3，∴EC=3cm.……8分18. （1）∵四边形ABCD 是平行四边形， ∴∠1＝∠C ，AD ＝CB ，AB ＝CD .………2分 ∵点E 、F 分别是AB 、CD 的中点，∴AE ＝21AB ，CF ＝21CD.∴AE ＝CF .…………4分∴△ADE ≌△CBF .………………………5分（2）当四边形BEDF 是菱形时，四边形 AGBD 是矩形. ∵四边形ABCD 是平行四边形，∴AD ∥BC .∵AG ∥BD ，∴四边形 AGBD 是平行四边形.……7分 ∵四边形 BEDF 是菱形，∴DE ＝BE . ∵AE ＝BE ， ∴AE ＝BE ＝DE .∴∠1＝∠2，∠3＝∠4.∵∠1＋∠2＋∠3＋∠4＝180°， ∴2∠2＋2∠3＝180°.∴∠2＋∠3＝90°.即∠ADB ＝90°.……9分 ∴四边形AGBD 是矩形.…………………10分19.DE=BG 且DE ⊥BG.………………2分 理由是：ABCD 、AEFG 是正方形 ∴AD=AB ，AE=AG ，∠DAB=∠GAE=90°，……4分 ∴∠DAB ＋∠BAE=∠GAE ＋∠BAE ， 即∠DAE=∠BAG∴△DAE ≌△BAG(SAS)∴DE=BG ……………………………6分 延长DH 交BG 于H ， ∵△DAE ≌△BAG ，∴∠ABH=∠EDA ，∠AED=∠BEH∴∠BEH ＋∠ABH=∠AED ＋∠EDA=90°……8分 ∴∠BHE=90°即DP ⊥EF ……………………10分20.解：（1）设直线DE 的解析式为y=kx ＋b∵点D （0,3）和E （6，0）在图象上∴360b k b =⎧⎨+=⎩→⎪⎩⎪⎨⎧=-=321b k ∴直线DE 的关系式为：y=12x -+3 ………………………2分 当y=2时，12-x+3=2得x=2 ∴点M 的坐标为（2,2）……………………………………4分 （2）由（1）知：m=2×2=4∴反比例函数的解析式为y= x4 …………………………6分将x=4代入y=12x -+3得y=1 即点N 坐标为（4,1），而4×1=4∴点N 在其图象上 ……………………………………………8分 （3）4≤m ≤8………………………………………………………10分 （4）y=x －1…………………………………………………………12分。

成都市2012—2013学年度上期八年级数学半期考试题考试时间：120分钟 试卷满分：150分A 卷（100分）一、选择题.（每题3分，共30分）1、下列数组中，不是勾股数的是（ ）A. 3、4、5B. 9、12、15C. 7、24、25D. 1.5、2、2.5 2、下列各式中正确的是（ ）A.7)7(2-=- B.39±= C.4)2(2=- D.33348=-3、在下列实数中：2π-，31，|－3|，4，7-0.8080080008…（每两个8之间依次多一个0），无理数的个数有（ ）A. 1个B. 2个C. 3个D. 4个4、下列语句正确的是（ ）A. - 9的平方根是 – 3B. 9 的平方根是 3C. 9的算数平方根是 – 3D. 9 的算术平方根是 3 5、下列说法中正确的是（ ）A. 四边都相等的四边形是正方形B. 有三个角是直角且有一组邻边相等的四边形是正方形C. 对角线相等且互相垂直的四边形是正方形D. 四个内角都相等的四边形是正方形 6、下列图形既是轴对称图形，又是中心对称图形的是（ ）A. 平行四边形B. 等边三角形C. 等腰梯形D. 菱 形 7、下列条件中，不能判定四边形ABCD 为平行四边形的条件是（ ）A. AB∥CD，AB=CDB. AB∥CD，AD∥BCC. AB=AD, BC=CDD. AB=CD AD=BC 8、正方形具有而菱形不一定具有的性质是 （ ） A. 对角线互相垂直 B. 对角线互相平分 C. 对角线相等 D. 对角线平分一组对角9、当a<-3时,化简2)12(-a +2)3(+a 的结果是( )A. 3a+2B. -3a-2C. 4-aD. a-4 10、已知一直角三角形的面积为10,两直边的和9,则斜边长为( )A. 7B. 9C. 29D. 41 二、填空题.（每题3分，共15分） 11、16的算术平方根是 .12、已知0)10(862=-+-+-z y x ,则由此z y x ,,为三边的三角形是 三角形。