工程力学1-4章
- 格式:ppt
- 大小:2.79 MB
- 文档页数:115

工程力学习题答案第一章 静力学基础知识思考题:1. ×;2. √;3. √;4. √;5. ×;6. ×;7. √;8. √习题一1.根据三力汇交定理,画出下面各图中A 点的约束反力方向。
解:(a )杆AB 在A 、B 、C 三处受力作用。
由于力p 和B R的作用线交于点O 。
如图(a )所示,根据三力平衡汇交定理,可以判断支座A 点的约束反力必沿通过A 、O 两点的连线。
(b )同上。
由于力p 和B R的作用线交于O 点,根据三力平衡汇交定理,可判断A 点的约束反力方向如下图(b )所示。
2.不计杆重,画出下列各图中AB 解:(a )取杆AB 为研究对象,杆除受力p外,在B 处受绳索作用的拉力B T ,在A 和E 两处还受光滑接触面约束。
约束力A N 和E的方向分别沿其接触表面的公法线,并指向杆。
其中力E N与杆垂直,力A N通过半圆槽的圆心O 。
AB 杆受力图见下图(a )。
(b)由于不计杆重,曲杆BC 只在两端受铰销B 和C 对它作用的约束力B N 和C N ,故曲杆BC 是二力构件或二力体,此两力的作用线必须通过B 、C 两点的连线,且B N =C N 。
研究杆A N 和B N,以及力偶m 的作用而平衡。
根据力偶的性质,A N 和B N必组成一力偶。
(d)由于不计杆重,杆AB 在A 、C 两处受绳索作用的拉力A T 和C T,在B 点受到支座反力B N 。
A T 和C T相交于O 点,根据三力平衡汇交定理,可以判断B N必沿通过B 、O 两点的连线。
见图(d).第二章力系的简化与平衡思考题:1. √;2. ×;3. ×;4. ×;5. √;6. ×;7. ×;8. ×;9. √.1.平面力系由三个力和两个力偶组成,它们的大小和作用位置如图示,长度单位为cm ,求此力系向O 点简化的结果,并确定其合力位置。
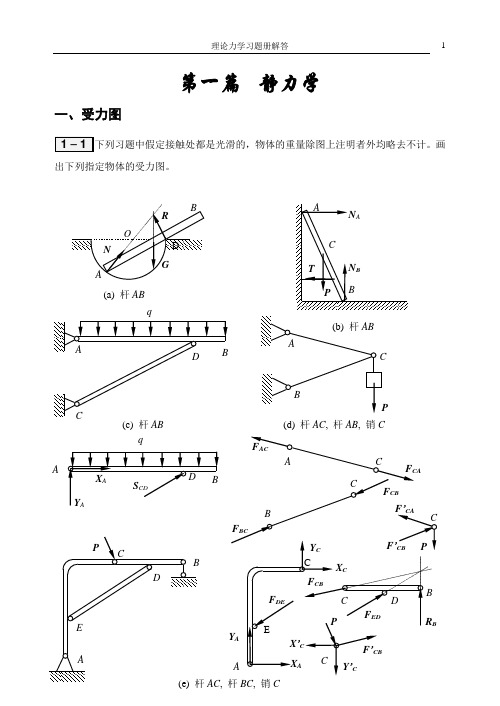
理论力学习题册解答 1第一篇静力学一、受力图出下列指定物体的受力图。
(a) 杆AB(d) 杆AC, 杆AB, 销Cq(c) 杆ABAqAC, 杆BC, 销CBF(d) AB , BCD , DEF理论力学习题册解答 3二、平面汇交力系如图所示图中方格的边长为1cm ,求力系的合力。
[解] 由解析法有N XR X 3.549cos 800cos 750450cos 500cos 10004321=+---==∑θθθθNYR Y 8.382sin 800sin 750sin 500sin 00014321-=--+==∑θθθθ 所以合力R 大小为: N R R R Y X 5.66922=+=R 方向为:2534'︒-==XYR R arctgαP=20KN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示,转动绞车物体便能升起。
设滑轮的大小及其中的摩擦略去不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡态时,试求拉杆AB 和支杆CB 所受的力。
[解]取滑轮B 为研究对象,受力如图所示,列平衡方程:030sin 30cos :0=︒-︒--=∑T F F X CB AB∑=︒--︒-=030cos 30sin :0T P FY CBP T =联立上述方程可解得:(压)拉);64.74(;64.54KN F KN F CB AB -==A 、B 的约束反力。
[解](a) AB 梁受力如图: (b) 构件受力如图:∑=-+⋅=02415,0AB R m A i∑=-⋅︒=045sin ,0Pa l R mA i解得: KN R R B A 5.1== 解得: ;2Pa R R B A ==四连杆机构OABO 1,在图示位置平衡,已知OA =40cm ,O 1B =60cm ,作用在曲柄OA 上的力偶矩大小为m 2=1NM,不计杆重,求力偶矩m 1的大小及连杆AB 所受的力。
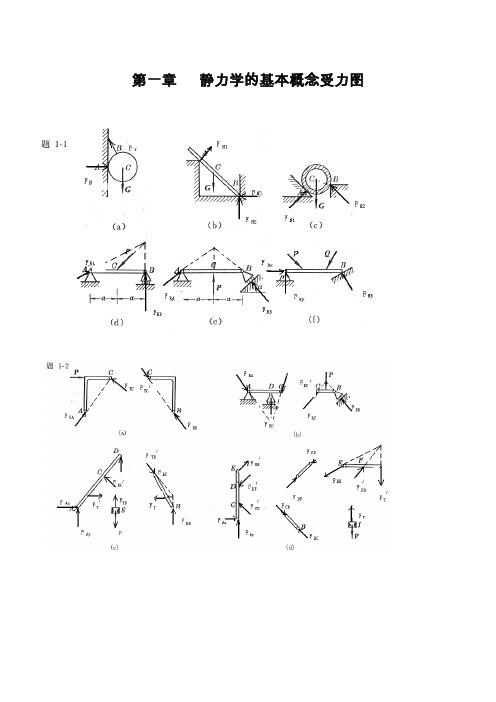
第一章静力学的基本概念受力图第二章 平面汇交力系2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故:22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+= 方向沿OB 。
2-3 解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解:(a )受力分析如图所示:由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解:受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以:5RA F KN= (压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得:7.32AB F KN=-(受压)27.3AC F KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D ,B 点分别列平衡方程(1)取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==(2)取B 点列平衡方程:由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象:由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得: 2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得:2.92RA F KN=1.33DC F KN=(压力)列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得: 1.67AC F KN=(拉力)1.0BC F KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。


第1章 工程静力学的基础例1:用小手锤拔起钉子的两种加力方式。
两种情形下,加在手柄上的力F 的数值都等于100N ,手柄的长度l =100 mm 。
试求:两种情况下,力F 对点O 之矩。
解: 图a 中的情形这种情形下,力臂: O 点到力F 作用线的垂直距离h 等于手柄长度l ,力F 使手锤绕O 点逆时针方向转动,所以F 对O 点之矩的代数值为图b 中的情形这种情形下,力臂 力F 使手锤绕O 点顺时针方向转动,所以F 对O 点之矩的代数值为例2:已知 :作用在托架的A 点力为F 以及尺寸 l 1, l 2 , α . 试求: 力F 对O 点之矩MO (F )解 : 可以直接应用力矩公式计算力F 对O 点之矩。
但是,在本例的情形下,不易计算矩心O 到力F 作用线的垂直距离h 。
如果将力F 分解为互相垂直的两个分力F l 和F 2,二者的数值分别为 这时,矩心O 至F l 和F 2作用线的垂直距离都容易确定。
30N 300100()m 30N m 10300N 100F 3⋅=⨯⨯===-Fl Fh m Ocos30l h =cos30300100cos30()m N 98.52cos30m 10300N 100cos30F 3⋅=⨯⨯⨯===-Fl Fh mO-sin45cos4521F F F F == sin45cos4521F F F F ==于是,应用合力之钜定理 mO (F ) = mO (F cos α)+mO (F sin α) 可以得到例3:具有光滑表面、重力为F W 的圆柱体,放置在刚性光滑墙面与刚性凸台之间,接触点分别为A 和B 二点。
试:画出圆柱体的受力图。
解:1.选择研究对象本例中要求画出圆柱体的受力图,所以,只能以圆柱体作为研究对象。
2.取隔离体将圆柱体从所受的约束中分离出来,即得到圆柱体的隔离体。
3.画受力图作用在圆柱体上的力,有:主动力-圆柱体所受的重力,沿铅垂方向向下,作用点在圆柱体的重心处;约束力-因为墙面和圆柱体表面都是光滑的,所以,在A 、B 二处均为光滑面约束,所以约束力垂直于墙面,指向圆柱体中心;圆柱与凸台间接触也是光滑的,也属于光滑面约束,约束力作用线沿二者的公法线方向,即沿B 点与O 点的连线方向,指向O 点。
工程力学教程(西南交通大学应用力学与工程系
著)课后答案下载
工程力学教程(西南交通大学应用力学与工程系著)内容提要第1章静力学基础
1-1 静力学中的基本概念
1-2 静力学公理
1-3 约束和约束力
1-4 研究对象和受力图
习题
第2章平面汇交力系
2-1 平面汇交力系合成与平衡的几何法
2-2 平面汇交力系合成与平衡的解析法
习题
第3章力矩与平面力偶系
3-1 关于力矩的概念及其计算
3-2 关于力偶的概念
3-3 平面力偶系的合成与平衡
习题
第4章平面一般力量
4-1 力线平移定理
4-2 平面一般力系向一点简化
4-3 分布荷载
4-4 平面一般力系的
工程力学教程(西南交通大学应用力学与工程系著)图书目录
本书是教育科学“十五”国家规划课题研究成果,根据“高等学校工科本科工程力学基本要求”编写而成,涵盖了理论力学和材料力学的主要内容。
本书共18章,包括静力学基础、平面汇交力系、力矩与平面力偶系、平面一般力系、重心和形心、内力和内力图、拉伸和压缩、扭转、弯曲、应力状态分析和强度理论、压杆的稳定性、点的运动、刚体的`基本运动、点的复合运动、刚体的平面运动、质点的运动微分方程、动力学普遍定理、动静法。
本书在讲述某些概念和方法的同时,给出了相关的思考题,供课堂讨论之用。
本书具有很强的教学适用性,有助于培养工程应用型人才。
本书可作为高等学校工科本科非机、非土类各专业中、少学时工程力学课程的教材,也可供高职高专与成人高校师生及有关工程技术人员参考。