2018年南平市初三质检数学试题及答案

2018年南平初中毕业班适应性检测数学试题及答案南平市2018年初中毕业班适应性检测数学试题参考答案及评分说明说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分．（4）评分只给整数分．选择题和填空题不给中间分．第Ⅰ卷一、选择题（本大题共10小题，每小题4分，共40分）（1）C ；（2）A；（3）C；（4）D；（5）D；（6）B ；（7）C；（8）B；（9）C；（10）A．第Ⅱ卷二、填空题（本大题共6小题，每小题4分，共24分）（11）如：（1，1）（答案不唯一）； （12）34； （13）5；（14）()2232+-=x y ； （15）10； （16）15．三、解答题（本大题共9小题，共86分）（17）（本小题满分8分）解：原式2224444a ab b ab a+-++=………………………… 2分2245b a +=， ……………………………………………4分 当32==b a ，时，原式22)3(425⨯+⨯=………………………………………6分 321220=+=． ………………………………………8分（18）（本小题满分8分）解：由①得，2<x ， ………………………………………3分 由②得，22-x ≥2-x ，……………………………………5分x ≥0 ， …………………………………… 6分所以不等式组的解集是0≤x ＜2． ……………………………8分（19）（本小题满分8分） 证明：∵△ABC ≌△BDE ，∴∠DBE=∠A , BE = AC ， …………………4分∵∠DBE=∠A ， ∴BE ∥AC ，…………………………………6分又∵BE = AC ，∴四边形ABEC 是平行四边形． …………8分（20）（本小题满分8分）（Ⅰ）确定点P ，E ，F ，各得1分，图形完整得1分，C B D E A（第19题图） F E P O D A C （第20题（Ⅰ）答题图）共4分；（Ⅱ）证明：∵∠DOC=∠ODP ，∴PD ∥OC ， ∴∠EDP=∠EFO ， …………………………5分∵PD =PE ， ∴∠PED=∠EDP ， …………………………6分∴∠PED=∠EFO ， …………………………7分∴OE=OF ． …………………………………8分 （21）（本小题满分8分）（Ⅰ）填空：a =2，b =10； …………………………………2分（Ⅱ）21015232251=⨯+⨯+⨯+⨯………………4分 答：这所学校平均每班贫困学生人数为2；（Ⅲ）设有2名贫困家庭学生的2个班级分别记为A 班和B 班，方法一： 列表：A 1A 2B 1B 2准确列表……………………………………………………………6分方法二： 树状图：A 212A 11B 2121B 2221B 1准确画出树状图 ……………………………………………………6分∴P （两名学生来自同一班级）＝31124=． ……………………8分 （22）（本小题满分10分） 解：（Ⅰ）把A （1，3）代入xy 12=中得，313=⨯=k ，A 1 （ A 1， A 2） （ A 1，B 1） （ A 1， B 2） A 2 （ A 2， A 1） （ A 2， B 1） （ A 2， B 2） B 1 （ B 1， A 1） （ B 1， A 2） （ B 1， B 2） B 2 （ B 2， A 1） （ B 2， A 2） （ B 2， B 1）Ay x O BC 1 C 2 C 3 （C （第22题∴反比例函数的解析式为xy 3=， ……3分 把B （c ，-1）代入xy 3=中，得3-=c ， 把A （1，3）,B （-3，-1）代入b ax y +=中得， ⎩⎨⎧-=+-=+133b a b a ，∴⎩⎨⎧==21b a ，∴一次函数的解析式为2+=x y ； ……6分 （Ⅱ）这样的点有4个，………………………8分C 2（3，1）或C 4（-3，-1）． (10)分（23）（本小题满分10分）（Ⅰ）证明：连接AC ，∵∠A+∠CDB =180， ………1分 ∠BDE+∠CDB =180°，………2分 ∴∠A=∠BDE ， ……………3分 ∵∠COE=2∠A ， ……………4分 ∴∠COE=2∠BDE ；…………5分 （Ⅱ）解：过C 点作CF ⊥AE 于F 点，∵∠BDE =60°， ∴∠A =60°， …………………………………………………………6分EA OBC D （第23题答题图）F又∵OA =OC ，∴△AOC 是等边三角形，∵OB =2，∴OA =AC =2，∴121===AO FO AF ， …………………………………………7分在Rt △AFC 中，∴ ，…………………………8分在Rt △CEF 中，EF =FO +OB +BE =5， ∴53tan ==EF CF E ． ………………………………………………10分（24）（本小题满分12分）（Ⅰ）证明：∵∠ADB=∠BEC=60°，∴等腰△ADB 和等腰△BEC 是等边三角形，………1分∴BD =BA，BE=BC，∠DBA=∠EBC=60°，………2分∴312222=-=-=AF ACCF E D CBA（第24∠DBA -∠EBA=∠EBC -∠EBA ，∴∠DBE=∠ABC ， …………………3分 ∴△DBE ≌△ABC （SAS ）；……………4分 （Ⅱ）解：（i ）∵∠ADB=90°， DB =DA ， ∴∠DBA=45°，同理∠EBC=45°， ∴∠DBA=∠EBC ，∴∠DBA -∠EBA=∠EBC -∠EBA ， ∴∠DBE=∠ABC ，……………………5分 又∵cos ∠DBA = cos ∠EBC ，∴22==BCBE AB DB ， ……………6分∴△DBE ∽△ABC ， …………………7分∴BC BE AC DE =，即222=DE ， ∴ ； ……………………8分 （ii ）223≤CD ≤227． ………12分E D CBA （第24题2=DE ED C B A（第24（25）（本小题满分14分）（Ⅰ）解：当p =2时，把x =2带入421+-=xy 中得，1=y ，∴A（2，0），……………………………………………………1分把y 2=2带入44122+-=x y （x >0）中得，x =4， ∴C（4，0），……………………………………………………2分∴AC =2； ……………………………………………………3分（Ⅱ）解：设)441,(),4,(22+-+-p p B p p A ，则)441,0(),4,0(22+-+-p F pE ，∵M （0，4）， ∴22)4(4p pME =+--=，4)441(422p p MF =+--=， (5)E D C BA（第24题分 当44121+-=p y时，444122+-=+-x p ，∴p xD21=， 当422+-=p y 时，441422+-=+-x p ， ，∴pxC2=，∴)4,2(2+-pp C ,)441,2(2+-p p D ，∴221pp p BD =-=， pp p AC =-=2， ……………………………………7分∴8412212122=⋅⋅=⋅⋅=∆∆p p p p MF BD MEAC SSBDMACM ；………………8分（Ⅲ）证明：方法一：设直线AD ：b kx y +=， 把)441,21(),4,(22+-+-p p D pp A 代入得：⎪⎩⎪⎨⎧+-=++-=+44121422p b kp p b kp ，解得⎪⎪⎩⎪⎪⎨⎧+=-=421232p b p k ，∴直线AD ：421232++-=p px y ； (10)分设直线BC ：b x k y '+'=， 把)441,(),4,2(22+-+-p p B pp C 代入得：⎪⎩⎪⎨⎧+-='+'+-='+'4414222p b k p p b k p ，解得⎪⎪⎩⎪⎪⎨⎧+='-='421432p b p k ，∴直线BC ：421432++-=p px y ；………………………12分∵直线AD 与BC 的交点为N(m,n)， ∴⎪⎪⎩⎪⎪⎨⎧++-=++-=421234214322p pm n p pm n ， (13)分∴043=pm ， ∵p >0，∴m=0，即m 为常数．…………………14分方法二： 设直线AD交y 轴于G 点，直线BC 交y 轴于H点，∵BF ∥CE ，∴△GFD ∽△GEA ，△HFB ∽△HEC ，…10分 ∴2121===p p AE DF GE GF ，212===p p CE BF HE HF ，∴HE HF GE GF =，………………………11分 ∴FEHF HFFE GF GF +=+， M D C B A O xyx=p F EG H （第25题y 1 y 2∴HFGF ，…………………………13分∴G、H点重合，∴G、H点就是直线AD与直线BC的交点N，∴m=0，即m为常数． (1)。

南平市2018年初中毕业班适应性检测数学试题参考答案及评分说明说明：（1） 解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2） 对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3） 若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分． （4） 评分只给整数分．选择题和填空题不给中间分．第Ⅰ卷一、选择题（本大题共10小题，每小题4分，共40分） （1）C ； （2）A ； （3）C ； （4）D ； （5）D ； （6）B ； （7）C ； （8）B ； （9）C ； （10）A ．第Ⅱ卷二、填空题（本大题共6小题，每小题4分，共24分） （11）如：（1，1）（答案不唯一）； （12）34； （13）5； （14）()2232+-=x y ； （15）10； （16）15． 三、解答题（本大题共9小题，共86分） （17）（本小题满分8分）解：原式2224444a ab b ab a +-++=………………………… 2分 2245b a +=， ……………………………………………4分当32==b a ，时，原式22)3(425⨯+⨯=………………………………………6分321220=+=． ………………………………………8分（18）（本小题满分8分）解：由①得，2<x ， ………………………………………3分由②得，22-x ≥2-x ，……………………………………5分x ≥0 ， …………………………………… 6分 所以不等式组的解集是0≤x ＜2． ……………………………8分（19）（本小题满分8分）证明：∵△ABC ≌△BDE ，∴∠DBE=∠A , BE = AC ， …………………4分 ∵∠DBE=∠A ，∴BE ∥AC ，…………………………………6分 又∵BE = AC ，∴四边形ABEC 是平行四边形． …………8分CB A（Ⅰ）确定点P ，E ，F ，各得1分，图形完整得1分，共4分； （Ⅱ）证明：∵∠DOC=∠ODP ，∴PD ∥OC ，∴∠EDP=∠EFO ， …………………………5分 ∵PD =PE ，∴∠PED=∠EDP ， …………………………6分 ∴∠PED=∠EFO ， …………………………7分 ∴OE=OF ． …………………………………8分（21）（本小题满分8分）（Ⅰ）填空：a =2，b =10； …………………………………2分（Ⅱ）21015232251=⨯+⨯+⨯+⨯………………4分答：这所学校平均每班贫困学生人数为2；（Ⅲ）设有2名贫困家庭学生的2个班级分别记为A 班和B 班， 方法一： 列表：准确列表……………………………………………………………6分准确画出树状图 ……………………………………………………6分 ∴P （两名学生来自同一班级）＝31124=． ……………………8分 F E PO D AC （第20题（Ⅰ）答题图）（22）（本小题满分10分） 解：（Ⅰ）把A （1，3）代入xy 12=中得，313=⨯=k ， ∴反比例函数的解析式为x y 3=， ……3分把B （c ，-1）代入xy 3=中，得3-=c ，把A （1，3）,B （-3，-1）代入b ax y +=中得， ⎩⎨⎧-=+-=+133b a b a ，∴⎩⎨⎧==21b a ， ∴一次函数的解析式为2+=x y ； ……6分（Ⅱ）这样的点有4个，………………………8分C 2（3，1）或C 4（-3，-1）． …………10分（23）（本小题满分10分）（Ⅰ）证明：连接AC ， ∵∠A+∠CDB =180， ………1分 ∠BDE+∠CDB =180°，………2分 ∴∠A=∠BDE ， ……………3分 ∵∠COE=2∠A ， ……………4分 ∴∠COE=2∠BDE ；…………5分（Ⅱ）解：过C 点作CF ⊥AE 于F 点，∵∠BDE =60°，∴∠A =60°， …………………………………………………………6分 又∵OA =OC ，∴△AOC 是等边三角形，∵OB =2，∴OA =AC =2，∴121===AO FO AF ， …………………………………………7分 在Rt △AFC 中，∴ ，…………………………8分在Rt △CEF 中，EF =FO +OB +BE =5， ∴53tan ==EF CF E ． ………………………………………………10分 （24）（本小题满分12分）（Ⅰ）证明：∵∠ADB=∠BEC=60°，∴等腰△ADB 和等腰△BEC 是等边三角形，………1分 ∴BD =BA ，BE=BC ，∠DBA=∠EBC=60°，………2分 ∴∠DBA -∠EBA=∠EBC -∠EBA ， ∴∠DBE=∠ABC ， …………………3分 ∴△DBE ≌△ABC （SAS ）；……………4分 （Ⅱ）解：（i ）∵∠ADB=90°， DB =DA ， ∴∠DBA=45°，同理∠EBC=45°， ∴∠DBA=∠EBC ，∴∠DBA -∠EBA=∠EBC -∠EBA ， ∴∠DBE=∠ABC ，……………………5分 312222=-=-=AF AC CF EA B CD （第23题答题图） F （第22题（Ⅱ）答题图）EDCBA（第24题图1）∴22==BC BE AB DB ， ……………6分 ∴△DBE ∽△ABC ， …………………7分∴BCBEAC DE =，即222=DE ， ∴ ； ……………………8分（ii ）223≤CD ≤227． ………12分（25）（本小题满分14分）（Ⅰ）解：当p =2时，把x =2带入421+-=x y 中得，01=y ， ∴A （2，0），……………………………………………………1分 把y 2=2带入44122+-=x y （x >0）中得，x =4， ∴C （4，0），……………………………………………………2分 ∴AC =2； ……………………………………………………3分 （Ⅱ）解：设)441,(),4,(22+-+-p p B p p A ， 则)441,0(),4,0(22+-+-p F p E ， ∵M （0，4），∴22)4(4p p ME =+--=，4)441(422p p MF =+--=，……………………………5分当44121+-=p y 时，444122+-=+-x p ，∴p x D 21=，当422+-=p y 时，441422+-=+-x p ， ，∴p x C 2=，EDCB A（第24题（ii ）答题图1）ED CBA（第24题（ii ）答题图2）2=DE E DCB A（第24题图2）∴)4,2(2+-p p C ,)441,2(2+-p pD ， ∴221pp p BD =-=，p p p AC =-=2， ……………………………………7分 ∴8412212122=⋅⋅=⋅⋅=∆∆ppp p MF BD ME AC S S BDM ACM；………………8分（Ⅲ）证明：方法一：设直线AD ：b kx y +=， 把)441,21(),4,(22+-+-p p D p p A 代入得：⎪⎩⎪⎨⎧+-=++-=+44121422p b kp p b kp ，解得⎪⎪⎩⎪⎪⎨⎧+=-=421232p b p k ，∴直线AD ：421232++-=p px y ；……………………10分设直线BC ：b x k y '+'=， 把)441,(),4,2(22+-+-p p B p p C 代入得：⎪⎩⎪⎨⎧+-='+'+-='+'4414222p b k p p b k p ，解得⎪⎪⎩⎪⎪⎨⎧+='-='421432p b pk ，∴直线BC ：421432++-=p px y ；………………………12分∵直线AD 与BC 的交点为N(m,n)， ∴⎪⎪⎩⎪⎪⎨⎧++-=++-=421234214322p pm n p pm n ， ………13分 ∴043=pm ，∵p >0， ∴m=0，即m 为常数．…………………14分 方法二： 设直线AD 交y 轴于G 点，直线BC 交y 轴于H 点，∵BF ∥CE ，∴△GFD ∽△GEA ，△HFB ∽△HEC ，…10分 ∴2121===p pAE DFGE GF ，（第25题（Ⅲ）答题图）212===p p CE BF HE HF ， ∴HEHF GE GF =，………………………11分 ∴FEHF HF FE GF GF +=+， ∴HF GF =，…………………………13分 ∴G 、H 点重合，∴G 、H 点就是直线AD 与直线BC 的交点N ， ∴m=0，即m 为常数． (1)。

南平市2017-2018学年第一学期九年级期末质量检测数学试题（满分：150分；考试时间：120分钟）★友情提示：① 所有答案都必须填在答题卡相应的位置上，答在本试卷上一律无效； ② 试题未要求对结果取近似值的，不得采取近似计算．一、选择题（本大题共10小题，每小题4分，共40分．每小题只有一个正确的选项，请在答题卡．．．的相应位置填涂） 1．在平面直角坐标系中，点M （1，﹣2）与点N 关于原点对称，则点N 的坐标为A ．（﹣2， 1）B ．（1，﹣2）C ．（2，-1）D ．（-1，2） 2．用配方法解一元二次方程0122=-+x x ，可将方程配方为A ．()212=+x B ．()012=+x C ．()212=-x D ．()012=-x3．下列事件中，属于随机事件的有①任意画一个三角形，其内角和为360°； ②投一枚骰子得到的点数是奇数； ③经过有交通信号灯的路口，遇到红灯； ④从日历本上任选一天为星期天．A ．①②③B ．②③④C ．①③④D ．①②④ 4．下列抛物线的顶点坐标为(4，－3)的是A ．()342-+=x y B ．()342++=x y C ．()342--=x y D ．()342+-=x y5．有n 支球队参加篮球比赛，共比赛了15场，每两个队之间只比赛一场，则下列方程中符合题意的是A ．()151=-n nB ．()151=+n nC ．()301=-n nD ．()301=+n n 6．某小组在“用频率估计概率”的实验中，统计了某种结果出现的频率，绘制了如图所示的折线图，那么符合这一结果的实验最有可能的是次数5000 4000 3000 2000 1000A ．袋子中有1个红球和2个黄球，它们只有颜色上的区别，从中随机地取出一个球是黄球B ．掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6C ．在“石头、剪刀、布”的游戏中，小宇随机出的是“剪刀”D ．掷一枚质地均匀的硬币，落地时结果是“正面向上”7．如果一个正多边形的中心角为60°，那么这个正多边形的边数是A ．4B ．5C ．6D ．78．已知点A （x 1，y 1），B （x 2，y 2）是反比例函数xy 1-=的图象上的两点，若x 1＜0＜x 2，则下列结论正确的是 A ．y 1＜0＜y 2B ．y 2＜0＜y 1C ．y 1＜y 2＜0D ．y 2＜y 1＜09．如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ， 且CO =CD ，则∠PCA =A ．30°B ．45°C ．60°D ．67.5° 10．如图，在Rt △ABC 和Rt △ABD 中，∠ADB =∠ACB =90°，∠BAC =30°，AB =4，AD =22，连接DC ，将Rt △ABC 绕点B 顺时针旋转一周，则线段DC 长的取值范围是 A ．2≤DC ≤4 B ．22≤DC ≤4 C ．222-≤DC ≤22 D ．222-≤DC ≤222+二、填空题（本大题共6小题，每空4分，共24分．将答案填入答题卡．．．的相应位置） 11．如图，在平面直角坐标系xoy 中，矩形OABC ，OA =2，OC =1，（第11题图）DCB OA P（第9题图）CDA B（第10题图）写出一个函数()0≠=k xky ，使它的图象与矩形OABC 的边有两个公共点，这个函数的表达式可以为 （答案不唯一）．12．已知关于x 的方程032=++a x x 有一个根为﹣2，a = ．13．圆锥的底面半径为7cm ，母线长为14cm ，则该圆锥的侧面展开图的圆心角为 °．14．设O 为△ABC 的内心，若∠A =48°，则∠BOC = °．15．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF =CD =4cm ，则球的半径为 cm ． 16． 抛物线c bx ax y ++=2（a >0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，则a 的取值范围是 ．三、解答题（本大题共9小题，共86分．在答题卡．．．的相应位置作答） 17．解方程（每小题4分，共8分）（1）022=+x x （2）01232=-+x x18．（8分）已知关于x 的方程 )0(03)3(2≠=+++k x k kx ．（1）求证：方程一定有两个实数根；（2）若方程的两个实数根都是整数，求正整数k 的值．19．（8分）有甲、乙两个不透明的布袋，甲袋中有3个完全相同的小球，分别标有数字0，1和2；乙袋中有3个完全相同的小球，分别标有数字1，2和3，小明从甲袋中随机取出1个小球，记录标有的数字为x ，再从乙袋中随机取出1个小球，记录标有的数字为y ，这样确定了点M 的坐标(x ，y )．D（第15题图）（1）写出点M 所有可能的坐标； （2）求点M 在直线3+-=x y 上的概率．20．（8分）如图，直线y =x +2与y 轴交于点A ，与反比例函数()0≠=k xky 的图象交于点C ，过点C 作CB ⊥x 轴于点B ，AO =2BO ，求反比例函数的解析式．21．（8分）如图，12×12的正方形网格中的每个小正方形的边长都是1，正方形的顶点叫做格点．矩形ABCD 的四个顶点A ，B ，C ，D 都在格点上，将△ADC 绕点A 顺时针方向旋转得到△AD ′C ′，点C 与点C ′为对应点．（1）在正方形网格中确定D ′的位置，并画出△AD ′C ′；（2）若边AB 交边C ′D ′于点E ，求AE 的长．22．（10分）在矩形ABCD 中，AB =8，BC =6，将矩形按图示方式进行分割，其中正方形AEFG 与正方形JKCI 全等，矩形GHID 与矩形EBKL 全等．（1）当矩形LJHF 的面积为43时，求AG 的长；（第21题图）LH I K JF DBCAG （第22题图）（2）当AG 为何值时，矩形LJHF 的面积最大．23．（10分）如图，点A ，C ，D ，B 在以O 点为圆心，OA 长为半径的圆弧上， AC=CD=DB ，AB 交OC 于点E ．求证：AE =CD ．24．（12分）如图，在等边△BCD 中，DF ⊥BC 于点F ，点A 为直线DF 上一动点，以B 为旋转中心，把BA 顺时针方向旋转60°至BE ，连接EC ． （1）当点A 在线段DF 的延长线上时，①求证：DA =CE ；②判断∠DEC 和∠EDC 的数量关系，并说明理由；（2）当∠DEC =45°时，连接AC ，求∠BAC 的度数．E DF BCA（第24题图）OABCDE（第23题图）25．（14分）如图，在平面直角坐标系xoy 中，二次函数c bx ax y ++=2（0≠a ）的图象经过A （0，4），B （2，0），C （-2，0）三点．（1）求二次函数的解析式；（2）在x 轴上有一点D （-4，0），将二次函数图象沿DA 方向平移，使图象再次经过点B ．①求平移后图象顶点E 的坐标； ②求图象 A ，B 两点间的部分扫过的面积．南平市2017-2018学年第一学期九年级期末质量检测数学试题参考答案及评分说明说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未（第25题图）改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分．（4）评分只给整数分．选择题和填空题不给中间分． 一、选择题（本大题共10小题，每小题4分，共40分）1．D ； 2．A ； 3．B ； 4．C ； 5．C ； 6．B ； 7．C ； 8．B ； 9．D ； 10．D ．二、填空题（本大题共6小题，每小题4分，共24分）11．如：xy 1=（答案不唯一，0＜k ＜2的任何一个数）； 12．2； 13．180； 14．114；15．2.5； 16．0＜a ＜3.三、解答题（本大题共9小题，共86分） 17.（每小题4分，共8分）(1) 解： 0)2(=+x x ……………………………………………………………2分∴2,021-==x x .……………………………………………………4分（2）解：1,2,3-===c b a∴ 161-34-22=⨯⨯=∆）（ ∴64232162±-=⨯±-=x …………………………………………2分 ∴1,3121-==x x . (4)分18．（8分）（1）证明：9634)3(22+-=⋅⋅-+=∆k k k k0)32≥-=k （，……………………………………………………2分 ∴方程一定有两个实数根. …………………………………………3分（2）解：3,3,=+==c k b k a ，22)3(34)3-=⋅⋅-+=∆∴k k k （，kk k k k k x 2)3(32)3()3(2-±--=-±+-=∴， kx x 3,121-=-=∴ ，………………………………………………6分 ∵方程的两个实数根都是整数，∴正整数31或=k ．…………………………………………………8分19．（8分）解：（1）方法一：列表：从表格中可知，点M 坐标总共有九种可能情况：（0,1），（0,2），（0,3），（1,1），（1,2），（1,3），（2,1），（2,2），（2,3）．……………………………………………………………3分 方法二：从树形图中可知，点M 坐标总共有九种可能情况：（0,1），（0,2），（0,3），（1,1），（1,2），（1,3），（2,1），（2,2），（2,3）．……………………………………………………………3分 （2）当x =0时，y=-0+3=3，当x =1时，y=-1+3=2，当x =2时，y=-2+3=1，……………………………………………………6分由（1）可得点M 坐标总共有九种可能情况，点M 落在直线y =-x +3上（记为事件A ）有3种情况．∴P(A )3193==．…………………………………………8分20．（8分）解： 当x =0时，y =2，∴A (0，2)，…………………………………2分∴A O=2，∵AO =2BO ，∴B O=1，………………………………………………4分 当x =1时，y =1+2=3，∴C (1，3)， ……………………………………………6分把C (1，3)代入xky =，解得：3=k xy 3:=∴反比例函数的解析式为…………………………………………………8分21．（8分）解：（1）准确画出图形；…………………………………………………1 0 2321321321甲袋：乙袋：3分（2）∵将△ADC 绕点A 顺时针方向旋转得到△AD ′C ′，点C 与点C ′为对应点，∴△ADC ≌△AD ′C ′，∴AC =AC ′，AD ′＝AD =5，CD ′＝CD =10，∠AD ′C ′＝∠ADC ＝90°，∠AC ′D ′＝∠ACD ，∵AB ∥CD ，∴∠BAC ＝∠ACD ，∵AB ⊥C C ′，AC =AC ′，∴∠BAC ＝∠C ′AB ， ∴∠AC ′D ′＝∠C ′AB，∴C ′E＝AE ．…………………………………………………5分222R E C BE B C BE C t '=+''∆中，在，x AE AB BE x AE -10-,===则设，222)-105x x =+（，……………………………………………………………………7分425:=x 解得.425的长为答：AE ……………………………………………………………………8分（第21题答题图）22．（10分）解：（1） 正方形AEFG 和正方形JKCI 全等，矩形GHID 和矩形EBKL 全等，设AG =x ，DG =6-x ，BE =8-x ，FL=x -(6-x )=2x -6，LJ =8-2x ， 方法1： LJ FL S LIH F ⋅=矩形 ，∴43)28)(62(=--x x ………………………………………………………………2分∴415,41321==x x ，∴AG =413或AG =415．………………………………………4分 方法2：AEFG D G H I ABCD LIH F S S S S 正方形矩形矩形矩形22--=)6)(8(2248432x x x ----=∴，…………………………………………………2分∴415,41321==x x ，∴AG =413或AG =415．………………………………………4分（2）设矩形LJHF 的面积为S ，)28)(62(x x S --=…………………………………………………………………6分482842-+-=x x1)27(42+--=x …………………………………………………………………8分04<-=a ， ∴S 有最大值，∴当AG =27 时，矩形LJHF 的面积最大．………………………………………10分ACE CAE AEC ACE ∠∠=∠∆︒--180中，在)290(180AOCAOC ∠--∠-=︒︒ 2-90AOC∠=︒，……………………………………………………………………6分AEC ACE ∠=∠∴， (7)分AE AC =∴， ……………………………………………………………………8分CD AC = ，CD AE =∴． (10)分方法二：连接OC ，OD ，∵AC=CD=DB ，∴DB CD AC 弧弧弧==，∴BOD COD AOC ∠=∠=∠，……………………………………………………2分∴AOC COD DOB COD COB ∠=∠=∠+∠=∠22，（第23题答题图）∵CAE COB ∠=∠2，∴CAE AOC ∠=∠，………………………………………4分∵∠CAO =∠CAE +∠EAO ，∠AEC =∠AOC +∠EAO ，∴∠CAO =∠AEC ，…………………………………………………………………6分OC OA AOC =∆中，在，∴∠ACO =∠CAO ，∴∠ACO =∠AEC ，AE AC =∴， ………………………………………………8分CD AC = ，CD AE =∴…………………………………………………………10分方法三：连接AD ，OC ，OD ， ∵AC=DB ，∴弧AC =弧BD ，∴∠ADC =∠DAB ，…………………………………………………………………2分 ∴CD ∥AB ，∴∠AEC =∠DCO ，…………………………………………………………………4分∵AC=CD ，AO=DO ， ∴CO ⊥AD ，∴∠ACO =∠DCO ，…………………………………………………………………6分∴∠ACO =∠AEC ，∴AC =AE ，……………………………………………………8分∵AC=CD ，∴AE =CD ．……………………………………………………………10分24．（12分）（1）①证明：∵把BA 顺时针方向旋转60°至BE ，∴=∠=ABE BE BA ，60°， ………………………………1分在等边△BCD 中，BC DB =∴，︒=∠60DBCFBA FBA DBC DBA ∠+︒=∠+∠=∠∴60，FBA CBE ∠+︒=∠60 ，CBE DBA ∠=∠∴，…………………………………………2分∴△BAD ≌△BEC ，∴DA =CE ；…………………………………………………3分 ②判断：∠DEC +∠EDC =90°．…………………………4分DC DB = ，BC DA ⊥，︒=∠=∠∴3021BDC BDA ，∵△BAD ≌△BEC ， ∴∠BCE =∠BDA =30°，……………………………………………………………5分在等边△BCD 中，∠BCD =60°，∴∠ACE =∠BCE +∠BCD ＝90°，∴∠DEC +∠EDC =90°．……………………6分（2）分三种情况考虑：①当点A 在线段DF 的延长线上时（如图1）， 由（1）可得， 为直角三角形DCE ∆，︒=∠∴90DCE ，︒︒︒=∠-=∠=∠459045DEC EDC DEC 时，当，DECEDC ∠=∠∴，CE CD =∴，EDF BCA（第24题答题图1）由（1）得DA =CE ，∴CD =DA ，CD BD DBC =∆中，在等边，CD DA BD ==∴︒=∠∴60BDC ，BC DA ⊥ ，︒=∠=∠=∠∴3021BDC CDA BDA ， ……………………………………………7分DA DB BDA =∆中，在，︒︒=∠=∠∴752-180BDA BAD ，DC DA DAC =∆中，在，︒︒=∠=∠∴752-180ADC DAC ，︒︒︒=+=∠+∠=∠∴1507575DAC BAD BAC ． (8)分②当点A 在线段DF 上时（如图2），BE BA B 至顺时针方向旋转为旋转中心，把以︒60 ， 60=∠=∴ABE BE BA ，，60=∠=∆DBC BC BD BDC ，中，在等边，ABEDBC ∠=∠∴，ABC ABE ABC DBC ∠∠=∠∠--，EBC DBA ∠=∠即，DBA ∆∴≌CBE ∆，CE DA =∴， …………………………9分90R =∠∆DFC DFC t 中，在， DF ∴＜DC ，∵DA ＜DF ，DA =CE ， ∴CE ＜DC ，由②可知为直角三角形DCE ∆，DFBCA（第24题答题图2）∴∠DEC ≠45°． ……………………………10分 ③当点A 在线段FD 的延长线上时（如图3）， 同第②种情况可得DBA ∆≌CBE ∆，ECB ADB CE DA ∠=∠=∴，，60=∠=∠∆BCD BDC BDC 中，在等边，BC DA ⊥ ，3021=∠=∠=∠∴BDC CDF BDF ，150180=∠-=∠∴︒BDF ADB ，150=∠=∠∴ADB ECB ，90=∠-∠=∠∴BCD ECB DCE ，︒︒︒=∠-=∠=∠459045DEC EDC DEC 时，当，DECEDC ∠=∠∴，CE CD =∴，∴AD =CD =BD ，……………………………………………11分 ∵ 150=∠=∠ADC ADB ，152-180=∠=∠∴︒ADB BAD ， 152-180=∠=∠︒CDA CAD ， 30=∠+∠=∠∴CAD BAD BAC ，.30150 或的度数为综上所述，BAC ∠ …………………12分EDFBCA（第24题答题图3）25．（14分）（1）得）代入（）（）（把c bx ax y C B A ++=20,2-,0,2,4,0，⎪⎩⎪⎨⎧=+-=++=0240244c b a c b a c ，…………………………2分 ⎪⎩⎪⎨⎧==-=401:c b a 解得，42+-=∴x y（2）设直线DA 得解析式为y =kx +d (k ≠0)，把A （0，4），D （-4，0）代入得，⎩⎨⎧=+-=044d k d ，⎩⎨⎧==41:d k 解得， ∴y =x +4，…………………………………………………………………………6分设E （m ，m +4），平移后的抛物线的解析式为：4)(2++--=m m x y ． 把B （2，0）代入得：04)-2-2=++m m （ 不符合题意，舍去），解得(0521==m m ， ∴E （5，9）． ……………………………………………………………………8分（3）如图，连接AB ，过点B 作BL ∥AD 交平移后的抛物线于点G ，连结EG ，∴四边形ABGE 的面积就是图象A ，B 两点间的部分扫过的面积．…………10分过点G 作GK ⊥x 轴于点K ，过点E 作EI ⊥y 轴于点I ，直线EI ，GK 交于点H ．（第25题答题图）方法一：由点A （0，4）平移至点E （5，9），可知点B 先向右平移5个单位，再向上平移5个单位至点G ．∵B （2，0），∴点G （7，5），…………………………………………………12分∴GK =5，OB =2，OK =7， ∴BK =OK -OB =7-2=5， ∵A （0,4），E （5,9）， ∴AI =9-4=5，EI =5， ∴EH =7-5=2，HG =9-5=4，∴G BK EH G AEI AO B IO KH ABG H ∆∆∆∆=S -S -S -S -S S 矩形四边形3025-8-635521-4221-5521-4221-97==⨯⨯⨯⨯⨯⨯⨯⨯⨯=答：图象A ，B 两点间的部分扫过的面积为30. ……………………………14分方法二：b x y BL '+=的解析式为设直线，02:0,2='+b B ）代入得（把点，2-='b ，2-=∴x y ，⎩⎨⎧+--=-=9)5(22x y x y 联立，⎩⎨⎧==02:11y x 解得，⎩⎨⎧==5722y x ， ∴点G （7，5）， …………………………………………………………………12分∴GK =5，OB =2，OK =7， ∴BK =OK -OB =7-2=5， ∵A （0,4），E （5,9）， ∴AI =9-4=5，EI =5，∴EH =7-5=2，HG =9-5=4，∴G BK EH G AEI AO B IO KH ABG H ∆∆∆∆=S -S -S -S -S S 矩形四边形3025-8-635521-4221-5521-4221-97==⨯⨯⨯⨯⨯⨯⨯⨯⨯=答：图象A ，B 两点间的部分扫过的面积为30. ……………………………14分。

南平市2017-2018学年第一学期九年级期末质量检测数学试题（满分：150分；考试时间：120分钟）★友情提示：① 所有答案都必须填在答题卡相应的位置上，答在本试卷上一律无效； ② 试题未要求对结果取近似值的，不得采取近似计算．一、选择题（本大题共10小题，每小题4分，共40分．每小题只有一个正确的选项，请在答题卡．．．的相应位置填涂） 1．在平面直角坐标系中，点M （1，﹣2）与点N 关于原点对称，则点N 的坐标为A ．（﹣2， 1）B ．（1，﹣2）C ．（2，-1）D ．（-1，2） 2．用配方法解一元二次方程0122=-+x x ，可将方程配方为A ．()212=+x B ．()012=+x C ．()212=-x D ．()012=-x3．下列事件中，属于随机事件的有①任意画一个三角形，其内角和为360°； ②投一枚骰子得到的点数是奇数； ③经过有交通信号灯的路口，遇到红灯； ④从日历本上任选一天为星期天．A ．①②③B ．②③④C ．①③④D ．①②④ 4．下列抛物线的顶点坐标为(4，－3)的是A ．()342-+=x y B ．()342++=x y C ．()342--=x yD ．()342+-=x y5．有n 支球队参加篮球比赛，共比赛了15场，每两个队之间只比赛一场，则下列方程中符合题意的是A ．()151=-n nB ．()151=+n nC ．()301=-n nD ．()301=+n n 6．某小组在“用频率估计概率”的实验中，统计了某种结果出现的频率，绘制了如A ．袋子中有1个红球和2从中随机地取出一个球是黄球B ．掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6C ．在“石头、剪刀、布”的游戏中，小宇随机出的是“剪刀”D ．掷一枚质地均匀的硬币，落地时结果是“正面向上”7．如果一个正多边形的中心角为60°，那么这个正多边形的边数是A ．4B ．5C ．6D ．78．已知点A （x 1，y 1），B （x 2，y 2）是反比例函数xy 1-=的图象上的两点，若x 1＜0＜x 2，则下列结论正确的是 A ．y 1＜0＜y 2 B ．y 2＜0＜y 1 C ．y 1＜y 2＜0 D ．y 2＜y 1＜09．如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ， 且CO =CD ，则∠PCA = A ．30°B ．45°C ．60°次数5000 4000 3000 2000 1000 （第6题图）D CB OAP（第9题图）D ．67.5°10．如图，在Rt △ABC 和Rt △ABD 中，∠ADB =∠ACB =90°，∠BAC =30°，AB =4，AD =22，连接DC ，将Rt △ABC 绕点B 顺时针旋转一周，则线段DC 长的取值范围是 A ．2≤DC ≤4 B ．22≤DC ≤4 C ．222-≤DC ≤22 D ．222-≤DC ≤222+二、填空题（本大题共6小题，每空4分，共24分．将答案填入答题卡．．．的相应位置） 11．如图，在平面直角坐标系xoy 中，矩形OABC ，OA =2，OC =1，写出一个函数()0≠=k xky ，使它的图象与矩形OABC 的边有两个公共点，这个函数的表达式可以为 （答案不唯一）． 12．已知关于x 的方程032=++a x x 有一个根为﹣2，a = ．13．圆锥的底面半径为7cm ，母线长为14cm ，则该圆锥的侧面展开图的圆心角为 °．14．设O 为△ABC 的内心，若∠A =48°，则∠BOC = °． 15．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF =CD =4cm ，则球的半（第11题图）CDAB（第10题图）D（第15题图）径为 cm ．16． 抛物线c bx ax y ++=2（a >0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，则a 的取值范围是 ．三、解答题（本大题共9小题，共86分．在答题卡．．．的相应位置作答） 17．解方程（每小题4分，共8分）（1）022=+x x （2）01232=-+x x18．（8分）已知关于x 的方程 )0(03)3(2≠=+++k x k kx ．（1）求证：方程一定有两个实数根；（2）若方程的两个实数根都是整数，求正整数k 的值．19．（8分）有甲、乙两个不透明的布袋，甲袋中有3个完全相同的小球，分别标有数字0，1和2；乙袋中有3个完全相同的小球，分别标有数字1，2和3，小明从甲袋中随机取出1个小球，记录标有的数字为x ，再从乙袋中随机取出1个小球，记录标有的数字为y ，这样确定了点M 的坐标(x ，y )． （1）写出点M 所有可能的坐标； （2）求点M 在直线3+-=x y 上的概率．20．（8分）如图，直线y =x +2与y 轴交于点A ，与反比例函数()0≠=k xky 的图象交于点C ，过点C 作CB ⊥x 轴于点B ，AO =2BO ，求反比例函数的解析式．21．（8分）如图，12×12的正方形网格中的每个小正方形的边长都是1，正方形的顶点叫做格点．矩形ABCD 的四个顶点A ，B ，C ，D 都在格点上，将△ADC 绕点A 顺时针方向旋转得到△AD ′C ′，点C 与点C ′为对应点． （1）在正方形网格中确定D ′的位置，并画出△AD ′C ′；（2）若边AB 交边C ′D ′于点E ，求AE 的长．22．（10分）在矩形ABCD 中，AB =8，BC =6，将矩形按图示方式进行分割，其中正方形AEFG 与正方形JKCI 全等，矩形GHID 与矩形EBKL 全等．（1）当矩形LJHF 的面积为43时，求AG 的长；（第21题图）LH I K JF DB CAG（第22题图）（2）当AG 为何值时，矩形LJHF 的面积最大．23．（10分）如图，点A ，C ，D ，B 在以O 点为圆心，OA 长为半径的圆弧上， AC=CD=DB ，AB 交OC 于点E ．求证：AE =CD ．24．（12分）如图，在等边△BCD 中，DF ⊥BC 于点F ，点A 为直线DF 上一动点，以B 为旋转中心，把BA 顺时针方向旋转60°至BE ，连接EC ． （1）当点A 在线段DF 的延长线上时，①求证：DA =CE ；②判断∠DEC 和∠EDC 的数量关系，并说明理由； （2）当∠DEC =45°时，连接AC ，求∠BAC 的度数．EDF BCA（第24题图）OABCDE（第23题图）25．（14分）如图，在平面直角坐标系xoy 中，二次函数c bx ax y ++=2（0≠a ）的图象经过A （0，4），B （2，0），C （-2，0）三点．（1）求二次函数的解析式；（2）在x 轴上有一点D （-4，0），将二次函数图象沿DA 方向平移，使图象再次经过点B ．①求平移后图象顶点E 的坐标；②求图象 A ，B 两点间的部分扫过的面积．（第25题图）南平市2017-2018学年第一学期九年级期末质量检测数学试题参考答案及评分说明说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分．（4）评分只给整数分．选择题和填空题不给中间分．一、选择题（本大题共10小题，每小题4分，共40分）1．D；2．A；3．B；4．C；5．C；6．B；7．C；8．B；9．D；10．D．二、填空题（本大题共6小题，每小题4分，共24分）11．如：xy 1=（答案不唯一，0＜k ＜2的任何一个数）； 12．2； 13．180； 14．114； 15．2.5； 16．0＜a ＜3. 三、解答题（本大题共9小题，共86分） 17.（每小题4分，共8分）(1) 解： 0)2(=+x x ……………………………………………………………2分∴2,021-==x x .……………………………………………………4分（2）解：1,2,3-===c b a∴ 161-34-22=⨯⨯=∆）（ ∴64232162±-=⨯±-=x …………………………………………2分 ∴1,3121-==x x . …………………………………………………4分18．（8分）（1）证明：9634)3(22+-=⋅⋅-+=∆k k k k0)32≥-=k （，............................................................2分 ∴方程一定有两个实数根. (3)分（2）解：3,3,=+==c k b k a ，22)3(34)3-=⋅⋅-+=∆∴k k k （，kk k k k k x 2)3(32)3()3(2-±--=-±+-=∴， kx x 3,121-=-=∴ ，………………………………………………6分 ∵方程的两个实数根都是整数，∴正整数31或=k ．…………………………………………………8分19．（8分）解：（1）方法一：列表：从表格中可知，点M 坐标总共有九种可能情况：（0,1），（0,2），（0,3），（1,1），（1,2），（1,3），（2,1），（2,2），（2,3）．……………………………………………………………3分 方法二：从树形图中可知，点M 坐标总共有九种可能情况：（0,1），（0,2），（0,3），（1,1），1 0 2321321321甲袋：乙袋：（1,2），（1,3），（2,1），（2,2），（2,3）．……………………………………………………………3分 （2）当x =0时，y=-0+3=3，当x =1时，y=-1+3=2，当x =2时，y=-2+3=1，……………………………………………………6分由（1）可得点M 坐标总共有九种可能情况，点M 落在直线y =-x +3上（记为事件A ）有3种情况．∴P(A )3193==．…………………………………………8分20．（8分）解： 当x =0时，y =2，∴A (0，2)，…………………………………2分∴A O=2，∵AO =2BO ，∴B O=1，………………………………………………4分当x =1时，y =1+2=3，∴C (1，3)， ……………………………………………6分把C (1，3)代入xky =，解得：3=k xy 3:=∴反比例函数的解析式为 (8)分21．（8分）解：（1）准确画出图形；…………………………………………………3分（第21题答题图）（2）∵将△ADC绕点A顺时针方向旋转得到△AD′C′，点C与点C′为对应点，∴△ADC≌△AD′C′，∴AC=AC′，AD′＝AD=5，CD′＝CD=10，∠AD′C′＝∠ADC＝90°，∠AC′D′＝∠ACD，∵AB∥CD，∴∠BAC＝∠ACD，∵AB⊥C C′，AC=AC′，∴∠BAC＝∠C′AB，∴∠AC ′D ′＝∠C ′AB ，∴C ′E ＝AE ．…………………………………………………5分222R E C BE B C BE C t '=+''∆中，在，x AE AB BE x AE -10-,===则设，222)-105x x =+（，……………………………………………………………………7分425:=x 解得.425的长为答：AE ……………………………………………………………………8分22．（10分）解：（1） 正方形AEFG 和正方形JKCI 全等，矩形GHID 和矩形EBKL 全等，设AG =x ，DG =6-x ，BE =8-x ，FL=x -(6-x )=2x -6，LJ =8-2x ， 方法1： LJ FL S LIH F ⋅=矩形 ，∴43)28)(62(=--x x ………………………………………………………………2分∴415,41321==x x ，∴AG =413或AG =415．………………………………………4分方法2：AEFG D G H I ABCD LIH F S S S S 正方形矩形矩形矩形22--=)6)(8(2248432x x x ----=∴，…………………………………………………2分∴415,41321==x x ，∴AG =413或AG =415．………………………………………4分（2）设矩形LJHF 的面积为S ，)28)(62(x x S --=…………………………………………………………………6分482842-+-=x x1)27(42+--=x …………………………………………………………………8分04<-=a ， ∴S 有最大值，∴当AG =27 时，矩形LJHF 的面积最大．………………………………………10分（第23题答题图）OC OA AOC =∆中，在，2-902180AOC AOC -ACO ∠=∠=∠∴︒︒，…………5分ACE CAE AEC ACE ∠∠=∠∆︒--180中，在)290(180AOCAOC ∠--∠-=︒︒ 2-90AOC∠=︒，……………………………………………………………………6分AEC ACE ∠=∠∴， ………………………………………………………………7分AE AC =∴， ……………………………………………………………………8分CD AC = ，CD AE =∴． (10)分方法二：连接OC ，OD ，∵AC=CD=DB ，∴DB CD AC 弧弧弧==，∴BOD COD AOC ∠=∠=∠，……………………………………………………2分∴AOC COD DOB COD COB ∠=∠=∠+∠=∠22，∵CAE COB ∠=∠2，∴CAE AOC ∠=∠，………………………………………4分∵∠CAO =∠CAE +∠EAO ，∠AEC =∠AOC +∠EAO ，∴∠CAO =∠AEC ，…………………………………………………………………6分OC OA AOC =∆中，在，∴∠ACO =∠CAO ，∴∠ACO =∠AEC ，AE AC =∴， ………………………………………………8分CD AC = ，CD AE =∴…………………………………………………………10分方法三：连接AD ，OC ，OD ， ∵AC=DB ，∴弧AC =弧BD ，∴∠ADC =∠DAB ，…………………………………………………………………2分 ∴CD ∥AB ，∴∠AEC =∠DCO ，…………………………………………………………………4分∵AC=CD ，AO=DO ， ∴CO ⊥AD ，∴∠ACO =∠DCO ，…………………………………………………………………6分 ∴∠ACO =∠AEC ，∴AC =AE ，……………………………………………………8分∵AC=CD ，∴AE =CD ．……………………………………………………………10分24．（12分）（1）①证明：∵把BA 顺时针方向旋转60°至BE ，∴=∠=ABE BE BA ，60°， ………………………………1分在等边△BCD 中，BC DB =∴，︒=∠60DBCFBA FBA DBC DBA ∠+︒=∠+∠=∠∴60，FBA CBE ∠+︒=∠60 ，CBE DBA ∠=∠∴，…………………………………………2分∴△BAD ≌△BEC ，∴DA =CE ；…………………………………………………3分 ②判断：∠DEC +∠EDC =90°．…………………………4分DC DB = ，BC DA ⊥，︒=∠=∠∴3021BDC BDA ，∵△BAD ≌△BEC ， ∴∠BCE =∠EDFBCA（第24题答题图1）BDA =30°，……………………………………………………………5分在等边△BCD 中，∠BCD =60°，∴∠ACE =∠BCE +∠BCD ＝90°，∴∠DEC +∠EDC =90°．……………………6分（2）分三种情况考虑：①当点A 在线段DF 的延长线上时（如图1）， 由（1）可得， 为直角三角形DCE ∆，︒=∠∴90DCE ，︒︒︒=∠-=∠=∠459045DEC EDC DEC 时，当，DECEDC ∠=∠∴，CE CD =∴，由（1）得DA =CE ，∴CD =DA ，CD BD DBC =∆中，在等边，CD DA BD ==∴︒=∠∴60BDC ，BC DA ⊥ ，︒=∠=∠=∠∴3021BDC CDA BDA ， ……………………………………………7分DA DB BDA =∆中，在，︒︒=∠=∠∴752-180BDA BAD ，DC DA DAC =∆中，在，︒︒=∠=∠∴752-180ADC DAC ，︒︒︒=+=∠+∠=∠∴1507575DAC BAD BAC ． (8)分②当点A 在线段DF 上时（如图2），BE BA B 至顺时针方向旋转为旋转中心，把以︒60 ，60=∠=∴ABE BE BA ，，60=∠=∆DBC BC BD BDC ，中，在等边，ABEDBC ∠=∠∴，ABC ABE ABC DBC ∠∠=∠∠--，EBC DBA ∠=∠即，DBA ∆∴≌CBE ∆，CE DA =∴， …………………………9分90R =∠∆DFC DFC t 中，在， DF ∴＜DC ，∵DA ＜DF ，DA =CE ， ∴CE ＜DC ，由②可知为直角三角形DCE ∆，∴∠DEC ≠45°． ……………………………10分 ③当点A 在线段FD 的延长线上时（如图3）， 同第②种情况可得DBA ∆≌CBE ∆，ECB ADB CE DA ∠=∠=∴，，60=∠=∠∆BCD BDC BDC 中，在等边，BC DA ⊥ ，3021=∠=∠=∠∴BDC CDF BDF ，EDFBCA（第24题答题图3）DFBCA（第24题答题图2）150180=∠-=∠∴︒BDF ADB ，150=∠=∠∴ADB ECB ，90=∠-∠=∠∴BCD ECB DCE ，︒︒︒=∠-=∠=∠459045DEC EDC DEC 时，当，DECEDC ∠=∠∴，CE CD =∴，∴AD =CD =BD ，……………………………………………11分 ∵ 150=∠=∠ADC ADB ，152-180=∠=∠∴︒ADB BAD ， 152-180=∠=∠︒CDA CAD ， 30=∠+∠=∠∴CAD BAD BAC ，.30150 或的度数为综上所述，BAC ∠ …………………12分25．（14分）（1）得）代入（）（）（把c bx ax y C B A ++=20,2-,0,2,4,0，⎪⎩⎪⎨⎧=+-=++=0240244c b a c b a c ，…………………………2分⎪⎩⎪⎨⎧==-=401:c b a 解得，42+-=∴x y（2）设直线DA 得解析式为y =kx +d (k ≠0)，把A （0，4），D （-4，0）代入得，⎩⎨⎧=+-=044d k d ，⎩⎨⎧==41:d k 解得， ∴y =x +4，…………………………………………………………………………6分设E （m ，m +4），平移后的抛物线的解析式为：4)(2++--=m m x y ．把B （2，0）代入得：04)-2-2=++m m （不符合题意，舍去），解得(0521==m m ， ∴E （5，9）． ……………………………………………………………………8分（3）如图，连接AB ，过点B 作BL ∥AD 交平移后的抛物线于点G ，连结EG ，∴四边形ABGE 的面积就是图象A ，B 两点间的部分扫过的面积．…………10分过点G 作GK ⊥x 轴于点K ，过点E 作EI ⊥y 轴于点I ，直线EI ，GK 交于点（第25题答题图）H ．方法一：由点A （0，4）平移至点E （5，9），可知点B 先向右平移5个单位，再向上平移5个单位至点G ．∵B （2，0），∴点G （7，5），…………………………………………………12分∴GK =5，OB =2，OK =7，∴BK =OK -OB =7-2=5，∵A （0,4），E （5,9），∴AI =9-4=5，EI =5，∴EH =7-5=2，HG =9-5=4，∴G BK EH G AEI AO B IO KH ABG H ∆∆∆∆=S -S -S -S -S S 矩形四边形3025-8-635521-4221-5521-4221-97==⨯⨯⨯⨯⨯⨯⨯⨯⨯=答：图象A ，B 两点间的部分扫过的面积为30. ……………………………14分方法二：b x y BL '+=的解析式为设直线，02:0,2='+b B ）代入得（把点，2-='b ，2-=∴x y ，⎩⎨⎧+--=-=9)5(22x y x y 联立，⎩⎨⎧==02:11y x 解得，⎩⎨⎧==5722y x ， ∴点G （7，5）， …………………………………………………………………12分∴GK =5，OB =2，OK =7，∴BK =OK -OB =7-2=5，∵A （0,4），E （5,9），∴AI =9-4=5，EI =5，∴EH =7-5=2，HG =9-5=4，∴G BK EH G AEI AO B IO KH ABG H ∆∆∆∆=S -S -S -S -S S 矩形四边形3025-8-635521-4221-5521-4221-97==⨯⨯⨯⨯⨯⨯⨯⨯⨯=答：图象A ，B 两点间的部分扫过的面积为30. ……………………………14分。

南平市2018-2019学年第一学期九年级期末质量检测数学试题（满分：150分；考试时间：120分钟）★友情提示：①所有答案都必须填在答题卡相应的位置上，答在本试卷上一律无效；②试题未要求对结果取近似值的，不得采取近似计算．一、选择题（本大题共10小题，每小题4分，共40分．每小题只有一个正确的选项，请在答题卡．．．的相应位置填涂）1. 下列图形中，既是轴对称图形又是中心对称图形的是A. B. C. D.2. 用配方法解方程2210x x--=，配方结果正确的是A. ()222x-= B. ()212x-=C. ()2+12x= D.()210x-=3. 同时抛掷两枚质地均匀的正方体骰子，每个骰子的六个面分别标有1，2，3，4，5，6这六个点数，下列事件为必然事件的是A. 朝上一面点数之和为12B. 朝上一面点数之和等于6C. 朝上一面点数之和小于13D. 朝上一面点数之和小于等于64. 如图，点A、B、C在⊙O上，过点C作⊙O的切线与OA的延长线交于点D，若32D∠=，则B∠的大小为A. 58B. 34C.32D.295. 关于二次函数()212y x=+-的图象，下列说法正确的是A. 对称轴是1x= B. 开口向下C. 顶点坐标是（1，-2）D. 与x轴有两个交点6. 1275年我国南宋数学家杨辉提出一个问题：直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及长一十二步（宽比长少一十二步），问阔及长各几步. 设阔（宽）为x 步，则所列方程正确的是A. 864)12(=+xx B. 864)12(=-xxC. 864)12)(12(=+-xx D. 86412=x第4题图7. 已知⊙O 的半径为5，直线l 与⊙O 相交，点O 到直线l 的距离为3，则⊙O 上到直线l 的距离为2的点共有 A. 1个B. 2个C. 3个D. 4个8. 如果点A ),3(1y -，B ),2(2y -，C ),2(3y 都在反比例函数)0(>=k xky 的图象上，那么 1y ，2y ，3y 的大小关系正确的是A. 3y <2y <1yB. 2y <1y <3yC. 1y <2y <3y D .1y <3y <2y9. 若正方形的边长为4，则其外接圆半径与内切圆半径的大小分别为A. ，2B. 4，2C. 4，D.，10.已知k 为非零的实数，则抛物线kk kx x y 1222++-=的顶点 A. 在一条直线上 B. 在某双曲线上C. 在一条抛物线上D. 无法确定二、填空题（本大题共6小题，每空4分，共24分．将答案填入答题卡．．．的相应位置）11. 一元二次方程22=x 的根是 ．12. 在一个不透明的口袋内只装有一些除颜色外完全相同的红球、白球和黑球，从中任意摸出一个球，摸到红球的概率是0.3，摸到白球的概率是0.4，那么摸到黑球的概率 是 ．13. 若点P (m ，-3)与点Q （2，n ）关于原点对称，则m n += ．14. 一个扇形的圆心角为80，面积是2cm 2π，则此扇形的半径是 cm ．15．已知反比例函数xky =（0≠k ），当1≤x ≤2时，函数的 最大值与最小值之差是1，则k 的值为 ． 16. 如图，四边形ABCD 中，AB =AC =AD ，若∠BAC =39°，则∠BDC= °.ADC第16题图三、解答题（本大题共9小题，共86分．在答题卡．．．的相应位置作答） 17．解方程（每小题4分，共8分）（1）x x 22=； （2）2550x x --=.18．（8分）已知关于x 的一元二次方程032=++m x x 有两个不相等的实数根，且m 为正整数，求m 的值.19．（8分）某中学食堂开设了两个窗口，窗口一提供四种食品：肉包、馒头、鸡蛋、油饼；窗口二提供两种食品：牛奶、豆浆. 约定：学生在一个窗口领一种食品后，再到另一个窗口领一种食品.（1）问：学生早餐领到的食品一共有几种不同的可能?（2）如果某天食堂师傅在两个窗口随机发放食品，请用列表或画树状图的方法，求出小王同学该天早餐刚好得到牛奶和馒头的概率.20．（8分）如图，△APB 内接于⊙O .（1）作∠APB 的平分线PC ，交⊙O 于点C （尺规作图，保留作图痕迹，不写作法）； （2）在（1）的条件下，若∠APB =120º，连接AC ，BC ，求证：△ABC 是等边三角形.第20题图21．（8分）如图，用48米篱笆围成一个外形为矩形的花园，花园一面利用院墙，中间用一道篱笆间隔成两个小矩形，院墙的长度为20米，平行于院墙的一边长为x 米，花园的面积为S 平方米．（1）求S 与x 之间的函数关系式；（2）问花园面积可以达到180平方米吗？如果能，花园的长和宽各是多少？如果不能，请说明理由.22．（10分）如图，AB 是半圆O 的直径，点D 是半圆上一点，连接OD ，AE ⊥OD 于点E ，设∠AOE =α，将△AEO 绕点O 顺时针旋转α角，得到△DHO ，若点D ，H ，B 在一条直线上，求α的值.23．（10分）如图，直线(0)y kxk =<与反比例函数(0,0)my m x x=<<的图象交于点A ，直线与y 轴正半轴的夹角为60，OA =2． （1）求反比例函数的解析式；（2）根据图象直接写出mkx x>的自变量的取值范围．xDCBA第21题图AOBHED第22题图第23题图24．（12分）如图，在边长为8的等边△ABC 中，点D 是AB 的中点，点E 是平面上一点，且线段DE =2，将线段EB 绕点E 顺时针旋转60º得到线段EF ，连接AF . （1）如图1，当BE =2时，求线段AF 的长； （2）如图2，① 求证：AF =CE ；② 求线段AF 的取值范围.25．（14分）我们把（a ，b ，c ）称为抛物线c bx ax y ++=2的三维特征值.已知抛物线1y 所对应的三维特征值为)031(，，b -，且顶点在直线2=x 上. （1）求抛物线1y 的解析式；（2）若直线t y =与抛物线1y 交于P 、Q 两点，当PQ <1≤2时，求t 的取值范围；（3）已知直线2=x 与x 轴交于点A ，将抛物线1y向右平移1）个单位得到抛物线2y ，且抛物线2y 与直线1=y 分别相交于M 、N 两点（M 点在N 点的左侧），与x轴交于C 、D 两点（C 点在D 点的左侧），求证：射线AN 平分∠MAD .第24题图1第24题图2南平市2018-2019学年第一学期九年级期末质量检测数学试题参考答案及评分说明说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分． （2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分． （3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分． （4）评分只给整数分．选择题和填空题不给中间分． 一、选择题（本大题共10小题，每小题4分，共40分）1．C ； 2．B ； 3．C ； 4．D ； 5．D ； 6．A ； 7．C ； 8．B ； 9．A ； 10．B ． 二、填空题（本大题共6小题，每小题4分，共24分）11．x = 12．0.3； 13．1； 14．3； 15．2±； 16．19.5°． 三、解答题（本大题共9小题，共86分） 17．（1）解：2-20x x =…………………………………………………………………1分()2=0x x -…………………………………………………………………2分12=0=2x x ，…………………………………………………………………4分（2）解：∵5,5,1-=-==c b a ， ……………………………………………………1分()254552⨯+-±=x ……………………………………………………2分2535±=x ， .2535,253521-=+=x x …………………………………………………4分 18．解：∵一元二次方程032=++m x x 有两个不相等的实数根，2=3-40m ∆>， …………………………………………………………4分∴94m < ，………………………………………………………………6分∵m 为正整数，∴=12m m =或.……………………………………………………………………8分19．（1）解：食堂早餐的食品一共有8种不同的可能.……………………………………2分(2) 方法一：肉包 馒头 鸡蛋 油饼牛奶豆浆 牛奶豆浆 牛奶豆浆牛奶豆浆………………………………………………6分∴（肉包，牛奶）（肉包，豆浆）（馒头，牛奶）（馒头，豆浆）（鸡蛋，牛奶）（鸡蛋，豆浆）（油饼，牛奶）（油饼，豆浆），………………7分∴()1=8P 得到牛奶和馒头. ………………………………………………………8分方法二：7分∴()1=8P 得到牛奶和馒头. ………………………………………………………8分 20． (1)作图………………………………………………………………………………3分(2)证明：∵PC 平分∠APB ，∠APB =120º，∴∠APC=∠CPB =60º ， ……………………………………………………4分 ∵∠ABC 与∠APC 同对弧AC ， ∴∠ABC=∠APC =60º ， ………………………………………………………5分 ∵∠CAB 与∠CPB 同对弧BCACP BO第20题答题图2第20题答题图1∴∠CAB=∠CPB =60º ，…………………………………………………………6分 ∴∠ACB=180º-∠ABC-∠CAB =60º，∴∠ACB=∠ABC=∠CAB ，……………………………………………………7分 ∴△ABC 是等边三角形. ………………………………………………………8分21．解：（1）∵()4803x x s -=，…………………………………………………………2分 ∴()21-160203s x x x =+<≤. ……………………………………………………3分 （2）花园面积可以达到180平方米， ……………………………………………4分 ∵ 21-161803x x +=， …………………………………………………………5分∴1218,30x x ==， ………………………………………………………………6分∵院墙的最大长度为m 20 ∴()230x =不符合题意舍去∴18x =. ……………………………………………………………………………7分 答：当18x =时，花园面积可以达到2180m . …………………………………………8分 22. 解：连接HB ，∵AE ⊥EO ， ∴∠AEO=90º，∵△AEO 绕点O 顺时针旋转得到△DHO ， ∴△AEO ≌△DHO ， ∴∠A=∠D ，∠DHO=∠AEO=90º ， ∠DOH=∠AOE ， …………………………………………………………………3分∵D 、H 、B 在一条直线上， ∴OH ⊥DB ，证法一：∵OD =OB ，∴∠B=∠D ，………………………………………………………………………4分 ∴∠A=∠B ，………………………………………………………………………5分 ∵∠AOE 与∠B 同对弧AD ，∴∠AOE =2∠B ，∴∠AOE =2∠A ， …………………………………………………………………7分 在Rt △AOE 中, ∠AOE +∠A=90º， ∴2∠A+∠A=90º，……………………………………………………………………8分 ∴∠A=30º， ……………………………………………………………………9分 ∴∠AOE=60º 即α=60º. ………………………………………………………10分 证法二：∵OD =OB ，OH ⊥DB ，O 第22题答题图∴OH平分∠BOD即∠BOH =∠DOH∵∠DOH=∠AOE ，∴∠DOH=∠AOE=∠BOH=60º………9分∴α=60º.………………………………10分23．解：（1）过A作AB⊥x轴垂足为B， (1)∵直线与y轴正半轴的夹角为60，∴∠AOB=30°，…………………………2分∴112AB OA==，……………………3分∴在Rt△AOB中，2O B=…………………4分∴()A， (5)∴m=， (6)∴y= (7)(2) 0x<< (10)24．解：(1)作AG⊥BC于G点，延长FE交AG于H∵AB=AC，∴∠BAG=30º，……………………1分∵EB绕点E顺时针旋转60º得到线段EF，∴∠BEF=60º，∴∠BEF=∠B，∴EF∥BC，…………………………2分∵AG⊥BC，∴AG⊥FH，…………………………3分在Rt△AEH中,∵AE=6,∠EAH=30º，∴132EH AE==,AH=在Rt△AFH中，AF===.……………………4分方法二：(1)连接FB,作FP⊥AB于P点，∵EB绕点E顺时针旋转60º得到线段EF，∴△EBF是等边三角形，…………………………1分又∵FP⊥AB，∴∠EFP=30º，（第24题答题图1）GFACAC第23题图xAOB∴112EP EF == ，……………………………2分 ∴AP =7，在Rt △EFP 中, PF ==………3分 在Rt △APF 中,AF ===…………………4分(2) ①连接FB ， ∵EB 绕点E 顺时针旋转60º得到线段EF ， ∴△EBF 是等边三角形，∴FB =EB , ∴∠FBE=∠ABC=60º…………………………………………………………6分 ∴∠FBE+∠EBA=∠ABC+∠EBA即∠FBA=∠EBC ，…………………………………………………………………………7分 又∵AB =BC ，∴△FBA ≌△EBC ，.................................................................................8分 ∴AF =CE ， (9)分②22AF ≤≤. ………………………………………………………12分 ∵DE =2,∴E 点在以D 为圆心，2为半径的圆上，且2342-34+≤≤CE ∵AF =CE∴22AF ≤≤.(回答合理均得分）25．解：（1）依题意可得211=-3y x bx +，………………………………………………1分 ∵1y 顶点在直线2=x 上， ∴-2123b=⎛⎫⨯- ⎪⎝⎭， FC∴43b =， ………………………………2分 ∴2114=-33y x x +.……………………3分 （2） 设直线PQ 与直线2=x 相交与E 点， ∴2PQ PE =， ………………………………………………………………………………4分 ∵PQ <1≤2，∴112PE <≤， …………………………………………………………5分 ∴当12PE =时，1352,224p p x y =-==，………………………………………………6分 当 1PE =时 ，211,1p p x y =-==， …………………………………………………7分 ∴ 514t ≤<. ………………………………………………………………………………9分 方法2：设214-=33x x t +， ∴ ()22=-34x t -+，∴122,2x x ==，…………………………………………………5分 ∴12PQ x x =-=6分 ∴ 1PQ =时，14-34t =，54t =， 2PQ =时，4-31t =，1t =，……………………………………………………………8分 ∴ 514t ≤<.…………………………………………………………………………………9分（3）设直线1=y 与1y 依次相交11,M N 于两点，由（2）可得11M N ,1M x ，∴()11,1M ，………………………………………………………………………10分由平移的性质可得11=2MN M N =,()2M ，…………………………11分∴2MA ==根据勾股定理可得………………………12分 证法一：∴=2MA MN =，∴∠MAN=∠MNA ，………………………………………………………………13分 ∵MN ∥CD ，∴∠MNA=∠NAD ,∴∠MAN=∠NAD ,∴射线AN 平分∠MAD . …………………………………………………………14分 证法二：过N 点作NP ⊥AM 于P 点, NQ ⊥CD 于Q 点, ∴NQ=1,∵.11=122AMN S AM NP MN ∆⋅=⋅， ∴NP =1 , ………………………………………………………………13分 ∴NP = NQ ,∵NP ⊥AM 于P 点, NQ ⊥CD ，∴射线AN 平分∠MAD . ………………………………………………14分。

2018年南平初中毕业班适应性检测数学试题及答案(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年南平初中毕业班适应性检测数学试题及答案(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年南平初中毕业班适应性检测数学试题及答案(word版可编辑修改)的全部内容。

南平市2018年初中毕业班适应性检测数学试题参考答案及评分说明说明：（1） 解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2） 对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3） 若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分．（4） 评分只给整数分．选择题和填空题不给中间分．第Ⅰ卷一、选择题（本大题共10小题，每小题4分，共40分)（1)C ； （2）A ； （3)C ； (4）D ； （5)D;(6）B ； (7)C ； (8）B; （9)C ； （10)A ．第Ⅱ卷二、填空题(本大题共6小题，每小题4分，共24分）(11）如：（1，1）（答案不唯一）; (12)34; （13）5; (14）()2232+-=x y ； （15）10； （16）15．三、解答题（本大题共9小题，共86分）(17)（本小题满分8分）解：原式2224444a ab b ab a +-++=………………………… 2分2245b a +=， ……………………………………………4分 当32==b a ，时, 原式22)3(425⨯+⨯=………………………………………6分321220=+=． ………………………………………8分（18）（本小题满分8分）解:由①得,2<x ， ………………………………………3分由②得,22-x ≥2-x ，……………………………………5分x ≥0 ， …………………………………… 6分所以不等式组的解集是0≤x ＜2． ……………………………8分（19）（本小题满分8分）A∵∠DBE=∠A ，∴BE ∥AC ，…………………………………6分又∵BE = AC ，∴四边形ABEC 是平行四边形． …………8分（20)(本小题满分8分)（Ⅰ）确定点P ，E ，F ,各得1分,图形完整得1分，共4分;（Ⅱ)证明：∵∠DOC=∠ODP ，∴PD ∥OC ，∴∠EDP=∠EFO ， …………………………5分∵PD =PE ，∴∠PED=∠EDP ， …………………………6分∴∠PED=∠EFO ， …………………………7分∴OE=OF ． …………………………………8分（21）（本小题满分8分）(Ⅰ）填空：a =2，b =10; …………………………………2分 （Ⅱ）21015232251=⨯+⨯+⨯+⨯………………4分 答:这所学校平均每班贫困学生人数为2；(Ⅲ）设有2名贫困家庭学生的2个班级分别记为A 班和B 班， 方法一：列表：准确列表……………………………………………………………6分 方法二：树状图：AABBF E P O D A C （第20题（Ⅰ）答题图）准确画出树状图 ……………………………………………………6分 ∴P (两名学生来自同一班级）＝31124=． ……………………8分 (22)（本小题满分10分）解：（Ⅰ）把A （1，3）代入xy 12=中得，313=⨯=k , xy 3=， ……3∴反比例函数的解析式为分 把B （c ，—1）代入x y 3=中，得3-=c ， 把A （1,3），B （—3，—1）代入b ax y +=中得， ⎩⎨⎧-=+-=+133b a b a ，∴⎩⎨⎧==21b a ,∴一次函数的解析式为2+=x y ;……6分（Ⅱ）这样的点有4个,………………………8分C 2（3，1）或C 4（-3，-1)． …………10分（23)（本小题满分10分)（Ⅰ)证明:连接AC , ∵∠A+∠CDB=180， ………1分 ∠BDE+∠CDB=180°，………2分 ∴∠A=∠BDE ， ……………3分 ∵∠COE=2∠A ， ……………4分 ∴∠COE=2∠BDE ；…………5分（Ⅱ）解：过C 点作CF ⊥AE 于F 点，∵∠BDE=60°,∴∠A=60°, …………………………………………………………6分 又∵OA =OC ，∴△AOC 是等边三角形，∵OB =2，∴OA =AC =2, ∴121===AO FO AF ， …………………………………………7分在Rt △AFC 中，∴ ，…………………………8分在Rt △CEF 中,EF =FO +OB +BE =5，∴53tan ==EF CFE ． ………………………………………………10分（24)（本小题满分12分）（Ⅰ)证明:∵∠ADB=∠BEC=60°，∴等腰△ADB 和等腰△BEC 是等边三角形，………1分312222=-=-=AF AC CF E A B CD （第23题答题图） F （第22题（Ⅱ）答题图）∴∠DBA —∠EBA=∠EBC —∠EBA , ∴∠DBE=∠ABC ， …………………3分∴△DBE ≌△ABC (SAS);……………4分（Ⅱ）解：（i ）∵∠ADB=90°， DB =DA ,∴∠DBA=45°，同理∠EBC=45°, ∴∠DBA=∠EBC ，∴∠DBA-∠EBA=∠EBC-∠EBA ，∴∠DBE=∠ABC ，……………………5分 又∵cos ∠DBA = cos ∠EBC ， ∴22==BC BE AB DB ， ……………6分 ∴△DBE ∽△ABC ， …………………7分∴BC BEAC DE =，即222=DE ， ∴ ; ……………………8分（ii ）223≤CD ≤227． ………12分（25）（本小题满分14分）（Ⅰ）解：当p =2时，把x =2带入421+-=x y 中得，01=y ， ∴A （2，0），……………………………………………………1分把y 2=2带入44122+-=x y （x >0）中得，x =4，∴C （4,0)，……………………………………………………2分∴AC =2； ……………………………………………………3分 （Ⅱ）解：设)441,(),4,(22+-+-p p B p p A ， ED CBA（第24题（ii ）答题图2）EDCBA（第24题（ii ）答题图1）2=DE EDB A（第24题图1）E DC BA（第24题图2）则)441,0(),4,0(22+-+-p F p E ， ∵M （0，4),∴22)4(4p p ME =+--=，4)441(422p p MF =+--=，……………………………5分当44121+-=p y 时，444122+-=+-x p ,∴p x D 21=， 当422+-=p y 时，441422+-=+-x p , ,∴p x C 2=，∴)4,2(2+-p p C ,)441,2(2+-p p D ，∴221pp p BD =-=,p p p AC =-=2， ……………………………………7分∴8412212122=⋅⋅=⋅⋅=∆∆p p p p MF BD MEAC S S BDMACM；………………8分(Ⅲ）证明：方法一：设直线AD ：b kx y +=，把)441,21(),4,(22+-+-p p D p p A 代入得:⎪⎩⎪⎨⎧+-=++-=+44121422p b kp p b kp ,解得⎪⎪⎩⎪⎪⎨⎧+=-=421232p b p k ， ∴直线AD :421232++-=p px y ；……………………10分 设直线BC ：b x k y '+'=， 把)441,(),4,2(22+-+-p p B p p C 代入得: ⎪⎩⎪⎨⎧+-='+'+-='+'4414222p b k p p b k p ，解得⎪⎪⎩⎪⎪⎨⎧+='-='421432p b p k ， ∴直线BC ：421432++-=p px y ；………………………12分 ∵直线AD 与BC 的交点为N （m ，n),∴⎪⎪⎩⎪⎪⎨⎧++-=++-=421234214322p pm n p pm n , ………13分 ∴043=pm ， ∵p 〉0，∴m=0，即m 为常数．…………………14分方法二： 设直线AD 交y 轴于G 点，直线BC 交y 轴于H 点，∵BF ∥CE ,∴△GFD ∽△GEA ，△HFB ∽△HEC ， (10)分∴2121===p pAE DF GE GF ， 212===p p CE BF HE HF , ∴HE HFGE GF =，………………………11分∴FEHF HF FE GF GF +=+， ∴HF GF =，…………………………13分 ∴G 、H 点重合，∴G 、H 点就是直线AD 与直线BC 的交点N ，∴m=0,即m 为常数． (1)（第25题（Ⅲ）答题图）。

南平市2017-2018学年第一学期九年级期末质量检测数学试题（满分：150分；考试时间：120分钟）★友情提示：① 所有答案都必须填在答题卡相应的位置上，答在本试卷上一律无效； ② 试题未要求对结果取近似值的，不得采取近似计算．一、选择题（本大题共10小题，每小题4分，共40分．每小题只有一个正确的选项，请在答题卡．．．的相应位置填涂） 1．在平面直角坐标系中，点M （1，﹣2）与点N 关于原点对称，则点N 的坐标为 A ．（﹣2， 1）B ．（1，﹣2）C ．（2，-1）D ．（-1，2）2．用配方法解一元二次方程0122=-+x x ，可将方程配方为A ．()212=+x B ．()012=+x C ．()212=-x D ．()012=-x3．下列事件中，属于随机事件的有①任意画一个三角形，其内角和为360°； ②投一枚骰子得到的点数是奇数； ③经过有交通信号灯的路口，遇到红灯； ④从日历本上任选一天为星期天． A ．①②③B ．②③④C ．①③④D ．①②④4．下列抛物线的顶点坐标为(4，－3)的是A ．()342-+=x y B ．()342++=x y C ．()342--=x y D ．()342+-=x y5．有n 支球队参加篮球比赛，共比赛了15场，每两个队之间只比赛一场，则下列方程中符合题意的是 A ．()151=-n n B ．()151=+n n C ．()301=-n nD ．()301=+n n6．某小组在“用频率估计概率”的实验中，统计了某种结果出现的频率，绘制了如图所示的折线图，那么符合这一结果的实验最有可能的是A ．袋子中有1个红球和2个黄球，它们只有颜色上的区别，从中随机地取出一个球是黄球B ．掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6C ．在“石头、剪刀、布”的游戏中，小宇随机出的是“剪刀”D ．掷一枚质地均匀的硬币，落地时结果是“正面向上”7．如果一个正多边形的中心角为60°，那么这个正多边形的边数是 A ．4 B ．5 C ．6 D ．78．已知点A （x 1，y 1），B （x 2，y 2）是反比例函数xy 1-=的图象上的两点，若x 1＜0＜x 2，则下列结论正确的是A ．y 1＜0＜y 2B ．y 2＜0＜y 1C ．y 1＜y 2＜0D ．y 2＜y 1＜0（第6题图）9．如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ， 且CO =CD ，则∠PCA =A ．30°B ．45°C ．60°D ．67.5° 10．如图，在Rt △ABC 和Rt △ABD 中，∠ADB =∠ACB =90°，∠BAC =30°，AB =4，AD =22，连接DC ，将Rt △ABC 绕点B 顺时针旋转一周，则线段DC长的取值范围是A ．2≤DC ≤4B ．22≤DC ≤4C ．222-≤DC ≤22D ．222-≤DC ≤222+二、填空题（本大题共6小题，每空4分，共24分．将答案填入答题卡．．．的相应位置） 11．如图，在平面直角坐标系xoy 中，矩形OABC ，OA =2， OC =1， 写出一个函数()0≠=k xky ，使它的图象与矩形OABC 的边有两个公共点，这个函数的表达式可以为 （答案不唯一）．12．已知关于x 的方程032=++a x x 有一个根为﹣2，a = ．13．圆锥的底面半径为7cm ，母线长为14cm ，则该圆锥的侧面展开图的圆心角为 °． 14．设O 为△ABC 的内心，若∠A =48°，则∠BOC = °．15．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF =CD =4cm ，则球的半径为cm ．16． 抛物线c bx ax y ++=2（a >0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，则a 的取值范围是 ．三、解答题（本大题共9小题，共86分．在答题卡．．．的相应位置作答）17．解方程（每小题4分，共8分）（1）022=+x x （2）01232=-+x x18．（8分）已知关于x 的方程 )0(03)3(2≠=+++k x k kx ．（1）求证：方程一定有两个实数根；（2）若方程的两个实数根都是整数，求正整数k 的值．19．（8分）有甲、乙两个不透明的布袋，甲袋中有3个完全相同的小球，分别标有数字0，1和2；乙袋中有3个完全相同的小球，分别标有数字1，2和3，小明从甲袋中随机取出1个小球，记录标有的数字为x ，再从乙袋中随机取出1个小球，记录标有的数字为y ，这样确定了点M 的坐标(x ，y )．（第11题图）DC B OAP（第9题图）CDAB（第10题图）D（第15题图）（1）写出点M 所有可能的坐标；（2）求点M 在直线3+-=x y 上的概率．20．（8分）如图，直线y =x +2与y 轴交于点A ，与反比例函数()0≠=k xky 的图象交于点C ，过点C 作CB ⊥x 轴于点B ，AO =2BO ，求反比例函数的解析式．21．（8分）如图，12×12的正方形网格中的每个小正方形的边长都是1，正方形的顶点叫做格点．矩形ABCD 的四个顶点A ，B ，C ，D 都在格点上，将△ADC 绕点A 顺时针方向旋转得到△AD ′C ′，点C 与点C ′为对应点． （1）在正方形网格中确定D ′的位置，并画出△AD ′C ′；（2）若边AB 交边C ′D ′于点E ，求AE 的长．22．（10分）在矩形ABCD 中，AB =8，BC =6，将矩形按图示方式进行分割，其中正方形AEFG 与正方形JKCI 全等，矩形GHID 与矩形EBKL 全等．（1）当矩形LJHF 的面积为43时，求AG 的长；（2）当AG 为何值时，矩形LJHF 的面积最大．23．（10分）如图，点A ，C ，D ，B 在以O 点为圆心，OA长为半径的圆弧上， AC=CD=DB ，AB 交OC 于点E ．求证：AE =CD ．24．（12分）如图，在等边△BCD 中，DF ⊥BC 于点F ，点直线DF 上一动点，以B 为旋转中心，把BA 顺时针方向旋转60BE ，连接EC ．（1）当点A 在线段DF 的延长线上时，①求证：DA =CE ；②判断∠DEC 和∠EDC （2）当∠DEC =45°时，连接AC ，求∠BAC 的度数．25．（14分）如图，在平面直角坐标系xoy 中，二次函数（第25题图）（第21题图） LH IK JF EDBCAG（第22题图）O ABCDE（第23题图）c bx ax y ++=2（0≠a ）的图象经过A （0，4），B （2，0），C （-2，0）三点．（1）求二次函数的解析式；（2）在x 轴上有一点D （-4，0），将二次函数图象沿DA 方向平移，使图象再次经过点B ．①求平移后图象顶点E 的坐标；②求图象 A ，B 两点间的部分扫过的面积．南平市2017-2018学年第一学期九年级期末质量检测数学试题参考答案及评分说明说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分． （4）评分只给整数分．选择题和填空题不给中间分． 一、选择题（本大题共10小题，每小题4分，共40分）1．D ； 2．A ； 3．B ； 4．C ； 5．C ； 6．B ； 7．C ； 8．B ； 9．D ； 10．D ． 二、填空题（本大题共6小题，每小题4分，共24分） 11．如：xy 1=（答案不唯一，0＜k ＜2的任何一个数）； 12．2； 13．180； 14．114； 15．2.5； 16．0＜a ＜3.三、解答题（本大题共9小题，共86分） 17.（每小题4分，共8分）(1) 解： 0)2(=+x x ……………………………………………………………2分∴2,021-==x x .……………………………………………………4分 （2）解：1,2,3-===c b a∴ 161-34-22=⨯⨯=∆）（ ∴64232162±-=⨯±-=x …………………………………………2分∴1,3121-==x x . …………………………………………………4分18．（8分）（1）证明：9634)3(22+-=⋅⋅-+=∆k k k k0)32≥-=k （，……………………………………………………2分∴方程一定有两个实数根. …………………………………………3分（2）解：3,3,=+==c k b k a ，22)3(34)3-=⋅⋅-+=∆∴k k k （，kk k k k k x 2)3(32)3()3(2-±--=-±+-=∴， kx x 3,121-=-=∴ ，………………………………………………6分∵方程的两个实数根都是整数，∴正整数31或=k ．…………………………………………………8分 19．（8分）解：（1）方法一：列表：从表格中可知，点M 坐标总共有九种可能情况：（0,1），（0,2），（0,3），（1,1），（1,2），（1,3），（2,1），（2,2），（2,3）．……………………………………………………………3分 方法二：从树形图中可知，点M 坐标总共有九种可能情况：（0,1），（0,2），（0,3），（1,1），（1,2），（1,3），（2,1），（2,2），（2,3）．……………………………………………………………3分 （2）当x =0时，y=-0+3=3， 当x =1时，y=-1+3=2，当x =2时，y=-2+3=1，……………………………………………………6分 由（1）可得点M 坐标总共有九种可能情况，点M 落在直线y =-x +3上（记为事 件A ）有3种情况．∴P(A )3193==．…………………………………………8分20．（8分）解： 当x =0时，y =2，∴A (0，2)，…………………………………2分∴A O=2，∵AO =2BO ，∴B O=1，………………………………………………4分 当x =1时，y =1+2=3，∴C (1，3)， ……………………………………………6分 把C (1，3)代入xky =，解得：3=k xy 3:=∴反比例函数的解析式为…………………………………………………8分 21．（8分）解：（1）准确画出图形；…………………………………………………3分（2）∵将△ADC 绕点A 顺时针方向旋转得到△AD ′C ′，点C 与点C ′为对应点，∴△ADC ≌△AD ′C ′，∴AC =AC ′，AD ′＝AD =5，CD ′＝CD =10，∠AD ′C ′＝∠ADC ＝90°，∠AC ′D ′＝∠ACD ， ∵AB ∥CD ，∴∠BAC ＝∠ACD ，∵AB ⊥C C ′，AC =AC ′，∴∠BAC ＝∠C ′AB ，∴∠AC ′D ′＝∠C ′AB ，∴C ′E ＝AE ．…………………………………………………5分 222R E C BE B C BE C t '=+''∆中，在，x AE AB BE x AE -10-,===则设， 222)-105x x =+（，……………………………………………………………………7分425:=x 解得.425的长为答：AE ……………………………………………………………………8分22．（10分）解：（1） 正方形AEFG 和正方形JKCI 全等，矩形GHID 和矩形EBKL 全等， 设AG =x ，DG =6-x ，BE =8-x ，FL=x -(6-x )=2x -6，LJ =8-2x ， 方法1： LJ FL S LIHF ⋅=矩形 ， ∴43)28)(62(=--x x ………………………………………………………………2分 ∴415,41321==x x ，∴AG =413或AG =415．………………………………………4分方法2：AEFG DGHI ABCD LIHF S S S S 正方形矩形矩形矩形22--=)6)(8(2248432x x x ----=∴，…………………………………………………2分 ∴415,41321==x x ，∴AG =413或AG =415．………………………………………4分（2）设矩形LJHF 的面积为S ，)28)(62(x x S --=…………………………………………………………………6分 482842-+-=x x1)27(42+--=x …………………………………………………………………8分04<-=a ，（第21题答题图）∴S 有最大值，∴当AG =27 时，矩形LJHF 的面积最大．………………………………………10分23．（10分）证明：方法一：连接OC ，OD ，∵AC=CD=DB ，∴DB CD AC 弧弧弧==，∴BOD COD AOC ∠=∠=∠，……………………………………………………2分 ∴AOC COD DOB COD COB ∠=∠=∠+∠=∠22，∵CAE COB ∠=∠2，∴CAE AOC ∠=∠，………………………………………4分OC OA AOC =∆中，在，2-902180AOC AOC -ACO ∠=∠=∠∴︒︒，…………5分ACE CAE AEC ACE ∠∠=∠∆︒--180中，在 )290(180AOC AOC ∠--∠-=︒︒2-90AOC ∠=︒，……………………………………………………………………6分 AEC ACE ∠=∠∴， ………………………………………………………………7分AE AC =∴， ……………………………………………………………………8分 CD AC = ，CD AE =∴．………………………………………………………10分 方法二：连接OC ，OD ，∵AC=CD=DB ，∴DB CD AC 弧弧弧==，∴BOD COD AOC ∠=∠=∠，……………………………………………………2分 ∴AOC COD DOB COD COB ∠=∠=∠+∠=∠22，∵CAE COB ∠=∠2，∴CAE AOC ∠=∠，………………………………………4分 ∵∠CAO =∠CAE +∠EAO ，∠AEC =∠AOC +∠EAO ，∴∠CAO =∠AEC ，…………………………………………………………………6分 OC OA AOC =∆中，在，∴∠ACO =∠CAO ，∴∠ACO =∠AEC ，AE AC =∴， ………………………………………………8分CD AC = ，CD AE =∴…………………………………………………………10分 方法三：连接AD ，OC ，OD ， ∵AC=DB ，∴弧AC =弧BD ，∴∠ADC =∠DAB ，…………………………………………………………………2分 ∴CD ∥AB ，∴∠AEC =∠DCO ，…………………………………………………………………4分 ∵AC=CD ，AO=DO ， ∴CO ⊥AD ，∴∠ACO =∠DCO ，…………………………………………………………………6分 ∴∠ACO =∠AEC ，∴AC =AE ，……………………………………………………8分 ∵AC=CD ，∴AE =CD ．……………………………………………………………10分 24．（12分）（1）①证明：∵把BA 顺时针方向旋转60°至BE ，∴=∠=ABE BE BA ，60°， ………………………………1分在等边△BCD 中，BC DB =∴，︒=∠60DBCFBA FBA DBC DBA ∠+︒=∠+∠=∠∴60，OABC DE（第23题答题图）DF BCAFBA CBE ∠+︒=∠60 ，CBE DBA ∠=∠∴，…………………………………………2分 ∴△BAD ≌△BEC ，∴DA =CE ；…………………………………………………3分 ②判断：∠DEC +∠EDC =90°．…………………………4分DC DB = ，BC DA ⊥，︒=∠=∠∴3021BDC BDA ，∵△BAD ≌△BEC ，∴∠BCE =∠BDA =30°，……………………………………………………………5分在等边△BCD 中，∠BCD =60°，∴∠ACE =∠BCE +∠BCD ＝90°，∴∠DEC +∠EDC =90°．……………………6分（2）分三种情况考虑：①当点A 在线段DF 的延长线上时（如图1）， 由（1）可得， 为直角三角形DCE ∆，︒=∠∴90DCE ， ︒︒︒=∠-=∠=∠459045DEC EDC DEC 时，当，DEC EDC ∠=∠∴，CE CD =∴，由（1）得DA =CE ，∴CD =DA ，CD BD DBC =∆中，在等边，CD DA BD ==∴ ︒=∠∴60BDC ，BC DA ⊥ ，︒=∠=∠=∠∴3021BDC CDA BDA ， ……………………………………………7分DA DB BDA =∆中，在，︒︒=∠=∠∴752-180BDA BAD ，DC DA DAC =∆中，在，︒︒=∠=∠∴752-180ADCDAC ， ︒︒︒=+=∠+∠=∠∴1507575DAC BAD BAC ． …………………………………8分②当点A 在线段DF 上时（如图2），BE BA B 至顺时针方向旋转为旋转中心，把以︒60 ，60=∠=∴ABE BE BA ，，60=∠=∆DBC BC BD BDC ，中，在等边，ABE DBC ∠=∠∴，ABC ABE ABC DBC ∠∠=∠∠--， EBC DBA ∠=∠即，DBA ∆∴≌CBE ∆，CE DA =∴， …………………………9分90R =∠∆DFC DFC t 中，在，DF ∴＜DC ， ∵DA ＜DF ，DA =CE ，∴CE ＜DC ，由②可知为直角三角形DCE ∆，∴∠DEC ≠45°． ……………………………10分 ③当点A 在线段FD 的延长线上时（如图3）， 同第②种情况可得DBA ∆≌CBE ∆， ECB ADB CE DA ∠=∠=∴，，60=∠=∠∆BCD BDC BDC 中，在等边，BC DA ⊥ ，DAEDFBCA（第24题答题图2）3021=∠=∠=∠∴BDC CDF BDF ，150180=∠-=∠∴︒BDF ADB ， 150=∠=∠∴ADB ECB ， 90=∠-∠=∠∴BCD ECB DCE ，︒︒︒=∠-=∠=∠459045DEC EDC DEC 时，当，DEC EDC ∠=∠∴， CE CD =∴，∴AD =CD =BD ，……………………………………………11分 ∵ 150=∠=∠ADC ADB ，152-180=∠=∠∴︒ADB BAD ， 152-180=∠=∠︒CDA CAD ， 30=∠+∠=∠∴CAD BAD BAC ，.30150 或的度数为综上所述，BAC ∠ …………………12分25．（14分）（1）得）代入（）（）（把c bx ax y C B A ++=20,2-,0,2,4,0，⎪⎩⎪⎨⎧=+-=++=0240244c b a c b a c ，…………………………2分 ⎪⎩⎪⎨⎧==-=401:c b a 解得，42+-=∴x y ． (4)（2）设直线DA 得解析式为y =kx +d (k ≠0)，把A （0，4），D （-4，0）代入得， ⎩⎨⎧=+-=044d k d ，⎩⎨⎧==41:d k 解得， ∴y =x +4，…………………………………………………………………………6分 设E （m ，m +4），平移后的抛物线的解析式为：4)(2++--=m m x y ． 把B （2，0）代入得：04)-2-2=++m m （ 不符合题意，舍去），解得(0521==m m ，∴E （5，9）． ……………………………………………………………………8分（3）如图，连接AB ，过点B 作BL ∥AD 交平移后的抛物线于点G ，连结EG ， ∴四边形ABGE 的面积就是图象A ，B 两点间的部分扫过的面积．…………10分 过点G 作GK ⊥x 轴于点K ，过点E 作EI ⊥y 轴于点I ，直线EI ，GK 交于点H ．方法一：由点A （0，4）平移至点E （5，9），可知点B 先向右平移5个单位，再向上平移5个单位至点G ． ∵B （2，0），∴点G （7，5），…………………………………………………12分（第25题答题图）∴GK =5，OB =2，OK =7， ∴BK =OK -OB =7-2=5，∵A （0,4），E （5,9）， ∴AI =9-4=5，EI =5， ∴EH =7-5=2，HG =9-5=4，∴GBK EHG AEI AOB IOKH ABGH ∆∆∆∆=S -S -S -S -S S 矩形四边形3025-8-635521-4221-5521-4221-97==⨯⨯⨯⨯⨯⨯⨯⨯⨯=答：图象A ，B 两点间的部分扫过的面积为30. ……………………………14分 方法二：b x y BL '+=的解析式为设直线，02:0,2='+b B ）代入得（把点，2-='b ，2-=∴x y ，⎩⎨⎧+--=-=9)5(22x y x y 联立，⎩⎨⎧==02:11y x 解得，⎩⎨⎧==5722y x ， ∴点G （7，5）， …………………………………………………………………12分∴GK =5，OB =2，OK =7， ∴BK =OK -OB =7-2=5，∵A （0,4），E （5,9）， ∴AI =9-4=5，EI =5， ∴EH =7-5=2，HG =9-5=4，∴GBK EHG AEI AOB IOKH ABGH ∆∆∆∆=S -S -S -S -S S 矩形四边形3025-8-635521-4221-5521-4221-97==⨯⨯⨯⨯⨯⨯⨯⨯⨯=答：图象A ，B 两点间的部分扫过的面积为30. ……………………………14分。

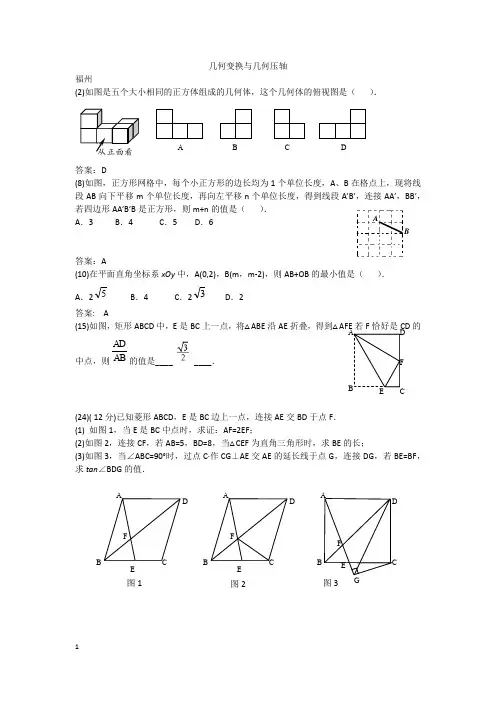
2018年南平市初三质检数学试题一、选择题（共40分）(1)下列各数中，比-2小3的数是( )．(A)1 (B)1- (C) 5- (D) 6-(2)我国南海总面积有3 500 000平方千米，数据3 500 000用科学记数法表示为( )． (A)3.5×106 (B)3.5×107 (C)35×105 (D)0.35×108 (3)如图，在2×2网格中放置了三枚棋子，在其他格点处再放置1枚棋子， 使图形中的四枚棋子成为轴对称图形的概率是( )．(A) 32 (B) 21 (C) 31 (D) 41(4)已知一个正多边形的内角是140°，则这个正多边形的边数是( )． (A)6 (B) 7 (C)8 (D)9(5)已知一次函数y 1=-2x ，二次函数y 2=x 2+1，对于x 的同一个值，这两个函数所对 应的函数值为y 1和y 2，则下列关系正确的是( )．(A)y 1>y 2 (B)y 1≥y 2 (C) y 1<y 2 (D) y 1≤y 2(6)如图，在△ABC 中，∠C=90°，AB=4，以C 点为圆心，2为半径作⊙C ，则AB 的中点 O 与⊙C 的位 置关系是( )．(A) 点O 在⊙C 外 (B) 点O 在⊙C 上 (C) 点O 在⊙C 内 (D) 不能确定 (7)下列说法正确的是( )．(A)为了审核书稿中的错别字，选择抽样调查 (B)为了了解某电视剧的收视率，选择全面调查 (C)“射击运动员射一次，命中靶心”是随机事件 (D)“经过有交通信号灯的路口，遇到红灯”是必然事件(8)某学校为绿化环境，计划植树220棵，实际劳动中每小时植树的数量比原计划多10%，结果提前2小时完成任务．设原计划每小时植树x 棵，依据题意,可列方程( )．(A)2220%)101(220+=+x x (B) 2220%)101(220-=+x x(C) 2220%10220=-x x (D) 2220%101220-=+xx(9)如图，是一圆锥的左视图，根据图中所示数据，可得圆锥侧面 展开图的圆心角的度数为( )． (A) 60° (B) 90° (C) 120° (D) 135°第3题第5题ABO第9题(10)已知一组数a 1，a 2，a 3，…，a n ，…其中a 1=1，对于任意的正整数n ，满足a n+1 a n ，+ a n+1 n a -=0， 通过计算a 2，a 3，a 4的值，猜想a n 可能是( )． (A)n1(B)n (C)n 2 (D)1 二、填空题（共24分）(11)写出一个正比例函数y =x 象上点的坐标__________．(12)关于x 的一元二次方程x 24-x +3m =0有两个实数根，则m =__________． (13)一组数据：3，4，4，6，6，6的中位数是__________． (14)将抛物线2)1(32-+=x y 向右平移3个单位，再向上平 移4个单位，那么得到的抛物线的表达式为__________．(15)如图，正方形ABCD 的面积为18，菱形AECF 的面积为6，则菱形的边长__________． (16)如图，在四边形ABCD 中，AB ∥CD ，AB=BC=BD=2，AD=1，则AC=__________． 三、解答题(共86分)(17)(8分)先化简，再求值：()()a b a b a --+422，其中a =2，b=3，(18)(8分)解不等式组：()⎩⎨⎧-≥-<-212063x x x(19)( 8分)如图，A ，B ，D 三点在同一直线上，△ABC ≌△BDE ，其中点A ，B ，C 的对应点分别是B ，D ，E ，连接CE ． 求证：四边形ABEC 是平行四边形．(20)( 8分)如图，已知∠AOC 内一点D ．(1)按要求面出图形：画一条射线DP ，使得∠DOC=∠ODP 交射线OA 于点P ，以P 点为圆心DP 半径画弧，交射线OA 于E 点，画直线ED 交射线OC 于F 点，得到△OEF ； (2)求证：OE=OF ．第15题AABCD第16题① ②CD AC(21)( 8分)为了有效地落实国家精准扶贫政策，切实关爱贫困家庭学生．某校对全校各班贫困家庭学生的 人数情况进行了调查．.发现每个班级都有贫困家庭学生，经统计班上贫困家庭学生人数分别有1名、 2名、3名、5名，共四种情况，井将其制成了如下两幅不完整的统计图： (1)填空：a =_______，b=_______； (2)求这所学校平均每班贫困学生人数； (3)某爱心人士决定从2名贫困家庭学 生的这些班级中，任选两名进行帮扶， 请用列表或画树状图的方法，求出被 选中的两名学生来自同一班级的概率．(22)如图，反比例函数xky =(k ≠0)与一次函数)0(≠+=a b ax y 相交于点A(1，3)，B(c ，1-) (1)求反比例函数与一次函数的解析式；(2)在反比例函数图象上存在点C ，使△AOC 为等腰三角形，这样的点有几个，请直接写出一个以 AC 为底边的等腰三角形顶点C 的坐标．(23)( 10分)如图，AB 为半圆O 的直径，弦CD 与AB 的延长线相交于点E ． (1)求证：∠COE=2∠BDE ；(2)当OB=BE=2，且∠BDE=60°时，求tan E ．贫困学生人数 班级数 1名 5 2名 2 3名 a 5名1ABO xym %1名 20% 2名 20%3名 5名 b %(24)( 12分)已知两条线段AC 和BC ，连接AB ，分别以AB 、BC 为底边向上画等腰△ABD 和等腰△BCE ，∠ADB=∠BEC=α．(1)如图1，当α=60°时，求证：△DBE ≌△ABC ； (2)如图2，当α=90°时，且BC=5，AC=2， ①求DE 的长；②如图3，将线段CA 绕点C 旋转，点D 也随之运动，请直接写出C 、D 两点之间距离的取值范围．(25)( 14分)已知抛物线421+-=x y (x >0)与44122+-=x y (x >0)有公共的顶点M(0，4)，直线 x =p (p >0)分别与掀物线y 1、y 2交于点A 、B ，过点A 作直线AE ⊥y 轴于点E ，交y 2于点C ． 过点B 作直线BF ⊥y 轴于点F ，交y 1于点D ． (1)当p =2时，求AC 的长；图1图2D(2)求BDMACM S S∆∆的值；(3)直线AD 与BC 的交点N(m ，n )， 求证：m 为常数．参考答案及评分说明（1）C ； （2）A ； （3）C ； （4）D ； （5）D ；（6）B ； （7）C ； （8）B ； （9）C ； （10）A ． （11）如：（1，1）（答案不唯一）； （12）34； （13）5； （14）()2232+-=x y ； （15）10； （16）15． 三、解答题（本大题共9小题，共86分） （17）（本小题满分8分）解：原式2224444a ab b ab a +-++=………………………… 2分 2245b a +=， ……………………………………………4分当32==b a ，时，原式22)3(425⨯+⨯=………………………………………6分321220=+=． ………………………………………8分（18）（本小题满分8分）解：由①得，2<x ， ………………………………………3分由②得，22-x ≥2-x ，……………………………………5分x ≥0 ， …………………………………… 6分 所以不等式组的解集是0≤x ＜2． ……………………………8分O yx y 1y 2C E BD F M x=p（19）（本小题满分8分）证明：∵△ABC ≌△BDE ，∴∠DBE=∠A , BE = AC ， …………………4分 ∵∠DBE=∠A ，∴BE ∥AC ，…………………………………6分 又∵BE = AC ，∴四边形ABEC 是平行四边形． …………8分（20）（本小题满分8分）（Ⅰ）确定点P ，E ，F ，各得1分，图形完整得1分，共4分；（Ⅱ）证明：∵∠DOC=∠ODP ，∴PD ∥OC ，∴∠EDP=∠EFO ， …………………………5分∵PD =PE ，∴∠PED=∠EDP ， …………………………6分 ∴∠PED=∠EFO ， …………………………7分 ∴OE=OF ． …………………………………8分（21）（本小题满分8分）（Ⅰ）填空：a =2，b =10； …………………………………2分（Ⅱ）21015232251=⨯+⨯+⨯+⨯………………4分答：这所学校平均每班贫困学生人数为2；（Ⅲ）设有2名贫困家庭学生的2个班级分别记为A 班和B 班， 方法一： 列表：准确列表……………………………………………………………6分 方法二： 树状图：CBEAEP ODA C（第20题（Ⅰ）答题图）A212A11B 2121B221B准确画出树状图 ……………………………………………………6分 ∴P （两名学生来自同一班级）＝31124=． ………………8分 （22）（本小题满分10分）解：（Ⅰ）把A （1，3）代入xy 12=中得，313=⨯=k ，∴反比例函数的解析式为x y 3=， ……3分把B （c ，-1）代入xy 3=中，得3-=c ，把A （1，3）,B （-3，-1）代入b ax y +=中得， ⎩⎨⎧-=+-=+133b a b a ，∴⎩⎨⎧==21b a ， ∴一次函数的解析式为2+=x y ； ……6分（Ⅱ）这样的点有4个，………………………8分C 2（3，1）或C 4（-3，-1）． …………10分（23）（本小题满分10分） （Ⅰ）证明：连接AC ，∵∠A+∠CDB =180， ………1分∠BDE+∠CDB =180°，………2分∴∠A=∠BDE ， ……………3分 ∵∠COE=2∠A ， ……………4分∴∠COE=2∠BDE ；…………5分（Ⅱ）解：过C 点作CF ⊥AE 于F 点，∵∠BDE =60°，∴∠A =60°， …………………………………………………………6分 又∵OA =OC ，∴△AOC 是等边三角形，∵OB =2，∴OA =AC =2，∴121===AO FO AF ， …………………………………………7分 在Rt △AFC 中，∴ ，…………………………8分在Rt △CEF 中，EF =FO +OB +BE =5， ∴53tan ==EF CF E ． (10)分 （24）（本小题满分12分）（Ⅰ）证明：∵∠ADB=∠BEC=60°，∴等腰△ADB 和等腰△BEC 是等边三角形，………1分 ∴BD =BA ，BE=BC ，∠DBA=∠EBC=60°，………2分312222=-=-=AF AC CF EAO B C D （第23题答题图） F （第22题（Ⅱ）答题图）ED∴∠DBA -∠EBA=∠EBC -∠EBA ，∴∠DBE=∠ABC ， …………………3分 ∴△DBE ≌△ABC （SAS ）；……………4分 （Ⅱ）解：（i ）∵∠ADB=90°， DB =DA ， ∴∠DBA=45°，同理∠EBC=45°， ∴∠DBA=∠EBC ，∴∠DBA -∠EBA=∠EBC -∠EBA ， ∴∠DBE=∠ABC ，……………………5分 又∵cos ∠DBA = cos ∠EBC ， ∴22==BC BE AB DB ， ……………6分 ∴△DBE ∽△ABC ， …………………7分∴BCBEAC DE =，即222=DE ， ∴ ； ……………………8分（ii ）223≤CD ≤227． ………12分（25）（本小题满分14分）（Ⅰ）解：当p =2时，把x =2带入421+-=x y 中得，01=y ， ∴A （2，0），……………………………………………………1分 把y 2=2带入44122+-=x y （x >0）中得，x =4， ∴C （4，0），……………………………………………………2分 ∴AC =2； ……………………………………………………3分 （Ⅱ）解：设)441,(),4,(22+-+-p p B p p A ， 则)441,0(),4,0(22+-+-p F p E ， ∵M （0，4），∴22)4(4p p ME =+--=，4)441(422p p MF =+--=，……………………………5分2=DE E DCBA（第24题图2）EDCBA（第24题（ii ）答题图1）ED CBA（第24题（ii ）答题图2）当44121+-=p y 时，444122+-=+-x p ，∴p x D 21=， 当422+-=p y 时，441422+-=+-x p ， ， ∴p x C 2=， ∴)4,2(2+-p p C ,)441,2(2+-p p D ， ∴221p p p BD =-=， p p p AC =-=2， ……………………………………7分∴8412212122=⋅⋅=⋅⋅=∆∆p p p p MF BD MEAC S S BDMACM ；………………8分 （Ⅲ）证明：方法一：设直线AD ：b kx y +=，把)441,21(),4,(22+-+-p p D p p A 代入得： ⎪⎩⎪⎨⎧+-=++-=+44121422p b kp p b kp ，解得⎪⎪⎩⎪⎪⎨⎧+=-=421232p b p k ， ∴直线AD ：421232++-=p px y ；……………………10分 设直线BC ：b x k y '+'=，把)441,(),4,2(22+-+-p p B p p C 代入得： ⎪⎩⎪⎨⎧+-='+'+-='+'4414222p b k p p b k p ，解得⎪⎪⎩⎪⎪⎨⎧+='-='421432p b p k ， ∴直线BC ：421432++-=p px y ；………………………12分 ∵直线AD 与BC 的交点为N(m,n)，∴⎪⎪⎩⎪⎪⎨⎧++-=++-=421234214322p pm n p pm n ， ………13分∴043=pm ， ∵p >0，∴m=0，即m 为常数．…………………14分方法二： 设直线AD 交y 轴于G 点，直线BC 交y 轴于H 点， ∵BF ∥CE ，∴△GFD ∽△GEA ，△HFB ∽△HEC ，…10分∴2121===p pAE DF GE GF ， 212===p p CE BF HE HF ， ∴HE HFGE GF =，………………………11分 ∴FEHF HF FE GF GF +=+， ∴HF GF =，…………………………13分∴G 、H 点重合，∴G 、H 点就是直线AD 与直线BC 的交点N ， ∴m=0，即m 为常数． ………………14分。

南平市2018-2019学年第一学期九年级期末质量检测数学试题（满分：150分；考试时间：120分钟）★友情提示：①所有答案都必须填在答题卡相应的位置上，答在本试卷上一律无效；②试题未要求对结果取近似值的，不得采取近似计算．一、选择题（本大题共10小题，每小题4分，共40分．每小题只有一个正确的选项，请在答题卡．．．的相应位置填涂）1. 下列图形中，既是轴对称图形又是中心对称图形的是A. B. C. D.2. 用配方法解方程2210x x--=，配方结果正确的是A. ()222x-= B. ()212x-=C. ()2+12x= D.()210x-=3. 同时抛掷两枚质地均匀的正方体骰子，每个骰子的六个面分别标有1，2，3，4，5，6这六个点数，下列事件为必然事件的是A. 朝上一面点数之和为12B. 朝上一面点数之和等于6C. 朝上一面点数之和小于13D. 朝上一面点数之和小于等于64. 如图，点A、B、C在⊙O上，过点C作⊙O的切线与OA的延长线交于点D，若32D∠=，则B∠的大小为A.58 B.34C.32 D.295. 关于二次函数()212y x=+-的图象，下列说法正确的是A. 对称轴是1x= B. 开口向下C. 顶点坐标是（1，-2）D. 与x轴有两个交点6. 1275年我国南宋数学家杨辉提出一个问题：直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及长一十二步（宽比长少一十二步），问阔及长各几步. 设阔（宽）为x 步，则所列方程正确的是A. 864)12(=+xx B. 864)12(=-xxC. 864)12)(12(=+-xx D. 86412=x第4题图7. 已知⊙O 的半径为5，直线l 与⊙O 相交，点O 到直线l 的距离为3，则⊙O 上到直线l 的距离为2的点共有 A. 1个B. 2个C. 3个D. 4个8. 如果点A ),3(1y -，B ),2(2y -，C ),2(3y 都在反比例函数)0(>=k xky 的图象上，那么 1y ，2y ，3y 的大小关系正确的是A. 3y <2y <1yB. 2y <1y <3yC. 1y <2y <3y D .1y <3y <2y9. 若正方形的边长为4，则其外接圆半径与内切圆半径的大小分别为A. 2B. 4，2C. 4，D.10.已知k 为非零的实数，则抛物线kk kx x y 1222++-=的顶点 A. 在一条直线上 B. 在某双曲线上C. 在一条抛物线上D. 无法确定二、填空题（本大题共6小题，每空4分，共24分．将答案填入答题卡．．．的相应位置）11. 一元二次方程22=x 的根是 ．12. 在一个不透明的口袋内只装有一些除颜色外完全相同的红球、白球和黑球，从中任意摸出一个球，摸到红球的概率是0.3，摸到白球的概率是0.4，那么摸到黑球的概率 是 ．13. 若点P (m ，-3)与点Q （2，n ）关于原点对称，则m n += ． 14. 一个扇形的圆心角为80，面积是2cm 2π，则此扇形的半径是 cm ．15．已知反比例函数xky =（0≠k ），当1≤x ≤2时，函数的 最大值与最小值之差是1，则k 的值为 ． 16. 如图，四边形ABCD 中，AB =AC =AD ，若∠BAC =39°，则∠BDC= °.ADC第16题图三、解答题（本大题共9小题，共86分．在答题卡．．．的相应位置作答） 17．解方程（每小题4分，共8分）（1）x x 22=； （2）2550x x --=.18．（8分）已知关于x 的一元二次方程032=++m x x 有两个不相等的实数根，且m 为正整数，求m 的值.19．（8分）某中学食堂开设了两个窗口，窗口一提供四种食品：肉包、馒头、鸡蛋、油饼；窗口二提供两种食品：牛奶、豆浆. 约定：学生在一个窗口领一种食品后，再到另一个窗口领一种食品.（1）问：学生早餐领到的食品一共有几种不同的可能?（2）如果某天食堂师傅在两个窗口随机发放食品，请用列表或画树状图的方法，求出小王同学该天早餐刚好得到牛奶和馒头的概率.20．（8分）如图，△APB 内接于⊙O .（1）作∠APB 的平分线PC ，交⊙O 于点C （尺规作图，保留作图痕迹，不写作法）； （2）在（1）的条件下，若∠APB =120º，连接AC ，BC ，求证：△ABC 是等边三角形.第20题图21．（8分）如图，用48米篱笆围成一个外形为矩形的花园，花园一面利用院墙，中间用一道篱笆间隔成两个小矩形，院墙的长度为20米，平行于院墙的一边长为x 米，花园的面积为S 平方米．（1）求S 与x 之间的函数关系式；（2）问花园面积可以达到180平方米吗？如果能，花园的长和宽各是多少？如果不能，请说明理由.22．（10分）如图，AB 是半圆O 的直径，点D 是半圆上一点，连接OD ，AE ⊥OD 于点E ，设∠AOE =α，将△AEO 绕点O 顺时针旋转α角，得到△DHO ，若点D ，H ，B 在一条直线上，求α的值.23．（10分）如图，直线(0)y kxk =<与反比例函数(0,0)my m x x=<<的图象交于点A ，直线与y 轴正半轴的夹角为60，OA =2． （1）求反比例函数的解析式；（2）根据图象直接写出mkx x>的自变量的取值范围．xDCBA第21题图AOBHED第22题图第23题图24．（12分）如图，在边长为8的等边△ABC 中，点D 是AB 的中点，点E 是平面上一点，且线段DE =2，将线段EB 绕点E 顺时针旋转60º得到线段EF ，连接AF . （1）如图1，当BE =2时，求线段AF 的长； （2）如图2，① 求证：AF =CE ；② 求线段AF 的取值范围.25．（14分）我们把（a ，b ，c ）称为抛物线c bx ax y ++=2的三维特征值.已知抛物线1y 所对应的三维特征值为)031(，，b -，且顶点在直线2=x 上. （1）求抛物线1y 的解析式；（2）若直线t y =与抛物线1y 交于P 、Q 两点，当PQ <1≤2时，求t 的取值范围； （3）已知直线2=x 与x 轴交于点A ，将抛物线1y向右平移1）个单位得到抛物线2y ，且抛物线2y 与直线1=y 分别相交于M 、N 两点（M 点在N 点的左侧），与x 轴交于C 、D 两点（C 点在D 点的左侧），求证：射线AN 平分∠MAD .第24题图1第24题图2南平市2018-2019学年第一学期九年级期末质量检测数学试题参考答案及评分说明说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分．（4）评分只给整数分．选择题和填空题不给中间分． 一、选择题（本大题共10小题，每小题4分，共40分）1．C ； 2．B ； 3．C ； 4．D ； 5．D ； 6．A ； 7．C ； 8．B ； 9．A ； 10．B ． 二、填空题（本大题共6小题，每小题4分，共24分）11．x = 12．0.3； 13．1； 14．3； 15．2±； 16．19.5°． 三、解答题（本大题共9小题，共86分）17．（1）解：2-20x x =…………………………………………………………………1分()2=0x x -…………………………………………………………………2分12=0=2x x ，…………………………………………………………………4分（2）解：∵5,5,1-=-==c b a ， ……………………………………………………1分()254552⨯+-±=x ……………………………………………………2分2535±=x .2535,253521-=+=x x ……………………………4分 18．解：∵一元二次方程032=++m x x 有两个不相等的实数根，2=3-40m ∆>， …………………………………………………………4分∴94m < ，………………………………………………………………6分∵m 为正整数，∴=12m m =或.……………………………………………………………………8分19．（1）解：食堂早餐的食品一共有8种不同的可能.……………………………………2分(2) 方法一：肉包 馒头 鸡蛋 油饼 ………………………………………………6分 ∴（肉包，牛奶）（肉包，豆浆）（馒头，牛奶）（馒头，豆浆）（鸡蛋，牛奶）（鸡蛋，豆浆）（油饼，牛奶）（油饼，豆浆），………………7分牛奶 豆浆 牛奶 豆浆 牛奶 豆浆 牛奶 豆浆∴()1=8P 得到牛奶和馒头. ………………………………………………………8分 方法二：7分∴()1=8P 得到牛奶和馒头. ………………………………………………………8分 20． (1)作图………………………………………………………………………………3分(2)证明：∵PC 平分∠APB ，∠APB =120º，∴∠APC=∠CPB =60º ， ……………………………………………………4分 ∵∠ABC 与∠APC 同对弧AC ， ∴∠ABC=∠APC =60º ， ………………………………………………………5分 ∵∠CAB 与∠CPB 同对弧BC ∴∠CAB=∠CPB =60º ，…………………………………………………………6分 ∴∠ACB=180º-∠ABC-∠CAB =60º，∴∠ACB=∠ABC=∠CAB ，……………………………………………………7分 ∴△ABC 是等边三角形. ………………………………………………………8分 21．解：（1）∵()4803x x s -=，…………………………………………………………2分 ACP BO第20题答题图2第20题答题图1∴()21-160203s x x x =+<≤. ……………………………………………………3分（2）花园面积可以达到180平方米， ……………………………………………4分∵ 21-161803x x +=， …………………………………………………………5分 ∴1218,30x x ==， ………………………………………………………………6分∵院墙的最大长度为m 20 ∴()230x =不符合题意舍去∴18x =. ……………………………………………………………………………7分 答：当18x =时，花园面积可以达到2180m . …………………………………………8分 22. 解：连接HB ，∵AE ⊥EO ， ∴∠AEO=90º，∵△AEO 绕点O 顺时针旋转得到△DHO ， ∴△AEO ≌△DHO ， ∴∠A=∠D ，∠DHO=∠AEO=90º ， ∠DOH=∠AOE ， …………………………………………………………………3分∵D 、H 、B 在一条直线上， ∴OH ⊥DB ，证法一：∵OD =OB ，∴∠B=∠D ，………………………………………………………………………4分 ∴∠A=∠B ，………………………………………………………………………5分 ∵∠AOE 与∠B 同对弧AD ，∴∠AOE =2∠B ，∴∠AOE =2∠A ， …………………………………………………………………7分 在Rt △AOE 中, ∠AOE +∠A=90º， ∴2∠A+∠A=90º，……………………………………………………………………8分 ∴∠A=30º， ……………………………………………………………………9分 ∴∠AOE=60º 即α=60º. ………………………………………………………10分 证法二：∵OD =OB ，OH ⊥DB ，∴OH 平分∠BOD 即∠BOH =∠DOH ，………………………………………7分∵∠DOH=∠AOE ，∴∠DOH=∠AOE=∠BOH=60º ………9分 ∴α=60º. ………………………………10分23．解：（1）过A 作AB ⊥x 轴垂足为B ，…………1分O 第22题答题图∵直线与y 轴正半轴的夹角为60，∴∠AOB =30°，…………………………2分 ∴112AB OA == ，……………………3分 ∴在Rt △AOB 中，O B = …………………4分∴()A ， …………………………5分∴m = ………………………………6分∴y =. ……………………………………7分(2) 0x < (10)24．解：(1)作AG ⊥BC 于G 点，延长FE 交AG 于H 点∵AB =AC ， ∴∠BAG=30º，……………………1分∵EB 绕点E 顺时针旋转60º得到线段EF ， ∴∠BEF=60º， ∴∠BEF=∠B ，∴EF ∥BC ， …………………………2分 ∵AG ⊥BC ，∴AG ⊥FH ， …………………………3分 在Rt △AEH 中,∵AE=6,∠EAH=30º， ∴132EH AE ==,AH == 在Rt △AFH 中，AF ===方法二：(1)连接FB,作FP ⊥AB 于P 点， ∵EB 绕点E 顺时针旋转60º得到线段EF ，∴△EBF 是等边三角形，…………………………1分 又∵FP ⊥AB ，∴∠EFP=30º， ∴112EP EF == ，……………………………2分 GAC∴AP=7，在Rt△EFP中, PF=3分在Rt△APF中,AF===…………………4分(2) ①连接FB，∵EB绕点E顺时针旋转60º得到线段EF，∴△EBF是等边三角形，∴FB=EB, ∴∠FBE=∠ABC=60º…………………………………………………………6分∴∠FBE+∠EBA=∠ABC+∠EBA即∠FBA=∠EBC，…………………………………………………………………………7分又∵AB=BC，∴△FBA≌△EBC，………………………………………………………………………8分∴AF=CE， (9)分②22AF≤≤. ………………………………………………………12分∵DE=2,∴E点在以D为圆心，2为半径的圆上，且2342-34+≤≤CE∵AF=CE∴22AF≤≤.(25．解：（1）依题意可得211=-3y x bx+∵1y顶点在直线2=x上，∴-2123b=⎛⎫⨯- ⎪⎝⎭，FC（第24题答题图2）∴43b =， ………………………………2分 ∴2114=-33y x x +.……………………3分（2） 设直线PQ 与直线2=x 相交与E 点， ∴2PQPE =， ……………………………………………………………4分 ∵PQ <1≤2，∴112PE <≤， …………………………………………………………5分 ∴当12PE =时，1352,224p p x y =-==，………………………………………………6分 当 1PE =时 ，211,1p p x y =-==， …………………………………………………7分 ∴ 514t ≤<. ………………………………………………………………………………9分 方法2：设214-=33x x t +， ∴ ()22=-34x t -+，∴ 122,2x x ==，…………………………………………………5分∴ 12PQ x x =-=，………………………………………………………………6分 ∴ 1PQ =时，14-34t =，54t =，2PQ =时，4-31t =，1t =，……………………………………………………………8分∴ 514t ≤<.…………………………………………………………………………………9分（3）设直线1=y 与1y 依次相交11,M N 于两点，由（2）可得11M N,1M x ，∴()11,1M ，………………………………………………………………………10分 由平移的性质可得11=2MN M N =,()2M +，…………………………11分 ∴2MA ==根据勾股定理可得………………………12分证法一：∴=2MA MN =，∴∠MAN=∠MNA ，………………………………………………………………13分 ∵MN ∥CD ，∴∠MNA=∠NAD , ∴∠MAN=∠NAD ,∴射线AN 平分∠MAD . …………………………………………………………14分 证法二：过N 点作NP ⊥AM 于P 点, NQ ⊥CD 于Q 点,∴NQ=1,∵.11=122AMN S AM NP MN ∆⋅=⋅， ∴NP =1 , ………………………………………………………………13分∴NP = NQ ,∵NP ⊥AM 于P点, NQ ⊥CD ，∴射线AN平分∠MAD. ………………………………………………14分。

南平市2017-2018学年第一学期九年级期末质量检测数学试题（满分：150分；考试时间：120分钟）★友情提示：① 所有答案都必须填在答题卡相应的位置上，答在本试卷上一律无效； ② 试题未要求对结果取近似值的，不得采取近似计算．一、选择题（本大题共10小题，每小题4分，共40分．每小题只有一个正确的选项，请在答．题卡．．的相应位置填涂） 1．在平面直角坐标系中，点M （1，﹣2）与点N 关于原点对称，则点N 的坐标为A ．（﹣2， 1）B ．（1，﹣2）C ．（2，-1）D ．（-1，2）2．用配方法解一元二次方程0122=-+x x ，可将方程配方为A ．()212=+x B ．()012=+x C ．()212=-x D ．()012=-x3．下列事件中，属于随机事件的有①任意画一个三角形，其内角和为360°； ②投一枚骰子得到的点数是奇数； ③经过有交通信号灯的路口，遇到红灯； ④从日历本上任选一天为星期天． A ．①②③B ．②③④C ．①③④D ．①②④4．下列抛物线的顶点坐标为(4，－3)的是A ．()342-+=x y B ．()342++=x y C ．()342--=x y D ．()342+-=x y5．有n 支球队参加篮球比赛，共比赛了15场，每两个队之间只比赛一场，则下列方程中符合题意的是A ．()151=-n nB ．()151=+n nC ．()301=-n nD ．()301=+n n6．某小组在“用频率估计概率”的实验中，统计了某种结果出现的频率，绘制了如图所示的折线图，那么符合这一结果的实验最有可能的是A ．袋子中有1个红球和2个黄球，它们只有颜色上的区别，从中随机地取出一个球是黄球B ．掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6C ．在“石头、剪刀、布”的游戏中，小宇随机出的是“剪刀”D ．掷一枚质地均匀的硬币，落地时结果是“正面向上”7．如果一个正多边形的中心角为60°，那么这个正多边形的边数是A ．4B ．5C ．6D ．78．已知点A （x 1，y 1），B （x 2，y 2）是反比例函数xy 1-=的图象上的两点，若x 1＜0＜x 2，则下列结论正确的是A ．y 1＜0＜y 2B ．y 2＜0＜y 1C ．y 1＜y 2＜0D ．y 2＜y 1＜09．如图，AB 为⊙O 的直径，PD 切⊙O 于点C ，交AB 的延长线于D ， 且CO =CD ，则∠PCA =A ．30°B ．45°C ．60°D ．67.5°（第6题图）DCB OAP（第9题图）10．如图，在Rt △ABC 和Rt △ABD 中，∠ADB =∠ACB =90°，∠BAC =30°，AB =4，AD =22，连接DC ，将Rt △ABC 绕点B 顺时针旋转一周，则线段DC 长的取值范围是 A ．2≤DC ≤4 B ．22≤DC ≤4C ．222-≤DC ≤22D ．222-≤DC ≤222+二、填空题（本大题共6小题，每空4分，共24分．将 答案填入答题卡．．．的相应位置） 11．如图，在平面直角坐标系xoy 中，矩形OABC ，OA =2， OC =1， 写出一个函数()0≠=k xky ，使它的图象与矩形OABC 的边有两个公共点，这个函数的表达式可以为 （答案不唯一）．12．已知关于x 的方程032=++a x x 有一个根为﹣2，a = ．13．圆锥的底面半径为7cm ，母线长为14cm ，则该圆锥的侧面展开图的圆心角为 °． 14．设O 为△ABC 的内心，若∠A =48°，则∠BOC = °．15．把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF =CD =4cm ，则球的半径为cm ．16． 抛物线c bx ax y ++=2（a >0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，则a 的取值范围是 ．三、解答题（本大题共9小题，共86分．在答题卡．．．的相应位置作答）17．解方程（每小题4分，共8分）（1）022=+x x （2）01232=-+x x18．（8分）已知关于x 的方程 )0(03)3(2≠=+++k x k kx ． （1）求证：方程一定有两个实数根；（2）若方程的两个实数根都是整数，求正整数k 的值． 19．（8分）有甲、乙两个不透明的布袋，甲袋中有3个完全相同的小球，分别标有数字0，1和2；乙袋中有3个完全相同的小球，分别标有数字1，2和3，小明从甲袋中随机取出1个小球，记录标有的数字为x ，再从乙袋中随机取出1个小球，记录标有的数字为y ，这样确定了点M 的坐标(x ，y )． （1）写出点M 所有可能的坐标；（2）求点M 在直线3+-=x y 上的概率．20．（8分）如图，直线y =x +2与y 轴交于点A ，与反比例函数()0≠=k xky 的图象交于点C ，过点C 作CB ⊥x 轴于点B ，AO =2BO ，求反比例函数的解析式．21．（8分）如图，12×12的正方形网格中的每个小正方形1，正方形的顶点叫做格点．矩形ABCD 的四个顶点A ，B ，C ，都在格点上，将（第21题图）（第11题图）CDABD（第15题图）△ADC 绕点A 顺时针方向旋转得到△AD ′C ′，点C 与点C ′为对应点． （1）在正方形网格中确定D ′的位置，并画出△AD ′C ′；（2）若边AB 交边C ′D ′于点E ，求AE 的长．22．（10分）在矩形ABCD 中，AB =8，BC =6，将矩形按图示方式进行分割，其中正方形AEFG 与正方形JKCI 全等，矩形GHID 与矩形EBKL 全等．（1）当矩形LJHF 的面积为43时，求AG 的长；（2）当AG 为何值时，矩形LJHF 的面积最大．23．（10分）如图，点A ，C ，D ，B 在以O 点为圆心，OA长为半径的圆弧上， AC=CD=DB ，AB 交OC 于点E ．求证：AE =CD ．24．（12分）如图，在等边△BCD 中，DF ⊥BC 于点F ，点A 为直线DF 上一动点，以B 为旋转中心，把BA 顺时针方向旋转60°至BE ，连接EC ．（1）当点A 在线段DF 的延长线上时，①求证：DA =CE ；②判断∠DEC 和∠EDC 的数量关系，并说明理由； （2）当∠DEC =45°时，连接AC ，求∠BAC 的度数．25．（14分）如图，在平面直角坐标系xoy 中，二次函数c bx ax y ++=2（0≠a ）的图象经过A （0，4），B （2，0），C （-2，0）三点． （1）求二次函数的解析式； （2）在x 轴上有一点D （-4，0），将二次函 数图象沿DA 方向平移，使图象再次经过点B ．①求平移后图象顶点E 的坐标；②求图象 A ，B 两点间的部分扫过的面积．南平市2017-2018学年第一学期九年级期末质量检测数学试题参考答案及评分说明（第25题图） LH I KJF E DB CA G（第22题图） E DFB CA （第24题图） A BC D E （第23题图）说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分． （4）评分只给整数分．选择题和填空题不给中间分． 一、选择题（本大题共10小题，每小题4分，共40分）1．D ； 2．A ； 3．B ； 4．C ； 5．C ； 6．B ； 7．C ； 8．B ； 9．D ； 10．D ． 二、填空题（本大题共6小题，每小题4分，共24分） 11．如：xy 1=（答案不唯一，0＜k ＜2的任何一个数）； 12．2； 13．180； 14．114； 15．2.5； 16．0＜a ＜3.三、解答题（本大题共9小题，共86分） 17.（每小题4分，共8分）(1) 解： 0)2(=+x x ……………………………………………………………2分 ∴2,021-==x x .……………………………………………………4分 （2）解：1,2,3-===c b a ∴ 161-34-22=⨯⨯=∆）（∴64232162±-=⨯±-=x …………………………………………2分∴1,3121-==x x . …………………………………………………4分18．（8分）（1）证明：9634)3(22+-=⋅⋅-+=∆k k k k0)32≥-=k （，……………………………………………………2分∴方程一定有两个实数根. …………………………………………3分（2）解：3,3,=+==c k b k a ，22)3(34)3-=⋅⋅-+=∆∴k k k （，kk k k k k x 2)3(32)3()3(2-±--=-±+-=∴， kx x 3,121-=-=∴ ，………………………………………………6分∵方程的两个实数根都是整数，∴正整数31或=k ．…………………………………………………8分 19．（8分）解：（1）方法一：列表：从表格中可知，点M （1,1），（1,2），（1,3），（2,1），（2,2），（2,3）．……………………………………………………………3分 方法二：从树形图中可知，点M 坐标总共有九种可能情况：（0,1），（0,2），（0,3），（1,1），（1,2），（1,3），（2,1），（2,2），（2,3）．……………………………………………………………3分 （2）当x =0时，y=-0+3=3， 当x =1时，y=-1+3=2，当x =2时，y=-2+3=1，……………………………………………………6分 由（1）可得点M 坐标总共有九种可能情况，点M 落在直线y =-x +3上（记为事 件A ）有3种情况．∴P(A )3193==．…………………………………………8分20．（8分）解： 当x =0时，y =2，∴A (0，2)，…………………………………2分 ∴A O=2，∵AO =2BO ，∴B O=1，………………………………………………4分 当x =1时，y =1+2=3，∴C (1，3)， ……………………………………………6分 把C (1，3)代入xky =，解得：3=k xy 3:=∴反比例函数的解析式为…………………………………………………8分 21．（8分）解：（1）准确画出图形；…………………………………………………3分（2）∵将△ADC 绕点A 顺时针方向旋转得到△AD ′C ′，点C 与点C ′为对应点， ∴△ADC ≌△AD ′C ′，∴AC =AC ′，AD ′＝AD =5，CD ′＝CD =10，∠AD ′C ′＝∠ADC ＝90°，∠AC ′D ′＝∠ACD ， ∵AB ∥CD ，∴∠BAC ＝∠ACD ，∵AB ⊥C C ′，AC =AC ′，∴∠BAC ＝∠C ′AB ，∴∠AC ′D ′＝∠C ′AB ，∴C ′E ＝AE ．…………………………………………………5分 222R E C BE B C BE C t '=+''∆中，在，x AE AB BE x AE -10-,===则设， 222)-105x x =+（，……………………………………………………………………7分（第21题答题图）425:=x 解得 .425的长为答：AE ……………………………………………………………………8分 22．（10分）解：（1） 正方形AEFG 和正方形JKCI 全等，矩形GHID 和矩形EBKL 全等， 设AG =x ，DG =6-x ，BE =8-x ，FL=x -(6-x )=2x -6，LJ =8-2x ， 方法1： LJ FL S LIHF ⋅=矩形 ， ∴43)28)(62(=--x x ………………………………………………………………2分 ∴415,41321==x x ，∴AG =413或AG =415．………………………………………4分方法2：AEFG DGHI ABCD LIHF S S S S 正方形矩形矩形矩形22--=)6)(8(2248432x x x ----=∴，…………………………………………………2分 ∴415,41321==x x ，∴AG =413或AG =415．………………………………………4分（2）设矩形LJHF 的面积为S ，)28)(62(x x S --=…………………………………………………………………6分482842-+-=x x1)27(42+--=x …………………………………………………………………8分04<-=a ， ∴S 有最大值，∴当AG =27 时，矩形LJHF 的面积最大．………………………………………10分23．（10分）证明：方法一：连接OC ，OD ， ∵AC=CD=DB ，∴DB CD AC 弧弧弧==，∴BOD COD AOC ∠=∠=∠，……………………………………………………2分 ∴AOC COD DOB COD COB ∠=∠=∠+∠=∠22，∵CAE COB ∠=∠2，∴CAE AOC ∠=∠，………………………………………4分 OC OA AOC =∆中，在，2-902180AOCAOC -ACO ∠=∠=∠∴︒︒，…………5分 ACE CAE AEC ACE ∠∠=∠∆︒--180中，在)290(180AOC AOC ∠--∠-=︒︒ 2-90AOC ∠=︒，……………………………………………………………………6分 AEC ACE ∠=∠∴， ………………………………………………………………7分 AE AC =∴， ……………………………………………………………………8分 CD AC = ，CD AE =∴．………………………………………………………10分 方法二：连接OC ，OD ，∵AC=CD=DB ，∴DB CD AC 弧弧弧==，∴BOD COD AOC ∠=∠=∠，……………………………………………………2分 ∴AOC COD DOB COD COB ∠=∠=∠+∠=∠22，∵CAE COB ∠=∠2，∴CAE AOC ∠=∠，………………………………………4分 ∵∠CAO =∠CAE +∠EAO ，∠AEC =∠AOC +∠EAO ，∴∠CAO =∠AEC ，…………………………………………………………………6分 OC OA AOC =∆中，在， ∴∠ACO =∠CAO ，∴∠ACO =∠AEC ，AE AC =∴， ………………………………………………8分O A BC DE （第23题答题图）CD AC = ，CD AE =∴…………………………………………………………10分 方法三：连接AD ，OC ，OD ， ∵AC=DB ，∴弧AC =弧BD ，∴∠ADC =∠DAB ，…………………………………………………………………2分 ∴CD ∥AB ，∴∠AEC =∠DCO ，…………………………………………………………………4分 ∵AC=CD ，AO=DO ， ∴CO ⊥AD ，∴∠ACO =∠DCO ，…………………………………………………………………6分 ∴∠ACO =∠AEC ，∴AC =AE ，……………………………………………………8分 ∵AC=CD ，∴AE =CD ．……………………………………………………………10分 24．（12分）（1）①证明：∵把BA 顺时针方向旋转60°至BE ，∴=∠=ABE BE BA ，60°， ………………………………1分 在等边△BCD 中，BC DB =∴，︒=∠60DBCFBA FBA DBC DBA ∠+︒=∠+∠=∠∴60， FBA CBE ∠+︒=∠60 ，CBE DBA ∠=∠∴，…………………………………………2分 ∴△BAD ≌△BEC ，∴DA =CE ；…………………………………………………3分 ②判断：∠DEC +∠EDC =90°．…………………………4分DC DB = ，BC DA ⊥，︒=∠=∠∴3021BDC BDA ，∵△BAD ≌△BEC ，∴∠BCE =∠BDA =30°，……………………………………………………………5分 在等边△BCD 中，∠BCD =60°，∴∠ACE =∠BCE +∠BCD ＝90°，∴∠DEC +∠EDC =90°．……………………6分 （2）分三种情况考虑：①当点A 在线段DF 的延长线上时（如图1），由（1）可得， 为直角三角形DCE ∆，︒=∠∴90DCE ， ︒︒︒=∠-=∠=∠459045DEC EDC DEC 时，当， DEC EDC ∠=∠∴，CE CD =∴，由（1）得DA =CE ，∴CD =DA ，CD BD DBC =∆中，在等边，CD DA BD ==∴ ︒=∠∴60BDC ，BC DA ⊥ ，︒=∠=∠=∠∴3021BDC CDA BDA ， ……………………………………………7分DA DB BDA =∆中，在，︒︒=∠=∠∴752-180BDA BAD ，DC DA DAC =∆中，在，︒︒=∠=∠∴752-180ADC DAC ，︒︒︒=+=∠+∠=∠∴1507575DAC BAD BAC ． …………………………………8分②当点A 在线段DF 上时（如图2），BE BA B 至顺时针方向旋转为旋转中心，把以︒60 ， 60=∠=∴ABE BE BA ，，60=∠=∆DBC BC BD BDC ，中，在等边， ABE DBC ∠=∠∴，ABC ABE ABC DBC ∠∠=∠∠--， EBC DBA ∠=∠即，DBA ∆∴≌CBE ∆，CE DA =∴， …………………………9分 90R =∠∆DFC DFC t 中，在，DF ∴＜DC ，E D FB C A（第24题答题图1） EDFB CA （第24题答题图2）∵DA ＜DF ，DA =CE ， ∴CE ＜DC ，由②可知为直角三角形DCE ∆，∴∠DEC ≠45°． ……………………………10分 ③当点A 在线段FD 的延长线上时（如图3）， 同第②种情况可得DBA ∆≌CBE ∆， ECB ADB CE DA ∠=∠=∴，，60=∠=∠∆BCD BDC BDC 中，在等边， BC DA ⊥ ，3021=∠=∠=∠∴BDC CDF BDF ，150180=∠-=∠∴︒BDF ADB ， 150=∠=∠∴ADB ECB ，90=∠-∠=∠∴BCD ECB DCE ，︒︒︒=∠-=∠=∠459045DEC EDC DEC 时，当， DEC EDC ∠=∠∴，CE CD =∴，∴AD =CD =BD ，……………………………………………11分 ∵ 150=∠=∠ADC ADB ，152-180=∠=∠∴︒ADB BAD ， 152-180=∠=∠︒CDA CAD ， 30=∠+∠=∠∴CAD BAD BAC ，.30150 或的度数为综上所述，BAC ∠ …………………12分25．（14分）（1）得）代入（）（）（把c bx ax y C B A ++=20,2-,0,2,4,0，⎪⎩⎪⎨⎧=+-=++=0240244c b a c b a c ，…………………………2分 ⎪⎩⎪⎨⎧==-=401:c b a 解得，42+-=∴x y ． (4)（2）设直线DA 得解析式为y =kx +d (k ≠0)，把A （0，4），D （-4，0）代入得，⎩⎨⎧=+-=044d k d ，⎩⎨⎧==41:d k 解得， ∴y =x +4设E （m ，m +4），平移后的抛物线的解析式为：4)(2++--=m m x y ． 把B （2，0）代入得：04)-2-2=++m m （ 不符合题意，舍去），解得(0521==m m ， ∴E （5，9）． ……………………………………………………………………8分（3）如图，连接AB ，过点B 作BL ∥AD 交平移后的抛物线于点G ，连结EG ，（第25题答题图）DF B C A（第24题答题图3）∴四边形ABGE 的面积就是图象A ，B 两点间的部分扫过的面积．…………10分 过点G 作GK ⊥x 轴于点K ，过点E 作EI ⊥y 轴于点I ，直线EI ，GK 交于点H ． 方法一：由点A （0，4）平移至点E （5，9），可知点B 先向右平移5个单位，再向上平移5个单位至点G ． ∵B （2，0），∴点G （7，5），…………………………………………………12分 ∴GK =5，OB =2，OK =7， ∴BK =OK -OB =7-2=5，∵A （0,4），E （5,9）， ∴AI =9-4=5，EI =5， ∴EH =7-5=2，HG =9-5=4，∴GBK EHG AEI AOB IOKH ABGH ∆∆∆∆=S -S -S -S -S S 矩形四边形3025-8-635521-4221-5521-4221-97==⨯⨯⨯⨯⨯⨯⨯⨯⨯=答：图象A ，B 两点间的部分扫过的面积为30. ……………………………14分 方法二：b x y BL '+=的解析式为设直线， 02:0,2='+b B ）代入得（把点，2-='b ，2-=∴x y ，⎩⎨⎧+--=-=9)5(22x y x y 联立，⎩⎨⎧==02:11y x 解得，⎩⎨⎧==5722y x ， ∴点G （7，5）， …………………………………………………………………12分 ∴GK =5，OB =2，OK =7， ∴BK =OK -OB =7-2=5，∵A （0,4），E （5,9）， ∴AI =9-4=5，EI =5， ∴EH =7-5=2，HG =9-5=4，∴GBK EHG AEI AOB IOKH ABGH ∆∆∆∆=S -S -S -S -S S 矩形四边形3025-8-635521-4221-5521-4221-97==⨯⨯⨯⨯⨯⨯⨯⨯⨯=答：图象A ，B 两点间的部分扫过的面积为30. ……………………………14分。

2018年南平市初三质检数学试题一、选择题（共40分）(1)下列各数中，比-2小3的数是( )．(A)1 (B)1- (C) 5- (D) 6-(2)我国南海总面积有3 500 000平方千米，数据3 500 000用科学记数法表示为( )． (A)3.5×106 (B)3.5×107 (C)35×105 (D)0.35×108 (3)如图，在2×2网格中放置了三枚棋子，在其他格点处再放置1枚棋子， 使图形中的四枚棋子成为轴对称图形的概率是( )． (A)32 (B) 21 (C) 31 (D) 41(4)已知一个正多边形的内角是140°，则这个正多边形的边数是( )． (A)6 (B) 7 (C)8 (D)9(5)已知一次函数y 1=-2x ，二次函数y 2=x 2+1，对于x 的同一个值，这两个函数所对 应的函数值为y 1和y 2，则下列关系正确的是( )． (A)y 1>y 2 (B)y 1≥y 2 (C) y 1<y 2 (D) y 1≤y 2(6)如图，在△ABC 中，∠C=90°，AB=4，以C 点为圆心，2为半径作⊙C ，则AB 的中点 O 与⊙C 的位 置关系是( )．(A) 点O 在⊙C 外 (B) 点O 在⊙C 上 (C) 点O 在⊙C 内 (D) 不能确定 (7)下列说法正确的是( )．(A)为了审核书稿中的错别字，选择抽样调查 (B)为了了解某电视剧的收视率，选择全面调查 (C)“射击运动员射一次，命中靶心”是随机事件(D)“经过有交通信号灯的路口，遇到红灯”是必然事件(8)某学校为绿化环境，计划植树220棵，实际劳动中每小时植树的数量比原计划多10%，结果提前2小时完成任务．设原计划每小时植树x 棵，依据题意,可列方程( )．(A)2220%)101(220+=+x x (B) 2220%)101(220-=+x x(C)2220%10220=-x x (D) 2220%101220-=+xx (9)如图，是一圆锥的左视图，根据图中所示数据，可得圆锥侧面 展开图的圆心角的度数为( )．(A) 60° (B) 90° (C) 120° (D) 135°(10)已知一组数a 1，a 2，a 3，…，a n ，…其中a 1=1，对于任意的正整数n ，满足a n+1 a n ，+ a n+1 n a -=0， 通过计算a 2，a 3，a 4的值，猜想a n 可能是( )． (A)n1(B)n (C)n 2 (D)1 二、填空题（共24分）(11)写出一个正比例函数y =x 象上点的坐标__________．第3题第5题AB第9题(12)关于x 的一元二次方程x 24-x +3m =0有两个实数根，则m =__________． (13)一组数据：3，4，4，6，6，6的中位数是__________． (14)将抛物线2)1(32-+=x y 向右平移3个单位，再向上平 移4个单位，那么得到的抛物线的表达式为__________．(15)如图，正方形ABCD 的面积为18，菱形AECF 的面积为6，则菱形的边长(16)如图，在四边形ABCD 中，AB ∥CD ，AB=BC=BD=2，AD=1，则AC=__________． 三、解答题(共86分)(17)(8分)先化简，再求值：()()a b ab a --+422，其中a =2，b=3，(18)(8分)解不等式组：()⎩⎨⎧-≥-<-212063x x x(19)( 8分)如图，A ，B ，D 三点在同一直线上，△ABC ≌△BDE ，其中点A ，B ，C 的对应点分别是B ，D ，E ，连接CE ． 求证：四边形ABEC 是平行四边形．(20)( 8分)如图，已知∠AOC 内一点D ．(1)按要求面出图形：画一条射线DP ，使得∠DOC=∠ODP 交射线OA 于点P ，以P 点为圆心DP 半径画弧，交射线OA 于E 点，画直线ED 交射线OC 于F 点，得到△OEF ； (2)求证：OE=OF ．(21)( 8分)为了有效地落实国家精准扶贫政策，切实关爱贫困家庭学生．某校对全校各班贫困家庭学生的 人数情况进行了调查．.发现每个班级都有贫困家庭学生，经统计班上贫困家庭学生人数分别有1名、 2名、3名、5名，共四种情况，井将其制成了如下两幅不完整的统计图： (1)填空：a =_______，b=_______；(2)求这所学校平均每班贫困学生人数； (3)某爱心人士决定从2名贫困家庭学 生的这些班级中，任选两名进行帮扶， 请用列表或画树状图的方法，求出被 选中的两名学生来自同一班级的概率．第15题 AA BCD第16题① ②CD AC(22)如图，反比例函数xky =(k ≠0)与一次函数)0(≠+=a b ax y 相交于点A(1，3)，B(c ，1-) (1)求反比例函数与一次函数的解析式；(2)在反比例函数图象上存在点C ，使△AOC 为等腰三角形，这样的点有几个，请直接写出一个以 AC 为底边的等腰三角形顶点C 的坐标．(23)( 10分)如图，AB 为半圆O 的直径，弦CD 与AB 的延长线相交于点E ． (1)求证：∠COE=2∠BDE ； (2)当OB=BE=2，且∠BDE=60°时，求tan E ．(24)( 12分)已知两条线段AC 和BC ，连接AB ，分别以AB 、BC 为底边向上画等腰△ABD 和等腰△BCE ，∠ADB=∠BEC=α． (1)如图1，当α=60°时，求证：△DBE ≌△ABC ； (2)如图2，当α=90°时，且BC=5，AC=2， ①求DE 的长；②如图3，将线段CA 绕点C 旋转，点D 也随之运动，请直接写出C 、D 两点之间距离的取值范围．AB O x y A BCDE 图1 A B C D E 图2 A B C DE图3(25)( 14分)已知抛物线421+-=x y (x >0)与44122+-=x y (x >0)有公共的顶点M(0，4)，直线 x =p (p >0)分别与掀物线y 1、y 2交于点A 、B ，过点A 作直线AE ⊥y 轴于点E ，交y 2于点C ．过点B 作直线BF ⊥y 轴于点F ，交y 1于点D ．(1)当p =2时，求AC 的长；(2)求BDMACM S S∆∆的值；(3)直线AD 与BC 的交点N(m ，n )， 求证：m 为常数．O y x y 1y 2C E BD F M x=p2018年南平市九年级学业（升学）质量检查参考答案及评分说明（1）C ； （2）A ； （3）C ； （4）D ； （5）D ； （6）B ； （7）C ； （8）B ； （9）C ； （10）A ． （11）如：（1，1）（答案不唯一）； （12）34； （13）5； （14）()2232+-=x y ； （15）10； （16）15． 三、解答题（本大题共9小题，共86分） （17）（本小题满分8分）解：原式2224444a ab b ab a +-++=………………………… 2分 2245b a +=， ……………………………………………4分当32==b a ，时，原式22)3(425⨯+⨯=………………………………………6分321220=+=． ………………………………………8分（18）（本小题满分8分）解：由①得，2<x ， ………………………………………3分由②得，22-x ≥2-x ，……………………………………5分x ≥0 ， …………………………………… 6分 所以不等式组的解集是0≤x ＜2． ……………………………8分（19）（本小题满分8分）证明：∵△ABC ≌△BDE ，∴∠DBE=∠A , BE = AC ， …………………4分 ∵∠DBE=∠A ，∴BE ∥AC ，…………………………………6分 又∵BE = AC ，∴四边形ABEC 是平行四边形． …………8分（20）（本小题满分8分）（Ⅰ）确定点P ，E ，F ，各得1分，图形完整得1分，共4分； （Ⅱ）证明：∵∠DOC=∠ODP ，∴PD ∥OC ，∴∠EDP=∠EFO ， …………………………5分 ∵PD =PE ，∴∠PED=∠EDP ， …………………………6分 ∴∠PED=∠EFO ， …………………………7分∴OE=OF ． …………………………………8分（21）（本小题满分8分）（Ⅰ）填空：a =2，b =10； …………………………………2分（Ⅱ）21015232251=⨯+⨯+⨯+⨯………………4分答：这所学校平均每班贫困学生人数为2；C BD EA（第19题图）EP O DAC （第20题（Ⅰ）答题图）（Ⅲ）设有2名贫困家庭学生的2个班级分别记为A 班和B 班， 方法一： 列表：准确列表……………………………………………………………6分 方法二： 树状图：A212A11B 2121B221B准确画出树状图 ……………………………………………………6分 ∴P （两名学生来自同一班级）＝31124=． ………………8分 （22）（本小题满分10分）解：（Ⅰ）把A （1，3）代入xy 12=中得，313=⨯=k ，∴反比例函数的解析式为x y 3=， ……3分把B （c ，-1）代入xy 3=中，得3-=c ，把A （1，3）,B （-3，-1）代入b ax y +=中得， ⎩⎨⎧-=+-=+133b a b a ，∴⎩⎨⎧==21b a ， ∴一次函数的解析式为2+=x y ； ……6分（Ⅱ）这样的点有4个，………………………8分C 2（3，1）或C 4（-3，-1）． …………10分（23）（本小题满分10分） （Ⅰ）证明：连接AC ，∵∠A+∠CDB =180， ………1分∠BDE+∠CDB =180°，………2分∴∠A=∠BDE ， ……………3分 ∵∠COE=2∠A ， ……………4分∴∠COE=2∠BDE ；…………5分（Ⅱ）解：过C 点作CF ⊥AE 于F 点，∵∠BDE =60°，∴∠A =60°， …………………………………………………………6分 又∵OA =OC ，∴△AOC 是等边三角形，∵OB =2，∴OA =AC =2，∴121===AO FO AF ， …………………………………………7分 在Rt △AFC 中，∴ ，…………………………8分在Rt △CEF 中，EF =FO +OB +BE =5， ∴53tan ==EF CF E ． (10)分 312222=-=-=AF AC CF EAO B C D （第23题答题图） F （第22题（Ⅱ）答题图）（24）（本小题满分12分）（Ⅰ）证明：∵∠ADB=∠BEC=60°，∴等腰△ADB 和等腰△BEC 是等边三角形，………1分 ∴BD =BA ，BE=BC ，∠DBA=∠EBC=60°，………2分 ∴∠DBA -∠EBA=∠EBC -∠EBA ，∴∠DBE=∠ABC ， …………………3分 ∴△DBE ≌△ABC （SAS ）；……………4分 （Ⅱ）解：（i ）∵∠ADB=90°， DB =DA ， ∴∠DBA=45°，同理∠EBC=45°， ∴∠DBA=∠EBC ，∴∠DBA -∠EBA=∠EBC -∠EBA ， ∴∠DBE=∠ABC ，……………………5分 又∵cos ∠DBA = cos ∠EBC ， ∴22==BC BE AB DB ， ……………6分 ∴△DBE ∽△ABC ， …………………7分∴BC BE AC DE =，即222=DE ， ∴ ； ……………………8分（ii ）223≤CD ≤227． ………12分（25）（本小题满分14分）（Ⅰ）解：当p =2时，把x =2带入421+-=x y 中得，01=y ， ∴A （2，0），……………………………………………………1分 把y 2=2带入44122+-=x y （x >0）中得，x =4， ∴C （4，0），……………………………………………………2分 ∴AC =2； ……………………………………………………3分 （Ⅱ）解：设)441,(),4,(22+-+-p p B p p A ， 则)441,0(),4,0(22+-+-p F p E ， 2=DE EDCBA（第24题图1）E DCBA（第24题图2）EDCBA（第24题（ii ）答题图1）ED CBA（第24题（ii ）答题图2）∵M （0，4），∴22)4(4p p ME =+--=，4)441(422p p MF =+--=，……………………………5分当44121+-=p y 时，444122+-=+-x p ，∴p x D 21=，当422+-=p y 时，441422+-=+-x p ， ，∴p x C 2=， ∴)4,2(2+-p p C ,)441,2(2+-p p D ， ∴221p p p BD =-=， p p p AC =-=2， ……………………………………7分∴8412212122=⋅⋅=⋅⋅=∆∆p p p p MF BD MEAC S S BDMACM ；………………8分（Ⅲ）证明：方法一：设直线AD ：b kx y +=，把)441,21(),4,(22+-+-p p D p p A 代入得： ⎪⎩⎪⎨⎧+-=++-=+44121422p b kp p b kp ，解得⎪⎪⎩⎪⎪⎨⎧+=-=421232p b p k ， ∴直线AD ：421232++-=p px y ；……………………10分 设直线BC ：b x k y '+'=，把)441,(),4,2(22+-+-p p B p p C 代入得： ⎪⎩⎪⎨⎧+-='+'+-='+'4414222p b k p p b k p ，解得⎪⎪⎩⎪⎪⎨⎧+='-='421432p b p k ， ∴直线BC ：421432++-=p px y ；………………………12分 ∵直线AD 与BC 的交点为N(m,n)，∴⎪⎪⎩⎪⎪⎨⎧++-=++-=421234214322p pm n p pm n ， ………13分 ∴043=pm ， ∵p >0，∴m=0，即m 为常数．…………………14分方法二： 设直线AD 交y 轴于G 点，直线BC 交y∵BF ∥CE ，∴△GFD ∽△GEA ，△HFB ∽△HEC ，…10分∴2121===p p AE DF GE GF ， 212===p p CE BF HE HF ， ∴HE HFGE GF =，………………………11分 ∴FEHF HFFE GF GF +=+，∴HF GF =，…………………………13分∴G 、H 点重合，∴G 、H 点就是直线AD 与直线BC 的交点N ， ∴m=0，即m 为常数． ………………14分（第25题（Ⅲ）答题图）。

顺昌县2018--2019学年第二学期初中第一次质量监测考试九年级 数学科试题（考试时间：120分钟；满分：150分）一、选择题（本大题10小题，每小题4分，共40分．每题只有一个选项）1．下列各数中，比﹣2小的数是（ ）A ．﹣1B ．0C ．﹣3D ．12．下列运算正确的是（ ） A ．2m 2+m 2＝3m 4B ．（mn 2）2＝mn 4C ．2m •4m 2＝8m 2D ．m 5÷m 3＝m 23、已知△ABC 和△A′B′C′是位似图形．△A′B′C′的面积为6 cm ²，△A′B′C′的周长是△ABC 的周长一半．则△ABC 的面积等于( )A ．24 cm ²B ．12 cm ²C ．6 cm ²D ．3 cm ²4．如图是由6个大小相同的小立方体搭成的几何体，这个几何体的左视图是（ ）A． B． C． D．5．在相同时刻的物高与影长成比例．小明的身高为1.5米，在地面上的影长为2米，同时一古塔在地面上的影长为40米，则古塔高为 ( ) (A)60米 (B)40米 (C)30米 (D)25米 6．下列事件属于必然事件的是（ ） A ．经过有交通信号的路口，遇到红灯B ．任意买一张电影票，座位号是双号C ．向空中抛一枚硬币，不向地面掉落D ．三角形中，任意两边之和大于第三边 7．为了美化校园，学校计划购买甲、乙两种花木共200棵进行绿化，其中甲种花木每棵80元，乙种花木每棵100元，若购买甲、乙两种花木共花费17600元，求学校购买甲、乙两种花木各多少棵？设购买甲种花木x 棵、乙种花木y 棵，根据题意列出的方程组正确的是（ ） A．B．C． D．8．若一次函数y ＝kx +b （k ≠0）的图象经过第一、三、四象限，则k ，b 满足（ ） A ．k ＞0，b ＜0B ．k ＞0，b ＞0C ．k ＜0，b ＞0D ．k ＜0，b ＜0学校： 班级： 姓名： 座号：·················密·············封············装············订············线·················9．如图，△ABC 的顶点A 在反比例函数y＝（x ＞0）的图象上， 顶点C 在x 轴上，AB ∥x 轴，若点B 的坐标为（1，3）， S △ABC ＝2，则k 的值为（ ）A ．4B ．﹣4C ．7D ．﹣710．如图1，在矩形ABCD 中，点E 在CD 上，∠AEB ＝90°， 点P 从点A 出发，沿A →E →B 的路径匀速运动到点B 停止， 作PQ ⊥CD 于点Q ，设点P 运动的路程为x ，PQ 长为y ， 若y 与x 之间的函数关系图象如图2所示，当x ＝6时， PQ 的值是（ ） A ．2B．C．D ．1二、填空题（本题6小题，每题4分，共24分） 11．△ABC 中，∠A ，∠B 都是锐角，若sinA ＝32，cosB ＝12，则∠C ＝____． 12．五张看上去无差别的卡片，正面分别写着数字1，2，2，3，5，现把它们的正面向下，随机地摆放在桌面上，从中任意抽出一张，则抽到数字“2”的卡片的概率是 ． 13．关于x 的一元二次方程2x 2﹣x ﹣k ＝0的一个根为1，则k 的值是 ．14．如图，△ABC 的两条中线AD 和BE 相交于点G ，过点E 作EF ∥BC 交AD 于点F ，那么FGAG＝________．15．如图，矩形OABC 的顶点A ，C 分别在坐标轴上，B （8，7），D （5，0），点P 是边AB 或边BC 上的一点，连接OP ，DP ，当△ODP 为等腰三角形时，点P 的坐标为 ． 16．如图，六个正方形组成一个矩形，A ，B ，C 均在格点上，则∠ABC 的正切值为_______．三、解答题（本题9题共86分）17、（8分）：sin45°＋cos30°3－2cos60°－sin60°(1－sin30°)．第14题图第15题图第16题图18．(8分)如图，M ，N 为山两侧的两个村庄，为了两村交通方便，根据国家的惠民政策，政府决定打一直线隧道．工程人员为了计算工程量，必须计算M ，N 两点之间的直线距离，选择测量点A ，B ，C ，点B ，C 分别在AM ，AN 上，现测得AM ＝1千米，AN ＝1.8千米，AB ＝54米，BC ＝45米，AC ＝30米，求M ，N 两点之间的直线距离．19．(8分)如图，在平面直角坐标系xOy 中，一次函数 y ＝kx ＋b 的图象与反比例函数y ＝mx 的图象交于A (2，3)，B (－3，n )两点．(1)求一次函数和反比例函数的解析式；(2)若P 是y 轴上一点，且满足△P AB 的面积是5，直接写出OP 的长．20．(8分) 一个几何体的三视图如下，主、左视图都是腰长为4，底边为2的等腰三角形，则这个几何体的侧面展开图的面积是多少？21．(8 分)如图，等边三角形ABC 的边长为6，在AC ，BC 边上各取一点E ，F ，使AE ＝CF ，连接AF ，BE 相交于点P .(1)求证：AF ＝BE ，并求∠APB 的度数； (2)若AE ＝2，试求AP ·AF 的值．22．（10分）如图为某景区五个景点A ，B ，C ，D ，E 的平面示意图，B ，A 在C 的正东方向，D 在C 的正北方向，D ，E 在B 的北偏西30°方向上，E 在A 的西北方向上，C ，D 相距1000m ，E 在BD 的中点处．（1）求景点B ，E 之间的距离；（2）求景点B ，A 之间的距离．（结果保留根号）23．(10分) 22．(10分)如图，AB 为⊙O 的直径，弦CD ⊥AB ， 垂足为E ，CF ⊥AF ，且CF ＝CE .(1)求证：CF 是⊙O 的切线； (2)若sin ∠BAC ＝25，求S △CBD S △ABC的值．24．（12分）菱形ABCD 中、∠BAD ＝120°，点O 为射线CA 上的动点，作射线OM 与直线BC 相交于点E ，将射线OM 绕点O 逆时针旋转60°，得到射线ON ，射线ON 与直线CD 相交于点F ．（1）如图①，点O 与点A 重合时，点E ，F 分别在线段BC ，CD 上，请直接写出CE ，CF ，CA 三条段段之间的数量关系； （2）如图②，点O 在CA 的延长线上，且OA＝AC ，E ，F 分别在线段BC 的延长线和线段CD 的延长线上，请写出CE ，CF ，CA 三条线段之间的数量关系，并说明理由； （3）点O 在线段AC 上，若AB ＝6，BO ＝2，当CF ＝1时，请直接写出BE 的长．25．（14分）如图，抛物线y ＝ax 2+2x +c （a ＜0）与x 轴交于点A 和点B （点A 在原点的左侧，点B 在原点的右侧），与y 轴交于点C ，OB ＝OC ＝3．（1）求该抛物线的函数解析式．（2）如图1，连接BC ，点D 是直线BC 上方抛物线上的点，连接OD ，CD ．OD 交BC 于点F ，当S △COF ：S △CDF ＝3：2时，求点D 的坐标． （3）如图2，点E 的坐标为（0，），点P 是抛物线上的点，连接EB ，PB ，PE 形成的△PBE 中，是否存在点P ，使∠PBE 或∠PEB 等于2∠OBE ？若存在，请直接写出符合条件的点P 的坐标；若不存在，请说明理由．2018-2019学年九下数学第一次月考评分标准出卷人：陶燕萍 审核：陈玉福、孙慎榕一、选择题本大题10小题，每小题4分，共40分1．C 2.D C 3.A 4.B 5.C 6.D 7.A 8.A 9 C 10.B二、填空题本题6小题，每题4分，共24分11、60° 12、 13、1 14、14 15、（8，4）或（，7） 16、317、．解：原式＝22＋323－2×12－32⎝⎛⎭⎫1－12 （3分） ＝24＋34－32＋34 （6分） ＝24. (8分) 18解：在△ABC 与△ANM 中，∠A ＝∠A ，AC AB ＝3054＝59，（1分）AM AN ＝11.8＝59，（2分）∴AC AB ＝AM AN ，∴AC AM ＝AB AN ，（3分）∴△ABC ∽△ANM ，（4分）∴AC AM ＝BC MN ，（5分）∴ACBC ＝AM MN ，即3045＝1MN ，(7分)解得MN ＝1.5，则M ，N 两点之间的直线距离是1.5千米（8分） 19解：(1)y ＝6x ， (2分) y ＝x ＋1 （4分）(2)对于一次函数y ＝x ＋1，令x ＝0求出y ＝1，即该函数与y 轴的交点为C (0，1)，∴OC ＝1，根据题意得S △ABP ＝12PC ×2＋12PC ×3＝5，解得PC ＝2，（6分）则OP ＝OC ＋PC ＝1＋2＝3或OP ＝PC －OC ＝2－1＝1（8分） 20解：由三视图知该几何体是母线长为4，(2分)底面直径为2的圆锥，（4分）其侧面展开图是扇形，其圆心角为90°（6分）∴这个几何体的侧面展开图的面积是面积为4π.（8分）21(1)∵△ABC 为等边三角形，∴AB ＝AC ，∠C ＝∠CAB ＝60°，又∵AE ＝CF ，∴△ABE ≌△CAF (SAS )，（2分）∴AF ＝BE ，∠ABE ＝∠CAF .又∵∠APE ＝∠BPF ＝∠ABP ＋∠BAP ，∴∠APE ＝∠BAP ＋∠CAF ＝60°，∴∠APB ＝180°－∠APE ＝120° （4分）(2)∵∠C ＝∠APE ＝60°，∠PAE ＝∠CAF ，∴△APE ∽△ACF ，（6分） ∴AP AC ＝AE AF ，即AP 6＝2AF，∴AP ·AF ＝12（8分） 22．解：（1）由题意得，∠C ＝90°，∠CBD ＝60°，∠CAE ＝45°，∵CD ＝1000，∴BC ＝＝1000，（3分）∴BD ＝2BC ＝2000，（4分）∵E 在BD 的中点处，∴BE ＝BD ＝1000（米）；（5分） （2）过E 作EF ⊥AB 与F ，在Rt △AEF 中，EF ＝AF ＝BE •sin60°＝1000×＝500，（7分）在Rt △BEF 中，BF ＝BE •cos60°＝500，（9分）∴AB ＝AF ﹣BF ＝500（﹣1）（米）．（10分）23解：(1)证明：连接OC ，∵CE ⊥AB ，CF ⊥AF ，CE ＝CF ，∴AC 平分∠BAF ，即∠BAF ＝2∠BAC ，(2分)∵∠BOC ＝2∠BAC ，∴∠BOC ＝∠BAF ，（3分）∴OC ∥AF ，∴CF ⊥OC ，∴CF 是⊙O 的切线 （5分）(2)解：∵AB 是⊙O 的直线，CD ⊥AB ，∴CE ＝ED ，BC ︵＝BD ︵，（6分）∴S △CBD ＝2S △CEB ，（7分）∠BAC ＝∠BCE ，又∠ACB ＝∠CEB ＝90°，∴△ABC ∽△CBE ，（8分）∴S △CBE S △ABC ＝(CB AB )2＝(sin ∠BAC )2＝(25)2＝425，（9分）∴S △CBD S △ABC ＝825.（10分）24．解：（1）如图①中，结论：CA ＝CE +CF ．理由：∵四边形ABCD是菱形，∠BAD＝120°∴AB＝AD＝DC＝BC，∠BAC＝∠DAC＝60°∴△ABC，△ACD都是等边三角形，（1分）∵∠DAC＝∠EAF＝60°，∴∠DAF＝∠CAE，∵CA＝AD，∠D＝∠ACE＝60°，∴△ADF≌△ACE（SAS），（2分）∴DF＝CE，∴CE+CF＝CF+DF＝CD＝AC，∴CA＝CE+CF．（3分）（2）结论：CF﹣CE＝AC．（4分）理由：如图②中，如图作OG∥AD交CF于G，则△OGC是等边三角形．∵∠GOC＝∠FOE＝60°，∴∠FOG＝∠EOC，（5分）∵OG＝OC，∠OGF＝∠ACE＝120°，∴△FOG≌△E OC（ASA），∴CE＝FG，∵OC＝OG，CA＝CD，∴OA＝DG，（6分）∴CF﹣EC＝CF﹣FG＝CG＝CD+DG＝AC+AC＝AC，（7分）（3）作BH⊥AC于H．∵AB＝6，AH＝CH＝3，∴BH＝3，（8分）如图③﹣1中，当点O在线段AH上，点F在线段CD上，点E在线段BC上时．∵OB＝2，∴OH＝＝1，∴OC＝3+1＝4，由（1）可知：CO＝CE+CF，∵OC＝4，CF＝1，∴CE＝3，∴BE＝6﹣3＝3．（9分）如图③﹣2中，当点O在线段AH上，点F在线段DC的延长线上，点E在线段BC上时．由（2）可知：CE﹣CF＝OC，∴CE＝4+1＝5，∴BE＝1．（10分）如图③﹣3中，当点O在线段CH上，点F在线段CD上，点E在线段BC上时．同法可证：OC＝CE+CF，∵OC＝CH﹣OH＝3﹣1＝2，CF＝1，∴CE＝1，∴BE＝6﹣1＝5．（11分）如图③﹣4中，当点O在线段CH上，点F在线段DC的延长线上，点E在线段BC上时．同法可知：CE﹣CF＝OC，∴CE＝2+1＝3，∴BE＝3，综上所述，满足条件的BE的值为3或5或1．（12分）25．解：（1）OB＝OC＝3，则：B（3，0），C（0，﹣3），把B、C坐标代入抛物线方程，解得抛物线方程为：y＝﹣x2+2x+3…①；（3分）（2）∵S△COF：S△CDF＝3：2，∴S△COF＝S△COD，即：x D＝x F，（4分）设：F点横坐标为3t，则D点横坐标为5t，点F在直线BC上，而BC所在的直线方程为：y＝﹣x+3，则F（3t，3﹣3t），（6分）则：直线OF所在的直线方程为：y＝x＝x，则点D（5t，5﹣5t），把D点坐标代入①，解得：t＝或，则点D的坐标为（1，4）或（2，3）；（8分）（3）①如图所示，当∠PEB＝2∠OBE＝2α时，过点E作∠PEB的平分线交x轴于G点，PE交x轴于H点，则：∠PEQ＝∠QEB＝∠ABE＝α，则∠HGE＝2α，设：GB＝m，则：OG＝3﹣m，GE＝m，在Rt△OGE中，由勾股定理得：EG2＝OG2+OE2，即：m2＝（3﹣m）2+（）2，解得：m＝，（10分）则：GE＝，OG＝，BE＝，∵∠PEQ＝∠ABE＝α，∠EHG＝∠EHG，∴△HGE∽△HEB，∴＝＝，设：GH＝x，HE＝4x，在Rt△OHE中，OH＝OG﹣HG＝﹣x，OE＝，EH＝4x，由勾股定理解得：x＝，则：OH＝，H（，0），（1）把E、H两点坐标代入一次函数表达式，解得EH所在直线的表达式为：y＝x﹣，将上式与①联立并解得：x＝，则点P（，）；（12分）②当∠PBE＝2∠OBE时，则∠PBO＝∠EBO，BE所在直线的k值为，则BE所在直线的k值为﹣，则：PB所在的直线方程为：y＝﹣x+3，将上式与①联立，解得：x＝，（x＝0已舍去），则点P（，），故：点P坐标为：（，或（，）．（14分）九年级数学试题第11 页（共11页）。

南平市2018-2019学年第一学期九年级期末质量检测数学试题（满分：150分；考试时间：120分钟）★友情提示：①所有答案都必须填在答题卡相应的位置上，答在本试卷上一律无效；②试题未要求对结果取近似值的，不得采取近似计算．一、选择题（本大题共10小题，每小题4分，共40分．每小题只有一个正确的选项，请在答题卡．．．的相应位置填涂）1. 下列图形中，既是轴对称图形又是中心对称图形的是A. B. C. D.2. 用配方法解方程2210x x--=，配方结果正确的是A. ()222x-= B. ()212x-=C. ()2+12x= D.()210x-=3. 同时抛掷两枚质地均匀的正方体骰子，每个骰子的六个面分别标有1，2，3，4，5，6这六个点数，下列事件为必然事件的是A. 朝上一面点数之和为12B. 朝上一面点数之和等于6C. 朝上一面点数之和小于13D. 朝上一面点数之和小于等于64. 如图，点A、B、C在⊙O上，过点C作⊙O的切线与OA的延长线交于点D，若32D∠=，则B∠的大小为A.58 B.34C.32 D.295. 关于二次函数()212y x=+-的图象，下列说法正确的是A. 对称轴是1x= B. 开口向下C. 顶点坐标是（1，-2）D. 与x轴有两个交点6. 1275年我国南宋数学家杨辉提出一个问题：直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及长一十二步（宽比长少一十二步），问阔及长各几步. 设阔（宽）为x 步，则所列方程正确的是A. 864)12(=+xx B. 864)12(=-xxC. 864)12)(12(=+-xx D. 86412=x第4题图7. 已知⊙O 的半径为5，直线l 与⊙O 相交，点O 到直线l 的距离为3，则⊙O 上到直线l 的距离为2的点共有 A. 1个B. 2个C. 3个D. 4个8. 如果点A ),3(1y -，B ),2(2y -，C ),2(3y 都在反比例函数)0(>=k xky 的图象上，那么 1y ，2y ，3y 的大小关系正确的是A. 3y <2y <1yB. 2y <1y <3yC. 1y <2y <3y D .1y <3y <2y9. 若正方形的边长为4，则其外接圆半径与内切圆半径的大小分别为A. 2B. 4，2C. 4，D.10.已知k 为非零的实数，则抛物线kk kx x y 1222++-=的顶点 A. 在一条直线上 B. 在某双曲线上C. 在一条抛物线上D. 无法确定二、填空题（本大题共6小题，每空4分，共24分．将答案填入答题卡．．．的相应位置）11. 一元二次方程22=x 的根是 ．12. 在一个不透明的口袋内只装有一些除颜色外完全相同的红球、白球和黑球，从中任意摸出一个球，摸到红球的概率是0.3，摸到白球的概率是0.4，那么摸到黑球的概率 是 ．13. 若点P (m ，-3)与点Q （2，n ）关于原点对称，则m n += ． 14. 一个扇形的圆心角为80，面积是2cm 2π，则此扇形的半径是 cm ．15．已知反比例函数xky =（0≠k ），当1≤x ≤2时，函数的 最大值与最小值之差是1，则k 的值为 ． 16. 如图，四边形ABCD 中，AB =AC =AD ，若∠BAC =39°，则∠BDC= °.ADC第16题图三、解答题（本大题共9小题，共86分．在答题卡．．．的相应位置作答） 17．解方程（每小题4分，共8分）（1）x x 22=； （2）2550x x --=.18．（8分）已知关于x 的一元二次方程032=++m x x 有两个不相等的实数根，且m 为正整数，求m 的值.19．（8分）某中学食堂开设了两个窗口，窗口一提供四种食品：肉包、馒头、鸡蛋、油饼；窗口二提供两种食品：牛奶、豆浆. 约定：学生在一个窗口领一种食品后，再到另一个窗口领一种食品.（1）问：学生早餐领到的食品一共有几种不同的可能?（2）如果某天食堂师傅在两个窗口随机发放食品，请用列表或画树状图的方法，求出小王同学该天早餐刚好得到牛奶和馒头的概率.20．（8分）如图，△APB 内接于⊙O .（1）作∠APB 的平分线PC ，交⊙O 于点C （尺规作图，保留作图痕迹，不写作法）； （2）在（1）的条件下，若∠APB =120º，连接AC ，BC ，求证：△ABC 是等边三角形.第20题图21．（8分）如图，用48米篱笆围成一个外形为矩形的花园，花园一面利用院墙，中间用一道篱笆间隔成两个小矩形，院墙的长度为20米，平行于院墙的一边长为x 米，花园的面积为S 平方米．（1）求S 与x 之间的函数关系式；（2）问花园面积可以达到180平方米吗？如果能，花园的长和宽各是多少？如果不能，请说明理由.22．（10分）如图，AB 是半圆O 的直径，点D 是半圆上一点，连接OD ，AE ⊥OD 于点E ，设∠AOE =α，将△AEO 绕点O 顺时针旋转α角，得到△DHO ，若点D ，H ，B 在一条直线上，求α的值.23．（10分）如图，直线(0)y kxk =<与反比例函数(0,0)my m x x=<<的图象交于点A ，直线与y 轴正半轴的夹角为60，OA =2． （1）求反比例函数的解析式；（2）根据图象直接写出mkx x>的自变量的取值范围．xDCBA第21题图AOBHED第22题图第23题图24．（12分）如图，在边长为8的等边△ABC 中，点D 是AB 的中点，点E 是平面上一点，且线段DE =2，将线段EB 绕点E 顺时针旋转60º得到线段EF ，连接AF . （1）如图1，当BE =2时，求线段AF 的长； （2）如图2，① 求证：AF =CE ；② 求线段AF 的取值范围.25．（14分）我们把（a ，b ，c ）称为抛物线c bx ax y ++=2的三维特征值.已知抛物线1y 所对应的三维特征值为)031(，，b -，且顶点在直线2=x 上. （1）求抛物线1y 的解析式；（2）若直线t y =与抛物线1y 交于P 、Q 两点，当PQ <1≤2时，求t 的取值范围； （3）已知直线2=x 与x 轴交于点A ，将抛物线1y向右平移1）个单位得到抛物线2y ，且抛物线2y 与直线1=y 分别相交于M 、N 两点（M 点在N 点的左侧），与x 轴交于C 、D 两点（C 点在D 点的左侧），求证：射线AN 平分∠MAD .第24题图1第24题图2南平市2018-2019学年第一学期九年级期末质量检测数学试题参考答案及评分说明说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分．（4）评分只给整数分．选择题和填空题不给中间分． 一、选择题（本大题共10小题，每小题4分，共40分）1．C ； 2．B ； 3．C ； 4．D ； 5．D ； 6．A ； 7．C ； 8．B ； 9．A ； 10．B ． 二、填空题（本大题共6小题，每小题4分，共24分）11．x = 12．0.3； 13．1； 14．3； 15．2±； 16．19.5°． 三、解答题（本大题共9小题，共86分）17．（1）解：2-20x x =…………………………………………………………………1分()2=0x x -…………………………………………………………………2分12=0=2x x ，…………………………………………………………………4分（2）解：∵5,5,1-=-==c b a ， ……………………………………………………1分()254552⨯+-±=x ……………………………………………………2分2535±=x .2535,253521-=+=x x ……………………………4分 18．解：∵一元二次方程032=++m x x 有两个不相等的实数根，2=3-40m ∆>， …………………………………………………………4分∴94m < ，………………………………………………………………6分∵m 为正整数，∴=12m m =或.……………………………………………………………………8分19．（1）解：食堂早餐的食品一共有8种不同的可能.……………………………………2分(2) 方法一：肉包 馒头 鸡蛋 油饼 ………………………………………………6分 ∴（肉包，牛奶）（肉包，豆浆）（馒头，牛奶）（馒头，豆浆）（鸡蛋，牛奶）（鸡蛋，豆浆）（油饼，牛奶）（油饼，豆浆），………………7分牛奶 豆浆 牛奶 豆浆 牛奶 豆浆 牛奶 豆浆∴()1=8P 得到牛奶和馒头. ………………………………………………………8分 方法二：7分∴()1=8P 得到牛奶和馒头. ………………………………………………………8分 20． (1)作图………………………………………………………………………………3分(2)证明：∵PC 平分∠APB ，∠APB =120º，∴∠APC=∠CPB =60º ， ……………………………………………………4分 ∵∠ABC 与∠APC 同对弧AC ， ∴∠ABC=∠APC =60º ， ………………………………………………………5分 ∵∠CAB 与∠CPB 同对弧BC ∴∠CAB=∠CPB =60º ，…………………………………………………………6分 ∴∠ACB=180º-∠ABC-∠CAB =60º，∴∠ACB=∠ABC=∠CAB ，……………………………………………………7分 ∴△ABC 是等边三角形. ………………………………………………………8分 21．解：（1）∵()4803x x s -=，…………………………………………………………2分 ACP BO第20题答题图2第20题答题图1∴()21-160203s x x x =+<≤. ……………………………………………………3分（2）花园面积可以达到180平方米， ……………………………………………4分∵ 21-161803x x +=， …………………………………………………………5分 ∴1218,30x x ==， ………………………………………………………………6分∵院墙的最大长度为m 20 ∴()230x =不符合题意舍去∴18x =. ……………………………………………………………………………7分 答：当18x =时，花园面积可以达到2180m . …………………………………………8分 22. 解：连接HB ，∵AE ⊥EO ， ∴∠AEO=90º，∵△AEO 绕点O 顺时针旋转得到△DHO ， ∴△AEO ≌△DHO ， ∴∠A=∠D ，∠DHO=∠AEO=90º ， ∠DOH=∠AOE ， …………………………………………………………………3分∵D 、H 、B 在一条直线上， ∴OH ⊥DB ，证法一：∵OD =OB ，∴∠B=∠D ，………………………………………………………………………4分 ∴∠A=∠B ，………………………………………………………………………5分 ∵∠AOE 与∠B 同对弧AD ，∴∠AOE =2∠B ，∴∠AOE =2∠A ， …………………………………………………………………7分 在Rt △AOE 中, ∠AOE +∠A=90º， ∴2∠A+∠A=90º，……………………………………………………………………8分 ∴∠A=30º， ……………………………………………………………………9分 ∴∠AOE=60º 即α=60º. ………………………………………………………10分 证法二：∵OD =OB ，OH ⊥DB ，∴OH 平分∠BOD 即∠BOH =∠DOH ，………………………………………7分∵∠DOH=∠AOE ，∴∠DOH=∠AOE=∠BOH=60º ………9分 ∴α=60º. ………………………………10分23．解：（1）过A 作AB ⊥x 轴垂足为B ，…………1分O 第22题答题图∵直线与y 轴正半轴的夹角为60，∴∠AOB =30°，…………………………2分 ∴112AB OA == ，……………………3分 ∴在Rt △AOB 中，O B = …………………4分∴()A ， …………………………5分∴m = ………………………………6分∴y =. ……………………………………7分(2) 0x < (10)24．解：(1)作AG ⊥BC 于G 点，延长FE 交AG 于H 点∵AB =AC ， ∴∠BAG=30º，……………………1分∵EB 绕点E 顺时针旋转60º得到线段EF ， ∴∠BEF=60º， ∴∠BEF=∠B ，∴EF ∥BC ， …………………………2分 ∵AG ⊥BC ，∴AG ⊥FH ， …………………………3分 在Rt △AEH 中,∵AE=6,∠EAH=30º， ∴132EH AE ==,AH == 在Rt △AFH 中，AF ===方法二：(1)连接FB,作FP ⊥AB 于P 点， ∵EB 绕点E 顺时针旋转60º得到线段EF ，∴△EBF 是等边三角形，…………………………1分 又∵FP ⊥AB ，∴∠EFP=30º， ∴112EP EF == ，……………………………2分 GAC∴AP=7，在Rt△EFP中, PF=3分在Rt△APF中,AF===…………………4分(2) ①连接FB，∵EB绕点E顺时针旋转60º得到线段EF，∴△EBF是等边三角形，∴FB=EB, ∴∠FBE=∠ABC=60º…………………………………………………………6分∴∠FBE+∠EBA=∠ABC+∠EBA即∠FBA=∠EBC，…………………………………………………………………………7分又∵AB=BC，∴△FBA≌△EBC，………………………………………………………………………8分∴AF=CE， (9)分②22AF≤≤. ………………………………………………………12分∵DE=2,∴E点在以D为圆心，2为半径的圆上，且2342-34+≤≤CE∵AF=CE∴22AF≤≤.(25．解：（1）依题意可得211=-3y x bx+∵1y顶点在直线2=x上，∴-2123b=⎛⎫⨯- ⎪⎝⎭，FC（第24题答题图2）∴43b =， ………………………………2分 ∴2114=-33y x x +.……………………3分（2） 设直线PQ 与直线2=x 相交与E 点， ∴2PQPE =， ……………………………………………………………4分 ∵PQ <1≤2，∴112PE <≤， …………………………………………………………5分 ∴当12PE =时，1352,224p p x y =-==，………………………………………………6分 当 1PE =时 ，211,1p p x y =-==， …………………………………………………7分 ∴ 514t ≤<. ………………………………………………………………………………9分 方法2：设214-=33x x t +， ∴ ()22=-34x t -+，∴ 122,2x x ==，…………………………………………………5分∴ 12PQ x x =-=，………………………………………………………………6分 ∴ 1PQ =时，14-34t =，54t =，2PQ =时，4-31t =，1t =，……………………………………………………………8分∴ 514t ≤<.…………………………………………………………………………………9分（3）设直线1=y 与1y 依次相交11,M N 于两点，由（2）可得11M N,1M x ，∴()11,1M ，………………………………………………………………………10分 由平移的性质可得11=2MN M N =,()2M +，…………………………11分 ∴2MA ==根据勾股定理可得………………………12分证法一：∴=2MA MN =，∴∠MAN=∠MNA ，………………………………………………………………13分 ∵MN ∥CD ，∴∠MNA=∠NAD , ∴∠MAN=∠NAD ,∴射线AN 平分∠MAD . …………………………………………………………14分 证法二：过N 点作NP ⊥AM 于P 点, NQ ⊥CD 于Q 点,∴NQ=1,∵.11=122AMN S AM NP MN ∆⋅=⋅， ∴NP =1 , ………………………………………………………………13分∴NP = NQ ,∵NP ⊥AM 于P点, NQ ⊥CD ，∴射线AN平分∠MAD. ………………………………………………14分。

数学试题参考答案及评分说明第1页(共6页)南平市2018年初中毕业班适应性检测数学试题参考答案及评分说明说明：（1）解答右端所注分数为考生正确做完该步应得的累计分数，全卷满分150分．（2）对于解答题，评卷时要坚持每题评阅到底，勿因考生解答中出现错误而中断本题的评阅．当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的考试要求，可酌情给分，但原则上不超过后面应得分数的一半，如果有较严重的错误，就不给分．（3）若考生的解法与本参考答案不同，可参照本参考答案的评分标准相应评分．（4）评分只给整数分．选择题和填空题不给中间分．第Ⅰ卷一、选择题（本大题共10小题，每小题4分，共40分）（1）C ；（2）A ；（3）C ；（4）D ；（5）D ；（6）B ；（7）C ；（8）B ；（9）C ；（10）A ．第Ⅱ卷二、填空题（本大题共6小题，每小题4分，共24分）（11）如：（1，1）（答案不唯一）；（12）34；（13）5；（14）()2232+-=x y ；（15）10；（16）15．三、解答题（本大题共9小题，共86分）（17）（本小题满分8分）解：原式2224444a ab b ab a +-++=…………………………2分2245b a +=，……………………………………………4分当32==b a ，时，原式223(425⨯+⨯=………………………………………6分321220=+=．………………………………………8分（18）（本小题满分8分）解：由①得，2<x ，………………………………………3分由②得，22-x ≥2-x ，……………………………………5分x ≥0，……………………………………6分所以不等式组的解集是0≤x ＜2．……………………………8分数学试题参考答案及评分说明第2页(共6页)（19）（本小题满分8分）证明：∵△ABC ≌△BDE ，∴∠DBE=∠A ,BE =AC ，…………………4分∵∠DBE=∠A ，∴BE ∥AC ，…………………………………6分又∵BE =AC ，∴四边形ABEC 是平行四边形．…………8分（20）（本小题满分8分）（Ⅰ）确定点P ，E ，F ，各得1分，图形完整得1分，共4分；（Ⅱ）证明：∵∠DOC=∠ODP ，∴PD ∥OC ，∴∠EDP=∠EFO ，…………………………5分∵PD =PE ，∴∠PED=∠EDP ，…………………………6分∴∠PED=∠EFO ，…………………………7分∴OE=OF ．…………………………………8分（21）（本小题满分8分）（Ⅰ）填空：a =2，b =10；…………………………………2分（Ⅱ）21015232251=⨯+⨯+⨯+⨯………………4分答：这所学校平均每班贫困学生人数为2；（Ⅲ）设有2名贫困家庭学生的2个班级分别记为A 班和B 班，方法一：列表：准确列表……………………………………………………………6分A 1A 2B 1B 2A 1（A 1，A 2）（A 1，B 1）（A 1，B 2）A 2（A 2，A 1）（A 2，B 1）（A 2，B 2）B 1（B 1，A 1）（B 1，A 2）（B 1，B 2）B 2（B 2，A 1）（B 2，A 2）（B 2，B 1）C BDE A （第19题图）F EP ODAC （第20题（Ⅰ）答题图）数学试题参考答案及评分说明第3页(共6页)方法二：树状图：准确画出树状图……………………………………………………6分∴P （两名学生来自同一班级）＝31124=．……………………8分（22）（本小题满分10分）解：（Ⅰ）把A （1，3）代入x y 12=中得，313=⨯=k ，∴反比例函数的解析式为x y 3=，……3分把B （c ，-1）代入x y 3=中，得3-=c ，把A （1，3）,B （-3，-1）代入b ax y +=中得，⎩⎨⎧-=+-=+133b a b a ，∴⎩⎨⎧==21b a ，∴一次函数的解析式为2+=x y ；……6分（Ⅱ）这样的点有4个，………………………8分C 2（3，1）或C 4（-3，-1）．…………10分（23）（本小题满分10分）（Ⅰ）证明：连接AC ，∵∠A+∠CDB =180，………1分∠BDE+∠CDB =180°，………2分∴∠A=∠BDE ，……………3分∵∠COE=2∠A ，……………4分∴∠COE=2∠BDE ；…………5分（Ⅱ）解：过C 点作CF ⊥AE 于F 点，∵∠BDE =60°，∴∠A =60°，…………………………………………………………6分又∵OA =OC ，∴△AOC 是等边三角形，∵OB =2，∴OA =AC =2，∴121===AO FO AF ，…………………………………………7分在Rt △AFC 中，∴，…………………………8分312222=-=-=AF AC CF E A O B C D （第23题答题图）F AyxO B C 1C 2C 3（C 4）（第22题（Ⅱ）答题图）数学试题参考答案及评分说明第4页(共6页)在Rt △CEF 中，EF =FO +OB +BE =5，∴53tan ==EF CF E ．………………………………………………10分（24）（本小题满分12分）（Ⅰ）证明：∵∠ADB=∠BEC=60°，∴等腰△ADB 和等腰△BEC 是等边三角形，………1分∴BD =BA ，BE=BC ，∠DBA=∠EBC=60°，………2分∴∠DBA -∠EBA=∠EBC -∠EBA ，∴∠DBE=∠ABC ，…………………3分∴△DBE ≌△ABC （SAS ）；……………4分（Ⅱ）解：（i ）∵∠ADB=90°，DB =DA ，∴∠DBA=45°，同理∠EBC=45°，∴∠DBA=∠EBC ，∴∠DBA -∠EBA=∠EBC -∠EBA ，∴∠DBE=∠ABC ，……………………5分又∵cos∠DBA =cos∠EBC ，∴22==BC BE AB DB ，……………6分∴△DBE ∽△ABC ，…………………7分∴BC BE AC DE =，即222=DE ，∴；……………………8分（ii ）223≤CD ≤227．………12分E DC B A（第24题（ii ）答题图1）E D CB A（第24题（ii ）答题图2）2=DE E D C B A （第24题图1）ED C B A （第24题图2）（25）（本小题满分14分）（Ⅰ）解：当p =2时，把x =2带入421+-=x y 中得，01=y ，∴A （2，0），……………………………………………………1分把y 2=2带入44122+-=x y （x >0）中得，x =4，∴C （4，0），……………………………………………………2分∴AC =2；……………………………………………………3分（Ⅱ）解：设)441,(),4,(22+-+-p p B p p A ，则)441,0(),4,0(22+-+-p F p E ，∵M （0，4），∴22)4(4p p ME =+--=，4)441(422p p MF =+--=，……………………………5分当44121+-=p y 时，444122+-=+-x p ，∴p x D 21=，当422+-=p y 时，441422+-=+-x p ，，∴p x C 2=，∴)4,2(2+-p p C ,)441,2(2+-p p D ，∴221p p p BD =-=，p p p AC =-=2，……………………………………7分∴8412212122=⋅⋅=⋅⋅=∆∆p p p p MF BD MEAC S S BDMACM ；………………8分（Ⅲ）证明：方法一：设直线AD ：b kx y +=，把)441,21(),4,(22+-+-p p D p p A 代入得：⎪⎩⎪⎨⎧+-=++-=+44121422p b kp p b kp ，解得⎪⎪⎩⎪⎪⎨⎧+=-=421232p b p k ，∴直线AD ：421232++-=p px y ；……………………10分设直线BC ：b x k y '+'=，把)441,(),4,2(22+-+-p p B p p C 代入得：⎪⎩⎪⎨⎧+-='+'+-='+'4414222p b k p p b k p ，解得⎪⎪⎩⎪⎪⎨⎧+='-='421432p b p k ，∴直线BC ：421432++-=p px y ；………………………12分∵直线AD 与BC 的交点为N(m,n)，∴⎪⎪⎩⎪⎪⎨⎧++-=++-=421234214322p pm n p pm n ，………13分∴043=pm ，∵p >0，∴m=0，即m 为常数．…………………14分方法二：设直线AD 交y 轴于G 点，直线BC交y 轴于H 点，∵BF ∥CE ，∴△GFD ∽△GEA ，△HFB ∽△HEC ，…10分∴2121===p pAE DF GE GF ，212===p p CE BF HE HF ，M D C BA O xy x=pF EG H（第25题（Ⅲ）答题图）y 1y 2∴HEHFGE GF =，………………………11分∴FEHF HF FE GF GF+=+，∴HF GF =，…………………………13分∴G 、H 点重合，∴G 、H 点就是直线AD 与直线BC 的交点N ，∴m=0，即m 为常数．………………14分。