运筹学 单纯形法表格形式
- 格式:doc
- 大小:252.50 KB
- 文档页数:9
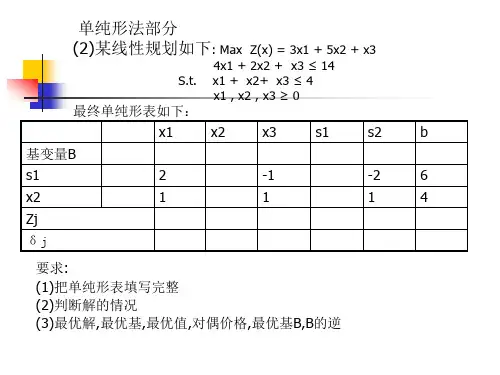





单纯形法(Simplex Method)是线性规划问题的一种求解方法。
下面我将以一个简单的线性规划问题为例,详细解释如何使用单纯形法求解。
例题:假设我们有一个简单的线性规划问题,目标是最小化目标函数 z = 3x + 2y,约束条件是 x + y <= 10, x >= 0, y >= 0。
首先,我们需要构建问题的数学模型。
数学模型可以表示为以下形式:z = 3x + 2yx + y <= 10x >= 0y >= 0然后,我们可以将这个线性规划问题表示为一个单纯形表。
单纯形表的形式如下:| c | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | ||---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---||x | y | z | u | v | w | x1 | x2 | x3 | ... | xn | s.x | s.y | s.z | c.val | b.x | b.y | b.z | dual.val | dual.x1 | dual.x2 | ... | dual.xn ||在这个表中,c 是目标函数的系数,b 是约束条件的系数,s 是松弛变量的系数,dual 是对偶问题的系数,c.val 是当前解的目标函数值,b.x, b.y, b.z 是约束条件的边界值,s.x, s.y, s.z 是松弛变量的值。
现在,我们可以将例题中的数据填入单纯形表:c = [3, 2, 1]b = [1, 0, -10]s = [1, 1, 0]dual = []然后,我们可以开始迭代求解。
在每一次迭代中,我们首先找到进入变量和离开变量,然后更新单纯形表中的数据。

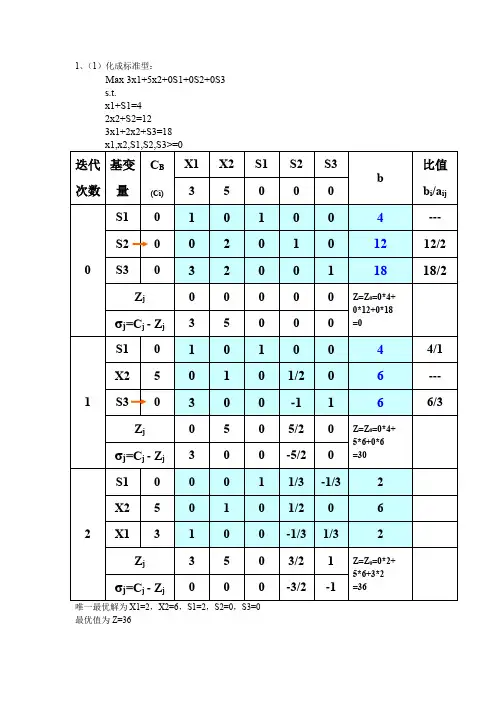



第3章05单纯形表法同学们大家好,前面我们讲了单纯形法的原理,它的整个过程看似很复杂,但实际上,单纯形法的全部计算过程,可以简单地在一张类似增广矩阵的表格上进行,这种表格我们称为单纯形表,所以,今天我们就来学习线性规划模型的单纯形表法。
给定一个可行基,可以画出一张单纯形表。
单纯形表的行标是n个变量以及右端项b,列标是m个基变量以及检验数行σ。
所以,用矩阵的形式把它表示出来,就如下表所示我们注意到,像B,所以,是与原方程组等价的。
最后一行是检验数C-C B B-1A,右下角是-C B B-1b,它恰好是这个基B所对应的可行解的目标函数值的相反数。
用单纯形表法求解线性规划模型时,有下面的步骤:单纯形表法求解线性规划问题的步骤:Step1.转换一般的线形规划模型为标准型,并写出A,b,C。
Step2找初始基本可行解,写出B,B-1,X B,C B。
Step3计算单纯形表中的各矩阵B-1A,B-1b,C-C B B-1A,-C B B-1b,并构造初始单纯形表。
Step4判断基本最优解。
Step5换基迭代,返回Step4。
第一步是将一般的线性规划模型转化为标准形,并写出约束矩阵A,右端项b,以及价值向量C。
第二步,找初始的基本可行解。
根据上一讲单纯形法的原理,你要注意的是,我们总是从约束矩阵A里面选一个单位阵出来作为初始基,在右端项非负的条件下,这样选出来的单位阵一定是可行基,也就是找到了初始的基本可行解。
而如果约束矩阵A中没有单位阵,我们将会通过引入人工变量构造出一个单位阵,这种构造方法我们将在后面进行详细介绍。
初始基选出来之后,我们就能写出B,B-1,以及基变量X B和基变量所对应的价值向量C B。
第三步,计算B-1A,B-1b,C-C B B-1A,-C B B-1b,这样就可以把初始单纯形表写出来。
第四步,判断当前的基本可行解是不是最优解?按照我们上一讲介绍的单纯形法的原理,如果检验数行中所有的检验数都小于等于0,当前的基本解就是最优解;如果有一个非基变量的检验数是正的,而且它所对应A中的列的项都小于等于0,那么这个时候是无界解。
P79,用单纯形法的表格形式求解第二章例1 1:在上表中有一个m*m 的单位矩阵,对应的基变量为s 1,s 2,s 3;●在s 1,s 2,s 3右边的C B 列中填入这些基变量的目标函数中相应的系数。
●2:← 在z j 行中填入第j 列与c B 列中对应的元素相乘相加所得的值,如z 2=0*1+0*1+0*1=0,所在z i 行中的第2位数填入0;← 在 j j jz c -=σ行中填入c j -z j 所得的值,如 050c 111-=-=z σ,01002-=σ,003-=σ,004-=σ,005-=σ← z 表示把初始基本可行解代入目标函数求得的目标函数值,即b 列*c B 列;3:4.5.6.初始基本可行解为s1=300,s2=400,s3=250,x1=0,x2=0;←由于250/1最小,因此确定s3为出基变量;σ>2σ,因此确定x2为←由于1入基变量。
出基变量所在行,入基变量所在列的交汇处为主元,这里是a32=1,在表中画圈以示区别.7:●第一次迭代,其变量为x2,s1,s2,通过矩阵行的初等变换,求出一个新的基本可行解。
●具体的做法:用行的初等变换使得x2的系数向量p2变换成单位向量,由于主元在p2的第3 分量上,所以这个单位向量是()Te1,=,也就是主元0,3素变成1。
在上表中第3个基变量s3已被x2代替,故基变量列中的第3个基变量应变为x2。
由于第0次迭代表中的主元a32已经为1,因此第3行不变。
为了使第1行的a12为0,只需把第3行*(-1)加到第1行即可。
同样可以求得第2行。
8:求得第1次迭代的基本可行解为s 1=50,s 2=150,x 2=250,x 1=0,s 3=0, z=25000.● 从上表可以看出,第一次迭的501=σ>0 ,因此不是最优解。
设x 1为入基变量,从此值可知b 1/a 11=50为最小正数,因此,s 1为出基变量,a 11为主元,继续迭代如下表所示。
P79,用单纯形法的表格形式求解第二章例1 1:
在上表中有一个m*m 的单位矩阵,对应的基变量为s 1,s 2,s 3;
●
在s 1,s 2,s 3右边的C B 列中填入这些基变量的目标函数中相应的系数。
●
2:
← 在z j 行中填入第j 列与c B 列中对应的元素相乘相加所得的值,如z 2=0*1+0*1+0*1=0,所在z i 行中的第2位数填入0;
← 在 j j j z c -=σ 行中填入c j -z j 所得的值,如 050c 111-=-=z σ,01002-=σ,003-=σ,004-=σ,005-=σ
← z 表示把初始基本可行解代入目标函数求得的目标函数值,即b 列*c B 列;
3:
4.
5.
6.
初始基本可行解为s1=300,s2=400,s3=250,x1=0,x2=0;
←由于250/1最小,因此确定s3为出基变量;
σ>2σ,因此确定x2为←由于1
入基变量。
出基变量所在行,入基变量所在列的交汇处为主元,这里是a32=1,在表中画圈以示区别.
7:
●第一次迭代,其变量为x2,s1,s2,通过矩阵行的初等变换,求出一个新的基本可行解。
●具体的做法:用行的初等变换使得x2的系数向量p2变换成单位向量,
由于主元在p2的第3 分量上,所以这个单位向量是()T
e1,
=,也就是主元
0,
3
素变成1。
在上表中第3个基变量s3已被x2代替,故基变量列中的第3个基变量应变为x2。
由于第0次迭代表中的主元a32已经为1,因此第3行不变。
为了使第1行的a12为0,只需把第3行*(-1)加到第1行即可。
同样可以求得第2行。
8:
求得第1次迭代的基本可行解为
s 1=50,s 2=150,x 2=250,x 1=0,s 3=0, z=25000.
● 从上表可以看出,第一次迭的501=σ>0 ,因此不是最优解。
设x 1为入基变量,从此值可知b 1/a 11=50为最小正数,因此,s 1为出基变量,a 11为主元,继续迭代如下表所示。
●。