层次分析法及Excel求解实验.
- 格式：ppt
- 大小：1.25 MB
- 文档页数：47
下载文档原格式
合集下载
物流选址层次分析法的应用步骤EXCEL版
0.005
<0.01
总权重
0.333 0.194 0.473
0.2000
0.333333333 1
最大特征根 λmax
5.02
CI
0.003809915 RI查表=1.12
第二步：基于交通因素的县域对比
因素-方案
A县（Z1） B县（Z2） C县（Z3）
A县（Z1）
1
3
0.5
B县（Z2）
0.3333
1
0.25
C县（Z3）
2
4
1
最大特征根 λmax
3.02
CI
权向量方根
0.595 RI查表=0.58
第五步：基于人口因素的县域对比
因素-方案 A县（Z1） B县（Z2） C县（Z3） 最大特征根
A县（Z1） 1 2 0.5 λmax
B县（Z2） C县（Z3） 权向量方根
WI
0.5
2
1.00
0.297
1
3
1.82
0.540
0.3333
1
0.55
0.163
3.01
CI
0.0046
RI查表=0.58
第六步：基于生产规模因素的县域对比
因素-方案
A县（Z1） B县（Z2） C县（Z3）
A县（Z1）
1
2
0.5
B县（Z2）
0.5
1
0.2
C县（Z3）
2
5
1
最大特征根 λmax
3.01
CI
权向量方根
WI
1.00
0.276
0.46
0.128
2.15 0.0028
1.层次分析法使用excel设计绩效考核
3层模型操作程序
在“建模”表上完成黄色区域操作
无真实数据的变量（计算方法取值为 1）备案：向表A、表B1~Bm输入层次 分析法需要的两两比较数据
有真实数据的变量（计算方法取值为 2）备案：把这类变量的全部数据保 存到"真实数据"工作表中，经过"筛 选"、"转换"、"幂阵"几个工作表放 大倍数后才能使用。
0.05 0.05 0.03
n RI
最终计算表(灰色
注：不必打开表"判断阵"、"A阵"、 "筛选"、"转换"、"幂阵"。
2 0.50
3 0.58
4 0.90
5 1.12
随机一致性表
6
7
8
9
1.24 1.32 1.41 1.45
10 1.49
11 1.52
12 1.54
13 1.56
14 1.58
最终计算表(灰色区域粘贴而来）
0.06 0.07 0.06 0.06 0.07 0.06
C 17 7 23
2 B3 0.24 0.06 1.58 0.07 0.07 0.08 0.04 0.07 0.03
0.06 0.08 0.15
0.05 0.07 0.04 0.04
0.08
返回 返回 返回
2 B4 0.14 0.06 1.58
C11 0.042 0.06
C12 0.053 0.06
C13 0.061 0.06
C14 0.046 0.06
C15 0.051 0.06
C16 0.042 0.06
C17 0.058 0.06
在“建模”表上完成黄色区域操作
无真实数据的变量（计算方法取值为 1）备案：向表A、表B1~Bm输入层次 分析法需要的两两比较数据
有真实数据的变量（计算方法取值为 2）备案：把这类变量的全部数据保 存到"真实数据"工作表中，经过"筛 选"、"转换"、"幂阵"几个工作表放 大倍数后才能使用。
0.05 0.05 0.03
n RI
最终计算表(灰色
注：不必打开表"判断阵"、"A阵"、 "筛选"、"转换"、"幂阵"。
2 0.50
3 0.58
4 0.90
5 1.12
随机一致性表
6
7
8
9
1.24 1.32 1.41 1.45
10 1.49
11 1.52
12 1.54
13 1.56
14 1.58
最终计算表(灰色区域粘贴而来）
0.06 0.07 0.06 0.06 0.07 0.06
C 17 7 23
2 B3 0.24 0.06 1.58 0.07 0.07 0.08 0.04 0.07 0.03
0.06 0.08 0.15
0.05 0.07 0.04 0.04
0.08
返回 返回 返回
2 B4 0.14 0.06 1.58
C11 0.042 0.06
C12 0.053 0.06
C13 0.061 0.06
C14 0.046 0.06
C15 0.051 0.06
C16 0.042 0.06
C17 0.058 0.06
层次分析法确定评价指标权重及Excel计算
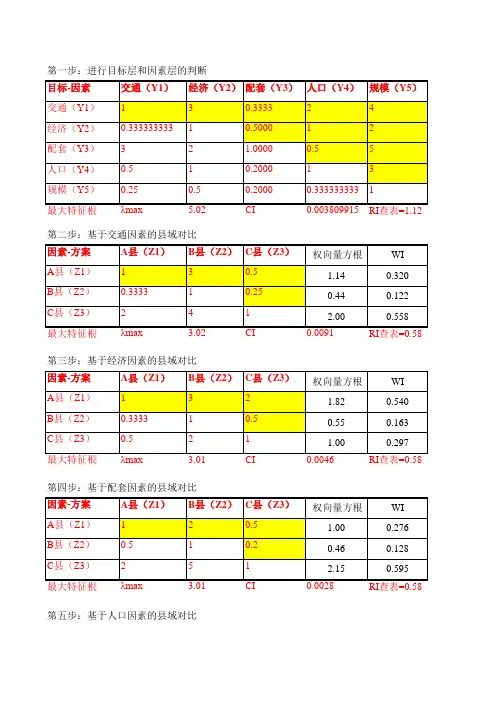
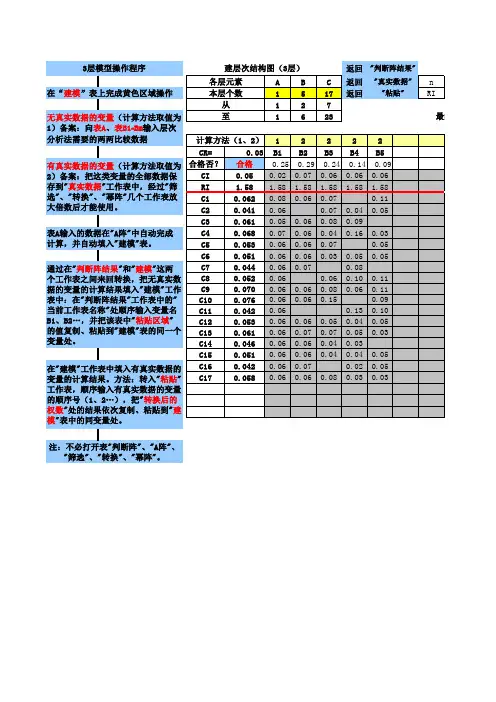
江苏科技信息February 2012表2判断矩阵摘要：文章介绍了层次分析法确定评价指标权重的过程和计算方法，建立的Excel 计算模板操作简单，方便推广，具有较强的实用性。
关键词：决策分析法；层次分析法；权重；Excel ；计算模板作者简介：曹茂林，扬州市环境监测中心站，高级工程师；研究方向：环境监测技术与环境科技管理。
■曹茂林层次分析法确定评价指标权重及Excel 计算层次分析法（Analytic hierarchy process ，简称AHP 法）是美国运筹学家T.L.Saaty 等人在20世纪70年代中期提出了一种定性和定量相结合的，系统性、层次化的多目标决策分析方法。
在环境科研实践中，AHP 法广泛应用于生态安全[1]、环境规划[2]、区域承载力[3]、化学品环境性能评价[4]等众多领域。
AHP 法的核心是将决策者的经验判断定量化，增强了决策依据的准确性，在目标结构较为复杂且缺乏统计数据的情况下更为实用。
应用AHP 法确定评价指标的权重，就是在建立有序递阶的指标体系的基础上，通过比较同一层次各指标的相对重要性来综合计算指标的权重系数。
具体步骤如下：1.构造判断矩阵同一层次内n 个指标相对重要性的判断由若干位专家完成。
依据心理学研究得出的“人区分信息等级的极限能力为7±2”的结论，AHP 法在对指标的相对重要性进行评判时，引入了九分位的比例标度，见表1。
判断矩阵A 中各元素a ij 为i 行指标相对j 列指标进行重要性两两比较的值。
显然，在判断矩阵A 中，a ij ＞0，a ii ＝1，a ij ＝1/a ji （其中i ，j=1,2,…，n ）。
因此，判断矩阵A 是一个正交矩阵，左上至右下对角线位置上的元素为1，其两侧对称位置上的元素互为倒数。
每次判断时，只需要作n(n-1)/2次比较即可。
表2是一个7阶判断矩阵，本文以此为例介绍应用Excel 计算指标权重并进行一致性检验的方法。
用电子表格(Excel)实现层次分析法(AHP)的简捷计算
用电子表格（Excel）实现层次分析法（AHP）的简捷计算先锋（华南农业大学林学院，广东广州510640）摘要：传统的层次分析法算法具有构造判断矩阵不容易、计算繁多重复且易出错、一致性调整比较麻烦等缺点。
层次分析法Excel 算法利用常用的办公软件电子表格（Excel）的运算功能，设置简明易懂的计算表格和步骤，使得判断矩阵的构造、层次单排序和层次总排序的计算以及一致性检验和检验之后对判断矩阵的调整变得十分简单。
从而可以为层次分析法的学习、应用、推广和改进探讨提供方便。
关键词：层次分析法Excel1 层次分析法（AHP）的应用难点层次分析法（Analytical Hierarchy Process,简称AHP）是美国匹兹堡大学教授A.L.Saaty ，于20 世纪70 年代提出的一种系统分析方法，它综合了定性与定量分析，模拟人的决策思维过程，具有思路清晰、方法简便、适用面广、系统性强等特点，是分析多目标、多因素、多准则的复杂大系统的有力工具。
层次分析法的基本原理简单说就是用下一层次因素的相对排序来求得上一层次因素的相对排序。
应用层次分析法解决问题的思路是：首先把要解决的问题分出系列层次，即根据问题的性质和要达到的目标将问题分解为不同的组成因素，按照因素之间的相互影响和隶属关系将各层次各因素聚类组合,形成一个递阶的有序的层次结构模型；然后对模型中每一层次每一因素的相对重要性，依据人们对客观现实的判断给予定量表示（也可以先进行定性判断，再予赋值量化），再利用数学方法确定每一层次全部因素相对重要性次序的权值；最后通过综合计算各层因素相对重要性的权值，得到最低层（方案层）相对于较高层（分目标或准则层）和最高层（总目标）的相对重要性次序的组合权值，以此进行进行方案排序，作为评价和选择方案的依据。
层次分析法在多个领域得到广泛应用，但在应用中也是确实存在着不少难点。
1.1 构造一个合适的判断矩阵不容易建立层次结构模型和构造判断矩阵是层次分析法的主要基本工作，构造判断矩阵是关键之关键。
层次分析法Excel演算实验
0.066666667 0.405480133 0.104729434
1
1 0.258284994
3.871692207
1
Awi/Wi 1.9354877 3.038511091 0.3182215 3.038511091 0.7848018 3.038511091
3.038511091
按行相乘
开3次方
年份 成分 2004 2005 2006 2007 2008 2009 2010 2011
人员成本 36% 35% 30% 28% 30% 28% 26% 23%
2004 2004 2004 2004 2004 2004 2004 2004
45% 40% 35% 30% 25% 20% 15% 10% 5% 0%
3.003694598
按行相乘
开3次方
权重Wi
Awi
15 2.466212074 0.648329014
0.1 0.464158883 0.122020192
0.666666667 0.873580465 0.229650794
3.803951422
1
Awi/Wi 1.94738 3.003694598 0.36651 3.003694598 0.68980 3.003694598
2002
2004
2006
成本A与其他6个因素比较
A,B
对于A：
A,C
对于A：
A,D
对于A：
A,E
对于A：
A,F
对于A：
A,G
对于A：
质量A与其他5个因素比较
A,B
对于A：
A,C
对于A：
9*1/5 28*1/3 20*1/4 25*1 17*5 29*1/2
用电子表格(Excel)实现层次分析法(AHP)的简捷计算
计算 判断矩阵 B1 B2 1 1/3 3 1 3 1 权重向量Wi 开N次方 0.4807 1.4422 1.4422 3.3652
A B1 B2 B3
B3 1/3 1 1
∏aij 0.11 3.00 3.00
B1 C1 C2
判断矩阵 C1 1 1
C2 1 1
权重向量Wi ∏aij 开N次方 权重Wi 1.00 1.0000 0.5000 1.00 1.0000 0.5000 2.0000 权重向量Wi 开N次方 权重Wi 1.7321 0.7500 0.5774 0.2500 2.3094 权重向量Wi 开N次方 权重Wi 1.7321 0.7500 0.5774 0.2500 2.3094
D1
D1
权重向量Wi 权重Wi 0.1429 0.4286 0.4286
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 0.4286 3.0000 0.0000 0.5149 0.0000 1.2857 3.0000 1.2857 3.0000
λ max= 3.0000
λ max= 1.3333
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 0.5000 2.0000 -0.8333 0.0000 0.0000 1.5000 2.0000
λ max= 1.3333
B2 C3 C4 CR
Wi
0.7500 0.2500 0.0000
λ max= 1.3333
λ max 一致性检验 (AW)i (AW)i/Wi C.I. R.I. C.R. 1.5000 2.0000 -0.8333 0.0000 0.0000 0.5000 2.0000
层次分析法中用方根法计算权重在Excel中的具体操作
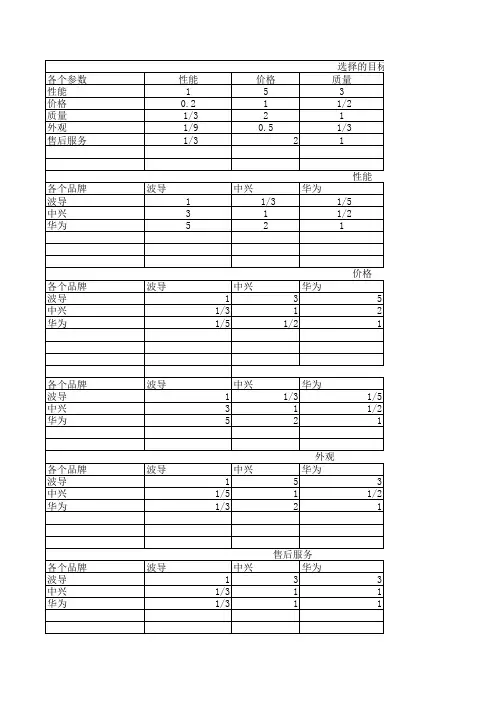
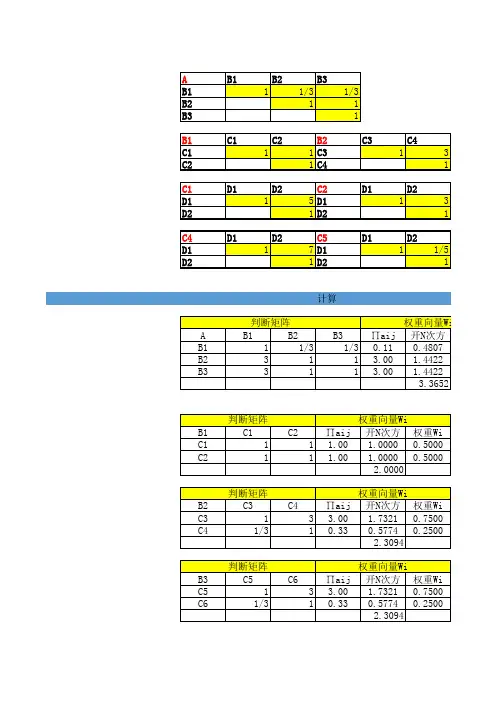
层次分析法中用方根法计算权重在Excel中的具体操作层次分析法中判断矩阵用方根法计算权重在Excel 中的具体操作Exce A B C D E F G H I J K L M Nl 表1总目子目子目子目子目M几何平均权重W AW AW/Wλ =(1/n)*CI=(λRI( 需要查CR=CI/RIij i i ii标标 1标 2标 3标 4数∑ {(AW i )/W i }-n)/(n-1)表 )2子目=B2*C2=GEOMEAN=MMULT=(K2-1)n=10标 11342*D2*E2(B2:E2)=G2/G6(B2:E2,H2:H5)=I2/H2=J6/n/(n-1)3子目=B3*C3=GEOMEAN=MMULT n=20标21/311/21/2*D3*E3(B3:E3)=G3/G6(B3:E3,H2:H5)=I3/H3 4子目=B4*C4=GEOMEAN=MMULT n=30.58标31/4212*D4*E4(B4:E4)=G4/G6(B4:E4,H2:H5)=I4/H45子目=B5*C5=GEOMEAN=MMULT n=40.90.0814694标41/221/21*D5*E5(B5:E5)=G5/G6(B5:E5,H2:H5)=I5/H5 6总和=SUM=SUM n=5 1.12(F2:F5)(J2:J5)树种经济社会生态技术按行相开 M ij的权重 W i AW i矩阵乘积（ AW i）/W iλ 最大特征CI 一般性RI 平均随机选择效益效益效益要求乘n 次方根指标一致性指标0.0733225经济0.4820 4.2199675208效益134224 2.21336452 2.070547 4.295277社会0.08330.1170n=10效益1/311/21/2330.537285160.478166 4.086325生态0.2177n=20效益1/421211920.938617 4.309704技术0.1831n=30.58要求1/221/211/20.84089640.7670944.188564总和 4.59154516.87987n=40.9CR随机一致性比率当CR<0.10 时，判断矩阵具有可以接受的一致性。
用电子表格(Excel)实现层次分析法(AHP)的简捷计算
用电子表格（Excel）实现层次分析法（AHP）的简捷计算准则层对目标层判断树种选择经济效益社会效益生态效益技术要求按行相乘开N次方权重W1经济效益134224 2.2133638390.482052062社会效益1/311/21/20.0833330.5372849660.117016155生态效益1/4212110.217791604技术要求1/221/211/20.8408964150.1831401794.591545221方案层对经济效益判断经济效益松树杉木桉树按行相乘开N次方权重W1AW1松树121/60.3333330.6933610.1428228040.429782771杉木1/211/90.0555560.3815710.0785984180.236518574桉树69154 3.7797630.778578777 2.3429013694.854696方案层对社会效益判断社会效益松树杉木桉树按行相乘开N次方权重W1AW1松树11/21/50.10.4641590.1220201920.366511392杉木211/30.6666670.873580.2296507940.68980085桉树53115 2.4662120.648329014 1.9473823573.803951方案层对生态效益判断生态效益松树杉木桉树按行相乘开N次方权重W1AW1松树1236 1.8171210.527836133 1.611811805杉木1/213 1.5 1.1447140.332515928 1.015377811桉树1/31/310.1111110.480750.1396479390.4264319593.442585方案层对技术要求判断技术要求松树杉木桉树按行相乘开N次方权重W1AW1松树11/23 1.5 1.1447140.3196182640.964702114杉木214820.558424543 1.685489843桉树1/31/410.0833330.436790.1219571930.368102753.581504层次总排序计算四准则ai经济效益 社会效益生态效益技术要求aibin三方案bin0.4820520.1170160.2177920.18314松树0.1428230.122020.5278360.3196180.0688480.0142783340.114958278杉木0.0785980.3325160.3325160.5584250.0378890.0389097350.072419177桉树0.7785790.6483290.1396480.1219570.3753160.0758649680.030414149层次总排序一致性检验CIi0.0046010.0018470.0268110.009147CI=∑aiCIi RI=∑aiRIi RIi0.51490.51490.51490.51490.009948670.5149 CRi0.0089360.0035880.052070.017765AW1AW1/W1CI=(入-n)/(n-1)CR=CI/RI 2.070547 4.2952770.073322510.89310.082099 0.478166 4.0863250.938617 4.3097040.767094 4.1885644.219968AW1/W1CI=(入-n)/(n-1)CR=CI/RI3.0092030.0046010.51490.0089364083.0092033.0092033.009203AW1/W1CI=(入-n)/(n-1)CR=CI/RI3.0036950.0018470.51490.0035876853.0036953.0036953.003695AW1/W1CI=(入-n)/(n-1)CR=CI/RI3.0536220.0268110.51490.0520698933.0536223.0536223.053622AW1/W1CI=(入-n)/(n-1)CR=CI/RI3.0182950.0091470.51490.0177653013.0182953.0182953.018295总排序Σaibin 0.0585350.251487 0.102270.251487 0.0223350.50393 CR=CI/RI0.019322。
层次分析法中用方根法计算权重在Excel中的具体操作
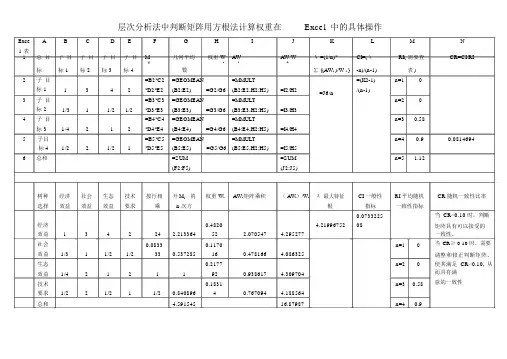
层次分析法中判断矩阵用方根法计算权重在Excel 中的具体操作Exce A B C D E F G H I J K L M Nl 表1总目子目子目子目子目M几何平均权重 W AW AW/Wλ =(1/n)*CI=(λRI( 需要查CR=CI/RIij i i ii标标 1标 2标 3标 4数∑ {(AW i )/W i }-n)/(n-1)表 )2子目=B2*C2=GEOMEAN=MMULT=(K2-1)n=10标 11342*D2*E2(B2:E2)=G2/G6(B2:E2,H2:H5)=I2/H2=J6/n/(n-1)3子目=B3*C3=GEOMEAN=MMULT n=20标 21/311/21/2*D3*E3(B3:E3)=G3/G6(B3:E3,H2:H5)=I3/H34子目=B4*C4=GEOMEAN=MMULT n=30.58标 31/4212*D4*E4(B4:E4)=G4/G6(B4:E4,H2:H5)=I4/H45子目=B5*C5=GEOMEAN=MMULT n=40.90.0814694标 41/221/21*D5*E5(B5:E5)=G5/G6(B5:E5,H2:H5)=I5/H56总和=SUM=SUM n=5 1.12(F2:F5)(J2:J5)树种经济社会生态技术按行相开 M ij的权重 W i AW i矩阵乘积（ AW i）/W iλ 最大特征CI 一般性RI 平均随机选择效益效益效益要求乘n 次方根指标一致性指标0.0733225经济0.4820 4.2199675208效益134224 2.21336452 2.070547 4.295277社会0.08330.1170n=10效益1/311/21/2330.537285160.478166 4.086325生态0.2177n=20效益1/421211920.938617 4.309704技术0.1831n=30.58要求1/221/211/20.84089640.767094 4.188564总和 4.59154516.87987n=40.9CR随机一致性比率当CR<0.10 时，判断矩阵具有可以接受的一致性。
Excel数据表数据技巧多层次分析
Excel数据表数据技巧多层次分析在进行Excel数据表数据分析时，我们经常需要使用各种技巧来逐层深入地分析数据。
本文将介绍一些常用的Excel数据表数据技巧，以帮助读者更好地进行多层次的数据分析。
一、数据表的创建与整理在进行数据分析前，我们首先需要创建一个数据表，并对数据进行整理，以便后续的分析。
在Excel中，我们可以通过以下步骤来创建和整理数据表：1. 打开Excel并创建一个新的工作表。
2. 在第一行中输入各列的名称，每个名称代表一个数据字段。
3. 在下面的行中逐行输入数据。
4. 如果有需要，可以通过筛选、排序等功能对数据进行整理。
二、数据透视表的使用数据透视表是Excel中一个非常强大的分析工具，它可以帮助我们对大规模数据进行多层次的分析。
以下是使用数据透视表进行数据分析的步骤：1. 选择需要进行分析的数据范围。
2. 在Excel菜单选项中选择“数据”-“数据透视表”。
3. 在数据透视表对话框中，将需要分析的字段拖放到行、列和值区域中。
4. 根据需要，可以对数据透视表进行进一步设置，如添加条件筛选、对值进行求和、计数等。
三、使用条件格式进行数据可视化数据可视化是数据分析的重要环节之一，在Excel中，我们可以通过条件格式来对数据进行可视化，以更好地发现数据的规律和趋势。
以下是使用条件格式进行数据可视化的步骤：1. 选择需要进行可视化的数据范围。
2. 在Excel菜单选项中选择“开始”-“条件格式”-“颜色规则”。
3. 在条件格式对话框中选择适当的规则和颜色，如根据值的大小设置颜色渐变等。
4. 确定条件格式后，应用到选定的数据范围中，从而实现数据可视化效果。
四、使用函数进行数据分析Excel提供了丰富的函数库，我们可以通过使用函数来进行数据分析。
以下是一些常用的数据分析函数及其使用方法：1. SUM函数：用于求取一组数值的总和，可以通过在单元格中输入“=SUM(数据范围)”来计算总和。
2. AVERAGE函数：用于求取一组数值的平均值，可以通过在单元格中输入“=AVERAGE(数据范围)”来计算平均值。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
P2
P3 I3 P1 P2 P3
1/2
1/7 P1 1 3 7
1
1/5 P2 1/3 1 5
5
1 P3 1/7 1/5 1
1.357
0.306 Wi 0.362 0.843 3.271
0.333
0.075 Wio 0.081 0.188 0.731
2018年10月7日星期日
PPT 16
判断矩阵中的bij是根据资料数据、专家的意见和系统分 析人 员的经验经过反复研究后确定。 应用层次分析法保持判断思维的一致性是非常重要的， 只要矩阵中的bij满足下面三条关系式时，就说明判断矩阵具 有完全的一致性。 bii = 1 bji = 1/ bij bij = bik/ bjk
2018年10月7日星期日
PPT 3
系统评价问题是由评价对象、评价主体、评价目的、评价 时期、评价地点及评价方法等要素构成的问题复合体。 评价对象——接受评价的事物、行为或对象系统。 评价主体——评定对象系统价值大小的个人或集体。 效用：某主体对某种利益和损失所独有的 感觉及反应。 评价的目的——系统评价所要解决的问题和所能发挥的作 用。
判断矩阵一致性指标C.I.(Consistency Index)
max n CI n 1
2018年10月7日星期日 PPT 17
0.230 0.648 0.122
1/2
I1 P1 P2 P3
P1 1 3 5
P2 1/3 1 3
P3 1/5 1/3 1
Wi 0.406 1.000 2.466
Wio 0.105 0.258 0.637
2018年10月7日星期日
PPT 15
I2 P1
P1 1
P2 2
P3 7
Wi 2.410
Wio 0.592
2018年10月7日星期日
PPT 11
在层次分析法中，为了使判断定量化，关键在于设法 使任意两个方案对于某一准则的相对优越程度得到定量描 述。一般对单一准则来说，两个方案进行比较总能判断出 优劣，层次分析法采用1-9标度方法，对不同情况的评比给 出数量标度。
2018年10月7日星期日
PPT 12
判断矩阵标度定义
2018年10月7日星期日
PPT 9
投资效果好（T）
（目的层）
风险程度（I1）
资金利润率（I2）
转产难易程度（I3）
（准则层）
产品1（P1）
产品2（P2）
产品3（P3）
（方案层）
2018年10月7日星期日
PPT 10
（3） 建立两两比较的判断矩阵 判断矩阵表示针对上一层次某单元（元素），本层次与它有 关单元之间相对重要性的比较。一般取如下形式：
PPT 7
层次分析法（AHP）特点 （1）分析思路清楚，可将系统分析人员的思维 过程系统化、数学化和模型化； （2）分析时需要的定量数据不多，但要求对问 题所包含的因素及其关系具体而明确； （3）这种方法适用于多准则、多目标的复杂问 题的决策分析，广泛用于地区经济发展方案比 较、科学技术成果评比、资源规划和分析以及 企业人员素质测评。
1.0 Ⅰ 效 用 Ⅱ Ⅲ
0
2018年10月7日星期日 PPT过程中所处的阶段。 期初评价、期中评价、期末评价、跟踪评价 评价地点——（1）评价对象所涉及到的及其占有的空间 或评价的范围。 （2）评价主体观察问题的角度和高度或评 价的立场。 评价方法——评价过程中所采用的方法。
2018年10月7日星期日
PPT 8
层次分析法（AHP）的具体步骤
（1）明确问题 在分析社会、经济的以及科学管理等领域的问题时，首 先要对问题有明确的认识，弄清问题的范围，了解问题所包 含的因素，确定出因素之间的关联关系和隶属关系。 （2） 递阶层次结构的建立 根据对问题分析和了解，将问题所包含的因素，按照是 否共有某些特征进行归纳成组，并把它们之间的共同特性看 成是系统中新的层次中的一些因素，而这些因素本身也按照 另外的特性组合起来，形成更高层次的因素，直到最终形成 单一的最高层次因素。
PPT 13
投资效果好（T）
风险程度（I1）
资金利润率（I2）
转产难易程度（I3）
产品1（P1）
产品2（P2）
产品3（P3）
T I1 I2 I3
2018年10月7日星期日
I1 1 3
判断矩阵及其分析处理举 例
I2 1 1/5 I3 2 5 1
PPT 14
Wi
Wio
1/3
0.874 2.466 0.464
2018年10月7日星期日
PPT 6
层次分析法（AHP）基本原理
AHP法首先把问题层次化，按问题性质和总目标将此问 题分解成不同层次，构成一个多层次的分析结构模型，分为 最低层（供决策的方案、措施等），相对于最高层（总目标） 的相对重要性权值的确定或相对优劣次序的排序问题。
2018年10月7日星期日
层次分析法及 Excel求解实验
马立坤
实验目的
学习层次分析法的基本原理与方法
掌握层次分析法建立数学模型的基本步骤
学会用excel求解层次分析法中的数学问题
无论是系统设计与开发、系统分析都会遇 到“多个方案比较”的问题。这个“多个方案 比较”的过程就是“系统评价过程”；在这个 过程中应采用的方法为“ 系统评价方法”。 系统评价--就是根据预定的系统目的，利用系 统模型和资料，根据技术、经济、环境等方面 的客观要求，从系统整体出发，分析对比各种 方案，选出技术上先进、经济上合理的最优方 案。
2018年10月7日星期日
PPT 5
层次分析法
层次分析法（AHP）的由来
美国运筹学家A.L.Saaty于本世纪70年代提出的层次分 析法（Analytical Hierar-chy Process，简称AHP方法)， 是一种定性与定量相结合的决策分析方法。 应用这种方法，决策者通过将复杂问题分解为若干层次 和若干因素，在各因素之间进行简单的比较和计算，就可以 得出不同方案的权重，为最佳方案的选择提供依据。
标度 1 3 5 7 9 含义 两个要素相比，具有同样重要性 两个要素相比，前者比后者稍微重要 两个要素相比，前者比后者明显重要 两个要素相比，前者比后者强烈重要 两个要素相比，前者比后者极端重要 上述相邻判断的中间值 两个要素相比，后者比前者的重要性标度
2， 4， 6， 8 倒数
2018年10月7日星期日