三点共线经典题型
- 格式:doc
- 大小:162.00 KB
- 文档页数:5

专题08三点共线充要条件一、结论1、设平面上三点O ,A ,B 不共线,则平面上任意一点P 与A ,B 共线的充要条件是存在实数 与,使得OP OA OB,且1 .特别地,当P 为线段AB 的中点时,1122OP OA OB .二、典型例题1.(2021·安徽·铜陵一中高三阶段练习(理))如图,ABC 中,D 为AB 上靠近B 的三等分点,点F 在线段CD 上,设AB a ,AC b ,AF xa yb ,则21x y的最小值为()A .6B .7C .4 D .4【答案】D 【解析】由于D 为AB 上靠近B 的三等分点,故23AD AB ,所以32x AF xa yb x AB y AC AD y AC,又因为点F 在线段CD 上,所以312x y ,故2121332()()422x x yy x y x y y x,由题意可知0,0x y ,故2132442x yx y y x,当且仅当322x y y x 时,即11,32x y时,等号取得,故选:D.【反思】本题重点C ,F ,D 三点共线,可以得到AF mAD nAC且1m n ,所以本题中AF xa yb 中的AF 如何化简成AF mAD nAC 才是本题的关键,又D 为AB 上靠近B 的三等分点,故23AD AB ,所以得到32x AF xa yb x AB y AC AD y AC这样,由C ,F ,D 三点共线,得到312x y ,进而才利用均值不等式求解最值.如何利用三点共线时解本题的快速捷径.三、针对训练举一反三一、单选题1.(2020·安徽·安庆市第二中学高一阶段练习)如图,在三角形OAB 中,P 为线段AB 上的一点,OP xOA yOB u u u r u u r u u u r ,且3BP PA,则()A .23x ,13yB .13x ,23yC .14x,34yD .34x,14y 【答案】D 【详解】因为3BP PA ,所以3331()4444OP OB BP OB BA OB OA OB OA OB ,又OP xOA yOB u u u r u u r u u u r ,,OA OB 不共线,所以31,44x y ,故选:D2.(2022·全国·高三专题练习)如图,在OAB 中,C 是AB 的中点,P 在线段OC 上,且2OC OP .过点P 的直线交线段,OA OB 分别于点N ,M ,且,OM mOB ON nOA ,其中,[0,1]m n ,则m n 的最小值为()A .12B .23C .1D .34【答案】C【详解】解:1()2OC OA OB u u u r u u r u u u r ,则11122OP ON OM n m,1144OP ON OM n m,又P ,M ,N 共线,∴11144n m.又,[0,1]m n ,∴ 111111214444m n m n m n n m n m ,当且仅当12m n 时取等号,故选:C.3.(2022·全国·高三专题练习)在ABC 中,3AC AD ,BE ED ,设(,)AE AB AC R,则 ()A .13B .13C .23D .43【答案】C 【详解】在三角形ABC 中,3AC AD ,BE ED ,可得111111()222326AE AB AD AB AC AB AC ,因为(,)AE AB AC R ,所以11,26,所以23 .故选:C.4.(2021·福建·厦门市湖滨中学高三期中).如图,在ABC 中,13AD DC,P 是线段BD上一点,若16AP m AB AC ,则实数m 的值为()A .13B .23C .2D .12【答案】A 【详解】设BP BD ,因为13AD DC,所以14AD AC ,则1()(1)4AP AB BP AB BD AB BA AD AB AC,又因为16AP m AB AC ,所以11146m,解得21,33m .故选:A.5.(2022·全国·高三专题练习)A ,B ,C 是圆O 上不同的三点,线段CO 与线段AB 交于点D (点O 与点D 不重合),若OC OA OB,R ,则 的取值范围是()A . 0,1B . 1, C.D .1,0 【答案】B 【详解】因为线段CO 与线段AB 交于点D ,所以,,O C D 三点共线,所以OC 与OD共线,设OC mOD ,则1m >,因为OC OA OB ,所以OA O OD B m ,可得OA OD O mB m ,因为,,A B D 三点共线,设AD t AB u u u r u u u r,所以OD OA t OB OA 即 1OD t OA tOB ,所以1t mtm,所以1m m ,可得1m ,所以 的取值范围是 1, .故选:B.6.(2021·四川成都·高三期中(文))如图所示,已知点G 是ABC 的重心,过点G 作直线分别与AB ,AC 两边交于M ,N 两点(点N 与点C 不重合),设AB xAM ,AC y AN,则111x y 的最小值为()A .2B.1C .32D.2 【答案】A 【详解】G ∵为ABC 的重心,21()32AG AB AC1()3xAM y AN又G ∵在线段MN 上,11133x y 3x y (1)2x y11111[(1)]()121x y x y x y 11(11)21x y y x1(22)22故选:A .7.(2021·山西大附中高三阶段练习(文))如图所示,已知点G 是ABC 的重心,过点G作直线分别与AB ,AC 两边交于M ,N 两点(点N 与点C 不重合),设xAB AM ,y AC AN,则11x y的值为()A .3B .4C .5D .6【答案】A 【详解】延长AG 交BC 与点H ,H 为BC 中点,G ∵为ABC 的重心,2211133333111123AG AH AB AC AB AC AM ANA x yxy M ANM G N ∵、、三点共线11133x y ,113x y故选:A8.(2021·福建省长汀县第一中学高三阶段练习)如图,在ABC 中,23AN NC,P 是BN 上一点,若13AP AB AC,则实数 的值为()A .13B .16C .23D .14【答案】B 【详解】由题意及图:1AP AB BP AB mBN AB m AN AB mAN m AB ,又23AN NC ,所以25AN AC,所以 215AP m AC m AB ,又13AP AB AC,所以12153m m,解得:51,66m .故选:B.二、填空题9.(2021·湖南·周南中学高二开学考试)在ABC 中,E 为AC 上一点,3AC AE ,P 为BE 上任一点,AD mAB ,AF nAC ,(0m ,0n ),若AP AD AF ,则当31m n取最小值时,四边形ADPF 的面积与ABC 的面积之比等于________.【答案】16##1:6【详解】解:由题意可知:3AP mAB nAC mAB nAE,而P ,B ,E 三点共线,则:31m n ,据此有:3131936612n m m n m n m n m n ,当且仅当12m,16n 时等号成立,取到最小值,此时12AD AB ,16AF AC,所以11sin sin 126116sin sin 22ADPF ABCAB AC ABC AD AF ABC S S AB AC ABC AB AC ABC .故答案为:16.10.(2021·黑龙江·大庆中学高一阶段练习)如图,经过OAB 的重心G 的直线与,OA OB 分别交于点P ,Q ,设,OP mOA OQ nOB,,m n R ,则11n m的值为________.【答案】3【详解】解:设,OA a OB b,由题意知211()()323OG OA OB a b ,11,33PQ OQ OP n b m a PG OG OP ma b,由P ,G ,Q 三点共线,得存在实数 使得PQ PG,即1133n b m a m a b,从而1,31,3m m n消去 ,得113n m .故答案为:3三、解答题11.(2021·全国·高一课时练习)如图,在AOB 中,14OC OA u u u r u u r ,12OD OB u u u r u u u r,AD 与BC 相交于点M ,设OA a,OB b,(1)试用a ,b表示向量OM :(2)在线段AC 上取一点E ,在BD 上取一点F ,使得EF 过点M ,设OE OA ,OF OB,求证:13177.【答案】(1)1377OM a ;(2)证明见解析.【详解】(1)解:由A ,M ,D 三点共线可知,存在实数1 使得11111122OM OA AM a AD a a b a b.由B ,M ,C 三点共线可知,存在实数2 使得22221144OM OB BM b BC b b a a b.由平面向量基本定理知21121412.解得126747,所以1377OM a b .(2)证明:若OE OA ,OF OB,则13137777OM a b OE OF.又因为E ,M ,F 三点共线,所以13177 .。

向量三点共线定理例题【中英文实用版】Title: Example Problems on the Collinearity of Three Points in Vector Space标题:向量空间中三点共线问题的例题Problem 1:Given vectors a = (2, 3), b = (4, 6), and c = (6, 9).Determine if these vectors are collinear.问题1:给定向量a=(2,3), b=(4,6), 和c=(6,9),判断这些向量是否共线。
Solution:To check if three vectors are collinear, we can use the cross product.If the cross product of two vectors is a zero vector, then the two vectors are parallel, and thus the three vectors are collinear.解:为了检查三个向量是否共线,我们可以使用向量叉乘。
如果两个向量的叉乘是一个零向量,那么这两个向量是平行的,因此三个向量共线。
Problem 2:Find the direction vector of the line containing points A(2, -1), B(4, 3), and C(6, 5).问题2:找到包含点A(2,-1), B(4,3), 和C(6,5)的直线的方向向量。
Solution:First, we find the vector AB and vector AC.Then, we divide vector AB and vector AC by their magnitudes to obtain their unit vectors.The unit vector of vector AB will be the direction vector of the line.解:首先,我们找到向量AB和向量AC。

第107课三点共线问题基本方法:三点共线问题解题策略一般有以下几种:①斜率法:若过任意两点的直线的斜率都存在,通过计算证明过任意两点的直线的斜率相等证明三点共线;②距离法:计算出任意两点间的距离,若某两点间的距离等于另外两个距离之和,则这三点共线;③向量法:利用向量共线定理证明三点共线;④直线方程法:求出过其中两点的直线方程,再证明第三点也在该直线上;⑤点到直线的距离法:求出过其中某两点的直线方程,计算出第三点到该直线的距离,若距离为0,则三点共线.⑥面积法:通过计算求出以这三点为三角形的面积,若面积为0,则三点共线.在处理三点共线问题时,离不开解析几何的重要思想:“设而不求思想”.一、典型例题1.已知椭圆22:12x C y +=,41,33M ⎛⎫ ⎪⎝⎭为椭圆上一点,若,R S 是椭圆C 上的两个点,线段RS 的中垂线l 的斜率为12且直线l 与RS 交于点P ,O 为坐标原点,求证:,,P O M三点共线.答案:见解析解析:因为线段RS 的中垂线l 的斜率为12,所以直线RS 的斜率为2-.所以可设直线RS 的方程为2y x m =-+.由222,1,2y x m x y =-+⎧⎪⎨+=⎪⎩得2298220x mx m -+-=.设点()11,R x y ,()22,S x y ,()00,P x y .所以1289m x x +=,()1212128222222299m m y y x m x m x x m m +=-+-+=-++=-⋅+=.所以120429x x m x +==,12029y y m y +==.因为0014y =,所以0014y x =.所以点P 在直线14y x =上.又点()0,0O ,41,33M ⎛⎫ ⎪⎝⎭也在直线14y x =上,所以,,P O M 三点共线.2.已知椭圆的焦点在x 轴上,它的一个顶点恰好是抛物线24x y =的焦点,离心率e =过椭圆的右焦点F作与坐标轴不垂直的直线l ,交椭圆于A 、B 两点.(1)求椭圆的标准方程;(2)设点(,0)M m 是线段OF 上的一个动点,且()MA MB AB +⊥ ,求m 的取值范围;(3)设点C 是点A 关于x 轴的对称点,在x 轴上是否存在一个定点N ,使得C 、B 、N 三点共线?若存在,求出定点N 的坐标,若不存在,请说明理由.答案:(1)2215x y +=;(2)805m <<;(3)在x 轴上存在定点5,02N ⎛⎫ ⎪⎝⎭,使得C 、B 、N 三点共线.解析:(1)设椭圆方程为22221(0)x y a b a b+=>>,由题意1b =,又e ===,∴25a =,故椭圆方程为2215x y +=.(2)由(1)得右焦点(2,0)F ,则02m ≤≤,设l 的方程为(2)y k x =-(0k ≠)代入2215x y +=,得2222(51)202050k x k x k +-+-=,∴220(1)0k ∆=+>,设1122(,),(,),A x yB x y 则21222051k x x k +=+,212220551k x x k -=+,且1212(4)y y k x x +=+-,2121()y y k x x -=-.∴11221212(,)(,)(2,)MA MB x m y x m y x x m y y +=-+-=+-+ ,2121(,)AB x x y y =-- ,由()MA MB AB +⊥ ,得()0MA MB AB +⋅= ,则12211221()(2)()()()0MA MB AB x x m x x y y y y +⋅=+--++⋅-= ,即12211221(2)()(4)()0x x m x x k x x k x x +--++-⋅-=,即2222220202(4)05151k k m k k k -+-=++,得2085m k m =>-,所以805m <<,∴当805m <<时,有()MA MB AB +⊥ 成立.(3)在x 轴上存在定点N ,使得C 、B 、N 三点共线.依题意11(,)C x y -,直线BC 的方程为211121()y y y x x y x x +=---,令0y =,则121122112121()N y x x y x y x x x y y y y -+=+=++, 点,A B 在直线:(2)l y k x =-上,∴1122(2),(2)y k x y k x =-=-,∴122112************(2)(2)22()(2)(2)()4N y x y x k x x k x x kx x k x x x y y k x k x k x x k +-⋅+-⋅-+===+-+-+-222222205202255151220451k k k k k k k k k k -⋅-⋅++==⋅-+,∴在x 轴上存在定点5,02N ⎛⎫ ⎪⎝⎭,使得C 、B 、N 三点共线.二、课堂练习1.抛物线2:4C y x =,已知斜率为k 的直线l 交y 轴于点P ,且与曲线C 相切于点A ,点B 在曲线C 上,且直线PB x 轴,P 关于点B 的对称点为Q ,判断点,,A Q O 是否共线,并说明理由.答案:点,,A Q O 共线,理由见解析解析:设直线:l y kx m =+,联立24y x y kx m⎧=⎪⎨=+⎪⎩,得()222240k x mk x m +-+=(*)由()()2222441610mk m k mk ∆=--=-=,解得1m =,则直线1:l y kx =+,得10,P k ⎛⎫ ⎪⎝⎭,211,4B k k ⎛⎫ ⎪⎝⎭,又P 关于点B 的对称点为Q ,故211,2Q k k ⎛⎫ ⎪⎝⎭,此时,(*)可化为222120k x x k -+=,解得21x k =,故12y kx k k =+=,即212,A k k ⎛⎫ ⎪⎝⎭,所以2OA OQ k k k ==,即点,,A Q O 共线.2.已知椭圆22143x y +=,点F 是椭圆的右焦点.是否在x 轴上存在定点D ,使得过D 的直线l 交椭圆于,A B 两点.设点E 为点B 关于x 轴的对称点,且,,A F E 三点共线?若存在,求D 点坐标;若不存在,说明理由.答案:存在定点()4,0D 满足条件,理由见解析解析:由题意易知直线l 斜率不为0.设直线l 方程为x my t =+,(),0D t ,联立22143x my t x y =+⎧⎪⎨+=⎪⎩,消去x 得()2223463120m y mt y t ++⋅+-=,设()11,A x y ,()22,B x y ,则()22,E x y -,则122212263431234mt y y m t y y m -⎧+=⎪+⎪⎨-⎪=⎪+⎩,且0∆>,由,,A F E 三点共线有()()2112110x y x y -+-=,即()()1212210my y t y y +-+=,()22231262103434t mt m t m m --∴⋅+-⋅=++,解得4t =,∴存在定点()4,0D 满足条件.三、课后作业1.已知抛物线2:4C y x =的焦点为F ,直线l 过点()1,0-,直线l 与抛物线C 相交于,A B 两点,点A 关于x 轴的对称点为D .证明:,,B F D 三点共线.解析:依题意,直线l 的斜率存在且不为零,设直线l 的方程为()10x my m =-≠,由214x my y x=-⎧⎪⎨=⎪⎩消去x 整理得2440y my -+=,设()()1122,,,A x y B x y ,则()11,D x y -,且12124,4y y m y y +==.又直线BD 的方程为()122221y y y y x x x x +-=--,即2222144y y y x y y ⎛⎫-=- ⎪ ⎪-⎝⎭,令0y =,得1214y y x ==.所以点()1,0F 在直线BD 上,即,,B F D 三点共线.2.已知椭圆:E 22162x y +=,其右焦点为F ,过x 轴上一点()3,0A 作直线l 与椭圆E 相交于,P Q 两点,设(1)AP AQ λλ=> ,过点P 且平行于y 轴的直线与椭圆E 相交于另一点M ,试问,,M F Q 是否共线,若共线请证明;反之说明理由.答案:,,M F Q 三点共线,理由见解析解析:设()11,P x y ,()22,Q x y ,则11(3,)AP x y =- ,22(3,)AQ x y =- ,由已知得方程组()12122211222233162162x x y y x y x y λλ-=-⎧⎪=⎪⎪⎪⎨+=⎪⎪⎪+=⎪⎩,注意到1λ>,解得2512x λλ-=,因为()()112,0,,F M x y -,所以11211211(2,)((3)1,),,22FM x y x y y y λλλλλ--⎛⎫⎛⎫=--=-+-=-=- ⎪ ⎪⎝⎭⎝⎭,又22(2,)FQ x y =- 21,2y λλ-⎛⎫= ⎪⎝⎭,所以FM FQ λ=- ,从而三点共线.3.已知椭圆22:1x y E +=,过定点()3,4P -且斜率为k 的直线交椭圆E 于不同的两点,M N ,在线段MN 上取异于,M N 的点H ,满足PMMHPN NH =,证明:点H 恒在一条直线上,并求出这条直线的方程.答案:210x y -+=,证明见解析解析:设()()()112200,,,,,M x y N x y H x y ,由PMMHPN NH =,得01122033x x x x x x -+=+-,整理可得()1212012236x x x x x x x ++=++设直线():3434l y k x kx k =++=++,联立2234132y kx k x y =++⎧⎪⎨+=⎪⎩,得()()()2222363433460k x k k x k +++++-=由题0∆>,∴()12263432k k x x k -++=+,()21223346k x x k +-=+,则22122218241812122463232k k k k x x k k --++-++==++,()()22121222692416125472728423+3232k k k k k x x x x k k ++---++==++,∴072846710312241212k k x k k k++===-+---,而P 在l 上,则001053433411212k y kx k k k k k =++=-+++=-+--,∴00210x y -+=,即H 恒在直线210x y -+=上.。

初中数学竞赛证明三点共线要证明三点共线,我们可以使用反证法。
假设有三个点A,B和C,我们要证明它们共线。
那么我们可以假设它们不共线,即A,B和C不在同一条直线上。
首先,我们可以连接AB和AC这两条线段。
这样我们就得到了一个三角形ABC。
在三角形ABC中,我们可以找到一个内角D,使得D是一个钝角。
我们假设D是钝角。
现在,我们将点B向点C移动。
点B移动到B',新的线段BB'与AC相交于点E。
由于AB'与AC相交于E,所以根据隐含的直角定理,我们可以得知E是一个直角,即∠AEB'=90°。
同理,我们将点C向点B移动,点C移动到C',新的线段CC'与AB相交于点F。
由于AC'与AB相交于F,我们可以得知F是一个直角,即∠AFC'=90°。
现在,我们来考虑线段BB'和CC'的关系。
根据直线的传递性,我们可以得知∠EAF'=∠CFB'。
同时,根据直角的性质,我们可以得知∠EAF'=∠CAF'和∠CFB'=∠CBF'。
因此,∠CBF'=∠CAF'。
现在,考虑三角形BC'F'和AC'F'。
根据共边原理,我们可以得知∠C'BF'=∠A'CF'和∠F'CB'=∠F'CA'。
因此,∠C'BF'=∠A'C F'。
现在,我们来考虑三角形BC'F'和BA'F'。
根据角边对应原理,我们可以得知∠C'BF'=∠B'AF'和∠F'CB'=∠F'BA'。
因此,∠C'BF'=∠B'AF'。
现在,我们来考虑线段ABB'和ACC'的关系。

平面向量中的三点共线的应用定理:1、a 0//≠b b a λ=⇔;2、A 、B 、C 三点共线BC AB λ=⇔()OC x OB x OC -+=⇔1。
例1:ABC ∆中,M 为边BC 上任意一点,N 为AM 中点,AC AB AN μλ+=,则μλ+的值为_____。
类型一:已知三点共线,则可得1=+y x 。
练习:1、ABC ∆中,G 为ABC ∆的重心,过G 作直线分别交直线AB 、AC 于M 、N 。
设AB x AM =,AC x AN =,则=+yx 11____。
2、在△ABC 中,NC AN =3,P 是线段BN 上一点,且AC n AB m AP +=,则n m 11+的最小值为_____。
例2:设a 、b 是两个不共线的单位向量,若向量c 满足()()b a c 222-3-+=λλ,31=-最小时,a 与b 的夹角的余弦值为_______。
类型二:注意到1=+y x ,可联想到三点共线。
练习:1、已知a +b +c =032=,a -b 与c 成120°的角,则(t a t -+1的最小值为_______。
2、在直角坐标系内,O 为原点,点A ,B 坐标分别为(1,0),(0,2),当实数p, q 满足111=+qp 时,若点C ,D 分别在x 轴,y 轴上,且OB q OD OA p OC ==,,则直线CD 恒过一个定点,这个定点的坐标为___________。
3、在△ABC 中,AB =4,AC =2,(2-2AB λλ+2,则对于△ABC 内一点P ,()PC PB PA +⋅的最小值为_____。
例3:如图,四边形ABCD 是正方形,延长CD 至E ,使DE=CD ,若点P 是以点A 为圆心,AB 为半径的圆弧(不超出正方形)上的任一点,设向量AE AB AP μλ+=,则μλ+的最小值为__________,最大值为_________。
类型三:利用1=+y x ,构造直线来求值。

高考数学二轮复习微专题(文理通用)多题一解之三点共线篇【知识储备】 1、共线向量定理:向量a (a ≠0)与b 共线的充要条件是存在唯一一个实数λ,使得b =λa 。
2、A ,B ,C 三点共线,O 为A ,B ,C 所在直线外一点,则OA →=λOB →+μOC →且λ+μ=1。
特别,当A 为线段BC 中点时,OA →=12OB →+12OC →。
3.向量共线的坐标表示:若a =(x 1,y 1),b =(x 2,y 2),则a ∥b ⇔x 1y 2-x 2y 1=0。
提示:a ∥b 的充要条件不能表示成x 1x 2=y 1y 2,因为x 2,y 2有可能等于0,应表示为x 1y 2-x 2y 1=0。
【走进高考】【例】【2019年高考全国Ⅰ卷理数】已知双曲线C :22221(0,0)x y a b a b-=>>的左、右焦点分别为F 1,F 2,过F 1的直线与C 的两条渐近线分别交于A ,B 两点.若1F A AB =u u u r u u u r ,120FB F B ⋅=u u ur u u u u r ,则C 的离心率为____.【答案】2【解析】法一:由1F A AB =u u u r u u u r可得1,,F A B 三点共线且A 为线段1F B 的中点,由题意知F 1,F 2的坐标分别为(,0),(,0)-c c ,设A 点的坐标为(,)-b x x a ,B 点的坐标为11(,)x y ,由1F A AB =u u u r u u u r 可得11(,(,)=)+--+b bx c x x x y x a a, 解得B 点的坐标为2(2,)+-b x c x a ,所以1222=(22,),2,()+-=-u u u r u u u u r b bF B x c x F B x x a a,又120FB F B ⋅=u u u r u u u u r ,则有22242(22)0++=b x x c x a (1),又2=(2)-⨯+b b x x c a a 可得4=-cx ,代入(1)式得223=b a ,∴该双曲线的离心率为2c e a ====. 法二:如图,由1,F A AB =u u u r u u u r得1.F A AB =又12,OF OF =得OA 是三角形12F F B 的中位线, 即22,2.BF OA BF OA =∥由120F B F B ⋅=u u u r u u u u r,得121,,F B F B OA F A ⊥∴⊥ ∴1OB OF =,1AOB AOF ∠=∠,又OA 与OB 都是渐近线,得21,BOF AOF ∠=∠又21πBOF AOB AOF ∠+∠+∠=,∴2160,BOF AOF BOA ∠=∠=∠=o又渐近线OB的斜率为tan 60ba=︒=∴该双曲线的离心率为2c e a ====.【名师点睛】本题结合平面向量考查双曲线的渐近线和离心率,渗透了逻辑推理、直观想象和数学运算素养,采取几何法,利用数形结合思想解题.解答本题时,通过向量关系得到1F A AB =和1OA F A ⊥,从而可以得到1AOB AOF ∠=∠,再结合双曲线的渐近线可得21,BOF AOF ∠=∠进而得到2160,BOF AOF BOA ∠=∠=∠=o从而由tan 60ba=︒=. 【例】【2019年高考全国Ⅰ卷理数】已知抛物线C :y 2=3x 的焦点为F ,斜率为的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求l 的方程;(2)若,求|AB |.【答案】(1)3728y x =-;(2)3. 【解析】设直线()()11223:,,,,2l y x t A x y B x y =+. (1)由题设得3,04F ⎛⎫⎪⎝⎭,故123||||2AF BF x x +=++,由题设可得1252x x +=.由2323y x t y x⎧=+⎪⎨⎪=⎩,可得22912(1)40x t x t +-+=,则1212(1)9t x x -+=-. 从而12(1)592t --=,得78t =-.所以l 的方程为3728y x =-. (2)法一:由题意设P 点的坐标为(,0)x ,则1122=(,),,()--=-u u u r u u u rAP x x y PB x x y ,323AP PB =u u u r u u u r由3AP PB =u u u r u u u r可得123y y =-.由2323y x t y x⎧=+⎪⎨⎪=⎩,可得2220y y t -+=. 所以122y y +=.从而2232y y -+=,故211,3y y =-=. 代入C 的方程得1213,3x x ==.故||3AB =.法二:过A 点、B 点分别向x 轴作垂线,垂足分别为M ,N ,易知AMP BNP ∆≈∆,由3AP PB =u u u r u u u r可得123y y =-.下同法一。

【题型综述】三点共线问题证题策略一般有以下几种:①斜率法:若过任意两点的直线的斜率都存在,通过计算证明过任意两点的直线的斜率相等证明三点共线;②距离法:计算出任意两点间的距离,若某两点间的距离等于另外两个距离之和,则这三点共线;③向量法:利用向量共线定理证明三点共线;④直线方程法:求出过其中两点的直线方程,在证明第3点也在该直线上;⑤点到直线的距离法:求出过其中某两点的直线方程,计算出第三点到该直线的距离,若距离为0,则三点共线.⑥面积法:通过计算求出以这三点为三角形的面积,若面积为0,则三点共线,在处理三点共线问题,离不开解析几何的重要思想:“设而不求思想”.【典例指引】类型一 向量法证三点共线例1 (优质试题北京理19)(本小题共14分)已知曲线C :22(5)(2)8m x m y -+-=(m R ∈)(Ⅰ)若曲线C 是焦点在x 轴上的椭圆,求m 的取值范围;(Ⅱ)设m =4,曲线C 与y 轴的交点为A ,B (点A 位于点B 的上方),直线4y kx =+与曲线交于不同的两点M ,N ,直线1y =与直线BM 交于点G ,求证:A ,G ,N 三点共线.MB 方程为:62M M kx y x x +=-,则316M M x G kx ⎛⎫⎪+⎝⎭,, ∴316M M x AG x k ⎛⎫=-⎪+⎝⎭,,()2N N AN x x k =+,, 欲证A G N ,,三点共线,只需证AG ,AN 共线 即3(2)6MN N M x x k x x k +=-+成立,化简得:(3)6()M N M N k k x x x x +=-+ 将①②代入易知等式成立,则A G N ,,三点共线得证。
类型二 斜率法证三点共线例2.(优质试题•上海模拟)已知抛物线y 2=4x 的焦点为F ,过焦点F 的直线l 交抛物线于A 、B 两点,设AB 的中点为M ,A 、B 、M 在准线上的射影依次为C 、D 、N . (1)求直线FN 与直线AB 的夹角θ的大小; (2)求证:点B 、O 、C 三点共线.∵k OB==,y1y2=﹣4,∴k OB=k OC,∴点B、O、C三点共线.类型三直线方程法证三点共线例3(优质试题•贵阳二模)已知椭圆C:=1(a>0)的焦点在x轴上,且椭圆C的焦距为2.(Ⅰ)求椭圆C的标准方程;(Ⅱ)过点R(4,0)的直线l与椭圆C交于两点P,Q,过P作PN⊥x轴且与椭圆C交于另一点N,F为椭圆C的右焦点,求证:三点N,F,Q在同一条直线上.==,即直线QN过点(1,0),又∵椭圆C的右焦点坐标为F(1,0),∴三点N,F,Q在同一条直线上.类型四多种方法证三点共线例4.(2017•保定一模)设椭圆x2+2y2=8与y轴相交于A,B两点(A在B的上方),直线y=kx+4与该椭圆相交于不同的两点M,N,直线y=1与BM交于G.(1)求椭圆的离心率;(2)求证:A,G,N三点共线.【扩展链接】1.给出()BQ BP AQ AP +=+λ,等于已知Q P ,与AB 的中点三点共线;2. 给出以下情形之一:①AC AB //;②存在实数,AB AC λλ=使;③若存在实数,,1,OC OA OB αβαβαβ+==+且使,等于已知C B A ,,三点共线; 3.【同步训练】1.已知椭圆E :+=1(a >)的离心率e=,右焦点F (c ,0),过点A(,0)的直线交椭圆E 于P ,Q 两点.(1)求椭圆E 的方程;(2)若点P 关于x 轴的对称点为M ,求证:M ,F ,Q 三点共线; (3)当△FPQ 面积最大时,求直线PQ 的方程.【思路点拨】(1)由椭圆的离心率公式,计算可得a 与c 的值,由椭圆的几何性质可得b 的值,将a 、b 的值代入椭圆的方程计算可得答案;(2)根据题意,设直线PQ的方程为y=k(x﹣3),联立直线与椭圆的方程可得(3k2+1)x2﹣18k2x+27k2﹣6=0,设出P、Q的坐标,由根与系数的关系的分析求出、的坐标,由向量平行的坐标表示方法,分析可得证明;(3)设直线PQ的方程为x=my+3,联立直线与椭圆的方程,分析有(m2+3)y2+6my+3=0,设P(x1,y1),Q(x2,y2),结合根与系数的关系分析用y1.y2表示出△FPQ的面积,分析可得答案.(3)设直线PQ的方程为x=my+3.由方程组,得(m2+3)y2+6my+3=0,2.已知椭圆C:+y2=1的左顶点为A,右焦点为F,O为原点,M,N是y轴上的两个动点,且MF⊥NF,直线AM和AN分别与椭圆C交于E,D两点.(Ⅰ)求△MFN的面积的最小值;(Ⅱ)证明;E,O,D三点共线.【思路点拨】(I)F(1,0),设M(0,t1),N(0,t2).不妨设t1>t2.由MF⊥NF,可得=0,化为:t1t2=﹣1.S△MFN=,利用基本不等式的性质即可得出.(II)A(﹣,0).设M(0,t),由(1)可得:N(0,﹣),(t≠±1).直线AM,AN的方程分别为:y=x+t,y=x﹣.分别与椭圆方程联立,利用一元二次方程的根与系数的关系可得kOE ,kOD.只要证明kOE=kOD.即可得出E,O,D三点共线.【详细解析】(I )F (1,0),设M (0,t 1),N (0,t 2).不妨设t 1>t 2.∵MF ⊥NF ,∴=1+t 1t 2=0,化为:t 1t 2=﹣1.∴S △MFN ==≥=1.当且仅当t 1=﹣t 2=1时取等号.3.已知焦距为2的椭圆W :+=1(a >b >0)的左、右焦点分别为A 1,A 2,上、下顶点分别为B 1,B 2,点M (x 0,y 0)为椭圆W 上不在坐标轴上的任意一点,且四条直线MA 1,MA 2,MB 1,MB 2的斜率之积为. (1)求椭圆W 的标准方程;(2)如图所示,点A ,D 是椭圆W 上两点,点A 与点B 关于原点对称,AD ⊥AB ,点C 在x 轴上,且AC 与x 轴垂直,求证:B ,C ,D 三点共线.【思路点拨】(1)由c=1,a2﹣b2=1,求得四条直线的斜率,由斜率乘积为,代入求得a和b的关系,即可求得a和b的值,求得椭圆W的标准方程;(2)设A,D的坐标,代入椭圆方程,作差法,求得直线AD的斜率,由kAD •kAB=﹣1,代入求得=,由kBD ﹣kBC=0,即可求证kBD=kBC,即可求证B,C,D三点共线.(2)证明:不妨设点A(x1,y1),D(x2,y2),B的坐标(﹣x1,﹣y1),C(x1,0),∵A,D在椭圆上,,=0,即(x1﹣x2)(x1+x2)+2(y1﹣y2)(y1+y2)=0,∴=﹣,由AD ⊥AB ,∴k AD •k AB =﹣1,•=﹣1,•(﹣,)=﹣1,∴=,∴k BD ﹣k BC =﹣=﹣=0,k BD =k BC ,∴B ,C ,D 三点共线. 4.给定椭圆C :+=1(a >b >0),称圆C 1:x 2+y 2=a 2+b 2为椭圆的“伴随圆”.已知A (2,1)是椭圆G :x 2+4y 2=m (m >0)上的点. (Ⅰ)若过点P (0,)的直线l 与椭圆G 有且只有一个公共点,求直线l 被椭圆G 的“伴随圆”G 1所截得的弦长;(Ⅱ)若椭圆G 上的M ,N 两点满足4k 1k 2=﹣1(k 1,k 2是直线AM ,AN 的斜率),求证:M ,N ,O 三点共线.【思路点拨】(Ⅰ)将A 代入椭圆方程,可得m ,进而得到椭圆方程和伴椭圆方程,讨论直线l 的斜率不存在和存在,设出l 的方程,代入椭圆方程运用判别式为0,求得k ,再由直线和圆相交的弦长公式,计算即可得到所求弦长;(Ⅱ)设直线AM ,AN 的方程分别为y ﹣1=k 1(x ﹣2),y ﹣1=k 2(x ﹣2),设点M (x 1,y 1),N (x 2,y 2),联立椭圆方程求得交点M ,M 的坐标,运用直线的斜率公式,计算直线OM ,ON 的斜⇐率相等,即可得证.5.已知椭圆,四点中恰有三点在椭圆C上(1)求椭圆的方程.(2)经过原点作直线(不与坐标轴重合)交椭圆于,两点,轴于点,点在椭圆C上,且求证:,三点共线.【思路点拨】根据椭圆上的点坐标求出椭圆方程;设出,,则,,再向量坐标化,得到,得到,最终得到;6.已知抛物线:()的焦点为,点为直线与抛物线准线的交点,直线与抛物线相交于、两点,点关于轴的对称点为.(1)求抛物线的方程;(2)证明:点在直线上.【思路点拨】(1)由交点坐标可得,求得可得抛物线方程;(2)设直线的方程为(),代入抛物线方程消去x整理得,再设,,进而得,可得直线的方程为,又,,故BD方程化为,令,得,即结论成立。

第26讲 三点共线问题知识与方法在解析几何中,三点共线一般用斜率相等或向量共线来计算:(1)斜率相等:A 、B 、C 三点共线AB AC k k ⇔=或直线AB 、AC 的斜率都不存在; (2)向量共线:A 、B 、C 三点共线AB AC ⇔∥.典型例题1.(★★★★)已知曲线()()22:528C m x m y −+−=()m ∈R .(1)若曲线C 是焦点在x 轴上的椭圆,求m 的取值范围;(2)设4m =,曲线C 与y 轴的交点分别为A 、B (点A 位于点B 的上方),直线4y kx =+与曲线C 交于不同的两点M 、N ,直线1y =与直线BM 交于点G ,求证:A 、G 、N 三点共线. 【解析】(1)原曲线方程可化为2218852x y m m +=−−,曲线C 是焦点在x 轴上的椭圆,所以88052m m >>−−,解得:752m <<. (2)当4m =时,曲线C 的方程为2228x y +=,由题意,()0,2A ,()0,2B −,联立22428kx x y y ++==⎧⎨⎩消去y 整理得:()222116240k x kx +++=,判别式()232230k ∆=−>,故232k >,设()11,4M x kx +,()22,4N x kx +,由韦达定理,1221621k x x k +=−+,1222421x x k =+, 直线MB 方程为1162kx y x x +=−,令1y =解得:1136x x kx =+,所以113,16x G kx ⎛⎫ ⎪+⎝⎭故113,16x AG kx ⎛⎫=−⎪+⎝⎭,()22,2AN x kx =+要证A 、G 、N 三点共线,只需证AG 与AN 共线, 即证()1221326x kx x kx +=−+成立,化简得:()121246kx x x x =−+①由1221621kx x k +=−+和1222421k x x k =+可得式①成立,所以A 、G 、N 三点共线.2.(★★★★)已知A 、B 分别为曲线222:1x C y a+=()0,0y a ≥>与x 轴的左、右两个交点,直线l 过点B且与x 轴垂直,S 为l 上异于B 的一点,连接AS 交曲线C 于点T . (1)若曲线C 为半圆,且T 为圆弧AB 的三等分点,求S 点的坐标;(2)如下图所示,M 是以BS 为直径的圆与线段BT 的交点,试问:是否存在a ,使得O 、M 、S 三点共线?若存在,求出a 的值;若不存在,说明理由.【解析】(1)当曲线C 为半圆时,1a =,由点T 为圆弧AB 的三等分点得60BOT ∠=︒或120°,当60BOT ∠=︒时,30SAB ∠=︒,又2AB =,所以在SAB △中,tan303SB AB =⋅︒=,故S ⎛ ⎝⎭当120BOT ∠=︒时,同理可求得点S 的坐标为(,综上所述,点S 的坐标为⎛ ⎝⎭或( (2)解法1:由题意,(),0A a −,(),0B a ,直线AS 不与坐标轴垂直,可设其方程为x my a =−()0m ≠,联立2222x a x m a ay y ⎧⎨+==−⎩消去x 整理得:()22220m a y may +−=,解得:0y =或222mam a+,所以222T may m a =+,从而()2222T T a m a x my a m a −=−=+,故()2222222,a m a ma T m a m a ⎛⎫−⎪ ⎪++⎝⎭, 联立x x amy a ⎧⎨==−⎩解得:2a y m =,所以2,a S a m ⎛⎫ ⎪⎝⎭,因为点M 在以BS 为直径的圆上,所以SM BM ⊥,又M 是圆与线段BT 的交点,所以SM BT ⊥,故O 、M 、S 三点共线等价于OS BT ⊥,即()222222221OS BTmam a k k m a m a am a +⋅=⋅=−−−+,结合0a >可解得:a =,所以存在a =,使得O 、M 、S 三点共线.解法2:显然AS 的斜率存在且大于0,故可设直线AS 的方程为()y k x a =+,联立()ay k x x a ⎧⎪⎨==+⎪⎩解得:2y ka =,所以(),2S a ka ,故直线OS 的斜率22OS ka k k a ==, 设()00,T x y ,则220021x y a +=,所以220021x y a=−,从而202200022222000011AT BT BTx y y y a k k k k x a x a x a x a a−⋅=⋅=⋅===−+−−− 所以直线BT 的斜率为21BT k a k=−,因为点M 是线段BT 与以BS 为直径的圆的交点,所以BT SM ⊥,从而211BT MS MS k k k a k=−⋅=−,故直线MS 的斜率为2MS k a k = 而O 、M 、S 三点共线等价于OS MS k k =,即22a k k =,所以a =,故存在a =使得O 、M 、S 三点共线.强化训练3.(★★★★)已知椭圆22154x y +=的右焦点为F ,设直线:5l x =与x 轴的交点为E ,过点F 的直线1l 与椭圆交于A 、B 两点,M 为线段EF 的中点.(1)若直线1l 的倾斜角为45°,求ABM △的面积S ;(2)过点B 作BN l ⊥于点N ,证明:A 、M 、N 三点共线.【解析】(1)由题意,()5,0E ,()1,0F ,()3,0M ,设()11,A x y ,()22,B x y , 若直线1l 的倾斜角为45°,则其方程为1y x =−,联立221541x y y x =−⎧⎪⎨+=⎪⎩消去x 整理得:298160y y +−=,判别式()284916640∆=−⨯⨯−=故12121299ABM S FM y y y y =⋅⋅−=−==△.(2)证法1:当1l y ⊥轴时,易得A 、M 、N 三点都在x 轴上,故A 、M 、N 三点共线, 当1l 不与y 轴垂直时,设其方程为1x my =+,联立221541x y x my =+=+⎧⎪⎨⎪⎩ 消去x 整理得:()22458160m y my ++−=,易得判别式0∆>,由韦达定理,122845my y m +=−+,1221645y y m =−+()13,MA x y =−,因为()25,N y ,所以()22,MN y =,要证A 、M 、N 三点共线,只需证MA 与MN 共线,即证()12132x y y −=,即()121320x y y −−=,也即()1211320my y y +−−=,故只需证()121220my y y y −+=而()1212221682204545m my y y y m m m ⎛⎫⎛⎫−+=⋅−−⋅−= ⎪ ⎪++⎝⎭⎝⎭,所以A 、M 、N 三点共线. 证法2:当1l y ⊥轴时,易得A 、M 、N 三点都在x 轴上,故A 、M 、N 三点共线, 当1l 不与y 轴垂直时,设其方程为1x my =+,联立221541x y x my =+=+⎧⎪⎨⎪⎩ 消去x 整理得:()22458160m y my ++−=,易得判别式0∆>,由韦达定理,122845m y y m +=−+,1221645y y m =−+ 由题意,()25,N y , 所以()()()()()()112112121212111123213232232323AM MN y x y y my y y y my y y y k k x x x x −−−+−+−−=−===−−−− 而()1212228162204545m y y my y m m m ⎛⎫⎛⎫+−=⋅−−⋅−= ⎪ ⎪++⎝⎭⎝⎭,故0AM MN k k −=,即AM MN k k =,所以A 、M 、N 三点共线.【反思】证明三点共线,常用证向量共线或证斜率相等的方法. 4.(★★★★)已知椭圆2222:1x y E a b+=()0a b >>的右焦点为F ,椭圆的上顶点和两个焦点的连线构成一.(1)求椭圆E 的标准方程;(2)若直线:l x my q =+()0m ≠与椭圆E 交于不同的两点A 、B ,设点A 关于椭圆长轴的对称点为1A ,试求1A 、F 、B 三点共线的充要条件.【解析】(1)由题意,2222122a cc b a b c=⎧⎪⎪⋅⋅=⎨⎪⎪−=⎩,解得:2a =,b 1c =,故椭圆E 的标准方程为22143x y +=. (2)由(1)知()1,0F ,设()11,A x y ,()22,B x y ,则()111,A x y −()1111,FA x y =−−,()221,FB x y =−−,1A 、F 、B 三点共线的充要条件是1F A 与FB 共线,即()()()122111x y x y −=−−,整理得:()1221120x y x y y y +++=①联立22143x my q x y =+⎧⎪⎨+=⎪⎩消去x 整理得:()2223463120m y mqy q +++−=判别式()()()2222223643431248340m q m q m q ∆=−+−=+−>,所以22340m q +−>②,由韦达定理,122634mq y y m +=−+,212231234q y y m −=+,所以()()()()()()122112122112121221x y x y y y my q y my q y y y my y q y y +++=+++−+=+−+()()()()2222312166403434m q q mq m q m m −+−−−===++因为0m ≠,所以4q =,代入式②得:24m >,即2m > 故A 、F 、B 三点共线的充要条件是4q =且2m >.。

�퐎 �퐎 APABOB OA OP OA OP OA OB11O 的中点,过点G 的直线分别交边D .724,所以1134AG AM AC .因为G 、M 、N 三点共线,所以本题考查利用三点共线求参数,考查了结论“若A 、B 、C 三点在一条直线上,点则下列说法正确的是(),A .C 可能是线段AB 的中点B .D 可能是线段AB 的中点C .C 、D 可能同时在线段AB 上D .C 、D 不可能同时在线段AB 的延长线上【答案】D【解析】由 AC AB R , AD AB R,可得:,,,A B C D 四点共线,对于选项A ,若C 是线段AB 的中点,则12AC AB ,则1,02 ,不满足112u,即选项A 错误;对于选项B ,若D 是线段AB 的中点,则12AD AB ,则10,2 ,不满足112u,即选B 错误;对于选项C ,若C 、D 同时在线段AB 上,则01,01 ,则112u ,不满足112u,即选项C 错误;对于选项D ,假设C 、D 同时在线段AB 的延长线上,则1,1 ,则112u,则不满足112u,即假设不成立,即C 、D 不可能同时在线段AB 的延长线上,即选项D 正确;故选:D.5.(多选题)如图,B 是AC 的中点,2BE OB,P 是平行四边形BCDE 内(含边界)的一点,且 ,OP xOA yOB x y R,则下列结论正确的为()A .当0x 时, 2,3yB .当P 是线段CE 的中点时,12x,52y C .若x y 为定值1,则在平面直角坐标系中,点P 的轨迹是一条线段D .x y 的最大值为1 【答案】BCD 【分析】。
三点共线经典题型例1如图△ABC,D是△ABC内的一点,延长BA至点E,延长DC至点F,使得AE=CF,G,H,M分别为BD,AC,EF的中点,如果G,H,M三点共线,求证:AB=CD.分析由三角形的中位线得,MS∥AE,MS=0.5AE,HS∥CF,HS=0.5CF由已知得HS=SM,从而得出∠SHM=∠SMH,则得出∠TGH=∠THG,GT=TH,最后不难看出AB=CD.解答:证明:取BC中点T,AF的中点S,连接GT,HT,HS,SM,∵GHM分别为BD,AC,EF的中点,∴MS∥AE,MS=0.5AE,HS∥CF,HS=0.5CF∵GT∥CD,HT∥AB,GT=0.5CD,HT=0.5AB,∴GT∥HS,HT∥SM∴∠SHM=∠TGH,∠SMH=∠THG,∴∠TGH=∠THG,∴GT=TH,∴AB=CD.例2如图,已知菱形ABCD,∠B=60°,△ADC内一点M满足∠AMC=120°,若直线BA与CM交于点P,直线BC与AM交于点Q,求证:P,D,Q三点共线.分析求证:P,D,Q三点共线就是证明平角的问题,可以求证∠PDA+∠ADC+∠CDQ=180°,根据△PAC∽△A MC,△AMC∽△ACQ,可以得出∠PAD=∠DCQ=60°;进而证明△PAD∽△DCQ,得出∠APD=∠CDQ,则结论可证解答连接PD,DQ,由已知∠PAC=120°,∠QCA=120°,∴△PAC∽△AMC,△AMC∽△ACQ.∴PA/AM=AC/MC,AC/AM=QC/MC∴AC2=PA•QC,又AC=AD=DC.∴PA/DC=AD/QC,又∠PAD=∠DCQ=60°,∴△PAD∽△DCQ,∴∠APD=∠CDQ.∴∠PDA+∠ADC+∠CDQ=180°,∴P,D,Q三点共线.本题是证明三点共线的问题,这类题目可以转化为求证平角的问题.并且本题利用相似三角形的性质,对应角相等.例3如图,△ABC内接于圆⊙,点D是圆⊙上异于A、B、C三点的任意一点,过D点作DP⊥AB,DQ⊥BC,DR⊥AC,交AB、BC、AC分别为P,Q,R.(1)求证:∠BDP=∠CDR;(2)求证:P,Q,R三点共线.分析(1)由已知中四边形ABDC为圆内接四边形,根据圆内接四边形性质,我们易得∠DBP=∠DCP,结合已知中DP⊥AB,DR⊥AC,根据等角的余角相等,即可得到答案.(2)由已知中DP⊥AB,DQ⊥BC,可判断出P、D、Q、B四点共圆,进而根据圆周角定理得到∠PQD=∠PBD,同理可得∠RQC=∠RDC,结合(1)中结论,我们易证明∠PQD+∠RQD=180°,进而得到P、Q、R三点共线.证明:(1)由已知可得四边形ABDC为圆内接四边形则∠DBP=∠DCP又∵DP⊥AB,DR⊥AC,∴∠BDP=90°-∠DBP,∠CDR=90°-∠DCP;∴∠BDP=∠CDR;(2)∵DP⊥AB,DQ⊥BC,∴P、D、Q、B四点共圆∴∠PQD=∠PBD同理可得∠RQC=∠RDC∵∠PBD+∠RDC=90°∴∠PQD+∠RQD=90°+∠CQD=180°故P、Q、R三点共线本题考查的知识点是圆内接四边形的判定与性质,其中根据已知条件判断出P、D、Q、B四点共圆,进而根据圆周角定理得到∠PQD=∠PBD,并同理得到∠RQC=∠RDC,是证明三点共线的关键.例4已知四边形ABCD是矩形,M、N分别是AD、BC的中点,P是CD上一点,Q是AB上一点,CP=BQ,PM与QN的交点为R.求证:R,A,C三点共线.分析延长RN交DC于T,连接RC交MN于O,易证PN=NT,PC=CT,进而根据O是MN 的中点所以R,C,O三点共线、A,O,C三点共线,可以证明R,A,C三点共线.证明:延长RN交DC于T,连接RC交MN于O,∵∠BNQ=∠CNT,BN=CN,∠NBQ=∠NCT,∴△BNQ≌△CNT(ASA),∴CT=BQ=CP,∴PN=NT,PC=CT,∵MN∥CD,∴MO=ON∴O是MN的中点所以R,C,O三点共线,又A,O,C三点共线,所以R,A,C三点共线本题考查了全等三角形的证明和全等三角形对应边相等的性质,矩形各内角为直角的性质,本题中求证R,C,O三点共线是解题的关键.例4如图,O,H分别是锐角△ABC的外心和垂心,D是BC边上的中点.由H向∠A及其外角平分线作垂线,垂足分别是E,F.求证:D,E,F三点共线.分析根据AE平分∠BAC,M为弦BC的中点,可证A、E、M三点共线,根据已知证明EG∥OA,DG∥OA,可证D、E、G三点共线,而F在EG上,故可证D、E、F三点共线.证明:如图,连接OA、OD,并延长OD交⊙O于M,则OD⊥BC,弦BC=弦CM∴A、E、M三点共线,又AE、AF是∠A及其外角平分线,∴AE⊥AF,∵HE⊥AE,HF⊥AF,∴四边形AEHF为平行四边形,∴AH与EF互相平分,设其交点为G,于是,AG=0.5AH=0.5EF=EG∵OA=OM,OD∥AH,∴∠OAM=∠OMA=∠MAG=∠GAE,∴EG∥OA ①又O、H分别是△ABC的外心和垂心,且OD⊥BC,∴OD=0.5AH=AG,∴四边形AODG为平行四边形,∴DG∥OA,②由①②可知,D、E、G三点共线,而F在EG上,∴D、E、F三点共线.本题考查了三角形外接圆的性质在证明三点共线问题中的运用.关键是利用平行线,圆周角定理,垂径定理证明三点共线.。

中考数学难点旋转最值三点共线问题旋转最值三点共线问题是中考数学中的难点之一。
解决这个问题需要掌握旋转、最值和共线等概念,以及相应的解题方法。
本文将为大家详细介绍这个难点问题的解题思路和步骤,帮助大家更好地应对中考数学考试。
1. 问题描述假设平面上有三个点A(x1, y1)、B(x2, y2)、C(x3, y3),我们需要找到一个旋转中心O,使得当点A绕O旋转时,点B和C始终保持共线。
我们需要求解旋转中心O的坐标。
2. 解题思路为了求解旋转中心O的坐标,我们可以从两个方面入手,分别是旋转角度和旋转中心的坐标。
首先,我们可以假设旋转中心O的坐标为(x, y),然后通过计算旋转角度来确定旋转中心的位置。
接下来,我们根据最值和共线的概念,构建方程组,进而求解旋转中心的坐标。
3. 计算旋转角度为了构建方程组,我们需要先确定旋转角度。
根据题目要求,点B和C始终保持共线,说明它们的斜率相等。
我们可以求解点B和C的斜率,然后通过斜率之间的关系来确定旋转角度。
斜率的计算公式为:k = (y2 - y1) / (x2 - x1)设斜率k1 = (y2 - y1) / (x2 - x1),斜率k2 = (y3 - y1) / (x3 - x1)由于点B和C始终共线,则k1 = k2,即 (y2 - y1) / (x2 - x1) = (y3 -y1) / (x3 - x1)化简上述方程,得到:(y2 - y1) * (x3 - x1) = (y3 - y1) * (x2 - x1)4. 求解旋转中心坐标通过4.计算旋转角度中的方程,我们得到了一个等式,然后我们将旋转中心的坐标代入该等式,从而求解旋转中心坐标。
具体步骤如下:将旋转中心坐标(x, y)代入方程,得到:(y2 - y1) * (x3 - x1) = (y3 - y1) * (x2 - x1)展开并整理得到:(x2 - x1) * y + (y2 - y1) * x = (x2 * y1 - x1 * y2) + (x1 * y3 - x3 * y1)由上述方程可知,旋转中心的坐标可以通过求解线性方程组来获得。
1. 题目:如图△ABC 的内心为I ,过点A 作直线BI 的垂线,垂足为H.设D ,E 分别为内切圆I 与边BC ,CA 的切点,求证:三点D ,H ,E 共线.解法一:四点共圆法 连接AI ,DI ,EI ,EH ,DH ∵∠AEI=∠AHI=90° ∴A ,I ,E ,H 四点共圆 ∴∠IEH=∠IAH ,又∵IE=ID ∴∠IEH=∠IAH=∠IDH又∵∠IBD+∠BID=90°,BI 平分∠ABC∴∠ABI+∠IHD+∠IDH=90°,∠ABI+∠BAI+∠IAH=90° ∴∠IHD=∠BAI=∠IAE ,∴D ,H ,E 共线解法二:相似三角形证角相等 延长IH 交AC 于G , 连接AI ,DI ,EI ,EH ,DH∵∠ABI=∠IBD ,∠BDI=∠BHD ∴△ABH ∽△IBD∴BI/AB=BD/BH ∴BI/BD=AB/BH ∴△ABI ∽△HBD ∴∠BHD=∠BAI (此时可用解法一) 又∵∠EHG=∠IAE∴∠EHG=∠BHD ∴D ,H ,E 共线解法三:三角形内心性质(同一法) 连接DE ,EH ,AI ,EI ∵A ,I ,H ,E 四点共圆 ∴∠AIB=AEH 又∵I 为△ABC 的内心 ∴∠AIB=∠AEH=90°+∠C/2又∵CD=CE ∴∠DEC=90°﹣∠C/2 ∴∠DEC+AEH=90° ∴H 在DE 上 ∴D ,H ,E 共线解法四:利用梅涅劳斯定理逆定理 连接DH ,EH ,延长BH 交AC 于G ,过G 作GK ∥BC ,交EH 于K 若BD /DC * CE/EG * GH/HB=1 即可证D ,H ,E 共线要证BD /DC * CE/EG * GH/HB=1 ∵DC=CE即证BD/EG=BH/GH ,即证BD/BH=EG/GH∵GK ∥BC ,△CED 为等腰三角形 ∴△EGK 也为等腰三角形 ∴EG=KG又∵△KGH ∽△DBH ∴BD/BH=KG/GH ∴BD/BH=EG/GH ∴D ,H ,E 共线2.如图,在菱形ABCD 中,∠A=120°,⊙O 为△ABC 的外接圆,M 为菱形外一点,连接MC 交AB 于E ,AM 交BC 的延长线.求证:点M 在⊙O 上<=>点D ,E ,F 共线解法一:三角形相似 连接AC ,DF ,DE∵M 在⊙O 上,∴∠AMC=∠ABC =∠ACB =60° ∴△AMC ∽△ACF∴MC /MA=CF/CA=CF/CD又∵∠AMC=∠BAC ,∴△AMC ∽△EAC ∴MC /MA=AC/AE=AD/AE ∴CE /CD=AD /AE 又∵∠BAD=∠BCD=120° ∴△CFD ∽△ADEFF∴∠ADE=∠DFB∵AD ∥BC ,∴∠ADF=∠DFB=∠ADE ∴F ,E ,D 三点共线。
黔西北州欣宜市实验学校二零二一学年度初三数学三点一共线不容无视□朱元生四边形是初中几何的重要内容之一,也是中考的必考内容,它既是三角形知识的延续,又是学好相似形和圆的根底。
在四边形问题的解答过程中,不少同学常常无视三点一共线这一关键点,为引起同学们的重视,现略举几例加以剖析,供学习时参考。
一、解题过程中没有说明三点一共线例1.如图1,在菱形ABCD中,对角线AC和BD相交于点O,OE⊥AB于点E,OF⊥BC于点F,OG⊥CD于点G,OH ⊥AD于点H,依次连接EF,FG,GH和HE,试证明四边形EFGH为矩形。
图1错解:因BD为菱形ABCD的对角线,所以∠ABD=∠CBD。
又因为OE⊥AB,OF⊥BC,由角平分线性质得OE=OF。
同理可得OF=OG,OG=OH,OH=OE即OE=OF=OG=OH所以四边形EFGH为平行四边形因为OE+OG=OF+OH,即EG=FH所以四边形EFGH为矩形剖析:在上面的解题过程中,先说明了四边形EFGH的“对角线〞EG和FH互相平分,可得四边形EFGH为平行四边形,再说明“对角线〞EG=FH,从而得到结论四边形EFGH为矩形。
外表上似乎推理严谨,无懈可击,其实不然,无论是,还是推理过程都没有说明E,O,G和F,O,H分别是同一条直线上的三点〔即三点一共线〕,所以上述解题过程中把EG和HF直接看做四边形EFGH的对角线是缺乏根据的,必须说明EG和FH分别是四边形EFGH的对角线后,上面的说理才能成立。
正解:因为OG⊥CD,AB∥CD,所以OG⊥AB又OE ⊥AB ,那么线段OE 和OG 在同一条直线上。
即E ,O ,G 三点一共线,从而EG 为四边形EFGH 的对角线。
同理可知,FH 也是四边形EFGH 的对角线。
下略,可参考错解。
例2.如图2,在梯形ABCD 中,AD ∥BC ,E ,F ,G ,H 分别是AB ,DC ,BD ,AC 的中点,连接EG ,GH ,HF ,试证明()GH BC AD =-12。
三点共线的常用处理方法例已知:A(-1,-1),B(1,3),C(2,5)。
证明:A,B,C三点共线。
(至少运用三种方法)一·向量法练习1`设(,12),(4,5),(10,)PA k PB PC k ===,则k =_____时,A,B,C 共线 2`如图`平行四边形ABCD 中,14BE BA =,15BF BD =, 求证: E 、F 、C 三点共线. .3. 已知,,A B C 三点不共线,对平面外任一点,满足条件122555OP OA OB OC =++ ,试判断:点P 与,,A B C 是否一定共面?2图已知ABCD ,从平面AC 外一点O 引向量,,,OE kOA OF KOB OG kOC OH kOD ==== ,(1)求证:四点,,,E F G H 共面; 二·夹角法练习.若1(2,3),(3,2),(,)2A B C m --三点共线 则m 的值为( )三·定比分点法练习1.(1)已知点A、B、C三点共线,O在直线AB外,设, , OA a OB b OC c ===,且存在实数m 使30ma b c -+= ,则点A分BC 所成的比为( )四·三角形法 五·函数法 六·斜率法练习.已知直线1:310l x y -+=,2:210l x my +-=.若1l ∥2l ,则实数m =______.已知过点(2,)A m -和(,4)B m 的直线与直线012=-+y x 平行,则m 的值为( )七·点到直线的距离法练习1·.已知A(-4,-6),B(-3,-1),C(5,a)三点共线,则a的值为()八·直线重合法九,点是否在直线上练习1·.若Na),C(1,3)共线,a∈,又三点A(a,0),B(0,4+求a的值十·反证法1.已知:a+b+c>0,ab+bc+ca>0,abc>0.求证:a>0,b>0,c>0.2`已知a ,b ,c ∈(0,1).求证:(1-a )b ,(1-b )c ,(1-c )a 不能同时大于14.3`求证:ABC ∆中不可能有两个角是直角。
证明三点共线问题的方法1、利用梅涅劳斯定理的逆定理例1、如图1,圆内接ΔABC 为不等边三角形,过点A 、B 、C 分别作圆的切线依次交直线BC 、CA 、AB 于1A 、1B 、1C ,求证:1A 、1B 、1C 三点共线。
解:记,,BC a CA b AB c ===,易知1111AC CCC BS AC C B S ∆∆=又易证11AC C CC B ∆∆.则11222AC C CC B S AC b S CB a∆∆⎛⎫== ⎪⎝⎭.同理12121212,BA c CB a A C b B A c ==.故1112221112221AC BA CB b c a C B A C B A a b c⋅⋅=⋅⋅=.由梅涅劳斯定理的逆定理,知1A 、1B 、1C 三点共线。
2、利用四点共圆(在圆内,主要由角相等或互补得到共线)例2 、如图,以锐角ΔABC 的一边BC 为直径作⊙O ,过点A 作⊙O 的两条切线,切点为M 、N ,点H 是ΔABC 的垂心.求证:M 、H 、N 三点共线。
(96中国奥数证明:射线AH 交BC 于D ,显然AD 为高。
记AB 与⊙O 的交点为E ,易知C 、H 、E 三点共线。
联结OM 、ON 、DM 、DN 、MH 、NH ,易知090AMO ANO ADO ∠=∠=∠=,∴A 、M 、O 、D 、N 五点共圆,更有A 、M 、D 、N 四点共圆, 此时,0+180AND ∠∠=AMD因为2AM AE AB AH AD =⋅=⋅(B 、D 、H 、E 四点共圆),即AM ADAH AM=;又MAH DAM ∠=∠,所以AMH ADM ∆∆,故AHM AMD ∠=∠同理,AHN AND ∠=∠。
因为0180AHM AHN AMD AND ∠+∠=∠+∠=,所以,M 、H 、N 三点共线。
3、利用面积法如果SS EMNFMN=∆∆,点E 、F 位于直线MN 的异侧,则直线MN 平分线段EF ,即M 、N 与EF 的中点三点共线。
向量三点共线定理例题三点一线的神秘向量舞步——一起探索共线定理的魅力嗨,朋友们!今天咱们要揭开一个数学王国中的小秘密,那就是“向量三点共线定理”。
这听起来似乎有点高深莫测,但只要你跟随我的脚步,保证让你恍然大悟,拍案叫绝。
就让我们在这段奇妙之旅中,领略数学的韵律与灵动吧!想象一下,在浩渺的几何空间里,有三个点A、B、C在跳一场别开生面的舞蹈。
每个点都像是一位舞者,手持着代表自身位置的向量指挥棒,翩翩起舞。
现在,我们假设这三个点之间存在着某种神秘的连线规则,只要它们仨能够通过各自的向量指挥棒指向同一条直线,那就意味着,它们已经完美演绎了这场“三点共线”的几何芭蕾。
那么,究竟怎样才算是“共线”呢?这就需要用到我们的向量大佬——向量三点共线定理。
简单来说,如果从点A到点B的向量AB和从点A到点C的向量AC满足这样的关系:存在某个实数λ(这个家伙就是我们的“比例因子”,相当于舞蹈编排中的节拍),使得向量AC等于λ乘以向量AB,即AC = λ·AB,那么,恭喜你,点A、B、C三位舞者就在同一直线上默契共舞了!比如说,有一次,在数学世界的璀璨舞台上,点A、B、C三剑客各据一隅。
我们计算得出,从A指向B的向量AB长度是5单位,而从A指向C的向量AC恰好是10单位,而且方向一致。
这时候,聪明如你一定想到了,既然AC是AB的两倍长,那λ不就是2吗?对喽,这样一来,根据向量三点共线定理,我们就知道A、B、C三位选手在同一直线上携手共舞,画面简直美不胜收!这就是向量三点共线定理在实际应用中的生动诠释,它就像一把钥匙,帮我们解锁了隐藏在几何图案背后的规律之美。
当你下次再看到三个点悄然排列,不妨试着用这条定理去探寻它们之间的微妙联系,或许你会发现,原来数学也可以如此贴近生活,如此富有诗意!所以,亲爱的朋友,下回当你面对复杂的几何问题时,别忘了召唤这位“向量三点共线定理”小助手哦!只要轻轻挥动它的魔法棒,任何看似杂乱无章的点阵都将化为曼妙的一线舞姿,让人为之惊叹:“哇塞,原来这就是共线的魅力所在!”。
三点共线经典题型
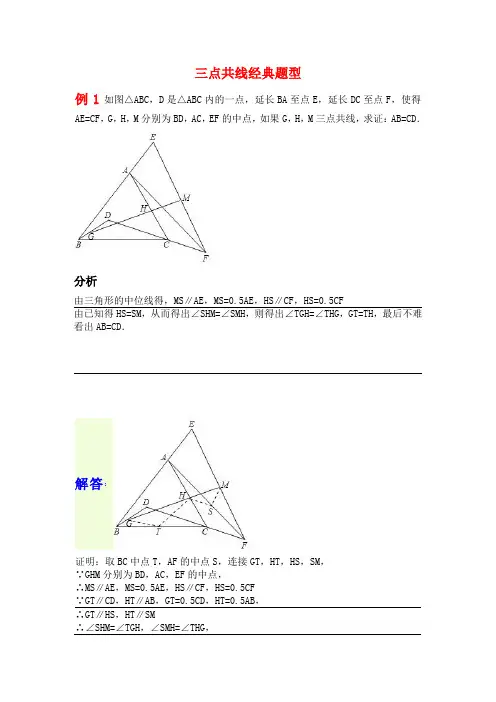
例1如图△ABC,D是△ABC内的一点,延长BA至点E,延长DC至点F,使得AE=CF,G,H,M分别为BD,AC,EF的中点,如果G,H,M三点共线,求证:AB=CD.
分析
由三角形的中位线得,MS∥AE,MS=0.5AE,HS∥CF,HS=0.5CF
由已知得HS=SM,从而得出∠SHM=∠SMH,则得出∠TGH=∠THG,GT=TH,最后不难看出AB=CD.
解答:
证明:取BC中点T,AF的中点S,连接GT,HT,HS,SM,
∵GHM分别为BD,AC,EF的中点,
∴MS∥AE,MS=0.5AE,HS∥CF,HS=0.5CF
∵GT∥CD,HT∥AB,GT=0.5CD,HT=0.5AB,
∴GT∥HS,HT∥SM
∴∠SHM=∠TGH,∠SMH=∠THG,
∴∠TGH=∠THG,
∴GT=TH,
∴AB=CD.
例2如图,已知菱形ABCD,∠B=60°,△ADC内一点M满足∠AMC=120°,若直线BA与CM交于点P,直线BC与AM交于点Q,求证:P,D,Q三点共线.
分析
求证:P,D,Q三点共线就是证明平角的问题,可以求证∠PDA+∠ADC+∠CDQ=180°,根据△PAC∽△AMC,△AMC∽△ACQ,可以得出∠PAD=∠DCQ=60°;进而证明△PAD∽△DCQ,得出∠APD=∠CDQ,则结论可证
解答连接PD,DQ,
由已知∠PAC=120°,∠QCA=120°,
∴△PAC∽△AMC,△AMC∽△ACQ.
∴PA/AM=AC/MC,AC/AM=QC/MC
∴AC2=PA•QC,又AC=AD=DC.
∴PA/DC=AD/QC,又∠PAD=∠DCQ=60°,
∴△PAD∽△DCQ,∴∠APD=∠CDQ.
∴∠PDA+∠ADC+∠CDQ=180°,
∴P,D,Q三点共线.
本题是证明三点共线的问题,这类题目可以转化为求证平角的问题.并且本题利用相似三角形的性质,对应角相等.
例3如图,△ABC内接于圆⊙,点D是圆⊙上异于A、B、C三点的任意一点,
过D点作DP⊥AB,DQ⊥BC,DR⊥AC,交AB、BC、AC分别为P,Q,R.
(1)求证:∠BDP=∠CDR;
(2)求证:P,Q,R三点共线.
分析
由已知中四边形ABDC为圆内接四边形,根据圆内接四边形性质,我们易得∠DBP=∠DCP,结合已知中DP⊥AB,DR⊥AC,根据等角的余角相等,即可得到答案.
(2)由已知中DP⊥AB,DQ⊥BC,可判断出P、D、Q、B四点共圆,进而根据圆周角定理得到∠PQD=∠PBD,同理可得∠RQC=∠RDC,结合(1)中结论,我们易证明∠PQD+∠RQD=180°,进而得到P、Q、R三点共线.
证明:(1)由已知可得四边形ABDC为圆内接四边形
则∠DBP=∠DCP
又∵DP⊥AB,DR⊥AC,
∴∠BDP=90°-∠DBP,∠CDR=90°-∠DCP;
∴∠BDP=∠CDR;
∵DP⊥AB,DQ⊥BC,
∴P、D、Q、B四点共圆
∴∠PQD=∠PBD
同理可得∠RQC=∠RDC
∵∠PBD+∠RDC=90°∴∠PQD+∠RQD=90°+∠CQD=180°
故P、Q、R三点共线
本题考查的知识点是圆内接四边形的判定与性质,其中根据已知条件判断出P、D、Q、B四点共圆,进而根据圆周角定理得到∠PQD=∠PBD,并同理得到∠RQC=∠RDC,是证明三点共线的关键.
例4已知四边形ABCD是矩形,M、N分别是AD、BC的中点,P是CD上一点,Q
是AB上一点,CP=BQ,PM与QN的交点为R.求证:R,A,C三点共线.
分析
延长RN交DC于T,连接RC交MN于O,易证PN=NT,PC=CT,进而根据O是MN 的中点所以R,C,O三点共线、A,O,C三点共线,可以证明R,A,C三点共线.
证明:延长RN交DC于T,连接RC交MN于O,
∵∠BNQ=∠CNT,BN=CN,∠NBQ=∠NCT,
∴△BNQ≌△CNT(ASA),
∴CT=BQ=CP,
∴PN=NT,PC=CT,
∵MN∥CD,
∴MO=ON
∴O是MN的中点所以R,C,O三点共线,
又A,O,C三点共线,所以R,A,C三点共线
本题考查了全等三角形的证明和全等三角形对应边相等的性质,矩形各内角为直角的性质,本题中求证R,C,O三点共线是解题的关键.
例4如图,O,H分别是锐角△ABC的外心和垂心,D是BC边上的中点.由H向∠A及其外角平分线作垂线,垂足分别是E,F.求证:D,E,F三点共线.
分析
根据AE平分∠BAC,M为弦BC的中点,可证A、E、M三点共线,根据已知证明EG∥OA,DG∥OA,可证D、E、G三点共线,而F在EG上,故可证D、E、F三点共线.
证明:如图,连接OA、OD,并延长OD交⊙O于M,
则OD⊥BC,弦BC=弦CM
∴A、E、M三点共线,
又AE、AF是∠A及其外角平分线,
∴AE⊥AF,
∵HE⊥AE,HF⊥AF,
∴四边形AEHF为平行四边形,
∴AH与EF互相平分,设其交点为G,
于是,AG=0.5AH=0.5EF=EG
∵OA=OM,OD∥AH,
∴∠OAM=∠OMA=∠MAG=∠GAE,
∴EG∥OA ①
又O、H分别是△ABC的外心和垂心,且OD⊥BC,
∴OD=0.5AH=AG,
∴四边形AODG为平行四边形,
∴DG∥OA,②
由①②可知,D、E、G三点共线,
而F在EG上,
∴D、E、F三点共线.
本题考查了三角形外接圆的性质在证明三点共线问题中的运用.关键是利用平行线,圆周角定理,垂径定理证明三点共线.。