SPC过程能力研究-X-R控制图(cpk自动计算)
- 格式：xls
- 大小：86.50 KB
- 文档页数：1
下载文档原格式
合集下载
SPC控制程序--范本
1. 目的：
为了不断地对生产过程进行改进并满足客户对生产过程的能力要求，特规定本程序来对生产过程的稳定状态和过程能力指数进行研究，以达到生产过程预防的效果。
2. 适用范围：
适用于与汽车产品特殊特性相关的关键过程的初始过程和稳定过程的能力研究，及过程控制；
3.定义
4. 职责
4.1 品质部
1)负责SPC过程控制；
2)制定与检讨SPC的操作规格，包括样本大小，抽样频率，管制界限等。
3)负责量测、记录、判读数据，并输入控制图的对应位置，将SPC异常通知给生产部，并要求停
止生产,当SPC数据超出规格限时，需立即组织相关部门采取改善措施；
4)确认SPC异常的回复及改善结果。
5)依客户要求定期向客户提交CPK报告；
6)负责保存及维护SPC相关数据。
7)负责对SPC作业相关人员作有关SPC作业规范的培训和异常判读培训。
4.2 生产部: 配合品质部进行SPC过程控制，并对异常情况采取相对应的改善对策。
4.3 APQP小组：负责策划使用哪种SPC控制图，和控制图样品取样数和取样频次。
5. 程序内容
6. 记录
各种控制图表。
Spc应用计算公式(超全)
SPC所有公式详细解释及分析SPC统计制程管制计量值管制图： Xbar-R(平均-全距)、Xbar-S(平均-标准差)、X-MR(个别值-移动全距)、EWMA、CUSUM等管制图。
计数值管制图：不良率p、不良数np、良率1-p、缺点数c、单位缺点数u等管制图。
常用分析工具：直方图、柏拉图、散布图、推移图、%GRR...等。
公式解说制程能力指数制程能力分析制程能力研究在于确认这些特性符合规格的程度，以保证制程成品不符规格的不良率在要求的水准之上，作为制程持续改善的依据。
制程能力研究的时机分短期制程能力研究及长期制程能力研究，短期着重在新产品及新制程的试作、初期生产、工程变更或制程设备改变等阶段；长期以量产期间为主。
制程能力指针 Cp 或 Cpk 之值在一产品或制程特性分配为常态且在管制状态下时，可经由常态分配之机率计算，换算为该产品或制程特性的良率或不良率，同时亦可以几 Sigma 来对照。
计数值统计数据的数量表示缺点及不良(Defects VS. Defectives)缺点代表一单位产品不符要求的点数，一单位产品不良可能有一个缺点或多个缺点，此为计点的品质指针。
例如描述一匹布或一铸件的品质，可用每公尺棉布有几个疵点，一铸件表面有几个气孔或砂眼来表达，无尘室中每立方公尺含微粒之个数，一片PCB有几个零件及几个焊点有缺点，一片按键有几个杂质、包风、印刷等缺点，这些都是以计点方式表示一单位产品的特性值。
不良代表一单位产品有不符要求的缺点，可能有一个或一个以上，此将产品分类为好与坏、良与不良及合格与不合格等所谓的通过－不通过(Go-NoGo)的衡量方式称为计件的品质指针。
例如单位产品必须以二分法来判定品质，不良的单位产品必须报废或重修，这是以计件方式来表示一单位产品的特值。
每单位缺点数及每百万机会缺点数(DPU VS. DPMO)一单位产品或制程的复杂程度与其发生缺点的机会有直接的关系，越复杂容易出现缺点；反之越简单越不容易出现缺点。
SPC教材(CP和CPK计算)
20/ 52
接上页
5、使不必要的变差最小 确保过程按预定的方式运行 确保输入的材料符合要求 恒定的控制设定值 注：应在过程记录表上记录所有的相关事件，如：刀具更新，新的材料批 次等，有利于下一步的过程分析。
21/ 52
均值和极差图（X-R）
1、收集数据
以样本容量恒定的子组形式报告，子组通常包括2-5件连续的产品， 并周性期的抽取子组。 注：应制定一个收集数据的计划，将其作为收集、记录及描图的依据。 1-1 选择子组大小，频率和数据 1-1-1 子组大小：一般为5件连续的产品，仅代表单一刀具/冲头/过程 流等。（注：数据仅代表单一刀具、冲头、模具等 生产出来的零件，即一个单一的生产流。） 1-1-2 子组频率：在适当的时间内收集足够的数据，这样子组才能 反映潜在的变化，这些变化原因可能是换班/操作人 员更换/材料批次不同等原因引起。对正在生产的产 品进行监测的子组频率可以是每班2次，或一小时一 次等。
是指按标准偏差为单位来描述的过程均值和规格界限 过程能力 (Process Capability) 的距离，用Z来表示。
移动极差 （Moving Range)
两个或多个连续样本值中最大值和最小值之差。
7/ 52
持续改进及统计过程控制概述 有反馈的过程控制系统模型
过程的呼声 人 设备 材料 方法 环境 统计方法 我们工作 的方式/资 源的融合
9/ 52
每件产品的尺寸与别的都不同
范围 范围 范围 但它们形成一个模型，若稳定，可以描述为一个分布
范围
分布可以通过以下因素来加以区分 位置 分布宽度
形状
或这些因素的组合
10/ 52
如果仅存在变差的普通原因， 随着时间的推移，过程的输 出形成一个稳定的分布并可 预测。
接上页
5、使不必要的变差最小 确保过程按预定的方式运行 确保输入的材料符合要求 恒定的控制设定值 注：应在过程记录表上记录所有的相关事件，如：刀具更新，新的材料批 次等，有利于下一步的过程分析。
21/ 52
均值和极差图（X-R）
1、收集数据
以样本容量恒定的子组形式报告，子组通常包括2-5件连续的产品， 并周性期的抽取子组。 注：应制定一个收集数据的计划，将其作为收集、记录及描图的依据。 1-1 选择子组大小，频率和数据 1-1-1 子组大小：一般为5件连续的产品，仅代表单一刀具/冲头/过程 流等。（注：数据仅代表单一刀具、冲头、模具等 生产出来的零件，即一个单一的生产流。） 1-1-2 子组频率：在适当的时间内收集足够的数据，这样子组才能 反映潜在的变化，这些变化原因可能是换班/操作人 员更换/材料批次不同等原因引起。对正在生产的产 品进行监测的子组频率可以是每班2次，或一小时一 次等。
是指按标准偏差为单位来描述的过程均值和规格界限 过程能力 (Process Capability) 的距离，用Z来表示。
移动极差 （Moving Range)
两个或多个连续样本值中最大值和最小值之差。
7/ 52
持续改进及统计过程控制概述 有反馈的过程控制系统模型
过程的呼声 人 设备 材料 方法 环境 统计方法 我们工作 的方式/资 源的融合
9/ 52
每件产品的尺寸与别的都不同
范围 范围 范围 但它们形成一个模型，若稳定，可以描述为一个分布
范围
分布可以通过以下因素来加以区分 位置 分布宽度
形状
或这些因素的组合
10/ 52
如果仅存在变差的普通原因， 随着时间的推移，过程的输 出形成一个稳定的分布并可 预测。
SPC(Cpk、Ppk)等工程能力计算公式
均值Ｘ图均值Ｘ图n A2d2D3D4A3c4B3B42 1.880 1.128- 3.267 2.6590.7979- 3.2763 1.023 1.693- 2.571 1.9540.8862- 2.56840.729 2.059- 2.282 1.6280.9213- 2.26650.577 2.326- 2.114 1.4270.9400- 2.08960.483 2.543- 2.004 1.2870.95150.030 1.97070.419 2.7040.076 1.924 1.1820.95940.118 1.88280.373 2.8470.136 1.864 1.0990.96500.185 1.81590.337 2.9700.184 1.816 1.0320.96930.239 1.761100.308 3.0780.223 1.7770.9750.97270.284 1.716110.285 3.1730.256 1.7440.9270.97540.321 1.679120.266 3.2580.283 1.7170.8860.97760.354 1.640130.249 3.3360.307 1.6930.8500.97940.382 1.618140.235 3.4070.328 1.6720.8170.98100.406 1.594150.223 3.4720.347 1.6530.7890.98230.428 1.572160.212 3.5320.363 1.6370.7630.98350.448 1.552170.203 3.5880.378 1.6220.7390.98450.446 1.534180.194 3.6400.391 1.6080.7180.98540.482 1.518190.187 3.6890.403 1.5970.6980.98620.497 1.503200.180 3.7350.415 1.5850.6800.98690.510 1.490210.173 3.7780.425 1.5750.6630.98760.523 1.477220.167 3.8190.434 1.5660.6470.98820.534 1.466230.162 3.8580.443 1.5570.6330.98870.545 1.455240.157 3.8950.451 1.5480.6190.98920.555 1.445250.153 3.9310.459 1.5410.6060.98960.565 1.435X±A 2R X±A 2R中位数Ｘ图单值Ｘ图n A 2d 2D 3D 4E 2d 2D 3D 42 1.880 1.128- 3.267 2.660 1.128- 3.2673 1.187 1.693- 2.574 1.772 1.693- 2.57440.796 2.059- 2.282 1.457 2.059- 2.282标准差估计值的除数UCL X ,LCL X = 全距Ｒ图 全距Ｒ图 中位数图计算控制限用的系数单值图LCL S = B 3s标准差估计值的除数计算控制限用的系数全距Ｒ图 子组容量计算控制限用的系数标准差估计值的除数计算控制限用的系数 Ｘ-Ｒ图 标准差Ｓ图 Ｘ-s图计算控制限用的系数计算控制限用的系数UCL S = B 4s控制图的常数和公式表δ=R/D 2δ= s/c 4子组容量计算控制限用的系数标准差估计值的除数计算控制限用的系数UCL X ,LCL X =UCL R = D 4R LCL R = D 3R50.691 2.326-2.114 1.290 2.326- 2.11460.548 2.534-2.004 1.184 2.534- 2.00470.508 2.7040.0761.924 1.1092.7040.076 1.92480.433 2.8470.1361.864 1.0542.8470.136 1.86490.412 2.9700.1841.816 1.0102.9700.184 1.816100.3623.0780.2231.7770.975 3.0780.223 1.777X±A 2RX±E 2R δ=R/d 2δ= R/d 2UCL R = D 4RUCL MR = D 4R LCL R = D 3RLCL MR = D 3R UCL ,LCL =UCL X ,LCL X =UCL P ,LCL P ==UCL np ,LCL np =UCL C ,LCL C =UCL U ,LCL U =Cpk＝( 1 － k ) ｘ Cp 或 MIN {CPU,CPL}Ppk＝( 1 － k ) ｘ Pp 或 MIN {PPU,PPL}单边规格(设计规格)因没有规格上限或下限,没有规格下限 Cp ＝ CPU ＝ Cpk,没有规格上限 Cp ＝ ()n P P P /13-±=()n P P P -±=13()P P n P n -±=13nUU 3±=CC 3±=格上限 Cp ＝ CPL ＝ Cpk。
SPC各值计算公式
SPC各值计算公式SPC（统计过程控制）是一种统计方法，用于检测和控制过程的稳定性和变异性。
SPC各值计算公式包括控制图参数和过程能力指数等。
以下是常见的SPC各值计算公式及其解释：1.控制图参数：a.X̄控制图上的中心线是过程的平均值的估计量。
计算公式为：X̄=ΣX/n，其中X是测量值的总和，n是样本大小。
b. R 控制图上的极差线是过程的极差的估计量。
计算公式为：R = Xmax - Xmin，其中Xmax和Xmin是样本中最大值和最小值。
c.S控制图上的标准偏差线是过程的标准偏差的估计量。
计算公式为：S=√(Σ(X-X̄)²/(n-1))，其中Σ(X-X̄)²是样本值与平均值的差的平方的总和。
d.UCL控制图上的上限控制限是过程的可接受上限。
计算公式为：UCL=X̄+3S，其中3是标准差的倍数，用于确定上限控制限。
e.LCL控制图上的下限控制限是过程的可接受下限。
计算公式为：LCL=X̄-3S，其中3是标准差的倍数，用于确定下限控制限。
2.过程能力指数：a.Cp过程能力指数是衡量过程发生误差在可接受范围内的能力。
计算公式为：Cp=(USL-LSL)/(6σ)，其中USL和LSL是规范上限和下限，σ是标准偏差的估计量。
b. Cpk 过程能力指数是衡量过程发生误差在可接受范围内的能力，同时考虑了过程的中心线偏移。
计算公式为：Cpk = min((USL - X̄) /(3σ), (X̄ - LSL) / (3σ))，其中USL和LSL是规范上限和下限，X̄是过程的平均值的估计量，σ是标准偏差的估计量。
c. Cpm 过程能力指数是衡量过程发生误差在可接受范围内的能力，同时考虑了过程的中心线偏移和过程的极差。
计算公式为：Cpm = (USL - LSL) / (6√((ΣR/n)² + σ²))，其中USL和LSL是规范上限和下限，ΣR/n是极差均值的估计量，σ是标准偏差的估计量。
X-R控制图实例
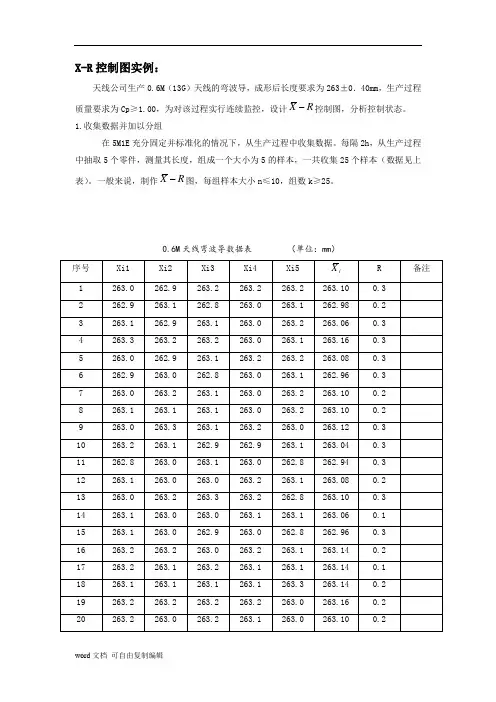
X-R控制图实例：天线公司生产0.6M（13G）天线的弯波导，成形后长度要求为263±0．40mm，生产过程X-控制图，分析控制状态。
质量要求为Cp≥1.00，为对该过程实行连续监控，设计R1.收集数据并加以分组在5M1E充分固定并标准化的情况下，从生产过程中收集数据。
每隔2h，从生产过程中抽取5个零件，测量其长度，组成一个大小为5的样本，一共收集25个样本（数据见上X-图，每组样本大小n≤10，组数k≥25。
表）。
一般来说，制作R0.6M天线弯波导数据表（单位：mm）2.计算每组的样本均值及极差（列于上表）。
计算总平均和极差平均：X=263.07 R=0.2283.计算控制线X图： CL=X=263.07UCL=X+A2R=263.07+0.577*0.228=263.20LCL=X-A2R=263.07-0.577*0.228=262.94R图：CL=R=0.228UCL=D4R=2.114*0.228=0.482LCL=D3R其中系数A2，D3，D4均从控制图系数表中查得，A2=0.577，D4=2.114，当n≤6时D3<0，此时LCL=——。
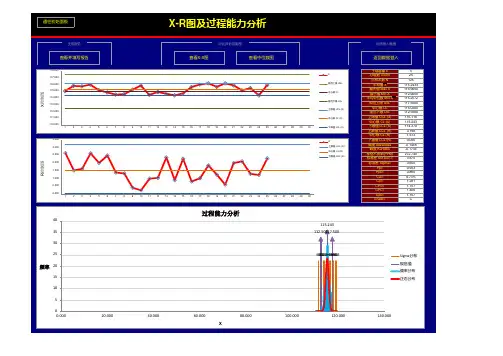
4.制作控制图分别做X图和R图，两张图画在同一张纸上，以便对照分析。
X图在上，R图在下，纵轴在同一直线上，横轴相互平行并且刻度对齐。
本题中R图的下控制界限线LCL＜0，但R要求R≥0，故LCL可以省略。
均值控制图（X图）极差控制图（R图）5.描点:根据各个样本的均值i X和极差Ri在控制图上描点(如上).6.分析生产过程是否处于统计控制状态.利用分析用控制图的判断原则，经分析生产过程处于统计控制状态。
7.计算过程能力指数因为：X=263.07，M=263, X≠M,所以：Cpk=(T-2ε)/6s,其中s=R/d2, ε=|X-M|s=R/d2=0.228/2.326=0.098ε=|X-M|=263.07-263=0.07修正后的过程能力指数Cpk=(T-2ε)/6s=（0.8-2*0.07）/6*0.098=1.228.由于波导管的长度尺寸，对于天线产品的质量影响，属于重要质量特性，1.67≥Cpk>1.33为理想状态， 1.33≥Cpk>1 为低风险状态。
Spc应用计算公式(超全)
SPC所有公式详细解释及分析SPC统计制程管制计量值管制图： Xbar-R(平均-全距)、Xbar-S(平均-标准差)、X-MR(个别值-移动全距)、EWMA、CUSUM等管制图。
计数值管制图：不良率p、不良数np、良率1-p、缺点数c、单位缺点数u等管制图。
常用分析工具：直方图、柏拉图、散布图、推移图、%GRR...等。
公式解说制程能力指数制程能力分析制程能力研究在于确认这些特性符合规格的程度，以保证制程成品不符规格的不良率在要求的水准之上，作为制程持续改善的依据。
制程能力研究的时机分短期制程能力研究及长期制程能力研究，短期着重在新产品及新制程的试作、初期生产、工程变更或制程设备改变等阶段；长期以量产期间为主。
制程能力指针 Cp 或 Cpk 之值在一产品或制程特性分配为常态且在管制状态下时，可经由常态分配之机率计算，换算为该产品或制程特性的良率或不良率，同时亦可以几 Sigma 来对照。
计数值统计数据的数量表示缺点及不良(Defects VS. Defectives)缺点代表一单位产品不符要求的点数，一单位产品不良可能有一个缺点或多个缺点，此为计点的品质指针。
例如描述一匹布或一铸件的品质，可用每公尺棉布有几个疵点，一铸件表面有几个气孔或砂眼来表达，无尘室中每立方公尺含微粒之个数，一片PCB有几个零件及几个焊点有缺点，一片按键有几个杂质、包风、印刷等缺点，这些都是以计点方式表示一单位产品的特性值。
不良代表一单位产品有不符要求的缺点，可能有一个或一个以上，此将产品分类为好与坏、良与不良及合格与不合格等所谓的通过－不通过(Go-NoGo)的衡量方式称为计件的品质指针。
例如单位产品必须以二分法来判定品质，不良的单位产品必须报废或重修，这是以计件方式来表示一单位产品的特值。
每单位缺点数及每百万机会缺点数(DPU VS. DPMO)一单位产品或制程的复杂程度与其发生缺点的机会有直接的关系，越复杂容易出现缺点；反之越简单越不容易出现缺点。
X-R控制图操作指南
精选ppt
2、收集数据
合理的子组大小、频率和数据
在控制时段内，按抽样容量/频率要求，收集产品工序 质量或过程特性数据125个或者100个，并按连续性将 数据分成25个子组，每个子组由4－5数据组成，每个 子组数据是在非常相似的生产条件下生产出来的，并 且相互之间不存在着系统的关系，因此，每组之间的 变差为普通原因造成的，对于所有的子组的样品应保 持恒定。
数据收集
精选ppt
2、收集数据
频率的选择
频率：在过程的初期研究中通常是连续
进行分组或很短时间间隔进行分组，检
查时间间隔内有否不稳定的因素存在。
当证明过程处于稳定时，子组间的时间
间隔可以增加。
分组频率大快了， 慢些！
精选ppt
3、 X-R图的位置及结构 1） X－R通常把数据栏位于X图和R 图的
UCL
精选ppt
X LCL
B）控制限之内的图形或趋势，当出现非随机有规律的图 形或趋势时，尽管所有极差都在控制限内，也表明出现 这种图形或趋势的时期内，过程质量异常或过程分布宽 度发生变化。
点链有下列现象之一表明过程已改变或出现这种趋势： a. 连续7点位于平均值的一侧； b. 连续7点上升(后点等于或大于前点)或下降； C、中心点一侧出现众多点（11点有10点，14点有12
3σ
σ
精选ppt
-σ -3σ
8、控制图报警程序和管理
当控制图出现警告信号时，由责任人员填写X-R控制
图异常报警表，交工艺人员作出分析并制定纠正措
施，质管部QA负责跟踪和考核。必要时，对超出控
制限的点确定为特殊原因引起的，必须对该点加以
删除，重新修订控制图，重新计算控制限。当控制
限变得越来越好时，应对此时的工艺参数形成文件
2、收集数据
合理的子组大小、频率和数据
在控制时段内，按抽样容量/频率要求，收集产品工序 质量或过程特性数据125个或者100个，并按连续性将 数据分成25个子组，每个子组由4－5数据组成，每个 子组数据是在非常相似的生产条件下生产出来的，并 且相互之间不存在着系统的关系，因此，每组之间的 变差为普通原因造成的，对于所有的子组的样品应保 持恒定。
数据收集
精选ppt
2、收集数据
频率的选择
频率：在过程的初期研究中通常是连续
进行分组或很短时间间隔进行分组，检
查时间间隔内有否不稳定的因素存在。
当证明过程处于稳定时，子组间的时间
间隔可以增加。
分组频率大快了， 慢些！
精选ppt
3、 X-R图的位置及结构 1） X－R通常把数据栏位于X图和R 图的
UCL
精选ppt
X LCL
B）控制限之内的图形或趋势，当出现非随机有规律的图 形或趋势时，尽管所有极差都在控制限内，也表明出现 这种图形或趋势的时期内，过程质量异常或过程分布宽 度发生变化。
点链有下列现象之一表明过程已改变或出现这种趋势： a. 连续7点位于平均值的一侧； b. 连续7点上升(后点等于或大于前点)或下降； C、中心点一侧出现众多点（11点有10点，14点有12
3σ
σ
精选ppt
-σ -3σ
8、控制图报警程序和管理
当控制图出现警告信号时，由责任人员填写X-R控制
图异常报警表，交工艺人员作出分析并制定纠正措
施，质管部QA负责跟踪和考核。必要时，对超出控
制限的点确定为特殊原因引起的，必须对该点加以
删除，重新修订控制图，重新计算控制限。当控制
限变得越来越好时，应对此时的工艺参数形成文件
SPC_过程能力控制
思考题：本公司的过程特性
• 质量数据：直通率，FOR，LRR（批拒收率），DR（不良率），不良品数，单 项不良品数，不良数，电流/电压值，尺寸，称重
• 制程参数：锡膏厚度，炉温（Peak温度、熔点以上保持时间），车间温、湿度 ，电批扭力，气压值，烙铁温度
• 生产数据：单位产量， Cycle Time（标准工时），耗料率/抛料率（报废率） ，结单率
特殊变异 (Special Variation) • 过程还不够稳定 • 需全检以保证质量
局部措施（Local Action） • 可改进约15%的制程问题 • 多由现场工作人员制定实施 • 一般成本较低
此过程变异在统计控制状态下, 其产品特性的分布有固定的分 布, 即: 位置、分布、形狀。
受控 vs. 失控
二、测量变差相对较小（测量系统的能力 保证）。
f(x)
68.27%
x
-1 µ +1
Normal Distribution
正
f(x)
态
分
95.45%
布
x
-2 µ +2
f(x)
-3
99.73%
x
µ
+3
正态分布
68.27%
0.135%
95.45% 99.73%
0.135%
-3σ -2σ -1σ μ
+1σ +2σ +3σ
i1
n
样本方差
样本标准差
n
2
(xi x)
S 2 i1
n 1
n
(xi x)2
S i1 n 1
为什么用样本估计总体的方差时，分母的n必须改为(n-1) ？
自由度（DF, Degree of Freedom）： 指当以样本的统计量来估计总体的参数时，样本中独立或能自由变化的 数据的个数称为该统计量的自由度。
SPC八大控制图自动生成表
过程能力分析
40
115.243
35 112.500 117.500
30
25
-6δ -5δ -4δ -3δ -2δ -δ +δ +2δ +3δ +4δ +5δ +6δ
Sigma分布 规范值 频率分布 正态分布
频率 20
15
10
5 0 0.000
20.000
40.000
60.000
80.000
100.000
120.000
140.000
X
Xቤተ መጻሕፍቲ ባይዱ
117.000 116.000 115.000 114.000
规范下限 LSL 规范上限 USL
X控制图
中心限 CL
113.000 112.000 111.000 110.000 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
通往初始面板
X-R图及过程能力分析
对比其他控制图 对照输入数据
生成报告
查看并填写报告
118.000
查看X-S图
查看中位数图
返回数据登入
子组容量 n 总组数 Count 总样本数 N 平均值 X 最大值 Max X 最小值 Min X 平均中位数 Mid X 规范上限 USL 中心限 CL 规范下限 LSL 上限值 UCL (X) 中心限 CL (X) 下限值 LCL (X) 上限值 UCL (R) 中心限 CL (R) 下限值 LCL (R) 偏度 Skewness 峰度 Kurtosis 预估不良率(PPM) 标准差 Std.Dev.= 标准差 Sigma= Pp= Ppk= Ca= Cp= CPU= CPL= Cpk= Grade= 5 25 125 115.2433 116.9600 112.9600 115.2572 117.5000 115.0000 112.5000 116.116 115.243 114.370 3.198 1.513 0.000 -0.1448 -0.1734 272.740 0.875 0.650 0.953 0.860 9.73% 1.281 1.157 1.406 1.157 C
CPK的计算
QE:
风险优等数 (RPN) = 严重度 * 发生率 * 难检度 页码:
制程名称/制程目的 预估失效模式 预估失效影响 严重度(S) 预估失效原因 发生率(O) 现行控 制 措 施 难 检 度 (D) RPN 建 议 控 制 措 施 责 任 人 完 成 日 期 状 态 改善后
Failure Mode Failure Mode of effect Failure Mode of cause Control(s) of cause (S*O*D) Control(s) Person Date 已采取之措施 [S] [O] [D] RPN
深蓝区域是距平均值小于一个标准差之内的数值范围。在正态分布中，此范围所占比率为 全部数值之 68%。对于正态分布，两个标准差之内（深蓝，蓝）的比率合起来为 95%。对于 正态分布，正负三个标准差之内（深蓝，蓝，浅蓝）的比率合起来为 99%。
意义
编辑
标准计算公式 假设有一组数值（皆为实数），其平均值为： 此组数值的标准差为： 样本标准差 在真实世界中，除非在某些特殊情况下，找到一个总体的真实的标准差是不现实的。 从一大组数值当中取出一样本数值组合 ，常定义其样本标准差： 样本方差 s^2 是对总体方差的无偏估计。s^2 中分母为 n - 1，是因为 s^2 的自由度为 n - 1 ， 这是由于存在约束条件。 这里示范如何计算一组数的标准差。例如一群儿童年龄的数值为 { 5,6,8,9 } ： 第一步，计算平均值 第二步，计算标准差
Ca=2*|规格中心值-实际中心值|/T=(（USL+LSL）/2-X)/(USL-LSL)/2,X 为实际平均数，USL 为最大要求值，LSL 为最小要求值， Cp=T/6 倍的标准差=（USL-LSL）/6δ，δ为标准差。 Cpk=（1-Ca）*Cp
SPC统计过程控制
如：5，9，10，4，7， R=10-4=6；
基本统计计量说明
6. 标准偏差s 、 指各数据偏离平均值的距离
s
2 ( X i X ) i 1 N
N
的平均数，反映数据离散程度，
总体标准偏差s
( X i X )
i 1
n
2
n 1
样本的标准偏差
如：5，9，10，4，7， 如：7，7，7，6，8， s=2.28； s=0.63；
式来影响过程的输出。如果系统内存在变差的特殊原因，随时 间的推移，过程的输出将不稳定。 如设备故障，原材料不合格，没有资格的操作工、未按照 作业指导书操作、工艺参数设定不对等。
二、基本的统计概念-波动 波动的区别 存在性 方向 影响大小 消除的难 易度 小 难
普通原因 始终
偏向
特殊原因 有时
或大或小 大
二、基本的统计概念-正态分布 正态分布-普通原因产生的变差
二、基本的统计概念-正态分布 正态分布-特殊原因产生的变差
二、基本的统计概念-CP&CPK指数 制程能力分析前提 过程处于统计稳定状态 过程中测量值服从正态分布 测量变差相对较小，一般可以忽略不计 工程及其他规范准确地代表顾客的需求， 设计目标值位于规范中心
的比率为99.73%。分散
幅度6 σ表示该工序具有 的实际加工精度。
CP值的大小可定量计算出该工序的不合格率，可反 映工序品质水平。
二、基本的统计概念-CP&CPK指数 CP值分析
过程刚好满 足规格要求 均值位移将 导致产品超 出规格
过程无法满 足规格要求 均值位移将 导致更多产 品超出规格
过程满足规格要求 小的值位移将导致 产品不会超出规格
基本统计计量说明
6. 标准偏差s 、 指各数据偏离平均值的距离
s
2 ( X i X ) i 1 N
N
的平均数，反映数据离散程度，
总体标准偏差s
( X i X )
i 1
n
2
n 1
样本的标准偏差
如：5，9，10，4，7， 如：7，7，7，6，8， s=2.28； s=0.63；
式来影响过程的输出。如果系统内存在变差的特殊原因，随时 间的推移，过程的输出将不稳定。 如设备故障，原材料不合格，没有资格的操作工、未按照 作业指导书操作、工艺参数设定不对等。
二、基本的统计概念-波动 波动的区别 存在性 方向 影响大小 消除的难 易度 小 难
普通原因 始终
偏向
特殊原因 有时
或大或小 大
二、基本的统计概念-正态分布 正态分布-普通原因产生的变差
二、基本的统计概念-正态分布 正态分布-特殊原因产生的变差
二、基本的统计概念-CP&CPK指数 制程能力分析前提 过程处于统计稳定状态 过程中测量值服从正态分布 测量变差相对较小，一般可以忽略不计 工程及其他规范准确地代表顾客的需求， 设计目标值位于规范中心
的比率为99.73%。分散
幅度6 σ表示该工序具有 的实际加工精度。
CP值的大小可定量计算出该工序的不合格率，可反 映工序品质水平。
二、基本的统计概念-CP&CPK指数 CP值分析
过程刚好满 足规格要求 均值位移将 导致产品超 出规格
过程无法满 足规格要求 均值位移将 导致更多产 品超出规格
过程满足规格要求 小的值位移将导致 产品不会超出规格
统计过程控制(SPC)案例分析
174
828
165．6
18
11
168
174
166
160
166
934
166．8
14
12
148
160
162
164
170
804
160．8
22
13
165
159
147
153
151
775
155．0
18
超限
14
164
166
164
170
164
828
165．6
6
15
162
158
154
168
172
814
162．8
18
16
49．52
49．49
49．53
49．47
49．502
0．06
23
49．50
49．47
49．48
49．56
49．50
49．502
0．09
24
49．48
49．50
49．49
49．53
49．50
49．500
0．05
25
49．50
49．55
49．57
49．54
49．46
49．524
0．11
总和值
平均值
1237．669
步骤七. 延长上述 图的控制线,进入控制用控制图阶段,对过程进行日常控制.
[例4]某厂生产一种零件，其长度要求为49．50±0．10mm，生产过程质量要求为Cp≥1，为对该过程实行连续监控，试设计 图。
某零件长度值数据表 （单位：mm）
序号
Xi1
828
165．6
18
11
168
174
166
160
166
934
166．8
14
12
148
160
162
164
170
804
160．8
22
13
165
159
147
153
151
775
155．0
18
超限
14
164
166
164
170
164
828
165．6
6
15
162
158
154
168
172
814
162．8
18
16
49．52
49．49
49．53
49．47
49．502
0．06
23
49．50
49．47
49．48
49．56
49．50
49．502
0．09
24
49．48
49．50
49．49
49．53
49．50
49．500
0．05
25
49．50
49．55
49．57
49．54
49．46
49．524
0．11
总和值
平均值
1237．669
步骤七. 延长上述 图的控制线,进入控制用控制图阶段,对过程进行日常控制.
[例4]某厂生产一种零件，其长度要求为49．50±0．10mm，生产过程质量要求为Cp≥1，为对该过程实行连续监控，试设计 图。
某零件长度值数据表 （单位：mm）
序号
Xi1
Xbar-R控制图-计算Cpk、Ppk用-MT制作
26 26
27 27
28 28
29 29
30 30
10.31
6 7 8
9.03 9.05 9.02 9.02 9.00 9.00 9.02 9.02 9.00 9.02 9.02 9.00 9.02 9.02 9.00 9.02 9.00 9.02 9.02 9.02 9.02 9.02 9.00 9.02 9.00 9.02 9.04 9.00 9.02 9.04 *样本容量小于7时，没有极差的下控制限 *For sample sizes of less than seven,there is no lower control 9.00 9.02 9.03 9.02 9.00 9.00 9.03 9.04 9.00 9.03 9.02 9.00 9.04 9.05 9.00 9.01 9.00 9.02 9.02 9.05 9.02 9.02 9.03 9.04 9.00 9.02 9.00 9.00 9.02 9.00 limit for ramges. 9.00 9.02 9.00 9.02 9.04 9.00 9.02 9.02 9.00 9.02 9.02 9.00 9.02 9.02 9.00 9.02 9.00 9.02 9.03 9.03 9.02 9.02 9.00 9.02 9.00 9.02 9.00 9.00 9.02 9.00 9.00 9.00 9.03 9.02 9.00 9.03 9.02 9.00 9.02 9.05 9.00 9.02 9.00 9.02 9.02 9.05 9.02 9.02 9.00 9.02 9.00 9.02 9.00 9.00 9.02 9.00 9.00 9.03 9.02 9.00 9.01 9.02 9.02 9.02 9.01 9.01 9.02 9.02 9.01 9.02 9.02 9.01 9.02 9.02 9.01 9.02 9.01 9.02 9.02 9.02 9.02 9.03 9.01 9.02 9.00 9.02 9.03 9.00 9.02 9.00 “
CPK-X-R图
冲孔 尺寸 11:00 15.900 16.000 16.000 16.100 16.200 80.20 16.04 0.300
16± 0.2
计算控制限日期 样本容量/频率 12:10 15.800 15.800 16.000 16.200 16.000 79.80 15.96 0.400 12:30 15.900 16.100 16.200 16.100 16.100 80.40 16.08 0.300 12:50 16.100 16.200 16.000 16.300 16.000 80.60 16.12 0.300 5件/1H 13:10 15.800 15.800 15.900 16.000 16.100 79.60 15.92 0.300
min(Cpk1,Cpk2)=
* 在确定过程能力之前，过程必须受控。 * 样本容量小于7时，没有极差的下控制线。 UCL X LCL UCL R LCL 16.18 16.18 16.18 16.18 16.18 16.18 15.99 15.99 15.99 15.99 15.99 15.99 15.80 15.80 15.80 15.80 15.80 15.80 0.6932857 0.6932857 0.6932857 0.6932857 0.6932857 0.6932857 0.329 0.329 0.329 0.329 0.329 0.329 0 0 0 0 0 0 16.18 16.18 15.99 15.99 15.80 15.80 0.693286 0.693286 0.329 0.329 0 0 16.18 16.18 16.18 15.99 15.99 15.99 15.80 15.80 15.80 0.693 0.6932857 0.6932857 0.329 0.329 0.329 0 0 0
过程能力均值-极差X-R控制图
注意！控制图中有点子出界，或出现7点链条情况!!!
过程能力尚可。
3 4.58 4.63 4.58 4.66 4.6125 0.0800 4 4.58 4.68 4.68 4.55 4.6225 0.1300 5 4.68 4.65 4.55 4.74 4.6550 0.1900 6 4.32 4.58 4.74 4.66 4.5750 0.4200 7 4.59 4.67 4.66 4.55 4.6175 0.1200 8 4.55 4.68 4.63 4.74 4.6500 0.1900 9 4.74 4.65 4.58 4.66 4.6575 0.1600 10 4.66 4.68 4.68 4.68 4.6750 0.0200 11 4.63 4.65 4.68 4.65 4.6525 0.0500 12 4.69 4.58 4.65 4.58 4.6250 0.1100 13 4.32 4.63 4.58 4.66 4.5475 0.3400 14 4.55 4.67 4.68 4.55 4.6125 0.1300 15 4.74 4.56 4.65 4.74 4.6725 0.1800 16 4.66 4.68 4.58 4.66 4.6450 0.1000 17 4.63 4.65 4.68 4.55 4.6275 0.1300 18 4.56 4.58 4.65 4.74 4.6325 0.1800 19 4.32 4.63 4.58 4.66 4.5475 0.3400 20 4.63 4.67 4.68 4.63 4.6525 0.0500 21 4.67 4.63 4.58 4.67 4.6375 0.0900 22 4.59 4.67 4.68 4.55 4.6225 0.1300 23 4.67 4.68 4.65 4.74 4.6850 0.0900 24 4.56 4.65 4.58 4.66 4.6125 0.1000 25 4.59 4.67 4.68 4.55 4.6225 0.1300