线性回归分析资料报告练习题

教学步骤及教学内容线性回归方程(参考公式：b＝∑i＝1nx i y i－n x y∑i＝1nx2i－n x2，a＝y－b x)1．实验测得四组(x，y)的值为(1,2)，(2,3)，(3,4)，(4,5)，则y与x之间的回归直线方程为()A.y^＝x＋1 B.y^＝x＋2 C.y^＝2x＋1 D.y^＝x－12．在比较两个模型的拟合效果时，甲、乙两个模型的相关指数R2的值分别约为0.96和0.85，则拟合效果好的模型是()A．甲B．乙C．甲、乙相同D．不确定3．某化工厂为预测产品的回收率y，需要研究它和原料有效成分含量x之间的相关关系，现取8对观测值，计算，得∑8i＝1x i＝52，∑8i＝1y i＝228，∑8i＝1x2i＝478，∑8i＝1x i y i＝1849，则其线性回归方程为()A.y^＝11.47＋2.62x B.y^＝－11.47＋2.62xC.y^＝2.62＋11.47x D.y^＝11.47－2.62x4．下表是某厂1～4月份用水量(单位：百吨)的一组数据：月份x 123 4用水量y 4.543 2.5由散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归直线方程是y^＝－0.7x＋a，则a等于______．5．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此作了四次试验，得到的数据如下：零件的个数x(个)234 5加工的时间y(小时) 2.534 4.5(1)在给定的坐标系中画出表中数据的散点图；(2)求出y关于x的线性回归方程y^＝bx＋a，并在坐标系中画出回归直线；(3)试预测加工10个零件需要多少小时？作业布置家长意见家长签名：2013 年＿月＿日（第＿次）审阅人：1。

统计学一元线性回归分析练习题一、内容提要本章介绍了回归分析的基本思想与基本方法。

首先，本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始，建立了回归分析的基本思想。

总体回归函数是对总体变量间关系的定量表述，由总体回归模型在若干基本假设下得到，但它只是建立在理论之上，在现实中只能先从总体中抽取一个样本，获得样本回归函数，并用它对总体回归函数做出统计推断。

本章的一个重点是如何获取线性的样本回归函数，主要涉及到普通最小二乘法的学习与掌握。

同时，也介绍了极大似然估计法以及矩估计法。

本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断，即进行所谓的统计检验。

统计检验包括两个方面，一是先检验样本回归函数与样本点的“拟合优度”，第二是检验样本回归函数与总体回归函数的“接近”程度。

后者又包括两个层次：第一，检验解释变量对被解释变量是否存在着显著的线性影响关系，通过变量的t检验完成；第二，检验回归函数与总体回归函数的“接近”程度，通过参数估计值的“区间检验”完成。

本章还有三方面的内容不容忽视。

其一，若干基本假设。

样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。

其二，参数估计量统计性质的分析，包括小样本性质与大样本性质，尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。

Goss-markov定理表明OLS估计量是最佳线性无偏估计量。

其三，运用样本回归函数进行预测，包括被解释变量条件均值与个值的预测，以及预测置信区间的计算及其变化特征。

二、典型例题分析例1、令kids表示一名妇女生育孩子的数目，educ 表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为kids??0??1educ??随机扰动项?包含什么样的因素？它们可能与教育水平相关吗？上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。

§1 回归分析一、基础过关1. 下列变量之间的关系就是函数关系的就是ﻩﻩﻩﻩﻩ( )A.已知二次函数y=ax2＋bx+c,其中a,c就是已知常数,取b为自变量,因变量就是这个函数的判别式Δ=b２-4acB、光照时间与果树亩产量C、降雪量与交通事故发生率D.每亩施用肥料量与粮食产量2. 在以下四个散点图中,其中适用于作线性回归的散点图为ﻩ( )A.①②Ｂ.①③ﻩ C.②③ﻩＤ.③④3、下列变量中,属于负相关的就是ﻩﻩﻩﻩﻩ( )A.收入增加,储蓄额增加Ｂ、产量增加,生产费用增加C.收入增加,支出增加D、价格下降,消费增加4、已知对一组观察值(xｉ,y i)作出散点图后确定具有线性相关关系,若对于y＝bx＋a,求得ｂ＝0、５1,错误!＝61、75,错误!＝3８、14,则线性回归方程为Ａ.y＝0.51x＋6.６５ﻩﻩﻩ B.ｙ＝６、65x＋0.51C.y＝0、５１x＋42、30ﻩﻩＤ、y＝42、３0x＋0.５15、对于回归分析,下列说法错误的就是ﻩﻩ( )A.在回归分析中,变量间的关系若就是非确定关系,那么因变量不能由自变量唯一确定B.线性相关系数可以就是正的,也可以就是负的C、回归分析中,如果ｒ2＝１,说明ｘ与ｙ之间完全相关D、样本相关系数ｒ∈(-1,１)６. 下表就是x与y之间的一组数据,则y关于x的回归方程必过ﻩﻩﻩ()A、点(2,3) ﻩﻩB、点(1、５,４)C、点(２.5,4) ﻩﻩＤ、点(2、5,5)7.若线性回归方程中的回归系数ｂ=0,则相关系数r=__＿＿____.二、能力提升８、若施化肥量x(kg)与小麦产量ｙ(kg)之间的线性回归方程为ｙ=2５0+4ｘ,当施化肥量为5０kg时,预计小麦产量为＿＿_____＿ｋg.9. 某车间为了规定工时定额,需确定加工零件所花费的时间,为此做了４次试验,得到的数据如下:若加工时间y(1)求加工时间与零件个数的线性回归方程;(2)试预报加工10个零件需要的时间.1０、在一段时间内,分５次测得某种商品的价格x (万元)与需求量y (t)之间的一组数据为:已知错误!x ｉy i ＝错误!错误!(1)画出散点图;(2)求出y 对x 的线性回归方程;(３)如果价格定为1、9万元,预测需求量大约就是多少？(精确到0、０１ t)、1１、某运动员训练次数与运动成绩之间的数据关系如下:(１)(２)求出回归方程;(3)计算相关系数并进行相关性检验;(4)试预测该运动员训练47次及55次的成绩、答案1.A2.B3.D 4、A ５、D 6.C 7.０ 8、y =－11、3+３6.９５ｘ ９.４5０10、解 (1)由表中数据,利用科学计算器得错误!=错误!＝3、5,＼ｘ＼ｔo(ｙ)=2.5+3＋４+4、５４=3、5,错误!x i ｙi =52、５,错误!x 错误!＝5４, b ＝错误!=5２、５－4×3、5×３.5５４－４×3.５2=0.7,a ＝错误!－ｂ错误!=1.0５,因此,所求的线性回归方程为y =０、７x ＋１、05、(2)将ｘ＝1０代入线性回归方程,得ｙ＝０、7×10+１、０５＝8、05(小时),即加工10个零件的预报时间为8、05小时、１１、解 (1)散点图如下图所示:(2)因为错误!＝错误!×9=1.8,错误!＝错误!×37＝7、4,错误!x i y ｉ＝62,错误!x 2i ＝16、６, 所以b =错误!=错误!=－11、5,a =错误!－b 错误!=7.4＋11、5×1、8＝28.1, 故y 对x 的线性回归方程为y ＝28、1-11.５x 、 (3)y ＝28.1－１１、5×1、9=6.25(ｔ).所以,如果价格定为1、9万元,则需求量大约就是6、25 t 、1２、解 (1)作出该运动员训练次数ｘ与成绩y 之间的散点图,如下图所示,由散点图可知,它们之间具有线性相关关系.(2)列表计算:次数ｘi成绩y i x2i ｙ2ｉx i y i3０３３34 1 0８9 1 1５6 1 12２3537 1 225 1 3691295３73９１369１52１1 44３3９４2 1 521１７64１63８４446 1 ９362 １１62 02446４8 2 116２3042 ２085０５1 2 50０ 2 601２5５0由上表可求得x＝39、25,错误!＝４0、８７5,错误!ｘ2i＝12 656,错误!y2i=１３731,错误!xｉyｉ＝１3180,∴b=错误!≈１、04１5,a＝ｙ－b错误!＝-０、00３88,∴线性回归方程为y=1、0４15x-0.003 88、(3)计算相关系数r=０、９９2 7,因此运动员的成绩与训练次数两个变量有较强的相关关系、(4)由上述分析可知,我们可用线性回归方程y＝1、041 ５x-０、０03 ８8作为该运动员成绩的预报值.将ｘ＝4７与ｘ＝5５分别代入该方程可得y＝４9与y＝５7、故预测该运动员训练4７次与55次的成绩分别为4９与57、1３.解∵ｓx=错误!,s y=错误!,∴l xyn＝rlｘyn·lｙyn=0、5×7、６×１５、2=5７、76、∴β1=＼f(＼f(ｌxy,ｎ),＼f(l xy,ｎ))＝57、７６7、62=1,β0＝错误!-β1错误!=7２-1×172＝－１00、故由身高估计平均体重的回归方程为ｙ=x-1００、由ｘ,y位置的对称性,得b=错误!=错误!＝0.25,∴a＝错误!-b错误!=17２-0、25×72＝154、故由体重估计平均身高的回归方程为x＝0、25y＋154、1.３可线性化的回归分析一、基础过关１. 某商品销售量y(件)与销售价格x(元/件)负相关,则其线性回归方程可能就是()A、y＝－10x＋２０0 B.y=１0x+2０0 Ｃ.y=－10x－２00ﻩﻩＤ、y＝１0ｘ-200２、在线性回归方程y=ａ+bx中,回归系数b表示ﻩﻩﻩﻩﻩ()A、当ｘ＝0时,ｙ的平均值Ｂ、x变动一个单位时,ｙ的实际变动量C、y变动一个单位时,x的平均变动量D、x变动一个单位时,y的平均变动量3.对于指数曲线ｙ＝a e bｘ,令u=lｎy,c=ｌn a,经过非线性化回归分析之后,可以转化成的形式为ﻩ()A.u=ｃ＋bｘB.u＝b＋cxＣ、ｙ=b+cxﻩD、ｙ＝c+bx4、下列说法错误的就是()A、当变量之间的相关关系不就是线性相关关系时,也能直接用线性回归方程描述它们之间的相关关系B.把非线性回归化为线性回归为我们解决问题提供一种方法Ｃ.当变量之间的相关关系不就是线性相关关系时,也能描述变量之间的相关关系Ｄ.当变量之间的相关关系不就是线性相关关系时,可以通过适当的变换使其转换为线性关系,将问题化为线性回归分析问题来解决5. 每一吨铸铁成本y c(元)与铸件废品率x％建立的回归方程ｙｃ=56+8ｘ,下列说法正确的就是()Ａ、废品率每增加１%,成本每吨增加64元 B.废品率每增加１％,成本每吨增加8%C.废品率每增加１％,成本每吨增加８元Ｄ、如果废品率增加1%,则每吨成本为56元６、为了考察两个变量ｘ与y之间的线性相关性,甲、乙两个同学各自独立地做1０次与１5次试验,并且利用线性回归方法,求得回归直线分别为l１与l2、已知在两个人的试验中发现对变量x的观测数据的平均值恰好相等,都为s,对变量y的观测数据的平均值也恰好相等,都为t.那么下列说法正确的就是( )A、直线l1与l２有交点(s,t) B.直线l1与l2相交,但就是交点未必就是点(ｓ,t)C.直线l1与l２由于斜率相等,所以必定平行D.直线l１与ｌ2必定重合二、能力提升７、研究人员对10个家庭的儿童问题行为程度(X)及其母亲的不耐心程度(Y)进行了评价结果如下,家庭1,2,３,4,5,6,7,8,9,１0,儿童得分:72,４０,5２,87,39,95,１2,６４,49,４６,母亲得分:７９,6２,53,89,8１,90,１0,82,7８,70、下列哪个方程可以较恰当的拟合ﻩﻩﻩﻩﻩﻩ()Ａ、y =0.７７１ 1x ＋26、528 B.ｙ=36.9５8ｌｎ ｘ－７４、604 Ｃ、y ＝1、177 ８x 1、014 ５ D.y =20、９24ｅ0、019 3x 8、 已知ｘ,y 之间的一组数据如下表:则ｙ与ｘ9. 已知线性回归方程为ｙ＝0.50ｘ-0.8１,则x ＝25时,ｙ的估计值为________、 10、在一次抽样调查中测得样本的5个样本点,数值如下表:(1)建立y 与x 之间的回归方程(2)当8x 时,y 大约就是多少11、某地区六年来轻工业产品利润总额y 与年次x 的试验数据如下表所示:由经验知,0y 关于x 的回归方程、(保留三位有效数字)三、探究与拓展1２.某商店各个时期的商品流通率y (％)与商品零售额ｘ(万元)资料如下:y 6 4、6 4 3、2 2、8x 19、５ 21、523.52５.５2７、5 y２、5 ２、4 ２、３ 2、２2、1散点图显示出x 与y ,流通率y 决定于商品的零售额x ,体现着经营规模效益,假定它们之间存在关系式:y ＝a ＋＼f(b,x )、试根据上表数据,求出a 与ｂ的估计值,并估计商品零售额为30万元时的商品流通率、ﻬ答案１、A 2、D 3、Ａ 4、A 5、C 6.A 7、B ８、(1、１6,2、４) 9、11、691０、解 画出散点图如图(1)所示,观察可知y 与x 近似就是反比例函数关系、设ｙ＝k x (k ≠0),令t =1x,则y ＝kt 、可得到y 关于t 的数据如下表:t 4 2 10、５ 0、25y16１２521画出散点图如图(2)所示,,易得: b =错误!≈４、13４ ４, a ＝错误!-b 错误!≈0、7９1 7, 所以ｙ＝4、134 4t ＋0、791 7,所以ｙ与x 的回归方程就是y ＝4、１3４ ４x +0.791 7、11、解 对y ＝ab ｘe 0两边取对数,得ｌn y =ln a e 0＋x ln b ,令z =ln y , 则ｚ与x 的数据如下表:由z =l ｎ ａｅ0+x ln 0即z =2、38+0.04７ 7ｘ,所以y =１0、8×1.０5x 、 １2、解 设u =＼ｆ(1,x ),则ｙ≈ａ+bu ,得下表数据:进而可得n =1０,＼x ＼to(ｕ)≈0、０60 4,错误!＝3、21,＼i ＼su(i ＝1,１０,ｕ)2i -10错误!2≈0、004 55７ 3,错误!i y i -1０错误! 错误!≈0、２56 ３5, b ≈０、2５6 350、０04 55７ 3≈56、２5, a ＝错误!－b ·错误!≈－0、18７ 5,所求的回归方程为ｙ=-0、18７ 5＋5６.２5x、当x ＝30时,y =1、687 5,即商品零售额为３０万元时,商品流通率为1、68７ 5%、。

第9章一元线性回归练习题一．选择题1．具有相关关系的两个变量的特点是（）A．一个变量的取值不能由另一个变量唯一确定B．一个变量的取值由另一个变量唯一确定C．一个变量的取值增大时另一个变量的取值也一定增大D．一个变量的取值增大时另一个变量的取值肯定变小2．下面的各问题中，哪个不是相关分析要解决的问题A．判断变量之间是否存在关系B．判断一个变量数值的变化对另一个变量的影响C．描述变量之间的关系强度 D.判断样本所反映的变量之间的关系能否代表总体变量之间的关系3.根据下面的散点图，可以判断两个变量之间存在（）A.正线性相关关系B. 负线性相关关系C. 非线性关系D. 函数关系4.下面的陈述哪一个是错误的（）A. 相关系数是度量两个变量之间线性关系强度的统计量B．相关系数是一个随机变量C．相关系数的绝对值不会大于1D．相关系数不会取负值5.根据你的判断，下面的相关系数取值哪一个是错误的（）A. -0.86B. 0.78C. 1.25D. 06.如果相关系数r=0,则表明两个变量之间（）A.相关程度很低B. 不存在任何关系C．不存在线性相关关系D.存在非线性关系7.下列不属于相关关系的现象是（）A.银行的年利息率与贷款总额B.居民收入与储蓄存款C.电视机的产量与鸡蛋产量D.某种商品的销售额与销售价格8.设产品产量与产品单位成本之间的线性相关系数为-0.87，这说明二者之间存在着（）A. 高度相关B.中度相关C.低度相关D.极弱相关9.在回归分析中，被预测或被解释的变量称为（）A.自变量B.因变量C.随机变量D.非随机变量10.对两变量的散点图拟合最好的回归线，必须满足一个基本的条件是（）A.2ˆ()yy∑-最小B.2)(ˆyy∑-最大C.2ˆ()yy∑-最大D.2)(ˆyy∑-最小11. 下列哪个不属于一元回归中的基本假定（）A.误差项i ε服从正态分布B. 对于所有的X ，方差都相同C. 误差项i ε相互独立D. 0)ˆ=-i i yy E （ 12.如果两个变量之间存在着负相关，指出下列回归方程中哪个肯定有误（ ）A.x y75.025ˆ-= B. x y 86.0120ˆ+-= C. x y 5.2200ˆ-= D. x y 74.034ˆ--= 13.对不同年份的产品成本拟合的直线方程为,75.1280ˆx y-=y 表示产品成本，x 表示不同年份，则可知（ ）A.时间每增加一个单位，产品成本平均增加1.75个单位B. 时间每增加一个单位，产品成本平均下降1.75个单位C.产品成本每变动一个单位，平均需要1.75年时间D. 产品成本每减少一个单位，平均需要1.75年时间 14.在回归分析中，F 检验主要是用来检验（ ）A ．相关关系的显著性 B.回归系数的显著性 C. 线性关系的显著性D.估计标准误差的显著性15.说明回归方程拟合优度的统计量是（ ）A. 相关系数B.回归系数C. 判定系数D. 估计标准误差16.已知回归平方和SSR=4854,残差平方和SSE=146,则判定系数R 2=( ) A.97.08% B.2.92% C.3.01% D. 33.25% 17. 判定系数R2值越大，则回归方程（ ）A 拟合程度越低B 拟合程度越高C 拟合程度有可能高，也有可能低D 用回归方程进行预测越不准确 18. 居民收入与储蓄额之间的相关系数可能是（ ） A -0.9247 B 0.9247 C -1.5362 D 1.536219.在对一元回归方程进行显著性检验时，得到判定系数R 2=0.80,关于该系数的说法正确的是（ ）A. 该系数越大，则方程的预测效果越好B. 该系数越大，则由回归方程所解释的因变量的变差越多C. 该系数越大，则自变量的回归对因变量的相关关系越显著D. 该回归方程中自变量与因变量之间的相关系数可能小于0.8 20.下列方程中肯定错误的是（ ）A. x y48.015ˆ-=，r=0.65 B. x y 35.115ˆ--=, r= - 0.81 C. x y85.025ˆ+-=, r=0.42 D. x y 56.3120ˆ-=, r= - 0.96 21. 若两个变量存在负相关关系，则建立的一元线性回归方程的判定系数R 2的取值范围是（ ）A.【0，1】B. 【-1，0】C. 【-1，1】D.小于0的任意数二． 填空题1.当从某一总体中抽取了一样本容量为30的样本，并计算出某两个变量的相关系数为0.8时，我们是否可认为这两个变量存在着强相关性（不能 ） ，理由是（因为该相关系数为样本计算出的相关系数，它的大小受样本数据波动的影响，它是否显著尚需检验 ）。

§1回归分析一、基础过关1．下列变量之间的关系是函数关系的是() A．已知二次函数y＝ax2＋bx＋c，其中a，c是已知常数，取b为自变量，因变量是这个函数的判别式Δ＝b2－4acB．光照时间和果树亩产量C．降雪量和交通事故发生率D．每亩施用肥料量和粮食产量2．在以下四个散点图中，其中适用于作线性回归的散点图为()A．①②B．①③C．②③D．③④3．下列变量中，属于负相关的是() A．收入增加，储蓄额增加B．产量增加，生产费用增加C．收入增加，支出增加D．价格下降，消费增加4．已知对一组观察值(x i，y i)作出散点图后确定具有线性相关关系，若对于y＝bx＋a，求得b＝0.51，x＝61.75，y＝38.14，则线性回归方程为A．y＝0.51x＋6.65 B．y＝6.65x＋0.51C．y＝0.51x＋42.30 D．y＝42.30x＋0.515．对于回归分析，下列说法错误的是()A．在回归分析中，变量间的关系若是非确定关系，那么因变量不能由自变量唯一确定B．线性相关系数可以是正的，也可以是负的C．回归分析中，如果r2＝1，说明x与y之间完全相关D．样本相关系数r∈(－1,1)6．下表是x和y之间的一组数据，则y关于x的回归方程必过() ArrayA.点(2,3) B．点(1.5,4)C．点(2.5,4) D．点(2.5,5)7．若线性回归方程中的回归系数b＝0，则相关系数r＝________.二、能力提升8．若施化肥量x(kg)与小麦产量y(kg)之间的线性回归方程为y＝250＋4x，当施化肥量为50 kg时，预计小麦产量为________ kg.9．某车间为了规定工时定额，需确定加工零件所花费的时间，为此做了4次试验，得到的数据如下：若加工时间y(1)求加工时间与零件个数的线性回归方程；(2)试预报加工10个零件需要的时间．10．在一段时间内，分5次测得某种商品的价格x (万元)和需求量y (t)之间的一组数据为：已知∑5i ＝1x i y i ＝62，∑i ＝1x 2i ＝16.6. (1)画出散点图；(2)求出y 对x 的线性回归方程；(3)如果价格定为1.9万元，预测需求量大约是多少？(精确到0.01 t)． 11．某运动员训练次数与运动成绩之间的数据关系如下：(1)(2)求出回归方程；(3)计算相关系数并进行相关性检验； (4)试预测该运动员训练47次及55次的成绩．答案1．A 2.B 3.D 4.A 5.D 6.C 7．0 8.y ＝－11.3＋36.95x 9．45010．解 (1)由表中数据，利用科学计算器得x ＝2＋3＋4＋54＝3.5， y ＝2.5＋3＋4＋4.54＝3.5，∑4i ＝1x i y i ＝52.5，∑4i ＝1x 2i ＝54， b ＝∑4i ＝1x i y i －4x y ∑4i ＝1x 2i －4x 2＝52.5－4×3.5×3.554－4×3.52＝0.7，a ＝y －b x ＝1.05，因此，所求的线性回归方程为y ＝0.7x ＋1.05.(2)将x ＝10代入线性回归方程，得y ＝0.7×10＋1.05＝8.05(小时)，即加工10个零件的预报时间为8.05小时．11．解 (1)散点图如下图所示：(2)因为x ＝15×9＝1.8，y ＝15×37＝7.4，∑5i ＝1x i y i ＝62，∑5i ＝1x 2i ＝16.6， 所以b ＝∑5i ＝1x i y i －5x y ∑5i ＝1x 2i －5x 2＝62－5×1.8×7.416.6－5×1.82＝－11.5，a ＝y －b x ＝7.4＋11.5×1.8＝28.1， 故y 对x 的线性回归方程为y ＝28.1－11.5x . (3)y ＝28.1－11.5×1.9＝6.25(t)．所以，如果价格定为1.9万元，则需求量大约是6.25 t.12．解 (1)作出该运动员训练次数x 与成绩y 之间的散点图，如下图所示，由散点图可知，它们之间具有线性相关关系．(2)列表计算：次数x i 成绩y i x 2i y 2i x i y i 30 30 900 900 900 33 34 1 089 1 156 1 122 35 37 1 225 1 369 1 295 37 39 1 369 1 521 1 443 39 42 1 521 1 764 1 638 44 46 1 936 2 116 2 024 46 48 2 116 2 304 2 208 50512 5002 6012 550由上表可求得x ＝39.25，y ＝40.875，∑8i ＝1x 2i ＝12 656，∑8i ＝1y 2i ＝13 731， ∑8i ＝1x i y i ＝13 180，∴b ＝∑8i ＝1x i y i －8x y∑8i ＝1x 2i －8x2≈1.041 5，a ＝y －b x ＝－0.003 88，∴线性回归方程为y ＝1.041 5x －0.003 88.(3)计算相关系数r ＝0.992 7，因此运动员的成绩和训练次数两个变量有较强的相关关系． (4)由上述分析可知，我们可用线性回归方程y ＝1.041 5x －0.003 88作为该运动员成绩的预报值． 将x ＝47和x ＝55分别代入该方程可得y ＝49和y ＝57.故预测该运动员训练47次和55次的成绩分别为49和57. 13．解 ∵s x ＝l xyn，s y ＝l xy n， ∴l xyn＝r l xy n ·l yyn ＝0.5×7.6×15.2＝57.76.∴β1＝l xyn l xy n＝57.767.62＝1， β0＝y －β1x ＝72－1×172＝－100.故由身高估计平均体重的回归方程为y ＝x －100.由x ，y 位置的对称性，得b ＝l xyn l xy n ＝57.7615.22＝0.25，∴a ＝x －b y ＝172－0.25×72＝154.故由体重估计平均身高的回归方程为x ＝0.25y ＋154.1.3 可线性化的回归分析一、基础过关1． 某商品销售量y (件)与销售价格x (元/件)负相关，则其线性回归方程可能是( )A ．y ＝－10x ＋200B ．y ＝10x ＋200C ．y ＝－10x －200D ．y ＝10x －200 2． 在线性回归方程y ＝a ＋bx 中，回归系数b 表示( )A ．当x ＝0时，y 的平均值B ．x 变动一个单位时，y 的实际变动量C ．y 变动一个单位时，x 的平均变动量D ．x 变动一个单位时，y 的平均变动量3． 对于指数曲线y ＝a e bx ，令u ＝ln y ，c ＝ln a ，经过非线性化回归分析之后，可以转化成的形式为 ( )A ．u ＝c ＋bxB ．u ＝b ＋cxC ．y ＝b ＋cxD ．y ＝c ＋bx4． 下列说法错误的是( )A ．当变量之间的相关关系不是线性相关关系时，也能直接用线性回归方程描述它们之间的相关关系B ．把非线性回归化为线性回归为我们解决问题提供一种方法C ．当变量之间的相关关系不是线性相关关系时，也能描述变量之间的相关关系D ．当变量之间的相关关系不是线性相关关系时，可以通过适当的变换使其转换为线性关系，将问题化为线性回归分析问题来解决5． 每一吨铸铁成本y c (元)与铸件废品率x %建立的回归方程y c ＝56＋8x ，下列说法正确的是 ( )A ．废品率每增加1%，成本每吨增加64元B ．废品率每增加1%，成本每吨增加8%C ．废品率每增加1%，成本每吨增加8元D ．如果废品率增加1%，则每吨成本为56元 6． 为了考察两个变量x 和y 之间的线性相关性，甲、乙两个同学各自独立地做10次和15次试验，并且利用线性回归方法，求得回归直线分别为l 1和l 2.已知在两个人的试验中发现对变量x 的观测数据的平均值恰好相等，都为s ，对变量y 的观测数据的平均值也恰好相等，都为t .那么下列说法正确的是 ( ) A ．直线l 1和l 2有交点(s ，t ) B ．直线l 1和l 2相交，但是交点未必是点(s ，t ) C ．直线l 1和l 2由于斜率相等，所以必定平行 D ．直线l 1和l 2必定重合 二、能力提升7． 研究人员对10个家庭的儿童问题行为程度(X )及其母亲的不耐心程度(Y )进行了评价结果如下，家庭1,2,3,4,5,6,7,8,9,10，儿童得分：72,40,52,87,39,95,12,64,49,46，母亲得分：79,62,53,89,81,90,10,82,78,70. 下列哪个方程可以较恰当的拟合( )A．y＝0.771 1x＋26.528 B．y＝36.958ln x－74.604C．y＝1.177 8x1.014 5 D．y＝20.924e0.019 3x8．已知x，y之间的一组数据如下表：则y与x9．已知线性回归方程为y＝0.50x－0.81，则x＝25时，y的估计值为________．10．在一次抽样调查中测得样本的5个样本点，数值如下表：（1）建立y与xx 时，y大约是多少（2）当811．某地区六年来轻工业产品利润总额y与年次x的试验数据如下表所示：y关于x的回归方程．(保留三位有效数字)三、探究与拓展12．某商店各个时期的商品流通率y(%)和商品零售额x(万元)资料如下：散点图显示出x 与y y 决定于商品的零售额x ，体现着经营规模效益，假定它们之间存在关系式：y ＝a ＋bx .试根据上表数据，求出a 与b 的估计值，并估计商品零售额为30万元时的商品流通率．答案1．A 2.D 3.A 4.A 5.C 6.A 7.B 8．(1.16,2.4) 9.11.6910．解 画出散点图如图(1)所示，观察可知y 与x 近似是反比例函数关系．设y ＝k x (k ≠0)，令t ＝1x，则y ＝kt .可得到y 关于t 的数据如下表：t 4 2 1 0.5 0.25 y1612521画出散点图如图(2)得：b ＝∑5i ＝1t i y i －5t y ∑5i ＝1t 2i －5t 2≈4.134 4，a ＝y －b t ≈0.791 7， 所以y ＝4.134 4t ＋0.791 7， 所以y 与x 的回归方程是y ＝4.134 4x＋0.791 7. 11．解 对y ＝ab x e 0两边取对数，得ln y ＝ln a e 0＋x ln b ，令z ＝ln y ， 则z 与x 的数据如下表：x 1 2 3 4 5 6 z2.432.472.522.572.612.67由z ＝ln a e 0＋x ln b 0即z ＝2.38＋0.047 7x ，所以y ＝10.8×1.05x . 12．解 设u ＝1x，则y ≈a ＋bu ，得下表数据：进而可得n ＝10，u ≈0.060 4，y ＝3.21，∑i ＝110u 2i －10u 2≈0.004 557 3， ∑i ＝110u i y i －10u y ≈0.256 35，b ≈0.256 350.004 557 3≈56.25， a ＝y －b ·u ≈－0.187 5，所求的回归方程为y ＝－0.187 5＋56.25x.当x ＝30时，y ＝1.687 5，即商品零售额为30万元时，商品流通率为1.687 5%.。

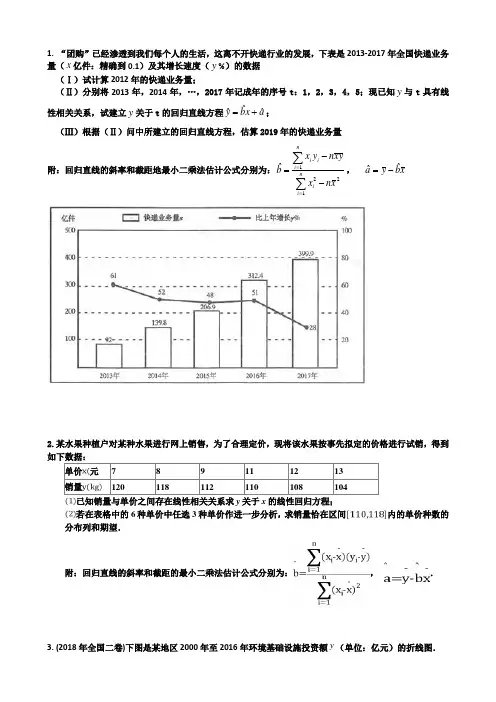
1. “团购”已经渗透到我们每个人的生活，这离不开快递行业的发展，下表是2013-2017年全国快递业务量（x 亿件：精确到0.1）及其增长速度（y %）的数据（Ⅰ）试计算2012年的快递业务量；（Ⅱ）分别将2013年，2014年，…，2017年记成年的序号t ：1，2，3，4，5；现已知y 与t 具有线性相关关系，试建立y 关于t 的回归直线方程a x b yˆˆˆ+=； （Ⅲ）根据（Ⅱ）问中所建立的回归直线方程，估算2019年的快递业务量附：回归直线的斜率和截距地最小二乘法估计公式分别为：∑∑==--=ni ini ii x n xy x n yx b1221ˆ， x b y aˆˆ-=2.某水果种植户对某种水果进行网上销售，为了合理定价，现将该水果按事先拟定的价格进行试销，得到如下数据：单价元 7 8 9 11 12 13 销量120118112110108104已知销量与单价之间存在线性相关关系求y 关于x 的线性回归方程； 若在表格中的6种单价中任选3种单价作进一步分析，求销量恰在区间内的单价种数的分布列和期望．附：回归直线的斜率和截距的最小二乘法估计公式分别为：， ．3. (2018年全国二卷)下图是某地区2000年至2016年环境基础设施投资额y （单位：亿元）的折线图．为了预测该地区2018年的环境基础设施投资额，建立了y 与时间变量t 的两个线性回归模型．根据2000年至2016年的数据（时间变量t 的值依次为1217，，…，）建立模型①：ˆ30.413.5y t =-+；根据2010年至2016年的数据（时间变量t 的值依次为127，，…，）建立模型②：ˆ9917.5y t =+． （1）分别利用这两个模型，求该地区2018年的环境基础设施投资额的预测值； （2）你认为用哪个模型得到的预测值更可靠？并说明理由．4.(2014年全国二卷) 某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：年份 2007 2008 2009 2010 2011 2012 2013 年份代号t 1 2 3 4 5 6 7 人均纯收入y 2.93.33.64.44.85.25.9（Ⅰ）求y 关于t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121niii ni i t t y y b t t ∧==--=-∑∑，ˆˆay bt =-5（2019 2卷）18．11分制乒乓球比赛，每赢一球得1分，当某局打成10∶10平后，每球交换发球权，先多得2分的一方获胜，该局比赛结束．甲、乙两位同学进行单打比赛，假设甲发球时甲得分的概率为0.5，乙发球时甲得分的概率为0.4，各球的结果相互独立．在某局双方10∶10平后，甲先发球，两人又打了X 个球该局比赛结束．(1)求P(X＝2)；(2)求事件“X＝4且甲获胜”的概率．。

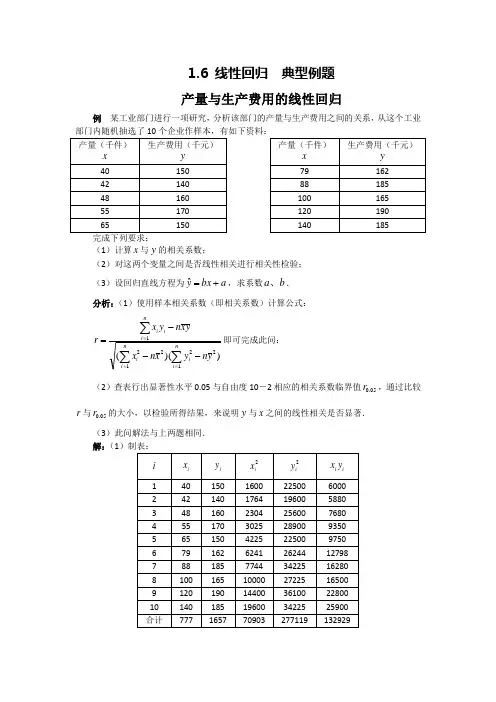
1.6 线性回归 典型例题 产量与生产费用的线性回归例 某工业部门进行一项研究，分析该部门的产量与生产费用之间的关系，从这个工业部门内随机抽选了10个企业作样本，有如下资料：完成下列要求：（1）计算x 与y 的相关系数；（2）对这两个变量之间是否线性相关进行相关性检验；（3）设回归直线方程为a bx y+=ˆ，求系数b a 、． 分析：（1）使用样本相关系数（即相关系数）计算公式：))((1222121∑∑∑===---=ni i n i i ni ii y n y x n x yx n yx r 即可完成此问：（2）查表行出显著性水平0.05与自由度10－2相应的相关系数临界值05.0r ，通过比较r 与05.0r 的大小，以检验所得结果，来说明y 与x 之间的线性相关是否显著．（3）此问解法与上两题相同．解：（1）制表：;806.0)7.16510277119)(7.771070903(7.1657.771013292922≈⨯-⨯-⨯⨯-=r即x 与y 的相关系数806.0≈r ；（2）查表显著性水平0.05，自由度10－2＝8相应的相关系数临界值6319.005.0=r ；因为，05.0r r >，所以，可以认为x 与y 之间具有线性相关关系．（3）;397.07.7710709037.1657.77101329292≈⨯-⨯⨯-=b .8.1347.77397.07.165=⨯-=a说明：如果会使用含统计的科学计算器，能简单得到∑∑∑∑∑-====10110110110110122,,,,,i i i i i ii iiiiy x y x y x 这些量，就无需有制表这一步，直接算出结果就行了制表的目的是为了准确无误而快速有效地得到r 和b 的值．顺便值得一提的是：电脑中的许多应用软件，特别是表格类软件是提供统计计算函数的，用起来非常方便．产品产量与单位成本的线性回归分析分析：这是一个实际应用的回归分析问题，其实就是找出回归方程，通过回归直线方程来分析产品产量与单位成本的关系．解：设回归直线方程为,ˆa bx y+=∑∑=======61121481,79,716426,621i ni i i i y x x y x ，所以代入公式，36.77621)8182.1(71,8182.15.51062167971621614812≈⨯--=-≈-=⎪⎭⎫⎝⎛⨯-⨯⨯-=a b ，故回归直线方程为：;82.136.77ˆx y-= 由于回归系数b 为－1.82，由回归系数b 的意义可知：产量每增加1000件，单位成本下降1.82元．说明：回归分析，说明y 与x 它们之间是一元线性回归关系．回归方程中的回归系数b 和a ，刻画了这x 与y 两个量之间的变化趋势，对它们所反映出的信息进行分析，就是回归分析．对求和符号的理解例 下列表达式中错误的是（ ）A ．∑=-+=-+nk n n na d k a 1112)1(])1([ B ．∑∑==++-=-n k nk k n n a na k a 11222)1()(C ．∑=-=nk nknC112 D ．∑=-+=nk n kk n k n b a b a C 1)( 分析：符号“∑” 表示若干个数相加，“∑=nk 1”的下标1=k ，上标n 的含义是：将“∑=nk 1”符号后的表达式中，含k 的部分分别取1，2，3，…，n 后所得式子依次加起来，即∑=++==nk n f f f k f k f 1).()2()1()()(Λ解：分别计算ABCD 知：∑∑==-+=-+++++=-+=-+n k nk d n n na d n n a d k n a d k a 111111.2)1()1210()1(])1([Λ∑∑∑∑∑======+-=+-=-n k nk n k n k nk na k ak a k ak a k a 112211222212)2()(∑∑∑∑====++-=++-=+-nk nk n k nk k n n a na k n n a na k k a 111122222.)1(2)1(22∑=-=-+++++=++++=nk n n n n n n n n n n n n k n C C C C C C C C C C13210321.121)(ΛΛ∑=-----+=+++++=nk nn n n n n k k n k n n n n n k kn k na Cb a b C b a C b a C b a C b aC 1022211.)(ΛΛ故只有D 是错误的。

1. 从20的样本中得到的有关回归结果是：SSR=60，SSE=40。

要检验x 与y 之间的线性关系是否显著，即检验假设：01:0H β=。

(1)线性关系检验的统计量F 值是多少? (2)给定显著性水平a ＝0.05，F a 是多少? (3)是拒绝原假设还是不拒绝原假设?(4)假定x 与y 之间是负相关，计算相关系数r 。

(5)检验x 与y 之间的线性关系是否显著?解：（1）SSR 的自由度为k=1；SSE 的自由度为n-k-1=18；因此：F=1SSR k SSE n k --=6014018=27 （2）()1,18F α=()0.051,18F =4.41 （3）拒绝原假设，线性关系显著。

（4），由于是负相关，因此r=-0.7746（5）从F 检验看线性关系显著。

2. 某汽车生产商欲了解广告费用(x)对销售量(y)的影响，收集了过去12年的有关数据。

通过计算得到下面的有关结果：(1)完成上面的方差分析表。

(2)汽车销售量的变差中有多少是由于广告费用的变动引起的?(3)销售量与广告费用之间的相关系数是多少?(4)写出估计的回归方程并解释回归系数的实际意义。

(5)检验线性关系的显著性(a＝0.05)。

（2）R2=0.9756，汽车销售量的变差中有97.56%是由于广告费用的变动引起的。

（3）r=0.9877。

（4）回归系数的意义：广告费用每增加一个单位，汽车销量就增加1.42个单位。

（5）回归系数的检验：p=2.17E—09＜α，回归系数不等于0，显著。

回归直线的检验：p=2.17E—09＜α，回归直线显著。

3. 根据两个自变量得到的多元回归方程为12ˆ18.4 2.014.74yx x =-++，并且已知n ＝10，SST ＝6 724.125，SSR ＝6 216.375，1ˆ0.0813s β=，2ˆs β＝0.056 7。

要求：(1)在a=0.05的显著性水平下，12,x x 与y 的线性关系是否显著? (2)在a ＝0.05的显著性水平下，1β是否显著?(3)在a ＝0.05的显著性水平下，2β是否显著?解（1）回归方程的显著性检验：假设：H 0：1β=2β=0 H 1：1β，2β不全等于0 SSE=SST-SSR=6 724.125-6 216.375=507.75 F=1SSR p SSE n p --=6724.1252507.751021--=42.85()2,7F α=4.74，F>()2,7F α，认为线性关系显著。

统计学一元线性回归分析练习题一、内容提要本章介绍了回归分析的基本思想与基本方法。

首先，本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始，建立了回归分析的基本思想。

总体回归函数是对总体变量间关系的定量表述，由总体回归模型在若干基本假设下得到，但它只是建立在理论之上，在现实中只能先从总体中抽取一个样本，获得样本回归函数，并用它对总体回归函数做出统计推断。

本章的一个重点是如何获取线性的样本回归函数，主要涉及到普通最小二乘法的学习与掌握。

同时，也介绍了极大似然估计法以及矩估计法。

本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断，即进行所谓的统计检验。

统计检验包括两个方面，一是先检验样本回归函数与样本点的“拟合优度”，第二是检验样本回归函数与总体回归函数的“接近”程度。

后者又包括两个层次：第一，检验解释变量对被解释变量是否存在着显著的线性影响关系，通过变量的t检验完成；第二，检验回归函数与总体回归函数的“接近”程度，通过参数估计值的“区间检验”完成。

本章还有三方面的内容不容忽视。

其一，若干基本假设。

样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。

其二，参数估计量统计性质的分析，包括小样本性质与大样本性质，尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则。

Goss-markov定理表明OLS估计量是最佳线性无偏估计量。

其三，运用样本回归函数进行预测，包括被解释变量条件均值与个值的预测，以及预测置信区间的计算及其变化特征。

二、典型例题分析例1、令kids表示一名妇女生育孩子的数目，educ 表示该妇女接受过教育的年数。

生育率对教育年数的简单回归模型为kids??0??1educ??随机扰动项?包含什么样的因素？它们可能与教育水平相关吗？上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗？请解释。

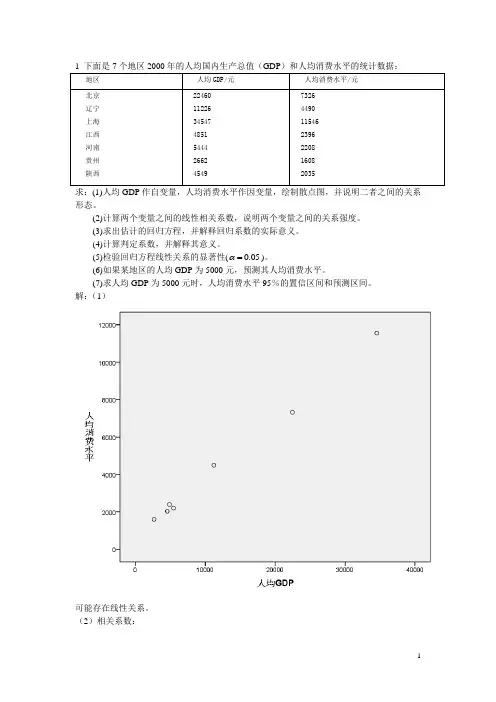
1 下面是7个地区2000年的人均国内生产总值（GDP）和人均消费水平的统计数据：地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求：(1)人均GDP作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。

(2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。

(3)求出估计的回归方程，并解释回归系数的实际意义。

(4)计算判定系数，并解释其意义。

(5)检验回归方程线性关系的显著性(0.05α=)。

(6)如果某地区的人均GDP为5000元，预测其人均消费水平。

(7)求人均GDP为5000元时，人均消费水平95％的置信区间和预测区间。

解：（1）可能存在线性关系。

（2）相关系数：（3）回归方程：734.6930.309y x=+回归系数的含义：人均GDP没增加1元，人均消费增加0.309元。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。

系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 （常量）734.693 139.540 5.265 0.003人均GDP（元）0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平（元）%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%（4）模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。

人均GDP对人均消费的影响达到99.6%。

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。