转动惯量和电机选择

什么时候需要考虑采用惯量计算电机功率你会了吗在伺服系统选型及调试中，常会碰到惯量问题。

其具体表现为：在伺服系统选型时，除考虑电机的扭矩和额定速度等等因素外，我们还需要先计算得知机械系统换算到电机轴的惯量，再根据机械的实际动作要求及加工件质量要求来具体选择具有合适惯量大小的电机；在调试时，正确设定惯量比参数是充分发挥机械及伺服系统最佳效能的前提。

此点在要求高速高精度的系统上表现尤为突出，这样，就有了惯量匹配的问题。

一、什么是惯量匹配1、根据牛顿第二定律：“进给系统所需力矩T = 系统传动惯量J ×角加速度θ角”。

加速度θ影响系统的动态特性，θ越小，则由控制器发出指令到系统执行完毕的时间越长，系统反应越慢。

如果θ变化，则系统反应将忽快忽慢，影响加工精度。

由于马达选定后最大输出T值不变，如果希望θ的变化小，则J应该尽量小。

2、进给轴的总惯量“J＝伺服电机的旋转惯性动量JM ＋电机轴换算的负载惯性动量JL。

负载惯量JL由（以平面金切机床为例）工作台及上面装的夹具和工件、螺杆、联轴器等直线和旋转运动件的惯量折合到马达轴上的惯量组成。

JM为伺服电机转子惯量，伺服电机选定后，此值就为定值，而JL则随工件等负载改变而变化。

如果希望J变化率小些，则最好使JL所占比例小些。

这就是通俗意义上的“惯量匹配”。

二、惯量匹配如何确定传动惯量对伺服系统的精度，稳定性，动态响应都有影响。

惯量大，系统的机械常数大，响应慢，会使系统的固有频率下降，容易产生谐振，因而限制了伺服带宽，影响了伺服精度和响应速度，惯量的适当增大只有在改善低速爬行时有利，因此，机械设计时在不影响系统刚度的条件下，应尽量减小惯量。

衡量机械系统的动态特性时，惯量越小，系统的动态特性反应越好；惯量越大，马达的负载也就越大，越难控制，但机械系统的惯量需和马达惯量相匹配才行。

不同的机构，对惯量匹配原则有不同的选择，且有不同的作用表现。

不同的机构动作及加工质量要求对JL与JM大小关系有不同的要求，但大多要求JL与JM的比值小于十以内。

电机转动惯量单位电机转动惯量是描述电机旋转惯性的物理量，通常用J表示，单位是kg·m²。

它是电机旋转惯性的度量，也是电机运动惯性的重要参数之一。

在电机的设计和运行过程中，电机转动惯量的大小对电机的性能和运行效率有着重要的影响。

电机转动惯量的大小取决于电机的结构和质量分布。

对于同一种类型的电机，转动惯量的大小与电机的转子质量、转子半径、转子质心位置、转子惯性矩等因素有关。

在电机的设计过程中，需要根据电机的使用要求和工作环境，合理地选择电机的转动惯量，以达到最佳的性能和效率。

电机转动惯量的大小对电机的性能和运行效率有着重要的影响。

首先，电机转动惯量的大小直接影响电机的加速度和减速度。

当电机需要快速启动或停止时，转动惯量越大，电机的加速度和减速度就越小，需要的时间就越长。

因此，在需要快速启动或停止的应用中，需要选择转动惯量较小的电机。

电机转动惯量的大小还影响电机的响应速度和精度。

当电机需要进行精确的位置控制时，转动惯量越小，电机的响应速度和精度就越高。

因此，在需要进行精确位置控制的应用中，需要选择转动惯量较小的电机。

电机转动惯量的大小还影响电机的能耗和寿命。

当电机需要进行长时间的运行时，转动惯量越大，电机的能耗就越高，寿命也会受到影响。

因此，在需要进行长时间运行的应用中，需要选择转动惯量较小的电机，以降低能耗和延长寿命。

在电机的设计和运行过程中，需要根据电机的使用要求和工作环境，合理地选择电机的转动惯量。

对于需要进行快速启动或停止的应用，需要选择转动惯量较小的电机；对于需要进行精确位置控制的应用，需要选择转动惯量较小的电机；对于需要进行长时间运行的应用，需要选择转动惯量较小的电机，以达到最佳的性能和效率。

电机转动惯量是电机旋转惯性的度量，也是电机运动惯性的重要参数之一。

在电机的设计和运行过程中，需要根据电机的使用要求和工作环境，合理地选择电机的转动惯量，以达到最佳的性能和效率。

在伺服系统选型及调试中，常会碰到惯量问题。

其具体表现为：在伺服系统选型时，除考虑电机的扭矩和额定速度等等因素外，我们还需要先计算得知机械系统换算到电机轴的惯量，再根据机械的实际动作要求及加工件质量要求来具体选择具有合适惯量大小的电机；在调试时，正确设定惯量比参数是充分发挥机械及伺服系统最佳效能的前提。

此点在要求高速高精度的系统上表现尤为突出，这样，就有了惯量匹配的问题。

一、什么是“惯量匹配”？1、根据牛顿第二定律：“进给系统所需力矩T = 系统传动惯量J ×角加速度θ角”。

加速度θ影响系统的动态特性，θ越小，则由控制器发出指令到系统执行完毕的时间越长，系统反应越慢。

如果θ变化，则系统反应将忽快忽慢，影响加工精度。

由于马达选定后最大输出T值不变，如果希望θ的变化小，则J应该尽量小。

2、进给轴的总惯量“J＝伺服电机的旋转惯性动量JM ＋电机轴换算的负载惯性动量JL。

负载惯量JL由（以平面金切机床为例）工作台及上面装的夹具和工件、螺杆、联轴器等直线和旋转运动件的惯量折合到马达轴上的惯量组成。

JM为伺服电机转子惯量，伺服电机选定后，此值就为定值，而JL则随工件等负载改变而变化。

如果希望J变化率小些，则最好使JL所占比例小些。

这就是通俗意义上的“惯量匹配”。

二、“惯量匹配”如何确定？传动惯量对伺服系统的精度，稳定性，动态响应都有影响。

惯量大，系统的机械常数大，响应慢，会使系统的固有频率下降，容易产生谐振，因而限制了伺服带宽，影响了伺服精度和响应速度，惯量的适当增大只有在改善低速爬行时有利，因此，机械设计时在不影响系统刚度的条件下，应尽量减小惯量。

衡量机械系统的动态特性时，惯量越小，系统的动态特性反应越好；惯量越大，马达的负载也就越大，越难控制，但机械系统的惯量需和马达惯量相匹配才行。

不同的机构，对惯量匹配原则有不同的选择，且有不同的作用表现。

不同的机构动作及加工质量要求对JL与JM大小关系有不同的要求，但大多要求JL与JM的比值小于十以内。

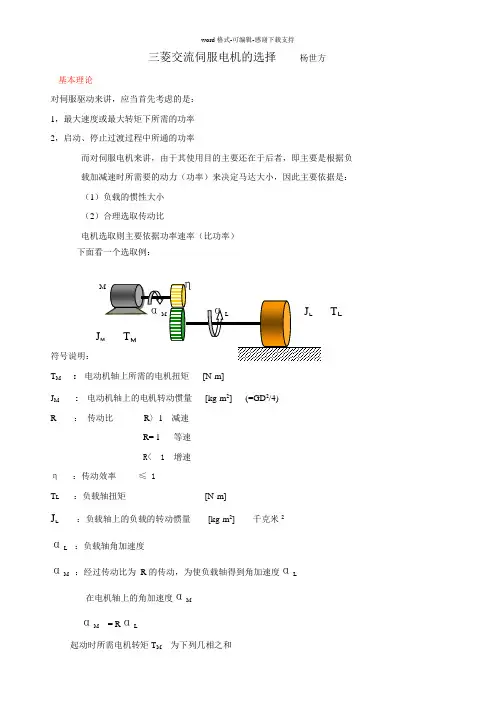
三菱交流伺服电机的选择杨世方基本理论对伺服驱动来讲，应当首先考虑的是：1，最大速度或最大转矩下所需的功率2，启动、停止过渡过程中所通的功率而对伺服电机来讲，由于其使用目的主要还在于后者，即主要是根据负载加减速时所需要的动力（功率）来决定马达大小，因此主要依据是：（1）负载的惯性大小（2）合理选取传动比电机选取则主要依据功率速率（比功率）下面看一个选取例：T L J符号说明：T M：电动机轴上所需的电机扭矩[N-m]J M: 电动机轴上的电机转动惯量[kg-m2] (=GD2/4)R ：传动比R〉1 减速R= 1 等速R< 1 增速η：传动效率≤ 1T L：负载轴扭矩[N-m]J L ：负载轴上的负载的转动惯量[kg-m2] 千克米2α：负载轴角加速度Lα：经过传动比为R的传动，为使负载轴得到角加速度αL M在电机轴上的角加速度αMα= RαLM起动时所需电机转矩T M为下列几相之和（1）用于电机本身加速的加速转矩T1[N-m]（2）使负荷加速的转矩T2[N-m]（3）为使负载轴（经过传动装置）得到转矩T L 所需要的转矩T3[N-m]T2和T3 不同，T3是正常运行时所需转矩则：T1= J M ·αM = J M ·R·αL根据，η·R·T2 = J L ·αL （牛顿定律）负载加速转矩：T2=（J L ·αL）/η·R正常运行时电机提供转矩：T3= T L/η·R电机起动转矩T M ≥T1+T2+T3 ≥J M ·R·αL +{（J L ·αL）+T L/η·R}---------(1)对上式右侧求R的偏微分，并使其等于零，即可求得（1）式右变最小值时的R0∂ T M / ∂ R =0R0= (J L ·αL+T L)/ J M·αL·η ------------------ （2）R0 称为最佳传动比，就是能使T M最小的传动比，选取这个传动比，电机所需的起动矩扭最小。

1、机电领域中伺服电机的选择原则现代机电行业中经常会碰到一些复杂的运动，这对电机的动力荷载有很大影响。

伺服驱动装置是许此，伺服电机的选择就变得尤为重要。

首先要选出满足给定负载要求的电动机，然后再从中按价格济指标选择最适合的电机。

各种电机的T- 曲线（1）传统的选择方法这里只考虑电机的动力问题，对于直线运动用速度v(t)，加速度a(t)和所需外力F(t)速度 (t)，角加速度 (t)和所需扭矩T(t)表示，它们均可以表示为时间的函数，与其他因素无关率P电机，最大应大于工作负载所需的峰值功率P峰值，但仅仅如此是不够的，物理意义上的功率但在实际的传动机构中它们是受限制的。

用峰值，T峰值表示最大值或者峰值。

电机的最大速度限，n上限= 峰值，最大/ 峰值，同样，电机的最大扭矩决定了减速比的下限，n下限=T峰值/T电大于n上限，选择的电机是不合适的。

反之，则可以通过对每种电机的广泛类比来确定上下限之间用峰值功率作为选择电机的原则是不充分的，而且传动比的准确计算非常繁琐。

（2）新的选择方法一种新的选择原则是将电机特性与负载特性分离开，并用图解的形式表示，这种表示方法使得驱动同系统间的比较更方便，另外，还提供了传动比的一个可能范围。

这种方法的优点：适用于各种负的特性分离开；有关动力的各个参数均可用图解的形式表示并且适用于各种电机。

因此，不再需要机是否能够驱动某个特定的负载。

在电机和负载之间的传动比会改变电机提供的动力荷载参数。

比如，一个大的传动比会减小外部扭而且，为输出同样的运动，电机就得以较高的速度旋转，产生较大的加速度，因此电机需要较大的适的传动比就能平衡这相反的两个方面。

通常，应用有如下两种方法可以找到这个传动比n，它会地协调起来。

一是，从电机得到的最大速度小于电机自身的最大速度电机，最大；二是，电机任机额定扭矩M额定。

2、一般伺服电机选择考虑的问题（1）电机的最高转速电机选择首先依据机床快速行程速度。

快速行程的电机转速应严格控制在电机的额定式中，为电机的额定转速（rpm）；n为快速行程时电机的转速（rpm）；为直线运行速度（m/min 电机/n丝杠；丝杠导程（mm）。

在伺服系统‎选型及调试‎中，常会碰到惯‎量问题。

其具体表现‎为：在伺服系统‎选型时，除考虑电机‎的扭矩和额‎定速度等等‎因素外，我们还需要‎先计算得知‎机械系统换‎算到电机轴‎的惯量，再根据机械‎的实际动作‎要求及加工‎件质量要求‎来具体选择‎具有合适惯‎量大小的电‎机；在调试时，正确设定惯‎量比参数是‎充分发挥机‎械及伺服系‎统最佳效能‎的前提。

此点在要求‎高速高精度‎的系统上表‎现尤为突出‎，这样，就有了惯量‎匹配的问题‎。

一、什么是“惯量匹配”？1、根据牛顿第‎二定律：“进给系统所‎需力矩T = 系统传动惯‎量J ×角加速度θ‎角”。

加速度θ影‎响系统的动‎态特性，θ越小，则由控制器‎发出指令到‎系统执行完‎毕的时间越‎长，系统反应越‎慢。

如果θ变化‎，则系统反应‎将忽快忽慢‎，影响加工精‎度。

由于马达选‎定后最大输‎出T值不变‎，如果希望θ‎的变化小，则J应该尽‎量小。

2、进给轴的总‎惯量“J＝伺服电机的‎旋转惯性动‎量JM ＋电机轴换算‎的负载惯性‎动量JL。

负载惯量J‎L由（以平面金切‎机床为例）工作台及上‎面装的夹具‎和工件、螺杆、联轴器等直‎线和旋转运‎动件的惯量‎折合到马达‎轴上的惯量‎组成。

JM为伺服‎电机转子惯‎量，伺服电机选‎定后，此值就为定‎值，而JL则随‎工件等负载‎改变而变化‎。

如果希望J‎变化率小些‎，则最好使J‎L所占比例‎小些。

这就是通俗‎意义上的“惯量匹配”。

二、“惯量匹配”如何确定？传动惯量对‎伺服系统的‎精度，稳定性，动态响应都‎有影响。

惯量大，系统的机械‎常数大，响应慢，会使系统的‎固有频率下‎降，容易产生谐‎振，因而限制了‎伺服带宽，影响了伺服‎精度和响应‎速度，惯量的适当‎增大只有在‎改善低速爬‎行时有利，因此，机械设计时‎在不影响系‎统刚度的条‎件下，应尽量减小‎惯量。

衡量机械系‎统的动态特‎性时，惯量越小，系统的动态‎特性反应越‎好；惯量越大，马达的负载‎也就越大，越难控制，但机械系统‎的惯量需和‎马达惯量相‎匹配才行。

伺服电机选型的原则和注意事项
为了满足机械设备对高精度、快速响应的要求，伺服电机应有较小的转动惯量和大的堵转转矩，并具有尽可能小的时间常数和启动电压，还应具有较长时间的过载能力，以满足低速大转矩的要求，能够承受频繁启动、制动和正、反转，如果盲目地选择大规格的电机，不仅增加成本，也会使得设计设备的体积增大，结构不紧凑，因此选择电机时应充分考虑各方面的要求，以便充分发挥伺服电机的工作性能；下面介绍伺服电机的选型原则和注意事项。

选用伺服电机型号的步骤1、明确负载机构的运动条件要求，即加／减速的快慢、运动速度、机构的重量、机构的运动方式等。

2、依据运行条件要求选用合适的负载惯最计算公式，计算出机构的负载惯量。

3、依据负载惯量与电机惯量选出适当的假选定电机规格。

4、结合初选的电机惯量与负载惯量，计算出加速转矩及减速转矩。

5、依据负载重量、配置方式、摩擦系数、运行效率计算出负载转矩。

6、初选电机的最大输出转矩必须大于加速转矩加负载转矩；如果不符合条件，必须选用其他型号计算验证直至符合要求。

7、依据负载转矩、加速转矩、减速转矩及保持转矩，计算出连续瞬时转矩。

8、初选电机的额定转矩必须大于连续瞬时转矩，如果不符合条件，必须选用其他型号计算验证直至符合要求。

9、完成选定。

伺服电机的选型计算方法 1、转速和编码器分辨率的确认。

2、电机轴上负载力矩的折算和加减速力矩的计算。

3、计算负载惯量，惯量的匹配，安川伺服电机为例，部分产品惯量匹配可达50倍，但实际越小越好，这样对精度和响应速度好。

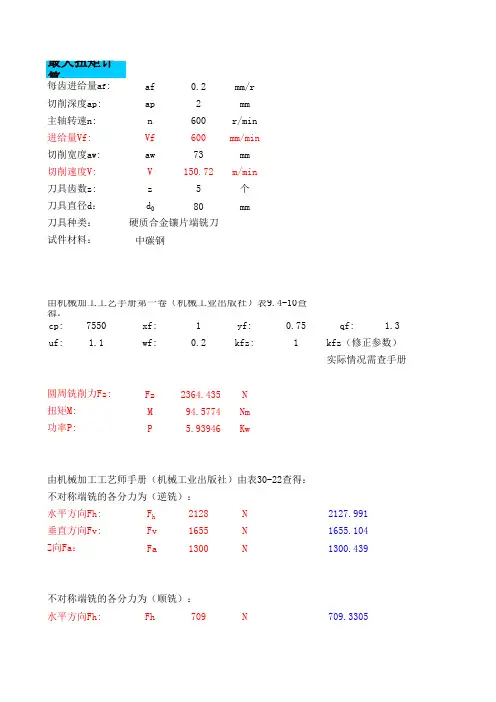
af 0.2mm/r ap 2mm n 600r/min Vf 600mm/min aw 73mm V 150.72m/min z 5个d 080mm中碳钢cp:7550xf:1yf:0.75qf: 1.3uf:1.1wf:0.2kfz:1Fz 2364.435N M 94.5774Nm P5.93946KwF h 2128N 2127.991 Fv 1655N 1655.104 Fa1300N1300.439Fh709N709.3305不对称端铣的各分力为（顺铣）：水平方向Fh:水平方向Fh:垂直方向Fv:Z向Fa：扭矩M:功率P:由机械加工工艺师手册（机械工业出版社）由表30-22查得：不对称端铣的各分力为（逆铣）：试件材料：由机械加工工艺手册第一卷（机械工业出版社）表9.4-10查得：kfz（修正参数）实际情况需查手册圆周铣削力Fz:切削宽度a w :切削速度V:刀具齿数z :刀具直径d：刀具种类：硬质合金镶片端铣刀最大扭矩计算：每齿进给量a f :切削深度a p:主轴转速n:进给量Vf:Fv 2128N 2127.991 Fa1300N1300.439ΔT 0.2s Vz 18m/min V 24m/min ax 2m/s 2ay 2m/s 2az1.5m/s 219.8KN 51KN 1004N/μmFmax=2303 N2302.57520 N0.015Fmin=537N536.75Fm=1714N1714.333最小载荷Fmin:当量载荷Fm:刚度系数K：1.确定当量载荷Fm:最大载荷Fmax:导轨滑块摩擦力f:摩擦系数μ：X向滚珠丝杠选择：设定滚珠丝杠副为FFZD-4008-3,公称直径40mm，导程8mm，丝杠外径38.6mm,钢珠直径5mm，底径34.9mm,循环数3，基本额定动负荷Ca为19.8KN,基本额定静负荷Coa为51KN，刚度系数K为1004N/基本额定动负荷Ca:基本额定静负荷Coa：加速时间ΔT：Z轴直线速度Vz：X和Y轴直线速度V：X向产生的加速度ax:Y向产生的加速度ay:Z向产生的加速度az:垂直方向Fv:Z向Fa：Cam=18.45709 KN250Km0.650.928mm δm1=5μm δm2=10μm20μm 50μm 取δm=5μm dm≥26mm 25.98754d 2m=34mm 33.8L=964mmFp=768N767.6667C=21μm 21.476Ft=5636N5635.52.5。

伺服电机的选型和转动惯量的计算引言：伺服电机是一种能够实现精确定位和速度控制的电动机。

在自动化控制系统中，伺服电机广泛应用于机械装置的定位与运动控制，如机床、工业机械手臂、机器人等。

为了确保控制系统的性能和稳定性，正确选型和计算转动惯量是非常重要的。

一、伺服电机选型1.负载特性分析：首先需要对负载特性进行分析，包括负载的质量、摩擦系数、惯性矩等。

这些参数影响到伺服电机的选择，如电机的额定转矩等。

在分析负载特性时需要考虑静态特性和动态特性。

2.运行速度要求：根据系统的运行速度要求，选择电机的额定转速。

如果要求快速响应，需要选择具有较高转速的电机；如果要求大转矩输出，需要选择具有较大额定转矩的电机。

3.控制方式：根据系统的控制方式，选择合适的伺服电机。

常见的控制方式有位置控制、速度控制和力控制。

不同的控制方式对电机的性能要求也不同。

4.转矩和转速曲线：了解电机的转矩和转速曲线，可以帮助选择合适的伺服电机。

转矩曲线决定了电机能够产生的最大转矩，转速曲线决定了电机能够输出的最大转速。

5.电机功率：根据负载特性和运行速度要求，计算出所需的电机功率。

一般情况下，应选择稍大于所需功率的电机，以保证系统的可靠性和安全性。

6.品牌和价格：最后根据伺服电机的品牌和价格进行选择。

国际知名品牌的产品质量较高，但价格也较高。

可以根据实际需求和预算进行选择。

转动惯量是描述物体抗拒改变转动状态的特性。

在伺服电机的选型和控制系统设计中，转动惯量是一个重要的参数。

计算转动惯量的一般公式为：J=m*r^2其中，J是转动惯量，m是物体的质量，r是物体相对转轴的距离。

如果物体是一个均匀的圆盘或圆柱体，根据其几何形状可以通过以下公式计算转动惯量：J=1/2*m*r^2其中，m是物体的质量，r是物体的半径。

如果物体是由多个部分组成，可以通过将各部分的转动惯量相加得到整体的转动惯量。

在实际应用中，还需要考虑其他因素对转动惯量的影响，如内部零件的分布、负载的摩擦系数等。

电机转动惯量
电动机转动惯量（Inertia of Motor）是指电机在转动时所受到的惯
性阻力，是反映电机转动能力的重要参数。

电动机转动惯量的数值代表着
电动机的载荷能力，电动机的转动惯量越大，其载荷能力越强。

通常情况下，电动机的转动惯量=电动机转子的惯量+负载的惯量。

电
动机转子的惯量主要受电机结构的影响，包括转子外形、转子转动部件的
重量等因素，负载的惯量由负载转动部件的重量和惯性系数决定。

电动机转动惯量越大，其载荷能力越强，转速变化也越小，而转动惯
量越小，电机的载荷能力越弱，转速变化越大，所以为了优化电机的性能，在选择电机的时候，应该尽量选择转动惯量比较大的电机。

750瓦电机允许转动惯量电机允许转动惯量是指在电机运转时，旋转部件产生的惯性力矩所需要克服的障碍。

对于750瓦电机来说，其转动惯量是一个重要的参数，影响着电机的运动特性和性能。

一、什么是转动惯量转动惯量（也称为转动惯性矩）是描述物体对于绕轴旋转时惯性特性的物理量。

它是指物体的质量在旋转中产生的惯性力矩大小，与物体的质量、形状和分布有关。

二、影响因素1.物体的质量：质量越大，转动惯量越大，即惯性力矩越大。

2.物体的形状：形状越复杂，转动惯量越大。

例如矩形和圆盘相比，相同质量的圆盘具有更大的转动惯量。

3.质量分布：质量分布越离轴心越远，转动惯量越大。

三、转动惯量的作用1.影响电机的启动和停止时间：转动惯量越大，电机的启动时间和停止时间越长，需要更多的能量来克服惯性力矩。

2.影响电机的加速度和减速度：转动惯量越大，电机的加速度和减速度越小，需要更长的时间来达到或停止旋转。

3.影响电机的动态响应：转动惯量越大，电机的动态响应越慢，旋转响应的灵敏度降低。

4.影响电机的能效：转动惯量越大，电机的能效越低，产生的能量损耗也越多。

四、如何减小转动惯量1.优化设计：通过改变物体的形状和质量分布，减小转动惯量。

例如，在设计电机转子时可以选择轻量化材料，减小质量。

2.降低负载：通过减少电机的负载，可以降低转动惯量。

例如，在设计机械系统时，可以采用轻量化、减少摩擦力和惯性力矩的方式来降低负载。

3.优化电机控制算法：通过优化电机控制算法，可以减小能量损耗，提高电机的能效。

五、结语750瓦电机的转动惯量是影响电机运动特性和性能的重要参数。

了解和减小转动惯量可以提高电机的启停时间、加速度和减速度，提高电机的动态响应和能效。

通过优化设计、降低负载和优化控制算法等方法，可以有效减小转动惯量，提高电机的运动效果。

电机制造商和工程师在设计和选择电机时，应充分考虑转动惯量这一指标，并根据具体需求进行合理的优化和调整。

机器人装夹过程及时间分配1花键母侧电机选型 1.1计算负载转动惯量：滚珠丝杠滚珠花键组合在工作过程中，花键侧电机带动丝杠花键轴及末端执行器旋转。

滚珠丝杠滚珠花键组合选择THK BNS2525A+1080L ，由资料得出：42=5.4210J Kgm -⨯螺母 42=5.1710J Kgm -⨯花键母3-4-42=5.921093010=5.510J Kgm -⨯⨯⨯⨯丝杠花键轴m =2.960.93=2.753kg ⨯丝杠花键轴=1.39m Kg 螺母 =1.25m Kg 花键母由模型得末端执行器部分相对丝杠花键轴转动惯量为：221 4.4210J Kgm -=⨯丝杠花键轴及两个花键母的转动惯量为：322 1.58410J kgm -=⨯同步带轮的转动惯量为：423 1.2110J Kgm -=⨯总惯量为：224123 4.5910J J J J Kgm -=++=⨯丝杠花键轴与减速器轴的距离为：90d mm =由平行轴定理2d c J J md =+由模型得末端执行器部分的质量为：m =4.1Kg 1得转动部分（包括花键母）相对减速器轴的转动惯量为：541222(m +2m 4.5910(4.1 2.7532 1.25)0.090.121J J m Kgm -=++=⨯+++⨯⨯=2丝杠花键轴花键母)d 其中1 4.1m Kg =（工件质量按最大1Kg 计算） 行星齿轮减速机构和同步带轮的转动惯量（已知）：44426 1.9710 1.2110 3.1810J Kgm ---=⨯+⨯=⨯综上所述，负载转动惯量J L1为：21560.1210.0003180.1213L J J J Kgm =+=+=1.2计算负载转矩 1.2.1加速转矩根据机器人在上下料，吹气以及位置检测过程中对末端执行器的运动要求，初定电机带动末端执行器旋转的工作过程中，加速时间为1t ，匀速时间为2t ，减速时间为1t ，如图所示。

选择同步带步进电机的型号时，一般需要考虑以下几个因素：
1. 负载要求：首先确定需要驱动的负载特性，包括负载的惯性、转动惯量、所需的扭矩和速度等。

这些参数将会影响到选择电机的型号和尺寸。

2. 步距角：步进电机的步距角是一个重要的参数，通常是1.8°或0.9°。

较小的步距角可以提供更精细的位置控制，但通常会降低最大转速和扭矩。

3. 驱动方式：确定使用同步带传动的方式，以便根据负载和速度要求来选择合适的同步带规格。

4. 环境条件：考虑电机所处的工作环境条件，如温度、湿度和其他环境因素，以便选择符合要求的防护等级。

5. 动力电源：确定可用的电源类型和电压范围，以便选择合适的电机型号和驱动器。

6. 可靠性要求：根据应用的要求，选择具有足够可靠性和寿命的电机产品。

在选择同步带步进电机时，还需要结合具体的应用场景和性能要求进行综合考虑，通常可以借助厂商提供的选型软件或者咨询相关的电机专业人士来进行详细的计算和选型。

如何减小负载转动惯量，提高伺服电机稳定性。

首先我们说说伺服电机如何选型，选伺服电机基本要从这五个因素考虑
第一扭矩，伺服电机额定扭矩至少要满足驱动负载扭矩的1.2倍；
第二转速，伺服电机额定转速要大于等于驱动负载所需转速；
第三惯量比，负载和伺服电机的惯量比最好控制在3:1之内；
第四编码器，根据设备回零和控制要求，选用增量式编码器还是绝对值编码器；
第五控制方式，根据运动控制器或者PLC控制方式，选用脉冲型、模拟量型还是网络型伺服驱动器。

具体负载扭矩和惯量如何计算，可以到公众号“建云工控”伺服下载页面查看伺服选型资料。

下面我们一起看一个伺服电机应用案例，或许会解开标题问题的谜底图1是伺服电机带动吸盘进行角度定位旋转，选用的伺服完全满足驱动负载要求，但是在运行过程偶尔有伺服啸叫和振动现象，之后重新手动修改和自动整定伺服参数后任然有上述问题。

图1
之后，通过软件监控伺服电机运行参数，发现负载和电机惯量比远远超出正常比例，最后确定负载的惯量和电机惯量不匹配造成上述问题。

下面我们通过模型图来讲解一下如何减小惯量比。

图2
图2是没有经过任何调整的原始机构，负载和电机的惯量比远远超过正常比例。

下面我们通过3种方法来减小惯量比。

第一，减小负载，如图3
图3
第,二，减小转动半径，如图4
图4
第三，在电机的额定扭矩能满足负载扭矩的情况下，增加配重，来减小转轴支点和负载中心点的距离，如图5
图5
最后总结一下，在不改变电机的情况下减小转动惯量有3个方法，在条件允许下减小负载，减小转动半径，减小转轴支点和负载中心距离。

ga12-n20电机的转动惯量ga12-n20电机是一种小型直流电机，常用于各种电子设备中。

在了解它的转动惯量之前，我们先来了解一下转动惯量的概念和意义。

转动惯量是物体绕轴旋转时所具有的惯性量度。

它与物体的质量和物体质量分布的方式有关。

转动惯量越大，物体的转动惯性越大，需要施加更大的力矩才能使其旋转，反之亦然。

ga12-n20电机的转动惯量是指该电机在转动过程中所具有的惯性量度。

它的数值大小决定了电机的转动灵敏度和响应速度。

转动惯量越小，电机的转动灵敏度越高，响应速度越快。

ga12-n20电机的转动惯量需要通过实验测量来获取。

一种常用的测量方法是利用牛顿第二定律和角加速度的关系。

测量者可以施加一个已知大小的力矩，使电机绕轴旋转，同时测量电机的角加速度。

通过测量数据的处理和计算，可以得到电机的转动惯量。

ga12-n20电机的转动惯量还与电机的结构和设计有关。

它的转动惯量取决于电机的质量分布方式、转子惯量和转子与轴之间的距离。

通常情况下，电机的转动惯量会由制造商提供，也可以通过计算机辅助设计软件进行计算。

了解转动惯量对于设计和控制电机的运动非常重要。

在设计电机驱动系统时，需要根据电机的转动惯量选择合适的驱动方式和参数，以实现所需的运动性能。

在控制电机的运动过程中，转动惯量的大小直接影响到电机的加速度和减速度，需要合理调节控制策略，以提高电机的运动性能和效率。

除了ga12-n20电机的转动惯量，我们还可以关注其他与电机性能相关的参数，例如额定电压、额定转速、额定电流等。

这些参数的选择和配置都会影响到电机的工作性能和使用寿命。

ga12-n20电机的转动惯量是电机设计和控制过程中一个重要的参数。

了解和掌握电机的转动惯量，可以帮助我们更好地设计和控制电机的运动，提高电机的性能和效率。

同时，也可以为电机的应用提供更多的参考和指导。

希望通过本文的介绍，能够增进对ga12-n20电机转动惯量的理解和认识。