下载文档原格式
运筹学第二章习题答案运筹学是一门应用数学学科，旨在通过数学模型和定量方法来解决实际问题。
在运筹学的学习中，习题是必不可少的一部分，通过解答习题可以加深对知识的理解和应用。
本文将针对运筹学第二章的习题进行解答，希望能够帮助读者更好地掌握运筹学的知识。
第一题：线性规划问题的基本要素包括目标函数、约束条件和决策变量。
请问线性规划问题的目标函数通常是什么形式？为什么？答：线性规划问题的目标函数通常是线性函数的形式。
这是因为线性函数具有简单的数学性质，容易求解和分析。
此外，线性函数的图像为直线，可以通过直观的图形方法来理解问题的解。
第二题：什么是单纯形法？请简要描述单纯形法的基本思想和步骤。
答：单纯形法是一种求解线性规划问题的常用方法。
其基本思想是通过不断地移动到更优解的顶点，直到找到最优解。
单纯形法的步骤如下：1. 初始解的选择：选择一个可行解作为初始解。
初始解可以通过图形方法或其他启发式算法得到。
2. 进行迭代：通过计算目标函数的改进方向来确定下一步移动的方向。
如果目标函数不能再改进，则停止迭代，当前解即为最优解。
3. 顶点的移动：通过改变决策变量的值，将当前解移动到相邻的顶点。
移动的方向和距离由迭代步骤中计算得到。
4. 检验最优性：对移动后的顶点进行最优性检验，判断是否达到最优解。
如果达到最优解，则停止迭代，当前解即为最优解；否则，返回第2步。
第三题：什么是整数规划问题？请举一个实际应用的例子，并说明为什么需要使用整数规划方法来解决。
答：整数规划问题是线性规划问题的一种扩展形式，要求决策变量的取值为整数。
整数规划问题通常用于需要离散决策的场景，如生产调度、资源分配等。
举个例子，假设某公司有多个项目需要进行投资，每个项目的投资金额和预期收益已知。
公司希望选择一些项目进行投资，使得总投资金额不超过公司的可用资金，并最大化预期收益。
由于项目的投资金额和收益都是整数，这就是一个整数规划问题。
使用整数规划方法来解决这个问题的原因是，如果将决策变量的取值限制为整数，可以更好地符合实际情况。
运筹学教程（第⼆版）（胡运权）课后答案（清华⼤学出版社）运筹学教程（第⼆版）习题解答第⼀章习题解答运筹学教程1.1 ⽤图解法求解下列线性规划问题。
并指出问题具有惟⼀最优解、⽆穷多最优解、⽆界解还是⽆可⾏解。
1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5 x 1 + 6 x 2≤ 82 5 ≤ x ? 1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3) 1 2 x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 21 2 ? ≥ 12 2 1 ? x , x ≥ 0 .? ?2 x 1 + x 2 ≤ 2st ?3x + 4 x (2) max Z = 3x 1 + 2 x 2x , x ≥ 0 1 2该问题⽆解≥ 12 2 1 ? ? 2 x 1 + x 2 ≤ 2st .?3 x +4 x ( 2 ) max Z = 3 x 1 + 2 x 2第⼀章习题解答3 2 1x = 1, x = 1, Z = 3是⼀个最优解⽆穷多最优解，1 2x , x ≥ 0 ? 2 1 ? ? ? 4 x 1 + 6 x 2 ≥ 6st .?2 x + 2 x ≥ 4 (1) min Z = 2 x 1 +3 x 2该问题有⽆界解1 2x , x ≥ 0 ? ≤ 2 2 1 ? .? 2 x 1 - x 2 ≥ 2st- 2 x + 3x (4) max Z = 5x 1 + 6 x 2第⼀章习题解答唯⼀最优解， x 1 = 10, x 2 = 6, Z = 16 ≤ 82 5 ≤ x ?1 ? 5 ≤ x ≤ 10 .?max Z = x 1 + x 26 x 1 + 10 x 2 ≤ 120st ?(3)第⼀章习题解答运筹学教程1.2 将下述线性规划问题化成标准形式。
《运筹学教程》第二章习题答案1、（1）解：引入松弛变量x4≥0,x5≥0,化不等式为等式为：minz=2X1 +3X2+4X3s.t. X1+3X2+2X3+X4=74X1+2X2+X5=9X1,X2,X4,X5≥0化自由变量为非负，令X3=X3′-X3〞，X3′，X3〞≥0 ：minz=2X1 +3X2+4X3′-4X3〞s.t. X1+3X2+2 X3′-2 X3〞+X4=74X1+2X2+X5=9X1,X2, X3′，X3〞，X4,X5 ≥0(2)解：引入松弛变量x5≥0,剩余变量X6≥0，化不等式为等式为：maxz=X1 -5X2+4X3- X4s.t. X1+2X3+X5=7X2-2X4-X6=9X1,X2，X4,X5 ，X6≥0化自由变量为非负，令X3=X3′-X3〞，X3′，X3〞≥0 ：maxz=X1 -5X2+4X3′-4X3〞- X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′，X3〞，X4,X5 , X6≥0化极大的目标函数为极小的目标函数：minz=-X1+5X2-4X3′+4X3〞+X4s.t. X1+2 X3′-2 X3〞+X5=7X2-2X4-X6=9X1,X2, X3′，X3〞，X4,X5 , X6≥02、(1)是不等式表示下图阴影区域，过阴影部分任意两点的直线仍在该区域内。
(2)不是不等式表示下图阴影区域，过阴影部分且通过曲线上部的直线上的点不完全在该区域内。
(3)不是 不等式表示下图阴影区域，过阴影部分且通过圆内部的直线上的点不完全在该区域内。
3、在以下问题中，指出一组基础变量，求出所有基础可行解以及最优解。
（1）123123123123m ax 2..2644,,0z x x x s t x x x x x x x x x =+-⎫⎪++≤⎪⎬+-≤⎪⎪≥⎭解：将上式化成标准形式，如下：1231234123512345m in 2..2644,,,,0p x x x s t x x x x x x x x x x x x x =--+⎫⎪+++=⎪⎬+-+=⎪⎪≥⎭从上式中可以得出系数矩阵为[]12345112101411A P P P P P ⎡⎤==⎢⎥-⎣⎦， 取基础变量为45,x x ，令非基变量123,,x x x =0，解方程组123412352644x x x x x x x x +++=+-+=得基础可行解(1)(0,0,0,6,4)T x =同理得基础解：(2)(0,6,0,0,20)T x =-，(3)(0,0,3,0,7)T x =，(4)(0,0,4,24,0)T x =-，(5)(0,1,0,5,0)Tx =，(6)1420(0,,,0,0)99Tx =，(7)(6,0,0,0,2)T x =-，(8)(4,0,0,2,0)Tx=，(9)202(,,0,0,0)33Tx =-，(10)142(,0,,0,0)33Tx =。
运筹学（第2版）习题答案2第1章 线性规划 P36~40第2章 线性规划的对偶理论 P68~69 第3章 整数规划 P82~84 第4章 目标规划 P98~100 第5章 运输与指派问题 P134~136 第6章 网络模型 P164~165 第7章 网络计划 P185~187 第8章 动态规划 P208~210 第9章 排队论 P239~240 第10章 存储论 P269~270 第11章 决策论 Pp297－298 第12章 博弈论 P325~326 全书360页由于大小限制，此文档只显示第6章到第12章，第1章至第5章见《运筹学课后答案1》习题六6.1如图6－42所示，建立求最小部分树的0－1整数规划数学模型。
【解】边[i ，j ]的长度记为c ij ，设⎩⎨⎧=否则包含在最小部分树内边0],[1j i x ij数学模型为：,12132323243434364635365612132434343546562324463612132446362335244656121324354656m in 52,22,233344,510ij ijij i j ij Z c x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x ==++≤++≤++≤++≤+++≤+++≤+++≤++++≤++++≤+++++≤=∑或,[,]i j ⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎩所有边6.2如图6－43所示，建立求v 1到v 6的最短路问题的0－1整数规划数学模型。
图6－42【解】弧(i ，j )的长度记为c ij ，设⎩⎨⎧=否则包含在最短路径中弧0),(1j i x ij数学模型为：,1213122324251323343524344546253545564656m in 100,00110,(,)ijiji jij Z cx x x x x x x x x x x x x x x x x x x x x x i j =⎧+=⎪---=⎪⎪+--=⎪⎪+--=⎨⎪++-=⎪⎪+=⎪=⎪⎩∑或所有弧 6.3如图6－43所示，建立求v 1到v 6的最大流问题的线性规划数学模型。
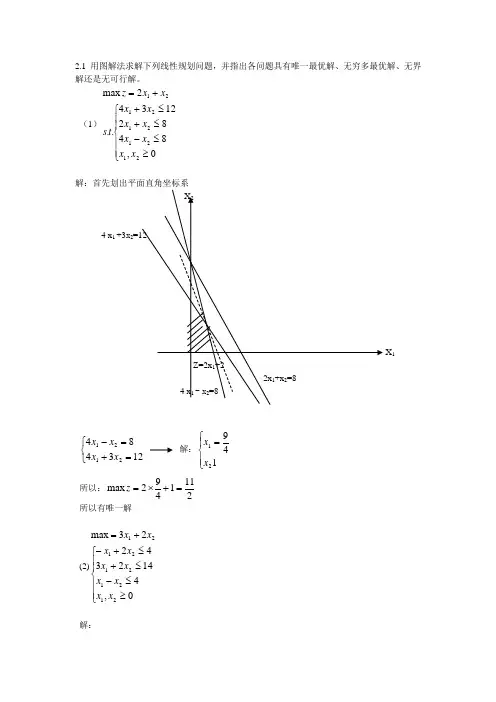
2.1 用图解法求解下列线性规划问题，并指出各问题具有唯一最优解、无穷多最优解、无界解还是无可行解。
（1）⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤++=0,84821234..2max 2121212121x x x x x x x x t s x x z解：首先划出平面直角坐标系4 x 1 +3x 2X 1⎩⎨⎧=+=-1234842121x x x x 解：⎪⎩⎪⎨⎧=14921x x 所以：2111492max =+⨯=z 所以有唯一解(2)⎪⎪⎩⎪⎪⎨⎧≥≤-≤+≤+-+=0,414234223max 2121212121x x x x x x x x x x 解：2=41⎩⎨⎧=+=+-1423422121x x x x 解得：⎪⎪⎩⎪⎪⎨⎧==4132521x x 所以:144132253max =⨯+⨯=z 因为直线02321=+x x 与直线142321=+x x 平行， 所以有无穷多最优解，max z=14（3） ⎪⎩⎪⎨⎧≥≤+-≤-+=0,432..32max 21212121x x x x x x t s x x z 解：（4）⎪⎩⎪⎨⎧≥-≤-≥-+=0,330..max 21212121x x x x x x t s x x z解：2.2将下列线性规划问题化为标准形式(1) s.t.⎪⎩⎪⎨⎧≥≤≤-+-=++-+-=无约束321321321321,0,0624322min x x x x x x x x x x x x z (2)⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束， 解：（1）令011≥-=x x )0'','('''33333≥-=x x x x x则上述形式可化为：)'''(32'2m ax 3321x x x x z --+=⎪⎩⎪⎨⎧≥=+--+=-++0,'',',,'6)'''('24)'''('..43321433213321x x x x x x x x x x x x x x t s（2）⎪⎪⎩⎪⎪⎨⎧≤≥-=-+-≤+-≥--+=0,0232132..23min 3213213132321x x x x x x x x x x t s x x x z 无约束， 解：令33'x x -= )0','','(322≥x x x 则上述形式可化为：')'''(23m ax 3221x x x x z ----=⎪⎪⎩⎪⎪⎨⎧≥=---=+--=+---0,,','',',2')'''(321')'''(3')'''(2..543221322153224322x x x x x x x x x x x x x x x x x x t s 2.3. 在下列线性规划问题中，找出所有基解，指出哪些是基可行解并分别代入目标函数，比较找出最优解。
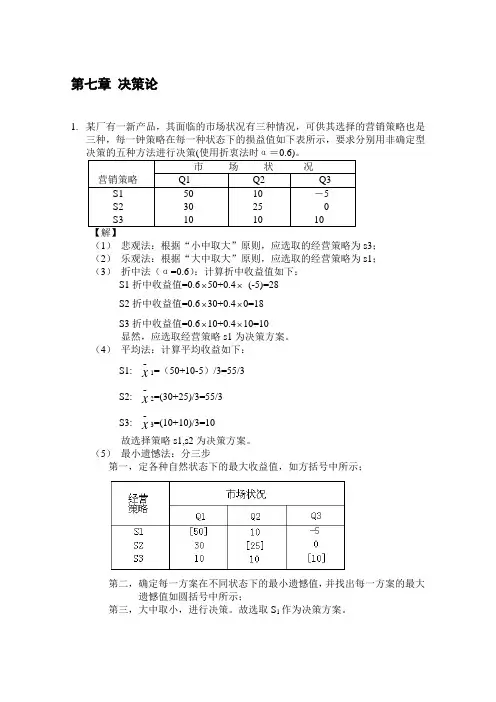
第七章 决策论1. 某厂有一新产品，其面临的市场状况有三种情况，可供其选择的营销策略也是三种，每一钟策略在每一种状态下的损益值如下表所示，要求分别用非确定型决策的五种方法进行决策(使用折衷法时α＝0.6)。
营销策略 市 场 状 况Q1 Q2 Q3S1 S2 S3 50 30 10 10 25 10 －50 10【解】（1） 悲观法：根据“小中取大”原则，应选取的经营策略为s3；（2） 乐观法：根据“大中取大”原则，应选取的经营策略为s1；（3） 折中法（α=0.6）：计算折中收益值如下：S1折中收益值=0.6⨯50+0.4⨯ (-5)=28S2折中收益值=0.6⨯30+0.4⨯0=18S3折中收益值=0.6⨯10+0.4⨯10=10显然，应选取经营策略s1为决策方案。
（4） 平均法：计算平均收益如下：S1:x _1=（50+10-5）/3=55/3 S2:x _2=(30+25)/3=55/3 S3:x _3=(10+10)/3=10 故选择策略s1,s2为决策方案。
（5） 最小遗憾法：分三步第一，定各种自然状态下的最大收益值，如方括号中所示；第二，确定每一方案在不同状态下的最小遗憾值，并找出每一方案的最大遗憾值如圆括号中所示；第三，大中取小，进行决策。
故选取S 1作为决策方案。
2．如上题中三种状态的概率分别为: 0.3, 0.4, 0.3, 试用期望值方法和决策树方法决策。
（1）用期望值方法决策：计算各经营策略下的期望收益值如下：故选取决策S2时目标收益最大。
（2）用决策树方法，画决策树如下：3. 某石油公司拟在某地钻井，可能的结果有三：无油(θ1)，贫油（θ2）和富油（θ3），估计可能的概率为：P (θ1) =0.5, P (θ2)=0.3，P (θ3)=0.2。
已知钻井费为7万元，若贫油可收入12万元，若富油可收入27万元。
为了科学决策拟先进行勘探，勘探的可能结果是：地质构造差(I1)、构造一般(I2)和构造好(I3)。
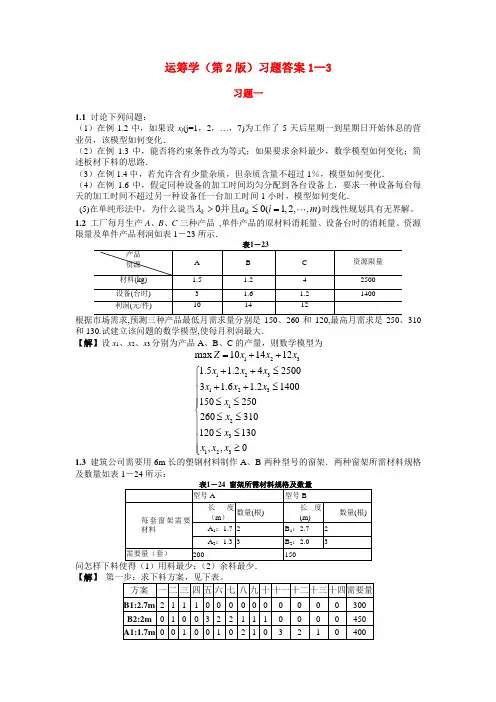
运筹学（第2版）习题答案1--3习题一1.1 讨论下列问题：（1）在例1.2中，如果设x j (j=1，2，…，7)为工作了5天后星期一到星期日开始休息的营业员，该模型如何变化．（2）在例1.3中，能否将约束条件改为等式；如果要求余料最少，数学模型如何变化；简述板材下料的思路．（3）在例1.4中，若允许含有少量杂质，但杂质含量不超过1％，模型如何变化．（4）在例1.6中，假定同种设备的加工时间均匀分配到各台设备上，要求一种设备每台每天的加工时间不超过另一种设备任一台加工时间1小时，模型如何变化．(5)在单纯形法中，为什么说当00(1,2,,)k ik a i m λ>≤=并且时线性规划具有无界解。
1.2 工厂每月生产A 、B 、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源限量及单件产品利润如表1－23所示．310和130.试建立该问题的数学模型,使每月利润最大．【解】设x 1、x 2、x 3分别为产品A 、B 、C 的产量，则数学模型为123123123123123max 1014121.5 1.2425003 1.6 1.21400150250260310120130,,0Z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤≤⎪⎨≤≤⎪⎪≤≤⎪≥⎪⎩ 1.3 建筑公司需要用6m 长的塑钢材料制作A 、B 两种型号的窗架．两种窗架所需材料规格及数量如表1－24所示：【解】设x j （j =1,2,…，14）为第j 种方案使用原材料的根数，则 （1）用料最少数学模型为14112342567891036891112132347910121314min 2300322450232400232346000,1,2,,14jj j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j ==⎧+++≥⎪++++++≥⎪⎪++++++≥⎨⎪++++++++≥⎪⎪≥=⎩∑ 用单纯形法求解得到两个基本最优解X (1)=( 50 ,200 ,0 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=534 X (2)=( 0 ,200 ,100 ,0,84 ,0,0 ,0 ,0 ,0 ,0 ,150 ,0 ,0 );Z=534 （2）余料最少数学模型为134131412342567891036891112132347910121314min 0.60.30.70.40.82300322450232400232346000,1,2,,14j Z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x j =+++++⎧+++≥⎪++++++≥⎪⎪++++++≥⎨⎪++++++++≥⎪⎪≥=⎩ 用单纯形法求解得到两个基本最优解X (1)=( 0 ,300 ,0 ,0,50 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0，用料550根 X (2)=( 0 ,450 ,0 ,0,0 ,0,0 ,0 ,0 ,0 ,0 ,200 ,0 ,0 );Z=0，用料650根 显然用料最少的方案最优。
第七章 决策论1. 某厂有一新产品，其面临的市场状况有三种情况，可供其选择的营销策略也是三种，每一钟策略在每一种状态下的损益值如下表所示，要求分别用非确定型决策的五种方法进行决策(使用折衷法时α＝0.6)。
营销策略 市 场 状 况Q1 Q2 Q3S1 S2 S3 50 30 10 10 25 10 －50 10【解】（1） 悲观法：根据“小中取大”原则，应选取的经营策略为s3；（2） 乐观法：根据“大中取大”原则，应选取的经营策略为s1；（3） 折中法（α=0.6）：计算折中收益值如下：S1折中收益值=0.6⨯50+0.4⨯ (-5)=28S2折中收益值=0.6⨯30+0.4⨯0=18S3折中收益值=0.6⨯10+0.4⨯10=10显然，应选取经营策略s1为决策方案。
（4） 平均法：计算平均收益如下：S1:x _1=（50+10-5）/3=55/3 S2:x _2=(30+25)/3=55/3 S3:x _3=(10+10)/3=10 故选择策略s1,s2为决策方案。
（5） 最小遗憾法：分三步第一，定各种自然状态下的最大收益值，如方括号中所示；第二，确定每一方案在不同状态下的最小遗憾值，并找出每一方案的最大遗憾值如圆括号中所示；第三，大中取小，进行决策。
故选取S 1作为决策方案。
2．如上题中三种状态的概率分别为: 0.3, 0.4, 0.3, 试用期望值方法和决策树方法决策。
（1）用期望值方法决策：计算各经营策略下的期望收益值如下：故选取决策S2时目标收益最大。
（2）用决策树方法，画决策树如下：3. 某石油公司拟在某地钻井，可能的结果有三：无油(θ1)，贫油（θ2）和富油（θ3），估计可能的概率为：P (θ1) =0.5, P (θ2)=0.3，P (θ3)=0.2。
已知钻井费为7万元，若贫油可收入12万元，若富油可收入27万元。
为了科学决策拟先进行勘探，勘探的可能结果是：地质构造差(I1)、构造一般(I2)和构造好(I3)。
根据过去的经验，地质构造与出油量间的关系如下表所示：P (I j|θi) 构造差(I1) 构造一般(I2) 构造好(I3)无油(θ1) 0.6 0.3 0.1贫油(θ2) 0.3 0.4 0.3富油(θ3) 0.1 0.4 0.5假定勘探费用为1万元, 试确定：(1)是否值得先勘探再钻井?(2)根据勘探结果是否值得钻井？【解】第一步第二步，画出决策树如下：第三步，计算后验概率首先，知，各种地质构造的可能概率是：再由得到，每一种构造条件下每一状态发生的概率：构造差（I 1） 构造一般（I 2） 构造好（I 3）0.73170.4286 0.20830.21950.3429 0.3750 0.04880.2286 0.4167合计 1.0 1.0 1.0根据决策表，若勘探得到结果为“构造差”，则有：E(s 1)=-7⨯0.7313+5⨯0.2195+20⨯0.0488=-3.0484若勘探得到结果为“构造一般”，则有：E(s 2)=-7⨯0.4286+5⨯0.3429+20⨯0.2286=3.2863若勘探得到结果为“构造好”，则有：E(s 3)=-7*0.2083+5*0.3750+20*0.4167=8.7509E(勘探)=∑=ni 1E(s i )P(I i )=-3.0484⨯0.41+3.2863⨯0.35+8.7509⨯0.24=2.0006已知，勘探成本为1万元，所以值得先勘探后钻井；同时，由于不钻井的期望收益为0，勘探后的结果为值得钻井。
4. 某企业拟从3名干部中选拔一人担任总经理助理，选拔的标准包括健康状况、业务知识、写作能力、口才、政策水平和工作作风6个方面。
这6个方面经过比较后得出的判断矩阵如下：⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=1132221133/1113/13/115/14/14/12/13512/112/1142112/114111A 经过对三个对象按每一标准权衡，得到的判断矩阵依次是：试应用AHP 方法，对三个候选人ABC 排出优先顺序。
⎪⎪⎪⎭⎫ ⎝⎛13/123142/14/11⎪⎪⎪⎭⎫ ⎝⎛1252/1145/14/11⎪⎪⎪⎭⎫ ⎝⎛113113/13/131⎪⎪⎪⎭⎫ ⎝⎛17/15/171353/11⎪⎪⎪⎭⎫ ⎝⎛17/17/1711711⎪⎪⎪⎭⎫ ⎝⎛15/19/1517/1971【解】对于C1矩阵：C1 P1P2P3P1 1 1/4 1/2 V1=0.5 W1=0.1365P2 4 1 3 V2=2.2894 W2=0.625P3 2 1/3 1 V3=0.8736 W3=0.2385∑V=3.663对于C2矩阵：C2 P1 P2P3P1 1 1/4 1/5 V1=0.3684 W1=0.0974P2 4 1 1/2 V2=1.2599 W2=0.3331P3 5 2 1 V3=2.1544 W3=0.570∑V=3.7827对于C3矩阵：C3P1P2P3P1 1 3 1/3 V1=1 W1=0.3189P21/3 1 1 V2=0.6934 W2=0.2211P3 5 2 1 V3=1.4422 W3=0.46∑V=3.1356对于C4矩阵：C4P1P2P3P1 1 1/3 5 V1=1.1856 W1=0.279P2 3 1 7 V2=2.7589 W2=0.6491P31/5 1/7 1 V3=0.3057 W3=0.0719∑V=4.2502对于C5矩阵：C5P1P2P3P1 1 1 7 V1=1.9129 W1=0.4667P2 1 1 7 V2=1.9129 W2=0.4667P31/7 1/7 1 V3=0.2733 W3=0.0667∑V=4.0991对于C6矩阵：C6P1P2P3P1 1 7 9 V1=3.9791 W1=0.772P21/7 1 5 V2=0.8939 W2=0.1734P31/9 1/5 1 V3=0.2811 W3=0.0545∑V=5.1541对于A矩阵：1 1 1 4 1 1/2 V1=1.1225 W1=0.16851 12 4 1 1/2 V2=1.2599 W2=0.18911 1/2 1 53 1/2 V3=1.2464 W3=0.18711/4 1/4 1/5 1 1/3 1/3 V4=0.334 W4=0.05011 1 1/3 3 1 1 V5=1 W5=0.15012 2 23 1 1 V 6=1.6984 W 6=0.255∑V=6.6612 进行层次总排序： C 1 C 2 C 3 C 4 C 5C 6 排序 结果 0.1685 0.1891 0.1871 0.0501 0.15010.255 P A 0.1365 0.0974 0.3189 0.279 0.46670.772 0.3821 P B 0.625 0.3331 0.2211 0.64910.46670.1734 0.3571 P C 0.2385 0.57 0.46 0.07190.0667 0.0545 0.2616 最终得出：3名候选人的优先顺序是A ﹥B ﹥C第八章 对策论1． 求解下列的矩阵对策，并明确回答它们分别是不是既约矩阵？有没有鞍点？（1） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---3258414122 （2） ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡612443122 （3） ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡6132445343221272 （4） ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡4532312265833427645608139 【解】（1） -2 12 -4 第二行优超于第三行1 4 8 第1列优超于第2列-5 2 3 不是既约矩阵这个矩阵对策有鞍点为a 21=1（2） 2 2 1 第二行优超于第一行3 4 4 不是既约矩阵，2 1 6 这个矩阵鞍点为a 21=3（3） 2 7 2 1 第三行优超于第二行2 234 第1列优超于第2列3 54 4 不是既约矩阵2 3 1 6 该矩阵对策有鞍点为a 31=3(4) 9 3 1 8 0 第二行优超于第五行6 5 4 67 第3列优超于第4列2 43 3 8 不是既约矩阵5 6 2 2 1 该矩阵对策有鞍点为a 23=43 2 3 5 42． 试证明在矩阵对策：⎥⎦⎤⎢⎣⎡=22211211a a a a A 中，不存在鞍点的充要条件是有一条对角线的每一元素大于另一条对角线上的每一元素。
3． 先处理下列矩阵对策中的优超现象，再利用公式法求解：A ＝⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡3880667864959379520503043 【解】对矩阵A 观察可知：3 4 0 3 0 第三行优超于第二行5 0 2 5 9 第四行优超于第一行7 3 9 5 9 故可划去第一行和第二行4 6 8 7 6 第1，2，4，5列都优超于第3列6 0 8 8 3 第2列优超于第4，5列故可划去第3，4，5列，得到：7 34 6 第一行优超于第三行，可划去第三行6 07 34 6解之：e=7+6-（4+3）=6 p 3=d-c/e=1/3 p 4=a-b/e=2/3q 1=d-b/e=1/2 q 2=a-c/e=1/2V G =ad-bc/e=5所以 p*=(0,0,1/3,2/3,0) q*=(1/2,1/2,0,0,0)T4． 利用图解法求解下列矩阵对策：（1）A ＝⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡2114672 （2）A ＝⎥⎦⎤⎢⎣⎡2581031 【解】（1） 假定局中人Ⅱ取混合策略（q ，1－q ）局中人I 随机地取纯策略a 1,a 2,a 3于是根据公式E(a i ，q)=∑ja ij q j 有：E(a 1 ,q)=a 11q+a 12(1-q)=a 12+(a 11-a 12)q=7-5qE(a 2 ,q)=a 21q+a 22(1-q)=a 22+(a 21-a 22)q=4+2qE(a 3 ,q)=a 31q+a 32(1-q)=a 32+(a 31-a 32)q=2+9q于是，可得到如下图示：按照大中取小准则，应有：7529E q E q =-⎧⎨=+⎩得5/143514q E =⎧⎪⎨=⎪⎩所以局中人Ⅱ的最优混合策略q *=5/149/14⎡⎤⎢⎥⎣⎦ 由图可知，当局中人I 出a2时，期望收益小于均衡收益E*，故令p2＝0 同时，因为q1>0，q2>0，所以有：2111373/14712373/14131p p p p p p ⨯+⨯=⎧⎪⨯+⨯=⎨⎪+=⎩得19/1435/14p p =⎧⎨=⎩ 所以p*＝(9/14，0，5/14) 【解】（2）E(p ,b 1)=a 11p+a 21(1-p)=a 21+(a 11-a 21)p=8-7pE(p ,b 2)=a 12p+a 22(1-p)=a 22+(a 12-a 22)p=5-2pE(p ,b 3)=a 13p+a 23(1-p)=a 23+(a 13-a 23)p=2+8p于是，有如下图示：按照小中取大准则，有：5228E p E p =-⎧⎨=+⎩得3/10245p E =⎧⎪⎨=⎪⎩所以p*=( 3/10,7/10) 由图可知，当局中人II 出b1时，期望收益大于均衡收益E*，故令q 1*=0又因为 p 1*=3/10﹥0 ,p 2*=7/10﹥03210322/5522322/5231q q q q q q +=⎧⎪+=⎨⎪+=⎩解得：24/531/5q q =⎧⎨=⎩ q*=(0 , 4/5 ,1/5)T5． 已知矩阵对策：A ＝⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡060800004 的解为：x*＝（6/13,3/13,4/13）,y*＝(6/13,4/13,3/13)T ，对策值为24/13，求下列矩阵对策的解：（1）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡2821022226 （2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------242226222 （3）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡203820442020202032 【解】（1）对于（1），根据定理8.6，因为A 1＝A ＋2所以，对策的值V G1=V G +k=24/13+2=50/13解为：X*=(6/13 ,3/13 ,4/13 )Y*=(6/13 ,4/13 ,3/13)T（2）因为对⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------242226222的第一列和第三列换位，得到：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------242622222=2060800004-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡ 所以，T(G B ) = T(G A ) 所以V GB V GA -2= V GB =24/13-26/13=-2/13 但由于列换了位，所以解应为：X*=(6/13 ,3/13 ,4/13) Y*=(3/13 ,4/13 , 6/13)T（3）6． 用行列式解法求解下列矩阵对策：（1）⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1140322210414301 （2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡032104321 【解】（1） 1 0 3 4 第四行优超于第二行-1 4 0 1 第1列优超于第4列2 2 23 划去第二行和第4列0 4 1 1得到： 1 0 3 第1列优超于第3列2 2 2 第二行优超于第一行0 4 1 划去第一行和第3列得到： 2 20 4 故鞍点为a 31=2（2） 1 2 34 0 12 3 0 此矩阵为既约矩阵先求局中人Ⅰ的混合策略：第1列减第2列，第2列减第3列得 -1 -1 a 1：12-1=11 , a 2：-3-1=-－4 , a 3：1+4=54 -1 策略的混合比为 11：4：5-1 3 所以p*=(11/20 ,4/20 ,5/20)=(11/20 ,1/5 ,1/4)再求局中人Ⅱ的混合策略：第一行减第二行，第二行减第三行得 -3 2 2 b 1：2+6=8 , b 2：-3-4=－7 , b 3：9-4=52 -3 1 策略的混合比为 8：7：5所以q*=（8/20，7/20，5/20）T=（2/5，7/20，1/4）T7． 试用线性规划方法求解下列矩阵对策：（1）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡446662428 （2）⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡121130202 【解】（1）（P ）⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥++≥++≥++++03,2,1134261413426121362218)321min(x x x x x x x x x x x x x x x (D)⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤++≤++≤++++03,2,1134241613626121342218)321max(y y y y y y y y y y y y y y y解之，X=(0 ,1/14 ,1/7) Y=(1/14 ,1/14 ,1/14) V G =1/∑Xi =14/3 所以，p*=V G X=(0 ,1/3 ,2/3)， q*=V G Y=(1/3 ,1/3 ,1/3)T(P)⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥++≥++≥++++03,2,1132121322310132012)321min(x x x x x x x x x x x x x x x (D)⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤++≤++≤++++03,2,1132211323101322012)321max(y y y y y y y y y y y y y y y解之，得到：X=(1/4 ,0 ,1/2) Y=(1/2 ,1/4 ,0) V G =1/∑Xi =4/3所以，p*=V G X=(1/3 ,0 ,2/3)，q*＝V G Y ＝(2/3 ,1/3 ,0)T8． 试写出“石头·剪刀·布”两碰吃游戏的赢得矩阵并求解双方的最优策略。
