利用导数解决恒成立能成立问题备课讲稿
- 格式:doc
- 大小:434.00 KB
- 文档页数:52


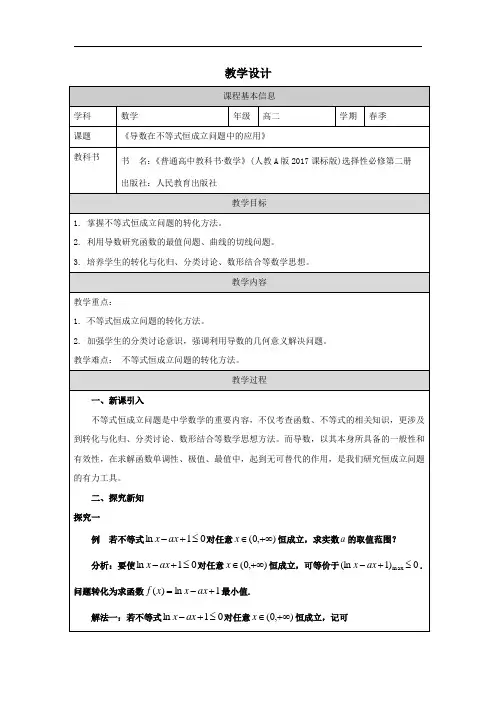


利用导数研究不等式恒成立(能成立)问题1.设函数f (x )=(1+x -x 2)e x (e =2.718 28…是自然对数的底数).(1)讨论f (x )的单调性;(2)当x ≥0时,f (x )≤ax +1+2x 2恒成立,求实数a 的取值范围.解:(1)f ′(x )=(2-x -x 2)e x =-(x +2)(x -1)e x .当x <-2或x >1时,f ′(x )<0;当-2<x <1时,f ′(x )>0.所以f (x )在(-∞,-2),(1,+∞)上单调递减,在(-2,1)上单调递增.(2)设F (x )=f (x )-(ax +1+2x 2),F (0)=0,F ′(x )=(2-x -x 2)e x -4x -a ,F ′(0)=2-a ,当a ≥2时,F ′(x )=(2-x -x 2)e x -4x -a ≤-(x +2)·(x -1)e x -4x -2≤-(x +2)(x -1)e x -x -2=-(x +2)·[(x -1)e x +1],设h (x )=(x -1)e x +1,h ′(x )=x e x ≥0,所以h (x )在[0,+∞)上单调递增,h (x )=(x -1)e x +1≥h (0)=0,即F ′(x )≤0在[0,+∞)上恒成立,F (x )在[0,+∞)上单调递减,F (x )≤F (0)=0,所以f (x )≤ax +1+2x 2在[0,+∞)上恒成立.当a <2时,F ′(0)=2-a >0,而函数F ′(x )的图象在(0,+∞)上连续且x →+∞,F ′(x )逐渐趋近负无穷,必存在正实数x 0使得F ′(x 0)=0且在(0,x 0)上F ′(x )>0,所以F (x )在(0,x 0)上单调递增,此时F (x )>F (0)=0,f (x )>ax +1+2x 2有解,不满足题意. 综上,a 的取值范围是[2,+∞).2.设函数f (x )=2ln x -mx 2+1.(1)讨论函数f (x )的单调性;(2)当f (x )有极值时,若存在x 0,使得f (x 0)>m -1成立,求实数m 的取值范围. 解:(1)函数f (x )的定义域为(0,+∞),f ′(x )=2x -2mx =-2(mx 2-1)x, 当m ≤0时,f ′(x )>0,∴f (x )在(0,+∞)上单调递增;当m >0时,令f ′(x )>0,得0<x <m m , 令f ′(x )<0,得x >m m , ∴f (x )在⎝⎛⎭⎫0,m m 上单调递增,在⎝⎛⎭⎫m m ,+∞上单调递减. (2)由(1)知,当f (x )有极值时,m >0,且f (x )在⎝⎛⎭⎫0,m m 上单调递增,在⎝⎛⎭⎫m m ,+∞上单调递减.∴f (x )max =f ⎝⎛⎭⎫m m =2ln m m -m ·1m +1=-ln m , 若存在x 0,使得f (x 0)>m -1成立,则f (x )max >m -1.即-ln m >m -1,ln m +m -1<0成立.令g (x )=x +ln x -1(x >0),∵g ′(x )=1+1x>0,∴g (x )在(0,+∞)上单调递增, 且g (1)=0,∴0<m <1.∴实数m 的取值范围是(0,1).3.(2020·西安质检)已知函数f (x )=ln x ,g (x )=x -1.(1)求函数y =f (x )的图象在x =1处的切线方程;(2)若不等式f (x )≤ag (x )对任意的x ∈(1,+∞)均成立,求实数a 的取值范围.解:(1)∵f ′(x )=1x,∴f ′(1)=1. 又∵f (1)=0,∴所求切线的方程为y -f (1)=f ′(1)(x -1),即为x -y -1=0.(2)易知对任意的x ∈(1,+∞),f (x )>0,g (x )>0.①当a ≥1时,f (x )<g (x )≤ag (x );②当a ≤0时,f (x )>0,ag (x )≤0,不满足不等式f (x )≤ag (x );③当0<a <1时,设φ(x )=f (x )-ag (x )=ln x -a (x -1),则φ′(x )=1x-a (x >1),令φ′(x )=0,得x =1a, 当x 变化时,φ′(x ),φ(x )的变化情况如下表:∴φ(x )max =φ⎝⎛⎭⎫1a >φ(1)=0,不满足不等式.综上所述,实数a 的取值范围为[1,+∞).4.已知函数f (x )=a x +x 2-x ln a (a >0,a ≠1).(1)求函数f (x )的极小值;(2)若存在x 1,x 2∈[-1,1],使得|f (x 1)-f (x 2)|≥e -1(e 是自然对数的底数),求实数a 的取值范围.解:(1)f ′(x )=a x ln a +2x -ln a =2x +(a x -1)ln a .∵当a >1时,ln a >0,函数y =(a x -1)ln a 在R 上是增函数,当0<a <1时,ln a <0,函数y =(a x -1)ln a 在R 上也是增函数,∴当a >1或0<a <1时,f ′(x )在R 上是增函数,又∵f ′(0)=0,∴f ′(x )>0的解集为(0,+∞),f ′(x )<0的解集为(-∞,0),故函数f (x )的单调递增区间为(0,+∞),单调递减区间为(-∞,0),∴函数f (x )在x =0处取得极小值1.(2)∵存在x 1,x 2∈[-1,1],使得|f (x 1)-f (x 2)|≥e -1,∴只需f (x )max -f (x )min ≥e -1即可.由(1)可知,当x ∈[-1,1]时,f (x )在[-1,0]上是减函数,在(0,1]上是增函数, ∴当x ∈[-1,1]时,f (x )min =f (0)=1,f (x )max 为f (-1)和f (1)中的较大者.f (1)-f (-1)=(a +1-ln a )-⎝⎛⎭⎫1a +1+ln a =a -1a-2ln a , 令g (a )=a -1a-2ln a (a >0), ∵g ′(a )=1+1a 2-2a =⎝⎛⎭⎫1-1a 2>0, ∴g (a )=a -1a-2ln a 在(0,+∞)上是增函数. 而g (1)=0,故当a >1时,g (a )>0,即f (1)>f (-1);当0<a <1时,g (a )<0,即f (1)<f (-1).∴当a >1时,f (1)-f (0)≥e -1,即a -ln a ≥e -1.由函数y =a -ln a 在(1,+∞)上是增函数,解得a ≥e ;当0<a <1时,f (-1)-f (0)≥e -1,即1a+ln a ≥e -1, 由函数y =1a +ln a 在(0,1)上是减函数,解得0<a ≤1e. 综上可知,所求实数a 的取值范围为⎝⎛⎦⎤0,1e ∪[e ,+∞).。
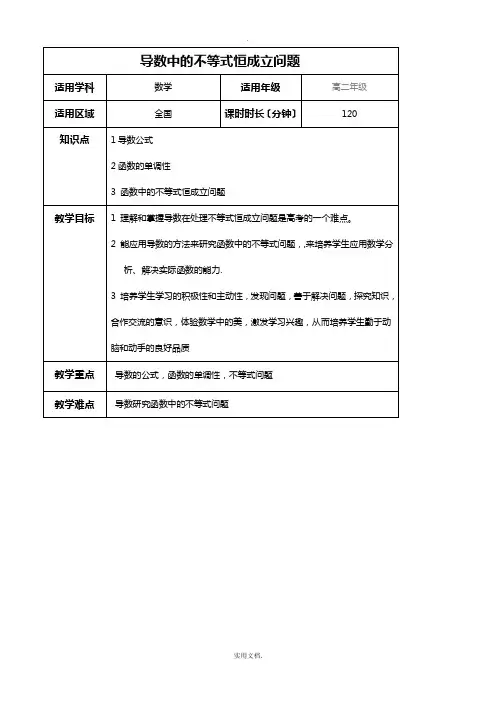
学习过程一、复习预习考纲要求:1.理解导数和切线方程的概念。
2.能在具体的数学环境中,会求导,会求切线方程。
3.特别是没有具体点处的切线方程,如何去设点,如何利用点线式建立直线方程。
4.灵活应用建立切线方程与其它数学知识之间的内在联系。
5. 灵活应用导数研究函数的单调性问题二、知识讲解1.导数的计算公式和运算法那么几种常见函数的导数:0'=C (C 为常数);1)'(-=n n nx x (Q n ∈);x x cos )'(sin =; x x sin )'(cos -=;1(ln )x x '=; 1(log )log a a x e x'=, ()x x e e '= ; ()ln x x a a a '= 求导法那么:法那么1 [()()]()()u x v x u x v x ±'='±'.法那么2 [()()]()()()()u x v x u x v x u x v x '='+', [()]'()Cu x Cu x '=法那么3: '2''(0)u u v uv v v v -⎛⎫=≠ ⎪⎝⎭复合函数的导数:设函数()u x ϕ=在点x 处有导数()x u x ϕ'=',函数()y f u =在点x 的对应点u 处有导数()u y f u '=',那么复合函数(())y f x ϕ=在点x 处也有导数,且x u x u y y '''⋅= 或(())()()x f x f u x ϕϕ'='⋅'2.求直线斜率的方法〔高中范围内三种〕(1) tan k α=〔α为倾斜角〕; (2) 1212()()f x f x k x x -=-,两点1122(,()),(,())x f x x f x ; (3)0()k f x '= 〔在0x x =处的切线的斜率〕;3.求切线的方程的步骤:〔三步走〕〔1〕求函数()f x 的导函数()f x ';〔2〕0()k f x '= 〔在0x x =处的切线的斜率〕;〔3〕点斜式求切线方程00()()y f x k x x -=-;4.用导数求函数的单调性:〔1〕求函数()f x 的导函数()f x ';〔2〕()0f x '>,求单调递增区间;〔3〕()0f x '<,求单调递减区间;〔4〕()0f x '=,是极值点。



第五节 利用导数解决不等式恒(能)成立问题考点1 恒成立问题分离参数法求范围若f (x )≥a 或g (x )≤a 恒成立,只需满足f (x )min ≥a 或g (x )max ≤a 即可,利用导数方法求出f (x )的最小值或g (x )的最大值,从而问题得解.已知f (x )=x ln x ,g (x )=x 3+ax 2-x +2. (1)求函数f (x )的单调区间;(2)若对任意x ∈(0,+∞),2f (x )≤g ′(x )+2恒成立,求实数a 的取值范围. [解] (1)因为函数f (x )=x ln x 的定义域为(0,+∞),所以f ′(x )=ln x +1.令f ′(x )<0,得ln x +1<0,解得0<x <1e ,所以f (x )的单调递减区间是(0,1e ).令f ′(x )>0,得ln x +1>0,解得x >1e ,所以f (x )的单调递增区间是(1e ,+∞).综上,f (x )的单调递减区间是(0,1e ),单调递增区间是(1e ,+∞).(2)因为g ′(x )=3x 2+2ax -1,由题意得2x ln x ≤3x 2+2ax +1恒成立.因为x >0,所以a ≥ln x -32x -12x 在x ∈(0,+∞)上恒成立.设h (x )=ln x -32x -12x (x >0),则h ′(x )=1x -32+12x 2=-(x -1)(3x +1)2x 2.令h ′(x )=0,得x 1=1,x 2=-13(舍).当x 变化时,h ′(x ),h (x )的变化情况如下表:x (0,1) 1 (1,+∞)h ′(x )+-h (x )极大值max =h (1)=-2,所以若a ≥h (x )在x ∈(0,+∞)上恒成立,则a ≥h (x )max =-2,即a ≥-2,故实数a 的取值范围是[-2,+∞).利用分离参数法来确定不等式f (x ,λ)≥0(x ∈D ,λ为实参数)恒成立问题中参数取值范围的基本步骤:(1)将参数与变量分离,化为f 1(λ)≥f 2(x )或f 1(λ)≤f 2(x )的形式. (2)求f 2(x )在x ∈D 时的最大值或最小值.(3)解不等式f 1(λ)≥f 2(x )max 或f 1(λ)≤f 2(x )min ,得到λ的取值范围.把参数看作常数利用分类讨论方法解决对于不适合分离参数的不等式,常常将参数看作常数直接构造函数,常用分类讨论法,利用导数研究单调性、最值,从而得出参数范围.已知函数f (x )=ln x -ax ,a ∈R . (1)求函数f (x )的单调区间;(2)若不等式f (x )+a <0在x ∈(1,+∞)上恒成立,求a 的取值范围. [解] (1)函数f (x )的定义域为(0,+∞),f ′(x )=1x -a . ①当a ≤0时,f ′(x )>0恒成立, 则f (x )只有单调递增区间是(0,+∞). ②当a >0时,由f ′(x )>0, 得0<x <1a ; 由f ′(x )<0,得x >1a ;所以f (x )的单调递增区间是(0,1a ),单调递减区间是(1a ,+∞).(2)f(x)+a<0在x∈(1,+∞)上恒成立,即ln x-a(x-1)<0在x∈(1,+∞)上恒成立.设g(x)=ln x-a(x-1),x>0,则g′(x)=1x-a,注意到g(1)=0,①当a≥1时,g′(x)<0在x∈(1,+∞)上恒成立,则g(x)在x∈(1,+∞)上单调递减,所以g(x)<g(1)=0,即a≥1时满足题意.②当0<a<1时,令g′(x)>0,得1<x<1a;令g′(x)<0,得x>1a.则g(x)在(1,1a)上单调递增,所以当x∈(1,1a)时,g(x)>g(1)=0,即0<a<1时不满足题意(舍去).③当a≤0时,g′(x)=1x-a>0,则g(x)在(1,+∞)上单调递增,所以当x∈(1,+∞)时,g(x)>g(1)=0,即a≤0时不满足题意(舍去).综上所述,实数a的取值范围是[1,+∞).已知f(x)=ax2-2ln x,a∈R.(1)讨论函数f(x)的单调性;(2)若对任意的x>0,2-f(x)≤2(a-1)x恒成立,求整数a的最小值.[解](1)由题意得f(x)的定义域为(0,+∞),且f′(x)=2ax2-2x.①当a≤0时,f′(x)<0,f(x)在(0,+∞)内单调递减.②当a>0时,令f′(x)=0,得x=aa 或x=-aa(负值舍去).当x∈(0,aa),f′(x)<0,f(x)单调递减;当x∈(aa,+∞),f′(x)>0,f(x)单调递增.(2)由题意得2-ax2+2ln x≤2(a-1)x,整理得2(ln x+x+1)≤a(2x+x2).因为x>0,所以原命题等价于a≥2(ln x+x+1)(2x+x2)在区间(0,+∞)内恒成立.令g(x)=2(ln x+x+1)2x+x2,则g′(x)=-2(x+1)(2ln x+x)(2x+x2)2,令h(x)=2ln x+x,易知h(x)在(0,+∞)内单调递增.又h(0.5)=-2ln 2+0.5<0,h(1)=1>0,故存在唯一的x0∈(0.5,1),使得h(x0)=0.当0<x<x0时,h(x)<0,即g′(x)>0,g(x)单调递增;当x>x0时,h(x)>0,即g′(x)<0,g(x)单调递减.故函数g(x)的极大值为g(x0),也为最大值,且2ln x0+x0=0,所以g(x)max=2(ln x0+x0+1)2x0+x20=x0+2x0(x0+2)=1x0,所以a≥1x0.又1x0∈(1,2),且a为整数,故整数a的最小值为2.考点2 能成立问题存在x ∈[a ,b ],f (x )≥a 成立⇔f (x )max ≥a . 存在x ∈[a ,b ],f (x )≤a 成立⇔f (x )min ≤a .存在x 1∈[a ,b ],对任意x 2∈[a ,b ],f (x 1)≤g (x 2)成立⇔f (x )min ≤g (x )min .已知函数f (x )=3ln x -12x 2+x ,g (x )=3x +a . (1)若f (x )与g (x )的图象相切,求a 的值;(2)若∃x 0>0,使f (x 0)>g ′(x 0)成立,求参数a 的取值范围.[解] (1)由题意得,f ′(x )=3x -x +1,g ′(x )=3,设切点为(x 0,f (x 0)),则k =f ′(x 0)=3x 0-x 0+1=3,解得x 0=1或x 0=-3(舍),所以切点为(1,12),代入g (x )=3x +a ,得a =-52.(2)设h (x )=3ln x -12x 2-2x .∃x 0>0,使f (x 0)>g (x 0)成立, 等价于∃x >0,使h (x )=3ln x -12x 2-2x >a 成立, 等价于a <h (x )max (x >0). 因为h ′(x )=3x -x -2=-x 2-2x +3x=-(x -1)(x +3)x,令⎩⎪⎨⎪⎧h ′(x )>0,x >0,得0<x <1;令⎩⎪⎨⎪⎧h ′(x )<0,x >0,得x >1. 所以函数h (x )=3ln x -12x 2-2x 在(0,1)上单调递增, 在(1,+∞)上单调递减,所以h (x )max =h (1)=-52, 即a <-52,因此参数a 的取值范围为(-∞,-52).(1)“恒成立”“存在性”问题一定要正确理解其实质,深刻挖掘内含条件,进行等价转化.(2)构造函数是求范围问题中的一种常用方法,解题过程中尽量采用分离参数的方法,转化为求函数的最值问题.已知函数f (x )=ax -e x(a ∈R ),g (x )=ln xx .(1)求函数f (x )的单调区间;(2)∃x 0∈(0,+∞),使不等式f (x )≤g (x )-e x 成立,求a 的取值范围. [解] (1)因为f ′(x )=a -e x ,x ∈R .当a ≤0时,f ′(x )<0,f (x )在R 上单调递减; 当a >0时,令f ′(x )=0得x =ln a .由f ′(x )>0得x <ln a ,所以f (x )的单调递增区间为(-∞,ln a ); 由f ′(x )<0得x >ln a ,所以f (x )的单调递减区间为(ln a ,+∞).(2)因为∃x 0∈(0,+∞),使不等式f (x )≤g (x )-e x ,则ax ≤ln x x ,即a ≤ln xx 2. 设h (x )=ln x x 2,则问题转化为a ≤(ln xx 2)max , 由h ′(x )=1-2ln xx 3, 令h ′(x )=0,则x = e.当x 在区间(0,+∞)内变化时,h ′(x ),h (x )的变化情况如下表:x (0,e) e (e ,+∞)h ′(x ) +0 -h (x )极大值12e由上表可知,当x =e 时,函数h (x )有极大值,即最大值为12e ,所以a ≤12e .。

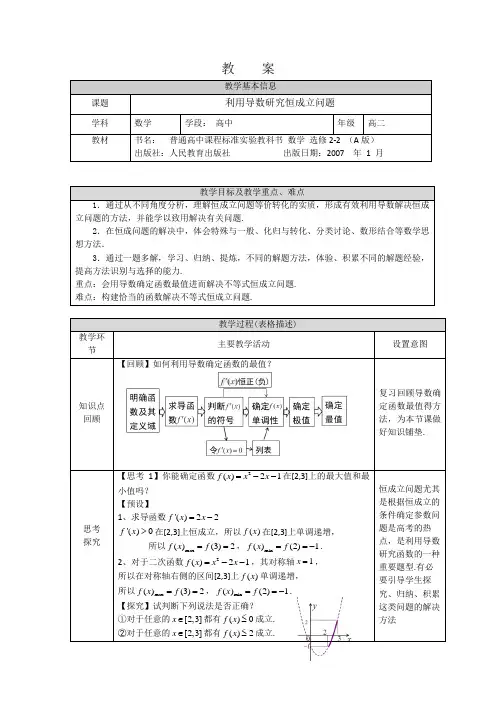
教案教学基本信息课题利用导数研究恒成立问题学科数学学段:高中年级高二教材书名:普通高中课程标准实验教科书数学选修2-2 (A版)出版社:人民教育出版社出版日期:2007 年1 月教学目标及教学重点、难点1.通过从不同角度分析,理解恒成立问题等价转化的实质,形成有效利用导数解决恒成立问题的方法,并能学以致用解决有关问题.2.在恒成问题的解决中,体会特殊与一般、化归与转化、分类讨论、数形结合等数学思想方法.3.通过一题多解,学习、归纳、提炼,不同的解题方法,体验、积累不同的解题经验,提高方法识别与选择的能力.重点:会用导数确定函数最值进而解决不等式恒成立问题.难点:构建恰当的函数解决不等式恒成立问题.教学过程(表格描述)教学环节主要教学活动设置意图知识点回顾【回顾】如何利用导数确定函数的最值?复习回顾导数确定函数最值得方法,为本节课做好知识铺垫.思考探究【思考1】你能确定函数2()21f x x x=--在[2,3]上的最大值和最小值吗?【预设】1、求导函数'()22f x x=-'()0f x>在[2,3]上恒成立,所以()f x在[2,3]上单调递增,所以max()(3)2f x f==,min()(2)1f x f==-.2、对于二次函数2()21f x x x=--,其对称轴1x=,所以在对称轴右侧的区间[2,3]上()f x单调递增,所以max()(3)2f x f==,min()(2)1f x f==-.【探究】试判断下列说法是否正确?①对于任意的[2,3]x∈都有()0f x≤成立.②对于任意的[2,3]x∈都有()2f x≤成立.恒成立问题尤其是根据恒成立的条件确定参数问题是高考的热点,是利用导数研究函数的一种重要题型.有必要引导学生探究、归纳、积累这类问题的解决方法思考 探究【探究】若对于任意的[2,3]x ∈都有()f x c ≤成立,你能确定实数c 的取值范围吗? 【预设】1、 一方面实数c 不小于()f x 在[2,3]的 所有函数值,c 大于等于()f x 在[2,3]上 的最大值即可;2、另一方面可以看成函数()y f x =与常数函数y c =函数值的大小关系,借助函数图象可以看出c 的取值范围.【思考2】对于函数2()21f x x x =-- .【探究】试判断下列说法是否正确?③对于任意的[2,3]x ∈都有()0f x ≥成立.④对于任意的[2,3]x ∈都有()-1f x ≥成立.【探究】若对于任意的[2,3]x ∈都有()f x m ≥成立,你能确定实数m 的取值范围吗? 【预设】1、一方面实数m 不大于()f x 在[2,3]上的所有函数值,m 小于等于()f x 在[0,2]上的最小值即可;2、另一方面,可以看成函数()y f x =与常数函数y m =函数值的大小关系,同样借助函数图象可以看出m 的取值范围.【思考3】已知函数31()3f x x x =-.下面两个说法是否正确?①对于任意的[0,2]x ∈,都有()0f x ≥成立? ②对于任意的[0,2]x ∈,都有()1f x ≤成立?【分析】判断两个说法是否正确的关键点是的什么? 利用导数确定函数()f x 在[0,2]上的最值,借助函数图象,做出判断.【预设】31()3f x x x =-,[0,2]x ∈,2'()1f x x =-,令'()0f x =,解得11x =,21x =-当x 变化时,'()f x ,()f x 的变化情况如下表:x0 (0,1)1 (1,2)2 '()f x -0 +()f x极小值23因为(0)0f =,2(2)3f =,所以max 2()3f x =,min 2()(1)3f x f ==-.【探究】从学生熟悉的简单的二次函数入手,再到三次函数复习巩固确定函数最值的方法,通过设问让学生思考判断一些结论是否正确,逐步帮助学生理解恒成立问题的本质,体会恒成立问题与函数最值的关系。
第04讲 利用导数研究不等式恒成立问题 (精讲+精练)目录第一部分:知识点精准记忆 第二部分:课前自我评估测试 第三部分:典型例题剖析 高频考点一:分离变量法 高频考点二:分类讨论法 高频考点三:等价转化法 第四部分:高考真题感悟第五部分:第04讲 利用导数研究不等式恒成立问题(精练)1、分离参数法用分离参数法解含参不等式恒成立问题,可以根据不等式的性质将参数分离出来,得到一个一端是参数,另一端是变量表达式的不等式; 步骤:①分类参数(注意分类参数时自变量x 的取值范围是否影响不等式的方向)②转化:若()a f x >)对x D ∈恒成立,则只需max ()a f x >;若()a f x <对x D ∈恒成立,则只需min ()a f x <. ③求最值.2、分类讨论法如果无法分离参数,可以考虑对参数或自变量进行分类讨论求解,如果是二次不等式恒成立的问题,可以考虑二次项系数与判别式的方法(0a >,0∆<或0a <,0∆<)求解.3、等价转化法当遇到()()f x g x ≥型的不等式恒成立问题时,一般采用作差法,构造“左减右”的函数()()()F x f x g x =-或者“右减左”的函数()()()H x g x f x =-,进而只需满足min ()0F x ≥,或者max ()0H x ≤,将比较法的思想融入函数中,转化为求解函数的最值的问题.1.(2022·全国·高二)设a 为正实数,函数322()34f x x ax a =-+,若(,2)x a a ∀∈,()0f x <,则a 的取值范围是( )A .[2,)+∞B .(2,)+∞C .(0,2]D .2(0,)32.(2022·全国·高二)若不等式4342x x a ->-对任意实数x 都成立,则实数a 的取值范围是( ) A .27a <-B .25a >-C .29a ≥D .29a >3.(2022·全国·高二)已知函数()22f x ax x a =-+,对[]1,2x ∀∈都有()0f x ≤成立,则实数a 的取值范围是( )A .(],0-∞B .4,5⎛⎤-∞ ⎥⎝⎦C .(],1-∞D .[]1,0-高频考点一:分离变量法1.(2022·全国·高三专题练习)设a R ∈,若不等式ln ax x >在()1,x ∞∈+上恒成立,则实数a 的取值范围是( ) A .()0,∞+B .1,e ⎛⎫+∞ ⎪⎝⎭C .()1,∞+D .()e,+∞2.(2022·内蒙古乌兰察布·高二期末(文))已知函数2()ln 2a f x x x =+,若对任意两个不等的正数1x ,2x ,都有1212()()4f x f x x x -≥-恒成立,则a 的取值范围为( )A .[)4∞+,B .()4.∞+C .(]4∞-,D .()4∞-,3.(2022·全国·高三专题练习)已知对(0,)x ∀∈+∞,不等式ln 1ax x ≥-恒成立,则实数a 的最小值是( ) A .eB .2eC .21e D .1e4.(2022·河南·高二阶段练习(理))已知当0x >时,()21e 1x x a x -≤--恒成立,则实数a 的取值范围是( )A .(],e 1-∞-B .(],1-∞C .(]2,e 1--D .(],2-∞-5.(2022·湖南·临澧县第一中学高二阶段练习)已知函数()ln af x x x=+(a 为常数) (1)讨论函数()f x 的单调性; (2)不等式()1f x ≥在2(]0,x ∈上恒成立,求实数a 的取值范围.6.(2022·重庆市育才中学高二阶段练习)已知函数()1ln f x ax x =--,a R ∈. (1)讨论函数()f x 在区间()1,e 的极值;(2)若函数()f x 在1x =处取得极值,对()0,x ∀∈+∞,()2f x bx ≥-恒成立,求实数b 的取值范围.7.(2022·四川省泸县第一中学高二阶段练习(理))已知函数()e 1()x f x ax a =-+∈R . (1)讨论函数()f x 的单调性与极值;(2)若对任意0x >,2()f x x x ≥--恒成立,求实数a 的取值范围.8.(2022·河南·三模(文))已知函数()e x f x ax b =++(e 是自然对数的底数),曲线()y f x =在点()()0,0f 处的切线为y a b =-. (1)求a ,b 的值;(2)若不等式()1f x mx >-在1,e e x ⎡⎤∈⎢⎥⎣⎦上恒成立,求正实数m 的取值范围.高频考点二:分类讨论法1.(2022·广西柳州·三模(文))已知函数()ln f x ax x =-. (1)讨论函数()f x 的单调性;(2)若1x =为函数()f x 的极值点,当[)e,x ∞∈+,不等式()()()1e x f x x m x -+≤-恒成立,求实数m 的取值范围.2.(2022·陕西西安·二模(文))已知函数()()1ln f x a x a x=+∈R . (1)当1a =时,求函数()f x 的单调减区间;(2)若不等式()f x x ≥对(]0,1x ∈恒成立,求实数a 的取值范围.3.(2022·河南·高二阶段练习(文))已知曲线()ln f x m x =+在1x =处的切线方程为()y h x =,且210e f ⎛⎫= ⎪⎝⎭.(1)求()h x 的解析式;(2)若0x ≥时,不等式()20e x ax h x --≥恒成立,求实数a 的取值范围.4.(2022·全国·高三专题练习)已知函数()e xf x =,曲线()y f x =在点()00,x y 处的切线为()yg x =.(1)证明:对于x R ∀∈,()()f x g x ≥; (2)当0x ≥时,()11axf x x≥++恒成立,求实数a 的取值范围.5.(2022·四川·树德中学高三开学考试(文))已知a ∈R ,设函数()()ln ln f x a x a x =++. (1)讨论函数()f x 的单调性; (2)若()2ln xf x a x a≤+恒成立,求实数a 的取值范围.6.(2022·贵州黔东南·一模(文))已知函数()22ln f x x a x =-.(1)讨论()f x 的单调性;(2)当x >1时,()1f x >恒成立,求a 的取值范围.高频考点三:等价转化法1.(2022·河南·民权县第一高级中学高三阶段练习(文))已知函数()1ln f x a x x=+,()()1e 1,x g x x mx a m x =+--∈R . (1)讨论f (x )的单调性;(2)当a =1时,若不等式()()f x g x ≤恒成立,求m 的取值范围.2.(2022·江苏·高二课时练习)已知函数()ln f x ax x =+,()()220g x a x a =>.若()()f x g x ≤对一切正实数x 都成立,求实数a 的取值范围.3.(2022·全国·高三专题练习)已知函数()()2ln f x x a x =+,()2g x ax x =+.(1)当0a =时,求函数()f x 的最小值;(2)当0a ≤时,若对任意1≥x 都有()()f x g x ≥成立,求实数a 的取值范围.4.(2022·江西·南昌市实验中学高二阶段练习(理))已知函数()2ln f x x a x =+,()2g x x x =+.(1)若()y f x =在点()()1,1M f 处的切线方程为30x y b -+=,求实数a 、b 的值; (2)若对任意1x >,都有()()f x g x ≤成立,求实数a 的取值范围.5.(2022·山东日照·高三期末)已知函数()ln f x x ax b =-+,中,a b ∈R . (1)当0a >时,求()f x 的单调区间;(2)若[]()1,0,2,ln 1a b x kx x x ϕ=∈=--,对任意实数[]()()1,e ,x f x x ϕ∈≥恒成立,求2k b -的最大值.高频考点四:最值法1.(2022·重庆市朝阳中学高二阶段练习)已知函数321()22f x x x x m =--+,其中.m R ∈(1)若函数()f x 的极小值为0,求实数m 的值; (2)当[1,2]x ∈-时,1()2f x 恒成立,求实数m 的取值范围.2.(2022·重庆市长寿中学校高二阶段练习)已知函数()()2ln 0f x a x ax a =+-> (1)求()f x 的最大值(2)若()0f x ≤恒成立,求a 的值3.(2022·江西·模拟预测(文))已知函数()222(0)exmx x f x m +-=>. (1)判断()f x 的单调性;(2)若对[]12,1,2x x ∀∈,不等式()()1224ef x f x -≤恒成立,求实数m 的取值范围.4.(2022·河南·高二阶段练习(文))已知函数()32f x x ax bx c =+++在23x =-与1x =处都取得极值.(1)求a ,b 的值;(2)若对任意[]1,2x ∈-,不等式()23f x c <恒成立,求实数c 的取值范围.5.(2022·全国·高三专题练习)已知函数()()()221n l 0f x ax a x a x=-+->. (1)讨论函数()f x 的单调性;(2)若对[]2,3a ∀∈,[]12,1,2x x ∀∈,不等式()()12ln 2m f x f x +>-恒成立,求实数m 的取值范围.6.(2022·全国·高三专题练习)已知曲线()()3,f x ax bx a b =+∈R 在点()()1,1f 处的切线方程是20y +=.(1)求()f x 的解析式;(2)若对任意[]12,2,3x x ∈-,都有()()12f x f x m -,求实数m 的取值范围.1.(2019·天津·高考真题(理))已知a R ∈,设函数222,1,()ln ,1,x ax a x f x x a x x ⎧-+=⎨->⎩若关于x 的不等式()0f x 在R 上恒成立,则a 的取值范围为 A .[]0,1B .[]0,2C .[]0,eD .[]1,e2.(2020·海南·高考真题)已知函数1()e ln ln x f x a x a -=-+.(1)当a e =时,求曲线()y f x =在点()()1,1f 处的切线与两坐标轴围成的三角形的面积; (2)若不等式()1f x ≥恒成立,求a 的取值范围.3.(2020·全国·高考真题(理))已知函数2()e x f x ax x =+-. (1)当a =1时,讨论f (x )的单调性;(2)当x ≥0时,f (x )≥12x 3+1,求a 的取值范围.4.(2019·全国·高考真题(文))已知函数f (x )=2sin x -x cos x -x ,f′(x )为f (x )的导数. (1)证明:f′(x )在区间(0,π)存在唯一零点; (2)若x ∈[0,π]时,f (x )≥ax ,求a 的取值范围.一、单选题1.(2022·河南南阳·高二期末(文))若函数()ln f x kx x =-在区间(1,)+∞单调递增,则k 的取值范围是( ) A .[1,)+∞ B .(1,)+∞ C .[2,)+∞ D .(,2)-∞-2.(2022·全国·高二)函数f (x )=13x 3-x 2+a ,函数g (x )=x 2-3x ,它们的定义域均为[1,+∞),并且函数f (x )的图象始终在函数g (x )图象的上方,那么a 的取值范围是( ) A .(0,+∞)B .(-∞,0)C .4,3⎛-+∞⎫ ⎪⎝⎭D .4,3⎛⎫-∞- ⎪⎝⎭3.(2022·全国·高三阶段练习(理))已知()xae f x x x =-,()0,x ∈+∞,且1x ∀,()20,x ∈+∞,且12x x <,()()12210f x f x x x -<恒成立,则a 的取值范围是( )A .12,e ∞-⎛⎤- ⎥⎝⎦B .2,e ⎡⎫+∞⎪⎢⎣⎭C .(2,e ⎤-∞⎦D .13,e ⎛⎫+∞ ⎪⎝⎭4.(2022·全国·高二)已知函数()()e 10xx a f a x =--≠在[]1,2上是减函数,则实数a 的取值范围是( )A .21,e ⎛⎤-∞ ⎥⎝⎦B .21,e ⎡⎫+∞⎪⎢⎣⎭C .210,e ⎛⎤⎥⎝⎦D .211,e e ⎡⎤⎢⎥⎣⎦5.(2022·重庆市清华中学校高二阶段练习)已知函数()()31e 1x f x x kx =--+,若对任意的()12,0,x x ∈+∞,且12x x ≠,都有()()()()11222112x f x x f x x f x x f x +>+,则实数k 的取值范围是( ) A .e ,3∞⎛⎫- ⎪⎝⎭B .e ,3⎛⎤-∞ ⎥⎝⎦C .1,3⎛⎫-∞ ⎪⎝⎭D .1,3⎛⎤-∞ ⎥⎝⎦6.(2022·山西临汾·二模(理))已知函数22,1()ln ,1x ax a x f x x a x x ⎧-+≤=⎨->⎩,若()0f x ≥恒成立.则a 的取值范围为( )A .[0,1]B .[0,2e]C .[1,2]D .[2,2e]7.(2022·浙江·义乌市商城学校高二阶段练习)已知m ,n 为实数,不等式ln 0x mx n --≤恒成立,则nm的最小值为( ) A .1-B .2-C .1D .28.(2022·宁夏中卫·一模(理))已知定义域为(0,)+∞的函数()f x 满足2()1()f x f x x x'+=,且2(e)e f =,e 为自然对数的底数,若关于x 的不等式()20f x a x x x--+≤恒成立,则实数a 的取值范围为( ) A .[1,)+∞B .[2,)+∞C .2,e e +⎡⎫+∞⎪⎢⎣⎭D .322,e e e ⎡⎫-+++∞⎪⎢⎣⎭二、填空题 9.(2022·全国·高二课时练习)当(]0,1x ∈时,不等式32430ax x x -++≥恒成立,则实数a 的取值范围是______.10.(2022·上海交大附中高二阶段练习)已知()2ln f x x ax a =-+,若对任意1≥x ,都有()0f x ≤,则实数a 的取值范围是______.11.(2022·江苏省石庄高级中学高二阶段练习)已知函数()ln x f x x =.若对任意[)12,,x x a ∞∈+,都有()()121ef x f x -≤成立,则实数a 的最小值是________.12.(2022·河南·民权县第一高级中学高三阶段练习(文))设函数f (x )在区间I 上有定义,若对12,x x I ∀∈和()0,1λ∀∈,都有()()()()()121211f x x f x f x λλλλ+-≤+-,那么称f (x )为I 上的凹函数,若不等号严格成立,即“<”号成立,则称f (x )在I 上为严格的凹函数.对于上述不等式的证明,19世纪丹麦数学家琴生给出了如下的判断方法:设定义在(a ,b )上的函数f (x ),其一阶导数为()f x ',其二阶导数为()f x ''(即对函数()f x '再求导,记为()f x ''),若()0f x ''>,那么函数f (x )是严格的凹函数(()f x ',()f x ''均可导).试根据以上信息解决如下问题:函数()21ln f x m x x x =++在定义域内为严格的凹函数,则实数m 的取值范围为___________. 三、解答题13.(2022·福建省厦门集美中学高二阶段练习)已知函数()ln f x x x =,(1)求过点(0,1)-的函数()f x 的切线方程(2)若对任意0x >,都有ln()x ax x a ≥-成立,求正数a 的取值范围.14.(2022·四川·成都外国语学校高二阶段练习(文))已知函数()()1ln f x x x =+(1)求函数()f x 的单调区间和极值;(2)若m Z ∈,()()1m x f x -<对任意的()1,x ∈+∞恒成立,求m 的最大值.15.(2022·陕西·武功县普集高级中学高三阶段练习(理))已知函数()()e ln 1x f x a x =+-+,()'f x 是其导函数,其中a R ∈.(1)若()f x 在(,0)-∞上单调递减,求a 的取值范围;(2)若不等式()()f x f x '≤对(,0)x ∀∈-∞恒成立,求a 的取值范围.16.(2022·四川达州·二模(文))已知()()e 1x f x mx m =+<-.(1)当2m =-时,求曲线()y f x =上的斜率为1-的切线方程;(2)当0x ≥时,()2213222m f x x ≥+-恒成立,求实数m 的范围.。
利用导数解决恒成立能成立问题利用导数解决恒成立能成立问题一利用导数解决恒成立问题不等式恒成立问题的常规处理方式?(常应用函数方程思想和“分离变量法”转化为最值问题,也可抓住所给不等式的结构特征,利用数形结合法)(1)恒成立问题若不等式()A x f >在区间D 上恒成立,则等价于在区间D 上()min f x A >若不等式()B x f <在区间D 上恒成立,则等价于在区间D 上()max f x B <1.若在x∈[1,+∞)上恒成立,则a 的取值范围是 ______ .2.若不等式x 4﹣4x 3>2﹣a 对任意实数x 都成立,则实数a 的取值范围 _________ .3.设a >0,函数,若对任意的x 1,x 2∈[1,e],都有f (x 1)≥g(x 2)成立,则a 的取值范围为 _________ .4.若不等式|ax 3﹣lnx|≥1对任意x∈(0,1]都成立,则实数a 取值范围是 _________ .15.设函数f(x)的定义域为D,令M={k|f(x)≤k恒成立,x∈D},N={k|f(x)≥k恒成立,x∈D},已知,其中x∈[0,2],若4∈M,2∈N,则a 的范围是_________ .6.f(x)=ax3﹣3x(a>0)对于x∈[0,1]总有f(x)≥﹣1成立,则a的范围为_________ .7.三次函数f(x)=x3﹣3bx+3b在[1,2]内恒为正值,则b的取值范围是_________ .8.不等式x3﹣3x2+2﹣a<0在区间x∈[﹣1,1]上恒成立,则实数a的取值范围是__ .9.当x∈(0,+∞)时,函数f(x)=e x的图象始终在直线y=kx+1的上方,则实数k的取值范围是_________ .10.设函数f(x)=ax3﹣3x+1(x∈R),若对于任意的x∈[﹣1,1]都有f(x)≥0成立,则实数a的值为_________ .11.若关于x 的不等式x 2+1≥kx 在[1,2]上恒成立,则实数k 的取值范围是 _________ .12.已知f (x )=ln (x 2+1),g (x )=()x ﹣m ,若∀x 1∈[0,3],∃x 2∈[1,2],使得f (x 1)≥g(x 2),则实数m 的取值范围是( )A . [,+∞)B . (﹣∞,]C . [,+∞)D . (﹣∞,﹣] 13.已知,,若对任意的x 1∈[﹣1,2],总存在x 2∈[﹣1,2],使得g (x 1)=f (x 2),则m 的取值范围是( )A . [0,]B . [,0]C . [,]D . [,1]二利用导数解决能成立问题若在区间D 上存在实数x 使不等式()A x f >成立,则等价于在区间D 上()max f x A >;若在区间D 上存在实数x 使不等式()B x f <成立,则等价于在区间D 上的()min f x B <.如14.已知集合A={x∈R|≤2},集合B={a∈R|已知函数f(x)=﹣1+lnx,∃x0>0,使f(x0)≤0成立},则A∩B=()A.{x|x <}B.{x|x≤或x=1}C.{x|x<或x=1}D.{x|x <或x≥1}15.设函数,(p是实数,e为自然对数的底数)(1)若f(x)在其定义域内为单调函数,求p的取值范围;(2)若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求p的取值范围.16.若函数y=f(x),x∈D同时满足下列条件:(1)在D内的单调函数;(2)存在实数m,n,当定义域为[m,n]时,值域为[m,n].则称此函数为D内可等射函数,设(a>0且a≠1),则当f (x)为可等射函数时,a的取值范围是.17.存在x<0使得不等式x2<2﹣|x﹣t|成立,则实数t 的取值范围是_________ .18.存在实数x,使得x2﹣4bx+3b<0成立,则b的取值范围是_________ .19.已知存在实数x使得不等式|x﹣3|﹣|x+2|≥|3a﹣1|成立,则实数a的取值范围是_ .20.存在实数a使不等式a≤2﹣x+1在[﹣1,2]成立,则a的范围为_________ .21.若存在x∈,使成立,则实数a的取值范围为______ .22.设存在实数,使不等式成立,则实数t的取值范围为_________ .23.若存在实数p∈[﹣1,1],使得不等式px2+(p﹣3)x ﹣3>0成立,则实数x的取值范围为_________ .24.若存在实数x使成立,求常数a的取值范围.25.等差数列{a n}的首项为a1,公差d=﹣1,前n项和为S n,其中a1∈{﹣1,1,2}(I )若存在n∈N,使S n=﹣5成立,求a1的值;.(II)是否存在a1,使S n<a n对任意大于1的正整数n均成立?若存在,求出a1的值;否则,说明理由.参考答案1若在x∈[1,+∞)上恒成立,则a的取值范围是(﹣∞,].考点:利用导数求闭区间上函数的最值;函数恒成立问题.专综合题.题:分析:把等价转化为lnx≥a﹣1﹣,得到lnx+≥a﹣1,从而原题等价转化为y=x+在x∈[1,+∞)上的最小值不小于a﹣1,由此利用导数知识能够求出a的取值范围.解答:解:∵=a ﹣1﹣,∴lnx+≥a﹣1,∵在x∈[1,+∞)上恒成立,∴y=x+在x∈[1,+∞)上的最小值不小于a﹣1,∵,令=0,得x=1,或x=﹣1(舍),∴x∈[1,+∞)时,>0,∴y=x+在x∈[1,+∞)上是增函数,∴当x=1时,y=x+在x∈[1,+∞)上取最小值1+=,故,所以a.故答案为:(﹣∞,].点评:本题考查实数的取值范围的求法,具体涉及到分离变量法、导数性质、等价转化思想等知识点的灵活运用,解题时要关键是在x∈[1,+∞)上恒成立等价转化为y=x+在x∈[1,+∞)上的最小值不小于a﹣1.2.若不等式x4﹣4x3>2﹣a对任意实数x都成立,则实数a 的取值范围(29,+∞).考点:利用导数求闭区间上函数的最值;函数恒成立问题.专题:计算题.分析:不等式恒成立,即较大的一边所取的最小值也大于较小的一边的最大值.因此记不等式的左边为F(x),利用导数工具求出它的单调性,进而得出它在R上的最小值,最后解右边2﹣a小于这个最小值,即可得出答案.解答:解:记F(x)=x4﹣4x3∵x4﹣4x3>2﹣a对任意实数x 都成立,∴F(x)在R上的最小值大于2﹣a求导:F′(x)=4x3﹣12x2=4x2(x﹣3)当x∈(﹣∞,3)时,F′(x)<0,故F(x)在(﹣∞,3)上是减函数;当x∈(3,+∞)时,F′(x)>0,故F(x)在(3,+∞)上是增函数.∴当x=3时,函数F(x)有极小值,这个极小值即为函数F(x)在R上的最小值即[F(x)]min=F(3)=﹣27因此当2﹣a<﹣27,即a>29时,等式x4﹣4x3>2﹣a 对任意实数x都成立故答案为:(29,+∞)点评:本题考查了利用导数求闭区间上函数的最值、函数恒成立问题等等知识点,属于中档题.3.设a>0,函数,若对任意的x1,x2∈[1,e],都有f(x1)≥g(x2)成立,则a的取值范围为[e﹣2,+∞).考点:利用导数求闭区间上函数的最值;函数恒成立问题.专题:综合题.分析:求导函数,分别求出函数f(x)的最小值,g(x)的最大值,进而可建立不等关系,即可求出a的取值范围.解答:解:求导函数,可得g′(x)=1﹣,x∈[1,e],g′(x)≥0,∴g(x)max=g(e )=e﹣1,令f'(x)=0,∵a>0,x=±当0<a<1,f(x)在[1,e]上单调增,∴f(x)min=f(1)=1+a≥e﹣1,∴a≥e﹣2;当1≤a≤e2,f(x)在[1,]上单调减,f(x)在[,e]上单调增,∴f(x)min=f()=≥e﹣1 恒成立;当a>e2时 f (x)在[1,e]上单调减,∴f(x)min=f(e)=e+≥e﹣1 恒成立综上a≥e﹣2故答案为:[e﹣2,+∞)点评:本题考查导数知识的运用,考查函数的最值,解题的关键是将对任意的x1,x2∈[1,e],都有f(x1)≥g (x2)成立,转化为对任意的x1,x2∈[1,e],都有f (x)min≥g(x)max.4.若不等式|ax3﹣lnx|≥1对任意x∈(0,1]都成立,则实数a取值范围是.考点:利用导数求闭区间上函数的最值;函数恒成立问题.专题:综合题;导数的综合应用.分析:令g(x)=ax3﹣lnx,求导函数,确定函数的单调性,从而可求函数的最小值,利用最小值大于等于1,即可确定实数a取值范围.解答:解:显然x=1时,有|a|≥1,a≤﹣1或a≥1.令g(x)=ax3﹣lnx,①当a≤﹣1时,对任意x∈(0,1],,g(x)在(0,1]上递减,g(x)min=g(1)=a≤﹣1,此时g(x)∈[a,+∞),|g (x)|的最小值为0,不适合题意.②当a≥1时,对任意x∈(0,1],,∴函数在(0,)上单调递减,在(,+∞)上单调递增∴|g(x)|的最小值为≥1,解得:.∴实数a取值范围是点评:本题考查导数知识的运用,考查函数的单调性与最值,考查分类讨论的数学思想,正确求导是关键.5.设函数f(x)的定义域为D,令M={k|f(x)≤k恒成立,x∈D},N={k|f(x)≥k恒成立,x∈D},已知,其中x∈[0,2],若4∈M,2∈N,则a 的范围是.考点:利用导数求闭区间上函数的最值;函数恒成立问题.专题:计算题;导数的概念及应用.分析:由题意,x∈[0,2]时,,确定的最值,即可求得a的范围.解答:解:由题意,x∈[0,2]时,,∴令,则g′(x)=x2﹣x=x(x﹣1)∵x∈[0,2],∴函数在[0,1]上单调递减,在[1,2]上单调递增∴x=1时,g(x)min=﹣∵g(0)=0,g(2)=∴g(x)max=∴2﹣a≤﹣且4﹣a≥∴故答案为:点评:本题考查新定义,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.6.f(x)=ax3﹣3x(a>0)对于x∈[0,1]总有f(x)≥﹣1成立,则a的范围为[4,+∞].考点:利用导数求闭区间上函数的最值.专题:计算题.分析:本题是关于不等式的恒成立问题,可转化为函数的最值问题来求解,先对x分类讨论:x=0与x≠0,当x≠0即x∈(0,1]时,得到:,构造函数,只需需a≥[g(x)]max,于是可以利用导数来求解函数g(x)的最值.解答:解:∵x∈[0,1]总有f(x)≥﹣1成立,即ax3﹣3x+1≥0,x∈[0,1]恒成立当x=0时,要使不等式恒成立则有a∈(0,+∞)当x∈(0,1]时,ax3﹣3x+1≥0恒成立,即有:在x∈(0,1]上恒成立,令,必须且只需a≥[g(x )]max由>0得,所以函数g(x)在(0,]上是增函数,在[,1]上是减函数,所以=4,即a≥4综合以上可得:a≥4.答案为:[4,+∞).点评:本题考查函数的导数,含参数的不等式恒成立为题,方法是转化为利用导数求函数闭区间上的最值问题,考查了分类讨论的数学思想方法.7.三次函数f(x)=x3﹣3bx+3b在[1,2]内恒为正值,则b的取值范围是.考点:利用导数求闭区间上函数的最值;函数恒成立问题.专题:计算题;转化思想.分析:方法1:拆分函数f(x),根据直线的斜率观察可知在[1,2]范围内,直线y2与y1=x3相切的斜率是3b的最大值,求出b的取值范围方法2:利用函数导数判断函数的单调性,再对b进行讨论,比较是否与已知条件相符,若不符则舍掉,最后求出b的范围解答:解:方法1:可以看作y1=x3,y2=3b(x﹣1),且y2<y1x3的图象和x2类似,只是在一,三象限,由于[1,2],讨论第一象限即可直线y2过(1,0)点,斜率为3b.观察可知在[1,2]范围内,直线y2与y1=x3相切的斜率是3b的最大值.对y1求导得相切的斜率3(x2),相切的话3b=3(x2),b的最大值为x2.相切即是有交点,y1=y2 3x2(x﹣1)=x3 x=1.5则b的最大值为x2=9/4,那么b<9/4.方法2:f(x)=x^3﹣3bx+3bf'(x)=3x^﹣3b b≤0时,f(x)在R上单调增,只需f(1)=1>0,显然成立;b>0时,令f'(x)=0 x=±√b﹣﹣﹣>f(x)在[√b,+∞)上单调增,在[﹣√b,√b]上单调减;如果√b≤1即b≤1,只需f(1)=1>0,显然成立;如果√b≥2即b≥4,只需f(2)=8﹣3b>0﹣﹣﹣>b<8/3,矛盾舍去;如果1<√b<2即1<b<4,必须f(√b)=b√b﹣3b√b+3b>0﹣b(2√b﹣3)>0√b<3/2b<9/4,即:1<b<9/4综上:b<9/4点评:考查学生的解题思维,万变不离其宗,只要会了函数的求导就不难解该题了.8.不等式x3﹣3x2+2﹣a<0在区间x∈[﹣1,1]上恒成立,则实数a的取值范围(2,+∞).考点:利用导数求闭区间上函数的最值;函数的单调性与导数的关系.专题:计算题.分析:变形为x3﹣3x2+2<a在闭区间∈[﹣1,1]上恒成立,从而转化为三次多项式函数在区间上求最值的问题,可以分两步操作:①求出f(x)=x3﹣3x2+2的导数,从而得出其单调性;②在单调增区间的右端求出函数的极大值或区间端点的较大函数值,得出所给函数的最大值,实数a要大于这个值.解答:解:原不等式等价于x3﹣3x2+2<a区间x∈[﹣1,1]上恒成立,设函数f(x)=x3﹣3x2+2,x∈[﹣1,1]求出导数:f/(x)=3x2﹣6x,由f/(x)=0得x=0或2可得在区间(﹣1,0)上f/(x)>0,函数为增函数,在区间(0,1)上f/(x)<0,函数为减函数,因此函数在闭区间[﹣1,1]上在x=0处取得极大值f(0)=2,并且这个极大值也是最大值所以实数a>2故答案为:(2,+∞)点评:本题利用导数工具研究函数的单调性从而求出函数在区间上的最值,处理不等式恒成立的问题时注意变量分离技巧的应用,简化运算.9.当x∈(0,+∞)时,函数f(x)=e x的图象始终在直线y=kx+1的上方,则实数k的取值范围是(﹣∞,1] .考点:利用导数求闭区间上函数的最值.专题:常规题型.分析:构造函数G(x)=f(x)﹣y=ex﹣kx+1求函数的导数,根据导数判断函数的单调性,求出最小值,最小值大于0时k的范围,即k的取值范围解答:解:G(x)=f(x)﹣y=ex﹣kx+1,G′(x)=ex﹣k,∵x∈(0,+∞)∴G′(x)单调递增,当x=0时G′(x)最小,当x=0时G′(x)=1﹣k 当G′(x)>0时G(x)=f(x)﹣y=ex﹣kx+1单调递增,在x=0出去最小值0所以1﹣k≥0 即k∈(﹣∞,1].故答案为:(﹣∞,1].点评:构造函数,利用导数求其最值,根据导数的正负判断其增减性,求k值,属于简单题.10.设函数f(x)=ax3﹣3x+1(x∈R),若对于任意的x∈[﹣1,1]都有f(x)≥0成立,则实数a的值为4 .考点:利用导数求闭区间上函数的最值.专题:计算题.分析:弦求出f′(x)=0时x的值,进而讨论函数的增减性得到f(x)的最小值,对于任意的x∈[﹣1,1]都有f(x)≥0成立,可转化为最小值大于等于0即可求出a 的范围.解答:解:由题意,f′(x)=3ax2﹣3,当a≤0时3ax2﹣3<0,函数是减函数,f(0)=1,只需f (1)≥0即可,解得a≥2,与已知矛盾,当a>0时,令f′(x)=3ax2﹣3=0解得x=±,①当x <﹣时,f′(x )>0,f(x)为递增函数,②当﹣<x<时,f′(x)<0,f(x)为递减函数,③当x>时,f(x)为递增函数.所以f()≥0,且f(﹣1)≥0,且f(1)≥0即可由f()≥0,即a•﹣3•+1≥0,解得a≥4,由f(﹣1)≥0,可得a≤4,由f(1)≥0解得2≤a≤4,综上a=4为所求.故答案为:4.点评:本题以函数为载体,考查学生解决函数恒成立的能力,考查学生分析解决问题的能力,属于基础题.11.若关于x的不等式x2+1≥kx在[1,2]上恒成立,则实数k的取值范围是(﹣∞,2] .考点:利用导数求闭区间上函数的最值.专题:计算题.分析:被恒等式两边同时除以x,得到k≤x+,根据对构函数在所给的区间上的值域,得到当式子恒成立时,k 要小于函数式的最小值.解解:∵关于x的不等式x2+1≥kx在[1,2]上恒成立,答:∴k≤x+,∵在[1,2]上的最小值是当x=2时的函数值2,∴k≤2,∴k的取值范围是(﹣∞,2]故答案为:(﹣∞,2].点评:本题考查函数的恒成立问题,解题的关键是对于所给的函数式的分离参数,写出要求的参数,再利用函数的最值解决.12.已知f(x)=ln(x 2+1),g(x)=()x﹣m,若∀x1∈[0,3],∃x2∈[1,2],使得f(x1)≥g(x2),则实数m的取值范围是()A.[,+∞)B.(﹣∞,]C.[,+∞)D.(﹣∞,﹣]考点:利用导数求闭区间上函数的最值.专题:计算题.分析:先利用函数的单调性求出两个函数的函数值的范围,再比较其最值即可求实数m 的取值范围.解答:解:因为x1∈[0,3]时,f(x1)∈[0,ln4];x2∈[1,2]时,g(x2)∈[﹣m,﹣m].故只需0≥﹣m⇒m≥.故选A.点评:本题主要考查函数恒成立问题以及函数单调性的应用,考查计算能力和分析问题的能力,属于中档题.13.已知,,若对任意的x1∈[﹣1,2],总存在x 2∈[﹣1,2],使得g (x1)=f(x2),则m的取值范围是()A.[0,]B.[,0]C.[,]D.[,1]考点:利用导数求闭区间上函数的最值;特称命题.专题:综合题.分析:根据对于任意x1∈[﹣1,2],总存在x2∈[﹣1,2],使得g(x1)=f(x2),得到函数g(x)在[﹣1,2]上值域是f(x)在[﹣1,2]上值域的子集,然后利用求函数值域的方法求函数f(x)、g(x)在[﹣1,2]上值域,列出不等式,解此不等式组即可求得实数a 的取值范围即可.解答:解:根据对于任意x1∈[﹣1,2],总存在x2∈[﹣1,2],使得g(x1)=f(x2),得到函数g(x)在[﹣1,2]上值域是f(x)在[﹣1,2]上值域的子集求导函数可得:f′(x)=x2﹣1=(x+1)(x﹣1),∴函数f(x)在[﹣1,1)上单调减,在(1,2]上单调增∴f(﹣1)=,f(1)=﹣,f(2)=,∴f(x)在[﹣1,2]上值域是[﹣,];m>0时,函数g(x)在[﹣1,2]上单调增,∴g(x)在[﹣1,2]上值域是[﹣m+,2m+]∴﹣m+≥﹣且≥2m+∴0<m≤m=0时,g(x)=满足题意;m<0时,函数g(x)在[﹣1,2]上单调减,∴g(x)在[﹣1,2]上值域是[2m+,﹣m+]∴2m+≥﹣且≥﹣m+∴﹣≤m<0综上知m的取值范围是[,]故选C.点本题主要考查了函数恒成立问题,以及函数的值域,评:同时考查了分类讨论的数学思想,属于中档题.14.已知集合A={x∈R|≤2},集合B={a∈R|已知函数f(x)=﹣1+lnx,∃x0>0,使f(x0)≤0成立},则A∩B=()A.{x|x<}B.{x|x≤或x=1}C.{x|x<或x=1}D.{x|x<或x≥1}考点:利用导数求闭区间上函数的最值;交集及其运算.专题:计算题.分析:解分式不等式求出集合A,根据集合B可得a≤x﹣xlnx 在(0,+∞)上有解.利用导数求得h(x)=x ﹣xlnx的值域为(﹣∞,1],要使不等式a≤xlnx 在(0,+∞)上有解,只要a小于或等于h(x)的最大值即可,即a≤1 成立,故B={a|a≤1},由此求得A∩B.解答:解:集合A={x∈R|≤2}={x|}={x| }={x|(x﹣1)(2x ﹣1)≥0,且2x﹣1≠0}={x|x<,或x≥1}.由集合B 可知f(x)的定义域为{x|x>0},不等式﹣1+lnx≤0有解,即不等式a≤x﹣xlnx 在(0,+∞)上有解.令h(x)=x﹣xlnx,可得h′(x)=1﹣(lnx+1)=﹣lnx,令h′(x)=0,可得 x=1.再由当0<x<1 时,h′(x)>0,当x>1 时,h′(x)<0,可得当x=1时,h(x)=x﹣xlnx 取得最大值为 1.要使不等式a≤x﹣xlnx 在(0,+∞)上有解,只要a小于或等于h(x)的最大值即可.即a≤1 成立,所以集合B={a|a≤1}.所以A∩B={x|x<,或 x=1}.故选C.点评:本题主要考查集合的表示方法、分式不等式的解法,利用导数判断函数的单调性,根据函数的单调性求函数的值域,两个集合的交集的定义和求法,属于中档题.15.设函数,(p是实数,e为自然对数的底数)(1)若f(x)在其定义域内为单调函数,求p的取值范围;(2)若在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立,求p的取值范围.考点:利用导数求闭区间上函数的最值;利用导数研究函数的单调性.专题:计算题.分析:(1)求导f′(x)=,要使“f(x)为单调增函数”,转化为“f′(x)≥0恒成立”,再转化为“p≥=恒成立”,由最值法求解.同理,要使“f(x)为单调减函数”,转化为“f′(x)≤0恒成立”,再转化为“p≤=恒成立”,由最值法求解,最后两个结果取并集.(2)因为“在[1,e]上至少存在一点x0,使得f(x0)>g(x0)成立”,要转化为“f(x)max>g(x)min”解决,易知g(x)=在[1,e]上为减函数,所以g(x)∈[2,2e],①当p≤0时,f(x)在[1,e]上递减;②当p≥1时,f(x)在[1,e]上递增;③当0<p<1时,两者作差比较.解答:解:(1)f′(x)=,要使“f(x)为单调增函数”,转化为“f′(x)≥0恒成立”,即p≥=恒成立,又,所以当p≥1时,f (x)在(0,+∞)为单调增函数.同理,要使“f(x)为单调减函数”,转化为“f′(x)≤0恒成立,再转化为“p≤=恒成立”,又,所以当p≤0时,f(x)在(0,+∞)为单调减函数.综上所述,f(x)在(0,+∞)为单调函数,p的取值范围为p≥1或p≤0(2)因g(x)=在[1,e]上为减函数,所以g (x)∈[2,2e]①当p≤0时,由(1)知f(x)在[1,e]上递减⇒f(x)max=f(1)=0<2,不合题意②当p≥1时,由(1)知f(x)在[1,e]上递增,f(1)<2,又g(x)在[1,e]上为减函数,故只需f(x)max>g(x)min,x∈[1,e],即:f(e)=p(e﹣)﹣2lne>2⇒p>.③当0<p<1时,因x﹣≥0,x∈[1,e]所以f(x)=p(x﹣)﹣2lnx≤(x﹣)﹣2lnx≤e﹣﹣2lne<2不合题意综上,p的取值范围为(,+∞)点评:本题主要考查用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题.16.若函数y=f(x),x∈D同时满足下列条件:(1)在D内的单调函数;(2)存在实数m,n,当定义域为[m,n]时,值域为[m,n].则称此函数为D内可等射函数,设(a>0且a≠1),则当f (x )为可等射函数时,a的取值范围是(0,1)∪(1,2).考点:利用导数求闭区间上函数的最值;函数的定义域及其求法;函数的值域.专题:新定义.分析:求导函数,判断函数为单调增函数,根据可等射函数的定义,可得m,n是方程的两个根,构建函数g(x)=,则函数g(x)=有两个零点,分类讨论,即可确定a的取值范围.解答:解:求导函数,可得f′(x)=a x>0,故函数为单调增函数∵存在实数m,n,当定义域为[m,n]时,值域为[m,n].∴f(m)=m,f(n)=n∴m,n 是方程的两个根构建函数g(x)=,则函数g(x)=有两个零点,g′(x)=a x﹣1①0<a<1时,函数的单调增区间为(﹣∞,0),单调减区间为(0,+∞)∵g(0)>0,∴函数有两个零点,故满足题意;②a>1时,函数的单调减区间为(﹣∞,0),单调增区间为(0,+∞)要使函数有两个零点,则g(0)<0,∴,∴a<2∴1<a<2综上可知,a的取值范围是(0,1)∪(1,2)故答案为:(0,1)∪(1,2).点评:本题考查新定义,考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,正确理解新定义是关键.17.存在x<0使得不等式x2<2﹣|x﹣t|成立,则实数t 的取值范围是(﹣,2).考点:绝对值不等式.专题:计算题.分析:本题利用纯代数讨论是很繁琐的,要用数形结合.原不等式x2<2﹣|x﹣t|,即|x﹣t|<2﹣x2,分别画出函数y1=|x﹣t|,y2=2﹣x2,这个很明确,是一个开口向下,关于y轴对称,最大值为2的抛物线;要存在x<0使不等式|x﹣t|<2﹣x2成立,则y1的图象应该在第二象限(x<0)和y2的图象有交点,再分两种临界讲座情况,当t≤0时,y1的右半部分和y2在第二象限相切;当t>0时,要使y1和y2在第二象限有交点,最后综上得出实数t的取值范围.解答:解:不等式x2<2﹣|x﹣t|,即|x﹣t|<2﹣x2,令y1=|x﹣t|,y1的图象是关于x=t对称的一个V字形图形,其象位于第一、二象限;y2=2﹣x2,是一个开口向下,关于y轴对称,最大值为2的抛物线;要存在x<0,使不等式|x﹣t|<2﹣x2成立,则y1的图象应该在第二象限和y2的图象有交点,两种临界情况,①当t≤0时,y1的右半部分和y2在第二象限相切:y1的右半部分即y1=x﹣t,联列方程y=x﹣t,y=2﹣x2,只有一个解;即x﹣t=2﹣x2,即x2+x﹣t﹣2=0,△=1+4t+8=0,得:t=﹣;此时y1恒大于等于y2,所以t=﹣取不到;所以﹣<t≤0;②当t>0时,要使y1和y2在第二象限有交点,即y1的左半部分和y2的交点的位于第二象限;无需联列方程,只要y1与y轴的交点小于2即可;y1=t﹣x与y轴的交点为(0,t),所以t<2,又因为t>0,所以0<t <2;综上,实数t的取值范围是:﹣<t<2;故答案为:(﹣,2).点评:本小题主要考查函数图象的应用、二次函数、绝对值不等式等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.18.存在实数x,使得x2﹣4bx+3b<0成立,则b的取值范围是b>或b<0 .考点:函数恒成立问题.专题:计算题;转化思想.分析:先把原命题等价转化为存在实数x,使得函数y=x2﹣4bx+3b的图象在X轴下方,再利用开口向上的二次函数图象的特点,转化为函数与X轴有两个交点,对应判别式大于0即可解题.解答:解:因为命题:存在实数x,使得x2﹣4bx+3b<0成立的等价说法是:存在实数x,使得函数y=x2﹣4bx+3b的图象在X轴下方,即函数与X轴有两个交点,故对应的△=(﹣4b)2﹣4×3b>0⇒b<0或b>.故答案为:b<0或b>.点评:本题主要考查二次函数的图象分布以及函数图象与对应方程之间的关系,是对函数知识的考查,属于基础题.19.已知存在实数x使得不等式|x﹣3|﹣|x+2|≥|3a﹣1|成立则实数a的取值范围是.考点:绝对值不等式.专题:数形结合;转化思想.分析:由题意知这是一个存在性的问题,须求出不等式左边的最大值,令其大于等于|3a﹣1|,即可解出实数a的取值范围解答:解:由题意借助数轴,|x﹣3|﹣|x+2|∈[﹣5,5]∵存在实数x使得不等式|x﹣3|﹣|x+2|≥|3a﹣1|成立,∴5≥|3a﹣1|,解得﹣5≤3a﹣1≤5,即﹣≤a≤2故答案为点评:本题考查绝对值不等式,求解本题的关键是正确理解题意,区分存在问题与恒成立问题的区别,本题是一个存在问题,解决的是有的问题,故取|3a﹣1|≤5,即小于等于左边的最大值即满足题意,本题是一个易错题,主要错误就是出在把存在问题当成恒成立问题求解,因思维错误导致错误.20.存在实数a使不等式a≤2﹣x+1在[﹣1,2]成立,则a的范围为(﹣∞,4] .考点:指数型复合函数的性质及应用.专题:计算题.分析:由x的范围可得1﹣x的范围,由此得到2﹣x+1 的范围,从而得到a的范围.解答:解:由于﹣1≤x≤2,∴﹣1≤1﹣x≤2,∴≤2﹣x+1 ≤4.∵存在实数a使不等式a≤2﹣x+1在[﹣1,2]成立,∴a≤4.故a的范围为(﹣∞,4],故答案为(﹣∞,4].点评:本题主要考查指数型复合函数的性质以及应用,属于中档题.21.若存在x∈,使成立,则实数a的取值范围为.考点:正弦函数的图象;函数的图象与图象变化.专计算题.题:分析:根据正弦函数的单调性,分别求出当0≤x≤和≤x≤0时|sinx|的范围,进而推知x∈时,|sinx|的最大值.进而可知要使成立,只需小于其最大值即可.解答:解:当0≤x≤时,0≤|sinx|=sinx≤当≤x≤0时,0≤sinx|=﹣sinx≤即当x∈,0≤|sinx|≤∴要使成立,则需<即故答案为:点评:本题主要考查了正弦函数的单调性.属基础题.22.设存在实数,使不等式成立,则实数t的取值范围为t.考点:函数恒成立问题.专题:计算题;函数的性质及应用.分析:考虑关键点x=1处,分为以下两端:①x∈(,1]时,t >;②x∈(1,3]时,t≥,综上所述,t>.解答:解:考虑关键点x=1处,分为以下两端:①x∈(,1]时,﹣x≥0,lnx≤0,于是t+﹣x>e﹣lnx,即 t>﹣+x+=x>,此时t>.②x∈(1,3]时,﹣x <0; lnx>0,于是t ﹣+x>e lnx,即 t>﹣x+x=,此时t≥,综上所述,t>.故答案为:t.点评:本题考查不等式的性质和应用,解题时要认真审题,仔细解答,注意分类讨论思想的合理运用.23.若存在实数p∈[﹣1,1],使得不等式px2+(p﹣3)x﹣3>0成立,则实数x的取值范围为(﹣3,﹣1).考点:函数恒成立问题;一元二次不等式的解法.分析:把已知不等式整理为关于p的一元一次不等式,而不等式左边为关于p的一次函数,根据一次函数的性质可得此函数的最值只有在[﹣1,1]的端点取得,根据题意不等式恒成立可得当p=﹣1时,最小值大于0即可,故把p=﹣1代入不等式,得到关于x的不等式,求出不等式的解集即可得到x的取值范围.解答:解:不等式px2+(p﹣3)x﹣3>0可以化为:p(x2﹣3x)﹣3x﹣3>0,这是一个关于p的一元一次不等式,函数p(x2﹣3x)﹣3x﹣3是关于p的一次函数,一次函数图象是直线,在定义域上是单调递增或递减,P∈[﹣1,1]时,函数p(x2﹣3x)﹣3x﹣3的最小值必定在端点﹣1或1处取到,不等式px2+(p﹣3)x﹣3>0总成立,只需最小值大于0即可.∴﹣x2+(﹣1﹣3)x﹣3>0,即x2+(1﹣3)x﹣3>0,解得:﹣3<x<﹣1,则实数x的取值范围为(﹣3,﹣1).故答案为:(﹣3,﹣1)点评:考查学生理解函数恒成立时的条件的能力,以及灵活运用一元二次不等式解法的能力.24.若存在实数x使成立,求常数a的取值范围.考点:二维形式的柯西不等式.专题:计算题.分析:利用柯西不等式,求出左边对应函数的最大值,即可确定常数a的取值范围.解答:解:由题意,由柯西不等式得=≤(3+1)(x+2+14﹣x)=64所以8,当且仅当x=10时取“=”,∵存在实数x使成立∴a<8∴常数a的取值范围是(﹣∞,8).。