数理方程：复习
- 格式：ppt
- 大小：1.85 MB
- 文档页数：78
下载文档原格式
合集下载
数理方程与特殊函数数理方程复习
r
球对称性导致球面波问题
2u t 2
a2
1 r2
r
(r 2
u ) r
u t 0
(r), ut
t 0
(r)
令 v = r u , 则有
2v u 2u r 2 2 r r r 2
所以
1 r
r
(r 2
u ) r
1 r
(2r
u r
r2
2u r 2 )
2v r 2
2u t 2
a2
1 r2
r
Ex20. 上半平面 y > 0 的格林函数
11
1
G(P, M0 )
2
[ln rPM0
ln rPM1
]
P M1
O M0
(x y) ( x0 , y0 )
( x0 , – y0 )
Ex21. 证明
J1/2( x)
2 cos x
x
证:
(1)m x n2m
J n ( x) m0 2n2m m!(n m 1)
n1
L
x
L2
h
Cn
2 L
L 0
4 (L ) n
L2
sin L
d
n≥1
Ex10. 用分离变量法求解
utt u
x
0
uxx 0,
0 x 1, u 0
x1
t
0
u
t0
sin(x),
ut
t0
0
Ex11. 求解方程
uuttx0
a 2uxx g, 0, u
xL
(0 0
x
L,
t
0)
u t0 0, ut t0 0
球对称性导致球面波问题
2u t 2
a2
1 r2
r
(r 2
u ) r
u t 0
(r), ut
t 0
(r)
令 v = r u , 则有
2v u 2u r 2 2 r r r 2
所以
1 r
r
(r 2
u ) r
1 r
(2r
u r
r2
2u r 2 )
2v r 2
2u t 2
a2
1 r2
r
Ex20. 上半平面 y > 0 的格林函数
11
1
G(P, M0 )
2
[ln rPM0
ln rPM1
]
P M1
O M0
(x y) ( x0 , y0 )
( x0 , – y0 )
Ex21. 证明
J1/2( x)
2 cos x
x
证:
(1)m x n2m
J n ( x) m0 2n2m m!(n m 1)
n1
L
x
L2
h
Cn
2 L
L 0
4 (L ) n
L2
sin L
d
n≥1
Ex10. 用分离变量法求解
utt u
x
0
uxx 0,
0 x 1, u 0
x1
t
0
u
t0
sin(x),
ut
t0
0
Ex11. 求解方程
uuttx0
a 2uxx g, 0, u
xL
(0 0
x
L,
t
0)
u t0 0, ut t0 0
数理方程总结完整终极版
00|()()t t u x ux t ϕψ===⎧⎪∂⎨=⎪∂⎩拉普拉斯算子：四种方法:分离变量法、 行波法、 积分变换法、 格林函数法 定解问题：初始条件.边界条件.其他 波动方程的初始条件:热传导方程的初始条件初始时刻的温度分布 :泊松方程和拉普拉斯方程的初始条件：不含初始条件，只含边界条件条件 波动方程的边界条件: (1)固定端：对于两端固定的弦的横振动，其为：或：(2)自由端：x =a 端既不固定，又不受位移方向力的作用.(3) 弹性支承端：在x =a 端受到弹性系数为k 的弹簧的支承。
定解问题的分类和检验：(1) 初始问题：只有初始条件，没有边界条件的定解问题；(2) 边值问题：没有初始条件，只有边界条件的定解问题；(3) 混合问题：既有初始条件，也有边界条件的定解问题。
• 解的存在性：定解问题是否有解；• 解的唯一性：是否只有一解；• 解的稳定性：定解条件有微小变动时，解是否有相应的微小k z j y i x ˆˆˆ∂∂+∂∂+∂∂=∇u u ∇=grad 2222222z y x ∂∂+∂∂+∂∂=∇⋅∇=∇22222y u x u u ∂∂+∂∂=∇0(,)|()t u M t M ϕ==0|0,x u ==(,)0u a t =变动。
分离变量法：基本思想：首先求出具有变量分离形式且满足边界条件的特解，然后由叠加原理作出这些解的线性组合，最后由其余的定解条件确定叠加系数。
把偏微分方程化为常微分方程来处理，使问题简单化。
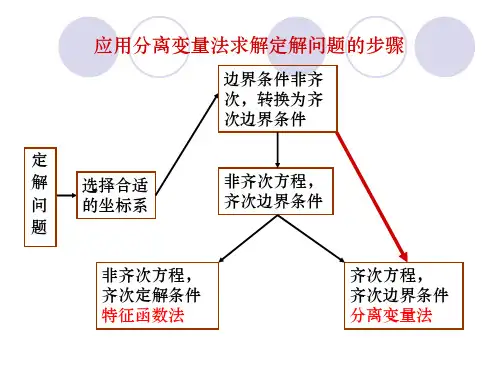
适用范围：波动问题、热传导问题、稳定场问题等分离变量法步骤：一有界弦的自由振动 二有限长杆上的热传导 三拉普拉斯方程的定解问题常用本征方程 齐次边界条件2''0(0)()0,/,1,2,sin k k X X X X l k l k X xλλββπβ+=⎧⎨==⎩====0,1,2,0,1,2,λ0,1,2,λ非齐次方程的求解思路用分解原理得出对应的齐次问题。
数理方程复习要点摘要
2 2u 2u 2 u a ( 2 2) 2 t x y
或 或
utt a 2 uxx
utt a2 (uxx uyy )
2 2u 2u 2u 2 u a ( 2 2 2) 2 t x y z
或
utt a2 (uxx uyy uzz )
Ay ( B B 2 AC ) x C 1 Ay ( B B 2 AC ) x C2
Ay Bx C1
返回
AC B 2 x C 2
退出
a 0 双曲型(波动) 方程
2
一维 二维 三维
2u 2u a2 2 t2 x
抛物型 uxx (2u u )x 2(2u u ) (2u u ) 4 2u 4u u 2u
x2 2 y C
x 2 2 y, x
uxy (2u u )y 2(2u u ) 4u 2u uyy (2u )y 2(2u ) 4u
退出
二阶线性偏微方程的一般形式
2u 2u 2u u u A 2 2B C 2 2D 2E Fu f ( x, t ) x xy y x y
双曲型方程 椭圆型方程 抛物型方程
A B AC B 2 0 B C A B AC B 2 0 B C A B B 2 AC 0 B C
X ( x ) X ( x ) 0 X (0) X ( L) 0
n 0,1, 2, 3,
2
X ( x ) X ( x ) 0 X (0) X ( L) 0
n 1, 2, 3,
或 或
utt a 2 uxx
utt a2 (uxx uyy )
2 2u 2u 2u 2 u a ( 2 2 2) 2 t x y z
或
utt a2 (uxx uyy uzz )
Ay ( B B 2 AC ) x C 1 Ay ( B B 2 AC ) x C2
Ay Bx C1
返回
AC B 2 x C 2
退出
a 0 双曲型(波动) 方程
2
一维 二维 三维
2u 2u a2 2 t2 x
抛物型 uxx (2u u )x 2(2u u ) (2u u ) 4 2u 4u u 2u
x2 2 y C
x 2 2 y, x
uxy (2u u )y 2(2u u ) 4u 2u uyy (2u )y 2(2u ) 4u
退出
二阶线性偏微方程的一般形式
2u 2u 2u u u A 2 2B C 2 2D 2E Fu f ( x, t ) x xy y x y
双曲型方程 椭圆型方程 抛物型方程
A B AC B 2 0 B C A B AC B 2 0 B C A B B 2 AC 0 B C
X ( x ) X ( x ) 0 X (0) X ( L) 0
n 0,1, 2, 3,
2
X ( x ) X ( x ) 0 X (0) X ( L) 0
n 1, 2, 3,
《方程的复习课》课件
二元一次方程组的应用
总结词
二元一次方程组在日常生活和科学研究中有着广泛的 应用，如路程问题、工资问题、经济问题等。
详细描述Байду номын сангаас
二元一次方程组在许多实际问题中都有应用，例如在路 程问题中，我们可以使用二元一次方程组来表示两个物 体的相对位置和速度；在工资问题中，我们可以使用二 元一次方程组来表示工人和雇主之间的利益关系；在经 济问题中，二元一次方程组可以用来描述供求关系、价 格变动等问题。此外，在物理学、化学、工程学等领域 中，二元一次方程组也经常被用来描述各种现象和规律 。
04
方程的解法技巧
消元法
总结词
通过消除两个变量，简化方程组的方 法。
详细描述
消元法是一种常用的解线性方程组的 方法，通过加减消元或代入消元的方 式，将方程组中的变量消除，从而得 到一个或多个简单的一元一次方程， 进而求解出方程组的解。
代入法
总结词
通过将一个方程的解代入另一个方程，求解 未知数的方法。
详细描述
代入法是解线性方程组的一种基本方法，通 过将一个方程的解代入另一个方程，将一个 未知数消除，从而将问题简化为一个一元一 次方程，进而求解出未知数的值。
公式法
总结词
通过对方程进行变形，将其转化为标准形式 ，然后使用公式求解的方法。
详细描述
公式法是一种通用的解线性方程组的方法， 通过对方程进行变形，将其转化为标准形式 ，然后使用公式求解未知数的值。这种方法 适用于任何线性方程组，但需要对方程进行
适当的变形。
图像法
总结词
通过绘制方程的图形，直观地求解未知数的方法。
详细描述
图像法是一种直观的解线性方程组的方法，通过绘制 方程的图形，可以直观地观察到方程的解。这种方法 适用于一些简单的线性方程组，但需要具备一定的几 何基础。
数理方程重点总结
X (0) A 0 B 1 0
断 言: B 0， 于 是 有
u
u
0,
0 (2)
x x0
x xl
X ( x) A sin x
又 由 边 界 条 件u
0， 得
x xl
sin l 0
于 是 ， 得 到 空 间 变 量 问题 的 本 征 值
l n
或
n
( n l
)2
(n 1,2,3,)
据此，解得H( y)
H ( y) cos y 1 y2 1 H (0) 6
(7)
将 （5） 、 （7） 代 入 （4） 式 ， 即 得 特 解
u( x, y) 1 x3 y2 cos y 1 y2 1 x2
6
6
再另附：直接积分法 求偏微分方程的通解
2u u
t
2 2xt
xt x
可 以 由 两 个 边 界 条 件 唯一 地 被 确 定 。
例如 f (x) x
W (x)
1 6a 2
x3
C1 x C2
W (0) M1
M1 C2
W (l) M2
l3 M2 6a2 C1l M1
据此，得到W ( x) 的解
C1
M2
M1
l3 6a 2
l
M2
l
M1
l2 6a 2
X X 0
(1)
u x
0 , u
x0
x
0
xl
(2)
(1) 式的通解为
X ( x) Acos x B sin x
(3)
对上式求导，得
X ( x) A sin x B cos x
X ( x) A sin x B cos x
数理方程总结完整版
该方程是非齐次方程。解决该类方程主要用特征函数法来 解决。以本题为例，来介绍一下特征函数法。
1.先求出该题目对应的齐次方程的特征函数， 即时当f（x，t）为零时。该题对应的齐次方 程为左一右一边界条件的齐次的一维波动方 n 程，其特征函数为X(x)=sin x, n 1, 2, 3... l n n 则设u（x，t） = Tn (t ) sin x, f ( x, t ) fn(t ) sin x, l l n 1 n 1 n n ( x) n sin x, ( x) n sin x, n 1, 2, 3... l l n 1 n 1
第二章 分离变量法
本章主要掌握三大类方程的解法，分别是有界弦的
自由振动方程，有限杆上的热传导方程，这两个方 程里包括“左几右几”的边界条件的，齐次或非齐 次边界条件的，齐次或非齐次方程的多种形式。 还有一个就是圆域内或扇形域内的二维拉普拉斯方 程，这类方程相对于比较简单，考试时的类型比较 固定。 1.有界弦的自由振动方程（方程是齐次的）的基本 解：
2 2u 2 u t 2 a x 2 f ( x, t ), 0 x l , t 0, u | x 0 u | x l 0, t 0, u u | t 0 ( x), | t 0 ( x), 0 x l. t
a 2 ( n 1/2) 2 2 t l2
(n 1/ 2) cos x l
④：“左二右二”的齐次边界条件的齐次方程：
2 u 2 u a , 0 x l , t 0, 2 t x u | x 0 0, u | x l 0, t 0, x x
l
1.先求出该题目对应的齐次方程的特征函数， 即时当f（x，t）为零时。该题对应的齐次方 程为左一右一边界条件的齐次的一维波动方 n 程，其特征函数为X(x)=sin x, n 1, 2, 3... l n n 则设u（x，t） = Tn (t ) sin x, f ( x, t ) fn(t ) sin x, l l n 1 n 1 n n ( x) n sin x, ( x) n sin x, n 1, 2, 3... l l n 1 n 1
第二章 分离变量法
本章主要掌握三大类方程的解法，分别是有界弦的
自由振动方程，有限杆上的热传导方程，这两个方 程里包括“左几右几”的边界条件的，齐次或非齐 次边界条件的，齐次或非齐次方程的多种形式。 还有一个就是圆域内或扇形域内的二维拉普拉斯方 程，这类方程相对于比较简单，考试时的类型比较 固定。 1.有界弦的自由振动方程（方程是齐次的）的基本 解：
2 2u 2 u t 2 a x 2 f ( x, t ), 0 x l , t 0, u | x 0 u | x l 0, t 0, u u | t 0 ( x), | t 0 ( x), 0 x l. t
a 2 ( n 1/2) 2 2 t l2
(n 1/ 2) cos x l
④：“左二右二”的齐次边界条件的齐次方程：
2 u 2 u a , 0 x l , t 0, 2 t x u | x 0 0, u | x l 0, t 0, x x
l
数理方程复习数理方程课件
复习
3. 在扇形区域内求下列定解问题
u 0,
0 ,r a
u(r,0) u(r, ) 0, r a
u(a, ) f ( ),
0
r2 r 0 0
u(0,)
(0)(r) ()(r) 0
u(r, ) (r)( )
(0) () 0
1 r
r
r
1 r2
0
1 r
1 r2
HUST 数学物理方程与特殊函数
复习
X X 0, 0 x l
X (0) 0,
X (l) 0
0
X 0 X (x) Ax B A B 0 X (x) 0
2 0 X 2 X 0
X (x) Acosx Bsin x
X (0) A 0 , X (l) Bsin l 0
0
l
l n
l
n
xd sin
0
l
x
2
n
x sin n
l
x |l0
2
n
l n
sin xdx
0
l
2l n
n2 2 cos l
x
|l0
2l
n2
2
(1)n 1
0, 4l
n2
2
,
n为偶数 n为奇数
u l
2 n1
2n
4l 1
2
2
e
2
n12
l2
2a2
t
cos
2n 1 x
l
HUST 数学物理方程与特殊函数
Bn
sin
n
Cnr
Байду номын сангаас
n
En
sin
数理方程-总结复习及练习要点(1)
数理方程-总结复习及练习要点(1)数理方程-总结复习及练习要点数理方程是数学中的一个重要分支，它研究的是各种用数学符号表示的方程簇，并探究其解法及相关性质。
在数学竞赛和高考中，数理方程是一个高频考查的内容，因此我们需要认真学习和掌握。
下面是数理方程的总结复习及练习要点。
一、知识点总结1. 一元一次方程：形如ax+b=0的方程，可以用解方程法、代入法、图像法等方法解决；2. 一元二次方程：形如ax²+bx+c=0的方程，可以用公式法、配方法、因式分解法、图像法等方法解决；3. 一元n次方程：形如a₁xⁿ+a₂xⁿ⁻¹+…+aₙ=0的方程，可以用因式分解法、求根公式、数形结合法等方法解决；4. 二元一次方程组：形如{ax+by=c,dx+ey=f}的方程组，可以用代数法、图像法、消元法等方法解决；5. 二元二次方程组：形如{ax²+by²+cx+dy+e=0,fx²+gy²+hx+iy+j=0}的方程组，可以用消元法、配方法等方法解决；6. 不等式：大于、小于、大于等于、小于等于等不同种类的不等式，可以分别用解不等式、求解集合、证明等方法解决。
二、练习要点1. 要经常进行例题训练，熟练记忆每种方程的解法以及相关性质；2. 要学会用复杂的方程题目中的一些特殊性质，如配方法中平方项差为完全平方、二次项系数一样等等；3. 要结合实际问题练习，尤其是二元一次方程组和不等式中，实际问题更容易引入数学领域；4. 要多用图像法、数形结合法等思维方式，能够脑补形状易于掌握方程性质；5. 在大型比赛中，要将时间合理分配，不要轻易卡在一些细节上，要有策略性地解决问题。
三、总结数理方程是数学考试的重要考点之一，掌握好方程的基本思想和方法，能够在比赛中占据更好的优势，同时也有助于我们更好地解决实际问题。
因此，我们要时常进行练习，加强对数理方程的理解和应用，才能在数学竞赛中获得更好的成绩。
数理方程复习
∞
J −1 / 2 ( x ) =
2 cos x πx
Ex12 推导出下面定解问题所连带的贝塞尔方程 （不解贝塞尔方程）
1 ⎧ 2 ⎪ utt = a ( uρρ + ρ uρ ), ( t > 0,0 < ρ < 1) ⎪ ⎪ ⎨ uρ |ρ =1 = 0, u |ρ = 0 < +∞ ⎪ u |t = 0 = 0, ut |t = 0 = 1 − ρ 2 ⎪ ⎪ ⎩
1 1 x + at u( x , t ) = [ϕ ( x + at ) + ϕ ( x − at )] + ∫x −atψ (ξ )dξ 2 2a x – at < 0 1 1 x + at u( x , t ) = [ϕ ( x + at ) − ϕ (at − x )] + ∫at − xψ (ξ )dξ 2 2a 7/16
− ( 1 + iλ ) x
dx
∞ 0
1 e ( 1 − iλ ) x = 1 − iλ
1 e − ( 1 + iλ ) x − −∞ 1 + iλ
1 1 2 = + = 1 − i λ 1 + iλ 1 + λ 2
13/16
例6 用付氏变换解热传导问题
⎧ ∂u ∂ 2u = a 2 2 + f ( x , t ), (− ∞ < x < +∞ , t > 0 ) ⎪ ∂x ⎨ ∂t ⎪u ⎩ t =0 = ϕ ( x )
∞
n≥1
6/16
达朗贝尔公式
∂ 2u ∂ 2u = a2 2 ∂t 2 ∂x ∂u u t = 0 = ϕ ( x ), ∂t
J −1 / 2 ( x ) =
2 cos x πx
Ex12 推导出下面定解问题所连带的贝塞尔方程 （不解贝塞尔方程）
1 ⎧ 2 ⎪ utt = a ( uρρ + ρ uρ ), ( t > 0,0 < ρ < 1) ⎪ ⎪ ⎨ uρ |ρ =1 = 0, u |ρ = 0 < +∞ ⎪ u |t = 0 = 0, ut |t = 0 = 1 − ρ 2 ⎪ ⎪ ⎩
1 1 x + at u( x , t ) = [ϕ ( x + at ) + ϕ ( x − at )] + ∫x −atψ (ξ )dξ 2 2a x – at < 0 1 1 x + at u( x , t ) = [ϕ ( x + at ) − ϕ (at − x )] + ∫at − xψ (ξ )dξ 2 2a 7/16
− ( 1 + iλ ) x
dx
∞ 0
1 e ( 1 − iλ ) x = 1 − iλ
1 e − ( 1 + iλ ) x − −∞ 1 + iλ
1 1 2 = + = 1 − i λ 1 + iλ 1 + λ 2
13/16
例6 用付氏变换解热传导问题
⎧ ∂u ∂ 2u = a 2 2 + f ( x , t ), (− ∞ < x < +∞ , t > 0 ) ⎪ ∂x ⎨ ∂t ⎪u ⎩ t =0 = ϕ ( x )
∞
n≥1
6/16
达朗贝尔公式
∂ 2u ∂ 2u = a2 2 ∂t 2 ∂x ∂u u t = 0 = ϕ ( x ), ∂t
华中科技大学数理方程课件——数理方程复习
HUST 数学物理方程与特殊函数
复习
4. 求解下列定解问题 x 0, y 0 u xy 1, u (0, y ) y 1, y 0 u ( x,0) 1, x0 解法一（积分变换法） 记 Ly [u( x, y)] U ( x, p) ，则 d d 1 x pU ( x, p) 1 1 p U ( x, p ) U ( x, p ) 2 C dx p dx p p 1 1 由于 U (0, p) Ly [ y 1] 2 ，于是 U ( x, p) x 1 1 p p p2 p2 p 从而所求解为：
n x l
n 2 n l 2 xd sin x x sin x |0 0 l n l n
l
l
0
sin
n为偶数 0, n l 2l n 2 2 cos x |0 2 2 (1) 1 4l , n为奇数 n l n n 2 2
l 4l u e 2 2 2 n1 2n 1
2hl2 2 l n Cn u ( x,0) sin xdx 2 c(l c)n 2 l 0 l
HUST 数学物理方程与特殊函数
复习
2. 解一维热传导方程，其初始条件及边界条件为 u (0, t ) u (l , t ) u ( x,0) x, 0, 0 x x 2 u 2 u , 0 x l, t 0 a 2 x t u (l , t ) u (0, t ) 0, 0, t 0 x x 0 xl u ( x,0) x, u( x, t ) X ( x)T (t ) u (0, t ) X (0)T (t ) 0 x T X a 2TX u (l , t ) X (l )T (t ) 0 T X x 2 aT X X (0) 0, X (l ) 0
数理方程总复习 复习1(第二章分离变量法)
∂u ∂ 2u = a 2 2 + f ( x, t ), 0 < x < l , t > 0, ∂t ∂x ( III ) u x =0 = u1 (t ), u x =l = u2 (t ), t ≥ 0, 0 ≤ x ≤ l. u t = 0 = ϕ ( x), 特点：非齐次边界
边界条件非齐 次，转换为齐 次边界条件 定 解 问 题 选择合适 的坐标系 非齐次方程， 齐次边界条件
非齐次方程， 齐次定解条件 特征函数法
齐次方程， 齐次边界条件 分离变量法
第二章、分离变量(fourier级数)法
分离变量法是数学物理方程的基本解法，主要讲：
(1)有限空间的分离变量法(fourier级数法)(本章) (2)无限空间的分离变量法(fourier积分法)(第三章积分变换法) (3) Laplace方程的圆上的定解问题－－在极坐标系下的分离变量法 (4)特征函数法－－在柱坐标系和球坐标系下的分离变量法 (第五、六章)
第三步：将展开式代入方程与初始条件，比较系数得到关于 Tn (t )的常微分方程定解问题，求解确定出Tn (t )。 (Laplace变换法、常数变易法)
方法三、齐次化原理
三、第三种类型定解问题( III )
2 ∂ 2u 2 ∂ u + f ( x, t ), 0 < x < l , t > 0, 2 =a 2 ∂x ∂t ( III ) u x =0 = u1 (t ), u x =l = u2 (t ), t ≥ 0, ∂u u = ψ ( x), 0 ≤ x ≤ l. t = 0 = ϕ ( x ), ∂t t =0
∂V 1 ∂ 2V A −α x − 2 2 = 2 e , 0 < x < l , t > 0, a ∂t a ∂x V x =0 = 0, V x =l = 0, t ≥ 0, V t =0 = 0, 0 ≤ x ≤ l. ∂W 1 ∂ 2W
西安理工大学研究生数理方程课件及复习题
A 0
，即一维热传导方程
为抛物型的，类似可得弦振动方程和二维Laplace方程分别 为双曲型和椭圆型的。
3.2、两个自变量的二阶微分方程的化简 下面我们通过自变量的变换，对方程在区域 内的某点 ( x0 , y0 ) 的近旁进行化简。
数学物理方程与特殊函数
第 章 典型方程和定解条件的推导
D( , ) x 假设上述变换是二次连续可微的，且 D ( x, y ) x
其中
u ( x dx, t ) u ( x, t ) u ( x, t ) 2u ( x, t ) dx dx 2 x x x x x
2 u ( x, t ) 2 u ( x, t ) T x 2 g dx t 2 dx
x l
u x
0
x l
u x (l , t ) 0
(3) 弹性支承端：在 x l 端受到弹性系数为 k 的弹簧的支承。
u T x
x l
k u x l
或
u u 0 x x l
数学物理方程与特殊函数
第 章 典型方程和定解条件的推导
B、热传导方程的边界条件 (1) 给定温度在边界上的值
数学物理方程与特殊函数
第 章 典型方程和定解条件的推导
2、边界条件——描述系统在边界上的状况
A、 波动方程的边界条件
(1)固定端：对于两端固定的弦的横振动，其为：
u |x0 0,
或： u (l , t ) 0
(2)自由端：x l 端既不固定，又不受位移方向力的作用。
u T x
0
第 章 典型方程和定解条件的推导
第一章 典型方程和 定解条件
高三数学参考方程知识点总结
高三数学参考方程知识点总结一、一元一次方程一元一次方程是指形式为ax+b=0的方程，其中a和b是已知常数，x是未知数。
解一元一次方程的基本方法是移项和化简，通过消去未知数的系数和常数项，求出方程的解。
二、一元二次方程一元二次方程是指形式为ax²+bx+c=0的方程，其中a≠0，a、b、c是已知常数，x是未知数。
解一元二次方程的常用方法有以下几种：1. 因式分解法：将方程进行因式分解，使得方程左边等于0，然后令每个因式等于0，求出方程的解。
2. 完全平方公式法：将方程变形为(a+b)²=c的形式，通过求解平方根的方式得到方程的解。
3. 直接开方法：将方程变形为x²=d的形式，通过对方程两边开平方的方式求解出x的值。
4. 公式法：利用求根公式x=(-b±√(b²-4ac))/2a求解方程的根。
三、一元高次方程一元高次方程是指形式为anxⁿ+an₋₁xⁿ⁻¹+...+a₀=0的方程，其中a₀、a₁、...、an是已知常数，x是未知数，n是大于等于2的整数。
解一元高次方程常用的方法有以下几种：1. 因式分解法：如果方程可以进行因式分解，将方程分解成一元一次方程的乘积形式，然后求解得到方程的解。
2. 提取公因式法：如果方程各项有公因式，可以通过提取公因式将方程化简为某个因式与一个更简单的方程的乘积形式。
3. 配方法：对于某些特殊的高次方程，可以通过配方法将其转化为已知的方程求解。
4. 换元法：通过进行变量代换，将原方程转化为一个更简单的方程，然后求解得到方程的解。
四、二元一次方程组二元一次方程组是由两个形式为ax+by=c的方程组成的方程组，其中a、b、c是已知常数，x和y是未知数。
解二元一次方程组的方法主要有以下几种：1. 消元法：通过逐步消除未知数的系数，使得方程组中只含有一个未知数的方程，然后通过代入法求解得到方程组的解。
2. 代入法：先解出其中一个未知数，然后代入到另一个方程中求解另一个未知数的值。
数理方程复习课件
x x x c1 e xe e dx c1
x e x xe x e x c1 x 1 c1 e
dy x 1 c1 e x dx
y x 1 c1 e x dx
所以原微分方程的通解为
n
性质5的推论常被当做级数发散的充分条件来使用。
即 lim un 0 级数 n 1 2n 1
n 1 因为lim un lim ， n n 2n 1 2
n 所以，级数 是发散的。 n 1 2n 1
三、 常数项级数的敛散性判别法
1、收敛准则：
定理 1 : 正项级数 un 收敛的充分必要条件
2、比较判别法: 定理 2 比较判别法 设 un 与 v n都是
正项级数, 且un v n n 1,2,
则 1) 当级数 v n 收敛时, un 也收敛 ;
2) 当级数 un 发散时, v n 也发散。
则微分方程的通解为 y e P x dx Q x e P x dx dx c
e
1 dx x
1 dx 1 x e dx c ln x
1 x dx c x ln x
三、通过适当的代换求解
dy x y 5 例 求 的通解 . dx x y 2
解
dy du 1 令 x y u, dx dx du u 5 代入原方程 1 dx u 2
解得u 2 14x C ,
2
2 代回u x y, 得 ( x y 2) 14x C1 ,
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
X '(l)T (t) 0
引入参数 得
T '' a 2T
X '' X
X ' (0) X ' (l) 0
分离变量： T '' a2T 0
X '' X 0
X
'(0)
X '(l )
0
（1） 0， X ( x) C1e x C2e x
由边值条件
(C1 C2 ) 0 (C1e l C2e
Tn(t )
An
cos
nat
l
Bn
sin
nat
l
n 1,2,
u0( x, t) A0 B0t
un
(
x,
t
)
(
An
cos
n
l
at
Bn
sin
n
l
at
)
cos
n
l
x
n 1,2,
特征函数
X
(
x)
C1
cos
nx
l
n 0,1,
T0(t) A0 B0t
Tn(t )
An
cos
nat
l
Bn
sin
nat
l ) 0
得C1 =C 2=0 从而 X ( x) 0 ， 0 无意义
（2）＝0，X ( x) C0 D0 x
由边值条件 X '(0) X '(l) 0 X ( x) C0
（3） 0，X ( x) C1 cos x C2 sin x
由边值条件
C2 0
C1sin
l 0
第一章 典型方程和定解条件的推导
1）了解概念:定解问题、初始条件、边界条件; 2）了解三类典型方程对初始条件、边界条件的要求： 波动方程，热传导方程，拉普拉斯方程； 3）根据问题的描述，要会写出定解问题。
波方程
2u( x,t ) t 2
- a2u( x,t)
f ( x,t),
x ,t 0
➢弦的自由横振动方程：
utt a2 uxx uyy uzz
热方程
u( x,t ) - a2u( x,t ) f ( x,t ), x ,t 0 t
若物体内部有热源
u(x,y,z,t) ：物体在空间位置 x 以及时刻 t 的温度。
➢二维齐次热传导方程
u t
a2
2u x 2
2u y2
➢三维非齐次热传导方程
u t
a
2
2u x2
2u y2
2u
z 2
f (x, y, z,t)
Laplace方程, 泊松方程
u( x) 0, x
稳定的热场
u( x) f ( x),
x
有源的稳定热场
第一类边界条件直接给出 u 在边界 S 上的值，即
u S
f1
.
第二类边界条件是给出 u 沿 S 的外法线方向的
a2uxx， 0 x u |x1 0；
1，
t 0；
u |to sin 2 x，ut |t0 x(1 x).
解：方程有通解表达式（分离变量具体步骤省略） ：
u(x，t) (cn cos n at dn sin n at)sin n x
其中， cn 2
C1 0 sin l 0 l n (n 1,2,...),
从而
n2
l2
2
X
(
x)
C1
cos
nx
l
特征值
n2
l2
2
n 0,1,2,
特征函数
X
(
x)
C1
cos
nx
l
n 0,1,
T 的方程 T '' a2T 0
其解为
T0'' 0
Tn''
n2 2a2
l2
Tn
0
n0
T0(t) A0 B0t
cos
n
l
x
(x)
把( x), ( x) 展开为傅立叶余弦级数，比较系数
( x)
0
2
n
n1
cos
n
l
x
n
2 l
l ( x)cos n x dx
0
l
A0
n1
An
cos
n
l
x
(x)
B0
n1
n a
l
Bn
cos
n
l
x
(x)
把( x), ( x) 展开为傅立叶余弦级数，比较系数
A0
0
2
1 l
l
( )d
0
B0
0
2
1 l
l
( )d
0
An
n
2 l
0l
(
)cos
n
l
d
Bn
2
n a
0l
(
)cos
n
l
d
f
(x)
a0 2
n1
an
cos
n
l
x
bn
sin
n
l
x
பைடு நூலகம்2 l
n x
an l
f ( x) cos
0
l
dx
bn
2 l
l
n x
f ( x)sin dx
0
l
例 求解定解问题：
uutt|x0
l
n 1,2,
u0( x, t) A0 B0t
un
(
x,
t
)
(
An
cos
n
l
at
Bn
sin
n
l
at
)
cos
n
l
x
n 1,2,
故
u( x, t)
A0
B0t
( An
n1
cos
n at
l
Bn
sin
n at )cos
l
n
l
x
代入初始条件:
A0
n1
An
cos
n
l
x
(x)
B0
n1
n a
l
Bn
件的定解问题。
分离变量法（I）
波动方程，热传导方程定解问题
例：两端自由的杆的自由纵振动问题.
uutxt
a2uxx x0 0
0 ux
xl
0
u t 0 ( x) ut t 0 ( x)
解：令 u( x, t) X ( x)T(t)
XT '' a2 X "T 0
X '(0)T (t) 0
方向导数，即
u n S
f2
第三类边界条件是给出
u
以及
u n
的线性组合在
边界的值，即
u n
u
S
f3 ,
0.
初始条件
➢弦振动问题：设初始位移、初始速度为( x), ( x) ,
则波动方程的初值条件为
u t0 ( x), ut t0 ( x)
➢热传导问题：若 f(M) 表示 t = 0 时物体内一点M 的温度，则热传导问题的初始条件为
u M ,t |t0 f M .
➢泊松方程和拉普拉斯方程：描述稳恒状态的，与时 间无关，所以不提初始条件。
注意：
➢ 不同类型的方程，相应初值条件的个数不同; ➢ 初始条件给出的应是整个系统的初始状态，
而非系统中个别点的初始状态。
u t0 ( x), ut t0 ( x)
➢叠加原理
设 L 是线性微分算子，若 ui 满足线性方程（或
2u t 2
a2
2u x 2
,
➢弦的强迫横振动方程：
2u t 2
a2
2u x 2
f (x,t)
➢均匀杆的纵向振动问题：以 u(x,t) 表示杆上各点 的纵向位移，则 u(x,t) 满足波方程。
二维波动方程（例如薄膜振动）和三维波动方程 （例如电磁波和声波的传播）：
utt a2 uxx uyy
线性定解条件）
Lui fi, i 1,2, ,n,
则它们的线性组合 u ciui
i 1
必满足方程（或定解条件） Lu ci fi
i 1
第二章 分离变量法
要求：
1. 掌握有界弦振动和有限长杆上热传导问题的分 离变量解法；
2. 了解矩形域和圆域内拉普拉斯方程的分离变量 法解法；
3. 掌握使用特征函数法解非齐次方程的定解问题 4. 掌握用辅助函数和叠加原理处理非齐次边界条