齿轮强度计算公式

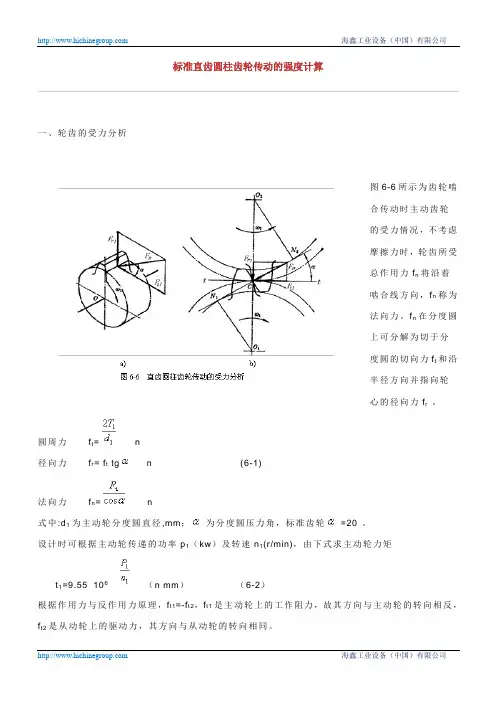
标准直齿圆柱齿轮传动的强度计算一、轮齿的受力分析图6-6所示为齿轮啮合传动时主动齿轮的受力情况，不考虑摩擦力时，轮齿所受总作用力f n将沿着啮合线方向，f n称为法向力。

f n在分度圆上可分解为切于分度圆的切向力f t和沿半径方向并指向轮心的径向力f r 。

圆周力f t=n径向力 f r= f t tg n (6-1)法向力 f n=n式中:d1为主动轮分度圆直径,mm；为分度圆压力角，标准齿轮=20°。

设计时可根据主动轮传递的功率p1（kw）及转速n1(r/min)，由下式求主动轮力矩t1=9.55×106×（n mm）（6-2）根据作用力与反作用力原理，f t1=-f t2，f t1是主动轮上的工作阻力，故其方向与主动轮的转向相反，f t2是从动轮上的驱动力，其方向与从动轮的转向相同。

同理，f r1=-f r2，其方向指向各自的轮心。

二、载荷与载荷系数由上述求得的法向力f n 为理想状况下的名义载荷。

由于各种因素的影响，齿轮工作时实际所承受的载荷通常大于名义载荷，因此，在强度计算中，用载荷系数k 考虑各种影响载荷的因素，以计算载荷f nc 代替名义载荷f n 。

其计算公式为(6-3)式中：k 为载荷系数，见表6-3。

表6-3 载荷系数k二、齿根弯曲疲劳强度计算齿根处的弯曲强度最弱。

计算时设全部载荷由一对齿承担，且载荷作用于齿顶，将轮齿看作悬臂梁，其危险截面可用30o 切线法确定，即作与轮齿对称中心线成30o 夹角并与齿根过渡曲线相切的两条直线，连接两切点的截面即为齿根的危险截面，如图6-7所示。

运用材料力学的方法，可得轮齿弯曲强度校核的公式为= ≤或σf =≤（6-4）或由上式得计算模数m的设计公式m≥ (6-5)式中:=b/d1称齿宽系数（b为大齿轮宽度），由表6-4查取；称为齿形系数，由图6-8查取；[]为弯曲许用应力，由式6-8计算。

表6-4齿宽系数=b/d1三、齿面接触疲劳强度计算齿面接触疲劳强度计算是为了防止齿间发生疲劳点蚀的一种计算方法，它的实质是使齿面节线处所产生的最大接触应力小于齿轮的许用接触应力，齿面接触应力的计算公式是以弹性力学中的赫兹公式为依据的，对于渐开线标准直齿圆柱齿轮传动，其齿面接触疲劳强度的校核公式为≤或≤ (6-6)将上式变换得齿面接触疲劳强度的设计公式d1≥ (6-7)式中：“±”分别用于外啮合、内啮合齿轮；z e为齿轮材料弹性系数，见表6-5；z h为节点区域系数，标准直齿轮正确安装时z h =2.5；[σh]为两齿轮中较小的许用接触应力，由式6-9计算；u为齿数比，即大齿轮齿数与小齿轮齿数之比。

变位齿轮传动的受力分析和强度计算原理与标准齿轮的相同，其计算公式也与标准齿轮相同
齿轮啮合节点位置发生变化，Z H 有变化
2/
2cos tan H Z a a =2/2cos tan H t t Z a a =/a a =/t t a a =高高高高高高 高x Σ=x 1+x 2=0：
Z H 高高高高高高高高高高高高高
或/a a >/t t a a >/a a </t t
a a <高x Σ>0高高高高高高高高Z H 高高高εα高高高Z ε高高高
高Z H 高高高εα高高高Z ε高高高或齿面接触强度提高。

当xΣ<0（负传动）时，或齿面接触强度降低。

角变位传动即x Σ=x 1+x 2≠0 ：
二、齿根弯曲强度齿根弯曲强度：
变位使齿形变化，齿根厚度和齿根圆角半径变化，引起计算系数Y Fa 和Y sa 的变化，影响齿根弯曲强度。

正变位齿轮的齿厚增大，Y Fa 减小，
齿根圆角半径减小，Y sa 增大。

正变位齿轮的齿根弯曲强度可有提高。

负变位使齿根弯曲强度降低。

变位使端面重合度系数εa 变化，Y ε也发生变化。

1. 齿面接触疲劳强度的计算齿面接触疲劳强度的计算中，由于赫兹应力是齿面间应力的主要指标，故把赫兹应力作为齿面接触应力的计算基础，并用来评价接触强度。

齿面接触疲劳强度核算时，根据设计要求可以选择不同的计算公式。

用于总体设计和非重要齿轮计算时，可采用简化计算方法；重要齿轮校核时可采用精确计算方法。

分析计算表明，大、小齿轮的接触应力总是相等的。

齿面最大接触应力一般出现在小轮单对齿啮合区内界点、节点和大轮单对齿啮合区内界点三个特征点之一。

实际使用和实验也证明了这一规律的正确。

因此，在齿面接触疲劳强度的计算中，常采用节点的接触应力分析齿轮的接触强度。

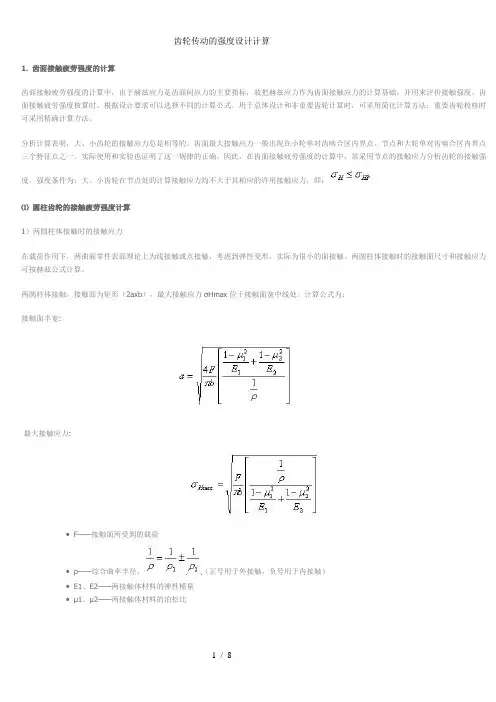
强度条件为：大、小齿轮在节点处的计算接触应力均不大于其相应的许用接触应力，即：⑴圆柱齿轮的接触疲劳强度计算1）两圆柱体接触时的接触应力在载荷作用下，两曲面零件表面理论上为线接触或点接触，考虑到弹性变形，实际为很小的面接触。

两圆柱体接触时的接触面尺寸和接触应力可按赫兹公式计算。

两圆柱体接触，接触面为矩形（2axb），最大接触应力σHmax位于接触面宽中线处。

计算公式为：接触面半宽:最大接触应力:•F——接触面所受到的载荷•ρ——综合曲率半径，（正号用于外接触，负号用于内接触）•E1、E2——两接触体材料的弹性模量•μ1、μ2——两接触体材料的泊松比2）齿轮啮合时的接触应力两渐开线圆柱齿轮在任意一处啮合点时接触应力状况，都可以转化为以啮合点处的曲率半径ρ1、ρ2为半径的两圆柱体的接触应力。

在整个啮合过程中的最大接触应力即为各啮合点接触应力的最大值。

节点附近处的ρ虽然不是最小值，但节点处一般只有一对轮齿啮合，点蚀也往往先在节点附近的齿根表面出现，因此，接触疲劳强度计算通常以节点为最大接触应力计算点。

参数直齿圆柱齿轮斜齿圆柱齿轮节点处的载荷为综合曲率半径为接触线的长度为，3）圆柱齿轮的接触疲劳强度将节点处的上述参数带入两圆柱体接触应力公式，并考虑各载荷系数的影响，得到：接触疲劳强度的校核公式为：接触疲劳强度的设计公式为：•KA——使用系数•KV——动载荷系数•KHβ——接触强度计算的齿向载荷分布系数•KHα——接触强度计算的齿间载荷分配系数•Ft——端面内分度圆上的名义切向力，N；•T1——端面内分度圆上的名义转矩，N.mm；•d1——小齿轮分度圆直径，mm；•b ——工作齿宽，mm，指一对齿轮中的较小齿宽；•u ——齿数比；•ψd——齿宽系数，指齿宽b和小齿轮分度圆直径的比值（ψd=b/d1）。

齿轮疲劳强度计算公式齿轮是一种广泛运用于机械设备传动系统中的机械元件。

由于长时间使用和不可避免的载荷，在齿轮中会出现疲劳现象。

其严重程度甚至可能导致齿轮的失效，因此在齿轮的设计和选择时，需要对齿轮的疲劳强度进行评估和计算。

下面我们介绍一下齿轮疲劳强度的计算公式和相关参考内容。

一、齿轮疲劳强度的计算公式齿轮的疲劳强度指齿轮在循环载荷作用下能承受的极限应力，是齿轮设计时必须考虑的重要参数。

目前，齿轮疲劳强度的计算公式主要包括两种：1. 安全性系数法安全性系数法是齿轮疲劳强度计算中最基本的方法，其计算公式为:S_h = K_h \cdot S_N式中，S_h 为齿轮疲劳强度，K_h 为齿轮强度系数，S_N 为材料的疲劳极限强度。

2. AGMA方法AGMA方法是美国齿轮制造商协会制定的齿轮强度计算方法，其计算公式为：S_h = S_F \cdot S_G \cdot S_I \cdot (1 + S_K \cdot S_H)式中，S_F 为载荷系数，S_G 为几何系数，S_I 为材料系数，S_K 为动载系数，S_H 为表面硬化系数。

二、齿轮疲劳强度计算参考内容齿轮疲劳强度的计算涉及到多个参数和方法，具体参考内容如下：1. 齿轮疲劳强度计算手册近年来，国内外多个机械设计机构纷纷出版齿轮疲劳强度计算手册，内容包括安全性系数法和AGMA方法，详细介绍了齿轮强度计算的各个参数如何确定、如何计算等，是齿轮设计师必备的参考资料。

2. 齿轮强度计算软件为了方便齿轮设计师进行疲劳强度计算，多家厂商推出了齿轮强度计算软件，其中不乏国内外知名企业，如Gearotic、KISSsoft等，可实现齿轮的一些增效功能，如自动计算载荷系数、自动选型等，提高了工作效率。

3. 材料手册齿轮的疲劳强度受到材料性能的影响，因此需要用到材料手册，了解不同种类材料的优缺点、极限应力等数据，为正确选择材料提供参考。

总的来说，齿轮疲劳强度的计算是齿轮设计中不可或缺的环节。

直齿轮箱尺寸变化影响传动强度分析阮超传递：功率P，转速n，扭矩T齿轮：齿数Z，齿宽b，模数m，材料强度σ 强度公式： 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2（体积关联） 条件变化： 1.齿轮箱外形尺寸不变，n2=3600r/min， m2=4mm，求P2？ 弯曲 模数变化4/3，转速变化3600/3000， P2=120*4/3KW 接触 体积不变，转速变化3600/3000，P2=120KW；弯曲变化机理：齿形变大 接触变化机理：P=T*n/9550已知：功率P1=100KW，转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递：功率P，转速n，扭矩T齿轮：齿数Z，齿宽b，模数m，材料强度σ 强度公式： 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2（体积关联） 条件变化： 2.齿轮箱齿数不变，n2=3600r/min， m2=4mm，求P2？ 弯曲 模数变化4/3，转速变化3600/3000， P =120*（4/3） KW 接触 模数变化4/3，转速变化3600/3000， P =120*（4/3） KW2 2 2 2弯曲变化机理：力臂和曲率半径增大 接触变化机理：单位齿宽负载和直径增大已知：功率P1=100KW，转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递：功率P，转速n，扭矩T齿轮：齿数Z，齿宽b，模数m，材料强度σ 强度公式： 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2（体积关联） 条件变化： 3.齿轮箱尺寸放大4/3倍，n2=3600r/min， 求P2？ 弯曲 模数变化4/3，转速变化3600/3000， P =120*（4/3） KW 接触 模数变化4/3，转速变化3600/3000， P =120*（4/3） KW2 2 3 3弯曲变化机理：齿宽b，模数m增大 接触变化机理：齿宽b，模数m增大已知：功率P1=100KW，转速n1=3000r/min,模数m1=3mm直齿轮箱尺寸变化影响传动强度分析阮超传递：功率P，转速n，扭矩T齿轮：齿数Z，齿宽b，模数m，材料强度σ 强度公式： 弯曲 T∝b(Zm)mσ 接触 T∝b(Zm)2σ2（体积关联） 条件变化： 4.齿轮材料选用1.2倍σ，n2=3600r/min， 求P2？ 弯曲 模数变化4/3，转速变化3600/3000， P =120*1.2KW 接触 模数变化4/3，转速变化3600/3000， P =120*（1.2） KW2 2 2弯曲变化机理：材料增强 接触变化机理：材料增强已知：功率P1=100KW，转速n1=3000r/min,模数m1=3mm。

圆柱齿轮传动的强度计算1 直齿圆柱齿轮传动的强度计算1.齿面接触疲劳强度计算为了保证在预定寿命内齿轮不发生点蚀失效，应进行齿面接触疲劳强度计算。

因此，齿轮接触疲劳强度计算准则为：齿面接触应力σH小于或等于许用接触应力σHP，即σH≤σHP赫兹公式由于直齿轮在节点附近往往是单对齿啮合区，轮齿受力较大，故点蚀首先出现在节点附近。

因此，通常计算节点的接触疲劳强度。

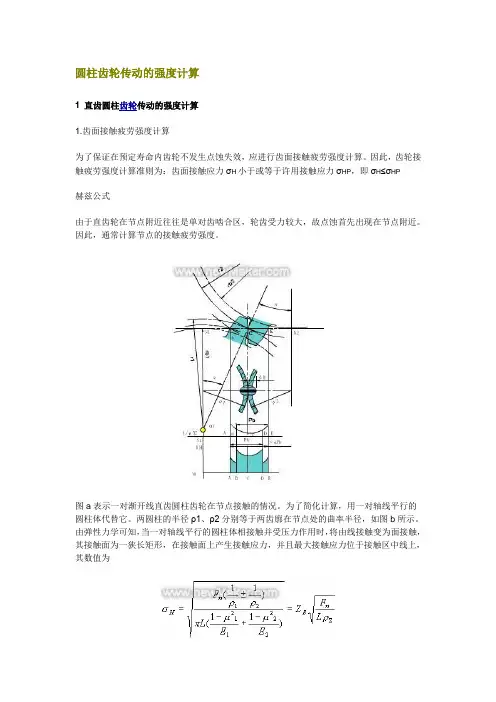
图a表示一对渐开线直齿圆柱齿轮在节点接触的情况。

为了简化计算，用一对轴线平行的圆柱体代替它。

两圆柱的半径ρ1、ρ2分别等于两齿廓在节点处的曲率半径，如图b所示。

由弹性力学可知，当一对轴线平行的圆柱体相接触并受压力作用时，将由线接触变为面接触，其接触面为一狭长矩形，在接触面上产生接触应力，并且最大接触应力位于接触区中线上，其数值为式中σH-接触应力（Mpa）Fn-法向力（N）L-接触线长度（mm）rS-综合曲率半径（mm）；±-正号用于外接触，负号用于内接触ZE-材料弹性系数（），，其中E1、E2分别为两圆柱体材料的弹性模量（MPa）；m1、m2分别为两圆柱体材料的泊松比。

上式表明接触应力应随齿廓上各接触点的综合曲率半径的变化而不同，且靠近节点的齿根处最大（图c、d）。

但为了简化计算，通常控制节点处的接触应力。

节点处的参数（1）综合曲率半径由图可知，，代入rE公式得式中：，称为齿数比。

对减速传动，u=i；对增速传动，u=1/i。

因，则有（2）计算法向力（3）接触线长度L引入重合度系数Ze，令接触线长度将上述参数代入最大接触应力公式得接触疲劳强度计算公式令，称为节点区域系数。

则得(1) 齿面接触疲劳强度的校核公式齿面接触疲劳强度的校核公式为(2) 齿面接触疲劳强度设计公式设齿宽系数，并将代入上式，则得齿面接触疲劳强度的设计公式式中:d1-小齿轮分度圆直径（mm）；ZE-材料弹性系数()，按下表查取；注：泊松比m1＝m2＝0.3Z H-节点区域系数，考虑节点处轮廓曲率对接触应力的影响，可由下左图查取。

锥齿轮接触疲劳强度公式1.2KTy u+'<[on]ow =Zg2H 0.85bd, 3u,齿面接触疲劳强度计算1)计算公式:按齿宽中点当量直齿圆柱齿轮计算，并取齿宽为0.85，则: 以齿轮大端参数代替齿宽中点当量直齿圆柱齿轮参数，代入整理得:4KToH =ZgZH,.tV'l2 , ≤[oH]e(1一0.5yR)du校核式:对于a=200的标准齿轮ZH=2.5。

故:KTow =5ZE, 12 3SloH]vg(1-0.5ug)dud≥2.92 3va(1一0.5y p尸u([on]设计式:2)参数说明)K=KAKvKQKBKv——按平均分度圆速度查取。

a——Ka =1k——锥齿轮齿向戟荷分布系数b)ZE、ZH、[oH]同直齿圆柱齿轮c)中R=b/R1/31．齿面接触疲劳强度计算1)计算公式:2KT.i__ u,+l<[o n]H = ZEZHZ.0.85bd2uv按齿宽中点当量直齿圆柱齿轮计算，并取齿宽为0.85b，则;以齿轮大端参数代替齿宽中点当量直齿圆柱齿轮:d=(1一0.S e , +lT, =T √u2+1u, =u2b =u gR =uo ed, vu2+i/代入整理得;=ZEZnZn4.7KT校核式;R(1一0.5yu ;)d; u4.7KTi(ZgZnZe设计式:d二.. 1_o5u o)u [o n]2参数说明a)K=KKy,KaKBKv---按平均分度圆速度查取。

Ka---按当量齿数计算K--锥齿轮齿向载荷分布系数b)ZE、Zw、Zg、[o]同直齿圆柱齿轮c) urw=b/R≤1/3。

斜齿轮弯曲强度公式斜齿轮是一种常见的齿轮类型，它在机械传动系统中得到了广泛的应用。

斜齿轮的弯曲强度是机械传动系统设计中的一个重要参数，它反映了斜齿轮在工作中承受弯曲应力的能力。

了解斜齿轮的弯曲强度公式可以帮助我们更好地设计和选型斜齿轮，提高机械传动系统的稳定性和可靠性。

一、斜齿轮的基本概念斜齿轮是指齿轮的齿线方向与齿轮轴线不垂直，而是成一个夹角。

夹角的大小称为螺旋角，用β表示。

根据螺旋角的方向，斜齿轮可分为左旋和右旋两种类型。

二、斜齿轮的弯曲强度斜齿轮在工作中，其齿部受到很大的弯曲应力，这种弯曲应力的大小与齿轮的几何参数、材料、转速等因素有关。

根据弹性力学理论，斜齿轮的弯曲强度可以表示为：σ = K ×σ′× Ym × Zm × [σ]其中，σ表示斜齿轮的弯曲强度；K表示弯曲强度系数，它与齿轮的几何参数、材料等因素有关；σ′表示齿轮的接触应力，即齿轮在接触区内的应力；Ym表示弯曲强度计算系数，它与齿轮的几何参数、转速等因素有关；Zm表示弯曲强度计算系数，它与齿轮的几何参数、转速等因素有关；[σ]表示齿轮材料的许用应力。

三、斜齿轮弯曲强度公式的推导弯曲强度计算系数的确定根据齿轮传动的原理，斜齿轮在工作中主要受到弯曲应力和接触应力两种作用。

弯曲应力的大小与齿轮的几何参数、材料、转速等因素有关，接触应力的大小与齿轮的几何参数、工作压力等因素有关。

因此，弯曲强度系数K可以通过以下公式计算：K = K1 × K2 × K3 × K4其中，K1表示弯曲系数，它与齿轮的几何参数、材料等因素有关；K2表示工作系数，它与工作压力、工作压力位置等因素有关；K3表示转速系数，它与齿轮的转速等因素有关；K4表示温度系数，它与齿轮的工作温度等因素有关。

弯曲强度计算系数的具体值弯曲强度计算系数K的具体值可以根据实际情况查表得到。

根据不同的设计条件和参数，弯曲强度计算系数K可以取不同的值。

直齿圆柱齿轮的强度计算受力分析：圆周力F t =112d T 径向力αtan ∙=t r F F 法向载荷αcos t n F F = 1T ：小齿轮传递的转矩，mm N ∙ 1d ：小齿轮的节圆直径，mm α：啮合角，对标准齿轮， 20=α齿根弯曲疲劳强度的计算： 校核公式：[]F d Sa Fa Sa Fa F z m Y Y KT bmd Y Y KT σφσ≤==21311122 计算公式：[]32112F d Sa Fa z Y Y KT m σφ≥d φ：齿宽系数，1d b d =φ Fa Y ：齿形系数 Sa Y ：应力校正系数齿面接触疲劳强度的计算： 校核公式：[]H E H uu bd KT Z σσ≤±∙=125.2211 设计公式：[]3211132.2⎪⎪⎭⎫ ⎝⎛∙±∙=H E d Z u u KT d σφ标准斜齿圆柱齿轮的强度计算 受力分析： 圆周力：112d T F T = 径向力：βαcos tan n t r F F ∙= 轴向力：βtan ∙=t a F F齿根弯曲疲劳强度计算： 校核公式：[]F n Sa Fa t F bm Y Y Y KF σεσαβ≤=设计计算：[]32121cos 2F Sa Fa d n Y Y z Y KT m σεφβαβ∙=齿面接触疲劳强度计算： 校核计算：H E H Z Z uu bd KT ∙±∙=111αεσ 设计计算：[]321112⎪⎪⎭⎫ ⎝⎛∙±∙≥H Sa Fa d Y Y u u KT d σεφαu ：齿数比标准锥齿轮的强度计算 受力分析：11212m t t d T F F == 121cos tan δαt a r F F F == 121cos tan δαt r a F F F == αcos 1t n F F =齿根弯曲疲劳强度计算： 校核公式：()[]F R Sa Fa t F bm Y Y KF σφσ≤-=5.01 设计公式：()[]32212115.014F Sa Fa R R Y Y u z KT m σφφ∙+-≥齿面接触疲劳强度计算： 校核公式：()[]H R R E H u d KT Z σφφσ≤-=31215.015设计公式：[]()321215.0192.2u KT Z d R R H E φφσ-∙⎪⎪⎭⎫ ⎝⎛≥。

一、轮齿的接触应力ζj 的计算：ζj=0.418√FE(1/ρz+1/ρb )/bF=F1/(cos αcos β)F1=2Tg/dd 为节圆的直径Tg 为计算载荷ρz 、ρb 分别为主从动齿轮节点处的曲率半径：直齿轮：ρz=r z sin α ρb= r b sin α斜齿轮：ρz=（r z sin α）/cos 2β ρb=（ r b sin α）/cos 2βr z r b为主，从动齿轮节圆半径 二、轮齿弯曲应力ζw 的计算：直齿轮：ζw=F1K ζK f /bty=2TgK ζK f /πm 3ZK c y斜齿轮：ζw=2Tgcos βK ζ/∏m 3n ZK c yK εK ε为重合度系数，一般取K ε=2.0K ζ集中应力系数，一般直齿轮取K ζ=1.65，斜齿轮取K ζ=1.50y 为齿形系数，一般在0.16---0.18之间K c 为齿宽系数，一般在4.5---8.0之间K f 为摩擦力系数，主动轮取1.1，从动轮取0.9 A B δf Fa LbX一、初选轴的直径已知中心距A。

第二轴与中间轴中部直径：d≈0.45A，轴的最大直径d和支承间距离L的比值：d/L=0.16--0.18；对二轴：d/L=0.18--0.21；第一轴花键部分直径d可按下试初选：d=K 3√T emax式中，K为经验系数，K=4.0---4.6；T emax为发动机最大转矩（N.m）二、轴的强度计算1.轴的刚度计算：轴在垂直面内绕度：f c=F1a2b2/3EIL轴在水平面内绕度：f s=F2a2b2/3EIL轴在水平面内转角: δ=F1ab（b-a）/3EIL式中，F1为齿轮齿宽中间平面上的径向力（N）,F2为齿轮齿宽中间平面上的圆周力（N），E为弹性模量，E=2.1×105MPa；I为惯性矩（mm4），对于实心轴，I=πd4/64;d为轴的直径（mm），花键外按平均直径计算；a，b为齿轮上的作用力矩A,B的距离（mm），L为支座间的距离（mm）。

标准齿轮计算公式1. 齿轮基本参数的计算。

在进行齿轮设计和计算时，首先需要确定一些基本参数，包括模数、齿数、齿宽等。

这些参数的计算可以通过以下标准公式进行：（1）模数的计算公式：\[ m = \frac{d}{z} \]其中，m为模数，d为齿轮的分度圆直径，z为齿数。

（2）齿宽的计算公式：\[ b = m \times z \]其中，b为齿宽。

（3）齿顶高和齿根高的计算公式：\[ h_t = m \]\[ h_f = 1.25 \times m \]其中，h_t为齿顶高，h_f为齿根高。

2. 齿轮传动比的计算。

齿轮的传动比是指两个齿轮的齿数之比，一般用i表示。

齿轮传动比的计算公式为：\[ i = \frac{z_2}{z_1} \]其中，z_1为驱动齿轮的齿数，z_2为被动齿轮的齿数。

3. 齿轮啮合角的计算。

齿轮啮合角是指齿轮啮合时齿廓线与径向的夹角，它的大小对齿轮传动的平稳性和噪音有着重要影响。

齿轮啮合角的计算公式为：\[ \alpha = \arccos \left( \frac{m}{d} \right) \]其中，α为齿轮啮合角，m为模数，d为齿轮的分度圆直径。

4. 齿轮齿形修形系数的计算。

齿轮齿形修形系数是用来修正齿轮齿形的参数，它的大小对齿轮的传动效率和运行平稳性有着重要影响。

齿轮齿形修形系数的计算公式为：\[ x = 0.5 \times \left( \frac{1}{\cos \alpha} \frac{1}{\cos^3 \alpha} \right) \]其中，x为齿形修形系数，α为齿轮啮合角。

5. 齿轮齿面接触疲劳强度的计算。

齿轮齿面接触疲劳强度是指齿轮齿面在啮合过程中所承受的接触应力，它的大小对齿轮的使用寿命有着重要影响。

齿轮齿面接触疲劳强度的计算公式为：\[ \sigma_H = \frac{2 \times P}{\pi \times m \times b \times J} \]其中，σ_H为齿面接触疲劳强度，P为传动功率，m为模数，b为齿宽，J为齿形修形系数。