合肥工业大学理论力学复习题
- 格式:docx
- 大小:197.46 KB
- 文档页数:17
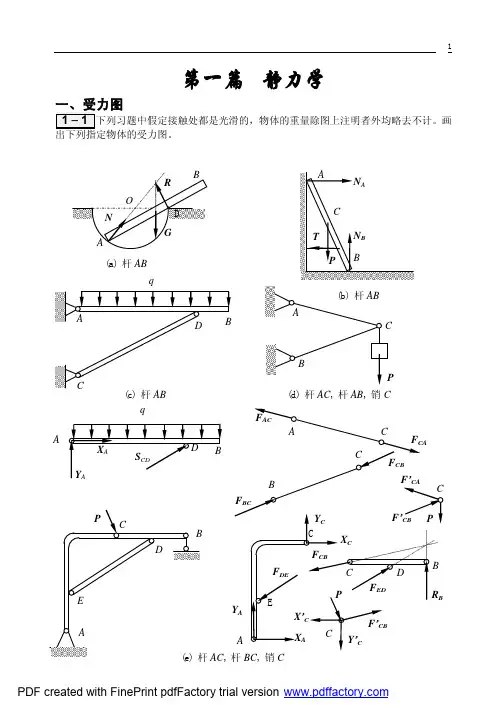
第一部分 静力学1、如图所示的平面桁架,在铰链H 处作用了一个20kN 的水平力,在铰链D 处作用了一个60kN 的垂直力。
求A 、E 处的约束力和FH 杆的内力。
E 20kN xF = E 52.5kN y F = A 7.5kN y F = HF 12.5kN F =-2、图示等边三角形ABC ,边长为l ,现在其三顶点沿三边作用三个大小相等的力F ,试求此力系的简化结果。
3、外伸梁ABC 上作用有均布载荷q =10 kN/m ,集中力F =20 kN ,力偶矩m =10 kN ⋅m ,求A 、B 支座的约束力4、一木板放在两个半径 r =0.25 m 的传输鼓轮上面。
在图示瞬时,木板具有不变的加速度 a =0.5 m/s2,方向向右;同时,鼓轮边缘上的点具有一大小为 3 m/s2 的加速度。
如果木板在鼓轮上无滑动,试求此木板的速度。
5、求图示分布载荷的合力及对A点之矩。
6、结构上作用载荷分布如图,q1=3 kN/m,q2=0.5 kN/m,力偶矩M=2 kN m,试求固定端A与支座B的约束力和铰链C的内力。
答案:Fnb=-0.5,Fcy=1.5,Fcx=0,Fay=2,Fax=-4.57、在刚架B点受一水平力作用。
设F=20 kN,刚架的重量略去不计。
求A、D处的约束力。
F答案:FA=22.4kN,FD=10 kN8、图中AD=DB=2 m,CD=DE=1.5 m,Q=120 kN,不计杆和滑轮的重量。
试求支座A和B 的约束力和BC杆的内力。
答案:FNB=105,Fax=120,Fay=15,Fbc=1509、某厂房用三铰刚架,由于地形限制,铰A及B位于不同高度。
刚架上的载荷已简化为两个集中力F1及F2。
试求C处的约束力。
答案()()()()122Cy CyF l a H F l b H h F F l H h ---+'==+12、图示平面结构由不计自重的三个刚体在D 、E 处铰接而成。
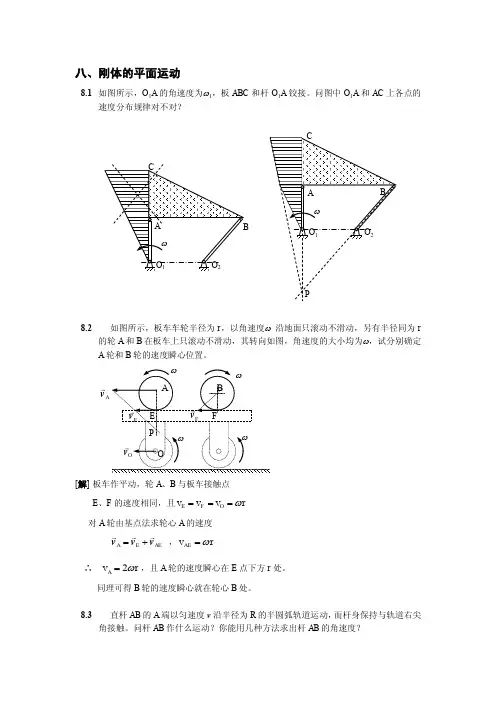
八、刚体的平面运动8.1 如图所示,O 1A 的角速度为ω1,板ABC 和杆O 1A 铰接。
问图中O 1A 和AC 上各点的速度分布规律对不对?8.2如图所示,板车车轮半径为r ,以角速度ω 沿地面只滚动不滑动,另有半径同为r 的轮A 和B 在板车上只滚动不滑动,其转向如图,角速度的大小均为ω,试分别确定A 轮和B 轮的速度瞬心位置。
[解] 板车作平动,轮A 、B 与板车接触点 E 、F 的速度相同,且r v v v O F E ω=== 对A 轮由基点法求轮心A 的速度 A E AE =+v v v ,r v AE ω=∴ r v A ω2=,且A 轮的速度瞬心在E 点下方r 处。
同理可得B 轮的速度瞬心就在轮心B 处。
8.3直杆AB 的A 端以匀速度v 沿半径为R 的半圆弧轨道运动,而杆身保持与轨道右尖角接触。
问杆AB 作什么运动?你能用几种方法求出杆AB 的角速度?E FPOE v Av Fv Ov[解] AB 杆作平面运动。
(一) 瞬心法AB 杆作平面运动,速度瞬心为P 。
Rv AP v AAB2==ω (二)基点法D A DA =+v v v ,DA v v AB A DA ωθ==sin又 DA =2R cos(90o -θ)=2R sin θ ∴ Rv AB 2=ω(三)自然法: d d AB tϕω=,而R S ϕ2= ∴d d 2d d S R v t t ϕ==, d d 2vt R ϕ= ∴ Rv AB 2=ω 8.4如图所示四连杆机构OABO 1中,OA=O 1B=AB/2,曲柄OA 的角速度ω=3rad/s 。
当OA 转到与OO 1垂直时,O 1B 正好在OO 1的延长线上,求该瞬时AB 杆的角速度ωAB 和曲柄O 1B 的角速度ω1。
[解]取AB 为研究对象,AB 作平面运动。
以A 为基点,画B 点速度合成图 由B A BA =+v v v(rad/s)32230sin o==∴⋅=⋅==ωωωωAB OAAB OA v v AB AB ABABBBvvvDAv Dv Dv111cos3022(rad/s)B BAv v OA O Bωωω=︒=⋅=∴=8.5图示曲柄摇机构中,曲柄OA以角速度oω绕O轴转动,带动连杆AC在摇块B内滑动,摇块及与其固结的BD杆绕B铰转动,杆BD长l;求在图示位置时摇块的角速度及D点的速度。
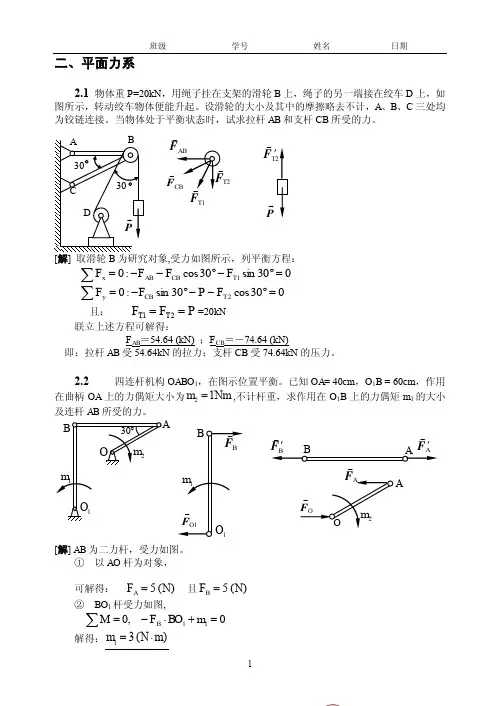
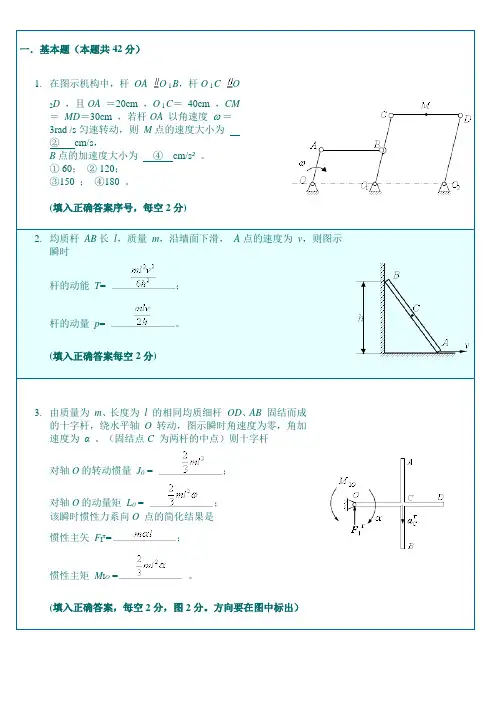
一.基本题(本题共42分)1. 在图示机构中,杆OA O l B ,杆O l C O2D,且OA =20cm ,O l C = 40cm ,CM = MD =30cm ,若杆OA 以角速度 = 3rad /s 匀速转动,则 M 点的速度大小为 ② cm/s ,B 点的加速度大小为 ④ cm/s 2 。
① 60; ② 120; ③150 ; ④180 。
(填入正确答案序号,每空2分)2. 均质杆 AB 长 l ,质量 m ,沿墙面下滑, A 点的速度为 v ,则图示瞬时杆的动能 T =;杆的动量 p =。
(填入正确答案每空2分)3. 由质量为 m 、长度为 l 的相同均质细杆 OD 、AB 固结而成的十字杆,绕水平轴 O 转动,图示瞬时角速度为零,角加速度为 α 。
(固结点C 为两杆的中点)则十字杆对轴O 的转动惯量 J 0 =;对轴O 的动量矩 L 0 = ; 该瞬时惯性力系向O 点的简化结果是 惯性主矢 F I τ=;惯性主矩 M I O = 。
(填入正确答案,每空2分,图2分。
方向要在图中标出)4. 图示三棱柱的截面是等腰直角三角形,尺寸如图。
A点作用一已知力 F ,方向如图,求该力在坐标轴 x 上的投影及对坐标轴 z 之矩。
F x =M Z (F ) =(每空2分)5. 在图示运动机构中,作平面运动的构件有 3 个,并在图中作出该瞬时各自的速度瞬心。
(三个瞬心各2分)6. 直角弯管 OAB 在平面内以匀角速度 = 2rad /s 绕O 点转动,动点M 以相对速度 v r =2 cm/s 沿弯管运动,b=5cm ,则图示瞬时动点的牵连速度 v e = cm/s ; 牵连加速度 a e =cm/s 2 ;科氏加速度 a c = 8 cm/s 2。
(各矢量方向必须在图中标出,每个矢量2分)7. 图示四连杆机构中,曲柄O l A 上作用力偶M ,B 铰上作用一集中力 P 。
已知 O 1A = AB =O 2B = l ,在图示瞬时机构处于平衡。

一、基本题(每小题6 分,共42 分)1. ( 填空题,6 分) 在边长为a的正方体的顶角B处作用集中力P,方向如图,求力系向O点简化的结果。
P x =[ ];P y = [-]P z =[ ];M x = [ ]M y = [ 0 ] ;M Z =[ -](每空 1 分)2. ( 填空题,5 分) 均质圆盘重P,半径为r,绕偏心轴以角速度 转动,轴O到圆心C的距离为 e ,则圆盘对轴O的动量矩为:L o =[]。
3. ( 选择题,5 分) 在图(a) 和图(b) 中,OA同为重为P 、长为l 的匀质杆,A B为无重细绳,两图中的OA杆均处于水平静止状态。
问在刚剪断细绳的瞬时,两图中OA杆的角加速度和O 点的支反力是否相同,则下列结论正确的情况是④。
①角加速度和支反力都不相同;②角加速度相同、支反力不同;③角加速度不同、支反力相同④角加速度和支反力都相同。
4. ( 简单计算题,10分) 重为R 的楔块放置在光滑的水平面上,与重为P,长为l 的均质杆AB用光滑铰链相连。
初始时刻A B杆处于铅直位置,整个系统静止;在微小扰动下杆AB 绕铰A转动,楔块在水平方向运动。
求(1) 当杆AB转过φ角度时楔块的水平位移x;(2) 用杆AB转动的角速度表示楔块水平运动的速度v。
解:由于系统在水平方向不受力,且系统初始静止。
取初始时刻系统的质心C0为坐标原点,设杆AB转过φ角度时楔块的水平位移为x,根据质心坐标守恒,有:(+ 4 分)(+ 5 分)解得:(+ 1 分)5. ( 简单计算题,10分) 匀质刚杆AC的长为l ,质量为m,弹簧刚度为k ,自由端固定一质量为M = m的物体。
试建立系统的运动方程,并确定系统作自由振动时的固有频率。
解一:用达朗贝尔原理。
以静平衡位置为参考位置,以刚杆的转角φ为广义位移,刚杆转动的角加速度为。
加惯性力系如图所示。
,,,(+3分)由有:整理得系统的运动方程:,或(+4分)由此可得固有频率:(+3分)解二:用能量法。

理论力学课程试题及答案理论力学是物理学中的一个重要分支,它主要研究宏观物体在力的作用下的运动规律。
理论力学课程通常包括静力学、动力学、运动学、能量守恒定律、动量守恒定律、角动量守恒定律等内容。
以下是一份理论力学课程的试题及答案,供学习者参考。
试题一、选择题(每题2分,共10分)1. 理论力学的研究对象是()A. 微观粒子B. 宏观物体C. 流体D. 热力学系统2. 在国际单位制中,力的单位是()A. 牛顿(N)B. 帕斯卡(Pa)C. 焦耳(J)D. 瓦特(W)3. 一个物体的动量是()A. 物体的质量与速度的乘积B. 物体的动能C. 物体的势能D. 物体的位移4. 根据牛顿第三定律,作用力与反作用力()A. 大小相等,方向相反B. 大小不等,方向相反C. 大小相等,方向相同D. 大小不等,方向相同5. 一个物体在水平面上做匀速直线运动,其受到的摩擦力()A. 等于物体的重力B. 等于物体的动能C. 等于物体的动量D. 与物体的牵引力大小相等,方向相反二、简答题(每题5分,共20分)1. 请简述牛顿运动定律的三个定律。
2. 什么是角动量守恒定律?它在什么条件下成立?3. 简述能量守恒定律,并说明其在实际应用中的重要性。
4. 何为虚功原理?它在解决静力学问题中有何作用?三、计算题(每题10分,共30分)1. 一个质量为2kg的物体在水平面上以3m/s的速度做匀速直线运动,若摩擦系数为0.1,请计算物体受到的摩擦力大小。
2. 一个质量为5kg的物体从静止开始自由下落,忽略空气阻力,求物体在2秒后的速度和位移。
3. 一个质量为3kg的物体在竖直平面内做圆周运动,其半径为1m,角速度为2rad/s,请计算物体在最高点时所需的最小速度。
四、解答题(每题15分,共30分)1. 一个质量为m的物体在竖直方向上受到一个向上的力F作用,物体向上做匀加速直线运动。
若物体的加速度为a,试证明牛顿第二定律在该情况下的表达式,并说明力F与物体质量m和加速度a之间的关系。

合肥工业大学工程力学专业《工程结构数值方法》2008年试卷A 答案2008年5月11 日上午考试(共8题,满分100分),考试时间:120分钟适用专业:工程力学05-1(本科),出题人:牛忠荣1.(8分)线弹性力学静力学问题有限元法计算列式的理论推导是如何采用弹性力学问题基本方程?答:弹性力学有限元的基本过程是:1.假设单元的位移场模式}]{[}{e N f δ=2.代入到几何方程得到}]{[}{eB δε=3.代入到物理方程得到}]{][[}{e B D δσ=4.代入到虚功方程,得到单元刚度方程}]{[][ee k F δ=5.叠加到总刚阵,得到结构的平衡方程}]{[][e e k F δ=6.引入位移边界条件后,解第5步得到的方程组,可以得到结点位移2.(12分)用有限元法计算图示平面刚架时, 试求:(1) 如何进行结点编号,使系统总刚度矩阵的带宽最小? K (2) 计算在你的结点编号下的系统总刚阵的半带宽。
K (3) 在结点编号确定后,按此顺序进行自由度编号,则图中结点水平位移A 对应的主对角元素在总刚阵中的列和行位置是多少? 那些单元对该K 元素的数值有贡献?答:(1)见图;(2)半带宽=;15143=+)((3)结点水平位移对应的A 主对角元素是;2828,k A 点周围的4个单元对有贡献。
2828,k xy 题2图1171353.(10分)弹性力学有限元中,平面等参数单元中的“等参数”概念是何意思? 该单元在跨相邻单元时,位移场连续吗? 应力场连续吗?答:在有限单元法中最普遍采用的是等参变换,即单元几何形状的变换和单元内的场函数采用相同数目的节点参数及相同的插值函数进行变换。
采用等参变换的单元称之为等参元。
所谓“等参元”是指几何形状插值形函数和单元上的位移插值形函数相同,参数个数相等。
相邻等参元之间,位移场是连续的,应力场不连续。
4.(10分)回答下列问题:(1)弹性力学平面问题8节点等参元,其单元自由度是多少个?单元刚阵元素是多少个?(2)弹性力学空间问题20节点等参元,其单元自由度是多少个?单元刚阵元素是多少个?(3)一般的平面刚架结构梁单元的自由度是多少个?单元刚阵元素是多少个?(4)一般的空间刚架结构梁单元的自由度是多少个?单元刚阵元素是多少个?答:1)自由度16个,刚阵元素16×16=256;2)自由度60个,刚阵元素60×60=3600;3)自由度6个,刚阵元素6×6=36;4)自由度12个,刚阵元素12×12=144.5.(10分)结构振动问题有限元离散的无阻尼自由振动方程为 0ΦM K 2=-)(ϖ式中是刚度矩阵,是质量矩阵,是结构固有频率,是振型n n ⨯K n n ⨯M ϖΦ向量。

大学理论力学期末考试题库及答案一、选择题(每题2分,共20分)1. 质点系的质心位置取决于()。
A. 质点系的总质量B. 质点系中各质点的质量C. 质点系中各质点的位置D. 质点系中各质点的速度答案:C2. 刚体的转动惯量与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状3. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B4. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的速度v为()。
A. v = v0 + atB. v = v0 - atC. v = v0 + 1/2atD. v = v0 - 1/2at5. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B6. 刚体绕固定轴转动时,其转动惯量与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状答案:C7. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的位移s为()。
A. s = v0t + 1/2at^2B. s = v0t - 1/2at^2C. s = v0t + at^2D. s = v0t - at^2答案:A8. 刚体绕固定轴转动时,其角加速度与()有关。
A. 质量B. 质量分布C. 质量分布和形状D. 形状答案:B9. 质点沿直线做匀加速运动,加速度为a,初速度为v0,则经过时间t后的位移s为()。
A. s = v0t + 1/2at^2B. s = v0t - 1/2at^2C. s = v0t + at^2D. s = v0t - at^2答案:A10. 两个质点组成的系统,若两质点间的作用力大小相等,方向相反,则这两个力()。
A. 是一对平衡力B. 是一对作用力和反作用力C. 是一对内力D. 不能确定答案:B二、填空题(每题2分,共20分)1. 质点系的质心位置取决于质点系中各质点的________和________。
理论力学期末复习题全套理论力学期末复习题一一、单选题1、F= 100N方向如图示,若将F沿图示x,y方向分解,则x向分力大小为()。
A) 86.6 N; B) 70.7 N; C) 136.6 N; D) 25.9 N。
2、某平面任意力系F1 =4KN,F2=3 KN,如图所示,若向A点简化,则得到() A.F’=3 KN,M=0.2KNm B.F’=4KN,M=0.3KNmC.F’=5 KN,M=0.2KNm D.F’=6 KN,M=0.3 KNm第1题图第2题图3、实验测定摩擦系数的方法,把物体放在斜面上,逐渐从零起增大斜面的倾角φ直到物体刚开始下滑为止,这时的φ就是对应的摩擦角φf,求得摩擦系数为()4、直角杆自重不计,其上作用一力偶矩为M的力偶,图(a)与图(b)相比,B点约束反力的关系为()。
A、大于B、小于C、相等D、不能确定图(a)图(b)5、圆轮绕固定轴O转动,某瞬时轮缘上一点的速度为v,加速度为a,如图所示。
试问哪些情况是不可能的?()A、(a)、(b)B、(b)、(c)C、(c)、(d)D、(a)、(d)6、杆AB的两端可分别沿水平、铅直滑道运动,已知B端的速度为vB,则图示瞬时B点相对于A点的速度为____________________。
A) B v sinθ; B) B v cosθ; C) B v ⁄ sin θ; D) B v ⁄ cos θ.第6题图 第7题图二、填空题7、图示物块重G=100N ,用水平力P 将它压在铅垂墙上,P=400N ,物块与墙间静摩擦系数fs=0.3,物块与墙间的摩擦力为F= 。
8、鼓轮半径R=0.5m ,物体的运动方程为x=52t (t 以s 计,x 以m 计),则鼓轮的角速度ω= ,角加速度α= 。
第8题图 第9题图 9、平面图形上任意两点的加速度A a 、B a 与A 、B 连线垂直,且A a ≠ B a ,则该瞬时,平面图形的角速度ω= 和角加速度α应为 。

《理论力学》——期末考试答案一、单选题1.力对点之矩决定于( )。
A.力的大小B.力臂的长短C.力的大小和力臂的长短D.无法确定正确答案:C2.动点相对于动坐标系的运动称为( )的运动。
A.牵连运动B.相对运动C.绝对运动D.圆周运动正确答案:B3.动点的牵连速度是指该瞬时牵连点的速度,它相对的坐标系是( )。
A.动坐标系B.不必确定的C.静坐标系D.静系或动系都可以正确答案:C4.在质点系动能定理中,应注意外力或内力做的功之和不等于合外力或( )做的功。
A.重力B.浮力C.合内力D.牵引力正确答案:C5.将平面力系向平面内任意两点进行简化,所得主矢量和主矩都相等,且主矩不为零,则该力系简化的最后结果为( )。
A.合力偶B.合力C.平衡力系D.无法进一步合成正确答案:A6.超静定结构的超静定次数等于结构中( )。
A.约束的数目B.多余约束的数目C.结点数D.杆件数正确答案:B7.静不定系统中,多余约束力达到3个,则该系统静不定次数为( )A.3次B.6次C.1次D.不能确定正确答案:A8.关于平面力偶系、平面汇交力系、平面一般力系,最多能够得到的相互独立的平衡方程的个数依次是( )。
A.2、1、3B.2、2、3C.1、2、2D.1、2、3正确答案:D9.平面任意力系向一点简化,应用的是( )。
A.力的平移定理B.力的平衡方程C.杠杆原理D.投影原理正确答案:A10.对于平面力系,一个平衡方程可解( )未知量。
A.1个B.2个C.3个D.不一定正确答案:A11.一平面力系由两组平面平行力系组成(这两组平面平行力系之间互不平行),若力系向某A点简化结果为一合力,下述说法正确的是( )。
A.这两组平面平行力系必然都各自向A点简化为一合力B.这两组平面平行力系可能都各自简化为一力偶C.可能一组平面平行力系向A点简化得到一个力和一个力偶,而另一组平面平行力系向A点简化得到一合力D.可能这两组平面平行力系都各自向A点简化得到一个力和一个力偶正确答案:D12.在任何情况下,在几何可变体系上增加一个二元体后构成的体系是几何( )体系。
五 轴向拉伸与压缩试求图示各杆横截面1-1、2-2、3-3上的轴力,并作轴N 1= 10kNN 2= -15kN N 3= -18kN一根中部对称开槽的直杆如图所示。
试求横截面1-1和2-2解: 1.轴力由截面法可求得,杆各横截面上的轴力为 P N -= 2.应力 63111111104201014----⨯⨯⨯-=-==A P A N σPa 175-=MPa ()6322222210410201014----⨯⨯-⨯-=-==A P A N σPa 350-=MPa一桅杆起重机如图所示。
起重杆AB 的横截面是外径为18 mm 的圆环,钢丝绳CB 的横截面面积为10 mm 2。
试求起重杆和钢丝绳横截面上的应力。
解: 1.轴力取节点B 为研究对象,受力如图所示,0=∑X : 045cos 30cos =++ P N N AB BC0=∑Y : 030sin 45sin =--AB N P由此解得: 83.2-=AB N kN , 04.1=BC N kN 2.应力起重杆横截面上的应力为 ()622310182041083.2-⨯-⨯⨯-==πσAN AB ABPa 4.47-=MPa 钢丝绳横截面上的应力为6310101004.1-⨯⨯==A N BC BC σPa 104=MPa 铜和钢的弹性模量分1001=GPa 和2102=E GPa 。
若杆的总伸长为126.0=l ∆ mm ,试求杆横截面上的应力和载荷P 。
解:1.横截面上的应力 由题意有 ⎪⎪⎭⎫⎝⎛+=+=∆+∆=∆2211221121E l E l A E Pl A E Pl l l l σ 由此得到杆横截面上的应力为9922111021040010100600126.0⨯+⨯=+∆=E l E l l σPa 9.15=MPa2.载荷62610404109.15-⨯⨯⨯⨯==πσA P N 20=kN200=E GPa解:1.最大正应力在BC 段的任一横截面上,即127.3M P aPa 102041040623min max =⨯⨯⨯==-σA N 2.杆的总伸长mm 57.0m 1020108001040104001020010404 444623623932221222121=⎪⎪⎭⎫⎝⎛⨯⨯+⨯⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛+=+=+=+=----ππππ∆∆∆d l d l E P d EPl d EPl EA Pl EA Pll l l BC AB BC AB BCAB BC ABAB 和AC 组成如图所示。
一、 是非题1、 力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
( √)2、 在理论力学中只研究力的外效应。
( √)3、 两端用光滑铰链连接的构件是二力构件。
( × )4、 作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
(× )5、 三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
( × )6、 约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
( × )7、 在有摩擦的情况下,全约束力与法向约束力之间的夹角称为摩擦角。
(× )8、 用解析法求平面汇交力系的平衡问题时,所建立的坐标系x ,y 轴一定要相互垂直。
( × )9、 一空间任意力系,若各力的作用线均平行于某一固定平面,则其独立的平衡方程最多只有3个。
( × )10、 一个质点只要运动,就一定受有力的作用,而且运动的方向就是它受力方向。
( × )11、 已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(× )12、 质点系中各质点都处于静止时,质点系的动量为零。
于是可知如果质点系的动量为零,则质点系中各质点必都静止。
( × )13、 作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
( × )14、 力对于一点的矩不因力沿其作用线移动而改变。
( √ )15、 在自然坐标系中,如果速度υ = 常数,则加速度α = 0。
( × )16、 设一质点的质量为m ,其速度 与x 轴的夹角为α,则其动量在x 轴上的投影为mvx =mvcos a 。
(√)17、 用力的平行四边形法则,将一已知力分解为F1和F2两个分力,要得到唯一解答,必须具备:已知F1和F2两力的大小;或已知F1和F2两力的方向;或已知F1或F2中任一个力的大小和方向。
理论力学期末考试复习资料题型及比例填空题(20%选择题(20%证明题(10%简答题(10%计算题(40% 第一章:质点力学(20~25%一•质点的运动学 I :(重点考查)非相对运动学 1、描述质点的运动需要确定参照系和坐标系。
参照系:没特别声明,一般以地球为参照系, 且认为地球是不动的, 即以静止坐标系为运动 的参考。
坐标系:根据问题的方便,通常选择直角坐标系(适用于三维,二维,一维的运动),极坐标系(适用于二维运动,题中明显有极径,极角等字眼或者有心力作用下质点的运动时采用极坐 标系),自然坐标系(适用于二维运动, 题中明显有曲率半径, 切向等字眼时,或者圆周曲线运动, 抛物线运动等通常采用自然坐标系)。
2、描述质点运动的基本物理量是位移(坐标)、速度、加速度,明确速度、加速度,轨道方程在三种坐标系下的求解,直角坐标系下步骤:(1) ,建立好坐标系(2) ,表示出质点的坐标(可能借助于中间变量,如直角坐标系中借助于角度)(3)对坐标求一阶导得速度,二阶导得加速度,涉及的未知量要利用题中所给的已知信 息求得。
若求轨道方程,先求得 x 、y 、z 随时间或其他共同变量(参数)的函数关系,消去共同 变量即可,其它坐标系下是一个道理。
若是采用处理二维运动的极坐标系和自然坐标系: 明确怎么建立这两种坐标系及速度、加速度表的达式和各项的意义(a ) 极坐标系:极轴(不变的),极角与极径(质点对质点的位矢大小)则随质点不断发生变化,特别需要明确的径向、横向的单位矢量i,j 的确定,径向即沿径矢延长方向,横向是垂直径向,指向极角增加的一侧,它们的方向随质点的运动不断发生变化,称为是活动坐标系; 我们只需应用相应的公式计算,并理解每一项的意义即可:速度: 径向,v r r 横向,v r加速度:径向a r r r 2 ,明确第一项是由于径向速度得大小改变而引起,第二项则是横向速度得方向发生改变而引起; 横向a , 2 r 第一项是混合项,其中之一表由横向速度得大小改变而引起,其中之二表由径向速度得方向改变而引起,而第二项则表示由横向速 度得大小变化而引起(b )自然坐标系:明确是把矢量分为切向和法向,活动坐标系的单位矢量i 沿切向,法向,并指向轨道弯曲的一侧:2法向a n v 描述速度方向随时间的变化率,只有运动轨迹为曲线就一定不为零。
第 1 页 共 4 页2008-2009 学年第 一 学期考试题(卷)2.如下图所示的平面机构,由摇杆A O 1、B O 2,“T 字形”刚架ABCD ,连杆DE 和竖直滑块E 组成,21O O 水平,刚架的CD 段垂直AB 段,且AB =21O O ,已知l BO AO ==21,DE=l 4 ,A O 1杆以匀角速度ω绕1O 轴逆时针定轴转动,连杆DE 的质量均匀分布且大小为M 。
根据刚体五种运动形式的定义,则“T 字形”刚架ABCD 的运动形式为 ,连杆DE 的运动形式为 。
在图示位置瞬时,若A O 1杆竖直,连杆DE 与刚架CD 段的夹角为o CDE 60=∠,则在该瞬时:A 点的速度大小为 ,A 点的加速度大小为 ,D 点的速度大小为 ,连杆DE 的速度瞬心到连杆DE 的质心即其中点的距离为 ,连杆DE 的角速度大小为 ,连杆DE 的动量大小为 ,连杆DE 的动能大小为 。
三、计算题(20分)如左下图所示,刚架结构由直杆AC 和折杆BC 组成,A 处为固定端,B 处为辊轴支座,C 处为中间铰。
所受荷载如图所示。
已知F=40 kN ,M= 20kN ·m ,q=10kN/m ,a=4m 。
试求A 处和B 处约束力。
四、计算题(20分)机构如右上图所示,1O 和2O 在一条竖直线上,长度mm A O 2001=的曲柄A O 1的一端A 与套筒A 用铰链连接,当曲柄A O 1以匀角速度s rad /21=ω绕固定轴1O 转动时,套筒A 在摇杆B O 2上滑动并带动摇杆B O 2绕固定轴2O 摆动。
在图示瞬时,曲柄A O 1为水平位置,02130=∠B O O 。
试求此瞬时:(1)摇杆B O 2的角速度2ω;(2)摇杆B O 2的角加速度2α五、计算题(20分)如下图所示,滚子A 沿倾角为θ=030的固定斜面作纯滚动。
滚子A 通过一根跨过定滑轮B 的绳子与物块C 相连。
滚子A 与定滑轮B 都为均质圆盘,半径相等均为r ,滚子A 、定滑轮B 和物块C 的质量相等均为m ,绳子的质量忽略不计。
一、是非题1、若有B A F F-=的两个力,作用在同一刚体上,则此二力是作用力与反作用力,或是一对平衡力。
( )2、若点的法向加速度为零,则该点轨迹的曲率必为零。
( )3、质点运动的方向一定是合外力的方向。
( )4、作用在同一刚体上的两个力 →1F 、 →2F ,若有→1F = - →2F ,则该二力是一对平衡的力,或者组成一个力偶。
( )5、一动点如果在某瞬时的法向加速度等于零,而其切向加速度不等于零,则该点一定作直线运动。
( )6、当质点处于相对平衡(即相对运动为匀速直线运动)时,作用在质点上的主动力、 约束力和牵连惯性力组成平衡力系。
( )二、选择题1、图示两个作用在三角形板上的平面汇交力系(图(a )汇交于三角形板中心,图(b )汇交于三角形板底边中点)。
如果各力大小均不等于零,则图(a )所示力系______________________; 图(b )所示力系______________________。
①可能平衡; ②一定不平衡; ③一定平衡; ④不能确定。
2、绳子的一端绕在滑轮上,另一端与置于水平面上的物块B 相连,若物块B 的运动方程为X =k t 2,其中k 为常数,轮子半径为R 。
则轮缘上A 点的加速度的大小为_____________。
① 2 k ;② (4 k 2 t 2 / R)1/2;③ (4 k 2+16 k 4 t 4 / R 2 )1/2; ④ 2 k +4 k 2 t 2 / R 。
3、船A 重P ,以速度v航行。
重Q 的物体B 以相对于船的速度ū空投到船上,设ū与水平面成600角,且与v在同一铅直平面内。
若不计水的阻力,则二者共同的水平速度为_________。
① ( Pv +0.5Qu ) / ( P +Q ); ② ( Pv +Qu ) / ( P +Q );③ ( ( P +Q ) v +Qu ) / ( P +Q)。
4、设力→F 在X 轴上的投影为F ,则该力在与X 轴共面的任一轴上的投影____________。
一.基本题(本题共42分)1. 在图示机构中,杆OA O l B ,杆O l C O2D,且OA =20cm ,O l C = 40cm ,CM = MD =30cm ,若杆OA 以角速度 = 3rad /s 匀速转动,则 M 点的速度大小为 ② cm/s ,B 点的加速度大小为 ④ cm/s 2 。
① 60; ② 120; ③150 ; ④180 。
(填入正确答案序号,每空2分)2. 均质杆 AB 长 l ,质量 m ,沿墙面下滑, A 点的速度为 v ,则图示瞬时杆的动能 T =;杆的动量 p =。
(填入正确答案每空2分)3. 由质量为 m 、长度为 l 的相同均质细杆 OD 、AB 固结而成的十字杆,绕水平轴 O 转动,图示瞬时角速度为零,角加速度为 α 。
(固结点C 为两杆的中点)则十字杆对轴O 的转动惯量 J 0 =;对轴O 的动量矩 L 0 = ; 该瞬时惯性力系向O 点的简化结果是 惯性主矢 F I τ=;惯性主矩 M I O = 。
(填入正确答案,每空2分,图2分。
方向要在图中标出)4. 图示三棱柱的截面是等腰直角三角形,尺寸如图。
A点作用一已知力 F ,方向如图,求该力在坐标轴 x 上的投影及对坐标轴 z 之矩。
F x =M Z (F ) =(每空2分)5. 在图示运动机构中,作平面运动的构件有 3 个,并在图中作出该瞬时各自的速度瞬心。
(三个瞬心各2分)6. 直角弯管 OAB 在平面内以匀角速度 = 2rad /s 绕O 点转动,动点M 以相对速度 v r =2 cm/s 沿弯管运动,b=5cm ,则图示瞬时动点的牵连速度 v e = cm/s ; 牵连加速度 a e =cm/s 2 ;科氏加速度 a c = 8 cm/s 2。
(各矢量方向必须在图中标出,每个矢量2分)7. 图示四连杆机构中,曲柄O l A 上作用力偶M ,B 铰上作用一集中力 P 。
已知 O 1A = AB =O 2B = l ,在图示瞬时机构处于平衡。
试用虚位移原理求 M 与 P 的关系。
解:给O 1A 杆以虚位移δθ,则相应地 A 点有 δr A = lδθ ,B 点有 δr B ,由虚功方程,∑δW F =0,∴ -Mδθ + Pδr B =0,又 [δr A ]AB =[δr B ]AB 得lδθcos30o =δr B cos30o得(正确给出虚位移得1分,列出虚功方程得3分,虚位移关系3分,答案1分)二、( 本题 18 分 )组合梁如图,已知 P =40kN ,M =24kN/m ,q = 6kN/m ,各部分自重不计。
试求① 固定端 A 处的约束反力;② 支座 B 处的约束反力;解:研究CD 段,有∑ M C (F ) =,F B ×1 - 1/2 × q× 3× 2 = 0, ∴研究系统,有 ∑ X =0, ∴∑ Y=0, F Ay - P + F B - 1/2 ×q × 3 = 0, ∴∑ M A(F ) =0, M A- P×1- M + F B ×4 - 1/2× q× 3× 5 = 0, ∴(每个方程4分,受力图2分;若方程正确,答案却错误,则扣1分)三、( 本题 20 分 )图示平面机构中曲柄长 OA =l ,绕 O 轴以匀角速度 ω 转动,通过长 AB =2l 的连杆带动磙子 B 沿水平面作纯滚动。
在图示位置,曲柄水平,且 OA ⊥OB 。
试求该瞬时① 连杆 AB 的角速度 ωAB 和磙子 B 的角速度 ωB ;② 连杆 AB 的角加速度 a AB 和磙子 B 的角加速度 a B 。
解:① AB 杆的瞬心为 O 点,v A = ωl , ∴ ,,∴(速度图2分;求出连杆AB的角速度ωAB得4分;求出磙子B的角速度ωB得4分)②对AB杆,以A 为基点,有,投影至BA轴上,得,,∴投影至y轴上,得,∴(加速度图2分;求出连杆AB的角加速度a AB得4分;求出磙子B的角加速度a B得4分)四、(本题20 分)均质圆轮A、C的重量均为P,半径均为R。
轮A上作用一矩为M = PR的常力偶,使系统由静止开始运动。
设绳子不可伸长,且不计质量及轴承摩擦。
试求①轮心 C 上升距离s时的速度和加速度;②两轮间绳子的张力。
解:①研究系统,由动能定理T2 - T1=∑WF式中得对时间求导得②研究轮A,由定轴转动微分方程J AαA= ∑ M A(F ),得(正确列出动能定理得8分;求出轮心速度得2分,求出轮心加速度得2分;求出两轮间绳子张力得8分)一、基本题 1 (18 分)图示结构中的各构件自重不计。
已知P=5kN ,M =5kN · m ,q =2.5kN/m ,。
试求各个支座以及 C 铰的约束反力。
解:以CB为对象:(方程2分)(方程2分)(答案1分)(方程2分)(答案1分)以AC 为对象:(受力图共2 分)(方程2分)(方程2分)(答案1分)(方程2分)(答案1分)二、基本题 2 (20 分)曲柄连杆机构带动摇杆O l D 绕O l 轴摆动。
已知:曲柄长OA =5cm ,绕O 轴转动的匀角速度 =10rad /s ,AB = BD = l = 10cm 。
在图示位置,曲柄与水平线间成90 °角,∠OAB=60 °,摇杆与水平线间成60 °角。
1.求摇杆的角速度2.求滑块B 的加速度和杆AD 的角加速度。
(速度图3分; 加速度图3分)解:由于AD杆瞬时平动,;(求出得 2 分)(求出得 2 分)又(求出得 3 分)以 A 为基点求 B 点的加速度,式中投影至y 轴上:即(求出得 3 分)投影至x 轴上:(求出得 3 分)(求出角加速度得 1 分)三、基本题 3 (20 分)图示两个均质圆轮质量同为 3 m ,半径均为R ,A 轮可绕A 轴转动;不可伸长的绳子绕在轮上,另一端与 B 轮的轮心 B 轴连接, B 轮轮心铰接一均质细杆BD 。
在轮 A 上作用一不变力偶M ( M=mg · R ,其中g 为重力加速度) ,带动轮 B 沿水平轨道纯滚动,并拖动杆BD 。
杆BD 质量为m ,其与水平面的夹角为45°,不计BD 杆D 端与地面的摩擦,并略去绳的重量和轴中的摩擦,。
试求1. A 轮的角加速度2.两个轮间绳子的拉力3.BD 杆端D 对支撑面的作用力解:(1)系统动能:而得:(列出系统的动能得 6 分)由动能定理:( 应用动能定理得 1 分)等号两边同时对t 求导,注意,得:即( 求出αA得2 分)显然( 求出加速度a B得1 分)(2)求绳子的拉力,以A轮为研究对象( 求出两个轮间绳子的拉力得 5 分) (3) 以DB 杆为研究对象得:(求出BD 杆端 D 对支撑面的作用力得 5 分)根据作用力与反作用力定理可知BD 杆端 D 对支撑面的作用力大小等于F D,方向相反,且作用在支撑面上。
四、渐进题(42 分)1.( 4 分) 图示有一边长为a 的正方体,在一顶角作用一力 F ,分别求力 F 在x 轴的投影F x和力F 对y 轴的矩M y( F ) 。
F x=M y ( F ) = ( 每空2 分)2.(本题5分)单自由度受迫振动实验仪器设备或元件有振动台、阻抗变换器、测振放大器、计算机、加速度传感器、数据处理软件、打印机等。
试指出图示单自由度系统自由振动实验框图中用序号代表的仪器或元件的名称。
①加速度传感器;②阻抗变换器;③测振放大器; ④ 计算机 ;⑤ 振动台 。
(每空 1分 )3. ( 7分) 圆轮以匀角速度 ω 沿直线纯滚动,M 为轮缘上的一点,试写出:1) 用直角坐标表示的 M 点的运动方程:(写出 M 点的运动方程得 3 分 )2) M 点的速度方向: 垂直于 M 点与瞬心的连线 ,并在图中画出。
( 得 2 分 )3) M 点的加速度方向的特点: 总是指向轮心 ,并在图中画出加速度方向。
( 得 2 分 )4. ( 9分) 图示机构各杆均质, AB 长 2 l ,质量为 2 m ;曲柄 OC 长 l ,质量为 m ,以角速度 ω 逆时针定轴转动,两滑快的质量不计。
试求图示瞬时“1) 系统的动量: ;2)系统的动能:;3) 系统对 O 点的动量矩: 。
1) 系统的动量:,(求出动量得 3 分)2) 系统的动能:(求出动能得 3 分)3) 系统对 O 点的动量矩:(求出动量矩得 3 分)5. (本题 8 分)图示半径为 R 的均质滑轮质量为 M ,可绕水平轴转动,在滑轮上绕一不可伸长的绳子,绳的一端悬挂质量为 m的重物,另一端固接在刚度系数为k 的弹簧上。
设绳与滑轮间无滑动,试利用拉格郎日方程列写重物运动微分方程并求重物振动的周期。
解: 以平衡位置为零势能点( 写出用广义坐标表示的动能得 3 分)( 写出势能的 1 分),, 代入拉格郎日方程得 ( 正确列写出拉格郎日方程得 2 分 )即运动微分方程: ( 正确写出重物运动微分方程得 1 分 )(求出周期得 1分)6. (本题 9分)图示机构由五根连杆与固定边AB 组成。
已知各杆及 AB 的长度均为 l ,两水平力 P 分别作用在 C 、 D 点,铅垂力Q 作用在EF 杆的中点,使系统保持正六边形平衡。
试用虚位移原理求力P 与Q之间的关系。
用解析法:取坐标系如图,选角ϕ为广义坐标,(建立坐标系、选好广义坐标得1 分)则点 D 、C 、G 的坐标及其变分为,,,(写出点 D 、 C 、G 的变分各得 1 分) 由虚功方程:(写出虚功方程得 3 分)由δϕ的任意性知:(求出力P与Q之间的关系得 2 分)。