2008复旦 高校自主招生数学试题及解答

昨天，一些面试完的考生向快学网（）回忆了部分面试题目。

1、同一架飞机，从纽约飞到上海和从上海飞到纽约，航线一样，哪一次航行时间短一点？2、如果你遇到了劫匪，你打算如何用智慧把他们制服？当媒体把你的事迹报道出去后，你觉得会产生哪些正面效应和负面效应？3、有理数和无理数的定义和区别是什么？如何证明根号2是无理数？4、平面镜在什么情况下，会出现头下脚上的情况。

5、在沙漠中如何给手提电脑供电？7、最近全社会都在关注儿童当乞丐的问题。

如果你是家长，你会把孩子送去当童乞么？9、你对“一沙一世界，一花一天堂”是怎么看的？10、你知道姓名、字、号的来历么？11、你有没有参加过社会活动？12、不打开酒瓶的盖子或塞子，怎么取里面的酒？13、有两辆重20吨的卡车，有一辆坏了，要一辆车拖着另一辆车走，在不用起重机的前提下，请问如何让这两辆车通过限重30吨的大桥？14、你对自己的人生有什么规划？15、你是如何选择你进复旦后学的专业的，是怎么考虑这些专业排列的先后顺序的？16、请用30秒钟时间准备，然后用英语背诵以前学过的一段文学作品。

17、你的自荐材料里写了你曾组织学生去敬老院参加社会活动，现在很多中学生不愿意参加社会活动，你是怎么组织同学去参加的?18、你如何看待当前的房价？毕业后会马上买房么？由父母付首付，子女付房贷，你认同吗？19、请快速地说出7的平方、7的3次方、7的四次方、7的5次方的结果分别是多少？20、请你对自己今天面试过程做个简单小结。

21、一位考生的首选专业是经济管理，面试官让他分析一下杭州的工业结构。

22、如果你是杭州市市长，你觉得杭州要怎样发展比较好？23、生物、化学、物理之间有什么共性？24、现在很多媒体在关注社会贫富差距的问题，你如何看待这个问题？25、一百年后的人到了现在，会发现哪些东西是未来没有的?26、让你一个人去荒原生存15天，你最想去做哪些事情？27、你如何考虑专业和毕业后择业的问题？28、看你的资料，你参加了很多次的社会实践活动，这些社会活动会不会影响你的学习？另外，在前两天上海考生的面试中，上海当地媒体也收集了部分面试题，快学网（）也刊登出来，给大家看一看。

第一讲近年来自主招生数学试卷解读集合与命题授课教师：范端喜第一部分近年来自主招生数学试卷解读一、各学校考试题型分析：交大：题型：填空题10题，每题5分；解答题5道，每题10分；考试吋间：试题难度：考试知识点分布：90分钟，满分100分；略高于高考，比竞赛一试稍简单；基本涵盖高屮数学教材高考所有内容，如：集合、函数、不等式、数列（包括极限）、三角、复数、排列组合、向量、二项式定理、解析几何和立体儿何复旦：题型：试题类型全部为选择题（四选一）；全考试吋间：总的考试吋间为3小吋（共200道选择题，总分1000分，其屮数学部分30题左右，，每题5分）；试题难度：基本相为于高考；考试知识点分布：除高考常规内容之外，还附加了一-些内容，如：行列式、矩阵等;考试重点：同济：题型：侧重于函数和方程问题、不等式、数列及排列组合等填空题8题左右，分数大约40分，解答题约5题，每题大约12分；考试吋间：90分钟，满分100分；试题难度：考试知识点分布：基本上相半于高考；常规高考内容二、试题特点分析：1. 突出对思维能力和解题技巧的考查。

例如，2007年交大冬令营自主招生试题中有这样一个问题：设/(x)二(1 + a)x4 + x3- (3a + 2)x2 - 4a ,试证明对任意实数a:(1) 方程/(x)二0总有相同实根；(2) 存在托，恒有/(X。

)工0・这两问解决的策略和方法是：换一个角度看成一个关于a的一次函数’ 关键步骤提示：/(a) = (x4一3兀2—4)° + (兀"+ x3 - 2x2—(% + 2)(兀一2)(兀~ + 1)Q +(x + 2)(兀—1)2. 注重数学知识和其它科目的整合，考查学生应用知识解决问题的能力。

通信工程中常用〃元数组...............a”)表示信息，其中q = 0或1, i、•设"=(q,a】,® ...... a；：), v = ...... b鳥,表示"和v中相对应的元素不同的个数.(1 ) ” = (0,0,0,0,0)问存在多少个5元数组v使得力(U(2)z/ = (l?Ll丄1)问存在多少个5元数组v使得67(Z/?V)=3；(3)令w = (0.0.0 ........ 0),"二(％6,4 ................. a“)，v = (b“b],b[ .......... b j,朴0求证：〃(2,小：)+ 〃(匕W)> d{u.v)・此问题与计算机中的“二进制”有关，前两问是排列组合计数问题，尤其是第三问有-定的挑战性。

18．（本题满分15分）本题共有2个小题，第1个题满分5分，第2小题满分10分．
已知函数f(x)=sin2x，g(x)=cos ，直线 与函数 的图像分别交于M、N两点．
（1）当 时，求｜MN｜的值；题满分16分）本题共有2个小题，第1小题满分8分，第2小题满分8分．
9．若函数 （常数 ）是偶函数，且它的值域为 ，则该函数的解析式 ．
10．已知总体的各个体的值由小到大依次为2，3，3，7，a，b，12，13.7，18.3，20，且总体的中位数为10.5．若要使该总体的方差最小，则a、b的取值分别是．
11．在平面直角坐标系中，点 的坐标分别为 ．如果 是 围成的区域（含边界）上的点，那么当 取到最大值时，点 的坐标是______．
………………………………5分
（2）
…………...8分
…………………………….11分
∵ …………13分
∴｜MN｜的最大值为 .……………15分
19、【解】（1） .…………….2分
由条件可知， 解得 …………6分
∵ …………..8分
（2）当 ……………10分
即
………………13分
故m的取值范围是 …………….16分
记 ．
（1）若 ，求 的值；
（2）求证：当 是正整数时， ；
（3）已知 ，且存在正整数 ，使得在 ， ， ， 中有4项为100．求 的值，并指出哪4项为100．
2008年全国普通高等学校招生统一考试
上海数学试卷（文史类）答案要点及评分标准
__________录入者：福建泉州第七中学 林志敏老师
一、（第1题至第11题）
21、【解】（1）
………………..2分
∵ ………………..4分

自主招生真题分类解析（下午课程）函数性态例1、若()f x 为R 上函数，且(10)(10)f x f x +=-，(20)(20)f x f x -=-+，则()f x 为（ ）(A) 奇函数且周期函数； (B) 奇函数且非周期函数； (C) 偶函数且周期函数； (D) 偶函数且非周期函数．例2、设()f x 和()g x 是定义在R 上的两个函数，12,x x 是R 上任意两个不等的实数.（1）设1212|()()||()()|f x f x g x g x +≥+恒成立，且()y f x =是奇函数， 判断函数()y g x =的奇偶性并说明理由；（2）设1212|()()||()()|f x f x g x g x -≥-恒成立，且()y f x =是周期函数， 判断函数()y g x =的周期性并说明理由；（3）设1212|()()||()()|f x f x g x g x ->-恒成立，且()y f x =是R 上的增函数， 判断函数()h x =()()f x g x +与函数'()()()h x f x g x =-在R 上的单调性并说明理由.例3、（交大2000联读）函数()f x =()x R ∈的反函数是_______________.例4、（交大2002保送）设()|lg |,,f x x a b =为实数，且0,,()()2()2a ba b a b f a f b f +<<==若满足，试写出a 与b 的关系，并证明在这一关系中存在b 满足34b <<.例5、（复旦2004保送）若存在M ，使任意t D ∈（D 为函数()f x 的定义域），都有()f x M ≤，则称函数()f x 有界．问函数11()sin f x x x =在1(0,)2x ∈上是否有界？例6、（交大2008冬令营）已知函数2()f x ax bx c =++(0)a ≠，且()f x x =没有实数根．那么(())f f x x =是否有实数根？并证明你的结论．导数积分例1、已知函数32()33(2)1f x x ax a x =++++有极大值又有极小值，则a 的取值范围是 .例2、设010211()cos ,()'(),()'(),,()'()n n f x x f x f x f x f x f x f x +====,,n N *∈则2008()f x ．例3、请您设计一个帐篷。

+y 2=1有交点,则11a 2+1b2 1,即有1a 2+1b2 1.2 隐性轨迹为抛物线例3 (2008年重庆文)函数f (x )=si n x5+4co s x(0 x 2 )的值域是( ).A [-14,14]B [-13,13]C [-12,12]D [-23,23]常规解法 令5+4cos x =t(1 t 3),则sin 2x =16-(t 2-5)216,当0 x时,si n x =16-(t 2-5)216=-t 4+10t 2-94,f (x )=si n x 5+4co s x=-t 4+10t 2-94t =-(t 2+9t2)+104-2t 29t 2+104=12,当且仅当t =3时取等号.同理可得当 <x 2 时,f(x ) -12,综上可知f (x )的值域为[-12,12],故选C.图3轨迹解法 令Y =f 2(x )=sin 2x 5+4cos x ,则Y =sin 2x 5+4cos x =1-cos 2x 5+4cos x设P (-4cos x ,cos 2x )则Y 表示两点P (-4cos x,cos 2x ),A (5,1)连线的斜率,而点P 的轨迹为抛物线y =x 216(0 y 1)的一段,如图3,当直线AP 平行于x 轴时,Y 取最小值;当直线AP 与抛物线相切时,Y 取最大值14,所以0 Y 14,即-12f (x )12.所以函数f (x )的值域为[-12,12].介绍几道2008年自主招生数学试题湖北省十堰市东风高级中学 442001 甘志国高校自主招生考试数学试题材料鲜活,试题的结构常以5~7道解答题的形式出现(如2008年清华大学、北京大学、浙江大学的自主招生试题),也有与本省高考数学试卷的形式类似的(如2008年山东大学自主招生试题),试题的难度一般略高于高考题.下面介绍几道2008年自主招生数学试题,且这里给出的解答多与原参考答案不同.题1(2008年北京大学自主招生数学试题)求证:边长为1的正五边形对角线长为1+52.原参考解答是用平面几何中的三角形相似证得的,下面给出一种三角解法.解 选择正五边形的两条共顶点的对角线及其一边组成等腰三角形,再作其底边上的高,又设这个正五边形对角线长为x,得si n18 =0.5x ,x =12si n18.下面求sin18 (实际上,有很多资料把si n18 =5-14作为特殊角的三角函数值列出此值为黄金分割数5-120.618的一半,挺好记的;高一数学老师应当介绍si n18 的值及其算法,并不难):由公式sin2 =2s i n cos ,cos3 =4cos 3 -3cos 及si n36 =cos54 ,立得2si n18 cos18 =4cos 318 -3co s18 ,2sin18 =4co s 218 -3=4(1-sin 218 )-3,4sin 218 +2sin18 -1=0,si n18 =5-14所以所求正五边形对角线长为x =12s i n18 =1+52.题2(2008年复旦大学自主招生数学试题)请证明2是一个无理数.证明 假设2是有理数,则可设2=mn(m,n 是两个互质的正整数),得m 2=2n 2,所以m 2是偶数,进而得m 也是偶54ZHONGXUESHUXUEZAZHI中学数学杂志 2009年第1期数(因为当m 是奇数时,m 2是奇数),又可得m 2(=2n 2)是4的倍数,n 2是偶数,n 也是偶数,得m,n 均是偶数,这与m,n 互质矛盾!说明2是无理数.以上证明初二学生即可弄懂,反证法教科书上虽然作了介绍,但平时训练的极少,所以学生对这种证法很陌生(而2008年高考数学江苏卷第19题第(2)问就是需要用反证法证明的题目),我们在平时的教学中应当重视这方面的训练.2还是人类历史上发现的第一个无理数,是Py thagoras (约公元前500年,希腊学者)学派的成员H i ppasus 所发现的,从而产生了数学史上的第一次危机,所以学生还应当尽可能的通过课外阅读等手段扩大知识面.题3 (2008年浙江大学自主招生数学试题),A ={(x,y )|(x -1)2+(y -2)254},B ={(x,y )||x -1|+2|y -2| a },A B,求a 的取值范围.原参考解答是:通过换元后可知,题意即,若{(x,y )|x 2+y 254} {(x,y )||x |+2|y | a },求正数a 的取值范围.再通过画图(由对称性,可以只考虑第一象限的图形),得圆x 2+y 254的圆心即坐标原点到直线x +2y =a 的距离不小于该圆的半径52,得所求a 的取值范围是[52,+ ).下面给出一种所用知识更少的解法.解 题意即,若(x -1)2+(y -2)2 54|x -1|+2|y -2| a,求实数a 的取值范围.因为(x -1)2+(y -2)2 54|y -2|54-(x -1)2,所以题设等价于|x -1|+254-(x -1)2 a 恒成立.设|x -1|=t ,得t 0,题设即函数z =t+5-4t 2(t 0)的最大值z m ax a,下面用两种方法求z m ax .法1 可得(z -t)2=5-4t 2,5t 2-2z t+(z 2-5)=0, =4z 2-20(z 2-5) 0-52z52,还可得当且仅当t =12即x =32或-12时,z =52,所以z m ax =52.法2 可得5-4t 2 0,0 t52,所以可设t =52s i n (02),得z =t +5-4t 2=52s i n +5cos ,=52(15s i n +25cos )=52si n ( + )(02),其中 =arccos15.由此也可得:当且仅当 + = 2即 =arcsin 15也即t =12就是x =32或-12时,z m ax =52.所以所求a 的取值范围是[52,+ ).题4 (2008年浙江大学自主招生数学试题)已知x >0,y >0,a =x +y,b =x 2+xy +y 2,c =mx y,问是否存在正数m 使得对于任意正数x,y,可使a 、b 、c 为一个三角形的三条边,如果存在,求出m 的值;如果不存在,请说明理由.解 因为a >b ,所以存在正数m 满足题意的充要条件是对于任意的正数x,y 有下式成立:x +y +x 2+xy +y 2>mxyx 2+xy +y 2+mx y >x +y可设y =k 2x,(k >0),得1+k 2+1+k 2+k 4>mk1+k 2+k 4+m k >1+k 2(k +1k )+(k +1k )2-1m i n>mm >(k +1k)-(k +1k )2-1m ax设k +1k =t ,得t 2,所以(t +t 2-1)m in >mm >(1t +t 2-1)m ax再由函数的单调性,可立得满足题意的正数m 存在,且m 的值有无数多个,其取值范围是(2-3,2+3).题5 (2008年南京大学自主招生数学试题)若正数a 、b 、c 满足a +b +c =1,求证:(a +1a )(b +1b )(c +1c) 100027.高中生在学习 不等式的证明 时,大多都证明过这样的题:若正数a、b 满足a +b =1,求证:(a +1a )(b +1b) 254.简证如下:先得0<ab (a +b 2)2=14,又函数f (x )=55中学数学杂志 2009年第1期ZHON GXUES HUXUEZAZHIx +1x 在(0,1)上是减函数,所以ab +1ab 14+4=174,再得(a +1a )(b +1b )=(ab +1ab )+(b a +a b ) 174+2=254,对于该题的深入研究,就会得到题5的问题.下面给出题5的两个简证,并推广其结论.证法1 因为在题5的不等式中,当且仅当a =b =c =13时取等号,为了使a +1a =a +1m a +1m a + +1ma (共m 个1m a )能使用均值不等式且等号能取到,应让a =1ma且a =13,得m =9,所以有如下证法:a +1a=a +19a +19a + +19a (共9个19a ) 1010a(9a)9,同理,有b +1b10 10b (9b )9,c +1c 10 10c(9c)9所以(a +1a )(b +1b )(c +1c ) 10310abc(93abc)9,再由0<abc(a +b +c 3)3=127,可得:(a +1a)(b +1b )(c +1c ) 100027(当且仅当a =b =c =13时取等号).由此思路,还可证得.推广1 若正数a 1,a 2, ,a n 满足ni=1a i =1,则ni=1(a i+1a i ) (n +1n )n (当且仅当a 1=a 2= =a n =1n 时取等号).证法2 (a +1a )(b +1b )(c +1c )=a 2+1b 2+1c 2+1=a 2b 2c 2+(a 2b 2+b 2c 2+c 2a 2)+(a 2+b 2+c 2)+1abca 2b 2c 2+3 (3a 2b 2c 2)2+3 (3a 2b 2c 2)+1abc =(3abc +13abc )3,再由0<abc(a +b +c 3)3=127,及函数f(x )=x +1x在(0,1)上是减函数,可得要证结论成立!推广2 若a,a 1,a 2, ,a nR +,ni=1a in a ,则ni=1(a i +aa i)ni=1a in+nani=1a in(当且仅当a 1=a 2= =a n 时取等号).证明ni=1(a i +aa i )=ni=1(a 2i +a)ni=1a i=1ni=1a i(a n +a n-11 i 1 na 2i 1+a n-21 i 1<i2 na 2i 1a 2i 2++a1 i 1<i 2< <i n-1 na 2i 1a 2i 2 a 2i n-1+a 21a 22 a 2n )=a n+nk =1a n-k1 i 1<i 2< <i k n(a i 1a i 2 a i k )2ni=1a i,注意到和式1 i 1<i 2< <i k n(a i 1a i 2 a i k )2是C k n 项的和,由均值不等式,得1 i 1<i 2< <i k n(a i 1a i 2 a i k )2 C k nC k n1 i 1<i 2< <i k n(a i 1a i 2 a i k)2=C k nC k n(a 1a 2 a n )2kC k n n=C k nnni=1a i2k(当且仅当a 1=a 2= =a n 时取等号).所以ni=1a i +aa ia n+nk =1an-kCk nnni=1a i2kn i=1a i=a +nni=1a i2nnn i=1a inni=1a i +a a inni=1a i +anni=1a in(当且仅当a 1=a 2= =a n 时取等号).又由均值不等式,得0<nni=1a ini=1a in(当且仅当a 1=a 2= =a n 时第一个 中取等号)再由函数f (x )=x +ax 在(0,a ]上是减函数,可得nni=1a i +anni=1a ini=1a i n+nani=1a i>0(当且仅当a 1=a 2= =a n 时 中取等号)从而可得推广2成立.(推广1显然是推广2的特例)56ZHONGXUESHUXUEZAZHI中学数学杂志 2009年第1期。

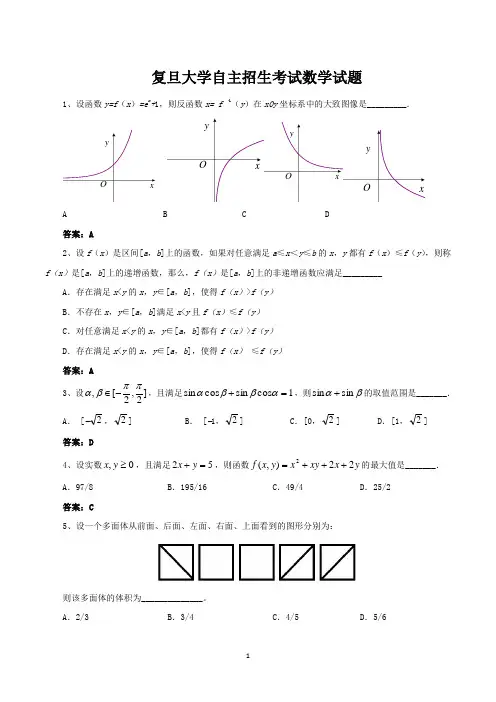
1、设函数y=f（x）=e x+1，则反函数OyxOyxO x答案：A2、设f（x）是区间[a，b]f（x）是[a，b]上的递增函数，那么，f（xA．存在满足x<y的x，y∈[a，b]B．不存在x，y∈[a，b]满足x<y且fC．对任意满足x<y的x，y∈[a，b]D．存在满足x<y的x，y∈[a，b]答案：A3、设]2,2[,ππβα-∈，且满足sinαA． [−2，2] B． [答案：D4、设实数0,≥yx，且满足2=+yxA．97/8 B．答案：C5则该多面体的体积为______________。

A．2/3 B．3/4答案：D6、在一个底面半径为1/2，高为1的圆柱内放入一个直径为1的实心球后，在圆柱内空余的地方放入和实心球、侧面以及两个底面之一都相切的小球，最多可以放入这样的小球个数是___________。

A ．32个；B ．30个；C ．28个；D ．26个答案：B7、给定平面向量（1，1），那么，平面向量（231-，231+）是将向量（1，1）经过________． A ．顺时针旋转60°所得； B ．顺时针旋转120°所得； C ．逆时针旋转60°所得；D ．逆时针旋转120°所得；答案：C8、在直角坐标系O xy 中已知点A 1（1，0），A 2（1/2，3/2），A 4（−1，0），A 5（−1/2，−3/2）和A6（1/2， −3/2）．问在向量−−→−ji A A （i ，j=1，2，3，4，5，6，i≠j）中，不同向量的个数有_____． A ．9个； B ．15个； C ．18个； D ．30个答案：C9、对函数f:[0，1]→[0，1]，定义f 1（x ）=f （x ），……，f n（x ） =f （f n −1（x ）），n=1，2，3，……．满足f n （x ）=x 的点x ∈[0，1]称为f 的一个n −周期点．现设⎪⎪⎩⎪⎪⎨⎧≤≤-≤≤=121,22,210,2)(x x x x x f 问f 的n −周期点的个数是___________．A ．2n 个；B ．2n 2个；C ．2n个；D ．2（2n−1）个．答案：C10、已知复数z 1=1+3i ，z 2=−3+3i ，则复数z 1z 2的幅角__________． A ．13π/12 B ．11π/12 C ．−π/4 D ．−7π/12答案：A11、设复数βαβαcos sin ,sin cos i w i z +=+=满足z w =3/2，则sin （β−α）=______． A ．±3/2B ．3/2，−1/2C ．±1/2D ．1/2，−3/2答案：D12、已知常数k 1，k 2满足0<k 1<k 2，k 1k 2=1．设C 1和C 2分别是以y =±k 1（x −1）+1和y =±k 2（x −1）+1为渐近线且通过原点的双曲线．则C 1和C 2的离心率之比e 1/e 等于_______．A ．222111k k ++ B ．212211k k ++ C ．1 D ．k 1/k 2答案：C13、参数方程0,)cos 1()sin (>⎩⎨⎧-=-=a t a y t t a x 所表示的函数y=f （x ）是____________．A ．图像关于原点对称；B ．图像关于直线x =π对称；C ．周期为2a π的周期函数D ．周期为2π的周期函数．答案：C14、将同时满足不等式x −k y −2≤0，2x +3y −6≥0，x +6y −10≤0 （k>0）的点（x ，y ）组成集合D 称为可行域，将函数（y +1）/x 称为目标函数，所谓规划问题就是求解可行域中的点（x ，y ）使目标函数达到在可行域上的最小值．如果这个规划问题有无穷多个解（x ，y ），则k 的取值为_____．A ．k≥1;B ．k≤2C ．k=2D ．k=1．答案：C15、某校有一个班级，设变量x 是该班同学的姓名，变量y 是该班同学的学号，变量z 是该班同学的身高，变量w 是该班同学某一门课程的考试成绩．则下列选项中正确的是________．A ．y 是x 的函数；B ．z 是y 的函数；C ．w 是z 的函数；D ．w 是x 的函数．答案：B16、对于原命题“单调函数不是周期函数”，下列陈述正确的是________． A ．逆命题为“周期函数不是单调函数”； B ．否命题为“单调函数是周期函数”； C ．逆否命题为“周期函数是单调函数”； D ．以上三者都不正确 答案：D17、设集合A={（x ，y ）|log a x +log a y >0}，B={（x ，y ）|y +x <a}．如果A∩B=∅，则a 的取值范围是_______ A ．∅ B ．a>0，a≠1 C ．0<a≤2， a≠1 D ．1<a≤2答案：D18、设计和X 是实数集R 的子集，如果点x 0∈R 满足：对任意a>0，都存在x ∈X 使得0<|x −x 0|<a ，则称x 0为集合X 的聚点．用Z 表示整数集，则在下列集合（1）{n/（n+1）|n ∈Z ， n≥0}， （2） R\{0}， （3）{1/n|n ∈Z ， n≠0}， （4）整数集Z 中，以0为聚点的集合有_____． A ．（2），（3）B ．（1），（4）C ．（1），（3）D ．（1），（2），（4）答案：A19、已知点A （−2，0），B （1，0），C （0，1），如果直线kx y =将三角形△ABC 分割为两个部分，则当k =______时，这两个部分得面积之积最大？A ．23-B ．43-C ．34-D ．32-答案：A20、已知x x x x f 2cos 3cos sin )(+=，定义域⎥⎦⎤⎢⎣⎡=ππ127,121)(f D ，则=-)(1x f_____A ．π12123arccos 21+⎪⎪⎭⎫ ⎝⎛-x B ．π6123arccos 21-⎪⎪⎭⎫ ⎝⎛-x C ．π12123arcsin 21+⎪⎪⎭⎫ ⎝⎛--x D ．π6123arcsin 21-⎪⎪⎭⎫ ⎝⎛-x 答案：A21、设1l ，2l 是两条异面直线，则直线l 和1l ，2l 都垂直的必要不充分条件是______ A ．l 是过点11l P ∈和点22l P ∈的直线，这里21P P 等于直线1l 和2l 间的距离 B ．l 上的每一点到1l 和2l 的距离都相等 C ．垂直于l 的平面平行于1l 和2lD ．存在与1l 和2l 都相交的直线与l 平行 答案：D22、设ABC −A’B’C’是正三棱柱，底面边长和高都为1，P 是侧面ABB’A’的中心，则P 到侧面ACC’A’的对角线的距离是_____A ．21B ．43C ．814D ．823答案：C23、在一个球面上画一组三个互不相交的圆，成为球面上的一个三圆组．如果可以在球面上通过移动和缩放将一个三圆组移动到另外一个三圆组，并且在移动过程中三个圆保持互不相交，则称这两个三圆组有相同的位置关系，否则就称有不同的位置关系．那么，球面上具有不同的位置关系的三圆组有______A ．2种B ．3种C ．4种D ．5种 答案：A24、设非零向量()()()321321321,,,,,,,,c c c c b b b b a a a a ===为共面向量，),,(31x x x x x = 是未知向量，则满足0,0,0=⋅=⋅=⋅x c x b x a的向量x 的个数为_____A ．1个B ．无穷多个C ．0个D ．不能确定 答案：B25、在Oxy 坐标平面上给定点)1,2(),3,2(),2,1(C B A ，矩阵⎪⎪⎭⎫⎝⎛-112k 将向量OC OB OA ,,分别变换成向量,,，如果它们的终点',','C B A 连线构成直角三角形，斜边为''C B ，则k 的取值为______A ．2±B ．2C ．0D ．0，−2 答案：B26、设集合A ，B ，C ，D 是全集X 的子集，A∩B≠∅，A∩C≠∅．则下列选项中正确的是______． A ．如果B D ⊂或C D ⊂，则D∩A≠∅； B ．如果A D ⊂，则C x D∩B≠∅，C x D∩C≠∅； C ．如果A D ⊃，则C x D∩B=∅，C x D∩C=∅； D ．上述各项都不正确．27、已知数列{}n a 满足21=a 且n a n ⎧⎫⎨⎬⎩⎭是公比为2的等比数列，则∑==nk k a 1______A ．221-+n nB ．22)1(1+-+n n C ．)1(22-+n n n D ．n n n 22)1(+-28、复平面上圆周2211=+--iz z 的圆心是_______ A ．3+i B ．3−iC ．1+iD ．1−i29．已知C 是以O 为圆心、r 为半径的圆周，两点P 、P *在以O 为起点的射线上，且满足|OP|∙|OP *|=r 2，则称P 、P *关于圆周C 对称．那么，双曲线22x y -=1上的点P （x ，y ）关于单位圆周C':x 2＋y 2=1的对称点P *所满足的方程是（A ）2244x y x y -=+（B ）()22222x y x y-=+（C ）()22442x y x y-=+（D ）()222222x y x y-=+30、经过坐标变换⎩⎨⎧+-=+=θθθθcos sin 'sin cos 'y x y y x x 将二次曲线06532322=-+-y xy x 转化为形如1''2222=±b y a x 的标准方程，求θ的取值并判断二次曲线的类型_______ A ．)(6Z k k ∈+=ππθ，为椭圆 B ．)(62Z k k ∈+=ππθ，为椭圆C ．)(6Z k k ∈-=ππθ，为双曲线D ．)(62Z k k ∈-=ππθ，为双曲线31、设k ， m ， n 是整数，不定方程mx+ny=k 有整数解的必要条件是____________ A ．m ，n 都整除kB ．m ，n 的最大公因子整除kC ．m ，n ，k 两两互素D ．m ，n ，k 除1外没有其它共因子。

2008年上海市普通高等学校春季招生考试数 学 试 卷考生注意：1．答卷前，考生务必将姓名、高考座位号、校验码等填写清楚．2．本试卷共有22道试题，满分150分．考试时间120分钟．一．填空题（本大题满分48分）本大题共有12题，只要求直接填写结果，每题填对得4分，否则一律得零分．1．已知集合{1A x x =<-或}23x ≤<，{}24B x x =-≤<，则AB = ． 【答案】{}4x x <【详解】略 2．计算：131lim 32n n n n +→∞+=+ ． 【答案】13【详解】 113131133lim lim 3232333n n n n n n n n n n n n ++→∞→∞++==++． 3．函数()1f x x =-的定义域是 ． 【答案】[2,1)(1,3]-【详解】 定义域满足22360110x x x x x -≤≤⎧-++≥⎧ ⇒⎨⎨≠-≠⎩⎩4．方程2cos 14x π⎛⎫-= ⎪⎝⎭在区间(0,)π内的解是 ． 【答案】712x π= 【详解】 12cos 1cos 44243x x x ππππ⎛⎫⎛⎫-=⇒-=⇒-= ⎪ ⎪⎝⎭⎝⎭．5．已知数列{}n a 是公差不为零的等差数列，11a =．若125a a a 、、成等比数列，则n a =．【答案】21n a n =-【详解】设公差为d ，则251,14a d a d =+=+，则21(14)(1)2d d d ⨯+=+⇒=．6．化简：cos sin 36ππαα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭． 【答案】cos α【详解】（方法一）：利用＂两角和公式＂直接求解；（方法二）：cos sin sin sin 36236πππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++=-+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ sin sin 2sin cos cos 666πππαααα⎛⎫⎛⎫=-++== ⎪ ⎪⎝⎭⎝⎭． 7．已知P 是双曲线22219x y a -=右支上的一点，双曲线的一条渐近线方程为30x y -=．设12F F 、分别为双曲线的左、右焦点．若23PF =，则1PF = ．【答案】5【详解】由双曲线的一条渐近线方程为30x y -=可得：2a =，又双曲线的定义知12112325PF PF a PF PF -=⇒-=⇒=．8．已知一个凸多面体共有9个面，所有棱长均为1，其平面展开图如右图所示，则该凸多面体的体积V = ．【答案】16+【详解】凸多面体为：下半部分为正方体3111V ==，上半部分为正四棱锥221132V =⨯⨯．9．已知无穷数列{}n a 前n 项和113n n S a =-，则数列{}n a 的各项和为 ．【答案】1-【详解】 由113n n S a =-可得：11113n n S a --=-，两式相减得并化简：112n n a a -=-， 又11113132a a a =-⇒=-．所以1lim 11n x a S q →∞==--． 10．古代“五行”学说认为：“物质分金、木、土、水、火五种属性，金克木，木克土，土克水，水克火，火克金．”将五种不同属性的物质任意排成一列，设事件A 表示“排列中属性相克的两种物质不相邻”，则事件A 出现的概率是 （结果用数值表示）． 【答案】112【详解】如下图，当左边的位置排定后（例如：金），第二位（除去金本身）只有“土、水”两种属性。

2008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页．第Ⅱ卷3至10页．考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上．2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．不能答在试题卷上．3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．参考公式：如果事件A B ，互斥，那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ，相互独立，那么 其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么 34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率 其中R 表示球的半径()(1)(012)k kn k k n P k C p p k n -=-= ，，，，一、选择题1．设集合{|32}M m m =∈-<<Z ，{|13}N n n M N =∈-=Z 则，≤≤（ ）A ．{}01，B ．{}101-，，C ．{}012，，D ．{}1012-，，， 2．设a b ∈R ，且0b ≠，若复数3()a bi +是实数，则（ ） A ．223b a = B ．223a b =C ．229b a =D ．229a b =3．函数1()f x x x=-的图像关于（ ）A ．y 轴对称B ． 直线x y -=对称C ． 坐标原点对称D ． 直线x y =对称4．若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ ） A ．a <b <cB ．c <a <bC ． b <a <cD ． b <c <a5．设变量x y ，满足约束条件：222y x x y x ⎧⎪+⎨⎪-⎩，，．≥≤≥，则y x z 3-=的最小值（ ）A ．2-B ．4-C ．6-D ．8-6．从20名男同学，10名女同学中任选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的概率为（ ） A ．929B ．1029C ．1929D ．20297．64(1(1-的展开式中x 的系数是（ ）A ．4-B ．3-C ．3D ．48．若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ ）A ．1BCD ．29．设1a >，则双曲线22221(1)x y a a -=+的离心率e 的取值范围是（ ） A． B．C ．(25)，D．(210．已知正四棱锥S ABCD -的侧棱长与底面边长都相等，E 是SB 的中点，则AE SD ，所成的角的余弦值为（ ） A ．13B．3C．3D ．2311．等腰三角形两腰所在直线的方程分别为20x y +-=与740x y --=，原点在等腰三角形的底边上，则底边所在直线的斜率为（ ） A ．3B ．2C ．13-D ．12-12．已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ ） A ．1B ．2C ．3D ．22008年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上． 13．设向量(12)(23)==，，，a b ，若向量λ+a b 与向量(47)=--，c 共线，则=λ ． 14．设曲线axy e =在点(01)，处的切线与直线210x y ++=垂直，则a = ． 15．已知F 是抛物线24C y x =：的焦点，过F 且斜率为1的直线交C 于A B ，两点．设FA FB >，则FA 与FB 的比值等于 ．16．平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件① ； 充要条件② ． （写出你认为正确的两个充要条件）三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分10分） 在ABC △中，5cos 13B =-，4cos 5C =． （Ⅰ）求sin A 的值；（Ⅱ）设ABC △的面积332ABC S =△，求BC 的长． 18．（本小题满分12分）购买某种保险，每个投保人每年度向保险公司交纳保费a 元，若投保人在购买保险的一年度内出险，则可以获得10 000元的赔偿金．假定在一年度内有10 000人购买了这种保险，且各投保人是否出险相互独立．已知保险公司在一年度内至少支付赔偿金10 000元的概率为41010.999-．（Ⅰ）求一投保人在一年度内出险的概率p ；（Ⅱ）设保险公司开办该项险种业务除赔偿金外的成本为50 000元，为保证盈利的期望不小于0，求每位投保人应交纳的最低保费（单位：元）．19．（本小题满分12分）如图，正四棱柱1111ABCD A B C D -中，124AA AB ==，点E 在1CC 上且EC E C 31=．（Ⅰ）证明：1AC ⊥平面BED ； （Ⅱ）求二面角1A DE B --的大小．20．（本小题满分12分）设数列{}n a 的前n 项和为n S ．已知1a a =，13nn n a S +=+，*n ∈N ．（Ⅰ）设3nn n b S =-，求数列{}n b 的通项公式；（Ⅱ）若1n n a a +≥，*n ∈N ，求a 的取值范围．21．（本小题满分12分）设椭圆中心在坐标原点，(20)(01)A B ，，，是它的两个顶点，直线)0(>=k kx y 与AB 相交于点D ，与椭圆相交于E 、F 两点．（Ⅰ）若6ED DF =，求k 的值；（Ⅱ）求四边形AEBF 面积的最大值． 22．（本小题满分12分） 设函数sin ()2cos xf x x=+．（Ⅰ）求()f x 的单调区间；（Ⅱ）如果对任何0x ≥，都有()f x ax ≤，求a 的取值范围．AB CD EA 1B 1C 1D 12008年普通高等学校招生全国统一考试 理科数学试题（必修+选修Ⅱ）参考答案和评分参考评分说明：1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要 考查内容比照评分参考制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和 难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数．选择题不给中间分．一、选择题1．B 2．A 3．C 4．C 5．D 6．D 7．B 8．B 9．B 10．C 11．A 12．C 二、填空题13．2 14．2 5．3+16．两组相对侧面分别平行；一组相对侧面平行且全等；对角线交于一点；底面是平行四边形．注：上面给出了四个充要条件．如果考生写出其他正确答案，同样给分．1．设集合{|32}M m m =∈-<<Z ，{|13}N n n M N =∈-=Z 则，≤≤（ ）A ．{}01，B ．{}101-，，C ．{}012，，D ．{}1012-，，， 【答案】B【解析】{}1,0,1,2--=M ，{}3,2,1,0,1-=N ，∴{}1,0,1-=N M 【高考考点】集合的运算，整数集的符号识别2．设a b ∈R ，且0b ≠，若复数3()a bi +是实数，则（ ） A ．223b a = B ．223a b =C ．229b a =D ．229a b =【答案】A【解析】i b b a ab a i b ab bi a a bi a )3()3(33)(322332233-+-=--+=+，因是实数且 0b ≠，所以2232303a b b b a =⇒=- 【高考考点】复数的基本运算3．函数1()f x x x=-的图像关于（ ） A ．y 轴对称 B ． 直线x y -=对称 C ． 坐标原点对称 D ． 直线x y =对称【答案】C 【解析】1()f x x x=-是奇函数，所以图象关于原点对称 【高考考点】函数奇偶性的性质4．若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ ） A ．a <b <cB ．c <a <bC ． b <a <cD ． b <c <a【答案】C【解析】由0ln 111<<-⇒<<-x x e ，令x t ln =且取21-=t 知b <a <c 5．设变量x y ，满足约束条件：222y x x y x ⎧⎪+⎨⎪-⎩，，．≥≤≥，则y x z 3-=的最小值（ ）A ．2-B ．4-C ．6-D ．8- 【答案】D【解析】如图作出可行域，知可行域的顶点是A （－2，2）、B(32,32)及C(－2，－2)于是8)(m in -=A z6．从20名男同学，10名女同学中任选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的概率为（ ） A ．929B ．1029C ．1929D ．2029【答案】D【解析】2920330110220210120=+=C C C C C P 7．64(1(1-的展开式中x 的系数是（ ）A ．4-B ．3-C ．3D ．4【答案】B【解析】324156141604262406-=-+=-+C C C C C C 【易错提醒】容易漏掉1416C C 项或该项的负号8．若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ ）A ．1B CD ．2【答案】B【解析】在同一坐标系中作出x x f sin )(1=及x x g cos )(1=在]2,0[π的图象，由图象知，当43π=x ，即43π=a 时，得221=y ，222-=y ，∴221=-=y y MN【高考考点】三角函数的图象，两点间的距离【备考提示】函数图象问题是一个常考常新的问题9．设1a >，则双曲线22221(1)x y a a -=+的离心率e 的取值范围是（ ）A ．B ．C ．(25)，D ．(2【答案】B【解析】222222)11(1)1()(a a a a a c e ++=++==，因为a 1是减函数，所以当1a >时 110<<a，所以522<<e ，即52<<e 【高考考点】解析几何与函数的交汇点 10．已知正四棱锥S ABCD -的侧棱长与底面边长都相等，E 是SB 的中点，则AE SD ，所成的角的余弦值为（ ）A ．13B ．3C D ．23【答案】C【解析】连接AC 、BD 交于O ，连接OE ，因OE ∥SD.所以∠AEO 为所求。

2009年上海高校自主招生考试数学试题解析浅谈上海高三毕业生应对高校自主招生的考试策略——自主招生考试数学试题解析华东师大二附中范端喜自从2006年复旦，交大等全国重点院校高考改革试“破冰”以来，各学校“深化自主选拔录取改革试验”招生方案不断出台。

全国自主招生学校数目不断增加，而且各学校自主招生规模比例也在增加，引起了上海乃至全国教育界，家长等瞩目。

更引起广大中学教师对其命题的高度关注。

下面是作为一名数学教师的我个人的一些认识，仅供参考。

1. 试卷特点分析1.1 基础知识和基本技能仍是考查的重点我们将基础知识，基本技能称之为“双基”。

大家知题，能力与“双基”有着辩证关系；没有扎实的“双基”，能力培养就成了无源之水，无本之木。

所以，“双基”训练是数学教学的重要任务之一，是培养学生能力的前提。

纵观复旦，交大，清华等高校近几年自主招生笔试题目，我们会发现，有60-70%左右的题目仍是比较基础的问题。

例如交大近三年来，填空题都是10题（50分），占试卷的一半，这些填空题比较常规，和高考试题难度相当。

复旦的30题左右的选择题中也多半是学生们平时训练过的一些比较熟悉的题型和知识点。

1.2 考查知识点的覆盖面广，但侧重点有所不同复旦，交大等高校近几年自主招生的试题，知识点的覆盖面还是很广的，基本上涉及到高中数学大纲的所有内容。

例如，函数，集合，数列，复数，三角，排列，组合，概率统计，向量，立体几何，解析几何等。

但毕竟高校自主招生试题命题是由大学数学教授完成的，更多会考虑到高等数学与初等数学的衔接，所以提请大家注意一下几个方面：函数和方程问题，排列组合和概率统计等。

笔者粗略统计了一下，2008年复旦自主招生试题中与函数和方程有关的试题多达10题，占31%。

复数。

复数通常在高考中要求也比较低，占的比分也较少，但在复旦自主招生中似乎复数仍占有一席之地（2008及2007年分别有2题和3题）。

矩阵和行列式。

目前还未纳入高考范围。

习题八5. 求下列各极限：10(1)y x y →→00(3)x y →→00(4)l ;x y →→222222001cos()(6)lim .()e x y x y x y x y +→→-++ 解：(1)原式0ln 2.=(3)原式=01.4x y →→=-(4)原式=002.x y →→=(6)原式=22222222222()00001()2lim lim 0.()e 2ex y x y x x y y x y x y x y ++→→→→++==+6. 讨论下列函数在原点O (0，0)处的连续性及偏导数：(3) 222222222,0,()0,0;x y x y z x y x y x y ⎧+≠⎪=+-⎨⎪+=⎩解：(3)若P (x ,y ) 沿直线y =x 趋于(0，0)点，则2222000lim lim 10x x y x x x z x x →→=→⋅==⋅+, 若点P (x ,y ) 沿直线y =-x 趋于(0，0)点，则22222220000()lim lim lim 0()44x x x y x x x x z x x x x →→→=-→-===⋅-++ 故00lim x y z →→不存在.故函数z 在O (0，0)处不连续.而…8. 求下列函数的偏导数： (1)z = x 2y +2xy; (6)u = z xy ;解：(1)223122,.z z x xy x x y y y∂∂=+=-∂∂ (6)1ln ln xy xy xy u u uz z y z z x xy z x y z-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂ 12.求曲线2244x y z y ⎧+=⎪⎨⎪=⎩在点（2，4，5）处的切线与正向x 轴所成的倾角.解：(2,4,5)1,1,2z zx x x ∂∂==∂∂ 设切线与正向x 轴的倾角为α, 则tan α=1. 故α=π4.13.求下列函数的二阶偏导数：(3)z = y x ;解：(3)222ln ,ln ,xx z z y y y y x x∂∂==∂∂ 21222112111,(1),1ln (1ln ),ln (1ln ).x x x x x x x x z z xy x x y y y z y xy y y x y x y y zy x y y y x y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂ 14.设f (x ,y ,z ) = xy 2+yz 2+zx 2,求(0,0,1),(0,1,0),(2,0,1).xx yz zzx f f f - 解：2(,,)2x f x y z y zx =+22(,,)2,(0,0,1)2,(,,)2(,,)2,(0,1,0)0,(,,)2(,,)2(,,)0,(2,0,1)0.xx xx y yz yz z zz zzx zzx f x y z z f f x y z xy z f x y z z f f x y z yz x f x y z yf x y z f ===+=-==+===22. 求下列复合函数的偏导数或全导数：(2)z ＝arc tanxy, x ＝u ＋v ,y ＝u －v , 求z u ∂∂,z v ∂∂；(3)ln(e e )xyu =+, y ＝x 3, 求d d u x;(4) u ＝x 2＋y 2＋z 2, x ＝e cos t t , y ＝e sin t t , z ＝e t, 求d d u t. 解：(2)222222211111x z z x z y y x v y u x u y uy x yu v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭ 2222222111(1)11.x z z x z yy v x v y vyx x y y y x ux y u v-∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e e e ex y x x x y x y x y x yx x u u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++ (4)d d d d d d d d u u x u y u z t x t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4e t t t t t t x t t y t t z =-+++⋅=.23. 设f 具有一阶连续偏导数，试求下列函数的一阶偏导数： (1)22(,e );xy u f x y =-解：(1)12122e 2e .xy xy uf x f y xf y f x∂''''=⋅+⋅⋅=+∂ 1212(2)e 2e .xy xy uf y f x yf x f y∂''''=⋅-+⋅⋅=-+∂ 29. 求下列隐函数的导数或偏导数：(4)333z xyz a -=，求22,z zx y∂∂∂∂.解：(4)设33(,,)3F x y z z xyz a =--, 则23,3,33,x y z F yz F xz F z xy =-=-=-故223,33x z F z yz yz x F z xy z xy∂-=-=-=∂-- 223,33y z F z xz xz y F z xy z xy∂-=-=-=∂--()()()()22222222322232222()zz z x x xz z xy xz y z y z xy y y z xy xzxzz x x xz z xy z xyx yzz xy xy z z xy ∂∂⎛⎫--- ⎪∂∂∂∂⎛⎫⎝⎭== ⎪-∂∂⎝⎭-⎛⎫⋅--- ⎪--⎝⎭==--31. 设11,0F y z x y ⎛⎫++= ⎪⎝⎭确定了函数z = z (x ,y ),其中F 可微，求,z z x y ∂∂∂∂.解：12122110x F F F F x x ⎛⎫'''=⋅+⋅=--⎪⎝⎭122122121222122221222110111y z x zy zF F F y F F F F F F F zx x F F x F F F F F y F zy y F F y F ⎛⎫''-=⋅+⋅ ⎪⎝⎭'''=⋅+⋅='-'∂∴=-=-=∂''''-''-∂=-=-=∂''。

复旦大学2008年优秀高中生文化水平选拔测试试卷答案及详解本试卷共30页，满分1000分；每题5分，共200题；考试时间为180分钟。

考生注意：1．答卷前，考生务必在试卷和答题卡上都用钢笔或圆珠笔填写姓名、中学名称、准考证号，并用2B铅笔在答题卡上正确涂写试卷类型(A卷或B卷)和准考证号。

2．本卷为单选题，由机器阅卷，答案必须全部涂在答题卡上。

在答题卡上，考生应将代表正确答案的小方格用铅笔涂黑。

注意试题题号和答题卡编号一一对应，不能错位。

答案需要更改时，必须将原选项用橡皮擦去，重新选择并填涂。

答案不能写在试卷上，写在试卷上一律不给分。

3．本卷每题答对得5分，不答得O分，答错扣2分！！1．[元]施惠《绿林寄迹》：“倚山为寨，号为拦路虎。

金银财宝，劫来如粪土。

”句中的“拦路虎”一语作____D____。

A．补语B．状语C．动宾短语的宾语D．宾语【解答】D 号：自称为。

为谓语。

所以，拦路虎应该是宾语2．下列各组词语中，没有错别字的一组是_C_____。

A．演绎必竞绊脚石目不暇接B．去逝耽搁爆发力举步维艰C．斡旋戏谑白内瘴运筹帷幄D．贸然简练纪录片舔犊情深【解答】CA毕竞 B 去世 D 舐犊情深3．鲁迅《月界旅行》七回：“那麦思敦更觉气色傲然，或饮或食，忽厢忽歌，大有，此间乐不思蜀‟之意。

”与句中“乐不思蜀”构成反向意义的是____B___。

A．留连忘返B．饮水思源C．乐而忘返D．乐不可支【解答】B乐不思蜀，是形容人因为处在悠闲自在的环境中而忘本，所以反义应该是饮水思源4．[明]归庄《万古愁》：“有几个狼奔豕突的燕和赵，有几个狗屠驴贩奴和盗。

”与句中“狼奔豕突”近义的是____D_____。

A．鱼贯丽行B．狼吞虎咽C．狼狈不堪D．抱头鼠串【解答】D象狼那样奔跑,象猪那样冲撞.形容成群的坏人乱冲乱撞,到处骚扰.比喻敌人奔逃时,惊慌状态.也比喻敌人乱冲乱窜，所以D符合5．张洁《爱，是不能忘记的》：“有人就会说你的神经出了毛病，或是你有什么见不得人的隐私，或是你政治上出了什么问题，或是你刁钻古怪，看不起凡人，不尊重千百年来的社会习惯，你准是个离经叛道的邪人。

2008年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．第Ⅰ卷1至2页．第Ⅱ卷3至10页． 考试结束后，将本试卷和答题卡一并交回．第Ⅰ卷注意事项：1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上．2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．不能答在试题卷上．3．本卷共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的． 参考公式：如果事件A B ，互斥，那么 球的表面积公式()()()P A B P A P B +=+24πS R =如果事件A B ，相互独立，那么 其中R 表示球的半径()()()P A B P A P B = 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么 34π3V R =n 次独立重复试验中事件A 恰好发生k 次的概率 其中R 表示球的半径()(1)(012)k k n kk n P k C p p k n -=-=，，，，一、选择题1．若sin 0α<且tan 0α>是，则α是（ ） A ．第一象限角 B ． 第二象限角 C ． 第三象限角 D ． 第四象限角2．设集合{|32}M m m =∈-<<Z ，{|13}N n n M N =∈-=Z 则，≤≤（ ）A ．{}01，B ．{}101-，，C ．{}012，，D ．{}1012-，，，3．原点到直线052=-+y x 的距离为（ ） A ．1B ．3C ．2D ．54．函数1()f x x x=-的图像关于（ ）A ．y 轴对称B ． 直线x y -=对称C ． 坐标原点对称D ． 直线x y =对称5．若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ ） A ．a <b <cB ．c <a <bC ． b <a <cD ． b <c <a6．设变量x y ，满足约束条件：222y x x y x ⎧⎪+⎨⎪-⎩，，．≥≤≥，则y x z 3-=的最小值为（ ）A ．2-B ．4-C ．6-D ．8-7．设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （ ） A ．1 B ．12C ．12-D ．1-8．正四棱锥的侧棱长为32，侧棱与底面所成的角为︒60，则该棱锥的体积为（ ） A ．3B ．6C ．9D ．189．44)1()1(x x +-的展开式中x 的系数是（ ）A ．4-B ．3-C ．3D ．410．函数x x x f cos sin )(-=的最大值为（ ） A ．1B ．2 C ．3D ．211．设ABC △是等腰三角形，120ABC ∠=，则以A B ，为焦点且过点C 的双曲线的离心率为（ ） A ．221+ B ．231+ C ． 21+ D ．31+12．已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ ） A ．1 B ．2C ．3D ．22008年普通高等学校招生全国统一考试文科数学(必修+选修I)第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．把答案填在题中横线上．13．设向量(12)(23)==，，，a b ，若向量λ+a b 与向量(47)=--，c 共线，则=λ ． 14．从10名男同学，6名女同学中选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的不同选法共有 种（用数字作答）15．已知F 是抛物线24C y x =：的焦点，A B ，是C 上的两个点，线段AB 的中点为(22)M ，，则ABF △的面积等于 ．16．平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件① ； 充要条件② ． （写出你认为正确的两个充要条件）三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分10分） 在ABC △中，5cos 13A =-，3cos 5B =． （Ⅰ）求sinC 的值；（Ⅱ）设5BC =，求ABC △的面积． 18．（本小题满分12分）等差数列{}n a 中，410a =且3610a a a ，，成等比数列，求数列{}n a 前20项的和20S ．19．（本小题满分12分）甲、乙两人进行射击比赛，在一轮比赛中，甲、乙各射击一发子弹．根据以往资料知，甲击中8环，9环，10环的概率分别为0.6，0.3，0.1，乙击中8环，9环，10环的概率分别为0.4，0.4，0.2．设甲、乙的射击相互独立．（Ⅰ）求在一轮比赛中甲击中的环数多于乙击中环数的概率；（Ⅱ）求在独立的三轮比赛中，至少有两轮甲击中的环数多于乙击中环数的概率． 20．（本小题满分12分）如图，正四棱柱1111ABCD A BC D -中，124AA AB ==，点E 在1CC 上且EC E C 31=． （Ⅰ）证明：1AC ⊥平面BED ； （Ⅱ）求二面角1A DE B --的大小． 21．（本小题满分12分）设a ∈R ，函数233)(x ax x f -=．（Ⅰ）若2=x 是函数)(x f y =的极值点，求a 的值；（Ⅱ）若函数()()()[02]g x f x f x x '=+∈，，，在0=x 处取得最大值，求a 的取值范围． 22．（本小题满分12分）设椭圆中心在坐标原点，(20)(01)A B ，，，是它的两个顶点，直线)0(>=k kx y 与AB 相交于点D ，与椭圆相交于E 、F 两点． （Ⅰ）若6ED DF =，求k 的值； （Ⅱ）求四边形AEBF 面积的最大值．AB CD EA 1B 1C 1D 12008年普通高等学校招生全国统一考试 文科数学试题（必修+选修Ⅰ）参考答案和评分参考评分说明：1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要 考查内容比照评分参考制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和 难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数．选择题不给中间分．一、选择题1．C 2．B 3．D 4．C 5．C 6．D 7．A 8．B 9．A 10．B 11．B 12．C 二、填空题13．2 14．420 15．216．两组相对侧面分别平行；一组相对侧面平行且全等；对角线交于一点；底面是平行四边形．注：上面给出了四个充要条件．如果考生写出其他正确答案，同样给分．1．若sin 0α<且tan 0α>是，则α是（ ） A ．第一象限角 B ． 第二象限角 C ． 第三象限角 D ． 第四象限角 【答案】C【解析】sin 0α<,α在三、四象限；tan 0α>，α在一、三象限，∴选C 2．设集合{|32}M m m =∈-<<Z ，{|13}N n n M N =∈-=Z 则，≤≤（ ）A ．{}01，B ．{}101-，，C ．{}012，，D ．{}1012-，，，【答案】B【解析】{}1,0,1,2--=M ，{}3,2,1,0,1-=N ，∴{}1,0,1-=N M 【高考考点】集合的运算，整数集的符号识别 3．原点到直线052=-+y x 的距离为（ ） A ．1B ．3C ．2D ．5【答案】D【解析】52152=+-=d【高考考点】点到直线的距离公式4．函数1()f x x x=-的图像关于（ ） A ．y 轴对称 B ． 直线x y -=对称 C ． 坐标原点对称 D ． 直线x y =对称【答案】C 【解析】1()f x x x=-是奇函数，所以图象关于原点对称 【高考考点】函数奇偶性的性质5．若13(1)ln 2ln ln x e a x b x c x -∈===，，，，，则（ ） A ．a <b <cB ．c <a <bC ． b <a <cD ． b <c <a【答案】C 【解析】由0ln 111<<-⇒<<-x x e，令x t ln =且取21-=t 知b <a <c6．设变量x y ，满足约束条件：222y x x y x ⎧⎪+⎨⎪-⎩，，．≥≤≥，则y x z 3-=的最小值为（ ）A ．2-B ．4-C ．6-D ．8-【答案】D【解析】如图作出可行域，知可行域的顶点是A （－2，2）、B(32,32)及C(－2，－2) 于是8)(min -=A z7．设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （ ）A ．1B ．12C ．12-D ．1-【答案】A【解析】ax y 2'=，于是切线的斜率a y k x 2'1===，∴有122=⇒=a a8．正四棱锥的侧棱长为32，侧棱与底面所成的角为︒60，则该棱锥的体积为（ ） A ．3 B ．6C ．9D ．18【答案】B【解析】高360sin 32＝︒=h ，又因底面正方形的对角线等于32，∴底面积为 6332212=⨯⨯⨯=S ，∴体积63631=⨯⨯=V【备考提示】在底面积的计算时，要注意多思则少算 9．44)1()1(x x +-的展开式中x 的系数是（ ）A ．4-B ．3-C ．3D ．4【答案】A【解析】41666141404242404-=-+=-+C C C C C C 【易错提醒】容易漏掉1414C C 项或该项的负号10．函数x x x f cos sin )(-=的最大值为（ ） A ．1 B ．2 C ．3D ．2【答案】B【解析】)4sin(2cos sin )(π-=-=x x x x f ，所以最大值是2【高考考点】三角函数中化为一个角的三角函数问题【备考提示】三角函数中化为一个角的三角函数问题是三角函数在高考中的热点问题 11．设ABC △是等腰三角形，120ABC ∠=，则以A B ，为焦点且过点C 的双曲线的离心率为（ ） A ．221+ B ．231+ C ． 21+ D ．31+【答案】B【解析】由题意BC c =2,所以c c AC 3260sin 220=⨯⨯=，由双曲线的定义，有c a c c BC AC a )13(2322-=⇒-=-=，∴231131+=-==a c e 【高考考点】双曲线的有关性质，双曲线第一定义的应用12．已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ ） A ．1 B ．2C ．3D ．2【答案】C【解析】设两圆的圆心分别为1O 、2O ，球心为O ，公共弦为AB ，其中点为E ，则21EO OO 为矩形，于是对角线OE O O =21,而3122222=-=-=AE OA OE ，∴321=O O 【高考考点】球的有关概念，两平面垂直的性质13．设向量(12)(23)==，，，a b ，若向量λ+a b 与向量(47)=--，c 共线，则=λ ． 【答案】 2【解析】λ+a b ＝)32,2(++λλ则向量λ+a b 与向量(47)=--，c 共线274322=⇒--=++⇔λλλ14．从10名男同学，6名女同学中选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的不同选法共有 种（用数字作答） 【答案】 420【解析】4202701501621026110=+=+C C C C15．已知F 是抛物线24C y x =：的焦点，A B ，是C 上的两个点，线段AB 的中点为(22)M ，，则ABF △的面积等于 ．【答案】 2 【解析】设过M的直线方程为)2(2-=-x k y ，由0)1(444)2(22222=-+-⇒⎩⎨⎧=-=-k kx x k xy x k y ∴k x x 421=+，2221)1(4kk x x -=，由题意144=⇒=k k ，于是直线方程为x y = 421=+x x ，021=x x ，∴24=AB ，焦点F （1，0）到直线x y =的距离21=d∴ABF △的面积是216．平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件：充要条件① ； 充要条件② ． （写出你认为正确的两个充要条件）【答案】两组相对侧面分别平行；一组相对侧面平行且全等；对角线交于一点；底面是平行四边形．注：上面给出了四个充要条件．如果考生写出其他正确答案，同样给分．三、解答题17．解：（Ⅰ）由5cos 13A =-，得12sin 13A =， 由3cos 5B =，得4sin 5B =． ··········································································· 2分所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=． ····································· 5分（Ⅱ）由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯===． ··········································· 8分 所以ABC △的面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=． ····················· 10分18．解：设数列{}n a 的公差为d ，则3410a a d d =-=-， 642102a a d d =+=+，1046106a a d d =+=+． ················································································ 3分 由3610a a a ，，成等比数列得23106a a a =，即2(10)(106)(102)d d d -+=+， 整理得210100d d -=，解得0d =或1d =．······················································································· 7分 当0d =时，20420200S a ==． ······································································ 9分 当1d =时，14310317a a d =-=-⨯=， 于是2012019202S a d ⨯=+207190330=⨯+=． ············································· 12分 19．解：记12A A ，分别表示甲击中9环，10环，12B B ，分别表示乙击中8环，9环，A 表示在一轮比赛中甲击中的环数多于乙击中的环数，B 表示在三轮比赛中至少有两轮甲击中的环数多于乙击中的环数，12C C ，分别表示三轮中恰有两轮，三轮甲击中环数多于乙击中的环数．（Ⅰ）112122A A B A B A B =++，··································································· 2分 112122()()P A P A B A B A B =++ 112122()()()P A B P A B P A B =++112122()()()()()()P A P B P A P B P A P B =++0.30.40.10.40.10.40.2=⨯+⨯+⨯=． ····························································· 6分（Ⅱ）12B C C =+， ······················································································ 8分22213()[()][1()]30.2(10.2)0.096P C C P A P A =-=⨯⨯-=，332()[()]0.20.008P C P A ===，1212()()()()0.0960.0080.104P B P C C P C P C =+=+=+=． ··························· 12分 20．解法一：依题设，2AB =，1CE =．（Ⅰ）连结AC 交BD 于点F ，则BD AC ⊥．由三垂线定理知，1BD AC ⊥． ········································································· 3分 在平面1ACA 内，连结EF 交1AC 于点G ，由于1AA ACFC CE== 故1Rt Rt A AC FCE △∽△，1AAC CFE ∠=∠， CFE ∠与1FCA ∠互余．于是1AC EF ⊥． 1AC 与平面BED 内两条相交直线BD EF ，都垂直， 所以1AC ⊥平面BED ． ·················································································· 6分 （Ⅱ）作GH DE ⊥，垂足为H ，连结1A H ．由三垂线定理知1A H DE ⊥，故1A HG ∠是二面角1A DE B --的平面角．························································ 8分EF =CE CF CG EF ⨯==EG ==． AB CDEA 1B 1C 1D 1 FH G13EG EF =，13EF FD GH DE ⨯=⨯=又1AC ==113AG AC CG =-=．11tan A GA HG HG∠== 所以二面角1A DE B --的大小为 ················································· 12分 解法二：以D 为坐标原点，射线DA 为x 轴的正半轴， 建立如图所示直角坐标系D xyz -．依题设，1(220)(020)(021)(204)B C E A ，，，，，，，，，，，．(021)(220)DE DB ==，，，，，，11(224)(204)AC DA =--=，，，，，． ······························ 3分 （Ⅰ）因为10AC DB =，10AC DE =， 故1AC BD ⊥，1AC DE ⊥． 又DBDE D =，所以1AC ⊥平面DBE ． ·················································································· 6分 （Ⅱ）设向量()x y z =，，n 是平面1DA E 的法向量，则DE ⊥n ，1DA ⊥n ．故20y z +=，240x z +=．令1y =，则2z =-，4x =，(412)=-，，n ． ····················································· 9分1AC <>，n 等于二面角1A DE B --的平面角， 11114cos 42AC AC AC <>==，n n n 所以二面角1A DE B --的大小为arccos42． ················································· 12分21．解：（Ⅰ）2()363(2)f x ax x x ax '=-=-．因为2x =是函数()y f x =的极值点，所以(2)0f '=，即6(22)0a -=，因此1a =． 经验证，当1a =时，2x =是函数()y f x =的极值点． ········································· 4分 （Ⅱ）由题设，3222()336(3)3(2)g x ax x ax x ax x x x =-+-=+-+． 当()g x 在区间[02]，上的最大值为(0)g 时，(0)(2)g g ≥，即02024a -≥．故得65a ≤． ································································································ 9分 反之，当65a ≤时，对任意[02]x ∈，， 26()(3)3(2)5g x x x x x +-+≤23(210)5xx x =+- 3(25)(2)5xx x =+- 0≤，而(0)0g =，故()g x 在区间[02]，上的最大值为(0)g ． 综上，a 的取值范围为65⎛⎤-∞ ⎥⎝⎦，． ··································································· 12分22．（Ⅰ）解：依题设得椭圆的方程为2214x y +=， 直线AB EF ，的方程分别为22x y +=，(0)y kx k =>． ····································· 2分 如图，设001122()()()D x kx E x kx F x kx ，，，，，，其中12x x <，且12x x ，满足方程22(14)4k x +=， 故21x x =-=．①由6ED DF =知01206()x x x x -=-，得021215(6)77x x x x =+==； 由D 在AB 上知0022x kx +=，得0212x k=+．所以212k =+， 化简得2242560k k -+=，解得23k =或38k =． ······················································································ 6分 （Ⅱ）解法一：根据点到直线的距离公式和①式知，点E F ，到AB的距离分别为1h ==2h ==······················································· 9分又AB ==AEBF 的面积为121()2S AB h h =+ 1525(14k =+==≤当21k =，即当12k =时，上式取等号．所以S 的最大值为 ························ 12分 解法二：由题设，1BO =，2AO =．设11y kx =，22y kx =，由①得20x >，210y y =->， 故四边形AEBF 的面积为BEF AEF S S S =+△△222x y =+ ···································································································· 9分===当222x y =时，上式取等号．所以S 的最大值为 ······································· 12分。

28.【简解】△ANE∽△CND, AE AN 1 E 为 AC 的三等分点；同理 M 也是其一个三等分点；三个 CD CN 2
1
11
非阴影部分面积都是 ；1-3× = 。选 A
6
62
29.【解析】T 中至少含有两个元素 与 A，除此之外，其他元素为{a1} ，{a2} ，{a3} ，{a1, a2} ，{a1, a3} ，
题.具体情况如下表所述：
问题
解决问题的学生数
代数学问题
20
几何学问题
18
三角学问题
18
代数学问题和几何学问题
7
代数学问题和三角学问题
8
几何学问题和三角学问题
9
其中有三位学生一个问题都没有解决.问三个问题都解决的学生数是___ ____.
A、5；
B、6；
C、7；
D、8
14.方程 3x2 ex 0 的实根_____.
{a3, a2} 六个中的若干 n 个；n=0 时有 1 个，n=1 时有 C61 =6 个，n=2 时有 C31C31 =9 个(集合中元素的个数只
F1
,
F2
分别为椭圆
x2 16
y2 9
1的左、右焦点，且点 P 是椭圆上的一点.若 F1, F2 ,P 是一个直角三角形
的三个顶点，则点 P 到 x 轴的距离为_______.
A、3；
B、 9 ； 4
C、 9 ； 5
D、 3 2
31.若空间三条直线两两成异面直线，则与 a, b, c 都相交的直线有_____.
2
16.【简解】将 y=

1
x 1
x 1
代入第一个式子，得到 x x = x 2 2 x ，x-

2008年全国普通高等学校招生统一考试（上海）数学试卷（理工农医类）一、填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分.1.不等式11x -＜的解集是___________________.2．若集合{|2}{|}A x x B x x a =≤=≥、满足{2}A B = ，则实数a = . 3．若复数z 满足(2)z i z =- (i 是虚数单位)，则z = .4．若函数()f x 的反函数为12()f x x -=(0)x >(x ＞0)，则(4)f = .5．若向量a b 、满足1,2,a b == 且a 与b 的夹角为3π，则a b + ＝___________________6．函数()sin 2f x x x π⎛⎫=++⎪⎝⎭的最大值是___________________. 7．在平面直角坐标系中，从六个点：(0,0)(2,0)(1,1)(0,2)(2,2)(3,3)A B C D E F 、、、、、中任取三个，这三点能构成三角形的概率是___________________（结果用分数表示）. 8．设函数f (x )是定义在R 上的奇函数.若当(0,)x ∈+∞时，()lg f x x =，则满足()0f x >的x 的取值范围是___________________.9．已知总体的各个体的值由小到大依次为2，3，3，7，a ，b ，12，13.7，18.3，20，且总体的中位数为10.5.若要使该总体的方差最小，则a 、b 的取值分别是___________________ .10．某海域内有一孤岛，岛四周的海平面（视为平面）上有一浅水区（含边界），其边界是长轴长为2a ,短轴长为2b 椭圆。

已知岛上甲、乙导航灯的海拔高度分别为12,h h ，且两个导航灯在海平面上的投岸恰好落在椭圆的两个焦点上。

现有船只经过该海域（船只的大小忽略不计），在船上测得甲、乙导航灯的仰角分别为12θθ、，那么船只已进入该浅水区的判别条件是___________________11．方程210x +-=的解可视为函数y x =1y x=的图像交点的横坐标。

2009年北京大学自主招生试题(2009-01-03 17:22:16)语文试题一.写出两个成语,要求曲解它的意思(例：度日如年：日子过得很好，每天都像在过年;文不加点：文章不加标点)二.从语法角度分析下列病句错在何处1.我们都有一个家,名字叫中国2.素胚勾勒出青花笔锋浓转淡三.对联博雅塔前人博雅(注：博雅塔是北大校园内一处景物）三.翻译古文(20分)吴人之归有绮其衣者衣数十袭届时而易之而特居于盗乡盗涎而妇弗觉犹日炫其华绣于丛莽之下盗遂杀而取之盗不足论而吾甚怪此妇知绮其衣而不知所以置其身夫使托身于荐绅之家健者门焉严扃深居盗乌得取唯其濒盗居而复炫其装此其所以死耳天下有才之士不犹吴妇之绮其衣乎托非其人则与盗邻盗贪利而耆杀故炫能于乱邦匪有全者杜袭喻繁钦曰子若见能不已非吾徒也钦卒用其言以免于刘表之祸呜呼袭可谓善藏矣钦亦可谓善听矣不尔吾未见其不为吴妇也附原文：书杜袭喻繁钦语后[1]·（清）林纾吴人之归，有绮其衣者[2]，衣数十袭[3]，届时而易之。

而特居于盗乡，盗涎而妇弗觉[4]，犹日炫其华绣于丛莽之下[5]，盗遂杀而取之。

盗不足论，而吾甚怪此妇知绮其衣，而不知所以置其身。

夫使托身于荐绅之家[6]，健者门焉，严扃深居，盗乌得取？唯其濒盗居而复炫其装[7]，此其所以死耳。

天下有才之士，不犹吴妇之绮其衣乎？托非其人，则与盗邻，盗贪利而耆杀[8]，故炫能于乱邦，匪有全者。

杜袭喻繁钦曰：“子若见能不已[9]，非吾徒也。

”钦卒用其言，以免于刘表之祸[10]。

呜呼！袭可谓善藏矣，钦亦可谓善听矣。

不尔，吾未见其不为吴妇也。

四.阅读理解是一篇选自鲁迅《野草》的文章,要求指出很多意像的象征意义求乞者我顺着剥落的高墙走路，踏着松的灰土。

另外有几个人，各自走路。

微风起来，露在墙头的高树的枝条带着还未干枯的叶子在我头上摇动。

微风起来，四面都是灰土。

一个孩子向我求乞，也穿着夹衣，也不见得悲戚，近于儿戏；我烦腻他这追着哀呼。

绝密★启用前2008年普通高等学校招生全国统一考试（上海卷）数学试卷（理工农医类）（满分150分，考试时间120分钟）考生注意1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题，用黑色字迹钢笔、水笔或圆珠笔作答非选择题.一. 填空题（本大题满分44分）本大题共有11题，只要求直接填写结果，每个空格填对得4分，否则一律得零分．1．不等式| x −1 |<1的解集是 .2．若集合A ={ x | x ≤2 }、B ={ x | x ≥a }满足A ∩B ={ 2 }，则实数a =_____________.3．若复数z 满足z =i(2−z)（i 是虚数单位），则z =_____________.4．若函数f(x)的反函数为f −1(x)=x 2（x >0），则f( 4 )= .5．若向量a ⃗、b ⃗⃗满足| a ⃗ |=1，| b ⃗⃗ |=2，且a ⃗与b ⃗⃗的夹角为π3，则| a ⃗+b ⃗⃗ |=__________. 6．函数f(x)=√3sin x +sin (π2+x)的最大值是 .7．在平面直角坐标系中，从六个点：A( 0,0 )、B( 2,0 )、C( 1,1 )、D( 0,2 )、E( 2,2 )、 F( 3,3 )中任取三个，这三点能构成三角形的概率是 (结果用分数表示).8．设函数f(x)是定义在R 上的奇函数. 若当x ∈( 0,+∞ )时，f(x)=lg x ，则满足 f(x)>0的x 的取值范围是 .9．已知总体的各个体的值由小到大依次为2，3，3，7，a ，b ，12，13.7，18.3，20，且 总体的中位数为10.5. 若要使该总体的方差最小，则a 、b 的取值分别是 .10．某海域内有一孤岛. 岛四周的海平面（视为平面）上有一浅水区（含边界），其边界 是长轴长为2a 、短轴长为2b 的椭圆. 已知岛上甲、乙导航灯的海拔高度分别为ℎ1、得 分 评 卷 人 得 分评 卷 人ℎ2，且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上. 现有船只经过该海 域（船只的大小忽略不计），在船上测得甲、乙导航灯的仰角分别为θ1、θ2，那么 船只已进入该浅水区的判别条件是 .11．方程x 2+√2x −1=0的解可视为函数y =x +√2的图像与函数y =1x 的图像交点的横坐标. 若方程x 4+ax −4=0的各个实根x 1,x 2,⋯,x k (k ≤4)所对应的点(x i ,4x i ) （i =1,2,⋯,k ）均在直线y =x 的同侧，则实数a 的取值范围是 .二. 选择题（本大题满分16分）本大题共有4 题，每题都给出 代号为A 、B 、C 、D 的四个结论，其中有且只有一个结论 是正确的，必须把正确结论的代号写在题后的圆括号内， 选对得4分，不选、选错或者选出的代号超过一个（不论 是否都写在圆括号内），一律得零分．12. 组合数C n r ( n >r ≥1,n 、r ∈Z )恒等于 [答] ( )(A) r+1n+1C n−1r−1. (B) ( n +1 )( r +1 )C n−1r−1. (C) nrC n−1r−1. (D) nr C n−1r−1. 13. 给定空间中的直线l 及平面α. 条件“直线l 与平面α内无数条直线都垂直”是“直 线l 与平面α垂直”的 [答] ( )(A) 充要条件. (B) 充分非必要条件.(C) 必要非充分条件. (D) 既非充分又非必要条件.14. 若数列{ a n }是首项为1，公比为a −32的无穷等比数列，且{ a n }各项的和为a ，则a 的值是 [答] ( )(A) 1. (B) 2. (C) 12. (D) 54.15. 如图，在平面直角坐标系中，Ω是一个与x 轴的正半轴、y 轴的正半轴分别相切于点C 、D 的定圆所围成的区域（含边界），A 、B 、C 、D 是该圆的四等分点. 若点P( x,y )、点P ′( x ′,y ′ )满足x ≤x ′且y ≥y ′，则称P 优于P ′. 如果Ω中的点Q 满足：不存在Ω中的其它点优 于Q ，那么所有这样的点Q 组成的集合是劣弧 [答] ( )(A) . (B) . (C) . (D) .三. 解答题（本大题满分90分）本大题共有6题，解答下列各题必须写出必要的步骤．16.（本题满分12分）AB BC CD DA如图，在棱长为2的正方体ABCD−A1B1C1D1中，E是BC1的中点. 求直线DE与平面ABCD所成角的大小（结果用反三角函数值表示）.[解]得分评卷人17.（本题满分13分）如图，某住宅小区的平面图呈圆心角为120∘的扇形AOB. 小区的两个出入口设置在点A 及点C处，且小区里有一条平行于BO的小路CD. 已知某人从C沿CD走到D用了10分钟，从D沿DA走到A用了6分钟. 若此人步行的速度为每分钟50米，求该扇形的半径OA的长（精确到1米）.[解]得分评卷人18.（本题满分15分）本题共有2个小题，第1小题满分6分，第2小题满分9分．−y2=1，P是C上的任意点.已知双曲线C:x24（1）求证：点P到双曲线C的两条渐近线的距离的乘积是一个常数；（2）设点A的坐标为( 3,0 )，求|PA|的最小值.[证明]（1）[解]（2）19.（本题满分16分）本题共有2个小题，第1小题满分8分，第2小题满分8分．.已知函数f(x)=2x−12|x|（1）若f(x)=2，求x的值；（2）若2f(2t)+mf(t)≥0对于t∈[ 1,2 ]恒成立，求实数m的取值范围. [解]（1）（2）20.（本题满分16分）本题共有3个小题，第1小题满分3分，第2小题满分5分，第3小题满分8分．设P( a,b ) ( b≠0 )是平面直角坐标系xOy中的点，l是经过原点与点( 1,b )的直线.记Q是直线l与抛物线x2=2py(p≠0)的异于原点的交点.（1）已知a=1,b=2,p=2. 求点Q的坐标；（2）已知点P( a,b ) ( ab≠0)在椭圆x24+y2=1上，p=12ab. 求证：点Q落在双曲线4x2−4y2=1上；（3）已知动点P( a,b ) 满足ab≠0，p=12ab. 若点Q始终落在一条关于x轴对称的抛物线上，试问动点P的轨迹落在哪种二次曲线上，并说明理由.[解]（1）[证明]（2）[解]（3）21.（本题满分18分）本题共有3个小题，第1小题满分3分，第 2小题满分7分，第3小题满分8分．已知以a 1为首项的数列{ a n }满足：a n+1={a n +c,a n <3,a n d,a n ≥3. （1）当a 1=1，c =1,d =3时，求数列{ a n }的通项公式；（2）当0<a 1<1，c =1,d =3时，试用a 1表示数列{ a n }前100项的和S 100；（3）当0<a 1<1m （m 是正整数），c =1m ，正整数d ≥3m 时，求证：数列a 2−1m , a 3m+2−1m ，a 6m+2−1m ，a 9m+2−1m 成等比数列当且仅当d =3m .[解]（1）（2）[证明]（3）2 0 0 8 年 全 国 普 通 高 等 学 校 招 生 统 一 考 试上海数学试卷(理工农医类)答案要点及评分标准说明1.本解答列出试题的一种或几种解法，如果考生的解法与所列解法不同，可参照解答中评分标准的精神进行评分．2.评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅，当考生的解答在某一步出现错误，影响了后继部分，但该步以后的解答未改变这一题的内容和难度时，可视影响程度决定后面部分的给分，这时原则上不应超过后面部分应给分数之半，如果有较严重的概念性错误，就不给分． 解答一、（第1题至第11题）1. ( 0,2 ).2. 2.3. 1+i .4. 2.5. √7.6. 2.7. 34. 8. ( −1,0 )∪( 1,+∞ ). 9. a =10.5,b =10.5. 10. ℎ1⋅cot θ1+ℎ2⋅cot θ2≤2a . 11. ( −∞,−6 )∪( 6,+∞ ). 二、（第12题至第15题） 题 号 12 131415 代 号DCBD三、（第16题至第21题）16．[解] 过E 作EF ⊥BC ，交BC 于F ，连接DF . ∵EF ⊥平面ABCD ，∴ ∠EDF 是直线DE 与平面ABCD 所成的角. …… 4分 由题意，得EF =12CC 1=1.∵ CF =12CB =1, ∴ DF =√5. …… 8分 ∵ EF ⊥DF ， ∴ tan ∠EDF =EF DF=√55. …… 10分 故直线DE 与平面ABCD 所成角的大小是arctan√55. …… 12分 17. [解法一] 设该扇形的半径为r 米. 连接CO . …… 2分由题意，得CD =500（米），DA =300（米），∠CDO =60°. …… 4分在△CDO 中，CD 2+OD 2−2⋅CD ⋅OD ⋅cos60°=OC 2， …… 6分 即5002+(r −300)2−2×500×(r −300)×12=r 2， …… 9分解得r =490011≈445（米）.答：该扇形的半径OA 的长约为445米. …… 13分 [解法二] 连接AC ，作OH ⊥AC ，交AC 于H . …… 2分 由题意，得CD =500（米），AD =300（米），∠CDA =120°. …… 4分 在△ACD 中，AC 2=CD 2+AD 2−2⋅CD ⋅AD ⋅cos120°=5002+3002+2×500×300×12=7002，∴ AC =700（米）， …… 6分 cos ∠CAD =AC 2+AD 2−CD 22⋅AC ⋅AD=1114. …… 9分在直角△HAO 中，AH =350（米），cos ∠HAO =1114， ∴ OA =AH cos ∠HAO=490011≈445（米）.答：该扇形的半径OA 的长约为445米. …… 13分 18. [解] （1）设P ( x 1,y 1)是双曲线上任意一点，该双曲线的两条渐近线方程分别是x −2y =0和x +2y =0. …… 2分 点P ( x 1,y 1)到两条渐近线的距离分别是11√5和11√5， …… 4分它们的乘积是11√511√5=| x 12−4y 12|5=45.∴ 点P 到双曲线C 的两条渐近线的距离的乘积是一个常数. …… 6分 （2）设P 的坐标为( x,y )，则|PA |2=(x −3)2+y 2 …… 8分 =(x −3)2+x 24−1=54( x −125)2+45. …… 11分∵ |x| ≥ 2， …… 13分 ∴ 当x =125时，|PA |2的最小值为45，即|PA |的最小值为2√55. …… 15分 19. [解] （1）当x <0时，f(x)=0；当x ≥0时，f(x)=2x −12x . …… 2分 由条件可知 2x −12x =2，即 22x −2⋅2x −1=0，解得 2x =1±√2. …… 6分 ∵ 2x >0，∴ x =log 2( 1+√2 ). …… 8分 （2）当t ∈[ 1,2 ]时，2t ( 22t −122t)+m ( 2t −12t )≥0， …… 10分即 m ( 22 t −1 )≥−( 24t −1 ).∵ 22 t −1>0， ∴ m ≥−( 22 t +1 ). …… 13分 ∵ t ∈[ 1,2 ],∴ −( 1+22 t )∈[ −17,−5 ]，故m 的取值范围是[ −5,+∞ ). …… 16分 20. [解]（1）当a =1,b =2,p =2时， 解方程组{x 2=4y,y =2x,得 {x =8,y =16,即点Q 的坐标为( 8, 16 ). …… 3分 [证明]（2）由方程组{x 2=1ab y,y =bx , 得 {x =1a ,y =b a ,即点Q 的坐标为( 1a ,ba ). …… 5分 ∵ P 是椭圆上的点，即 a 24+b 2=1， ∴ 4 ( 1a)2−4 ( ba)2=4a 2( 1−b 2)=1.因此点Q 落在双曲线4x 2−4y 2=1上. …… 8分 （3）设Q 所在抛物线的方程为 y 2=2q(x −c)，q ≠0. …… 10分 将Q ( 1a ,ba )代入方程，得b 2a 2=2q ( 1a −c )，即b 2=2qa −2qca 2. …… 12分当qc =0时，b 2=2qa ，此时点P 的轨迹落在抛物线上； 当qc =12时，( a −12c )2+b 2=14c 2，此时点P 的轨迹落在圆上； 当qc >0且qc ≠12时，( a−12c )214c 2+b 2q 2c=1，此时点P 的轨迹落在椭圆上；当qc <0时，( a−12c )214c 2−b 2( −q 2c)=1，此时点P 的轨迹落在双曲线上.…… 16分21. [解]（1）由题意得a n ={1,n =3k −2,2,n =3k −1,3,n =3k, ( k ∈Z +) . …… 3分（2）当0<a 1<1时，a2=a1+1，a3=a1+2，a4=a1+3，a5=a13+1，a6=a13+2，a7=a13+3，…，a3k−1=a13k−1+1，a3k=a13k−1+2，a3k+1=a13k−1+3 ，……… 6分∴S100=a1+( a2+a3+a4)+( a5+a6+a7)+⋯+( a98+a99+a100)=a1+( 3a1+6)+( a1+6)+( a13+6)+⋯+( a1331+6)=a1+a1(3+1+13+⋯+1331)+6×33=12(11−1331)a1+198. …… 10分（3）当d=3m时，a2=a1+1m；∵a3m=a1+3m−1m =a1−1m+3<3<a1+3=a3m+1，∴a3m+2=a13m+1m；∵a6m=a13m −1m+3<3<a13m+3=a6m+1，∴a6m+2=a19m2+1m；∵a9m=a19m2−1m+3<3<a19m2+3=a9m+1，∴a9m+2=a127m3+1m.∴a2−1m =a1，a3m+2−1m=a13m，a6m+2−1m=a19m2，a9m+2−1m=a127m3.综上所述，当d=3m时，数列a2−1m ，a3m+2−1m，a6m+2−1m，a9m+2−1m是公比为13m的等比数列. ……13分当d≥3m+1时，a3m+2=a1+3d ∈( 0,1m)，a6m+2=a1+3d +3∈(3,3+1m)，a6m+3=a1+3d+3d∈( 0,1m)，a9m+2=a1+3d+3d+3m−1m∈( 3−1m,3 ). ……15分由于a3m+2−1m <0，a6m+2−1m>0，a9m+2−1m>0，故数列a2−1m ，a3m+2−1m，a6m+2−1m，a9m+2−1m不是等比数列.所以，数列a2−1m ，a3m+2−1m，a6m+2−1m，a9m+2−1m成等比数列当且仅当d=3m. ……18分1.不等式|1|1x-<的解集是.【答案】(0,2)【解析】由11102x x -<-<⇒<<.2.若集合A ＝{x |x ≤2}、B ＝{x |x ≥a }满足A ∩B ＝{2}，则实数a ＝ . 【答案】2 【解析】由{2}, 22AB A B a =⇒⇒=只有一个公共元素.3.若复数z 满足z ＝i (2-z)（i 是虚数单位），则z ＝ . 【答案】1i +【解析】由2(2)11iz i z z i i =-⇒==++.4.若函数f (x )的反函数为f －1(x )＝x 2（x ＞0），则f (4)＝ . 【答案】2【解析】令12(4)()44(0)2f t f t t t t -=⇒=⇒=>⇒=. 5.若向量\s\up6(()、\s\up6(()满足|\s\up6(()|＝1，|\s\up6(()|＝2，且\s\up6(()与\s\up6(()的夹角为，则|\s\up6(()+\s\up6(()|＝ .【解析】222||()()2||||2||||cos7||73a b a b a b a a b b a b a b a b a b π+=++=++=++=⇒+=.6.函数f (x )＝sin x +sin(+x )的最大值是 . 【答案】2【解析】由max ()cos 2sin()()26f x x x x f x π=+=+⇒=.7.在平面直角坐标系中，从六个点：A(0,0)、B(2,0)、C(1,1)、D(0,2)、E(2,2)、F(3,3)中任取三个，这三点能构成三角形的概率是 （结果用分数表示）.【答案】34【解析】已知 A C E F B C D 、、、共线；、、共线；六个无共线的点生成三角形总数为：36C ；可构成三角形的个数为：33364315C C C --=，所以所求概率为：3336433634C C C C --=；8.设函数f (x )是定义在R 上的奇函数，若当x ∈(0,+∞)时，f (x )＝lg x ，则满足f (x )＞0的x 的取值范围是 . 【答案】(1,0)(1,)-+∞【解析】 0 ()0 1 ()00 1 x f x x f x x >>⇔><⇔<<当时，；；由f (x )为奇函数得： 0 ()010 ()0 1 x f x x f x x <>⇔-<<<⇔<-⇒当时，；结论；9.已知总体的各个体的值由小到大依次为2,3,3,7,a ,b ,12，13.7，18.3，20，且总体的中位数为10.5，若要使该总体的方差最小，则a 、b 的取值分别是 . 【答案】10.5,10.5a b ==【解析】根据总体方差的定义知，只需且必须10.5,10.5a b ==时，总体方差最小； 10.某海域内有一孤岛，岛四周的海平面（视为平面）上有一浅水区（含边界），其边界是长轴长为2a ，短轴长为2b 的椭圆，已知岛上甲、乙导航灯的海拔高度分别为h 1、h 2，且两个导航灯在海平面上的投影恰好落在椭圆的两个焦点上，现有船只经过该海域（船只的大小忽略不计），在船上测得甲、乙导航灯的仰角分别为θ1、θ2，那么船只已进入该浅水区的判别条件是 . 【答案】1122cot cot 2h h aθθ⋅+⋅≤【解析】依题意，12||||2MF MF a+≤1122cot cot 2h h aθθ⇒⋅+⋅≤；11.方程x 2+x －1＝0的解可视为函数y ＝x +的图像与函数y ＝的图像交点的横坐标，若x 4+ax－4＝0的各个实根x 1，x 2，…，x k (k ≤4)所对应的点(x i ,)（i ＝1,2,…,k ）均在直线y ＝x 的同侧，则实数a 的取值范围是 . 【答案】(,6)(6,)-∞-+∞【解析】方程的根显然0x ≠，原方程等价于34x a x +=，原方程的实根是曲线3y x a=+与曲线4yx=的交点的横坐标；而曲线3y x a=+是由曲线3y x=向上或向下平移||a个单位而得到的。

2008年交大冬令营数学试题2008.1.1一．填空题1．若21()21x x f x -=+，1()()g x f x -=，则3()_______5g =． 2．函数218x y x +=+的最大值为__________． 3．等差数列中，81353a a =，则前n 项和n S 取最大值时，n 的值为__________．4．复数||1z =,若存在负数a 使得2220z az a a -+-=，则________a =．5．若1cos sin 2x x -=，则33cos sin ________x x -=． 6．数列{}n a 的通项公式为n a =，则这个数列的前99项之和99_______S =．7．2(1)(1)x x ++++……9899(1)(1)x x ++++中3x 的系数为________．8．数列{}n a 中，00a =，112a =-，26a =，334a =-，420a =，556a =-，642a =，778a =-，872a =，此数列的通项公式为_______n a =． 9．甲、乙两厂生产同一种商品．甲厂生产的此商品占市场上的80%，乙厂生产的占20%；甲厂商品的合格率为95%，乙厂商品的合格率为90%．若某人购买了此商品发现为次品，则此次品为甲厂生产的概率为__________．10．若曲线221:0C x y -= 与 222:()1C x a y -+=的图像有3个交点，则_______a =．二．解答题1．30个人排成矩形，身高各不相同．把每列最矮的人选出，这些人中最高的设为a ；把每行最高的人选出，这些人中最矮的设为b ．（１）a 是否有可能比b 高？（２）a 和b 是否可能相等？2．已知函数2()f x ax bx c =++(0)a ≠，且()f x x =没有实数根．那么(())f f x x =是否有实数根？并证明你的结论．3．世界杯预选赛中，中国、澳大利亚、卡塔尔和伊拉克被分在A 组，进行主客场比赛．规定每场比赛胜者得三分，平局各得一分，败者不得分．比赛结束后前两名可以晋级． （１）由于4支队伍均为强队，每支队伍至少得3分．于是甲专家预测：中国队至少得10分才能确保出线；乙专家预测：中国队至少得11分才能确保出线．问：甲、乙专家哪个说的对？为什么？（２）若不考虑()1中条件，中国队至少得多少分才能确保出线？4．通信工程中常用n 元数组123(,,,)n a a a a ……表示信息，其中0i a =或1，i n N ∈、．设123(,,)n u a a a a =……，123(,,)n v b b b b =……，(,)d u v 表示u 和v 中相对应的元素不同的个数．（１）(0,0,0,0,0)u =问存在多少个5元数组v 使得(,)1d u v =；（２）(1,1,1,1,1)u =问存在多少个5元数组v 使得(,)3d u v =；（３）令0(0,0,00)n w =个……，123(,,)n u a a a a =……，123(,,)n v b b b b =……， 求证：(,)(,)(,)d u w d v w d u v +≥．5．曲线()220y px p =>与圆22(2)3x y -+=交于A B 、两点，线段AB 的中点在y x =上，求p ．2008年交大冬令营数学试题参考答案2008.1.1一．填空题1．若21()21x x f x -=+，1()()g x f x -=，则3()_______5g =．2 2．函数218x y x +=+的最大值为__________．143．等差数列中，81353a a =，则前n 项和n S 取最大值时，n 的值为__________．204．复数||1z =,若存在负数a 使得2220z az a a -+-=，则________a =．12- 5．若1cos sin 2x x -=，则33cos sin ________x x -=．11166．数列{}n a 的通项公式为n a =，则这个数列的前99项之和99_______S =．9107．2(1)(1)x x ++++……9899(1)(1)x x ++++中3x 的系数为________．4100C =39212258．数列{}n a 中，00a =，112a =-，26a =，334a =-，420a =，556a =-，642a =，778a =-，872a =，此数列的通项公式为_______n a =．(1)(1)(1)n n n n --+9．甲、乙两厂生产同一种商品．甲厂生产的此商品占市场上的80%，乙厂生产的占20%；甲厂商品的合格率为95%，乙厂商品的合格率为90%．若某人购买了此商品发现为次品，则此次品为甲厂生产的概率为__________．2310．若曲线221:0C x y -= 与 222:()1C x a y -+=的图像有3个交点，则a = ．1± 二．解答题1．30个人排成矩形，身高各不相同．把每列最矮的人选出，这些人中最高的设为a ；把每行最高的人选出，这些人中最矮的设为b ．（１）a 是否有可能比b 高？（２）a 和b 是否可能相等？1． 解：()1不可能① 若a 、b 为同一人，有a b =；② 若a 、b 在同一行、列，则均有a b ≤；③ 若a 、b 不在同一行、列，同如图1以5*6的矩形为例，记a 所在列与b 所在行相交的人为x 。