圆的面积专项练习题10

专项练习09：圆（计算题）【考点预览】圆周长的计算含圆的组合图形周长的计算圆面积的计算含圆的组合图形面积的计算【专项练习】圆周长的计算1．求下面各圆的周长(单位：cm)（1）（2）2．如下图所示，求半圆形的周长。

含圆的组合图形周长的计算3．计算如图图形的周长。

4．求下图阴影部分的周长。

(单位：厘米)5．求下面操场的周长。

6．求下面图形的周长。

(单位：厘米)7．求下图阴影部分的周长（单位：厘米）8．求阴影部分的周长。

（单位：cm）9．计算如图中阴影部分的周长。

（1）（2）圆面积的计算10．求出下面各圆的面积。

（1）（2）含圆的组合图形面积的计算11．下面这个运动场的两端是半圆形，中间是长方形，请计算出运动场的面积。

12．求阴影部分的面积（单位：cm）。

13．如下图，圆形模板中减掉一个正方形，圆的直径为8厘米，求图中阴影部分面积。

14．如图，AB=10厘米，求阴影部分的周长和面积。

15．求下面图形阴影部分的周长和面积。

16．计算如图图形涂色部分的面积。

17．计算阴影部分的面积。

（单位：厘米）18．计算右面图形阴影部分的面积。

19．计算下图中阴影部分的面积。

20．求下图中阴影部分的面积。

21．求出下面图形中的阴影部分的面积。

22．求阴影部分的面积。

(单位：cm，π取3.14)23．如下图，正方形的边长是4cm，四个同样大小圆的圆心分别是正方形的四个顶点，求阴影部分的面积。

参考答案1．（1）解：2×3.14×3.2=20.096(cm) （2）解：9×3.14=28.26(cm)2．解：3.14×10÷2+10=3.14×5+10=15.7+10=25.7（cm）答：半圆的周长是25.7厘米。

3．解：2×6×3.14＝12×3.14＝37.68（厘米）答：它的周长是37.68厘米。

4．解：4×3.14÷2=12.56÷2=6.28（厘米）8×3.14÷2=25.12÷2=12.56（厘米）（4+8）×3.14÷2=37.68÷2=18.84（厘米）6.28+12.56+18.84=37.68（厘米）5．解：64×3.14+100×2=200.96+200=400.96（m）答：操场的周长是400.96米。

六年级数学上册《圆的面积周长》填空题专项练习1、围成圆的曲线的长叫做圆的（）。

2、测量圆的周长的方法有直接测量法、（）、（）等；这些方法都有一定的（），而且测得的数据也有一定的误差。

3、圆的（周长）与（）的比值是一个固定的数，叫做（），用字母（）表示，在实际问题中一般取近似值，约等于（）。

4、半圆的周长指的是圆的周长的（）加上（）条直径或2条（）。

5、已知圆的（）或（），可以直接套用公式求周长。

6、圆的周长的计算公式：C=（）和C=（）。

7、半圆的周长的计算公式：C半圆=（）或C半圆=（）。

8、圆的半径扩大到原来的三倍，直径就扩大到原来的（）倍，周长就扩大到原来的（）倍。

9、圆周率是一个（）。

10、圆的直径是10cm，该圆的周长是（）cm。

11、如果用S表示圆的面积，那么圆的面积计算公式是S=（）。

12、要求圆的面积，最直接的条件是圆的（）。

13、已知圆的直径或周长求圆的面积，要先计算出圆的（），再代入公式（）计算圆的面积。

14、以同一点为圆心画两个（）不相等的圆，两圆之间的部分叫（）。

15、已知外圆与内圆的半径，可直接套用公式S环=（）或S环=（）计算圆环的面积。

16、如果小圆的直径等于大圆的半径，那么小圆周长与大圆周长的比是（）：（），小圆的面积是大圆面积的（）。

17、用一根长12.56cm的铁丝，围成一个圆。

圆的面积是（）cm2。

18、一个圆的直径扩大3倍，其周长扩大（）倍，其面积扩大）倍。

19、正方形的面积S=（），圆的面积S=（）。

20、“外方内圆”是指在正方形内画一个（），这个图形的（）等于正方形的边长。

21、“外圆内方”是指在圆内画一个最大的（），这个图形的（）的长度等于圆的直径。

22、“外方内圆”时，正方形和圆之间部分的面积是（）。

23、“外圆内方”时，正方形与圆之间部分的面积是（）。

24、在一张长为3米，宽为2米的长方形铁板上割下一个最大的圆，剩下的面积是（）平方米。

25、在一个边长为4米的纸板上剪下一个最大的圆，剩下的纸板的面积是（）平方米。

圆的专项练习题一、选择题（每题3分，共30分）1. 圆的周长公式是（）。

A. C = πrB. C = 2πrC. C = 4πrD. C = πd2. 半径为5厘米的圆的周长是（）厘米。

A. 31.4B. 15.7C. 62.8D. 94.23. 圆的面积公式是（）。

A. S = πr²B. S = 2πrC. S = πrD. S = πd²4. 半径为3厘米的圆的面积是（）平方厘米。

A. 9πB. 18πC. 28.26D. 56.525. 一个扇形的半径为4厘米，圆心角为30°，其面积是（）平方厘米。

A. 2πB. 4πC. 6πD. 8π6. 圆的直径是半径的（）倍。

A. 1B. 2C. 3D. 47. 圆的内接四边形的对角线（）。

A. 互相垂直B. 互相平分C. 相等D. 互相垂直且相等8. 圆的切线在切点处与半径（）。

A. 垂直B. 平行C. 重合D. 相交9. 圆的外切四边形的对边（）。

A. 相等B. 互相垂直C. 平行D. 互相垂直且相等10. 圆的弧长公式是（）。

A. L = rθB. L = πrθC. L = 2πrθD. L = πr/θ二、填空题（每题2分，共20分）11. 圆的周长是半径的________倍。

12. 如果圆的周长为40π厘米，那么它的半径是________厘米。

13. 一个圆的直径为10厘米，它的面积是________平方厘米。

14. 圆的内接正六边形的边长等于圆的________。

15. 圆的内接正三角形的边长是半径的________倍。

16. 圆的外切正六边形的边长等于圆的________。

17. 圆的外接正三角形的边长是半径的________倍。

18. 圆的切线与圆相切于一点，这一点叫做圆的________。

19. 圆的内切圆与外接圆的半径之和等于________。

20. 圆的内切正多边形的边数越多，其形状越接近于________。

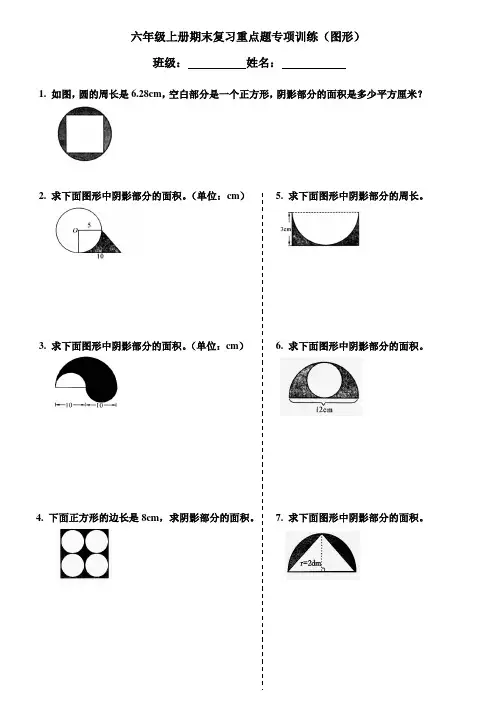
六年级上册期末复习重点题专项训练（图形）
班级：姓名：
1. 如图，圆的周长是6.28cm，空白部分是一个正方形，阴影部分的面积是多少平方厘米？
2. 求下面图形中阴影部分的面积。

（单位：cm） 5. 求下面图形中阴影部分的周长。

3. 求下面图形中阴影部分的面积。

（单位：cm）
6. 求下面图形中阴影部分的面积。

4. 下面正方形的边长是8cm，求阴影部分的面积。

7. 求下面图形中阴影部分的面积。

8. 求下面图形中阴影部分的面积。

9. 下面中阴影部分的面积是6平方厘米，
求圆的面积。

10. 求下面图形中阴影部分的面积。

11. 求下面图形中阴影部分的周长
或面积。

（单位：cm）12. 求下面图形中阴影部分的面积。

13. 求下面图形中阴影部分的面积。

14. 求下面图形中阴影部分的面积。

（单位：cm）
15. 求下面图形中阴影部分的面积。

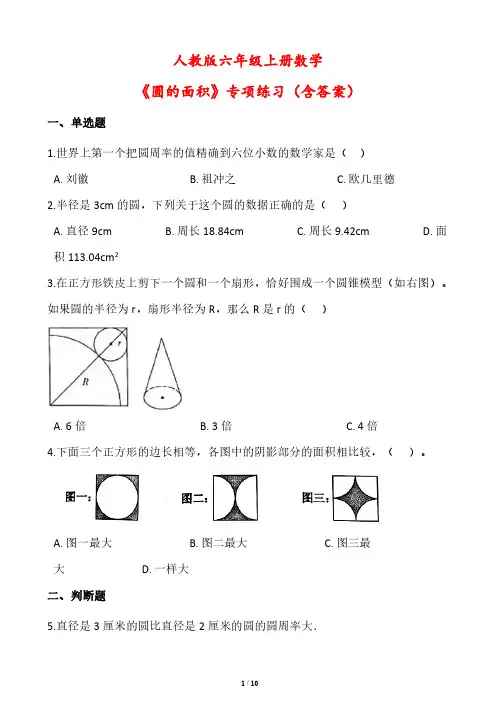
人教版六年级上册数学《圆的面积》专项练习（含答案）一、单选题1.世界上第一个把圆周率的值精确到六位小数的数学家是（）A. 刘徽B. 祖冲之C. 欧几里德2.半径是3cm的圆，下列关于这个圆的数据正确的是（）A. 直径9cmB. 周长18.84cmC. 周长9.42cmD. 面积113.04cm23.在正方形铁皮上剪下一个圆和一个扇形，恰好围成一个圆锥模型（如右图）。

如果圆的半径为r，扇形半径为R，那么R是r的（）A. 6倍B. 3倍C. 4倍4.下面三个正方形的边长相等，各图中的阴影部分的面积相比较，（）。

A. 图一最大B. 图二最大C. 图三最大 D. 一样大二、判断题5.直径是3厘米的圆比直径是2厘米的圆的圆周率大．6.一个圆的周长是它直径的π倍。

7.当圆的半径是2 cm时，它的周长和面积相等。

8.圆周长是直径的3.14倍．三、填空题9.圆的公式C=________=________，S＝________10.画一个直径是5厘米的圆，圆规两脚之间的距离是________厘米。

如果要画一个周长是12.56厘米的圆，圆规两脚之间的距离应该是________厘米，这个圆的面积是________平方厘米。

11.如图，把一个圆平均分成16份，剪开后拼成一个近似三角形，已知三角形的周长大约是19.14厘米，则圆的面积是________平方厘米。

12.在长8厘米，宽6厘米的长方形里面画一个最大的圆，圆的周长是________厘米，面积是________平方厘米。

13.把一个圆形纸片分成若干等份，然后拼成近似的长方形，量出长方形的长是15.7厘米，这个圆形纸片的面积大约是________。

四、解答题14.求下图阴影部分的面积。

（1）（2）（3）15.小明在纸上设计了一个图案（图中阴影部分），这个图案的面积是多少？五、应用题16.从一张正方形纸上剪下一个周长是18.84厘米的最大圆，求被剪掉的纸屑的面积。

参考答案一、单选题1.【答案】B【解析】【解答】世界上第一个把圆周率的值精确到六位小数的数学家是祖冲之。

六年级数学上册典型例题系列之第五单元圆：求阴影部分的面积专项练习（解析版）专项练习一：S整体-S空白=S阴影1.求图中阴影部分的面积（单位：厘米）。

解析：图一：S阴影=S半圆-S三角形半径：10÷2=5（cm）3.14×52÷2-5×5÷2=39.25-12.5=26.75（平方厘米）图二：S阴影=S梯形-S扇形（8+4）×4÷2-3.14×42÷4=24-12.56=11.44（平方厘米）图三：S阴影=S梯形-S半圆（6+10）×3÷2-3.14×32÷2=24-14.13=9.87（平方厘米）2.求图中阴影部分的面积（单位：厘米）。

解析：S阴影=S正方形-S圆4×4-3.14×22=3.44（平方厘米）3.下图中，正方形的边长是2厘米，四个圆的半径都是1厘米，圆心分别是正方形的四个顶点。

求出阴影部分的面积。

解析：S阴影=S正方形-S圆2×2-3.14×12=0.86（平方厘米）4.如图，正方形ABCD的对角线AC=2厘米，扇形ACB是以AC为直径的半圆，扇形DAC是以D为圆心，AD为半径的圆的一部分，求阴影部分的面积。

解析：S阴影=S扇形+S半圆-S正方形S半圆：3.14×（2÷2）2÷2=1.57（平方厘米）S扇形：3.14×2÷4=1.57（平方厘米）S正方形：2×2÷2=2（平方厘米）S阴影：1.57+1.57-2=1.14（平方厘米）专项练习二：割补法1.求图中阴影部分的面积（单位：厘米）。

解析：8×4÷2=26（平方厘米）2.如图，大正方形的边长是4cm，求图中阴影部分的面积（单位：厘米）。

解析：4×2=8（平方厘米）3.如图，正方形边长为2厘米，求阴影部分的面积。

五年级圆的周长及面积专项练习题一. 填空题1.圆中最长的线段是6厘米,这个圆的周长是（）厘米。

2.画一个周长为37.68厘米的圆，圆规两脚间的距离应是（）。

3.一个圆的半径扩大2倍，直径扩大（）倍，周长扩大（）倍。

4.一个圆的周长为12.56厘米，将它切成两个半圆后，每个半圆的周长为（）厘米。

5.一只大挂钟的时针长60厘米，分针长80厘米，一天内这只大挂钟分针尖端经过路程总长（）米。

6.用面积为9平方分米的正方形铁皮，剪成一个面积最大的圆形铁片，铁片的周长为（）分米。

7.把一个圆分割成两个相等的半圆后，它的周长增加了6厘米，原来这个圆的面积是（）。

8.在一张长60厘米、宽40厘米的长方形纸片中，最多能剪（）个直径为4厘米的圆。

9.两个圆的半径之和是6厘米，已知大圆周长是25.12厘米，小圆的周长是（）厘米。

10.在一个长10厘米，宽5厘米的长方形里，画一个最大的圆，这个圆的半径是（）分米。

11.圆的半径从10厘米减少到8厘米，周长减少（）厘米。

12.一个圆的周长、直径、半径的和是18.56厘米，这个圆的半径是（）厘米。

13.一根电线长94.2厘米,用它围成一个正方形,边长是(),用它围成一个等边三角形,边长是( ),用它围一个圆，半径是（）。

14.把一个圆分成32等份，然后剪开拼成一个近似的长方形。

这个长方形的长相当于（），长方形的宽就是圆的（）。

因为长方形的面积是（），所以圆的面积是（）。

15.一个半圆的直径是2分米，它的周长是（），面积是（）。

16.甲圆半径是乙圆半径的3倍，甲圆的周长是乙圆周长的（）倍，甲圆面积是乙圆面积的（）倍。

二. 操作题。

如图所示，已知正方形的边长是3厘米，求阴影部分周长。

三. 应用题。

17.一个圆形花圃，直径为12米，在它的周围沿外侧铺一条2米宽的小路，在小路的外侧围上篱笆，篱笆有多长？18.一个直径为24米的花坛周围有4米宽的路，在这条路的两旁按间隔1.57米栽一棵柏树，共可栽柏树多少棵？19.一个圆形游乐场的周长是62.8米，后半径减少1米，周长减少多少米？20.已知半圆的半径是5米，求这个半圆的周长？21.用塑料绳把四个酒瓶捆三圈,(接头处忽略不计),已知每个瓶底直径是6厘米,至少需要多少厘米的塑料绳?22.一个圆形的铁环，外直径是40厘米，内直径是20厘米，做这样一个铁环需要用多大的铁皮？23.一个圆形花圃直径8米，用四分之三种兰花，兰花的种植面积是多少？24.在一张周长为4厘米的正方形硬纸板上，剪一个最大的圆，剩下部分的面积是多少平方厘米？25.用两根长12.56厘米的铁丝分别围成一个正方形和一个圆，哪个面积大？大多少？26.一个水缸的缸口是一个圆形，直径是0.75米。

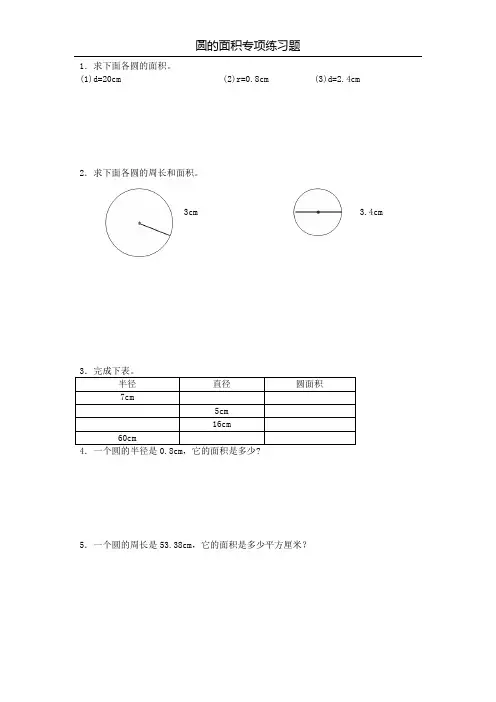
(1)d=20cm (2)r=0.8cm (3)d=2.4cm2．求下面各圆的周长和面积。

3cm 3.4cm半径直径圆面积7cm5cm16cm60cm5．一个圆的周长是53.38cm，它的面积是多少平方厘米？(1)d=4cm (2)r=1.6cm (3)d=0.8cm2．求下面各圆的周长和面积。

15cm 1.4cm半径直径圆面积4cm8cm14cm40cm5．一个圆的周长是78.5cm，它的面积是多少平方厘米？(1)d=20cm (2)r=0.6cm (3)r=3.6cm2．求下面各圆的周长和面积。

10cm 5.2cm半径直径圆面积4cm3cm14cm10cm5．一个圆的周长是53.38cm，它的面积是多少平方厘米？(1)r=16cm (2)d=1.2cm (3)d=3.2cm2．求下面各圆的周长和面积。

10cm 1.4cm半径直径圆面积7cm7cm8cm10cm5．一个圆的周长是37.68cm，它的面积是多少平方厘米？(1)d=14cm (2)d=3.4cm (3)r=1.6cm2．求下面各圆的周长和面积。

11cm 4.4cm半径直径圆面积7cm5cm16cm80cm5．一个圆的周长是72.22cm，它的面积是多少平方厘米？(1)r=16cm (2)d=2.2cm (3)d=3.2cm2．求下面各圆的周长和面积。

5cm 5.2cm半径直径圆面积6cm7cm16cm20cm5．一个圆的周长是50.24cm，它的面积是多少平方厘米？(1)r=20cm (2)r=1.4cm (3)d=0.4cm2．求下面各圆的周长和面积。

11cm 5cm半径直径圆面积2cm6cm4cm10cm5．一个圆的周长是65.94cm，它的面积是多少平方厘米？(1)r=4cm (2)r=1cm (3)r=1.2cm2．求下面各圆的周长和面积。

12cm 2.6cm半径直径圆面积7cm8cm16cm60cm5．一个圆的周长是9.42cm，它的面积是多少平方厘米？。

圆的面积专项练习1、右图中各个圆的面积都是 12 平方厘米，求阴影部分的面积之和是多少？2、一个圆形的养鱼池的周长是 62.8 米，如果每平方米投放鱼苗 15 尾，那么这个养鱼池一共要投放鱼苗多少尾？3、用一块 10 米长的席子围成一个底面是圆形的粮囤的底面，已知两头相接的重叠处占去 0.58 米，求这个粮囤的占地面积。

4、如图，一个圆形环岛的直径是 50m，中间是一个直径为 10m的圆形画坛，其他地方是草坪。

草坪的占地面积是多少？5、一个长方形和一个圆的周长相等，已知长方形的长是 10 厘米，宽是 5.7 厘米。

圆的面积是多少？6、通过实验发现：圆的面积是正方形面积的（）倍（1）正方形的面积是 20 平方厘米，那么圆的面积是多少？（2）圆的面积是 7.85 平方米，那么正方形的面积是多少？7、看图计算。

（1）左图中的两个阴影部分的面积相等，求 AB的长。

（2）左图中圆的半径是 3 厘米，求阴影部分的面积。

9、梯形面积是 51平方厘米，求图中阴影影部分的面积。

（单位：厘米）10、如图，在一个直径 4 分米的半圆形钢板上剪取一个最大的直角三角形。

这个三角形的面积是半圆面积的几分之几？11、将圆平均分成若干个小扇形，剪拼成一个近似的长方形（如右图）。

（1）如果长方形的长是 6.28厘米，圆的面积是多少？（2）如果圆的半径是 10 厘米，阴影部分的周长和面积分别是多少？13、有一只直径为 60 厘米的油桶从墙脚的一边滚到另一边，仓库的宽是 10.02 米，需要滚多少圈？13、下左图中，直角三角形 AOB的面积是 12 平方厘米，那么圆的面积是多少平方厘米？14、上右图中，半圆中三角形 ABO的面积 (S1)是 11 平方厘米， O为圆心，半径长 5 厘米，求阴影部分的面积。

完整版)北师大版六年级上册数学圆的面积专项练习题一、填空题。

1、把一个圆分成若干等份，剪开拼成一个近似的长方形。

这个长方形的长相当于（圆的直径），长方形的宽就是圆的（半径）。

因为长方形的面积是（圆的面积），所以圆的面积是（长方形面积）。

2、圆的直径是6厘米，它的周长是（18π）厘米，面积是（9π）平方厘米。

3、圆的周长是25.12分米，它的面积是（50.24π）平方厘米。

4、甲圆半径是乙圆半径的3倍，甲圆的周长是乙圆周长的（3倍），甲圆面积是乙圆面积的（9倍）。

5、一个圆的半径是8厘米，这个圆的面积是（64π）平方厘米。

6、周长相等的长方形、正方形、圆，（圆）面积最大。

7、圆的半径由6厘米增加到9厘米，圆的面积增加了（45π）平方厘米。

8、要在一个边长为10厘米的正方形纸板里剪出一个最大的圆，剩下的面积是（100-25π）平方厘米。

9、要在底面半径是12厘米的圆柱形水桶外面打上一个铁丝箍，接头部分是8厘米，需用铁丝（24π）厘米。

10、用圆规画一个圆，如果圆规两脚之间的距离是7厘米，画出的这个圆的周长是（14π）厘米，这个圆的面积是（49π）平方厘米。

11、圆的半径扩大3倍，它的直径扩大（6倍），周长扩大（3倍），面积就扩大（9倍）。

12、用长12.56厘米的铁丝分别围成一个正方形、圆、长方形，（圆）的面积最大。

13、一个半圆的直径是8厘米，这个半圆的面积是（16π）平方厘米。

14、一个正方形的边长是6厘米，在这个正方形里面画一个最大的圆，圆的面积是（9π）平方厘米。

15、一根铁丝可围成边长是3.14厘米的正方形，如果用这根铁丝围成一个圆，圆的半径是（1.57）厘米，面积是（7.77π）平方厘米。

16、两个半径不同的同心圆，内半径是3厘米，外直径是8厘米，圆环的面积是（46.24π）平方厘米。

17、一个圆的半径是2CM，它的周长是（4π）CM，面积是（4π）CM2.18、用5米长的绳子将一只羊拴在一根木桩上，这只羊的最大活动面积是（19.63π）平方米。

初三数学圆专项练习题大全圆是数学中一个重要的几何概念，它在几何题中经常出现。

为了帮助初三学生更好地掌握圆的知识，以下是一份初三数学圆专项练习题的大全，包括了常见的圆的性质、弧与弦的关系、切线与割线等内容。

希望同学们通过这些练习题的训练，能够熟练掌握圆的相关知识，并能灵活运用于解题中。

1. 圆的面积计算题(1) 已知圆的半径为r，求圆的面积。

(2) 已知圆的直径为d，求圆的面积。

2. 圆的周长计算题(1) 已知圆的半径为r，求圆的周长。

(2) 已知圆的直径为d，求圆的周长。

3. 相关性质题(1) 在一个圆内，连接圆心和圆上一点A，再连接另一点B在圆上，证明线段AB是圆的半径。

(2) 若两圆相交于点A和点B，那么点A、点B与两圆心连线的关系是什么？(3) 圆的切线与半径的关系是什么？(4) 圆的割线与半径的关系是什么？4. 圆的切线与弦的关系题(1) 若AB是圆的切线，C是弦上一点，证明AB与直径AC的夹角等于角ACB。

(2) 若AD是圆的直径，B是圆上一点，证明ACB是直角。

5. 多边形与圆的关系题(1) 若一个正多边形的每个顶点均位于同一个圆上，那么这个正多边形的内角和是多少度？(2) 若一个正多边形的内角和等于360度，那么这个正多边形的每个顶点都位于同一个圆上吗？6. 圆的切线长度计算题(1) 已知切点A到圆心的距离为r，切线段AB的长度为x，求x的值。

7. 圆的弦长计算题(1) 已知弦CD的长度为x，求弦AB的长度。

8. 圆的切线长与切点到圆心距离关系题(1) 切线段AB长为12，切点到圆心的距离为5，求切点到圆的切线的长度。

以上是一部分初三数学圆专项练习题的大全，希望同学们能够认真训练，掌握圆的相关性质和计算方法。

通过不断的练习和巩固，相信你们一定能够在数学中取得更大的进步！。

圆的专项练习题一、选择题1. 圆的周长公式是（）。

A. C = πdB. C = 2πrC. C = πrD. C = 2πd2. 圆的面积公式是（）。

A. S = πr²B. S = 2πrC. S = πdD. S = πd²3. 半径为5厘米的圆的周长是（）厘米。

A. 31.4B. 15.7C. 62.8D. 3144. 半径为3厘米的圆的面积是（）平方厘米。

A. 28.26B. 9C. 4.5D. 285. 圆的直径是半径的（）倍。

A. 2B. 1/2C. 1/3D. 3二、填空题6. 半径为2厘米的圆的周长是________厘米。

7. 半径为4厘米的圆的面积是________平方厘米。

8. 如果一个圆的周长是31.4厘米，那么它的半径是________厘米。

9. 一个圆的直径是8厘米，那么它的半径是________厘米。

10. 如果一个圆的面积是78.5平方厘米，那么它的半径是________厘米。

三、计算题11. 一个圆形花坛的直径是20米，求这个花坛的周长和面积。

12. 一个圆形的钟表的半径是10厘米，求这个钟表的周长和面积。

13. 一个圆形水池的半径是15米，如果沿着水池的边缘铺设一条1米宽的小路，求这条小路的面积。

四、应用题14. 一个圆形的花园，半径为10米，现在要在花园周围铺设一条宽2米的环形小路，求这条小路的面积。

15. 一个圆形的水池，半径为5米，现在要在水池的中心建造一个圆形的喷泉，喷泉的半径为2米，求喷泉占据的面积。

五、解答题16. 某工厂需要制作一个圆形的金属盖子，直径为1米，求这个盖子的周长和面积。

17. 一个圆形的花坛，半径为15米，现在要在花坛的周围铺设一条宽1米的环形小路，求这条小路的面积。

18. 一个圆形的操场，半径为30米，如果沿着操场的边缘铺设一条宽5米的跑道，求这条跑道的面积。

六、证明题19. 证明：在一个圆中，任意两个直径所夹的圆心角相等。

北师大版六年级数学上册同步提优常考题专项训练第一单元《圆》第4课时《圆的面积》一、单选题1.如图，阴影部分占整个图形的（）A. B.【答案】B【解析】【解答】，如图，阴影部分占整个图形的。

故答案为：B。

【分析】观察图可知，通过剪拼的方法，可以将两部分阴影部分组合成一个正方形，图中正方形是长方形面积的一半，据此解答。

2.在解决下面问题的过程中，没有运用转化策略的是（）。

A. 计算异分母分数加减法时，先通分。

B. 推导圆面积计算公式时，把圆剪拼成近似长方形。

C. 用竖式计算整数加减法。

【答案】C【解析】【解答】解：A：计算异分母分数加减法时，就是把异分母分数转化成同分母分数；B：把圆剪拼成近似长方形，就是把圆转化成长方形；C：用竖式计算整数加减法，没有运用转化策略。

故答案为：C。

【分析】转化的策略就是把新知识转化成原来学过的知识来解决问题。

3.如图中，三角形ABC是等腰直角三角形，图中阴影部分和空白部分的面积相比较，（）A. 阴影部分的面积大B. 空白部分的面积大C. 面积一样大D. 无法判断【答案】B【解析】【解答】采用移补的办法，将三角形外面的阴影部分移到三角形内部变成两个三角形的面积比较，由于这个三角形是等腰直角三角形，移补之后阴影部分的面积为三角形ABC的一半，而空白部分面积大于三角形ABC的一半，故答案为：B【分析】采用移补的方法将这两个不规范的图形变成规范的图形，如图：4.数学课上，同学们把一个圆形纸片沿它的半径平均分成若干份以后剪开，用它们拼成一个面积不变的近似的长方形．这个长方形的周长是16.56厘米，这个圆形纸片的面积是（）平方厘米．A. 12.56B. 16.56C. 8.28【答案】A【解析】【解答】解：设圆形纸片的半径是r厘米。

3.14×r×2+2r=16.568.28r=16.56r=16.56÷8.28r=2圆面积：3.14×22=12.56（平方厘米）。

2023-2024学年六年级数学上册典型例题系列第五单元：圆环面积的实际应用专项练习1．一个花坛，半径5米，在它周围有一条宽2米的环形鹅卵石小路，小路的面积是多少平方米？【答案】75.36平方米【分析】由题意可知，小路是环形，小圆的半径为5米，大圆的半径＝小圆的半径＋环宽，最后利用“22S R r 环形 ”求出小路的面积，据此解答。

【详解】5＋2＝7（米）3.14×（72－52）＝3.14×（49－25）＝3.14×24＝75.36（平方米）答：小路的面积是75.36平方米。

【点睛】本题主要考查环形面积公式的应用，熟记公式是解答题目的关键。

2．在一个半径为8米的圆形空地中央修建了一个半径为2米的圆形喷泉（如下图），剩下的部分栽花（阴影部分），栽花的面积是多少平方米？（π取3.14）【答案】188.4平方米【分析】栽花的部分是个圆环，根据S 圆环＝π（R 2－r 2），列式解答即可。

【详解】3.14×（82－22）＝3.14×（64－4）＝3.14×60＝188.4（平方米）答：栽花的面积是188.4平方米。

【点睛】关键是掌握并灵活运用圆环面积公式。

3．一座电视塔的圆形塔底的半径是30米，现在要在它的周围种上10米宽的环形草坪（如图），草坪的面积是多少平方米？【答案】2198平方米【分析】由图可知，大圆半径为30＋10＝40米，小圆半径为30米，利用“22S R r 环形 ”求出环形草坪的面积，据此解答。

【详解】30＋10＝40（米）3.14×（402－302）＝3.14×（1600－900）＝3.14×700＝2198（平方米）答：草坪的面积是2198平方米。

【点睛】熟练掌握环形的面积计算公式是解答题目的关键。

4．公园有一个圆形花坛，量得它的周长是50.24米，要在花坛的四周铺一条宽1米的小路，这条小路的面积是多少平方米？另在小路的外围围一圈栏杆，需要栏杆多少米？【答案】53.38平方米；56.52米【分析】小路的形状是个圆环，根据“2r C π=÷÷”求出花坛的半径，即内圆半径，内圆半径＋路宽＝外圆半径，根据“22S R r 环形π”求出小路的面积，最后利用“C 2r π=圆形”求出栏杆的长度，据此解答。

五年级专项练习圆的面积提优（较难）【知识梳理】1. 封闭曲线圆所围成的平面的大小叫做圆的面积。

如果用S 表示圆的面积，那么2r S π=。

2. 弧与扇形：圆上两点之间的部分叫做弧，一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。

顶点在圆心的角叫做圆心角。

用扇S 表示扇形面积，则2360r n S π⨯=扇（n 为扇形圆心角的度数）； 3. 环形：）（环形22-r R S π=（R 为外圆半径，r 为内圆半径）【典型例题】例1：求下图中阴影部分的面积。

（单位：厘米）例2：求右图中阴影部分的面积。

（单位：厘米）例3：如右下图，正方形的面积是8平方厘米，求圆的面积。

例4.如右下图，已知阴影部分的面积是15平方厘米，求环形的面积。

【竞赛探究】例1：三角形ABC是直角三角形，AB是圆的直径，并且AB=20厘米。

阴影1比阴影2大18平方厘米，求BC的长度。

【举一反三】1.求右下图中阴影部分的面积。

（单位：厘米）2.求右下图阴影部分的面积。

（单位：厘米）3.如右下图，三角形ABC是等腰直角三角形，D是半圆周上的中点，BC是半圆的直径，且AB=BC=10，求阴影部分的面积。

一、现代文阅读1．现代文阅读阅读下面文字，完成下列小题。

话说筋骨梅万林①所谓筋骨，包括筋肉和骨头两个部分。

一个人如果没有筋骨，或者筋骨软弱，即使长再多的肌肉，也终究寸步难行，甚至连独立支撑也很勉强。

如果某人被骂作没有骨头，那便是他的奇耻大辱了。

②因此，筋骨之重要，不仅关乎一个人的生存与否，而且更关乎一个人的生存要义。

所以，在古人眼里，一个能担当大义的人，摆在面前的第一道关口必是劳其筋骨。

这里，筋骨早已超出了身体本身的含义，而上升到了人生乃至境界的层面。

③对于一个艺术家而言，要创作出更多更优质的文艺作品，有筋骨必然是摆在谋篇布局之前的第一道关口。

古人云，言之无文，行而不远。

在我看来，这里的“文”，不仅指文采，而且更主要的还是指文章能否“载道”，而欲有所承载，离了筋骨是万万不能的。

求阴影部分的面积—圆的面积专项练习1．求下面图形阴影部分的面积。

（环形宽1m）2．求下图阴影部分的周长和面积。

3．求阴影部分的面积。

（单位：厘米）4．求下面各图形中阴影部分的面积。

5．求阴影部分的面积。

（单位：厘米）6．求出下面图形的面积（单位：厘米）。

7．求出下面图形阴影部分的周长和面积。

8．计算阴影部分的面积和周长。

（单位：厘米）9．计算下面图形阴影的面积。

10．求阴影部分的面积。

（单位：cm）11．求阴影面积。

（单位：厘米）12．求下图阴影部分的面积。

（单位：米）13．求阴影部分的面积。

14．求下面各图形阴影部分的面积。

（1）（2）15．求下图中阴影部分的面积。

16．求下图阴影部分的面积。

(单位：cm)17．求下图中阴影部分的周长和面积.18．求下列图形中阴影部分的面积．（单位：米）19．求阴影部分的面积．（单位：厘米）20．正方形边长8cm，求阴影部分面积．21．求下面图形中阴影部分的面积（单位：厘米）22．求下面图形中阴影部分的面积（单位：厘米）．23．计算下面图中阴影部分的面积．参考答案1．40.82平方米阴影部分圆环的面积S ＝π（R 2－r 2），其中r ＝6m ，R ＝6＋1＝7（米），代入数据计算即可。

6＋1＝7（米）；3.14×（72－62）＝3.14×13＝40.82（平方米）2．C ＝113.04cm ；S ＝113.04cm 2；C ＝50.82dm ；S ＝102.05dm 2（1）圆环的周长＝外圆周长＋内圆周长，根据圆的周长公式：=2C r π即可解答； （2）圆环的面积根据面积公式：()22=S R r π-即可解答；（3）半圆环面积＝外圆的一半弧长＋内圆的一半弧长＋外圆直径－内圆直径，根据圆的周长公式：=C d π即可解答；（4）求半圆环面积，先求出整个圆环面积，然后除以2即可解答。

（1）圆环周长：3.14×2×10＋3.14×2×8＝（10＋8）×3.14×2＝56.52×2＝113.04（cm）圆环面积：3.14×（102－82）＝3.14×36＝113.04（cm2）（2）半圆环的周长：（3.14×18÷2）＋（3.14×8÷2）＋（18－8）＝28.26＋12.56＋10＝50.82（dm）半圆环的面积：3.14×[（18÷2）2－（8÷2）2]÷2＝3.14×（92－42）÷2＝3.14×65÷2＝102.05（dm2）3．339.12平方厘米圆环面积＝π（R2－r2），据此解答。

六年级圆的面积20题专项练习学校:___________姓名：___________班级：___________考号：___________一、计算题1．如图，圆的周长是25.12厘米，圆的面积正好和长方形的面积相等，这个长方形的长是多少厘米？2．列式求如图阴影部分的面积。

3．求下面图形的周长。

（单位：厘米）4．求阴影面积。

5．如图，求它的周长和面积。

6．求阴影部分的周长和面积。

7．求下图中阴影部分的面积。

（π取3.14，单位：cm）8．求下图阴影部分的面积。

（单位：厘米）9．求下图阴影部分的面积。

（ 取3.14）（单位：厘米）10．如图所示，已知圆的周长是18.84厘米，0为圆心，平行四边形ABCD的面积为42平方厘米，线段DE∶EC＝1∶3。

求阴影部分的面积。

（π取3.14）11．计算下图阴影部分的面积。

12．看图计算阴影部分面积（单位：cm）（π取3.14）13．求阴影部分的面积（单位，厘米）14．计算下图阴影部分的面积。

15．求下图阴影部分的面积和周长。

（单位：米）16．如图，求阴影部分的面积。

（单位：厘米）17．一个长方形和一个半圆组成如图所示的图形，长方形长6厘米，宽4厘米，求这个图形的周长和面积。

18．已知直角三角形面积是12平方厘米，求阴影部分的面积。

19．三角形ABC 是等腰直角三角形，以BC 为直径，BC 中点O 为圆心画半圆，D 为半圆周的中点，连结AD ，已知10AB BC ==厘米，求阴影部分的面积。

20．求下图涂色部分的面积。

（单位：m ）本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

答案第1页，总1页 参考答案1．12.56厘米2．13.74平方厘米3．15.42厘米4．7.725．37.68厘米；56.52平方厘米6．周长：30.84cm ；面积：36cm ²7．2.28cm 28．6.88平方厘米9．1.14平方厘米10．634平方厘米 11．6.88平方分米12．7.72平方厘米13．13.5平方厘米14．2.28cm 215．面积343平方米；周长101.4米16．13.12平方厘米17．周长22.28厘米；面积17.72平方厘米 18．5.13平方厘米19．57.125平方厘米20．343m 2。

人教版六年级数学上册第五单元圆的面积专项卷一、仔细推敲，选一选。

(每小题3分，共15分)1．一个圆的周长和一个正方形的周长都是6.28分米，则圆的面积( )正方形的面积。

A．大于B．小于C．等于D．无法确定2．周长相等的正方形、长方形和圆，面积最大的是( )。

A．正方形B．长方形C．圆D．无法确定3．一个环形铁片如图，计算铁片的面积，列式正确的是( )。

A．3.14×[52＋(8÷2)2] B．3.14×[52－(8÷2)2]C．3.14×(8－5)2D．3.14×(8＋5)24．下面各图中，阴影部分面积相等的是( )。

A．只有①和②B．只有③和④C．都不相等D．①②③④5．下面说法正确的是( )。

①两个圆的面积相等，它们的周长也一定相等。

②圆的面积大于半圆形的面积。

③6个圆心角是60°的扇形，一定可以拼成一个圆。

④圆的半径扩大到原来的3倍，面积扩大到原来的9倍。

A．①和②B．②和③C．①和④D．③和④二、认真审题，填一填。

(每小题4分，共24分)1．一个圆的半径是10cm，它的周长是( )cm，它的面积是 ( )cm2。

2．一个扇形的圆心角是90°，它的面积是所在圆面积的( ) 。

3．把一个圆形纸片平均分成若干(偶数)份，剪开后可以拼成一个近似的长方形，拼成的图形的长相当于圆的( )，宽相当于圆的( )。

4．一个圆的周长是25.12 cm，它的半径是( )cm，面积是 ( )cm2。

5．在一张长3厘米、宽2厘米的长方形纸片上剪去一个最大的圆，剩下的面积是( )平方厘米。

6．一个圆形挂钟钟面上的分针长6cm，分针从12走到6，扫过的面积是( )cm2；如果分针从12走到1，那么扫过的面积是( )cm2。

三、细心的你，算一算。

(共28分)1．求下面图形的周长和面积。

(每小题5分，共10分)(1)(2)2．求下面各图形阴影部分的面积。

圆的面积专项练习60题（有答案）1．求图中半圆的面积．2．正方形的边长为6cm．3．小东量得一棵树的树干最粗处的周长是125.6cm，该树干最粗处横截面的面积是多少？4．如图，以圆的半径为边长的正方形的面积是25平方厘米，求圆的面积．5．小明每分62.8米的速度绕一个圆形游泳池游一周，恰好用了5分钟．这个游泳池的面积是多少平方米？6．钟表有分针长12厘米，经过30分后，分针针尖走过的路程是多少厘米？分针针尖所扫过的面积是多少平方厘米？7．如图，长方形与圆的面积相等，圆的周长是12.56cm，阴影部分的面积是多少平方厘米？（π取3.14）8．一小区有一直径是8米的圆形花坛，现在沿着它的外沿修一条宽2米的小路，小路的面积是多少平方米？9．在一张边长为10厘米的正方形纸上，画一个最大的圆并剪下来．圆的面积是多少平方厘米？剩余面积是多少？10．一个车轮滚动10圈前进了62.8米，它的面积是多少？11．在一片草地上拴着一头牛．若拴牛的绳子长4米（不含打结部分）．这头牛最多可以吃到多少平方米的草？12．求环形的面积．（单位：分米）13．在一个正方形内画一个最大的圆，已知正方形的面积是20平方厘米，圆的面积是多少？14．一块环形铁皮的外直径是12厘米，内直径是外直径的三分之一，这块铁皮的面积是多少？15．一个农民新开挖一个圆形水池，水池的周长是50.24米，求水池占地的面积是多少平方米？16．学校围绕一个半径7米的圆形花坛铺一条1米宽的石子小路，求小路面积为多少平方米？如果每平方米投资150元，求修这条小路要投资多少元？17．在一个直径是16米的圆心花坛周围，有一条宽为2米的小路围绕，小路的面积是多少平方米？18．在面积为20平方厘米的正方形内画一个最大的圆，圆的面积是多少？19．一个圆形花圃的周长是50.24米，在它里面留出的面积种菊花．菊花的占地面积是多少？20．一个圆形游乐场的周长是62.8米，扩建时，半径增加了1米，面积增加了多少平方米？21．一个圆形喷水池的周长是62.8m，这个喷水池的占地面积是多少平方米？22．一个圆形花园的直径是6米，在它周围有一条宽l米的环形鹅卵石小路．这条小路的面积是多少平方米？23．台钟的时针长4厘米，分针长5厘米，分别转动圈，它们所扫过的面积相差多少平方厘米？24．小圆周长为3.14分米，大圆周长是小圆周长的2倍，大圆面积是多少？25．在一个圆里画一个最大的正方形，已知正方形的面积是40平方厘米，圆的面积是多少？26．一个环形内圆半径是3米，外圆周长是37.68米，这个环形的面积是多少平方米？27．将一个圆沿一条直径剪成两部分，每一个部分的周长是41.12厘米，求这个圆的面积．28．在长1.8米、宽1.2米的纸板上，你能截出几个半径为30厘米的圆？并计算材料的利用率？29．现有一根长62.8米的绳子，要围成一块尽量大的土地，你认为怎么围，围成的是什么图形？面积是多少？30．有一个圆形花坛，直径是16m，在它的周围修建一条2m宽的小路．（圆周率取值3）（2）沿环形小路的边缘每隔5m装一盏灯，一共要安装多少盏灯？31．在一个直径为18米的圆形草地周围铺一条宽4米的环形道路，求这条环形路的面积是多少？32．一块正方形草地，边长是20米，在两个相对的角上各有一棵树，树上各拴一只羊，拴羊的绳长与草地边长相等，两只羊都能吃到草的草地面积是多少平方米？（提示：先根据题意画出图再解答）．33．一个圆和一个扇形的半径相等，已知圆的面积是30平方厘米，扇形的圆心角是36°．求扇形的面积．34．一个圆形花坛周长是31.4米，花坛中40%的土地种植月季花，种月季花的面积是多平方米？35．如下图，正方形的面积是2平方分米，求圆的面积．36．用席子围成一个地面周长是18.84米的圆柱形粮囤．这个粮囤占地面积有多大？37．一块圆形菜地，直径20米，现在要在菜地上覆盖一层塑料薄膜，至少需要薄膜多少平方米？如果每平方米薄膜价格0.5元，这些薄膜要花多少元？38．求下图阴影部分的周长和面积．39．在面积为20平方厘米的正方形内画一个最大的圆，圆的面积是多少？40．一个圆形花圃的周长是50.24米，在它里面留出的面积种菊花．菊花的占地面积是多少？41．台钟的时针长4厘米，分针长5厘米，分别转动圈，它们所扫过的面积相差多少平方厘米？42．在一个圆里画一个最大的正方形，已知正方形的面积是40平方厘米，圆的面积是多少？43．将一个圆沿一条直径剪成两部分，每一个部分的周长是41.12厘米，求这个圆的面积．44．一张长方形纸，正好可以剪两个同样大小的最大的圆，告诉你什么条件你就能求剩余纸的面积？45．一个长方形的长8厘米，宽4.56厘米，与这个长方形周长相等的圆的面积是多少？46．在一张正方形纸上剪四个相等的最大的圆，用这些圆片做手工材料，这张纸的利用率是多少？47．在长6cm，宽4cm的长方形中，画一个最大的半圆，求这个半圆的周长和面积．48．已知：圆与长方形面积相等，长方形长6.28米，求阴影部分面积．（π取3.14）49．一个圆形的水池，周长188.4米，现在要在周围加宽1米，加宽后的面积比原来面积增加了多少平方米？50．将一个边长是3.14米正方形变成一个圆形，围成圆形的面积是多少？51．一根绳子剪去后，还剩12.56分米，如果将剪去的绳子围成一个圆，这个圆的面积是多少平方分米？52．在一张长32厘米，宽24厘米的长方形纸片上能剪出多少个直径为4厘米的圆？剩下部分的面积是多少？53．图中阴影部分的面积是小圆面积的，是大圆面积的，已知阴影部分的面积是12平方厘米，求如图总面积．54．如图，以墙壁为一边，用竹篱笆围一个半圆形羊圈，已知篱笆总长是94.2米，这个羊圈的面积是多少平方米？55．一种重机枪的有效射程是1500米，如果它做72°的水平扫射，求它的控制面积是多少平方米？56．一个挂钟分针长5厘米，时针长4厘米，从6时走到18时，时针扫过的面积是平方厘米？57．把一个圆转化成一个近似的长方形，转化后的长方形的周长比圆多10厘米，求这个圆的面积是多少平方厘米？58．一张长方形纸片，长60厘米，宽40厘米．用这张纸剪下一个尽可能大的圆．这个圆的面积是多少平方厘米？剩下的面积是多少平方厘米？59．一根长50.24米的绳子，正好绕一棵树干8圈，树干横截面的面积是多少平方米？60．在一块正方形的地，边长20米，在它的中央有一个圆形花圃，直径是6米，在它的四周建一条最大的环形走道，环形走道的面积是多少平方米？如果每平方米的造价是250元，这条走道的造价是多少元？参考答案：1．3.14×（）2÷2，=3.14×9÷2，=14.13（平方厘米）．答：半圆的面积是14.13平方厘米．2．3.14×（6÷2）2，=3.14×9，=28.26（平方厘米）；答：圆的面积是28.26平方厘米．3．125.6÷3.14÷2=20（厘米），3.14×202，=3.14×400，=1256（平方厘米）；答：该树干最粗处横截面的面积是1256平方厘米．4．3.14×25=78.5（平方厘米）；答：圆的面积是78.5平方厘米5．62.8×5=314（米）；r=C÷2π，=314÷（2×3.14），=50（米）；S=πr2，=3.14×502，=7850（平方米）；答：这个游泳池的面积是7850平方米6．c=2πr，=2×3.14×12，=75.36（厘米），75.36÷2=37.68（厘米）；s=πr2，=3.14×122，=452.16（平方厘米），452.16÷2=226.08（平方厘米）；答：分针针尖走过的路程是37.68厘米．分针针尖所扫过的面积是226.08平方厘米．7．圆的半径为：12.56÷3.14÷2=2（厘米），圆的面积为：3.14×22=12.56（平方厘米），阴影部分的面积：12.56×（1﹣），=12.56×，=9.42（平方厘米）．答：阴影部分的面积是9.42平方厘米8．根据题干分析可得：3.14×（62﹣42），=3.14×（36﹣16），=3.14×20，=62.8（平方米），答：小路的面积是62.8平方米9．圆的面积：3.14×（10÷2）2，=3.14×25，=78.5（平方厘米）；答：这个圆的面积是78.5平方厘米．剩余面积为：10×10﹣78.5，=100﹣78.5，=21.5（平方厘米），答：圆的面积是78.5平方厘米，剩下的面积是21.5平方厘米10．车轮的半径为：62.8÷10÷3.14÷2，=6.28÷3.14÷2，=2÷2，=1（米），车轮的面积为：3.14×12=3.14（平方米），答：这个车轮的面积是3.14平方米11．3.14×42，=3.14×16，=50.24（平方米）；答：这头牛最多可以吃到50.24平方米的草12．3.14×82﹣3.14×52，=3.14×（64﹣25），=3.14×39，=122.46（平方分米），答：这个环形的面积是122.4613．设正方形的边长为a ，圆的半径为，则a2=20平方厘米，圆的面积=3.14×，=3.14×，=3.14×5，=15.7（平方厘米）；答：圆的面积是15.7平方厘米14．12÷3=4（厘米），22=3.14×32，=100.48（平方厘米）；答：这块铁皮的面积是100.48平方厘米15．已知C=50.24米，r=C÷2÷π=50.24÷2÷3.14=8（米）；S=πr2=3.14×82=3.14×64，=200.96（平方米）；答：这个圆形水池占地面积是200.96平方米16．内圆面积：3.14×72=153.86（平方米），外圆面积：3.14×（7+1）2=3.14×64=200.96（平方米），小路面积：200.96﹣153.86=47.1（平方米）．投资钱数：47.1×150=7065（元），答：这条小路的面积是47.1平方米，修这条小路要投，7065元17．16÷2=8（米），8+2=10（米），3.14×（102﹣82），=3.14×（100﹣64），=3.14×36，=113.04（平方米）．答：小路的面积是113.04平方米．18．设这个圆的半径为r厘米，则正方形的边长就是2r，根据正方形的面积是20平方厘米可得：2r×2r=20，整理可得：r2=5，所以圆的面积是：3.14×5=15.7（平方厘米），答：圆的面积是15.7平方厘米19．圆形花圃的半径：50.24÷3.14÷2=16÷2，=8（米），圆形花圃的面积是：3.14×82=3.14×64，=200.96（平方米），菊花的占地面积：200.96×=25.12（平方米）．答：菊花的占地面积是25.12平方米20．内圆半径：62.8÷3.14÷2=10（米）；增加的面积：3.14×[（10+1）2﹣102]=3.14×[121﹣100]=3.14×21=65.94（平方米）；答：面积增加了65.94平方米21．3.14×（62.8÷3.14÷2）2，=3.14×102，=314（平方米）；答：它的占地面积是314平方米．22．6÷2=3（米），3+1=4（米），所以小路的面积为：3.14×（42﹣32），=3.14×（16﹣9），=3.14×7，=21.98（平方米）；答：这条小路的面积是21.98平方米23．×3.14×（52﹣42），=×3.14×9，=7.065（平方厘米），答：相差7.065平方厘米．24．小圆的半径：3.14÷3.14÷2=0.5（分米）；大圆的半径：0.5×2=1（分米）；大圆的面积：3.14×12=3.14（平方分米）；答：大圆的面积是3.14平方分米25．设圆的半径为r，则正方形的面积：2r×r÷2×2=2r2，又因“正方形的面积是40平方厘米”，所以2r2=40平方厘米，r2=20平方厘米；圆的面积：πr2=3.14×20=62.8（平方厘米）；答：圆的面积是62.8平方厘米26．外圆的半径为：37.68÷3.14÷2=12÷2，=6（米），圆环的面积为：3.14×62﹣3.14×32=3.14×（36﹣9），=3.14×27，=84.78（平方米），答：这个环形的面积是84.78平方米27．41.12÷（3.14+2），=41.12÷5.14，=8（厘米）；3.14×82，=3.14×64，=200.96（平方厘米）．答：这个圆的面积是200.96平方厘米28．1.8米=180厘米，1.2米=120厘米．180÷（30×2）=3个，120÷（30×2）=2个，3×2=6个；圆的面积3.14×302×6=16956平方厘米，纸板的面积180×120=22600平方厘米，16956÷22600=78.5%；答：能截出6个半径为30厘米的圆；材料的利用率是78.5%29．围成圆的半径为：62.8÷3.14÷2=10（米），围成圆的面积为：3.14×102=314（平方米），答：把绳子围成圆形面积最大，面积是314平方米．30．（1）16÷2=8（米），8+2=10（米），3×（102﹣82），=3×（100﹣64），=3×36，=108（平方米）；答：这条小路的面积是108平方米．（2）3×10×2÷5，=60÷5，=12（盏）；答：一共要安装12盏灯31．18÷2=9（米），9+4=13（米），3.14×（132﹣92），=3.14×（169﹣81），=3.14×88，=276.32（平方米）；答：这条环形路的面积是276.32平方米32．（×3.14×202﹣×20×20）×2，=（314﹣200）×2，=114×2，=228（㎡）．答：两只羊都能吃到的草地面积是228㎡．33．30÷3.14=r2，，=，=3（平方厘米）；答：扇形的面积是3平方厘米34．圆形花坛的半径：31.4÷3.4÷2=5（米）；圆形花圃的面积：52×3.14，=25×3.14，=78.5（平方米）；种月季花的面积：78.5×40%=31.4（平方米），答：种月季花的面积是31.4平方米35．πr2=3.14×2=6.28（平方分米）；答：圆的面积是6.28平方分米36．18.84÷3.14÷2=3（米），3.14×32，=3.14×9，=28.26（平方米），答：这个粮囤占地面积是28.26平方米．37．（1）这层塑料薄膜的面积：3.14×（10÷2）2=78.5（平方米）；（2）这些薄膜要的钱数：0.5×78.5=39.25（元）．答：至少需要薄膜78.5平方米，这些薄膜要花39.25元38．大半圆的半径：（4+8）÷2=12÷2=6（分米）；阴影部分的面积：3.14×62÷2﹣3.14×（4÷2）2÷2﹣3.14×（8÷2）2÷2，=3.14×36÷2﹣3.14×4÷2﹣3.14×16÷2，=56.52﹣6.28﹣25.12，=25.12（平方分米）；阴影部分的周长：3.14×（4+8）÷2+3.14×4÷2+3.14×8÷2，=3.14×12÷2+6.28+12.56，=18.84+6.28+12.56，=37.68（分米）；答：阴影部分的周长是37.68分米，面积是25.12平方分米39．设这个圆的半径为r厘米，则正方形的边长就是2r，根据正方形的面积是20平方厘米可得：2r×2r=20，整理可得：r2=5，所以圆的面积是：3.14×5=15.7（平方厘米），答：圆的面积是15.7平方厘米40．圆形花圃的半径：50.24÷3.14÷2=16÷2，=8（米），圆形花圃的面积是：3.14×82=3.14×64，=200.96（平方米），菊花的占地面积：200.96×=25.12（平方米）．答：菊花的占地面积是25.12平方米41．×3.14×（52﹣42），=×3.14×9，=7.065（平方厘米），答：相差7.065平方厘米42．设圆的半径为r，则正方形的面积：2r×r÷2×2=2r2，又因“正方形的面积是40平方厘米”，所以2r2=40平方厘米，r2=20平方厘米；圆的面积：πr2=3.14×20=62.8（平方厘米）；答：圆的面积是62.8平方厘米13．41.12÷（3.14+2），=41.12÷5.14，=8（厘米）；3.14×82，=3.14×64，=200.96（平方厘米）．答：这个圆的面积是200.96平方厘米44．最大的圆是以这个长方形的宽为直径的圆，而剩下纸的面积=长方形的面积﹣两个圆的面积，所以只要知道这个长方形的长和宽就能求得剩余纸的面积45．2×（8+4.56）=25.12（厘米），25.12÷3.14÷2=4（厘米），3.14×42=3.14×16=50.24（平方厘米）．答：与这个长方形周长相等的圆的面积是50.24平方厘米46．设正方形纸的边长为a，圆半径=a，圆面积=π（a）2=πa2，正方形面积=a2，利用率=4×πa2÷a2，=0.785，=78.5%；答：这张纸的利用率是78.5%47．3.14×6÷2+6，=9.42+6，=15.42（厘米）；3.14×÷2，=3.14×9÷2，=14.13（平方厘米）；答：这个半圆的周长是15.42厘米，面积是14.13平方厘米．48．圆的半径是：6.28÷3.14=2（米），3.14×22×，=3.14×3，=9.42（平方米），答：阴影部分的面积是9.42平方厘米．49．188.4÷3.14÷2=30（米），3.14×（30+1）2﹣3.14×302，=3.14×961﹣314×900，=3017.54﹣2826，=191.54（平方米）．答：加宽后的面积比原来面积增加了191.54平方米．50．正方形的周长：3.14×4=12.56（米），圆的半径：12.56÷3.14÷2=2（米），圆的面积：3.14×22=12.56（平方米）；答：围成圆形的面积是12.56平方米51．圆的周长是：12.56÷（1﹣）×，=12.56÷×，=6.28（分米）；半径是：6.28÷3.14÷2=1（分米），面积是：3.14×12=3.14（平方分米）；答：这个圆的面积是3.14平方分米52．（32÷4）×（24÷4），=8×6，=48（个），32×24﹣3.14×（4÷2）2×48，=768﹣12.45×48，=768﹣602.88，=165.12（平方厘米），答：可以剪出48个这样的圆，剩下的面积是165.12平方厘米53．大圆的面积是为12÷=60（平方米），小圆的面积为12÷=30（平方厘米），60+30﹣12，=90﹣12，=78（平方厘米）．答：这幅图的总面积是78平方厘米．54．半圆形羊圈的半径为：94.2÷3.14=30（米），半圆形羊圈的面积为：3.14×302÷2=1413（平方米），答：这个羊圈的面积是1413平方米．55．×3.14×15002，=3.14×450000，=1413000（平方米）；答：它的控制面积是1413000平方米56．3.14×42，=3.14×16，=50.24（平方厘米），答：时针扫过的面积是50.24平方厘米．57．圆的半径是：10÷2=5（厘米），圆的面积是：3.14×52，=3.14×25，=78.5（平方厘米）．答：圆的面积是78.5平方厘米58．3.14×（40÷2）2，=3.14×400，=1256（平方厘米）；60×40﹣1256，=2400﹣1256，=1144（平方厘米）．答：这个圆的面积是1256平方厘米，剩下的面积是1144平方厘米．59．50.24÷8=6.28，6.28÷3.14÷2=1（米），3.14×12=3.14（平方米）；答：树干横截面的面积是3.14平方米．60．3.14×（20÷2）2﹣3.14×（6÷2）2，=3.14×100﹣3.14×9，=3.14×91，=285.74（平方米），285.74×250=71435（元），答：环形走道的面积是285.74平方米；这条走道的造价是71425元．11。

2011—2012学年上学期六年级数学导学案编号_5 使用时间_________编写人李卫华审核人________ 班级_____小组______姓名_______________【学习目标】1、掌握给出圆的半径求圆的面积的方法2、掌握给出圆的直径求圆的面积的方法3、掌握给出圆的周长求圆的面积的方法【预习自学】课前准备小练习3.14×1²= 3.14×2²= 3.14×3²=3.14×4²= 3.14×5²= 3.14×6²=3.14×7²= 3.14×8²= 3.14×9²=1、已知圆的半径怎样求圆的面积？2、已知圆的直径怎样求圆的面积？3、已知圆的周长怎样求圆的面积？4、已知半圆的半径怎样求圆的面积？5、已知半圆的直径怎样求圆的面积？6、已知半圆的周长怎样求圆的面积？【讨论合作】1、已知一个圆的半径为1厘米，这个圆的面积是多少平方厘米？2、已知一个圆的半径为2厘米，这个圆的面积是多少平方厘米？3、已知一个圆的直径为2厘米，这个圆的面积是多少平方厘米？4、已知一个圆的直径为4厘米，这个圆的面积是多少平方厘米？5、已知一个半圆的半径为1厘米，这个半圆的面积是多少平方厘米？6、已知一个半圆的周长为10.28厘米，这个半圆的面积是多少平方厘米？7、已知一个圆的周长为12.56厘米，这个圆的面积是多少平方厘米？8、已知一个圆的周长为21.98厘米，这个圆的面积是多少平方厘米？【展示提升】1、完成上面内容后，与你的组员交流一下，看看你们的结果一样么？2、把你们不一样的内容与组员交流讨论一下。

3、展示要求：使用普通话，声音洪亮，站姿挺拔，自信大方。

讲解思路清晰，重点突出，允许组内补充。

板书，字体端正，不得重复展示。

【当堂达标】1、补充下列表格圆圆圆2、一个盘的半径是3.21厘米，它的面积是多少厘米？3、一个圆的周长是7.85米，它的面积是多少平方米？4、用圆规画一个圆，如果圆规两脚之间的距离是7厘米，画出的这个圆的周长是多少厘米？这个圆的面积是多少平方厘米？5、一种铝制面盆是用直径30厘米的圆形铝板冲压而成的，要做1000个这样的面盆至少需要多少平方米的铝板？6、一张长30厘米，宽20厘米的长方形纸，在纸上剪一个最大的圆。