南昌工程学院xxxx年专升本考试大纲汇总

江西理工大学2010年“专升本”考试自主命题课程考试大纲科目一、《高等数学》考试大纲一. 主要内容1。

函数与极限函数；数列的极限；函数的极限；无穷小与无穷大；极限运算法则极限存在准则，两个重要极限；无穷小的比较；函数的连续性；闭区间上连续函数的性质。

2．导数与微分导数的概念及其性质；函数的和、差、积、商的求导法则；复合函数的求导法则；高阶导数、隐函数的导数以及由参数方程所确定的函数的导数；函数的微分。

3、中值定理与导数的应用中值定理；洛必塔法则；函数的单调性和曲线的凹凸性；函数的极值和最大值、最小值；函数图形的描绘。

4、不定积分不定积分的概念与性质；换元积分法；分部积分法；有理函数的不定积分。

5、定积分及其应用定积分的概念与性质；微积分基本公式；定积分的换元法及分部积分法；定积分在几何上的应用；反常（广义）积分。

6、微分方程微分方程的基本概念；可分离变量的微分方程；齐次方程；一阶线性微分方程；二阶常系数齐次线性微分方程；二阶常系数非齐次线性微分方程。

7、向量代数与空间解析几何向量及其线性运算；点的坐标与向量的坐标；数量积、向量积；平面及其方程；空间直线及其方程。

8、多元函数微分法及其应用多元函数的基本概念；偏导数；全微分；多元复合函数的求导法则；隐函数的求导公式；多元函数微分法的几何应用举例；多元函数的极值及其求法。

9、重积分二重积分的概念与性质；二重积分的计算。

10、无穷级数常数项级数的概念与性质；常数项级数的审敛法；幂级数；函数展开成幂级数。

二. 基本要求1 。

函数与极限a．理解初等函数的概念。

熟练掌握函数的四种特性。

会建立简单问题的函数关系式。

b．理解数列极限的描述性定义。

熟练掌握数列极限的计算。

c．理解函数极限的描述性定义。

熟练掌握极限的四则运算法则。

理解无穷小与无穷大的概念，掌握无穷小的性质及阶的比较。

熟练掌握极限的收敛准则。

熟练掌握两个重要极限。

d．了解函数的连续性。

知道闭区间上连续函数的性质。

南昌工程学院2020年专升本考试大纲《平面构成》一、总体要求及考核目的《平面构成》是判定应试者是否具备应有的艺术修养、审美能力、观察能力、造形能力、形的组织表现能力和技法运用能力的专业基础考试科目，学生应按本大纲的要求准备考试。

科目考试旨在测试考生能否切中主题，并运用创新思维进行形的创造和平面综合设计能力。

二、考试范围1.形式美的基本法则2.点、线、面二维抽象构成3.平面构成形的秩序组合设计4.平面构成综合设计三、考试形式为了较好地考核学生艺术设计的综合应用能力，同时兼顾科学性、客观性，本考试参考教育部本科专业的培养标准和要求，依据考试目标设计考试方向、考点内容和考查范围，以平面构成现场设计创作为考试形式。

四、考试内容及评分标准1.考试内容：平面构成设计与创作（手绘）（画面尺寸大小为25*25厘米）2.评分标准：试卷满分150分（1）具有独创性,画面完整，整体效果好、表现手法较熟练，刻画较深入，具有一定的表现性,能突出表达主题。

（35分）（2）造形新颖、构成形式合理,布局均衡，具有设计感及丰富的视觉效果。

（30分）（3）黑白灰关系合理、运用有个性，对比又调和，视感觉舒适。

（30分）（4）画面主体形象突出，细节丰富，表现手法有创意。

（30分）（5）点线面构成合理，表现较为抽象。

（25分）五、考试要求1.考试用具与材料：考试用纸由考场提供（八开素描纸）；黑色水笔和绘画工具自备（包括画板或画夹、绘图板、小水桶、铅笔、尺、橡皮、勾线笔、白色水分颜料、黑色水粉颜料等各类表现技法所需的工具）。

2.黑白灰关系合理，表现技法不限。

注意事项：不得在试卷纸上留有任何可疑记号，包括喷洒固定液体。

六、考试时间考试时间为：120分钟。

七、参考书目[1]洪雯，敖芳，罗倩倩.平面构成-中国高等院校“十三五”艺术设计系列规划教材[M].北京：中国青年出版社，2017年.[2]于国瑞.平面构成[M].北京：清华大学出版社，2019年.。

英语
计算机基础
高等数学B
29
保险学
会计、会计电算化、 国际经济与贸易、市场营销、物流、旅游管理、房地产经营管理、电子商务、会计与审计、统计实务、保险实务等经管类专科专业
英语
计算机基础
高等数学B
人文
与艺
术学
院
30
广播电视新闻学
文秘、新闻采编与制作、影视多媒体技术、国际商务国际经济与贸易、广播电视技术、摄影摄像技术、影像技术、影视动画、影视广告、主持与播音、编导、电视节目制作、电视制作管理、旅游管理、现代教育技术、商务英语、旅游英语、多媒体设计与制作、广告设计与制作、动漫设计与制作、计算机多媒体技术、广播电视网络技术
英语
计算机基础
高等数学A
18
自动化
水电站动力设备与管理、发电厂及电力系统、机电一体化、电气自动化
英语
计算机基础
高等数学A
19
机械电子工程
模具设计与制造、数控技术、机电一体化、电气自动化
英语
计算机基础
高等数学A
信息
工程
学院
20
通信工程
通信技术
英语
计算机基础
高等数学A
21
电子信息工程
应用电子技术
英语
计算机基础
水信息技术、水利水电建筑工程
英语
计算机基础
高等数学A
3
测绘工程
工程测量技术
英语
计算机基础
高等数学A
4
水土保持与荒漠化防治
水土保持、园林技术、水利水电建筑工程、水利工程、灌溉与排水技术
英语
计算机基础
高等数学B
5
园 林
园林技术、城镇规划、水土保持、建筑装饰工程技术

南昌工程学院2020年专升本考试大纲《音乐与舞蹈专业技能》一、考试方式：现场面试二、考试内容：考试内容包括三个部分：一是节奏视唱，二是舞蹈表演，三是声乐演唱或器乐演奏任选其一。

总分150分，三部分考试成绩折合计算。

总分=节奏视唱成绩*0.5+舞蹈表演成绩*0.5+声乐演唱或器乐演奏成绩*0.5。

1、节奏视唱：常用节奏，长度为4—8小节，现场抽题视唱。

2、舞蹈表演：舞蹈剧目不超过3分钟(可在中国古典舞、民族民间舞、芭蕾舞、现代舞、当代舞中任选)，所用音乐由考生自备CD盘,并且CD盘上仅有本次考试所用音乐，考试中如发生CD盘音质不清楚等问题,一律由考生本人负责。

3、声乐演唱或器乐演奏任选其一：声乐演唱自选歌曲一首，要求清唱，唱法不限，曲目长度限3分钟以内；器乐演奏自选器乐曲一首（自带乐器，现场提供钢琴），要求能展现考生的器乐演奏能力，曲目长度限3分钟以内。

以上考试项目，每位考生只有一次考试机会,因自身原因中断或失误,不得重考。

三、评分标准：1、节奏视唱90-100分：学生视唱准确，速度稳定，总体完整、流畅。

80-89分：学生视唱比较准确，个别节奏有误（一小节以内），速度稳定，偶尔中断，但总体完整，流畅。

70-79分：学生视唱比较准确，个别节奏有误（两小节以内），速度基本稳定，偶尔中断（3次左右），但总体流畅。

60-69分：学生视唱基本准确，部分节奏有误（不超过总长度的一半），速度不稳，途中有中断（4次左右），但能衔接至结束。

60分以下：学生视唱不准确，部分节奏有误（超过总长度的一半），速度不稳，时快时慢，途中有中断（4次以上），全曲的完整性较差。

2、舞蹈表演90-100分：女生身高166-170cm，男生身高176-180cm；五官端正，身材比例好，气质佳，舞台形象好。

表演作品难度较大，较好地把握舞蹈风格、韵律、舞姿优美，动作规范流畅，完成技巧好。

80-89分：女生身高162cm以上(含)，男生身高172cm以上(含)；五官端正，身材比例好，气质较好，舞台形象较好。

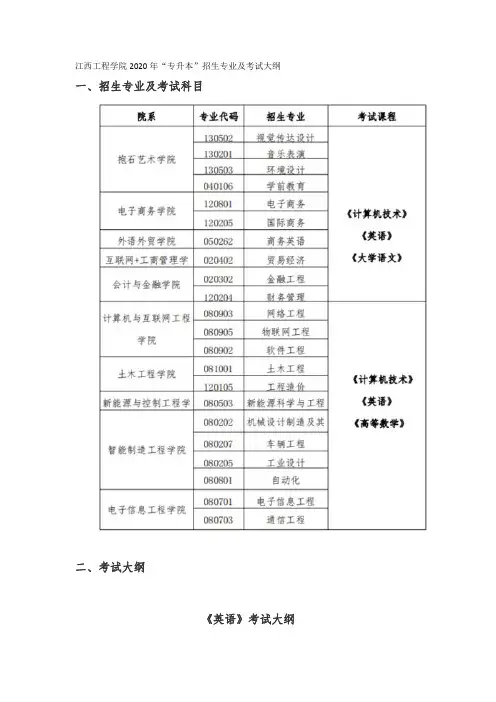
江西工程学院2020年“专升本”招生专业及考试大纲一、招生专业及考试科目二、考试大纲《英语》考试大纲一、考试方式：闭卷考试二、考试时间：120分钟三、考试总分：150分四、考试范围：根据《关于做好全省2020年普通高校专升本考试招生工作的通知》文件要求，英语考试科目由省教育考试院统一组织命题、制卷（英语科目考试大纲参照高职高专英语教学的相关要求）。

《计算机技术》考试大纲一、考试方式：闭卷考试二、考试时间：100分钟三、考试总分：150分四、考试范围：(一)计算机公共基础知识1.计算机发展与社会：(1)计算机技术发展过程及发展趋势；(2)计算机的应用范围及不同应用领域的特点；(3)使用计算机时应该遵守的道德规范及应该具备的防护意识。

2.计算机系统组成及计算机硬件：(1)计算机语言的分类；理解信息在计算机内的表示与存储方式、进制的概念及数制间的相互转换；(2)计算机系统的基本组成；(3)软件的分类及常用软件的功能；(4)计算机基本工作方式(存储程序原理)；(5)计算机各基本部件的功能与主要技术指标；(6)设备管理的基本概念及常见设备的工作方式。

（7）总线、接口、外部设备、计算机硬件组装及启动过程、冯·诺依曼体系结构、嵌入式系统的应用领域等知识。

3.操作系统的功能和使用：(1)操作系统的基本概念、功能和分类；(2)Windows操作系统的基本概念和常用术语：文件、文件夹、库、目录、路径等；(3)Windows操作系统文件及文件夹的相关操作(新建、复制、移动、删除、查找、重命名、更改属性、隐藏等操作)；(4)Windows操作系统桌面外观的设置：任务栏、桌面背景、分辨率、屏幕保护等相关操作及设置；(5)Windows操作系统控制面板的使用：用户账户、防火墙、键盘、鼠标、输入法、日期和时间、字体、文件夹选项等相关设置。

4.Linux操作系统、iOS操作系统、Android操作系统、虚拟机及VMware等知识。

江西2023年专升本考纲
江西2023专升本考试大纲2023年江西专升本考试大纲旨在指导考生准备参加2023年江西专升本考试，为考生提供参考。

本大纲涵盖了江西2023年专升本考试的基本原则和要求，并根据考试内容分为三个部分：综合素质测试、专业课程考试和综合实践活动考试。

一、综合素质测试部分综合素质测试主要考察考生的英语和逻辑思维能力，包括英语语法、词汇、阅读理解和逻辑思维等内容。

考试形式为闭卷，时间为90分钟。

二、专业课程考试部分专业课程考试主要考察考生在本专业研究的知识技能，考试内容包括：专业专业基础理论、知识及应用、专业专业技能及应用等。

考试形式为闭卷，时间为120分钟。

三、综合实践活动考试部分综合实践活动考试是考察考生的实践能力，包括实践任务模拟、实践任务步骤指导、实践任务报告等内容。

考试形式为开卷，时间为120分钟。

本大纲旨在为考生提供参考，以便考生更好地为2023年江西专升本考试做好准备。

考生可以参考本大纲，结合考试实际情况，制定个人研究计划，充分利用备考时间，努力提高自身知识和能力，以期取得好的考试成绩。

通过本大纲，考生可以更好地了解2023年江西专升本考试的考试内容，更好地规划备考过程，努力备考。

只要考生能够按照本大纲的要求认真备考，相信考生一定能够取得满意的成绩，实现自己的梦想。

南昌工程学院2019年专升本考试大纲《高等数学A》本大纲规定了我校专升本考试对《高等数学A》的总体要求，考生应按本大纲的要求，了解或理解“高等数学”中函数、极限和连续、一元函数微分学、一元函数积分学、向量代数与空间解析几何、多元函数微积分学、常微分方程的基本概念与基本理论；学会、掌握或熟练掌握上述各部分的基本方法.应注意各部分知识的结构及知识的内在联系；应具有一定的抽象思维能力、逻辑推理能力、运算能力、空间想象能力；能运用基本概念、基本理论和基本方法正确地推理证明，准确地计算；能综合运用所学知识分析并解决简单的实际问题.本大纲对内容的要求由低到高，对概念和理论分为“了解”和“理解”两个层次；对方法和运算分为“会”、“掌握”和“熟练掌握”三个层次.复习考试内容一、函数、极限和连续（一）函数1．知识范围（1）函数的概念: 函数的定义,函数的定义域及值域，函数的表示法,分段函数,隐函数，复合函数.（2）函数的四个特性：有界性,奇偶性, 单调性,周期性.（3）反函数的概念: 反函数的定义,反函数的图像.（4）基本初等函数: 幂函数,指数函数,对数函数,三角函数,反三角函数.（5）函数的四则运算与复合运算.（6）初等函数.2．要求（1）理解函数的概念,会求函数的表达式、定义域及函数值；会求分段函数的定义域、函数值，会作出简单的分段函数的图像.（2）理解并掌握函数的单调性、奇偶性、有界性和周期性.（3）熟练掌握函数的四则运算与复合运算.（4）掌握基本初等函数的性质及其图像.（5）了解初等函数的概念.（6）会建立简单实际问题的函数关系式.（二）极限1．知识范围（1）数列极限的概念: 数列,数列极限的定义（2）数列极限的性质: 唯一性,有界性,四则运算法则,夹逼定理,单调有界数列极限存在定理.（3）函数极限的概念: 函数在一点处极限的定义,左、右极限及函数在一点处极限极限存在的充要条件,无穷远处函数的极限,函数极限的几何意义.（4）函数极限的性质: 唯一性,四则运算法则,夹逼定理.（5）无穷小量与无穷大量: 无穷小量与无穷大量的定义,无穷小量与无穷大量的关系,无穷小量的性质,无穷小的比较.（6）两个重要极限.2．要求（1）理解极限的概念.会求函数在一点处的左极限与右极限，理解函数在一点处极限存在的充分必要条件.（2）了解极限的有关性质，掌握极限的四则运算法则.（3）理解无穷小量、无穷大量的概念，掌握无穷小量的性质、无穷小量与无穷大量的关系.会进行无穷小量阶的比较（高阶、低阶、同阶和等价）.会运用等价无穷小量代换求函数极限.（4）熟练掌握用两个重要极限求极限的方法.（三）连续1．知识范围（1）函数连续的概念: 函数在一点处连续的定义,左连续与右连续,函数在一点处连续的充分必要条件, 函数的间断点及其分类.（2）函数在一点处连续的性质: 连续函数的四则运算,复合函数的连续性,反函数的连续性.（3）闭区间上连续函数的性质: 有界性定理,最大值与最小值定理,介值定理，零点定理.（4）初等函数的连续性.2．要求（1）理解函数在一点处连续与间断的概念，理解函数在一点处连续与极限存在的关系，掌握判断函数（含分段函数）在一点处的连续性的方法.（2）会求函数的间断点及确定其类型.（3）掌握闭区间上连续函数的性质，会用介值定理推证一些简单命题.（4）理解初等函数在其定义区间上的连续性，会利用连续性求极限.二、一元函数微分学（一）导数与微分1．知识范围（1）导数概念: 导数的定义,左导数与右导数,函数在一点处可导的充分必要条件.导数的几何意义与物理意义,可导与连续的关系.（2）求导法则与导数的基本公式: 导数的四则运算,反函数的导数,导数的基本公式.（3）求导方法: 复合函数的求导法,隐函数的求导法,对数求导法,由参数方程确定的函数的求导法,求分段函数的导数.（4）微分: 微分的定义,微分与导数的关系,微分法则及一阶微分形式不变性.2．要求（1）理解导数的概念及其几何意义，会求曲线上一点处的切线方程与法线方程，了解可导性与连续性的关系，掌握用定义求函数在一点处的导数的方法.（2）熟练掌握导数的基本公式、四则运算法则及复合函数的求导方法，会求反函数的导数.（3）掌握隐函数求导法、对数求导法以及由参数方程所确定的函数的求导方法，会求分段函数的导数.（4）理解高阶导数的概念，会求简单函数的n阶导数.（5）理解函数的微分概念，掌握微分法则，了解可微与可导的关系，会求函数的一阶微分.（二）微分中值定理及导数的应用1．知识范围（1）微分中值定理: 罗尔（Rolle）定理,拉格朗日（Lagrange）中值定理.（2）洛必达（L’Hospital）法则.（3）函数单调性的判定法.（4）函数的极值与极值点最大值与最小值.（5）函数的凹凸性、拐点.（6）曲线的水平渐近线与铅直渐近线.2．要求（1）理解罗尔定理、拉格朗日中值定理及它们的几何意义.会用罗尔定理证明方程根的存在性.会用拉格朗日中值定理证明简单的不等式.（2）熟练掌握用洛必达法则求未定式的极限的方法.（3）掌握利用导数判定函数的单调性及求函数的单调增、减区间的方法，会利用函数的单调性证明简单的不等式.（4）理解函数极值的概念，掌握求函数的极值、最大值与最小值的方法，会解简单的应用问题.（5）会求曲线的水平渐近线与铅直渐近线.（6）会判断曲线的凹凸性，会求曲线的拐点.三、一元函数积分学（一）不定积分1．知识范围（1）不定积分: 原函数与不定积分的定义,原函数存在定理,不定积分的性质. （2）基本积分公式.（3）换元积分法 : 第一换元法（凑微分法）,第二换元法.（4）分部积分法.（5）一些简单有理函数的积分.2．要求（1）理解原函数与不定积分的概念及其关系，掌握不定积分的性质，了解原函数存在定理.（2）熟练掌握不定积分的基本公式.（3）熟练掌握不定积分第一换元法、第二换元法（限于三角代换与简单的根式代换）及分部积分法.（4）会求简单有理函数的不定积分.（二）定积分1．知识范围（1）定积分的概念: 定积分的定义及其几何意义,可积条件.（2）定积分的性质.（3）定积分的计算: 变上限积分牛顿—莱布尼茨（Newton-Leibniz）公式, 换元积分法, 分部积分法（4）无穷区间的广义积分.（5）定积分的应用:平面图形的面积,旋转体体积.2．要求（1）理解定积分的概念及其几何意义，了解函数可积的条件.（2）掌握定积分的基本性质.（3）理解变上限积分是变上限的函数，掌握变上限积分求导数的方法.（4）熟练掌握牛顿—莱布尼茨公式.（5）掌握定积分的换元积分法与分部积分法.（6）理解无穷区间的广义积分的概念，掌握其计算方法.（7）掌握直角坐标系下用定积分计算平面图形的面积以及平面图形绕坐标轴旋转所生成的旋转体体积.四、向量代数与空间解析几何（一）向量代数1．知识范围（1）向量的概念: 向量的定义,向量的模,单位向量,向量的坐标表示法,向量的方向角及方向余弦.（2）向量的线性运算:向量的加法,向量的减法,向量的数乘.（3）向量的数量积: 二向量的夹角,二向量垂直的充分必要条件.（4）二向量的向量积,二向量平行的充分必要条件.2．要求（1）理解向量的概念，掌握向量的坐标表示法，会求单位向量、方向余弦. （2）熟练掌握向量的线性运算、向量的数量积与向量积的计算方法.（3）熟练掌握二向量平行、垂直的充分必要条件.（二）平面与直线1．知识范围（1）平面方程: 点法式方程，一般式方程，截距式方程.（2）两平面的位置关系（平行、垂直和斜交）.（3）点到平面的距离.（4）空间直线方程：点向式方程或对称式方程,参数式方程,一般式方程.（5）两直线的位置关系（平行、垂直）.（6）直线与平面的位置关系（平行、垂直和直线在平面上）.2．要求（1）会求平面的点法式方程、一般式方程.会判定两平面的垂直、平行.会求两平面的夹角.（2）会求点到平面的距离.（3）了解直线的一般式方程，会求直线的点法式方程、参数方程.会判定两直线平行、垂直.（4）会判定直线与平面间的关系（垂直、平行、直线在平面上）.（三）简单的二次曲面1．知识范围球面,柱面,旋转抛物面.2．要求了解球面、母线平行于坐标轴的柱面、旋转抛物面、圆锥面的方程及其图形.五、多元函数微积分学（一）多元函数微分学1．知识范围（1）多元函数：多元函数的定义,二元函数的几何意义,二元函数极限与连续的概念（2）偏导数与全微分：偏导数,全微分,二阶偏导数.（3）复合函数的偏导数.（4）隐函数的偏导数.（5）二元函数的无条件极值与条件极值.（1）要求（1）了解多元函数的概念、二元函数的几何意义.会求二元函数的表达式及定义域.了解二元函数的极限与连续概念（对计算不作要求）.（2）理解偏导数概念，了解偏导数的几何意义，了解全微分概念，了解全微分存在的必要条件与充分条件.（3）掌握二元函数的一、二阶偏导数计算方法.（4）掌握复合函数一阶偏导数的求法.（5）掌握由方程所确定的隐函数的一阶偏导数的计算方法.（6）会求二元函数的全微分.（7）会求二元函数的无条件极值.会用拉格朗日乘数法求二元函数的条件极值.（二）二重积分1．知识范围（1）二重积分的概念：二重积分的定义二重积分的几何意义.（2）二重积分的性质.（3）二重积分的计算. 2．要求（1）理解二重积分的概念及其性质.（2）掌握二重积分在直角坐标系及极坐标系下的计算方法.六、常微分方程（一）一阶微分方程 1．知识范围（1）微分方程的概念：微分方程的定义,阶,解,通解,初始条件,特解.（2）可分离变量的方程，齐次方程. （3）一阶线性方程. 2．要求（1）理解微分方程的定义，理解微分方程的阶、解、通解、初始条件和特解. （2）掌握可分离变量方程的解法. （3）掌握齐次微分方程的解法. （4）掌握一阶线性方程的解法. （二）可降价方程 1．知识范围（1）),(y x f y '='' 型方程.2．要求（1）会用降阶法解),(y x f y '='' 型方程.（三）二阶线性微分方程 1．知识范围（1）二阶线性微分方程解的结构. （2）二阶常系数齐次线性微分方程. （3）二阶常系数非齐次线性微分方程. 2．要求（1）理解二阶线性微分方程解的结构. （2）掌握二阶常系数齐次线性微分方程的解法. （3）掌握二阶常系数非齐次线性微分方程的解法.考试形式及试卷结构试卷总分：100分 考试时间：90分钟 考试方式：闭卷，笔试试卷内容比例：函数、极限和连续 约18% 一元函数微分学 约18% 一元函数积分学 约20%多元函数微积分（含向量代数与空间解析几何）约30% 常微分方程 约14%试卷题型及比例：选择题 约20% ，填空题 约25% ，解答题及证明题 约55试题难易比例：容易题 约20% ，中等难度题 约60%，较难题 约20%。

南昌工程学院2020年专升本考试大纲《大学语文》一、考核目标主要考核学生的语文基础知识和阅读、分析浅近文言文、经典现代文学作品的能力以及议论文写作的能力。

二、考核内容考核内容分为四个部分：语言知识、文学知识、阅读分析、议论文写作。

（一）语言知识（简答题20分）1、了解现代汉语含义、地位及普通话和方言的基本知识。

2、了解现代汉语语音、文字相关知识。

3、掌握现代汉语词汇和语法基础知识。

4、理解现代汉语语用和修辞基本知识。

（二）文学知识（填空题20分）1、熟悉古代诗词歌赋中的名篇名句。

2、熟悉古代其他文体的重要作品、作者、出处及名句。

3、了解现当代文学流派和文学现象。

（三）阅读分析[古典诗词赏析（20分）+古文阅读（30分）+现代文阅读（20分）]1、对古代诗词歌赋中的名篇能进行美学意义上的欣赏，并能用流畅、优美的文字表达出来。

2、能通读古代其他文体中的著名作品，能用现代汉语将它们翻译过来，能体会文章的内在含义。

3、能对现代文学作品的内容大意，段落层次，主旨或中心论点，哲理内涵，人物形象，故事情节，作者的思想观点、感情态度，作品所用的表现手法（对比、衬托、比兴、白描、象征等），修辞手法（比喻、比拟、对偶、排比、夸张、层递、反复、设问、反诘、引用等）能进行准确深刻的欣赏分析。

（四）议论文写作（40分）1、根据所给材料，拟定论题。

2、用现代汉语完成写作。

三、考试方式与试卷结构1、考试方式：闭卷、笔试。

2、试卷分数：试卷满分150分。

3、考试时间：120分钟。

四、主要参考教材《大学语文》，杨萌，北京理工大学出版社。

南昌工学院专升本考试大纲《大学语文》一、考试目的与要求《大学语文》是高等院校非中文专业的公共必修课，是为培养和检验学生的阅读能力及写作能力而设置的一门综合性文化基础课程。

本课程考试主要考查考生识记、理解、分析综合、鉴赏评价、表达应用的能力，具体分为语文基础知识、阅读理解和实际写作能力考察三部分。

二、考试范围及要求（一）基础知识1.语言知识（1）能够识记、理解常用的文言词语，掌握文言文作品中词类活用、一词多义、通假字、古今字等语言现象及常见的特殊句式，能够将简单的文言文翻译成规范的现代文。

（2）了解汉语语法规范，掌握准确、简明、连贯、得体的语言表达方法。

（3）掌握文言文、现代文中常见的修辞手法。

2.文学知识掌握古今中外重要作家、作品的相关知识。

例如：作家的时代、国别、字号、代表作、诗文集名称、文学主张、艺术成就等；代表作品的出处、编著年代、基本内容、主要特色和在文学史上的地位等。

（二）阅读理解能力1.了解作品的题材，理解并概括段落大意及作品的主旨。

2.能准确地分析一篇作品的材料、表现手法和表达技巧，能联系作品说明常见辞格的修辞作用。

3.能结合不同文体的特点，分析作品语言的特色，体味富有表现力的语言的含义和表情达意的作用。

（三）实际写作能力1.以议论文和抒情性散文为考试备选文种。

2.能准确、合理地理解题意。

3.思想健康、中心明确、材料具体。

4.结构完整、条理清楚。

5.语言通顺、连贯、得体。

6.字数不少于800字。

三、考试篇目《甲骨》、《现代汉语再认识》、《“新婚燕尔”是何方“燕”》（外三则）、《怀李叔同先生》、《十八岁出门远行》、《回答》、《世说新语》（三则）、《诗经》（二首）、《当你老了》、《蝶恋花?辛苦最怜天上月》、《三年之丧》、《论语》、《活着》（节选）、《江城子?记梦》、《梦狼》、《一个陌生女人的来信》（节选）。

四、教材及主要参考书《大学语文实验教程》黄春慧主编，上海交通大学出版社。

五、试卷结构（一）试卷总分：100分（二）考试时间：120分钟（三）试卷内容比例：基础知识约25%阅读理解能力约35%实际写作能力约40%（四）试题难易比例容易题约40%中等难度题约50%较难题约10%。

5）钢结构用钢材
6）钢筯混凝土结构用钢
2、了解
1）钢材的拉伸性能
第八章 沥青
一 、学习目的和要求
通过本章的学习，要求学生熟悉沥青材料的基本知识以及以沥青为基础的一些防水材料。
二 、课程内容
1、石油沥青
A、课程内容与考核标准：
绪论
一、学习目的和要求
通过本章的学习，要求学生明确该课程的基本知识，了解该课程的基本框架。
二、课程内容
1、熟悉建筑材料的概念及分类
2、了解建筑材料在建筑业中的地位和发展概况
3、了解本课程的学习内容和方法
2．拉伸、压缩和剪切
了解轴向拉伸与压缩的概念，能熟练地计算轴力，并画出轴力图，熟练地计算直杆横截面和斜截面上的应力。掌握材料的拉伸与压缩的力学性能。能熟练地计算轴向拉伸与压缩的变形。能熟练地掌握轴向拉伸与压缩时的强度计算。掌握简单静不定问题的求解方法。掌握剪切和挤压的概念及其实用计算。
3．扭转
二 、课程内容
1、石灰
2、建筑石膏
三、考核知识点
1、分类、生产
2、石膏的性质和技术要求
3、石膏的应用
4、生石灰的熟化
5、石灰的硬化过程
6、建筑石灰的技术性质
四、考核要求
7、和易性的选用原则
8、混凝土的抗压强度
9、抗压强度标准值与强度等级
10、混凝土的强度的影响因素
11、减水剂
12、配合比设计的步骤与方法
四、考核要求
1、掌握
1）砼用水泥的技术要求
2、煤沥青
3、改性沥青
4、沥青防水材料
三、考核知识点
1、石油沥青的主要技术性质

江西专升本考纲2023
2023年江西专升本考纲包括7门考试科目，分别是政治、历史、
地理、物理、化学、生物和普通话。

每科考试皆为考试90分钟，共
360分。

政治、历史、地理、物理考试皆为选择题，每题5分，共各
120分；化学、生物考试为客观题、主观题混合考试，客观题每题3分，主观题每题10分，共各120分；普通话考试则是以作文和口语为主，
分别占50分，阅读、写作占20分。

总体考试规律是，政治、历史、
地理、物理考试每题有4个选项；化学、生物考试的客观题每题有4
个选项；普通话考试有2-3幅图片，要求考生根据图片进行描述，并
进行同义词转换、完成对话等操作。

此外，考生在报考江西专升本考试时，需要通过教育部提供的考
试网站进行在线报名等工作，该网站上还提供考试报名、考试成绩查
询等功能。

考生需要准备好有效身份证明文件以及能够提供应急保障
的紧急联系人，确保可以正常参加考试。

最后，考生在参加江西专升本考试时，应按照规定时间严格答题，完成所有题目，确保能够取得较高的成绩。

南昌工程学院2021年专升本考试大纲《高等数学B 》I 复习考试说明本大纲对内容的要求由低到高，对概念和理论分为“了解”和“理解”两个层次；对方法和运算分为“会”、“掌握”和“熟练掌握”三个层次. II 复习考试内容 一、函数、极限和连续 （一）函数 1．知识范围 （1）函数的概念函数的定义,函数的表示法,分段函数,隐函数.（2）函数的性质 单调性,奇偶性,有界性,周期性. （3）反函数反函数的定义,反函数的图像.（4）基本初等函数幂函数,指数函数,对数函数,三角函数,反三角函数.（5）函数的四则运算与复合运算. （6）初等函数. （7）常用经济函数. 2．要求（1）理解函数的概念.（2）掌握函数的四个性质.单调性、奇偶性、有界性和周期性. （3）了解函数)(x f y = 与其反函数)(1x fy -=之间的关系（定义域、值域、图像），会求单调函数的反函数. （4）熟练掌握函数的四则运算与复合运算. （5）熟练掌握基本初等函数的性质及其图像. （6）了解初等函数的概念.（7）会建立简单实际问题的函数关系式（需求函数、供给函数、成本函数、收益函数和利润函数）. （二）极限 1．知识范围（1）数列极限的概念 数列,数列极限的定义.（2）数列极限的性质 唯一性,有界性,四则运算法则,夹逼定理,单调有界数列极限存在定理.（3）函数极限的概念 函数在一点处极限的定义,左、右极限及其与极限的关系,趋于无穷时函数的极限.（4）函数极限的性质 唯一性,四则运算法则,夹逼定理.（5）无穷小量与无穷大量 无穷小量与无穷大量的定义,无穷小量与无穷大量的关系,无穷小量的性质，无穷小量的阶. （6）两个重要极限. 2．要求（1）理解极限的概念.会求函数在一点处的左极限与右极限，理解函数在一点处极限存在的充分必要条件.（2）了解极限的有关性质，掌握极限的四则运算法则.（3）理解无穷小量、无穷大量的概念，掌握无穷小量的性质、无穷小量与无穷大量的关系.会进行无穷小量阶的比较（高阶、低阶、同阶和等价）.会运用常见的等价无穷小量代换求极限.（4）熟练掌握用两个重要极限求极限的方法. （三）连续 1．知识范围（1）函数连续的概念函数在一点处连续的定义,左连续与右连续,函数在一点处连续的充分必要条件,函数的间断点及其分类.（2）函数在一点处连续的性质连续函数的四则运算,复合函数的连续性,反函数的连续性.（3）闭区间上连续函数的性质有界性定理,最值定理,介值定理、零点定理. （4）初等函数的连续性.2．要求（1）理解函数在一点处连续与间断的概念，理解函数在一点处连续与极限存在的关系，掌握判断函数（含分段函数）在一点处的连续性的方法.（2）会求函数的间断点及确定其类型(第一类间断点、第二类间断点).（3）掌握在闭区间上连续函数的性质，会用介值定理推证一些简单命题.（4）理解初等函数在其定义区间上的连续性，会利用连续性求极限.二、一元函数微分学（一）导数与微分1．知识范围（1）导数的概念导数的定义,左导数与右导数,函数在一点处可导的充分必要条件.导数的几何意义,可导与连续的关系.（2）求导法则与导数的基本公式导数的四则运算,反函数的导数,导数的基本公式.（3）求导方法复合函数的求导法,隐函数的求导法,对数求导法,由参数方程确定的函数的求导法,求分段函数的导数.（4）高阶导数高阶导数的定义,高阶导数的简单计算.（5）微分微分的定义,微分与导数的关系,微分法则，一阶微分形式不变性. 2．要求（1）理解导数的概念及其几何意义，了解可导性与连续性的关系，掌握用定义求函数在一点处的导数的方法.（2）会求曲线上一点处的切线方程与法线方程. （3）熟练掌握导数的基本公式、四则运算法则及复合函数的求导方法，会求反函数的导数.（4）掌握隐函数求导法、对数求导法以及由参数方程所确定的函数的求导方法，会求分段函数的导数.（5）理解高阶导数的概念，会求简单函数的二阶导数.（6）理解函数的微分概念，掌握微分法则，了解可微与可导的关系，会求函数的一阶微分.（二）微分中值定理及导数的应用1．知识范围（1）微分中值定理罗尔(Rolle）定理,拉格朗日（Lagrange）中值定理.（2）洛必达（L’Hospital）法则.（3）函数单调性的判定法.（4）函数的极值与极值点，最大值与最小值.（5）曲线的凹凸性及拐点.（6）曲线的水平渐近线与铅直渐近线.（7）导数在经济上的应用.2．要求（1）理解罗尔定理、拉格朗日中值定理及它们的几何意义.会用罗尔定理证明方程根的存在性.会用拉格朗日中值定理证明简单的不等式.（2）熟练掌握用洛必达法则求未定式的极限的方法.（3）掌握利用导数判定函数的单调性及求函数的单调增、减区间的方法，会利用函数的单调性证明简单的不等式.（4）理解函数极值的概念.掌握求函数的极值、最大值与最小值的方法，会解简单的应用问题.（5）会判断曲线的凹凸性，会求曲线的拐点.（6）会求曲线的水平渐近线与铅直渐近线.（7）会作出简单函数的图形.（8）会边际分析和弹性分析.三、一元函数积分学（一）不定积分1．知识范围（1）不定积分原函数与不定积分的定义,原函数存在定理,不定积分的性质. （2）基本积分公式.（3）换元积分法第一换元法（凑微分法）,第二换元法.（4）分部积分法.（5）一些简单有理函数的积分.2．要求（1）理解原函数与不定积分的概念及其关系，掌握不定积分的性质，了解原函数存在定理.（2）熟练掌握不定积分的基本公式.（3）熟练掌握不定积分第一换元法，掌握第二换元法（限于三角代换与简单的根式代换）.（4）熟练掌握不定积分的分部积分法.（5）会求简单有理函数的不定积分.（二）定积分1．知识范围（1）定积分的概念定积分的定义及其几何意义.（2）定积分的性质.（3）定积分的计算变上限积分牛顿—莱布尼茨（Newton-Leibniz）公式换元积分法分部积分法.（4）定积分的应用平面图形的面积,旋转体体积,物体沿直线运动时变力所作的功. 2．要求（1）理解定积分的概念及其几何意义.（2）掌握定积分的基本性质.（3）理解积分变限函数，掌握积分变限函数的求导方法.（4）熟练掌握牛顿—莱布尼茨公式.（5）掌握定积分的换元积分法与分部积分法.（6）掌握直角坐标系下用定积分计算平面图形的面积以及平面图形绕坐标轴旋转所生成的旋转体体积.会用定积分解决一些简单的经济问题.四、常微分方程1.知识范围（1）微分方程的基本概念.（2）一阶微分方程.（3）可降阶的高阶微分方程.（4）二阶线性微分方程.2．要求（1）理解微分方程的基本概念.（2）掌握可分离变量方程、齐次微分方程和一阶线性微分方程解法.（3）会解可降阶的高阶微分方程.（4）掌握二阶常系数线性齐次微分方程及自由项较简单的二阶常系数线性齐次微分方程的解法.五、空间解析几何与向量代数1、知识范围：（1）平面的方程点法式方程、一般式方程、截距式方程.（2）直线的方程一般式方程、点向式方程、参数式方程.（3）判定两平面的垂直、平行，判定两直线平行、垂直的位置关系.（4）曲面及方程柱面方程旋转曲面方程.2．要求（1）熟练掌握平面方程及直线方程.（2）掌握面与面、线与线的位置关系.（3）掌握母线平行与坐标轴的柱面方程的特征.（4）熟练掌握将坐标平面内曲线绕坐标轴旋转的曲面方程.六、多元函数微分学（1）多元函数的概念、二元函数的极限.（2）多元函数偏导数及全微分.（3）多元函数极值和条件极值的概念，求函数的极值，二元函数极值存在的必要条件及二元函数极值存在的充分条件，拉格朗日乘数法.2、要求：（1）会求简单二元函数的极限.（2）掌握多元函数的一阶偏导数及二元函数的二阶偏导数计算.（4）掌握用拉格朗日乘数法求解函数的极值及最值.七、二重积分1、知识范围：（1）二重积分的概念与性质.（2）二重积分的计算法.（3）二重积分的应用.2、要求：（1）了解二重积分的概念，二重积分的性质、二重积分的中值定理.（2）掌握二重积分计算（直角坐标法和极坐标法）.（3）会利用二重积分求解两个曲面所围立体的体积.III 考试形式及试卷结构试卷总分：100分考试时间：120分考试方式：闭卷，笔试试卷内容比例：函数、极限和连续约15% 一元函数微分学约15% 一元函数积分学约20% 微分方程约10% 空间解析几何与向量代数约5%多元函数微分学约20% 二重积分约15%试卷题型比例：选择题约18%填空题约24%解答题约50%证明题约8%试题难易比例：容易题约30%中等难度题约50%；较难题约20%。

南昌工程学院2016年专升本考试大纲《素描》(一)目的和要求通过表现物体的形体、结构、比例、运动、空间位置、明暗关系等造型手段来塑造形象。

通过素描考试，考查考生的造型能力。

要求考生在考试时间内，明确的表现视觉感受和对造型的理解。

(二)考试范围（选取其中一门）1、静物素描：内容以日常用品为主。

2、人物素描：限头像、胸像、半身带手，原则上不考全身像。

(三)工具和材料：1、铅笔（不能用炭笔、炭精棒等）；2、自带画夹(或画板)；3、纸张：4开素描纸(由考场提供)；4、画面上不得喷洒任何固定液体。

(四)考试时间150分钟(五)评分满分为100分(六)评分标准：A类卷（90～100分）：1.符合试题规定及要求；2.造型准确，有较强的表现和塑造能力（包括比例、动态、结构透视、特征、神态、空间关系等）；3.正确理解对象结构及体面关系，并能完整地表现；4.画面色调对比明朗，素描关系准确，表现生动，形体刻画深入，画面整体效果好。

B类卷（75～89分）：1.符合试题规定及要求；2.造型比较准确（包括比例、动态、结构透视、特征、神态、空间关系等）；3.对对象结构及体面关系理解比较正确，并能较好地表现；4.画面色调对比比较明朗，素描关系比较准确，表现比较生动，具备一定的形体刻画能力，略有缺点，但画面整体效果较好。

C类卷（60～74分）：1.基本符合试题规定及要求；2.基本具备造型能力（包括比例、动态、结构透视、特征、神态、空间关系等），但把握欠准确；3.对对象结构及体面关系有基本认识，但理解和表现上有欠缺；4.画面色调对比不够明朗，素描关系基本准确，表现缺乏生动，形体刻画能力不够，存在某些缺点，画面整体效果一般。

D类卷（59分以下）：1.不符合试题规定及要求；2.不具备基本的造型能力（包括比例、动态、结构透视、特征、神态、空间关系等）；3.对对象结构和体面关系缺乏基本认识，理解和表现不到位；4.画面整体效果差。

南昌工程学院2020年专升本课程考试大纲
《管理学》
考试要求：
1、本考试大纲适用于报考南昌工程学院市场营销和人力资源管理两个专业专升本入学考试。

2、要求考生具备扎实的管理学理论基础、合理的知识结构，掌握管理学基本概念、基本原理与基本方法，熟悉管理理论的发展历程和现代管理理论的基本观点，对决策、组织、领导、控制和创新职能有较深的认识；能够运用管理的基本理论来分析和解决企业经营管理问题。

考试方式：
笔试、闭卷。

答题时间：
120分钟。

考试内容比例：（卷面成绩150分）
1、主要题型：单项选择题、判断题、论述题和案例分析题等。

2、单项选择题：约30%；判断题：约10%；论述题：约40%，案例分析题：约20%。

基本内容及范围:
1、管理与管理学
管理的定义，管理工作的内容，管理的本质，管理学的研究对象，管理学的学习意义和方法。

2、管理理论
泰勒的科学管理理论，法约尔的一般管理理论，韦伯的科层组织理论；巴纳德的系统管理理论；西蒙的决策管理理论以及权变管理理论等。

3、决策
决策的概念，决策的要素，决策的过程，决策的影响因素；决策与计划的区别与联系，计划的本质与特征，计划的作用，计划的编制过程
4、组织
组织设计的任务、原则和影响因素，组织结构各形式的优缺点；管理幅度与管理层次；集权与分权。

5、领导
领导与管理的区别，领导的权力来源，管理方理论，领导者角色理论，激励的定义，激励理论。

6、控制
控制的内涵性，有效控制的目标，控制过程。

参考教材：《管理学》编写组编（陈传明主编，徐向艺、赵丽芬副主编），高等教育出版社，2019年1月。

各专业招 生计划总 人数包含 享受专项 政策考生 的录取指 标。其中， 建档立卡 贫困家庭 毕业生专 升本专项 计划占 10%，退役 士兵专升 本专项计 划占 5%， 获奖学生 专升本专 项计划占 5%。Fra bibliotek考试科目
考试时长
备注
科目一：《英语》 科目二：《大学语文》 科目三：《平面构成》
科目一：《英语》
科目二：《大学语文》 1.《英语》、《大
科目三：《音乐与舞 学语文》、《平
蹈专业技能》
面构成》、《管
理学》:120 分
钟。
2.《音乐与舞
蹈专业技能》
分组考试。
科目一：《英语》 科目二：《大学语文》 科目三：《管理学》
附件 1：2020 年专升本招生专业、计划分配、考试科目与时长
专业 类别
艺 术 体 育 类
文 理 类
招生专业及代 码
环境设计 （130503）
数字媒体艺术 （130508）
音乐学 （130202）
人力资源管理 （120206）
市场营销 （120202）
招生计 划总人
数 45
45
30
40
40
普通 计划 40 40 25
28
27
招生计划分配（人） 退伍 获奖学生（含高 士兵 水平运动员）
1
2
1
2
1
2
3
2
4
2
建档 立卡
2 2 2
7
7
拟招专科专业及代码
室内艺术设计 650109 展示艺术设计 650110 环境艺术设计 650111 公共艺术设计 650112 数字媒体艺术设计 650104 摄影与摄像艺术 650124 动漫设计 650120 游戏设计 650121 广告设计与制作 650103 艺术设计 650101 舞蹈表演 650207 舞蹈编导 650216 音乐教育 670112K 音乐表演 650219 人力资源管理 690202 物流管理 630903 工商企业管理 630601 建设工程管理 540501 国际经济与贸易 630502 酒店管理 640105 财务管理 630301 应用英语 670203 市场营销 630701 电子商务 630801 旅游管理 640101 工商企业管理 630601 会计 630302 会展策划与管理 640301 商务英语 670202 工程造价 540502

2020年“专升本”考试科目及考试大纲序号专业类别考试科目1理工类英语、计算机基础、高等数学2经管类英语、计算机基础、管理学原理3艺术类4体育类英语、计算机基础、大学语文5文史类6法学类《英语》考试大纲一、考试方式：闭卷考试二、考试时间：120分钟三、考试总分：100分四、考试范围1.语法和词汇：考查考生对英语基础知识的运用，测试考生对英语语法、词汇知识和较为简单表达方式的掌握情况。

重点考查从句复合句、非谓语动词、虚拟语气、倒装、反义疑问句、时态和语态、词组搭配、词义辨析。

题型为单项选择题和填空题。

2.阅读理解能力：考查考生阅读各类题材文章并从书面文字材料获取信息的能力。

考生应能够(1)理解文章的主旨和大意；(2)了解事实和细节；(3)根据文章所给信息进行判断和推理；(4)根据上下文推断单词和短语的含义；(5)理解作者的意图、观点和态度。

3.翻译能力：考查考生准确将汉语翻译成英语的能力，要求考生根据全句意思将汉语译成英语。

翻译须符合英语的语法结构和表达习惯，用词准确。

能恰当地运用参考书目中所学的单词、词组和句型翻译句子。

4.应用文写作能力：考查考生对于应用文的掌握，例如感谢信、邀请信、祝贺信、道歉信、投诉信、求职信、推荐信等英语应用文的基本写作格式、结构和常用句型，注重词汇和语法使用的准确性，文章要求有连贯性和逻辑性。

五、考试题型选择题、填空题、阅读理解题、翻译题、作文题等。

六、参考教材：1.《大学英语综合教程I》，宋乃康主编,陕西人民教育出版社，2 009年3月第1版。

2.《大学英语综合教程Ⅱ》，宋乃康主编,陕西人民教育出版社，2 010年。

《计算机基础》考试大纲一、考试方式：闭卷考试二、考试时间：100分钟三、考试总分：100分四、考试范围：(一)计算机公共基础知识1.计算机发展与社会：(1)计算机技术发展过程及发展趋势；(2)计算机的应用范围及不同应用领域的特点；(3)使用计算机时应该遵守的道德规范及应该具备的防护意识。

2023年江西专升本考试大纲
一、报考资格
1、具有高中学历的在校生、非在校生和成人教育学生；
2、报考者应具备良好的学习习惯和学习能力，有较强的学习自觉性；
3、报考者应具有良好的政治表现和道德品质；
4、报考者应具备良好的身心健康状况，能够适应大学学习和生活；
5、报考者应具备有关法律法规规定的其他条件。

二、考试科目
1、语文：阅读理解、写作、文言文阅读；
2、数学：数学分析、线性代数、概率论、数学建模；
3、英语：阅读理解、词汇、语法、写作；
4、政治：思想政治理论、政治经济学、中国近现代史；
5、历史：世界历史、中国古代史、中国近现代史；
6、地理：世界地理、中国地理；
7、物理：物理学基础、物理实验；
8、化学：化学基础、化学实验；
9、生物：生物学基础、生物实验；
10、选修课：可以根据学校要求选择必修课程或者选修课程，如：体育、艺术、计算机等。

三、考试形式
1、笔试：笔试考试时间为2个小时，共有120道题，每题1分，共120分；
2、综合考试：综合考试时间为2个小时，共有50道题，每题
2分，共100分；
3、口试：口试考试时间为15分钟，考试内容包括政治、历史、地理、文学等；
4、实践考试：实践考试时间为2个小时，。