戴维宁定理和诺顿定理

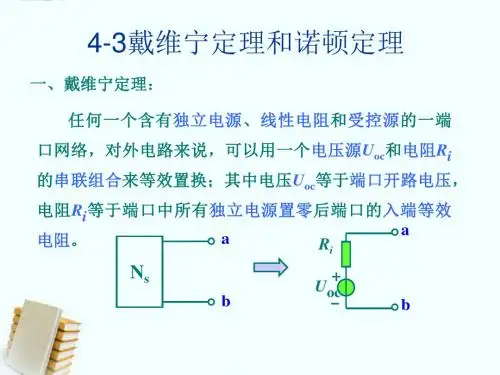
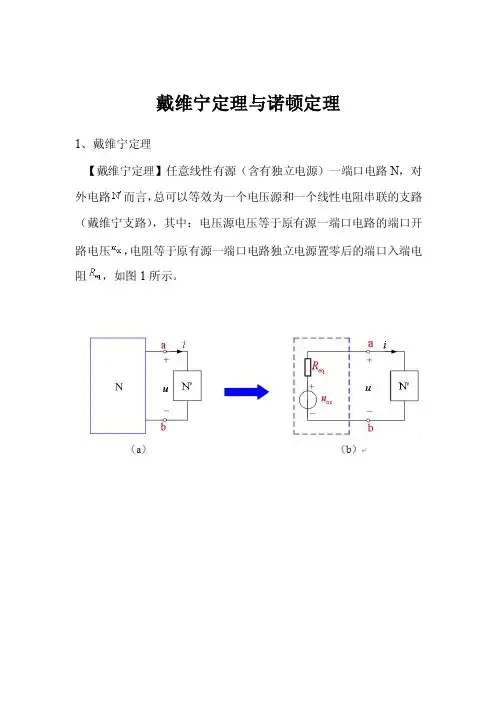
戴维宁定理与诺顿定理1、戴维宁定理【戴维宁定理】任意线性有源（含有独立电源）一端口电路N，对外电路而言，总可以等效为一个电压源和一个线性电阻串联的支路（戴维宁支路），其中：电压源电压等于原有源一端口电路的端口开路电压，电阻等于原有源一端口电路独立电源置零后的端口入端电阻，如图1所示。

2、诺顿定理【诺顿定理】任意线性有源（含有独立电源）一端口电路N，对外电路而言，总可以等效为一个电流源和一个线性电阻并联的支路（诺顿支路），其中：电流源的电流等于原有源一端口电路的端口短路电流，电阻等于原有源一端口电路独立电源置零后的端口入端电阻，如图4-3-2所示。

【戴维宁定理和诺顿定理的参数关系】根据戴维宁支路和诺顿支路的互换关系，不难得到在图4-3-1和4-3-2所规定的参考方向下，有。

3、戴维宁与诺顿定理的应用【戴维宁定理和诺顿定理的应用】戴维宁定理与诺顿定理常用来获得一个复杂网络的最简单等效电路，特别适用于计算某一条支路的电压或电流，或者分析某一个元件参数变动对该元件所在支路的电压或电流的影响等情况。

【应用的一般步骤】1.    把代求支路以外的电路作为有源一端口网络。

2.    考虑戴维宁等效电路时，计算该有源一端口网络的开路电压。

3.    考虑诺顿等效电路时，计算该有源一端口网络的短路电流。

4.    计算有源一端口网络的入端电阻。

5.    将戴维宁或诺顿等效电路代替原有源一端口网络，然后求解电路。

【例4-3-1】用戴维宁定理计算当图4-3-3中电阻R分别为，时，流过的电流分别是多少？解（1）计算图4-3-3中端口ab的戴维宁等效电路。

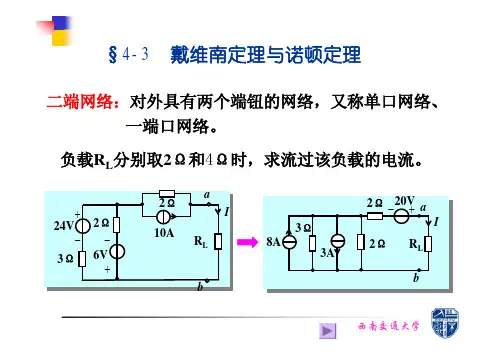
§4-3 戴维南定理与诺顿定理二端网络：对外具有两个端钮的网络，又称单口网络、一端口网络。

负载R L 分别取2Ω和4Ω时，求流过该负载的电流。

当R L ＝2Ω时，AI 522.326=+=当R L ＝4Ω时，AI 75.342.326=+=戴维南定理：任何一个含有独立电源的线性电阻二端网络，对外电路来说，总可以等效为一个电压源串电阻的支路，该电压源等于原二端网络的开路电压u oc ，电阻R o 等于该网络中独立电源置零后在端口处的等效电阻。

u oc R oR o 戴维南定理的证明：端口a 、b 处的电压为u ，电流为i替代定理ii s =i+-u oc+-oc u ′叠加定理i s =i＋N 0 —N 中独立电源为零后的网络。

当网络N 中的电源作用时：oc u u ='0'=i 当电流源i s 作用时：0''''iR R i u ab −=−=i i =''叠加定理：iR u u u u oc 0'''−=+=u ocR b诺顿定理：任何一个含有独立电源的线性电阻二端网络，对外电路来说，总可以等效为一个电流源并电阻的电路，其中电流源等于原二端网络端口处的短路电流i sc ，电阻R o 等于该网络中独立电源置零后在端口处的等效电阻。

诺顿定理的证明：替代定理u s =u′叠加定理u s =u ＋网络N 中电源作用：sc i i ='(短路电流)0'=u u s 作用时：00''R u R u R u i s ab s −=−=−=uu =''所以0'''R ui i i i sc −=+=ai sc一、电路中不含受控源的情况：例4－4：求a 、b 端的戴维南及诺顿等效电路。

33解：（1）求开路电压u ocAi 5.433621=++=Vi u oc 5.176352=−+×=3Ωb（2）求R 0将独立电源置零戴维南等效电路如图17.5V3.5ΩabΩ=+×+=5.333332o Ri sc321V0=u 等效电阻R o 的求法同前a5A536321)213131(−−=++u Aui sc 552=+=（3）例4－5：问R L 取何值可获最大功率？最大功率是多少？2A5Ω5ΩL解：先求R L 左侧电路的戴维南等效电路。

戴维宁定理和诺顿定理戴维南定理（Thevenin’s theorem）：含独立电源的线性电阻单口网络N，就端口特性而言，可以等效为一个电压源和电阻串联的单口网络。

电压源的电压等于单口网络在负载开路时的电压uoc；电阻R0是单口网络内全部独立电源为零值时所得单口网络N0的等效电阻。

戴维南定理（又译为戴维宁定理）又称等效电压源定律，是由法国科学家L·C·戴维南于1883年提出的一个电学定理。

由于早在1853年，亥姆霍兹也提出过本定理，所以又称亥姆霍兹-戴维南...对于含独立源，线性电阻和线性受控源的单口网络（二端网络），都可以用一个电压源与电阻相串联的单口网络（二端网络）来等效，这个电压源的电压，就是此单口网络（二端网络）的开路电压，这个串联电阻就是从此单口网络（二端网络）两端看进去，当网络内部所有独立源均置零以后的等效电阻。

uoc 称为开路电压。

Ro称为戴维南等效电阻。

在电子电路中，当单口网络视为电源时，常称此电阻为输出电阻，常用Ro表示；当单口网络视为负载时，则称之为输入电阻，并常用Ri表示。

电压源uoc 和电阻Ro的串联单口网络，常称为戴维南等效电路。

当单口网络的端口电压和电流采用关联参考方向时，其端口电压电流关系方程可表为：U=R0i+uoc。

戴维南定理和诺顿定理是最常用的电路简化方法。

由于戴维南定理和诺顿定理都是将有源二端网络等效为电源支路，所以统称为等效电源定理或等效发电机定理。

诺顿定理(Norton’s theorem)：含独立源的线性电阻单口网络N，就端口特性而言，可以等效为一个电流源和电阻的并联。

电流源的电流等于单口网络从外部短路时的端口电流isc；电阻R0是单口网络内全部独立源为零值时所得网络N0的等效电阻。

诺顿定理与戴维南定理互为对偶的定理。

定理指出，一个含有独立电源线性二端网络N, 就其外部状态而言,可以用一个独立电流源isc 和一个松弛二端网络N0的并联组合来等效。

戴维宁定理和诺顿定理
1 戴维宁定理
戴维宁定理是数学家汤姆森·戴维宁（Thomas Davidet Alain Davie）提出的一个有关不可划分系统的重要概念，是系统理论的基础定理之一。

他的定理强调的是当系统的每个部分处于完整和可更改的状态时，它们将把整个系统从不可再划分进行分割，从而使系统被认为是不可再分割的。

它用来区分一般形式和不可分割形式之间的关系，它的定理是：当一个系统的每一部分是完整的（可更改的）时，它们将把整个系统从不可再划分状态分割出来；但是，如果系统的任意一部分是不可更改的，它将被认为是不可分割的。

戴维宁定理也可用于更改现有系统，可以帮助把它们划分为更加可控制的组件，这有助于在系统推出时获得最佳性能或改善系统稳定性。

2 诺顿定理
诺顿定理是英国数学家约翰·诺顿（John von Neumann）提出的另一个重要定理，在他的重要著作《决策理论》中有精彩的讨论。

他的定理认为，当一个系统的每个部分是完整的，可以控制的，协调的时，它们将使该系统从可再划分变得不可再划分。

诺顿定理也强调了
系统是由可控制的，可调整的组件构成的，而且每个组件可以协调运作以最小化系统的总能耗，同时可以更加有效地运行系统。

诺顿定理也可以帮助系统的设计者更加有效地运用系统的资源，可以更有效地快速解决难题。

它也可以帮助改善和协调系统的性能，同时明确的表示出系统的控制计划。

总之，戴维宁定理和诺顿定理都是系统理论建筑中重要的概念，旨在帮助系统设计者更加有效地理解和利用系统资源，以改善系统性能，可以有效地帮助快速解决系统问题，也可以为系统构建带来一定的帮助。

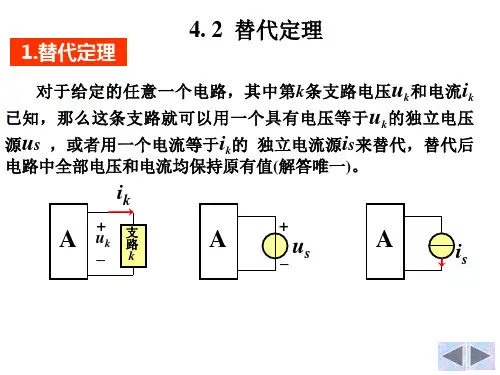
戴维南定理和诺顿定理的验证
戴维南定理和诺顿定理是电路理论中两个重要的定理，它们分别用于求解有源二端网络的等效电路和电流控制电路。

下面是对这两个定理的验证：
戴维南定理的验证：
1. 构建一个有源二端网络，其中包含一个电阻和一个电压源。

2. 将电压源视为短路，用短路代替它，得到一个等效电路。

3. 对等效电路进行电压测量，计算出等效电压和等效电阻，并与原始电路的电压和电阻进行比较。

4. 验证等效电压和等效电阻是否相等，以此验证戴维南定理的正确性。

诺顿定理的验证：
1. 构建一个有源二端网络，其中包含一个电阻和一个电流源。

2. 将电流源视为开路，用开路代替它，得到一个等效电路。

3. 对等效电路进行电流测量，计算出等效电流和等效电阻，并与原始电路的电流和电阻进行比较。

4. 验证等效电流和等效电阻是否相等，以此验证诺顿定理的正确性。

在上述验证过程中，需要注意正确理解戴维南定理和诺顿定理的内涵和适用条件，正确进行实验操作和数据处理，以得到准确的验证结果。

同时，也需要注意实验中的安全问题，确保实验过程的顺利进行。

戴维南定理和诺顿定理一、戴维南定理出发点：对于一个复杂的含有独立源的电路，如果只要计算某条支路上的电压和电流，那么就可以把电路分解成两个部分，把该条支路作为一个部分，把电路的其余部分作为另一个部分，并用一个含源二端网络 Ns 来表示。

试图找到一个简化的等效电路去替换 Ns ，则该支路上的电压和电流的计算就会简单得多。

1 、戴维南定理图 4.3-1 （ a ）中， Ns 是含源二端网络，欲计算电阻 R 的端电压 u 和端电流 i 。

根据替代定理，可以用一个电流为 i 的理想电流源去替代外电路，如图 4.3-1 （ b ）所示，替代之后，电路中其他支路上的电压和电流则保持不变。

用叠加定理计算 a 、 b 端钮的电压 u 。

当含源二端网络 Ns 中的独立源单独作用时，外部的电流源 i 应视为开路，这时的电路如图 4.3-1 （ c ）所示。

显然，这时的端钮电压就是含源二端网络 Ns 的开路电压。

当外部的电流源 i 单独作用时，把含源二端网络 Ns 中的所有独立源都视为 0 ，这时Ns 中只剩下线性电阻和线性受控源等元件，没有独立源，成为一个无源二端网络，用 N 表示，其电路如图 4.3-1 （ d ）所示。

显然，无源二端网络 N 可以等效为一个电阻，这个电阻称为含源二端网络 Ns 的等效内阻用 Ro 表示。

这时电阻的端电压为。

根据叠加定理，得图 4.3-1 （ a ）电路中电阻的端电压为戴维南定理（Thevenin's theorem ）：对于一个线性的含源二端网络，对外电路而言，它可以用一个理想电压源和一个内阻相串联的支路来等效，这条支路称为戴维南等效支路，又称戴维南模型。

其中，等效电压源的电压为该含源二端网络的开路电压，等效内阻为该含源二端网络中所有独立源都取 0 时的等效电阻。

2 、戴维南模型参数的计算1 、电压的计算先画出含源二端网络 Ns 开路时的电路，然后再计算开路电压。

2 、等效内阻的计算（ 1 ）如果无源二端网络 N 中没有受控源，可以用电阻网络的等效方法，如电阻的串、并联方法等。

戴维南定理和诺顿定理
戴维南定理：如果有一个一端口网络，它的里面可能包括独立源，线性电阻，线性受控源，以及它们的各种可能的复杂组合。

它能够等效成为一个串联的连接，这个串联的连接是一个独立电压源，这个电压源就是这个一端网络的开路电压和一个电阻。

这个电阻的阻值，就是这个网络所有独立源都置0以后的入端电阻。

电压为Uoc，电阻为Ri。

诺顿定理：内部包含独立源，线性电阻和线性受控源的一端口网络可以等效为一个电流源和一个电导的并联形式。

这个电流叫Isc，是这个端口短路时候流过的电流。

电导是Gi，是从ab端口往里看的等效电导。