下载文档原格式
高频电子线路第2章 小信号选频放大器2.1 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解]90-612110.035610Hz 35.6MHz 2π2π102010f LCH F-===⨯=⨯⨯6312640.71010022.4k 22.361022.36k 201035.610Hz35.610Hz 356kH z100p H R Q Ff BW Q ρρ--===Ω=⨯Ω=Ω⨯⨯===⨯=2.2 并联谐振回路如图P2.2所示，已知：300pF,390μH,100,C L Q ===信号源内阻s100k ,R =Ω负载电阻L200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解]011465kHz 2π2π390μH 300PF f LC ≈==⨯0.70390μH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω42k Ω371.14k Ω390μH/300 PF /465kHz/37=12.6kHzp e s p Le e e R Q R R R R R Q BWf Q ρρ=========== 2.3 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ，应在回路两端并接一个多大的电阻?。
[解] 6262120115105μH (2π)(2π1010)5010L H f C--===⨯=⨯⨯⨯⨯6030.7101066.715010f Q BW ⨯===⨯ 2236022*********.78.11010p oU f Q f U ∙∙⎛⎫⎛⎫∆⨯⨯=+=+= ⎪ ⎪⨯⎝⎭⎝⎭ 当0.7300kHz BW=时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯ 由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.4并联回路如图P2.4所示,已知：360pF,C =1280μH,L ==100,Q 250μH,L = 12=/10,n N N =L1k R =Ω。
(pF)).(L C H)(.QR则L Ω取R Δf f Q (kHz)Δf MHz解：f..159101*********11591014321010010100101010121010990101211362620603670036700=⨯⨯⨯⨯===⨯⨯⨯====⨯⨯===⨯-⨯==--ωμω时，产生并联谐振。
C L 或ωC L )当(时，产生串联谐振。
C L 或ωC L )当(时，产生并联谐振。
C L 或ωC L )当解：(22021101220211012202110111311211123======-ωωωR R C L R )LC ωL(j ωR )LC ωLR(j ωC L R C j ωR L j ωR )C j ωL)(R j ω(R 证明：Z =+=-+-++=+++++=-2112111133220020020000)()()()()())()()()())318010404501053514321121535100160512405354501605151431223202222μH .C C L 故采用后一个不合理舍去pF -得C C C 由pF得C C C 由解：=⨯+⨯⨯⨯⨯='+==+=⨯+=+=⨯+--ω。
()()()()mV V Q V V mA .R V I μH ..C L ..R C 解：Q-Sm Com Lom -om om --21210121220510111210100105114321121251010010511432115330312260200126000=⨯⨯====⨯===⨯⨯⨯⨯===⨯⨯⨯⨯⨯⨯==-ωω()()()()()()Ωj ..j .C jR Z Ω.....Q LQ L R pF C pF .L C C C C .V V Q μH .C 解：L X X X X X X X S C 796747102001014321747174710010253101432152102531014322001001025310143211100101025310100101432116312606666000626200122620-=⨯⨯⨯⨯-=-==⨯⨯⨯⨯-⨯⨯⨯⨯=-==→=⨯⨯⨯⨯==+⋅====⨯⨯⨯⨯==------ωωωωω()()()。
⾼频电⼦线路课后答案（胡宴如-狄苏燕）说明所有习题都是我们上课布置的作业题，所有解答都是本⼈⾃⼰完成，其中难免有错误之处，还望⼤家海涵。
第2章⼩信号选频放⼤器已知并联谐振回路的1µH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解] 900.035610Hz 35.6MHz f ===?=3640.722.4k 22.361022.36k 35.610Hz35.610Hz 356kH z100p R Q f BW Q ρρ===Ω=?Ω=Ω?===?=并联谐振回路如图所⽰，已知：300pF,390µH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解] 0465kHz 2π2π390µH 300PFf LC≈==?0.70390µH100114k Ω300PF////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω390µH/300 PF /465kHz/37=12.6kHzp e s p Le e e R Q R R R R R Q BW5105µH (2π)(2π1010)5010L H f C --===?= 6030.7101066.715010f Q BW ?===?2236022*********.78.11010p oU f Q f U ?=+=+= ? ?????当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-?===?====?Ω=Ω⽽471266.72.131021.2k 2π105010p R Q ρ-===?Ω=Ω由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω?Ω===Ω-Ω-Ω并联回路如图所⽰,已知：360pF,C =1280µH,L ==100,Q 250µH,L =12=/10,n N N =L 1k R =Ω。
第2章 小信号选频放大器2.1填空题(1)LC 并联谐振回路中，Q 值越大，其谐振曲线越尖锐,通频带越窄,选择性越好。
(2)LC 并联谐振回路谐振时，回路阻抗为最大且为纯电阻,高于谐振频率时间阻抗呈容性，低于谐振频率时间阻抗感性。
(3)小信号谐振放大器的负载采用谐振回路,工作在甲类状态，它具有选频作用。
(4)集中选频放大器由集成宽带放大器和集中选频滤波器组成，其主要优点是接近理想矩形的幅频特性，性能稳定可靠，调整方便。
2.2 已知并联谐振回路的1μH,20pF,100,L C Q ===求该并联回路的谐振频率0f 、谐振电阻p R 及通频带0.7BW 。
[解]900.035610Hz 35.6MHz f ===⨯=3640.722.4k 22.361022.36k 35.610Hz35.610Hz 356kH z100p R Q f BW Q ρρ==Ω=⨯Ω=Ω⨯===⨯=2.3 并联谐振回路如图P2.3所示，已知：300pF,390μH,100,C L Q ===信号源内阻s 100k ,R =Ω负载电阻L 200k ,R =Ω求该回路的谐振频率、谐振电阻、通频带。
[解]0465kHz f ≈==0.70114k Ω////100k Ω//114.k Ω//200k Ω=42k Ω42k Ω371.14k Ω/465kHz/37=12.6kHzp e s p Le e e R Q R R R R R Q BWf Q ρρ========== 2.4 已知并联谐振回路的00.710MHz,C=50pF,150kHz,f BW ==求回路的L 和Q 以及600kHz f ∆=时电压衰减倍数。
如将通频带加宽为300 kHz ，应在回路两端并接一个多大的电阻? [解] 6262120115105μH (2π)(2π1010)5010L H f C --===⨯=⨯⨯⨯⨯6030.7101066.715010f Q BW ⨯===⨯8.1p oU U ∙∙= 当0.7300kHz BW =时6030.746120101033.33001033.31.061010.6k 2π2π10105010e e e ef Q BW Q R Q f C ρ-⨯===⨯====⨯Ω=Ω⨯⨯⨯⨯而471266.72.131021.2k 2π105010p R Q ρ-===⨯Ω=Ω⨯⨯⨯ 由于,p e pRR R R R =+所以可得10.6k 21.2k 21.2k 21.2k 10.6k e p p eR R R R R Ω⨯Ω===Ω-Ω-Ω2.6 并联谐振回路如图P2.6所示。
说明所有习题都是我们上课布置的作业题，所有解答都是本人自己完成，其中难免有错误之处，还望大家海涵。
第2章小信号选频放大器2. 1已知并联谐振回路的厶=1迟C = 2OpF,0 = lOO,求该并联回路的谐振频率九、谐振电阻心及通频带创匕“。
［解］X = 一= = 一1——-=0.0356 X109 Hz = 35.6 MHz2 托应27U>/10^//X20X10-,2FR =Q = 1叫10 H = 22.4kQ = 22.36x10s Q = 22.36kQ卩 i V20xl0-|2FBW（｝7丄=血6小）Hz =35.6xl04Hz = 356kHzQ 1002.2并联谐振回路如图P2. 2所示，已知：C = 300pF.L = 390nH.0 = 100.信号源内阻尺=1009负载电阻&=2OOM1求该回路的谐振频率、谐振电阻、通频带。
［解］f 。
a —!= = 一— = 465 kHz2ny/LC 2^90 pH x 300 PF/? =0 =100 390pH =114kQ “ P \ 300 PFR.^RJIRIIR, c s p L=100 RQ//114. kQ//200 kQ=42 kQ O _R — "kQ _42kQ _“ rp J390pH/300 PF 1.14RQB\V Q7 = fJQ e = 465 kHz/37=12.6 kHz2. 3已知并联谐振回路的九=10MHz.C=50pF, B% = 150kHz.求回路的£和0以及 V =600kHz 时电压衰减倍数。
如将通频带加宽为300 kHz,应在回路两端并接一 个多大的电阻？ ［解］ L =——= -------- 丄 ------ =5X 10-67/=5M H (2JT f Q fC (2JTX 10X 106)2X 50X 10-12丄」竺斗6.7BW 01 15OxlO 3<1 z^^2x600xl03 YUofo丿10x10° 丿当 BW <)7 = 300 kHz 时L _ loxio- _333 J B%7300X 10’ 'R«=Q JP = ° -66 7R =Q ・p = --------- 「 ---------- =2」3xl04Q = 21.2kQ卩 尸 27TX1O* x 50x10"由于R 严企■，所以可得R + Rp/? = ^=1(),6k Ox21.2kQ = 212knRp-& 21.2kQ-10.6kQ2.4 并联回路如图P2. 4所示，已知：C = 360pE 厶=280pH. Q=100•厶=50pH ・ zNJN 严心&“心。
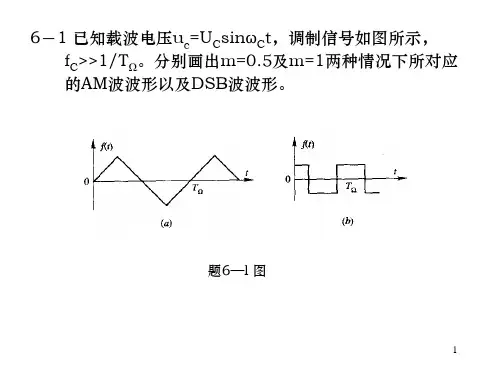
第六章 频谱搬移电路6－1.已知调制信号为载波信号为调幅的比例系数为试 1）写出调幅定义的数学表达式2）写出普通调幅波的数学表达式。
并画出其频谱图。
DSB/SC 调幅波的数学表达式。
并画出其频谱图。
SSB/SC 调幅波的数学表达式。
并画出其频谱图。
【解】：1）g(t)=+2）同理各波形频谱略。
6－2.有一调幅波方程式为：（1） 试求它所包含的各分量的频率与振幅。
（2） 给出这调幅波包络的形状，并求出峰值与谷值调幅度。
【解】：（1）载波频率为，振幅为25V ；第一边频为，振幅为 第二边频为，振幅为t U u Ω=ΩΩcos tU u c c c ωcos =a kc U a k tU ΩΩcos tt U Uk U t u c ca c AM ωcos )cos 1()(Ω+=Ωtt U k t u c a DSB ωcos cos )(Ω=Ω)sin cos cos (cos 21)(t t t t U k t u c c a SSBU ωωΩ-Ω=∧Ω)sin sin cos (cos 21t t t t U k c c a ωωΩ-Ω=ΩtU k c a )cos(21Ω+=ΩωtU k t u c a SSBD )cos(21)(Ω-=Ωωtt t u 5102sin )100002cos 3.050002cos 7.01(25πππ-+=510Hz Hz )500010(5±V75.87.02521=⨯⨯Hz)1000010(5±V75.33.02521=⨯⨯6－3.已知负载电阻上调幅波的表达式如下：伏 求：（1） 载波电压的振幅值U=? （2） 已调波电压的最大振幅值＝？ （3） 已调波电压的最小振幅值＝？（4） 调幅指数＝？ （5） 若负载电阻＝计算：负载电阻上吸收的载波功率＝？负载电阻上吸收的两个边频功率之和＝？ 【解】：（1）U ＝100V（2）＝（1+）U ＝(1+0.25)100＝125V （3）＝（1-）U ＝(1-0.25)100=75V（4）＝25/100＝0.25（5）＝＝＝5W＝＝0.16WLR tt t u c ωcos )cos 5.2100()(Ω+=maxU minU am LR ΩK 1LR cP LR sideP maxU am ⨯minU am ⨯am cP LR U221100021002⨯sideP ca P m 2412⨯5)25.0(212⨯⨯≈6－4.已知调幅波表达式。
第6章 角度调制与解调电路6.1填空题(1) 用低频调制信号去改变载波信号的频率和相位，分别称为 调频 和 调相 ，它们都是频谱的 非线性 变换。
(2) 单频调制时，调频信号的调频指数m f 与调制信号的 振幅 成正比，与调制信 号的 频率 成反比；最大频偏Δf m 与调制信号的 振幅 成正比，与 频率 无关。
(3) 取差值的混频器输入信号为u s (t)=0.3cos[（2π×107t ）+7sin(2π×103t)]V ，本振信号u L (t)=cos(2π×1.2×107t)V ，则混频器输出信号的载频为 0.2×107 Hz ，调频指数m f 为 7 ，最大频偏Δf m 为 7 ×103 Hz ，频带宽度为 16 ×103 Hz 。
(4) 3倍频器输入调频信号u s (t)=U sm cos[(2π×105t)+2sin(2π×102t)]V ，则3倍频器输出信号的载频为 3×105 Hz ，最大频偏为 3× 2 ×102 Hz ，频带宽度为 14×102 Hz 。
(5) 斜率鉴频是先将调频信号变换成 调频调幅 信号，然后用 包络检波器 进行解调得到原调制信号。
(6) 乘积型相位鉴频器由 频相变换网络 、 相乘器 和 低通滤波器 等组成。
6.2 已知调制信号3()8cos(2π10)V u t t Ω=⨯，载波电压6()5cos(2π10)V c u t t =⨯，3f 2π10rad/s V k =⨯，试求调频信号的调频指数f m 、最大频偏m f ∆和有效频谱带宽BW ，写出调频信号表示式。
[解] 3m 3m 2π108810Hz 2π2πf k U f Ω⨯⨯∆===⨯3m 33632π1088rad 2π102(1)2(81)1018kHz ()5cos(2π108sin 2π10)(V)f f FM k U m BW m F u t t t Ω⨯⨯===Ω⨯=+=+⨯==⨯+⨯6.3 已知调频信号72()3cos[2π105sin(2π10)]V o u t t t =⨯+⨯，3f 10πrad/s V k =g ，试：(1) 求该调频信号的最大相位偏移f m 、最大频偏m f ∆和有效频谱带宽BW ；(2) 写出调制信号和载波电压表示式。
[解] (1) 5f m =5100500Hz=2(+1)2(51)1001200Hzm f f m F BW m F ∆==⨯==+⨯= (2) 因为mf f k U m Ω=Ω，所以352π1001V π10f m fm U k ΩΩ⨯⨯===⨯，故27()cos 2π10(V)()3cos 2π10(V)c u t t u t t Ω=⨯=⨯40 6.4 已知载波信号m c ()cos()c u t U t ω=，调制信号()u t Ω为周期性方波，如图P6.4所示，试画出调频信号、瞬时角频率偏移()t ω∆和瞬时相位偏移()t ϕ∆的波形。
[解] FM ()u t 、()t ω∆和()t ϕ∆波形如图P6.4(s)所示。
6.5 调频信号的最大频偏为75 kHz ，当调制信号频率分别为100 Hz 和15 kHz 时，求调频信号的f m 和BW 。
[解] 当100Hz F =时，37510750100m f f m F ∆⨯===2(1)2(7501)100Hz 150kHz f BW m F =+=+⨯= 当15kHz F =时，33751051510m f f m F ∆⨯===⨯32(51)1510Hz 180kHz BW =+⨯⨯=6.6 已知调制信号3()6cos(4π10)V u t t Ω=⨯、载波电压8()2cos(2π10)V c u t t =⨯，p 2rad /V k =。
试求调相信号的调相指数p m 、最大频偏m f ∆和有效频谱带宽BW ，并写出调相信号的表示式。
[解] m 2612rad p p m k U Ω==⨯=3m 383124π10Hz=24kHz2π2π2(1)2(121)210Hz=52kHz ()2cos(2π1012cos 4π10)VΩ⨯⨯∆===+=+⨯⨯=⨯+⨯p p PM m f BW m F u t t t 6.7 设载波为余弦信号，频率25MHz c f =、振幅m 4V U =，调制信号为单频正弦波、频率400Hz F =，若最大频偏m 10kHz f ∆=，试分别写出调频和调相信号表示式。
[解] FM 波：3101025400m f f m F ∆⨯===6()4cos (2π251025cos 2π400)V FM u t t t =⨯⨯-⨯图P6.4图P6.4(s)41PM 波：25mp f m F∆== 6()4cos (2π251025sin 2π400)V PM u t t t =⨯⨯+⨯6.8 直接调频电路的振荡回路如图P6.8所示。
变容二极管的参数为：B 0.6V U =，2γ=，jQ 15pF C =。
已知20μH L =，6V Q U =，30.6cos(10π10)V u t Ω=⨯，试求调频信号的中心频率c f 、最大频偏m f ∆和调频灵敏度F S 。
[解] 66129.19310Hz 9.193MHz 2π2π20101510c jQf LC --===⨯=⨯⨯⨯m 6m 0.60.09090.660.09099.19310Hz=0.8356MHz 0.8356MHz1.39MHz/V 0.6Vc B Q m c C m F U m U U f m f f S U ΩΩ===++∆==⨯⨯∆=== 6.9变容二极管直接调频电路如图P6.9(a)所示，变容二极管的特性如图P6.9(b)所示。
当调制电压u Ω=cos(2π×10³t)v 时，试求调频信号的中心频率fc 和最大频偏Δfm 。
图P6.9[解]振荡部分的等效电路如图P6.9(s)所示图P6.842图P6.9(s)U Q =-2V C jQ =10pF C Σ=15.09pF ，所以fc=18.15MHz 当Ωt=0时，u Ω=1V , Cj=20pF, fmin=14.81MHz 当Ωt=π时，u Ω=-1V ，Cj=5pF, fmax=21.496MHz 由此可得Δfm=(21.496-14.81)／2=3.34MHz6.10 变容二极管直接调频电路如图P6.10所示，画出振荡部分交流通路，分析调频电路的工作原理，并说明各主要元件的作用。
当Cjq=20pf 时，求调频信号的中心频率fc.[解] 振荡部分的交流通路如图P6.10(s)所示。
电路构成克拉泼电路。
()U t 通过C L 加到变容二极管两端，控制其j c 的变化，从而实现调频，为变容二极管部分接入回路的直接调频电路。
图P6.10中，2R 、1C 为正电源去耦合滤波器，3R 、2C 为负电源去耦合滤波器。
4R 、5R 构成分压器，将-15 V 电压进行分压，取4R 上的压降作为变容二极管的反向偏压。
C L 为高频扼流圈，用以阻止高频通过，但通直流和低频信号；5C 为隔直流电容，6C 、7C 为高频旁43路电容。
fc=93.67MHz6.11变容二极管直接调频电路如图P6.11所示，试画出振荡电路简化交流通路；分析电路的工作原理，并说明电路的特点。
图P6.11[解]振荡电路简化交流通路如图P6.11(s)所示。
图P6.11(s)由图可见，它构成电容三点式振荡电路。
调制信号uΩ通过高频扼流圈加到对接的两只变容管两端，使其等效电容值随uΩ变化，振荡频率随之变化，实现调频作用。
该电路的主要特点是采用两只变容管对接，并部分接入振荡回路，以减小高频振荡电压对变容管特性的影响，可提高中心频率的稳定度，改善调频特性的线性度。
6.12图P6.12所示为晶体振荡器直接调频电路，画出振荡部分交流通路，说明其工作原理，同时指出电路中各主要元件的作用。
[解]由于1000 pF电容均高频短路，因此振荡部分交流通路如图P6.12(s)所示。
它由44变容二极管、石英晶体、电容等组成并联型晶体振荡器。
当()U tΩ加到变容二极管两端，使jC发生变化，从而使得振荡频率发生变化而实现调频。
由jC对振荡频率的影响很小，故该调频电路频偏很小，但中心频率稳定度高。
图P6.12中稳压管电路用来供给变容二极管稳定的反向偏压。
6.13晶体振荡器直接调频电路如图P6.13所示，试画交流通路，说明电路的调频工作原理。
[解]振荡部分的交流通路如图P6.13(s)所示，它构成并联型晶体振荡器。
变容二极管与石英晶体串联，可微调晶体振荡频率。
由于jC随()U tΩ而变化，故可实现调频作用。
6.14图P6.14所示为单回路变容二极管调相电路，图中，3C为高频旁路电容，m()cos(2π)u t U FtΩΩ=，变容二极管的参数为2γ=，1VBU=，回路等效品质因数15eQ=。
试求下列情况时的调相指数pm和最大频偏mf∆。
(1)m0.1VUΩ=、1000HzF=；(2)m0.1VUΩ=、2000HzF=；(3)m0.05VUΩ=、1000HzF=。
[解](1) m20.1150.3rad91ep c eB QU Qm m QU UγγΩ⨯⨯====++0.31000300Hzm pf m F∆==⨯=(2) 0.3rad,0.32000600Hzp mm f=∆=⨯=(3)20.05150.15rad,0.151000150Hz91p mm f⨯⨯==∆=⨯=+456.15 某调频设备组成如图P6.15所示，直接调频器输出调频信号的中心频率为10 MHz ，调制信号频率为1 kHz ，最大频偏为1.5 kHz 。
试求：(1) 该设备输出信号()o u t 的中心频率与最大频偏；(2) 放大器1和2的中心频率和通频带。
[解] (1) (10540)10MHz=100MHz c f =⨯-⨯1.5kHz 510=75kHz m f ∆=⨯⨯(2)1111.5kHz10MHz,==1.5,=2(1.5+1)1=5kHz 1kHz f f m BW =⨯22275kHz100MHz,==75,=2(75+1)1=152kHz 1kHzf f m BW =⨯6.16 鉴频器输入调频信号63()3cos[2π10+16sin (2π10)]V s u t t t =⨯⨯，鉴频灵敏度S D =-5mv /kHz ，线性鉴频范围max 2=50kHz f ∆，试画出鉴频特性曲线及鉴频输出电压波形。
[解] 已知调频信号的中心频率为310kHz ，鉴频灵敏度S D = -5mv /kHz ，因此可在图P6.16(a)中3=10kHz f 处作一斜率为-5mV/kHz 的直线即为该鉴频器的鉴频特性曲线。
