关于CDS的流水作业排序问题

流水线作业排序问题/productioncontrol/200908091604.html流水作业排序问题的基本特征是每个工件的加工路线都一致。

在流水生产线上制造不同的零件，遇到的就是流水作业排序问题。

我们说加工路线一致，是指工件的流向一致，并不要求每个工件必须经过加工路线上每台机器加工。

如果某些工件不经某些机器加工，则设相应的加工时间为零。

一般说来，对于流水作业排序问题，工件在不同机器上的加工顺序不尽一致。

但本节要讨论的是一种特殊情况，即所有工件在各台机器上的加工顺序都相同的情况。

这就是排列排序问题。

流水作业排列排序问题常被称作“同顺序”排序问题。

对于一般情形，排列排序问题的最优解不一定是相应的流水作业排序问题的最优解，但一般是比较好的解；对于仅有2台和3台机器的特殊情况，可以证明，排列排序问题下的最优解一定是相应流水作业排序问题的最优解。

这里只讨论排列排序问题。

但对于2台机器的排序问题，实际上不限于排列排序问题。

一、最长流程时间Fmax的计算这里所讨论的是n／m／P /Fmax，问题，其中n为工件数，m为机器数，P表示流水线作业排列排序问题，Fmax为目标函数。

目标函数是使最长流程时间最短，最长流程时间又称作加工周期，它是从第一个工件在第一台机器开始加工时算起，到最后一个工件在最后一台机器上完成加工时为止所经过的时间。

由于假设所有工件的到达时间都为零(ri=0，i= 1，2，…，n)，所以Fmax等于排在末位加工的工件在车间的停留时间，也等于一批工件的最长完工时间Cmax。

设n个工件的加工顺序为S＝(S1，S2，S3，…，Sn)，其中Si为第i位加工的工件的代号。

以表示工件Si在机器M k上的完工时间, 表示工件Si在Mk上的加工时间，k= 1，2，…，m；i=1，2，…，n，则可按以下公式计算：在熟悉以上计算公式之后，可直接在加工时间矩阵上从左向右计算完工时间。

下面以一例说明。

例9．4 有一个6／4／p／F max问题，其加工时间如表9—6所示。

)
华中科技大学管理学院
一、基本概念
4、排序问题的假设条件
• 一个工件不能同时在几台不同的机器上加工。 • 工件在加工过程中采取平行移动方式。 • 不允许中断。 • 每道工序只在一台机器上完成。 • 每台机器同时只能加工一个工件。 • 工件数、机器数和加工时间已知，加工时间与加工
顺序无关。
)
华中科技大学管理学院
一个实例： D=
2,1,3 2,2,1 2,3,2
241
T= 345
i {Ot} Tk
T’k
T*
M*
Oj
1 1,1,1 0
2
0
M1 1,1,1
2,1,3 0
3
0
M3
2 1,2,3 2
6
2,1,3 0
3
0
M3 2,1,3
3 1,2,3
3
7
3
M3 1,2,3
2,2,1 3
7
3
M1
4 1,3,2 7 2,2,1 3
四、一般n/m/P/ Fmax问题的 启发式算法
2、关键工件法：
• 计算Pi= Pij ，找出Pi最长的工件，将之作为 关键工件C。
• 对其余工件，若Pi1≤Pim ，则按Pi1由小到大排 成序列SA。若Pi1> Pim ，则按Pim由大到小排成 序列SB。
• 顺序（SA，C，SB）即为近优解。
)
四、一般n/m/P/ Fmax问题的 启发式算法
1、Palmer法
m
• 计算工件斜度指标i ： i [k (m 1) / 2]pik
m : 机器数
k 1
pik ：工件i在机器k上的加工时间。 i=1,2, ,n

-、流水作业排序1. 最长流程时间的计算例：有一个6/4/F/Fmax 问题，其加工时间如下表所示，当按顺序 加工 S=(6, 1, 5, 2, 4, 3) 时,求Fmax工件代号i 14 6 35 2 P 订 4 5 3 4 8 5 P 「23 9 1 3 7 5 PQ7 6 8 2 5 g563924解：列出加工时间矩阵根 据 公式Gsi 二max{Gk-i )si , C KSM }+ P sik,计算各行加丄时间，最后得出结果 Fmax=CmsnFmax=572•两台机器排序冋题的最优算法(Johnson 算法)例：求下表所示的6/2/F/Fmax 的最优解将工件2排在第1位 2将工件 将工件 将工件将工件将工件 3排在第 5排在第 6排在第 4排在第 最优加6位2位 3位5位4位2 56 1 4 S=(2, 5, 6, 1,4,33由上表可计算出，Fmax =283.—般n/m/F/Fmax问题的最优算法(一)Palmar算法(入i二刀[k-(m+l)/2]P ik k二1, 2,…,m按入i不增的顺序排列」】件)例：有一个4/3/F/Fmax问题，其加工时间如下表所示，用Palmar求解.解：入i二刀[k-(3+l)/2]P ik , k=l,2 , 3入i二-Pil+ Pi3于是,入1=-PU+ P13 =-1+4=3入2二-P21+ P23 =2+5二3入3二-P31+ P33 =-6+8=2入4二-P41+ P43 =-3+2二T按入i不增的顺序排列工件，得到加工顺序(1, 2, 3, 4)和(2, 1, 3, 4 )，经计算,二者都是最优顺序，Fmax=28(二)关键工件法例：有一个4/3/F/Fmax问题，其加工时间如下表所示,用关键工件法求解.3■ ■Pa Pit 24解：由上表可知，力口 u工时间最长的是3号工件，Pil<=Pi3的工件为1和2,按Pil不减的顺序排成Sa=(l,2),Pil>Pi3 的工件为4号工件，Sb= (4),这样得到加工顺序为(1,2, 3,4 )。

2）采用预订系统
对特定期间的服务需求做出较准确的估计
3）采用差异定价措施
5 调整服务能力的策略
1）进行有效的人员班次排序 2）利用临时工或兼职人员 3）招聘和培养多技能的员工
为何“集中使用”可以提高服务质量？
独立的系统
在此等待
“集中使用”系统
在此等待
减少等待时间的办法
减少平均服务时间 减少服务时间的可变性 增加服务人员 减少平均到达人数 通过顾客预约等办法来减少到达的可变性 集中使用服务资源 更好地计划和调度
i M1 M2
1 8 3
2 4 2
3 7 6
4 1 9
5 3 2
6 10 5
CWU-HRM
人力系
多工件多设备的排序问题启发算法
关键工件法
1983年提出 1.
2.
3.
计算每个工件的总加工时间Pi，找出加工时间最长 的工件C为关键工件 余下的工件，如果 Pi1 Pim 则按照Pi1 不减的顺 序排成序列S1，如果 Pi1 >Pim 则按照Pim 不增的顺 序排成序列S2， 序列（ S1 ，C， S2，）为所求排序
2) 最高优先权法则(Highest Priority Principle) 为减少等待顾客离队可能，应让顾客知道预期等待 火警、救护车 时间的信息，并使顾客得到定期更新的信息。
4 调整顾客到达率的措施
1）利用预约系统
控制顾客到达时间 实现最高程度的服务能力利用率 减少顾客等待的时间 提高服务水平
CWU-HRM
例
人力系
I Pi1 Pi2 Pi3 Pi
1 1 8 4 13
2 2 4 5 11
3 6 2 8 16

②③④ 8 6 12 156 10 5 7
②③④
minti1≥ maxti2
G
18 9 11 18
可得右下表：
H
7 11 10 13
按约翰逊法： 可得最优解为：②一④一③ 一①
设备零件 ① A 车床 15 B 铣床 3 C 磨床 4
②③④ 8 6 12 156 10 5 7
计算加工周期：
最优排序为：
Fi2 计算的根据：一个零件在设备(2)上加工必须等到该零件在设 备(1)上加工完并且设备(2)加工完前一个零件之后才能开始
故:从表中可以看出，最大流程时间( 零件的总加工周期）为40
3 三台设备流水型排序问题及解法
1）问题：n种零件在三台 设备零件 ①
设备上加工，其工艺顺
序均相同。
A 车床 15
31
等待时间 0
2
5
9
14
22
预定交货期 8
13 24 6
23
32
交货延期 0
0
0
8
0
0
加工顺序
12
3
4
5
6
零件号
③⑥①④②
⑤
作业时间 2
3
4
5
8
9
流程时间 2
5
9
14 22
31
等待时间 0
2
5
9
14
22
预定交货期 8
13 24 6
23
32
交货延期 0
0
0
8
0
0
答：最大流程时间：31 最大等待时间：22 平均流程时间=(2+5+9+14+22+31)／6＝13.83 平均等待时间=(0+2+5+9+1+14+22)/6=8.67 最大交货延期：8 总交货延期：( 0+0+0+8+0+0)=8

《生产与运作管理》试卷五一、填空题（本大题共7小题，每空2分，共计28分）1.用Johnson算法求下列6/2/F/F max问题的最优排序为，对应的F max。

i J1J2J3J4J5J6P i15 1 8 5 3 4Pi27 2 2 4 7 62.某装配线每天实际工作时间为480分钟，日产量为40台产品。

该装配线共有9道装配作业，各作业之间的关系及标准时间如下所示：那么它的节拍、最小工作地数、平衡的评价指标分别为、和。

作业 A B C D E F G H I紧前作业— A B B A C F DE GH时间（分）7 4 3 8 5 9 8 11 33.某产品流水生产，计划日产量为150件，两班生产，每班规定有12分钟停歇时间，计划废品率为5%，那么该产品生产的节拍的计算公式应为。

4.已知每件A产品需2件C部件，第6周C部件的库存量为110件，如A产品在第7周的计划订单投入量为190件，则C部件的净需求量为。

5.某超市的某种食用油平均日需求量为1000瓶，并且食用油的需求情况服从标准差为20瓶／天的正态分布，如果提前期是固定常数5天，如果该超市确定的客户服务水平不低于95%，请结合所提供的客户服务水平与安全系数对应关系的常用数据（见下表），计算出该食用油的订货点是；安全库存是。

服务水平0.9998 0.99 0.98 0.95 0.90 0.80 0.70安全系数 3.5 2.33 2.05 1.65 1.29 0.84 0.556.某装配车间零件需求率为490个/月，零件由厂内生产，生产率为900个/月，生产准备费为100元/每批，存储费为0.5元/个/月。

则经济生产批量、每月平均成本、最佳循环时间和最大库存水平分别为、和、。

7.n/3/P/C max表示。

二、简答题（本大题共4小题，每小题5分，共计20分）1.简述MRP的运算逻辑，并说明如何与OPT相结合。

2.按照对象专业化原则建立生产单位的优缺点是什么？3.简述OPT的三个财务指标和三个作业指标是什么？OPT的九原则是什么？4.简述网络计划方法的优点。

k=2，3，…，m i=1，2，…，n ◆当ri=0，i=1，2，…，n时
C3(2)
P23
Fmax= Cm(sn)
GWM-PPT V2010.1
汇报人：杨猛
2、最长流程时间Fmax的计算
例题:6/4/p/ Fmax，其加工时间如表1所示
J1(精灵 精灵) 精灵 M1(冲压) M2(焊装) M3(涂装) M4(总装) M4( ) 4 4 5 4 J2(炫丽 炫丽) 炫丽 2 5 8 2 J3(酷熊 酷熊) 酷熊 3 6 7 4 J4(凌傲 凌傲) 凌傲 1 7 5 3 4 4 5 3
序列A为（2，5，6，1），序列B为（4，3），构 成最优顺序为（2，5，6，1，4，3）
J2 M1 M2
GWM-PPT V2010.1
J5 3 7
J6 4 4
J1 5 7
汇报人：杨猛
J4 5 4
J3 8 2
1 2
3、n/m/p/ Fmax问题的启发式算法
J1 M1 M2 M3 M4 3 7 4 5 J2 12 4 8 7 J3 9 6 7 11 J4 4 8 1 5 J5 5 5 3 9 J6 6 10 12 2
汇报人：杨猛
J4 113 727 535 338
J3 316 633 742 446
22 57 512 113
三、约翰逊算法及其启发式算法
GWM-PPT V2010.1
汇报人：杨猛
1、n/2/P/Fmax 约翰逊算法
◆Johnson算法:一短、二看、三排序
J3 J1 M1 M2 2 8 7 3 J2 5 4 J1 J3 8 2 3 7
表1
J5(腾翼） J6（哈弗） 腾翼） （哈弗） 腾翼 2 5 5 1

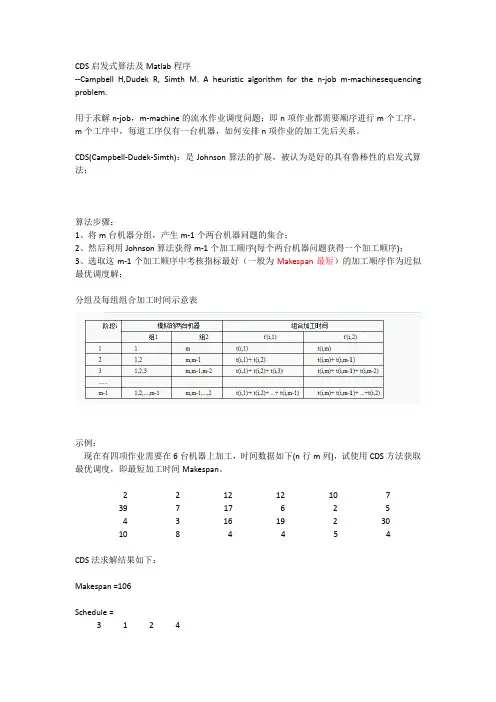
CDS启发式算法及Matlab程序--Campbell H,Dudek R, Simth M. A heuristic algorithm for the n-job m-machinesequencing problem.用于求解n-job，m-machine的流水作业调度问题；即n项作业都需要顺序进行m个工序，m个工序中，每道工序仅有一台机器，如何安排n项作业的加工先后关系。

CDS(Campbell-Dudek-Simth)：是Johnson算法的扩展，被认为是好的具有鲁棒性的启发式算法；算法步骤：1、将m台机器分组，产生m-1个两台机器问题的集合；2、然后利用Johnson算法获得m-1个加工顺序(每个两台机器问题获得一个加工顺序)；3、选取这m-1个加工顺序中考核指标最好（一般为Makespan最短）的加工顺序作为近似最优调度解；分组及每组组合加工时间示意表示例：现在有四项作业需要在6台机器上加工，时间数据如下(n行m列)，试使用CDS方法获取最优调度，即最短加工时间Makespan。

2 2 12 12 10 739 7 17 6 2 54 3 16 19 2 3010 8 4 4 5 4CDS法求解结果如下：Makespan =106Schedule =3 1 2 43 1 2 43 1 2 43 1 2 4可以看出，分组后的5（m-1）组两机器问题中，通过Johnson法获取的最优调度中，有4组获得了最优调度： 3 1 2 4也验证了CDS法具有较高的Matlab程序--CDS.mfunction [Makespan,Schedule]=CDS(PT)[n,m]=size(PT);if n<=1error('The job qty must large than 2')endPT=double(PT);%Create new 2-stage-machine timeNewPT(1:n,1:2,1:m-1)=0.0;for i=1:m-1for j=1:iNewPT(:,1,i)=NewPT(:,1,i)+PT(:,j);NewPT(:,2,i)=NewPT(:,2,i)+PT(:,m-j+1);endend%Calculate the m-1 group 2-machine problem using Johnson Rulefor i=1:m-1[MidMakespan(i),MidSchedule(i,:)]=Johnson(NewPT(:,:,i)');end%Calculate the Makespan of the m-1 MidSchedulefor i=1:m-1StartTime(1:m,1:n)=0;StartTime(1,MidSchedule(i,1))=0;for j=2:nStartTime(1,MidSchedule(i,j))=StartTime(1,MidSchedule(i,j-1))+PT(MidSchedule(i,j-1),1);endfor k=2:mStartTime(k,MidSchedule(i,1))=StartTime(k-1,MidSchedule(i,1))+PT(MidSchedule(i,1),k-1);for j=2:nStartTime(k,MidSchedule(i,j))=max(StartTime(k,MidSchedule(i,j-1))+PT(MidSchedule(i,j-1),k),...StartTime(k-1,MidSchedule(i,j))+PT(MidSchedule(i,j),k-1));endendMMidMakespan(i)=StartTime(m,MidSchedule(i,n))+PT(MidSchedule(i,n),m); end% Sort the Makespan and obtain the optimal Schedule[Best,BestIndex]=sort(MMidMakespan);OptNum=1;Makespan=MMidMakespan(BestIndex(1));Schedule=MidSchedule(BestIndex(1),:);%Statistic the total optimal shedulesfor i=2:m-1if MMidMakespan(BestIndex(i))==MMidMakespan(BestIndex(1))OptNum=OptNum+1;Schedule(OptNum,:)=MidSchedule(BestIndex(i),:);endend。

∑ 模型 １ ｒｊ，Ｃｍａｘ !Ｙ
Ｄｊ （π＊ ）的 最 优 算 法，且
证 明 了 其 可 行 性 ；原 晋 江 、慕 运 动 等 人 在 文 献 ［５］中
证明了模 型 １ ｒｊ，Ｄｍａｘ（π＊ ）!ｋ Ｃｍａｘ 的 可 行 性，且
给 出 了 它 的 多 项 式 时 间 算 法 ．Ｊｏｈｎｓｏｎ 在 文 献 ［６］中
１ 引 言 和 问 题 阐 述
重新排序问题是决策者在使得目标函数值为 最优的前提下，对 原 始 的 工 件 集 最 优 排 序，这 时 有 一 批 新 的 工 件 来 到 ，需 要 把 新 到 达 的 工 件 插 入 到 原 有 的 序 列 中 一 起 进 行 加 工 ，则 原 有 的 工 件 可 能 产 生 一 定 的 错 位 ，一 般 要 求 在 不 打 乱 太 多 原 始 工 件 位 置 的基础上 进 行 重 新 排 序，使 得 目 标 函 数 值 达 到 最 优．流水作业排序是每个工件需要在每个处理 机 上 加工，且要求 每 个 工 件 的 加 工 顺 序 相 同．本 文 是 将 重新排序的思想方法应用到流水作业排序模型中， 主要考虑了两台机器的流水作业重新排序的问题． 对于两台机器的流水作业最大完工时间最小的排 序 问 题 ，假 设 原 始 工 件 集 已 经 在 使 得 目 标 函 数 为 最 优的前提下，进行 了 最 优 排 序，新 的 工 件 在 零 时 刻 到达，此时需要将 新 工 件 和 原 始 工 件 在 一 起 加 工， 则须考虑原始工 件 的 错 位，使 得 在 错 位 约 束 下，得 到全部工件的最大完工时间最小的重新排序问题． Ｈａｌｌ和 Ｐｏｔｔｓ［１］第 一 次 明 确 提 出 了 时 间 错 位 和 序 列 错 位 的 概 念 ，进 而 提 出 了 最 大 错 位 和 总 错 位 的 月

作业：用Palmer法求解
2、关键工件法
（1）计算每个工件的总加工时间，找出加工时间最长 的工件C，将其作为关键工件； （2）对于余下的工件若Pi1≤Pim，则按Pi1 不减的顺序排 成一个序列Sa ，若Pi1＞Pim， 则按Pim 不增的顺序排列成 一个序列Sb。 （3）顺序（ Sa，C，Sb）即为所求顺序。
K = 1
m
i [k (3 1) / 2]Pik
k 1
m
i [k 2]Pik
k 1
m
=(1-2) Pi1+(2-2) Pi2+(3-2) Pi3
=- P i1 + P i3
λi =- P i1 + P i3 λ1 = - P 11 + P 13= -1+4 = 3 λ2 = -P21 + P23= -2 + 5= 3 λ3 =- P31 + P33 = -6 + 8 = 2 λ4 =-P 41+P43 = -3 + 2 = -1 按λi不增的顺序排列，得到加工顺序 （1，2，3，4）和（2，1，3，4）， 两者均为最优顺序，Fmax=28。
例：有一个4/3/P/ Fmax 问题，其加工时间如下 表所示，用Palmer法求解。
表11 加工时间矩阵 -5 i Pi1 Pi2 Pi3 1 1 8 4 2 2 4 5 3 6 2 8 4 3 9 2
解
i [k (m 1) / 2]Pik , (k 1,2,3, )
k 1
M2
M3 M4
t1 t2 t3 t T平顺
4
时间 第1个工序的所有工件加工完成的时刻为基准，向前推（n-1）个t2时间，作为

i ti1 ti 2 ti 3 ti 4
6 2，2 5，7 5，12 1，13 表 2 顺序 S 下的加工时间矩阵 1 5 2 4，6 4，11 5，17 4，21 4，10 4，15 5，22 3，25 2，12 5，20 8，30 2，32 4 1，13 7，27 5，35 3，38 3 3，16 6，33 7，42 4，46
当 ri = 0 ， i = 1,2, L , n 时，最大流程时间为
-782-
（1） （2） （3）
Fmax = csn m
当由式（3）得出 csn m 时， Fmax 就求得了。
（4）
在熟悉以上计算公式之后， 可直接在加工时间矩阵上从左到右计算完工时间。 下面 以一例说明。 例 1 有一个 6 / 4 / P / Fmax 问题，其加工时间如表 1 所示。当按顺序 S = (6,1,5,2,
j =1
m
hij ： J i 在 M j 上的等待时间， J i 的总等待时间为 H i = ∑ hij ；
j =1
m
ri ： J i 的到达时间，指 J i 从外部进入车间，可以开始加工的最早时间； d i ： J i 的完工期限； cij ： J i 在 M j 上的完工时间； Ci ： J i 的完工时间， Ci = ri + ∑ (hij + tij ) = ri + H i + Ti ；
计算的 Matlab 程序如下： clc,clear t=[4 2 3 1 4 2 4 5 6 7 4 5 5 8 7 5 5 5 4 2 4 3 3 1]'; s=[6 1 5 2 4 3]; st=t(s,:); %提出指定顺序的时间矩阵 [n,m]=size(st); c(1,:)=cumsum(st(1,:)); %计算 c 的第一行 c(2:n,1)=c(1,1)+cumsum(st(2:n,1)); %计算 c 的第一列的除第 1 个元素外其它元素

J3 8 2
1 2
8
26 J3
J4
M2 3
J5J4 22
J3 26 28
5
10
15
20
25
30 时间
2、最长流程时间Fmax 的计算
◆ 最长流程时间（加工周期） 从第一个工件在第一台机器开始加工时算起，到最后一个 工件在最后一台机器上完成加工时为止所经过的时间 ◆ 假设所有工件的到达时间都为零 ri= 0, i= 1, 2, ……n Fmax等于排在末位加工的工件在车间的停留时间，也等于 一批工件的最大完工时间Cmax ◆ 设n 个工件的加工顺序为 S= ( S1, S2,……Sn） Si为排第i 位加工的工件的代号
1、名词术语 2、假设条件 3、符号说明 4、排序问题的分类和表示方法 5、排序问题的评价标准（目标函数）
1、名词术语
（1）排序（Sequencing） ：确定工件在机器上的加工顺序。 （2）编制作业计划（Scheduling） 确定工件的加工顺序，并确定机器加 工每个工件的开始时间和完成时间 （3）调度（控制）（Controlling） 对生产过程实施控制所采取的行动 •派工（Dispatching）——按作业计划的要求，将具体生产任务安 排到具体的机床上加工 •赶工（Expediting）——在实际进度落后于计划进度时采取的行动 排序的各个名词来自加工制造业，（机器、工件、工序、加工 时间），但此时它们的含义已经扩大了。如机器可以是人、计算机等 服务者。
5、排序问题的评价标准（目标函数）
（1）以按时交货作为目标函数 平均延迟时间 L 平均延误时间 T 最大延误时间Tmax 延误的工件数n （2）以工件的完工时间和工件的流程时间为目标函数 最大完工时间Cmax 最长流程时间Fmax 平均完工时间 C 平均流程时间 F （3）其他目标函数 在制品占用量最小 总调整时间最小 延期罚款最小 生产费用最小 总利润最大 设备利用率最大

作业排序的优先规则知识梳理在进行作业排序时，需用到优先调度规则。

这些规则可能很简单，仅需根据一种数据信息对作业进行排序。

这些数据可以是加工时间、交货日期或到达的顺序。

其它的规则，尽管也同样简单但可能需要更多的信息，通常是需要一个指标，比如最小松弛时间规则和关键比率规则。

还有另外的规则，比如约翰逊规则，在一个机器序列上应用作业排序，并需要一个计算程序来规定作业的顺序。

1、F CFS （先到优先）按订单送到的先后顺序进行加工。

2、S OT （最短作业时间优先）这个规则等同于SPT （最短加工时间）规则。

3、D date （交货期优先）最早交货期最早加工。

4、S TR （剩余时间最短优先）剩余时间是指交货期前所剩余时间减去加工时间所得的差值。

5、RAN （随机排序）主管或操作工通常随意选择一件他们喜欢的进行加工。

6、LCFS （后到优先）该规则经常作为缺省规则使用。

因为后来的工单放在先来的上面，操作人员通常是先加工上而的工单。

“n个作业一一单台工作中心的问题”或“n/1”，理论上，排序问题的难度随着工作中心数量的增加而增大，而不是随着作业数量的增加而增大，对n的约束是其必须是确定的有限的数。

例：n个作业单台工作中心排序问题。

在一周的开始，有5位顾客提交了他们的订单。

原始数据间=3+7+9+15+16二50 （天）平均流程时间二50/5=10天将每个订单的交货日期与其流程时间相比较，发现只有A 订单能按时 交货。

订单B, C, D 和E 将会延期交货，延期时间分别为1,2, 6, 14 天。

每个订单平均延期(0+1+1+2+6+14) /5二4. 6天。

平均流程时间=36/5=7. 5天SOT 规则的平均流程时间比FCFS 规则的平均流程时间小。

另外，订单E 和C 将在交货R 期前完成，订单A 仅延期1天。

每个订单的平均 延期时间为(0+0+1+4+7) /5=2. 4天。

方案二 利用S0T (最短作业时间)规则，流程时间为:间=1+3+6+10+16=36 （天）。

如何进行作业排序
参考资料：轻松管生产
《轻松管生产》是2006年广东经济出版社出版的图书。
内容介绍
作业排序就是安排作业的活动、资源利用或者配置设施的时间表。它是从工作中心的角度，来控 制加工工件的作业顺序或作业优先级。作业排序包括决定工件加工顺序以及安排相应机器设备来 进行加工。
方法/步骤
1.作业排序方法类型 一个作业排序系统区别于另一个作业排序系统的特征是:在决定排序时，生产能力是如何考虑的。 作业排序系统既能用无限负荷，也一可以用有限负荷。无限负荷指的是当将工作分配到工作中心 时，只考虑它需要多少时间，而不直接考虑完成这份工作所需的资源是否有足够的能力，也不考 虑在工作中心中，每个资源完成这项工作的实际顺序。有限负荷方法实际上是根据对每一个订单 所需的调整和运行时间对句种资源进行详细的排序。实质上，这个系统明确地规定了在工作日的 何一时刻，何一种资源要做的工作。理论上讲，当采用有限负荷时，所有的计划都是一可行的。 另一个区别作业排序系统的特征是看作业排序是基于前向排序还是后l句的顺序进行排序。前向 排序系统刊一以告诉我们汀单能够完成的最早时间，是最常用的排序方法。后向排序系统是从未 来的某个时期(可能是一个交货日期)开始，按照从后向前的顺序进行排序。
方法/步骤
(8)将工作中心的输入信息和工人们的实际能力相匹配。
参考资料：约翰逊法
约翰逊法，又名约翰逊规则，是作业排序中的一种排序方法。这种方法适用的条件是：n个工件 经过二、三台设备（有限台设备）加工，所有工件在有限设备上加工的次序相同。
参考资料：基于遗传算法与仿真的生产作业排序系统研究与开发
参考资料：排序问题
排序问题(sequencing problem)亦称工件加工日程表问题，是一类典型的组合优化问题。设用m 台机器加工n个工件，给定了加工每个工件所用机器的次序，以及每台机器加工每个工件所需要 的时间、问题是确定工件在每台机器上的加工次序以使预先选定的目标函数达到最小，这个目标 函数通常是完成时间、平均完成时间、机器的空间时间等的一个非降函数。排序问题有两个类型： 1.流水作业，这时要求每个工作在机器上的加工次序都一样；2.工件作业，这时每个工件在机器 上的加工次序不必一致。流水作业可以看做是工件作业的一种特殊情形，三台或以上机器的排序 问题多为NP完全问题.因此是很困难的 。

机械制造行业中的流水作业排序问题作者：马超来源：《中国科技博览》2013年第35期【摘要】企业要管理好，生产计划很重要。

保证生产交期和提高生产效率的前提条件，就是要有一个完整合理的生产计划，制定好详细的生产计划对生产的顺利进行有举足轻重的作用。

无论何种生产型态，首先要重视计划，实施有计划地生产。

无计划意味着无序，无序的结果便是无效率，最终是无效益。

而解决好生产过程中的排序问题就是完成生产计划的重要保障。

【关键词】排序生产作业计划 Palmer法关键工件法 CDS法中图分类号：TH 文献标识码：A 文章编号：1009―914X（2013）35―393―01一、生产作业计划与流水作业排序问题生产作业计划是根据企业年度、季度计划的要求，来具体地安排车间、工段、班组乃至工作地在月、旬、日以及昼夜、轮班和小时的工作任务。

对于大型机械制造企业，生产作业计划一般分为公司级生产作业计划和车间级生产作业计划两级。

一般来说，公司生产制造部负责编制和下达公司级生产作业计划，各车间的作业计划员在接到公司级生产作业计划以后，要负责编制本车间的生产作业计划，并将车间级生产作业计划分解落实到各个班组及各个工作地，将车间的生产任务变成各个班组、各个工作地的生产任务。

每个工作地生产作业计划的完成，保证了车间生产作业计划的完成；每个车间生产作业计划的完成，保证了公司级生产计划的完成；公司级生产计划的完成，保证了公司生产经营计划的完成。

假如某个车间需要生产n种零部件，这n种零部件需要经过m台设备进行加工，并且每种零部件在每台设备上的加工时间各不相同。

那么怎样编排这n种零部件的加工顺序可以使总加工时间最短，这是排序要解决的问题。

一般说来，排序只是确定工件在机器上的加工顺序，而编制生产作业计划，则不仅包括确定工件的加工顺序，而且还包括确定机器加工每个工件的开始时间和完工时间。

可以说解决好排序问题是顺利完成生产作业计划的保障。

二、排序问题的表示方法通常我们用4个参数来表示不同的排序问题，4个参数表示法为：n/m/p/Fmax其中，n为零部件数，m为设备（或机器数），p表示流水作业排列排序问题，Fmax则表示目标函数，通常是使其值最小。

生产作业排序的问题引言在制造业或生产行业中，作业排序是一项重要的管理任务。

作业排序的目的是合理、高效地安排生产作业，确保生产线的顺畅运行和最大化生产效率。

然而，由于生产作业的多样性和复杂性，作业排序的问题变得相当困难。

本文将探讨生产作业排序问题的背景、相关算法和解决方案。

背景生产作业排序是指将待处理的生产作业按特定的规则进行排列，以最小化生产周期、最大化生产效率。

当涉及到多个生产作业时，这个问题变得尤为复杂。

常见的作业排序问题包括单机调度问题、流水线调度问题和工序调度问题。

单机调度问题单机调度问题是指在单一设备或机器上安排多个作业的问题。

其目标是使得每个作业的完成时间最小化或工期最短。

常用的调度算法包括最早截止时间优先（EDD）算法、最短处理时间优先（SPT）算法和最长处理时间优先（LPT）算法。

流水线调度问题流水线调度问题是指在多个设备或工序之间安排多个作业的问题。

其目标是使得整个生产线的生产效率最大化。

常见的流水线调度问题包括多品种无等待流水线调度问题和有限缓冲流水线调度问题。

解决这些问题的方法包括最早完成时间优先（EFT）算法、最短工序时间优先（SOT）算法和最大可完工期（MTWR）算法。

工序调度问题工序调度问题是指在多个工序上安排多个作业的问题。

其目标是使得整个生产过程的吞吐量最大化。

常见的工序调度问题包括并行机调度问题和流水车间调度问题。

解决这些问题的方法包括遗传算法、模拟退火算法和禁忌搜索算法。

算法与解决方案为了解决生产作业排序问题，研究者们提出了多种算法和解决方案。

以下是一些常用的算法和解决方案：1.基于优先级规则的算法：根据作业的特定属性（如截止时间、处理时间等）确定作业的优先级。

常用的优先级规则有最早截止时间优先（EDD）规则、最短处理时间优先（SPT）规则和最长处理时间优先（LPT）规则。

2.遗传算法：模拟生物遗传过程，通过交叉、变异等操作产生新的解，并根据解的适应度进行选择。

C A
0＋1＝ 1
1＋2＝ 3 3＋3＝ 6
B
D 合计
4
5
8
6
6＋4＝10
10＋5＝15
10－8＝2
15－6＝9
平均作业数＝35/15＝2.33
15
35
12
排序 准则
EDD 交货 期最 早准 则
任务 排序
加工 时间
交货 期
通过时间
延误时间
E A D C B 合计
1 3 5 2 4 15 5 3 1
A
3
9
16 17
22
B
3
0
5
17
23
27
30
(a) J1 - J2 - J3- J4 - J5
A B 3 2 6 8 7 6 1 4 5 3
30
1
A
7
14
19
22
B
1
5 7
15
21 24 26 26
(b) J4 - J2 - J3- J5 - J1 A 1 6 7 5 3 B 4 8 6 3 2
(a) J1 - J2 - J3- J4 - J5
A
B
0 30
(b) J4 - J2 - J3- J5 - J1
A B 26
可以看出，初始作业顺序的总加工周期是30，用约 翰逊法排出的作业顺序总加工周期是26，显然后者 的结果优于前者。
习题
• 假设有A，B，C，D，E五种零件，每种零件均需 先在甲设备上加工，再在乙设备上加工。甲、 乙设备各一台，零件加工时间如下表所示。问 如何加工使总加工时间最短？最短时间是多少？ 整个加工过程中甲乙两台设备的空闲时间是多 少？
单台机器的排序问题