下载文档原格式
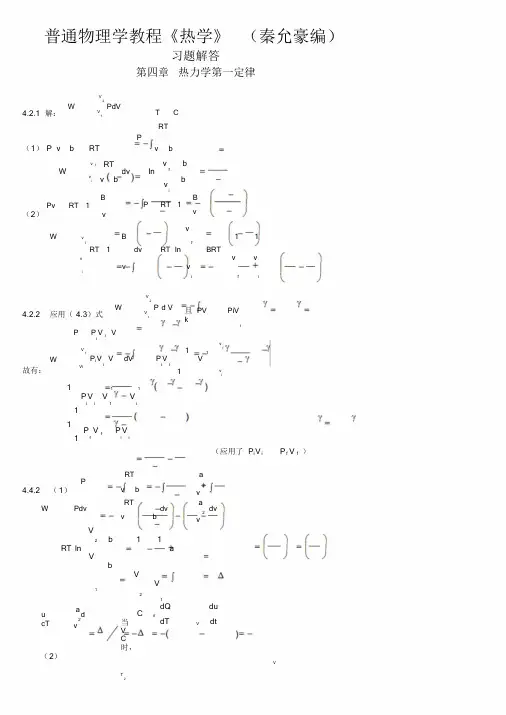
普通物理学教程《热学》 （秦允豪编）习题解答第四章 热力学第一定律V24.2.1 解：WV1PdVT CRT P（1） P v bRT vbWvvi fRT v bdv lnv fvibbB Pv RT 1 （2）vPRT 1B vWvvB11 ffRT 1dv RT lnBRTvvvvviifiV24.2.2 应用（ 4.3）式WV1P d V且PVPiVkiPP V i i V故有：VfWVi1 P i V VdV P VViii11vfvi11 1P V VViifi11 1 P fVfP Vii（应用了 P i V iP f V f ）4.4.2 （1）PRT vba 2vWPdvRT vbdv a 2 vdv V2b 1 1RT lnaVbVV121u cTa 2 vd当VC时，C VdQdT Vdu dt（2）VT2∴C CV QT1C d T C T4.4.3 水蒸气的凝结热即为定压状况下单位质量物质相变时吸收（或释放）的热量，在等压下此值即为比焓变化，即：l HV h 2545 .0 100 .59 2444 .4 m kJ（系统放热）4.4.4 铜升温过程，是等压过程T2H QT T12 2P C dT a bT dT aT bTPT T21 12T1a T2 T1b2T 222T114 2 22.310 1200 300 5. 92 1200 300212. 47107 J mol4.4.5Q hP NH1 3 1 33 h h 29154 8669 8468 46190 .5 J mol2 2N H2 2 2 214.4.6 在定压情况下，1molH 2 和12molO2化合生成1mol 水时吸收的热量为5 1Q （系统放热Q ' Q ）H 2 .858 10 J mol每产生一个水分子有两个电子自阴极到阳极，生成 1 m ol 水有2 N A 电子到阳极。
总电量为q 19 232 （q 2N e ）1 .60 10 6 .02 10 CA两极间电压为， A q19 23A 1 .229 2 1 .60 10 6 .02 1082.84%5Q' 2. 858 104.4.7 设 1 m ol 固体状态方程为：v v aT bP0 ，内能表示为：u CT aPT ，a 均为常数。
普通物理学教程《热学》（秦允豪编）习题解答 第一章 导论1.3.1设一定容气体温度计是按摄氏温标刻度的，它在 0.0405MPa 和 0.0553MPa ,试问（1）当气体的压强为 0.0101MPa （2）当温度计在沸腾的硫中时 （0.1013MPa 下的硫的沸点为 444.5）, = 0.0405MPa ；t s =100 C P s 二 0.0553MPa k = tga = —s ― =C , t p =P ,P s-P100 C t v 二 P - P⑵由Ps - P i1.3.2 有一支液体温度计，在 0.1013MPa 下，把它放在冰水混 合物中的示数t0=- 0.3C ；在沸腾的水中的示数 t0= 101.4C 。
试问放在真实温度为 66.9 C 的沸腾的甲醇中的示数是多少？若 用这支温度计测得乙醚沸点时的示数是为 34.7 C,则乙醚沸点 的真实温度是多少？在多大一个测量范围内，这支温度计的读 数可认为是准确的（估读到0.1 C ）分析：此题为温度计的校 正问题。
依题意：大气压为0.1013Mpa 为标准大气压。
冰点It p —tj t p ' E - t sTi 十't s -t it p2、真实温度t i =0 C 汽占 t s•) I “八'、=100 C,题设温度计为未经校证的温度计，t i二-0.3 Ct s =101.4 C1）标准温度为t ^ 66.9 C ，求示数温度t^ ?（2）当示数为t P • 34.7 C ，求标准温度tP 解：X为测温物质的测温属性量设t s -右是等分的，故t X 乂 X （是线性的）, t p- t i 对标准温度计t s- t It (X pc XX - X i X s _Xj(1)tp- 1非标准温度计t s '-t i 'tpT'tsT' ••••••( 3)(2)下水的沸点时的压强分别为时的待测温度是多少？ 气体的压强是多少？解： （1）ti=0 C, R1、示数温度: 0.1013MPa 下的冰点及 0.1013MPa 题设的温度计在（(1 )、( 2)两式得:t s -t i66 9 _0 “101.4 0.3 -0.3 =68.01 C100-0t p '-t i ' PtsT Jts ti（答案）67.7 C(2)(3)34 7 + 0 3101.4 0.3 100一°^3441C3、（ 1）两曲线交汇处可认为 tp =tp ',代入（3）t p -0 t p - 0.3 t p 0.3100墾=a+blg R' 1.3.4 已知： T 求：当R'=1000门时，T =?解：令 X =lg R' =lg1000 =lg103 =3141 已知：P 。
秦允豪热学第四章习题答案秦允豪热学第四章习题答案热学作为一门物理学科，研究的是物体的热现象和热力学规律。
而在学习热学的过程中，习题是不可或缺的一部分。
本文将为大家提供秦允豪热学第四章习题的答案，希望能够帮助大家更好地理解和掌握热学知识。
第一题：一个理想气体在等温过程中，其体积由V1变为V2，求该过程中气体对外界做功的大小。
答案：根据理想气体的状态方程PV=constant，可知P1V1 = P2V2。
由于等温过程中温度保持不变，所以P1 = P2。
因此，对外界做功的大小为W = P1(V2 - V1) = P2(V2 - V1)。
第二题：一个物体的质量为m，温度由T1降低到T2，求该过程中物体释放的热量。
答案：根据热容的定义，热量Q = mcΔT，其中c为物体的比热容，ΔT为温度变化。
由于温度由T1降低到T2，所以ΔT = T2 - T1。
因此，物体释放的热量为Q = mc(T2 - T1)。
第三题：一个理想气体在等压过程中，其体积由V1变为V2，求该过程中气体吸收的热量。
答案：根据理想气体的状态方程PV=constant，可知P1V1 = P2V2。
由于等压过程中压强保持不变，所以P1 = P2。
根据热容的定义，热量Q = ncΔT，其中n为气体的物质量，c为气体的摩尔热容，ΔT为温度变化。
由于等压过程中压强保持不变，所以ΔT = T2 - T1。
因此，气体吸收的热量为Q = nc(T2 - T1)。
第四题：一个物体的质量为m，温度由T1升高到T2，求该过程中物体吸收的热量。
答案：根据热容的定义，热量Q = mcΔT，其中c为物体的比热容，ΔT为温度变化。
由于温度由T1升高到T2，所以ΔT = T2 - T1。
因此，物体吸收的热量为Q = mc(T2 - T1)。
通过以上习题的解答，我们可以看出热学中的一些基本概念和公式的应用。
热学作为一门重要的物理学科，不仅在理论上具有广泛的应用，而且在实际生活中也有着重要的意义。
第四章热力学第一定律(题号有所不同)5－1.0.020Kg的氦气温度由升为，若在升温过程中：（1）体积保持不变；（2）压强保持不变；（3）不与外界交换热量，试分别求出气体内能的改变，吸收的热量，外界对气体所作的功，设氦气可看作理想气体，且，解：理想气体内能是温度的单值函数，一过程中气体温度的改变相同，所以内能的改变也相同，为：热量和功因过程而异，分别求之如下：（1）等容过程：V=常量A＝0由热力学第一定律，（2）等压过程：由热力学第一定律，负号表示气体对外作功，（3）绝热过程Q＝0由热力学第一定律5－2.分别通过下列过程把标准状态下的0.014Kg氮气压缩为原体积的一半；（1）等温过程；（2）绝热过程；（3）等压过程，试分别求出在这些过程中气体内能的改变，传递的热量和外界对气体所作的功，设氮气可看作理想气体，且，解：把上述三过程分别表示在P-V图上，（1）等温过程理想气体内能是温度的单值函数，过程中温度不变，故由热一、负号表示系统向外界放热（2）绝热过程由或得由热力学第一定律另外，也可以由及先求得A（3）等压过程，有或而所以＝＝＝由热力学第一定律，也可以由求之另外，由计算结果可见，等压压缩过程，外界作功，系统放热，内能减少，数量关系为，系统放的热等于其内能的减少和外界作的功。
5－3 在标准状态下的0.016Kg的氧气，分别经过下列过程从外界吸收了80cal的热量。
（1）若为等温过程，求终态体积。
（2）若为等容过程，求终态压强。
（3）若为等压过程，求气体内能的变化。
设氧气可看作理想气体，且解：（1）等温过程则故（2）等容过程（3）等压过程5－4 为确定多方过程方程中的指数n，通常取为纵坐标，为横坐标作图。
试讨论在这种图中多方过程曲线的形状，并说明如何确定n。
解：将两边取对数或比较知在本题图中多方过程曲线的形状为一直线，如图所示。
直线的斜率为可由直线的斜率求n。
或即n可由两截距之比求出。
5－5 室温下一定量理想气体氧的体积为，压强为。
3121131211332332=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+-=a a a a a a 普通物理学教程《热学》（秦允豪编）习题解答第二章 分子动理学理论的平衡态理论2.2.1解：（a ）归一化()⎰⎰-===aa aA Adx dx x f 12，a A 21=或：可直接由面积求。
()⎰=⋅==12A a dx x f S ，a A 21= ()[]⎰⎰====+-04122aa x a dx a x dx x xf x()()()()()⎰⎰⎰⎰⎰--+=+-==00aa a adxx xf dx x xf dx x xf dx x f x dx x f x x()⎰⎰=⨯+=⎥⎥⎦⎤⎢⎢⎣⎡+=+=--a aa a a a a a x x a xdx a xdx a 022020202212122212121()232226121a x a dx x a dx x f x x aa ====-⎰⎰（b ）()⎰⎰=⋅==a aa A a Adx dx x f 20212，a A 21=（或12=⋅a A ） ()()⎰=⋅==a z aa a dx x xf x 2222121 ()()⎰=⋅=⋅⋅==a a a a a a dx x f x x 20233223486123121（c ）()⎰=⨯⋅=1212A a dx x f ，a A 1= 确定()x f 的关系，由121211x x y y x x y y --=--，得 ()02a aax x f -+=()aa x a x f 02-= ()()()⎰⎰⎰-++==+--aa a a dxx ax a dx x ax a dx x xf x 02022211aa x ax a x ax a 032203223121131211⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡+=-()()()⎰⎰⎰-++==-a a dx x ax a dx x ax a dx x f x x 032023222211 aa x ax a x ax a 043204324131141311⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡+=-24444261413141311aa a a a a =⎪⎭⎫ ⎝⎛-+-=（d ）()⎰=⋅⋅=1221a A dx x f ,a A 1= 依题意得解析式()a x a A x f 0= ()()aaa x a A x f 22--=()()⎰⎰⎰--==a aa a xdxa x a A dx x a A dx x xf x 022202 a a a a a xA x a A x a A 2223032233+-= ()()22333241831a a a a a a a-++-=a a a =+-=32 ()⎰⎰⎰⎰+-==a a a a a a dxx A dx x a A dx x a A dx x f x x 20022233222aa a a a xa x a x a 23242042324141+-= ()()3344242832164141a a a a a a a a -+--=22226731441541a a a a =+-=2.2.2 ()242x Aex f xπα-=，将()x f 归一化，求A 。
普通物理学教程《热学》（秦允豪编）习题解答第二章 分子动理学理论的平衡态理论2.2.1在图2,22中列出了某量x 的值的三种不同的概率分布函数的图线。
试对于每一种图线求出常数A 的值，使在此值下函数成为归一化函数，然后计算x 和x 2的平均值，在(a)的情况下还求出x 的平均值。
（修改：定积分需加上下限）解：（a ）归一化()⎰⎰-===aa aA Adx dx x f 12，a A 21=或：可直接由面积求。
()⎰=⋅==12A a dx x f S )⎰=⋅==12A a dx x f S )⎰=⋅==12A a dx x f S ，a A 21= ()[]⎰⎰====+-04122aa x a dx a x dx x xf x()aax x f x dx-=⎰)()()()()⎰⎰⎰⎰⎰--+=+-==00aa aadxx xf dx x xf dx x xf dx x f x dx x f x x()⎰⎰=⨯+=⎥⎥⎦⎤⎢⎢⎣⎡+=+=--a aa a a a a a x x a xdx a xdx a 022020202212122212121()232226121ax a dx x a dx x f x x aa ====-⎰⎰（b ）220()21aaf x dx Adx a A =⋅=⎰⎰，a A 21=（或12=⋅a A ） ()()⎰=⋅==a z aa a dx x xf x 2222121 ()()⎰=⋅=⋅⋅==a a a a a a dx x f x x 20233223486123121（c ）()⎰=⨯⋅=1212A a dx x f ，a A 1= 确定()x f ，由121211x x y y x x y y --=--，得 ()02a aa x x f -+=()aa x a x f 02-= ()()()⎰⎰⎰-++==+--aa a a dxx ax a dx x ax a dx x xf x 0202221103121131211332332=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛+-=a a a a a a aa x ax a x ax a 032203223121131211⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡+=-22()aax x f x dx -=⎰)()()⎰⎰⎰-++==-a a dxx ax a dx x ax a dx x f x x 032023222211aa x ax a x ax a 043204324131141311⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡+=-24444261413141311a a a a a a =⎪⎭⎫ ⎝⎛-+-=2.2.2 量的概率分布函数具有形式()242x Aex f xπα-= ,式中 A 和 是常数，试写出的值出现在 7.9999到8.0001范围内的概率P 的近似表示式。
.第一章温度1-1定容气体温度计的测温泡浸在水的三相点槽内时,个中气体的压强为50mmHg.（1）用温度计测量300K的温度时,气体的压强是若干？（2）当气体的压强为68mmHg时,待测温度是若干？解：对于定容气体温度计可知：(1)(2)1-3用定容气体温度计测量某种物资的沸点.本来测温泡在水的三相点时,个中气体的压强;当测温泡浸入待测物资中时,测得的压强值为,当从测温泡中抽出一些气体,使减为200mmHg时,从新测得,当再抽出一些气体使减为100mmHg时,测得.试肯定待测沸点的幻想气体温度.解：依据从幻想气体温标的界说：依以上两次所测数据,作T-P图看趋向得出时,T约为亦即沸点为400.5K.题1-4图1-6水银温度计浸在冰水中时,水银柱的长度为;温度计浸在滚水中时,水银柱的长度为.（1）在室温时,水银柱的长度为若干？（2）温度计浸在某种沸腾的化学溶液中时,水银柱的长度为,试求溶液的温度.解：设水银柱长与温度成线性关系：当时,代入上式当,（1）（2）1-14水银气压计中混进了一个空气泡,是以它的读数比现实的气压小,当准确的气压计的读数为时,它的读数只有.此时管内水银面到管顶的距离为.问当此气压计的读数为时,现实气压应是若干.设空气的温度保持不变.题1-15图解：设管子横截面为S,在气压计读数为和时,管内空气压强分离为和,依据静力均衡前提可知,因为T.M不变依据方程有,而1-25一抽气机转速转/分,抽气机每分钟可以或许抽出气体,设容器的容积,问经由若干时光后才干使容器的压强由降到.解：设抽气机每转一转时能抽出的气体体积为,则当抽气机转过一转后,容器内的压强由降到,疏忽抽气进程中压强的变更而近似以为抽出压强为的气体,因而有,当抽气机转过两转后,压强为当抽气机转过n转后,压强设当压强降到时,所需时光为分,转数1-27把的氮气压入一容积为的容器,容器中本来已充满同温同压的氧气.试求混杂气体的压强和各类气体的分压强,假定容器中的温度保持不变.解：依据道尔顿分压定律可知又由状况方程且温度.质量M不变.第二章气体分子活动论的根本概念2-4 容积为2500cm3×1015个氧分子,有×1015个氮分子和×10-7g的氩气.设混杂气体的温度为150℃,求混杂气体的压强.解：依据混杂气体的压强公式有PV=（N 氧+N 氮+N 氩）KT个中的氩的分子个数：N 氩=15231001097.410023.640103.3⨯=⨯⨯⨯=-N M 氩氩μ（个）∴ P=（1.0+4.0+4.97）10152231033.225004231038.1--⨯=⨯⨯⋅Pa 41075.1-⨯≅mmHg2-5一容器内有氧气,其压强P=1.0atm,温度为t=27℃,求 (1) 单位体积内的分子数： (2) 氧气的密度; (3) 氧分子的质量; (4) 分子间的平均距离; (5) 分子的平均平动能. 解：(1)∵P=nKT∴n=252351045.23001038.110013.10.1⨯=⨯⨯⨯⨯=-KT P m -3(2)l g RTP /30.1300082.0321=⨯⨯==μρ(3)m 氧=23253103.51045.2103.1-⨯≅⨯⨯=n ρg (4) 设分子间的平均距离为d,并将分子算作是半径为d/2的球,每个分子的体积为v 0. V 0=336)2(34d d ππ=∴71931028.41044.266-⨯=⨯⨯==ππn d cm (5)分子的平均平动能ε为：ε14161021.6)27273(1038.12323--⨯=+⨯⨯==KT （尔格）2-12 气体的温度为T = 273K,压强为 P=×10-2atm,密度为ρ×10-5g(1) 求气体分子的方均根速度.(2) 求气体的分子量,并肯定它是什么气体.解：（1）s m P RT V /485332===ρμ（2）mol g mol kg PRTn PN A /9.28/109.283=⨯===-ρμ 该气体为空气2-19 把尺度状况下224升﹒l 2mol-2-1.解：在尺度状况西224l 的氮气是10mol 的气体,所以不竭紧缩气体时,则其体积将趋于10b,即0.39131,分子直径为： 内压强P 内=8.90703913.039.122≅=V a atm 注：一摩尔现实气体当不竭紧缩时（即压强趋于无穷大）时,气体分子不成能一个挨一个的慎密分列,因而气体体积不克不及趋于分子本身所有体积之和而只能趋于b.第三章 气体分子热活动速度和能量的统计散布律3-1 设有一群粒子按速度散布如下：试求(1)平均速度V;（2）方均根速度2V （3）最可几速度Vp 解：（1）平均速度：18.32864200.5200.4800.3600.2400.12≅++++⨯+⨯+⨯+⨯+⨯=V (m/s)(2) 方均根速度37.322≅∑∑=ii i N V N V(m/s)3-2 盘算300K 时,氧分子的最可几速度.平均速度和方均根速度.解：s m RT V P /395103230031.8223=⨯⨯⨯==-μ3-13 N 个设想的气体分子,其速度散布如图3-13所示（当v ＞v 0时,粒子数为零）.（1）由N 和V 0求a.00之间的分子数.（1） 求分子的平均速度.解：由图得分子的速度散布函数：N V Va 0 (00V V 〈〈) Na (002V V V 〈〈)f(v)= 0 (02V V 〉)(1) ∵dv V Nf dN )(=∴aV aV V V a advdV V VadV V f N N VV V 00200202321)(0=+=+==⎰⎰⎰∞(2) 00之间的分子数3-21 收音机的腾飞前机舱中的压力计批示为1.0atm,温度为270C;腾飞后压力计指导为0.80atm,温度仍为27 0C,试盘算飞机距地面的高度.解：依据等温气压公式： P=P0e -有In = - ∴ H = - In •个中In =In = -0.223,空气的平均分子量u=29. ∴××103(m)3-27 在室温300K 下,一摩托车尔氢和一摩尔氮的内能各是若干？一克氢和一克氮的内能各是若干？×103(J) ×103(J)可见,一摩气体内能只与其自由度（这里t=3,r=2,s=0）和温度有关.一克氧和一克氮的内能： ∴××103(J)3-30 某种气体的分子由四个原子构成,它们分离处在正四面体的四个极点：（1）求这种分子的平动.迁移转变和振动自由度数.（2）依据能均分定理求这种气体的定容摩尔热容量.解：（1）因n个原子构成的分子最多有3n个自由度.个中3个平动自由度,3个迁移转变自由度,3n-1个是振动自由度.这里n=4,故有12个自由度.个中3个平动.个迁移转变自由度,6个振动自由度.(2) 定容摩尔热容量：Cv= (t+r+2s)R = ×18×2= 18（Cal/mol•K）第四章气体内的输运进程4－2.氮分子的有用直径为,求其在尺度状况下的平均自由程和持续两次碰撞间的平均时光.解：＝代入数据得：－（m）＝代入数据得：＝（s）4－4.某种气体分子在时的平均自由程为.（1）已知分子的有用直径为,求气体的压强.（2）求分子在的旅程上与其它分子的碰撞次数.解：（1）由得：代入数据得：（2）分子走旅程碰撞次数（次）4－6.电子管的真空度约为HG,设气体分子的有用直径为,求时单位体积内的分子数,平均自由程和碰撞频率.解：（2）（3）若电子管中是空气,则4－14.今测得氮气在时的沾次滞系数为试盘算氮分子的有用直径,已知氮的分子量为28.解：由《热学》（）式知：代入数据得：4－16.氧气在尺度状况下的集中系数：.求氧分子的平均自由程.解：代入数据得4－17.已知氦气和氩气的原子量分离为4和40,它们在尺度状况嗲的沾滞系数分离为和,求：（1）氩分子与氦分子的碰撞截面之比;（2）氩气与氦气的导热系数之比;（3）氩气与氦气的集中系数之比.解：已知（1）依据（2）因为氮氩都是单原子分子,因而摩尔热容量C雷同（3）现P.T都雷同,第五章热力学第必定律5-21. 图5-21有一除底部外都是绝热的气筒,被一地位固定的导热板隔成相等的两部分A和B,个中各盛有一摩尔的幻想气体氮.今将80cal 的热量迟缓地同底部供应气体,设活塞上的压强始终保持为1.00atm,求A部和B部温度的转变以及各接收的热量(导热板的热容量可以疏忽).若将地位固定的导热板换成可以自由滑动的绝热隔板,反复上述评论辩论.解：(1)导热板地位固定经底部向气体迟缓传热时,A部气体进行的是准静态等容进程,B部进行的是准表态等压进程.因为隔板导热,A.B两部气体温度始终相等,因而（2）绝热隔板可自由滑动B部在1大气压下整体向上滑动,体积保持不变且绝热,所以温度始终不变.A部气体在此大气压下吸热膨胀5－25.图5-25,用绝热壁作成一圆柱形的容器.在容器中央置放一无摩擦的.绝热的可动活塞.活塞两侧各有n 摩尔的幻想气体,开端状况均为p0.V0.T0.设气体定容摩尔热容量C v为常数,将一通电线圈放到活塞左侧气体中,对气体迟缓地加热,左侧气体膨胀同时通度日塞紧缩右方气体,最后使右方气体压强增为p0.问：（1）对活塞右侧气体作了若干功？（2）右侧气体的终温是若干？（3）左侧气体的终温是若干？（4）左侧气体接收了若干热量？解：（1）设终态,阁下两侧气体和体积.温度分离为V左.V右.T左.T 右,两侧气体的压强均为p0对右侧气体,由p0 =p右得则外界（即左侧气体）对活塞右侧气体作的功为（2）（3）（4）由热一左侧气体吸热为5-27 图5-27所示为一摩尔单原子幻想气体所阅历的轮回进程,个中AB为等温线.已知3.001, 求效力.设气体的解:AB,CA为吸引进程,BC为放热进程.又且故%5-28 图5-28(T-V图)所示为一幻想气体(已知)的轮回进程.个中CA为绝热进程.A点的状况参量(T, )和B点的状况参量(T, )均为已知.(1)气体在A B,B C两进程中各和外界交流热量吗?是放热照样吸热?(2)求C点的状况参量(3)这个轮回是不是卡诺轮回?(4)求这个轮回的效力.解:(1)A B是等温膨胀进程,气体从外界吸热,B C是等容降温进程,气体向外界放热.从又得(3)不是卡诺轮回(4)==5-29 设燃气涡轮机内工质进行如图5-29的轮回进程,个中1-2,3-4为绝热进程;2-3,4-1为等压进程.试证实这轮回的效力为又可写为个中是绝热紧缩进程的升压比.设工作物资为幻想气体, 为常数.证:轮回中,工质仅在2-3进程中吸热,轮回中,工质仅在4-1进程中放热轮回效力为从两个绝热进程,有或或由等比定理又可写为5-31 图5-31中ABCD为一摩尔幻想气体氦的轮回进程,全部进程由两条等压线和两条等容线构成.设已知A点的压强为 2.0tam,体积为 1.01,B点的体积为2.01,C点的压强为 1.0atm,求轮回效力.设解:DA和AB两进程吸热,===6.5atmlBC和CD两进程放热==%5-33 一制冷机工质进行如图5-33所示的轮回进程,个中ab,cd分离是温度为, 的等温进程;cb,da为等压进程.设工质为幻想气体,证实这制冷机的制冷系数为证:ab,cd两进程放热, 而Cd,da两进程吸热, ,而则轮回中外界对体系作的功为从低温热源1,(被致冷物体)接收的热量为制冷系数为证实进程中可见,因为,在盘算时可不斟酌bc及da两进程.第六章热力学第二定律6-24 在一绝热容器中,质量为m,温度为T1的液体和雷同质量的但温度为T2的液体,在必定压强下混杂后达到新的均衡态,求体系从初态到终态熵的变更,并解释熵增长,设已知液体定压比热为常数CP.解：两种不合温度液体的混杂,是不成逆进程,它的熵变可以用两个可逆进程熵变之和求得.设T1>T2,（也可设T1<T2,成果与此无关）,混杂后均衡温度T知足下式mC p(T1－T)=mC p(T－T1)∴ T = (T1＋T2)温度为T1的液体准静态等压降温至T,熵变成温度为T2的液体准静态等压升温至T熵变成由熵的可加性,总熵变成：△S=△S＋△S=mC p(ln＋ln)=mC p ln=mC p ln因（T1－T2）2>0 即T12－2T1T2＋T22>0T12＋2T1T2＋T22－4T1T2>0由此得（T1＋T2）2>4T1T2所以,△S>0因为液体的混杂是在绝热容器内,由熵增长道理可见,此进程是不成逆.6-26 如图6—26,一摩尔幻想气体氢（γ=1.4）在状况1的参量为V1=20L,T1=300K.图中1—3为等温线,1—4为绝热线,1—2和4—3均为等压线,2—3为等容线,试分离用三条路径盘算S3－S1：（1）1—2—3（2）1—3（3）1—4—3解：由可逆路径1—2—3求S3－S1C p ln－C v ln=R ln=R ln=8.31 ln=5.76 J·K－1（2）由路径1—3求S3－S1=5.76 J·K－1因为1—4为可逆绝热进程,有熵增道理知S4－S1=0从等压线4—3= =从绝热线1—4 T1v1γ－1或则即故=5.76 J·K－1盘算成果标明,沿三条不合路径所求的熵变均雷同,这反应了一切态函数之差与进程无关,仅决议处.终态.6-28 一现实制冷机工作于两恒温热源之间,热源温度分离为T1=400K,T2=200K.设工作物资在没一轮回中,从低温热源接收热量为200cal,向高温热源放热600cal.（1）在工作物资进行的每一轮回中,外界对制冷机作了若干功？（2）制冷机经由一轮回后,热源和工作物资熵的总变更（△S b）（3）如设上述制冷机为可逆机,经由一轮回后,热源和工作物资熵的总变更应是若干？（4）若（3）中的饿可逆制冷机在一轮回中从低温热源接收热量仍为200cal,试用（3）中成果求该可逆制冷机的工作物资向高温热源放出的热量以及外界对它所作的功.解：（1）由热力学第必定律,外界对制冷机作的功为A=Q1-Q2=600-200=400cal=1672J(2)经一轮回,工作物资又回到初态,熵变成零,热源熵变是高温热源熵变△S1与低温热源熵变△S2之和.所以,经一轮回后,热源和工作物资的熵的总变更为△S b=（3）视工资与热源为一绝热系,若为可逆机,由熵增长道理知,全部体系的总熵变成零.即△S0=0（4）由（3）知,对于可逆机即工质想高温热源放出的热量.而外界对它的功为A=Q1'-Q2=400-200=200cal=836J盘算成果标明,,当热源雷同,从低温热源取相等的热量时,可逆制冷机比现实制冷机所需的外功少。
