热学第四章习题参考答案

普通物理学教程《热学》（秦允豪编）习题解答第四章 热力学第一定律4.2.1 解：⎰-=21V V PdVW C T =（1）()RT b v P =-b v RTP -=⎪⎪⎭⎫ ⎝⎛---=--=⎰b v b v dv bv RTW i f v v fi ln（2）⎪⎭⎫ ⎝⎛-=v B RT Pv 1 ⎪⎭⎫ ⎝⎛-=v B RT P 1 ⎪⎪⎭⎫ ⎝⎛-+-=⎪⎭⎫ ⎝⎛--=⎰i f i f v v v v BRT v v RT dv v B RT W f i11ln 14.2.2 应用（4.3）式⎰-=21V V PdVW 且k PiV PV i ==γγ γγ-=V V P P i i故有：fifv v i i V Vii i V V P dV V V P W γγγγγ----=-=⎰111()()i i f f i f i i V P V P V V V P --=--=--111111γγγγγ （应用了γγf f i i V P V P =）4.4.2 （1）2v ab v RT P --=⎰⎰⎰+--=-=dvv adv b v RT Pdv W 2aV V b V b V RT ⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛---=121211ln （2）d v a cT u +-=2当C V =时，V V V dt du dT dQ C ⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛= ∴C C V =TC CdT Q T T ∆==⎰214.4.3 水蒸气的凝结热即为定压状况下单位质量物质相变时吸收（或释放）的热量，在等压下此值即为比焓变化，即：()kJh mHl V 4.244459.1000.2545-=--=∆-=∆= （系统放热）4.4.4 铜升温过程，是等压过程()212121221T T T T T T P P bT aT dT bT a dT C Q H ⎪⎭⎫⎝⎛+=+===∆⎰⎰()()2122122T T b T T a -+-=()()122447107.2300120092.5213001200103.2-⋅=-⨯⨯+-⨯⨯=mol J4.4.515.46190846823866921291542321223-⋅-=⎪⎭⎫⎝⎛⨯+⨯--=+-=mol J h h h Q H N NH P4.4.6 在定压情况下，21molH 和221molO 化合生成mol 1水时吸收的热量为 1510858.2-⋅⨯-=∆=mol J H Q （系统放热Q Q -='）每产生一个水分子有两个电子自阴极到阳极，生成mol 1水有A N 2电子到阳极。

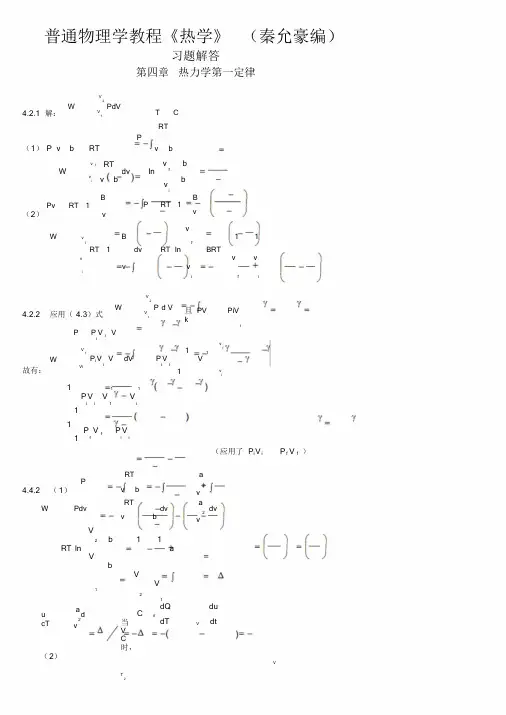
普通物理学教程《热学》 （秦允豪编）习题解答第四章 热力学第一定律V24.2.1 解：WV1PdVT CRT P（1） P v bRT vbWvvi fRT v bdv lnv fvibbB Pv RT 1 （2）vPRT 1B vWvvB11 ffRT 1dv RT lnBRTvvvvviifiV24.2.2 应用（ 4.3）式WV1P d V且PVPiVkiPP V i i V故有：VfWVi1 P i V VdV P VViii11vfvi11 1P V VViifi11 1 P fVfP Vii（应用了 P i V iP f V f ）4.4.2 （1）PRT vba 2vWPdvRT vbdv a 2 vdv V2b 1 1RT lnaVbVV121u cTa 2 vd当VC时，C VdQdT Vdu dt（2）VT2∴C CV QT1C d T C T4.4.3 水蒸气的凝结热即为定压状况下单位质量物质相变时吸收（或释放）的热量，在等压下此值即为比焓变化，即：l HV h 2545 .0 100 .59 2444 .4 m kJ（系统放热）4.4.4 铜升温过程，是等压过程T2H QT T12 2P C dT a bT dT aT bTPT T21 12T1a T2 T1b2T 222T114 2 22.310 1200 300 5. 92 1200 300212. 47107 J mol4.4.5Q hP NH1 3 1 33 h h 29154 8669 8468 46190 .5 J mol2 2N H2 2 2 214.4.6 在定压情况下，1molH 2 和12molO2化合生成1mol 水时吸收的热量为5 1Q （系统放热Q ' Q ）H 2 .858 10 J mol每产生一个水分子有两个电子自阴极到阳极，生成 1 m ol 水有2 N A 电子到阳极。

总电量为q 19 232 （q 2N e ）1 .60 10 6 .02 10 CA两极间电压为， A q19 23A 1 .229 2 1 .60 10 6 .02 1082.84%5Q' 2. 858 104.4.7 设 1 m ol 固体状态方程为：v v aT bP0 ，内能表示为：u CT aPT ，a 均为常数。

秦允豪热学第四章习题答案秦允豪热学第四章习题答案热学作为一门物理学科，研究的是物体的热现象和热力学规律。

而在学习热学的过程中，习题是不可或缺的一部分。

本文将为大家提供秦允豪热学第四章习题的答案，希望能够帮助大家更好地理解和掌握热学知识。

第一题：一个理想气体在等温过程中，其体积由V1变为V2，求该过程中气体对外界做功的大小。

答案：根据理想气体的状态方程PV=constant，可知P1V1 = P2V2。

由于等温过程中温度保持不变，所以P1 = P2。

因此，对外界做功的大小为W = P1(V2 - V1) = P2(V2 - V1)。

第二题：一个物体的质量为m，温度由T1降低到T2，求该过程中物体释放的热量。

答案：根据热容的定义，热量Q = mcΔT，其中c为物体的比热容，ΔT为温度变化。

由于温度由T1降低到T2，所以ΔT = T2 - T1。

因此，物体释放的热量为Q = mc(T2 - T1)。

第三题：一个理想气体在等压过程中，其体积由V1变为V2，求该过程中气体吸收的热量。

答案：根据理想气体的状态方程PV=constant，可知P1V1 = P2V2。

由于等压过程中压强保持不变，所以P1 = P2。

根据热容的定义，热量Q = ncΔT，其中n为气体的物质量，c为气体的摩尔热容，ΔT为温度变化。

由于等压过程中压强保持不变，所以ΔT = T2 - T1。

因此，气体吸收的热量为Q = nc(T2 - T1)。

第四题：一个物体的质量为m，温度由T1升高到T2，求该过程中物体吸收的热量。

答案：根据热容的定义，热量Q = mcΔT，其中c为物体的比热容，ΔT为温度变化。

由于温度由T1升高到T2，所以ΔT = T2 - T1。

因此，物体吸收的热量为Q = mc(T2 - T1)。

通过以上习题的解答，我们可以看出热学中的一些基本概念和公式的应用。

热学作为一门重要的物理学科，不仅在理论上具有广泛的应用，而且在实际生活中也有着重要的意义。

第四章热力学第一定律(题号有所不同)5－1.0.020Kg的氦气温度由升为，若在升温过程中：（1）体积保持不变；（2）压强保持不变；（3）不与外界交换热量，试分别求出气体内能的改变，吸收的热量，外界对气体所作的功，设氦气可看作理想气体，且，解：理想气体内能是温度的单值函数，一过程中气体温度的改变相同，所以内能的改变也相同，为：热量和功因过程而异，分别求之如下：（1）等容过程：V=常量A＝0由热力学第一定律，（2）等压过程：由热力学第一定律，负号表示气体对外作功，（3）绝热过程Q＝0由热力学第一定律5－2.分别通过下列过程把标准状态下的0.014Kg氮气压缩为原体积的一半；（1）等温过程；（2）绝热过程；（3）等压过程，试分别求出在这些过程中气体内能的改变，传递的热量和外界对气体所作的功，设氮气可看作理想气体，且，解：把上述三过程分别表示在P-V图上，（1）等温过程理想气体内能是温度的单值函数，过程中温度不变，故由热一、负号表示系统向外界放热（2）绝热过程由或得由热力学第一定律另外，也可以由及先求得A（3）等压过程，有或而所以＝＝＝由热力学第一定律，也可以由求之另外，由计算结果可见，等压压缩过程，外界作功，系统放热，内能减少，数量关系为，系统放的热等于其内能的减少和外界作的功。

5－3 在标准状态下的0.016Kg的氧气，分别经过下列过程从外界吸收了80cal的热量。

（1）若为等温过程，求终态体积。

（2）若为等容过程，求终态压强。

（3）若为等压过程，求气体内能的变化。

设氧气可看作理想气体，且解：（1）等温过程则故（2）等容过程（3）等压过程5－4 为确定多方过程方程中的指数n，通常取为纵坐标，为横坐标作图。

试讨论在这种图中多方过程曲线的形状，并说明如何确定n。

解：将两边取对数或比较知在本题图中多方过程曲线的形状为一直线，如图所示。

直线的斜率为可由直线的斜率求n。

或即n可由两截距之比求出。

5－5 室温下一定量理想气体氧的体积为，压强为。

第四章思考题4-1 容器被闸板分割为A 、B 两部分。

A 中气体参数为P A 、T A ，B 为真空。

现将隔板抽去，气体作绝热自由膨胀，终压将为P 2，试问终了温度T 2是否可用下式计算？为什么?122()k k A Ap T T p -=答：气体作绝热自由膨胀是不可逆绝热过程，因此终了温度T 2不可用上式计算。

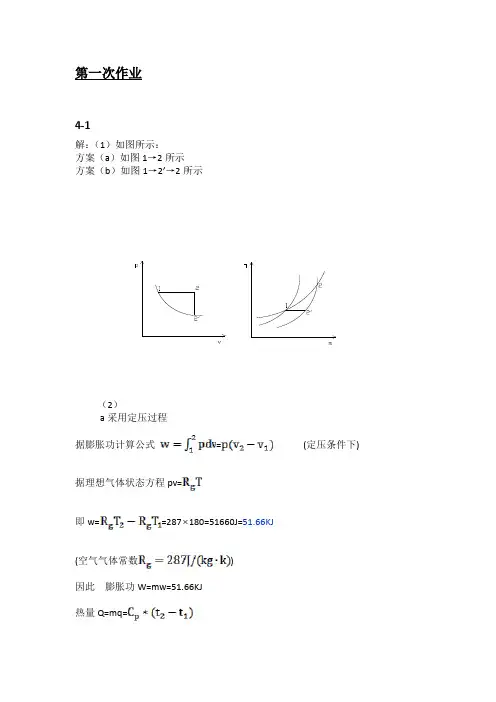
4-2 今有任意两过程a-b ，b-c ，b 、c 两点在同一定熵线上，如图所示。

试问：Δｕab 、Δｕac 哪个大？再设b 、c 两点在同一条定温线上，结果又如何？答：由题可知，因b 、c 两点在同一定熵线上T b >T c , ｕb >ｕc . Δｕab >Δｕac 。

若b 、c 两点在同一条定温线上，T b =T c , ｕb =ｕc . Δｕab =Δｕac 。

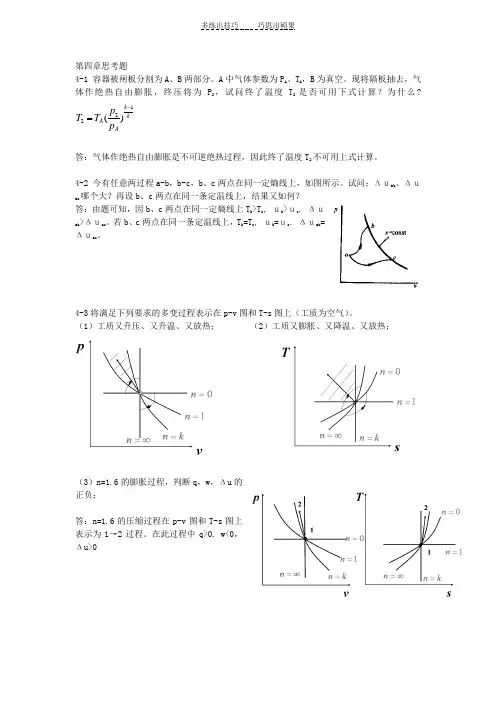
4-3将满足下列要求的多变过程表示在p-v 图和T-s 图上（工质为空气）。

（1）工质又升压、又升温、又放热； （2）工质又膨胀、又降温、又放热；（3）n=1.6的膨胀过程，判断q ，w ，Δu 的正负；答：n=1.6的压缩过程在p-v 图和T-s 图上表示为1→2过程。

在此过程中q>0, w<0，Δu>0（4）n=1.3的压缩过程，判断q ，w ，Δu 的正负。

答：n=1.3的压缩过程在p-v 图和T-s 图上表示为1→2过程。

在此过程中q<0，w<0，Δu>04-4将p-v 图表示的循环，如图所示，表示在T －s 图上。

图中：2-3，5-1，为定容过程；1-2，4-5为定熵过程；3-4为定压过程。

答：T-s 图如图所示4-5 以空气为工质进行的某过程中，加热量的一半转变为功，试问过程的多变指数n 为多少？试在p-v 图和T-s 图上画出该过程的大概位置（比热容比可视为定值）。

答：多变过程中，遵循热力学第一定律q u w =∆+，由题可知12q u =∆，由于v 21()1n -k q c T T n =--，所以()v 21v 21()()21n -k c T T c T T n -=--即：()121n -k n =-，0.6n =4-6如果采用了有效的冷却方法后，使气体在压气机汽缸中实现了定温压缩，这时是否还需要采用多级压缩？为什么？（6分） 答：还需要采用多级压缩，由余隙效率可知，12111n v p c p λ⎡⎤⎛⎫⎢⎥=-- ⎪⎢⎥⎝⎭⎢⎥⎣⎦，余隙使一部分气缸容积不能被有效利用，压力比越大越不利。

热学习题答案第四章：热力学第一定律(内容对应参考书的第五章)1. （P 192。

1）0.020Kg 的氦气温度由17C ︒升为27C ︒。

若在升温过程中：（1）体积保持不变；（2）压强保持不变；（3）不与外界交换热量，试分别求出气体内能的改变，吸收的热量，外界对气体所做的功。

设氦气可看作理想气体，且R C m v 23,=。

解：已知=︒=C T 171290K ，K C T 300272=︒=，()mol molKg KgM5/104020.03=⨯==-μν（1）体积保持不变：外界对气体做功0=A ，内能的变化()()()cal R R T T C U m v 1507529030023512,≈=-⨯=-=∆ν，根据热力学第一定律，由0=A 有系统吸收热量()cal R U Q 15075≈=∆= （或者=623.55J ）；（2）压强保持不变：由P ＝常数，及理想气体状态方程RT PV ν=有 外界对气体做功()()()cal R T T R V V P PdV A V V 10050212121-≈-=-=-=-=⎰ν，内能的变化()()cal R T T C U m v 1507512,≈=-=∆ν， 由热力学第一定律，得系统吸收热量：()cal R A U Q 250125≈=-∆=；此问也可以先求A 和()12T T C Q P -=，而后再由第一定律得Q A U +=∆。

（3）不与外界交换热量：由于理想气体内能的变化只由温度决定，则 内能的变化仍然是()()cal R T T C U m v 1507512,≈=-=∆ν，但由0=Q ，根据热力学第一定律知此时外界对系统所做的功完全转化为系统内能的增加量，即外界对气体做功()()cal R T T C U A m v 1507512,≈=-=∆=ν。

注意：此题很简单，目的在于理解理想气体内能无论在什么样的准静态过程下都只由温度决定。