等腰梯形的性质专项练习30题(有答案)ok
- 格式:doc
- 大小:270.50 KB
- 文档页数:11


等腰梯形三线合一专项综合练习等腰梯形是指具有两边长度相等的梯形,三线合一是指将等腰梯形的面积、周长和内切圆半径联系在一起进行综合练的题目。
下面介绍一些常见的练内容。
一、求等腰梯形的面积等腰梯形的面积可以通过底边长度和高来计算。
假设底边长度为$a$,高为$h$,则等腰梯形的面积$S$可以计算为:$S = \frac{(a + b)h}{2}$二、求等腰梯形的周长等腰梯形的周长可以通过各边长度来计算。
假设底边长度为$a$,上底边长度为$b$,两个斜边的长度分别为$c$,则等腰梯形的周长$C$可以计算为:$C = a + b + 2c$三、求等腰梯形的内切圆半径等腰梯形的内切圆半径可以通过底边长度和高来计算。
假设底边长度为$a$,高为$h$,则等腰梯形的内切圆半径$r$可以计算为:$r = \frac{h}{2}$四、综合练题示例以下是一个综合练题示例:已知一个等腰梯形的底边长度$a = 8$ cm,上底边长度$b =6$ cm,高$h = 5$ cm,请计算这个等腰梯形的面积、周长和内切圆半径。
解答:- 面积$S = \frac{(a + b)h}{2} = \frac{(8 + 6) \times 5}{2} =35$ 平方厘米- 周长$C = a + b + 2c = 8 + 6 + 2 \times c$- 内切圆半径$r = \frac{h}{2} = \frac{5}{2} = 2.5$ 厘米综上所述,该等腰梯形的面积为35平方厘米,周长为$a + b +2c$,内切圆半径为2.5厘米。
以上是等腰梯形三线合一专项综合练习的简要介绍和示例题目。
通过练习这些题目,可以更好地理解和应用相关的概念和计算方法。

等腰梯形的判定测试题:一、选择题1.以下结论中,正确的选项是〔 〕A .等腰梯形的两个底角相等B .两个底角相等的梯形是等腰梯形C .一组对边平行的四边形是梯形D .两条腰相等的梯形是等腰梯形2.如下图,等腰梯形ABCD 的对角线AC ,BD 相交于点O ,那么图中全等三角形有〔 〕A .2对B .3对C .4对D .5对3.如图,线段AC ,BD 相交于点O ,欲使四边形ABCD 成为等腰梯形,•需满足的条件是〔 〕A .AO=CO ,BO=DOB .AO=CO ,BO=DO ,∠AOB=90°C .AO=DO<BO=COD .AO=DO ,∠AOD=90°4.课外活动课上,•教师让同学们制作了一个对角线互相垂直的等腰梯形形状的风筝,其面积为450cm ,那么两条对角线所用的竹条长度之和至少为〔 〕A .302cmB .30cmC .60cmD .602cm5.四边形ABCD 中,∠A,∠B,∠C,∠D 的度数比是1:2:2:3,那么这个四边形是〔 〕A .平行四边形B .等腰梯形C .菱形D .直角梯形二、填空题1.等腰梯形上底,下底和腰分别为4,•10,•5,•那么梯形的高为_____,•对角线为______.2.一个等腰梯形的上底长为5cm ,下底长为12cm ,一个底角为60°,那么它的腰长为____cm ,周长为______cm .3.在四边形ABCD 中,AD∥BC,但AD≠BC,假设使它成为等腰梯形,那么需要添加的条件是______4.梯形ABCD 中,AD ∥BC 、AB =CD ,AC 丄BD 于点O ,∠BAC =60°,假设BC =错误!未找到引用源。
,那么此梯形的面积为__________DA BC EF5如下图,在梯形ABCD 中,AB ∥CD ,E 是BC 的中点,EF ⊥AD 于点F ,AD=4,EF=5,那么梯形ABCD 的面积是___________6.形ABCD 中如下图),AB ∥DC.∠DAB =90°,∠ABC =60°,EF 为中位线。

等腰梯形的性质定理和判定定理及其证明配套练习1. 下列命题中,错误的是()A .矩形的对角线互相平分且相等B .对角线互相垂直的四边形是菱形C .等腰梯形的两条对角线相等D .等腰三角形底边上的中点到两腰的距离相等2. 用含 30o 角的两块同样大小的直角三角板拼图形,下列四种图形:①平行四边形,②菱形,③矩形,④直角梯形.其中可以被拼成的图形是( )A .①②B .①③C.③④D.①②③3. 顺次连接等腰梯形四边中点所得到的四边形是()A.等腰梯形B.直角梯形C.矩形 D.菱形4. 已知梯形的两底边长分别为 6 和 8,一腰长为 7,则另一腰长 a 的取值范围是 .E5. 如图,在等腰梯形 ABCD 中, AD ∥ BC ,B60o , ADAB .点ADPE ,F 分别在 AD , AB 上, AEBF , DF 与 CE 相交于 P ,则DPEF6. 如图,在平行四边形ABCD 中,点 E , F 分别在 AB ,CDDFCBC上移动,且 AE CF,则四边形BFDE ...)不可能 是(A .矩形B .菱形C .梯形D .平行四边形A E B7. 如图,四边形 ABCD 是矩形, F 是 AD 上一点, E 是 CB延长线上一点,且四边形AECF 是等腰梯形.下列结论中不一定正确的是()AF D...A. AE FCB. ADBCC.AEBCFDD. BEAFEBC8. 下列说法正确的是()A .有两个角为直角的四边形是矩形B .矩形的对角线互相垂直C .等腰梯形的对角线相等D .对角线互相垂直的四边形是菱形A9. 如图,将一张等腰直角三角形纸片沿中位线DE 剪开后,可以拼成的四边形是()EA .矩形或等腰梯形B.矩形或平行四边形DC .平行四边形或等腰梯形D.矩形或等腰梯形或平行四边形BCC10. 在等腰梯形 ABCD 中, AB ∥ DC ,AD BC 5,DC 7,AB 13 ,点P 从D 点 A 出发,以 3 个单位 /s 的速度沿 ADDC 向终点 C 运动,同时点 Q 从点 BPAQB出发,以 1 个单位 /s 的速度沿 BA 向终点 A 运动.在运动期间,当四边形 PQBC为平行四边形时,运动时间为() A . 3sB . 4s C. 5s D . 6s11. 已知:如图,在等腰 △ ABC中, AB AC , BD AC CEAB, 垂足分别为点D E连接 DE.求,,证:四边形 BCDE 是等腰梯形.AFE12. 如图,在正六边形ABCDEF 中,对角线 AE 与 BF 相交于点 M , BD 与CE 相交AME DNDBCBC于点 N .( 1)观察图形,写出图中两个不同形状的特殊四边形;....( 2)选择( 1)中的一个结论加以证明.A13. 如图 1,△ ABC 是直角三角形, 如果用四张与 △ ABC 全等的三角 形纸片恰好拼成一个等腰梯形,如图2,那么在 Rt △ ABC 中,AC的AB值是.BC14. 如图,在梯形ABCD 中, AD ∥ BC,对角线 BD 平分 ABC ,图 1图 2BAD 的平分线 AE 交 BC 于 E ,F ,G 分别是 AB ,AD 的中点.AGD( 1)求证: EFEG ;F( 2)当 AB 与 EC 满足怎样的数量关系时,EG ∥ CD ?并说明理由.B E C15. 如图,在等腰梯形 ABCD 中, AB ∥ CD , E ,F 是边 AB 上两点,且 AE BF , DE 与 CF 相交于梯形 ABCD 内一点 O .DC( 1)求证: OE OF ;O( 2)当 EF CD 时,请你连接 DF , CE ,判断四边形DCEF 是什么样ABF E的四边形,并证明你的结论.16. 如图,已知等腰梯形 ABCD 中, AD ∥ BC ,∠A 110o,则 ∠C ()ADA. 90oB. 80oC. 70oD. 60oBC17. 如图,梯形 ABCD 中, AB ∥ CD , AD = CD , E 、 F 分别是 AB 、BC 的中点,若∠ 1 = 35 ,则∠ D =.18. 如图,等腰梯形ABCD 中, AD ∥BC ,点 E 是AD 延长线上一点, DE BC .( 1)求证: EDBC ;( 2)判断 △ ACE 的形状(不需要说明理由) .A D EB C。

等腰梯形的性质与判定 试题一、选择题1 .下列命题错误的是( )A.矩形是平行四边形;B.相似三角形一定是全等三角形C.等腰梯形的对角线相等D.两直线平行,同位角相等2 .顺次连结等腰梯形各边中点得到的四边形是A 矩形B 菱形C 正方形D 平行四边形 3 .如图,锐角三角形ABC 中(AB>AC),AH⊥BC,垂足为H,E 、D 、F 分别是各边的中点,则四边形EDHF 是( )A.梯形B.等腰梯形C.直角梯形D.矩形4 .等腰梯形的下底是上底的3倍,高与上底相等,这个梯形的腰与下底所夹角的度数为A.30°B.45°C.60°D.135°5 .若等腰梯形的两底差等于一腰长,那么它的腰与下底的夹角为A.︒30B.︒45C.︒60D.︒756 .等腰梯形的腰长为13cm,两底差为10cm,则高为 ( )A 、69cmB 、12cmC 、69cmD 、144cm7 .在等腰梯形ABCD 中,AD∥BC,AD=3,BC=7,AB=CD,E 为CD 的中点,四边形ABED 的周长与△BCE 的周长之差为2,则AB 的长为( ).A.8B.3C.6D.78 .如图8,等腰梯形ABCD 中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD 的面积是(•)二、填空题9 .如图1,请写出等腰梯形ABCD(AB∥CD)特有而一般梯形不具有的三个特征: ________,________,________.10.等腰梯形ABCD 中,AD∥BC,AB=6,AD=5,BC=8,且AB∥DE,则△DEC 的周长是____________.11.等腰梯形的对角线互相垂直,若高为8,则梯形的面积是_______.12.如图 2所示,在等腰梯形ABCD 中,∠B=450,已知腰长是3cm,则∠ADC=______度,高DE=_____。13.等腰梯形ABCD 中,AB∥CD,对角线AC 与BD 相交与O,请写出图中一对相等的线段___________。14.顺次连结等腰梯形四边的中点,所得四边形是____________;15.等腰梯形的一个锐角为60°, 一腰长为24cm,•一底长为39cm,•则另一底长为_______. 16.若等腰梯形ABCD 的上、下底之和为4,并且两条对角线所夹锐角为60,则该等腰梯形的面积为___________(结果保留根号的形式).三、解答题17.如图,在等腰梯形ABCD 中,AB ∥CD ,延长底边AB 到E ,使得BE =DC .求证:AC =CE.18.如图,将等腰梯形ABCD 的一条对角线BD 平移到CE 的位置,(1)试猜猜线段AE 与AD 、BC有怎样的数量关系?为什么?(2)ΔACE 是等腰三角形吗?为什么?19.如图,等腰梯形ABCD 中,AB∥CD,AD=BC,对角线AC⊥BD 于O,若DC=4cm,AB=9cm 。求梯形的高。O DCB A A B CDE答案一、选择题1 .B点拨:两三角形全等是两三角形,相似的一种特例,所以全等一定相似,但相似不一定全等.2 .B3 .B4 .B5 .C6 .A;7 .C 解析:如图所示,四边形ABCD的周长=AB+BE+DE+AD,△BCE的周长=BC+EC+BE,两者之差为2,即AB+BE+DE+AD-(BC+EC+BE)=AB+AD-BC=AB+3-7=2,所以AB=6.BEDC A8 .A二、填空题9 .略10.15 ;11.解析:如图所示,过点D分别作DF⊥BC于F点,DE∥AC交BC•延长线于点E.∵梯形ABCD,AD∥BC,∴四边形ACED是平行四边形,∴DE=AC,AD=CE.∵AB=CD,∴AC=BD(等腰梯形对角线相等),∴BD=DE.∵BD⊥AC,∴BD⊥DE,∴∠DBF=∠DEF=45°,∴DF=BF=FE.∴S梯形ABCD=12(AD+BC)DF=12BE×DF=12(2DF)×DF=DF2.∵DF=8,∴S梯形ABCD=64. 答案:64BE DC A F 12.323 13.AC=BD 等;14.菱形15.如图所示,过D 点作DE∥AB 交BC 于点E.∵AD∥BC,∴四边形ABED 是平行四边形,∴∠DEC=∠B,∴AB=ED,AD=BE.∵∠B=∠C=60°,AB=DC=24cm,∴△ECD 是等边三角形,∴CD=ED=E C=24cm.若AD=39cm,则BC=BE+EC=AD+EC=63cm;若BC=39cm,则AD=BE=BC-EC=15cm,且均符合三边关系定理,∴另一底长应为63cm 或15cm.答案:63cm 或15cmBE DC A 16.三、解答题 17.证明:在等腰梯形ABCD 中∵ AB ∥CD AD =CB ,∴ ∠DAB =∠CBA又 ∵∠CDA +∠DAB =180°∠CBA +∠CBE =180°∴∠CDA=∠CBE又∵ BE=DC∴△ADC ≌△CBE∴AC =CE18.(1) AE=AD+BC ∵BD平移到CE ∴ 四边形DBCE是平行四边形∴ DE=BC ∴AE=AD+DE=AD+BC 。(2) ∵ BD=CE AC=BD ∴AC=CE ∴△ACE是等腰三角形。19.解:过C作CE∥BD交AB的延长线于E,过C作CF⊥AB于FAB∥CD, CE∥BD∴CE=BD , BE=CD=4等腰梯形ABCD中,AC=BD ∴CE=ACAC⊥BD, CE∥BD ∴CE⊥AC∴△ACE是等腰直角三角形∴CF=12AE=12(AB+BE)∵AB=9cm ∴CF=12(9+4)=132cm即梯形的高为132cm。。


等腰梯形练习题在数学学习中,我们经常会遇到各种几何图形的练习题。
其中,等腰梯形是一种常见的几何图形,它具有特定的性质和计算方法。
本文将为大家提供一些关于等腰梯形的练习题,帮助大家巩固和应用相关的知识。
例题一:已知等腰梯形的上底长为15 cm,下底长为25 cm,高为10 cm,求等腰梯形的面积和周长。
解答:等腰梯形的面积可以通过上底和下底的平均值与高的乘积来计算。
根据题目给出的数据,我们可以得出等腰梯形的面积计算公式:面积 = (上底 + 下底) ×高 ÷ 2。
代入数值,计算出等腰梯形的面积:(15 + 25) × 10 ÷ 2 = 200 平方厘米。
等腰梯形的周长可以通过上底、下底和斜边的长度之和来计算。
由于等腰梯形的两边是等长的,所以斜边可以通过勾股定理计算得出。
根据题目给出的数据,我们可以得出等腰梯形的周长计算公式:周长 = 上底 + 下底 + 斜边1 + 斜边2。
斜边1和斜边2可以通过勾股定理计算得出,即:斜边= √(腰长的平方 + 高的平方)。
代入数值,计算出等腰梯形的周长:周长= 15 + 25 + √(10×10 + 10×10) + √(10×10 + 10×10)= 15 +25 + √200 + √200 ≈ 73.65 厘米。
例题二:已知等腰梯形的面积为90 平方厘米,上底长为12 cm,下底长未知,高为10 cm,求等腰梯形的下底长和周长。
解答:根据例题一的解答,我们知道等腰梯形的面积公式为:面积 = (上底 + 下底)×高 ÷2。
代入已知数据,可得到方程:90 = (12 + 下底)× 10 ÷ 2,进一步计算得到:90 = 6 + 5 下底,解方程可得下底≈ 16.8。
下底长约为16.8 cm。
等腰梯形的周长计算方式同例题一,根据已知数据计算:周长= 12 + 16.8 + √(10×10 + 8.4×8.4)+ √(10×10 + 8.4×8.4)≈ 46.18 厘米。

习题精选制卷人:歐陽文化、歐陽理複;制卷時間:二O二二年二月七日[自主演练,各个击破]等腰梯形的性质1.以下说法中,不正确的选项是〔〕A.等腰梯形同一底上的两个等角相等B.等腰梯形的对角线相等C.对角线相等的四边形是等腰梯形D.同一底上的两个角相等的梯形是等腰梯形2.等腰梯形的上底与高相等,下底是上底的3倍,那么一个底角是〔〕A.30°B.45°C.60°D.75°3.假如等腰梯形两底之差等于一腰的长,那么这个等腰梯形的底角是〔〕A.60°B.30°C.45°D.15°4.在以下四个图形中,不是中心对称图形的是〔〕A.平行四边形B.矩形C.菱形D.等腰梯形5.梯形ABCD中,DC∥AB,E为腰BC的中点,假设AB=8,CD=2,AE把梯形分为△ABE 和四边形ADCE,它们的周长相差4,那么梯形的腰AD的长为〔〕A.12B.10C.2或者10D.2或者126.等腰梯形有一角为120°,腰长为3cm,一底边长为4cm,那么另一底边长为_______。
7.等腰梯形ABCD中,AD ∥ BC,AB=CD,且AC ⊥ BD,梯形的高为5,那么S梯形ABCD=_________。
★等腰梯形的断定8.在四边形ABCD中,AD∥ BC,AB=DC,那么四边形ABCD是〔〕A.等腰梯形B.平行四边形C.直角梯形D.等腰梯形或者平行四边形9.以下说法中,正确的选项是〔〕A.对角线相等的四边形是矩形或者等腰梯形B.一组对边平行,另一组对边相等的四边形是等腰梯形C.两组对角分别互补的四边形是等腰梯形D.等腰梯形是轴对称图形,经过两底中点的直线是它的对称轴[互动探究,拓展延伸][学科综合]10.如图32-4-1所示,己知四边形ABCD是矩形,四边形ABDE是等腰梯形,AE ∥ BD,证明:∠C= ∠DEB。
[创新思维]〔一〕新形题11.某校方案修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种图案,你认为符合条件的是〔〕A.等腰三角形B.正三角形C.等腰梯形D.菱形〔二〕课本习题变式题12.〔课本P153习题2题变式题〕如图32-4-2,在梯形ABCD中,AD ∥BC,AB=DC,对角线AC、BD交于点O。
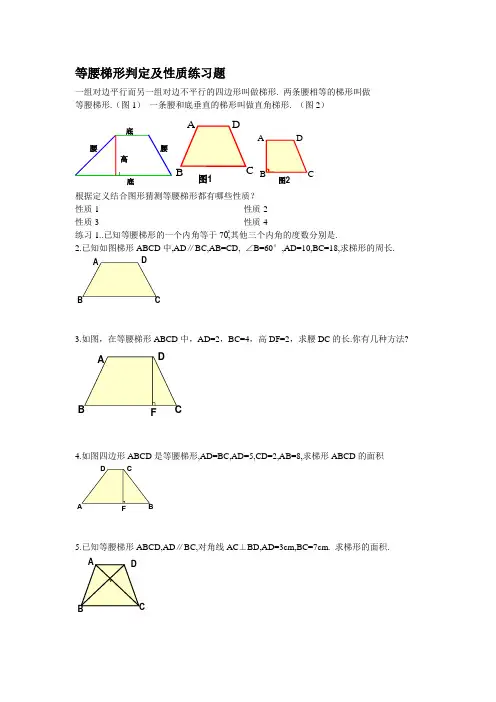
等腰梯形判定及性质练习题一组对边平行而另一组对边不平行的四边形叫做梯形. 两条腰相等的梯形叫做 等腰梯形.(图1) 一条腰和底垂直的梯形叫做直角梯形. (图2) 底底腰腰高图1图2A根据定义结合图形猜测等腰梯形都有哪些性质?性质1_________________________________性质2_________________________________ 性质3_________________________________性质4______________________练习1..已知等腰梯形的一个内角等于70ْ,其他三个内角的度数分别是. ________________2.已知如图梯形ABCD 中,AD ∥BC,AB=CD, ∠B=60°,AD=10,BC=18,求梯形的周长.3.如图,在等腰梯形ABCD 中,AD=2,BC=4,高DF=2,求腰DC 的长.你有几种方法?F4.如图四边形ABCD 是等腰梯形,AD=BC,AD=5,CD=2,AB=8,求梯形ABCD的面积5.已知等腰梯形ABCD,AD ∥BC,对角线AC ⊥BD,AD=3cm,BC=7cm. 求梯形的面积.如何判断一个梯形是不是等腰梯形?方法1___________________________。
方法2___________________________。
方法3___________________________。
练习:1 判断正误:(1)有两个角相等的梯形一定是等腰梯形.( )(2)两条对角线相等的梯形一定是等腰梯形. ( )(3)如果一个梯形是轴对称图形,则它一定是等腰梯形. ( )(4) 一组对边平行,另一组对边相等的四边形一定是等腰梯形. ( )(5)对角互补的梯形一定是等腰梯形.( )2、填空题(1)两条对角线相等且相互平分的四边形是__________(2) 平行四边形 ABCD 中,∠A 和∠C 是对角,如果∠A+∠C=200°,则∠B= __________ 。

等腰梯形的判定专项练习30题(有答案)1.如图,四边形ABCD中,已知AB∥CD,AD∥EC,∠CEB=∠CBE,四边形ABCD是等腰梯形吗?如果是,请说明理由.2.如图,在梯形ABCD中,AE⊥BC于E,DF⊥BC于F,且BE=CF.(1)求证:梯形ABCD为等腰梯形;(2)若AD=AE=2,BC=4,求腰AB的长.3.在矩形ABCD中,△ABD沿对角线BD对折,A与A′重合,AD=8,AB=6,A′D与BC相交于O.(1)求证:△A′BO≌△DOC.(2)求BO的长.(3)求证:四边形A′CDB为等腰梯形.4.等腰△ABC中,AB=AC,E、F分别在AB、AC上,AE=AF,试证明四边形EBCF是等腰梯形.5.如图,四边形ABCD是矩形,把矩形沿直线BD折叠,点C落在点E处,连接DE,DE与AD交于点M.(1)证明四边形ABDE是等腰梯形;(2)写出等腰梯形ABDE与矩形ABCD的面积大小关系,并证明你的结论.6.如图所示,已知在梯形ABCD中,AD∥BC,∠ABC=60°,BD平分∠ABC,且BD⊥DC.(1)求证:梯形ABCD是等腰梯形;(2)当CD=1时,求等腰梯形ABCD的周长.7.如图,E、F分别是矩形ABCD的对角线以AC、BD上两点,且AE=DF.求证:(1)△BOE≌△COF;(2)四边形BCFE是等腰梯形.8.如图,在梯形ABCD中,AB∥CD,BD平分∠ADC,过点A作AF∥BD,交CD的延长线于点F,若∠F=∠C.(1)求证:梯形ABCD是等腰梯形;(2)当∠BDC=30°,AD=5时,求CD的长.9.已知正方形ABCD中,E、F分别是对角线AC、BD的三等分点(1)求证:四边形BCFE是等腰梯形;(2)若正方形ABCD的对角线长为9cm,求等腰梯形BCFE的面积.10.如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,AC、BD交于F,过点F作EF∥AB,交AD 于点E.求证:四边形ABFE为等腰梯形.11.如图,▱ABCD,点E是DC边上的一点,∠AED=∠D,说明:四边形ABCE是等腰梯形.12.如图,已知在平行四边形ABED中,AE是对角线,∠B=∠EAD,延长BE至点C,使EC=BE,并连接DC.(1)求证:四边形ABCD是等腰梯形;(2)若AB=AD=4,求梯形ABCD的面积.13.如图,D、E、F分别是△ABC各边的中点,AH是△ABC的高,(1)求证:四边形DHEF是等腰梯形;(2)若DF=HC,求证:H是BE的中点.14.如图,▱ABCD中,AE平分∠BAD交BC于E,EF∥AB交AD于F,试问:(1)四边形ABEF是什么图形?请说明理由;(2)当∠B为多少度数时,四边形AECD是等腰梯形?请说明理由.15.如图,梯形ABCD中,AD∥BC,E是AD的中点,且EB=EC.求证:梯形ABCD是等腰梯形.(要求写出证明过程中的主要依据)16.如图,直角梯形ABCD中,AD∥BC,∠DCB=90°,BC=2AD,对角线AC与BD相交于点P,过点P作PE∥BC 交AB于点E.(1)求证:四边形EBCP是等腰梯形.(2)若直角梯形ABCD的面积为72,AB=10,求△ADC的周长.17.如图,在梯形ABCD中,AD∥BC,∠B=∠C,E是BC边的中点.请你探索线段AE与DE间的数量关系,并说明理由.18.如图,AB=AC,过点A的直线DE∥CB,且CD⊥AC,BE⊥AB.梯形BCDE是等腰梯形吗?为什么?19.如图,在等腰梯形ABCD中,点E、F分别在两腰AD、BC上,且EF∥DC,梯形CDEF是等腰梯形吗?为什么?20.已知:如图,△ABC中,AB=AC,BD、CE分别为∠ABC、∠ACB的角平分线,猜一猜,四边形BCDE是怎样的四边形?证明你的结论.21.如图,AD是△ABC中BC边上的高线,E、F、G分别是AB、BC、AC的中点.求证:四边形EFDG为等腰梯形.22.如图,在梯形ABCD中,AB∥DC,DB平分∠ADC,过点A作AE∥BD,交CD的延长线于点E,且∠C=2∠E,∠BDC=30°,AD=3,求CD的长.23.如图,在梯形ABCD中,AB∥CD,若M为DC中点,且∠1=∠2,试说明梯形ABCD是等腰梯形.24.如图所示,在平行四边形ABCD中,延长DC到点E,使BE=BC;(1)四边形ABED是否为等腰梯形,请说明理由;(2)若∠D=60°,AB=3,过点C作CF⊥BE,垂足为F,且CF=,求DE的长及平行四边形ABCD的面积.25.如图在梯形ABCD中,AD∥BC,∠B=∠C,DE交BC于点E,AD=BE.(1)AB=DE吗?为什么?(2)梯形ABCD是等腰梯形吗?为什么?26.如图,在梯形ABCD中,AD∥BC,CA平分∠BCD,DE∥AC,交BC的延长线于点E,∠B=2∠E,求证:AB=DC.27.已知,如图,△ABC中,AB=AC,直线DE∥BC分别交AB,AC的延长线于D、E,四边形BDEC是等腰梯形吗?为什么?28.如图,在矩形ABCD中,AC、BD相交于点O,E、F分别是OA、OD的中点.试判断四边形EBCF的形状,并证明你的结论.29.如图,直角梯形ABCD中,AD∥BC,AB=cm,AD=24cm,BC=26cm,∠B=90°,动点P从A开始沿AD 边向D以1cm/s的速度运动,动点Q从点C开始沿CB以3cm/s的速度向点B运动.P、Q同时出发,当其中一点到达顶点时,另一点也随之停止运动,设运动时间为ts,问:(1)t=_________时,四边形PQCD是平行四边形.(2)是否存在一个t值,使PQ把梯形ABCD分成面积相等的两部分?若存在请求出t的值.(3)当t为何值时,四边形PQCD为等腰梯形.(4)连接DQ,是否存在t值使△CDQ为等腰三角形?若存在请直接写出t的值.30.如图,点E是正方形ABCD的对角线AC上一点,CF⊥BE,垂足为F,交BD与点G,四边形ABGE是等腰梯形吗?为什么?参考答案:1.四边形ABCD是等腰梯形(2分)∵在四边形ABCD中AB∥CD∴四边形ABCD是梯形∵AD∥EC∴∠A=∠CEB(3分)∵∠CEB=∠CBE即∠B=∠CEB(4分)∴∠A=∠B(5分)∴四边形ABCD是等腰梯形.2.1)证明:在梯形ABCD中,AD∥BC(1分)又∵AE⊥BC,DF⊥BC,∴AE=DF且∠AEB=∠DFC=90°(3分)在Rt△ABE和Rt△DCF中,∵∴Rt△ABE≌Rt△DCF,(4分)∴AB=DC,即梯形ABCD为等腰梯形(5分)(2)又∵AE⊥BC,DF⊥BC,∴∠AEF=∠DFE=90°.又AD∥BC,∴∠EAD=90°,∴四边形AEFG为矩形,∴AD=EF.(6分)∵AD=AE=2,BC=4,∴BE==1,(7分)∴AB===.得腰AB 的长为.3.(1)证明:在△A′BO与△DOC中,,∴△A′BO≌△DOC(AAS);(2)解:BO+OC=8,OB2=OD2=OC2+36,解得BO=6.25(4分)(3)证明:∵△A′BO≌△DOC,∴OB=OD,OC=OA′,∴,∴A′C∥DB,又∵A′B=CD,∴四边形A′CDB为等腰梯形.4.∵AB=AC且AE=AF,∴AB﹣AE=AC﹣AF即EB=FC.(2分)∵AB=AC,∴∠B=∠C=,∴∠AEF=∠B.(6分)∴EF∥BC而EB不平行FC.∴四边形EBCF是等腰梯形5.(1)∵四边形ABCD是矩形,∴AD=BE,AB=ED,AD∥BC.∴△ADB≌△DBC≌△EDB,∠EBD=∠DBC,∠ADB=∠EBD.(2分)∴DM=BM,AM=EM.∴△AMB≌△EMD.∴AB=DE.AM=EM,∴∠EAM=∠AEM,∵DM=BM,∴∠BDM=∠MBD,又∵∠AME=∠BMD,∴∠EAD=∠MDB,∴AE∥BD.∵AE≠BD,∴四边形ABDE是等腰梯形.(5分)(2)∵△ABC的面积=△BDC的面积=△BDE的面积,∵S梯形ABDE=S△ABM+S△AME+S△BDE,∵AE<BD,∴△AEM的面积<△BDM的面积.∴等腰梯形ABDE小于矩形ABCD的面积.6.(1)证明:∵BD平分∠ABC,∴∠ABD=∠CBD,∵∠ABC=60°,∴∠CBD=30°,∵BD⊥DC,∴∠BDC=90°,∴∠C=60°,∴梯形ABCD是等腰梯形;(2)解:过点D作DE∥AB,∵AD∥BC,∴四边形ABED为平行四边形,∵CD=1,∴BC=2,∵∠C=60°,∴△DCE为等边三角形,∴CE=BE=1,AD=1,∴等腰梯形ABCD的周长=AD+AB+CD+BC=1+1+1+2=5.7.(1)矩形ABCD的对角线AC、BD相交于O,∴OB=OC,OA=OD,又∵AE=DF,∴OE=OF,在△BOE和△COF中,,∴△BOE≌△COF(SAS);(2)在等腰△EOF中,∠OEF=,在等腰△AOD中,∠OAD=,∴∠OEF=∠OAD,又∵∠OCB=∠OAD,∴∠OEF=∠OCB,∴EF∥BC.又由题意知,EF≠BC,∴四边形BCFE是梯形.由(1)△BOE≌△COF,∴BE=CF,∴四边形BCFE是等腰梯形8.(1)证明:∵BD平分∠ADC,∴∠ADC=2∠BDC.∵AF∥BD,∴∠F=∠BDC,∴∠ADC=2∠F.又∵∠F=∠C,∴∠ADC=∠C.则梯形ABCD是等腰梯形(同一底上的两个角相等的梯形是等腰梯形)(2)解:由(1)知∠C=2∠F=2∠BDC=60°,BC=AD=5,在△BCD中,∵∠C=60°,∠BDC=30°,∴∠DBC=90°.则CD=2BC=10即为所求9.(1)证明:∵E、F分别是对角线AC、BD的三等分点,∴==,∴EF∥BC,∴四边形BCFE是梯形,∴BF=BD,CE=AC,∴BF=CE,∴四边形BCFE是等腰梯形;(2)解:∵正方形ABCD的对角线长为9cm,∴设正方形边长为x ,=9,x=.梯形的上底为,高为×=,下底为.∴梯形的面积为:×(+)×=.10.过D作DM垂直于AB,垂足为M,∵AB∥DC,∠ABC=90°,AB=2DC,∴BM=MA,∵AM=BM,∠BMD=∠AMD,DM=DM,∴△AMD≌△BMD,∴BD=AD,三角形ABD为等腰三角形,∴∠DAB=∠DBA,∵EF∥AB,∴四边形ABFE是等腰梯形11.∵四边形ABCD是平行四边形,∴DC∥AB,AD=BC,∵∠AED=∠D,∴AD=AE,∴AE=BC,即CE∥AB,AE=BC,∴四边形AECB是等腰梯形12.(1)∵四边形ABED是平行四边形,∴AD=BE,AD∥BE,∴∠EAD=∠AEB,∵∠B=∠EAD,∴∠AEB=∠B,∴AB=AE,∵EC=BE,AD=BE,∴AD=EC,∴四边形AECD是平行四边形,∴AE=CD,∵AE=AB,∴AB=CD,∵AD∥BC,∴四边形ABCD是等腰梯形;(2)解:∵AB=AD=4,AB=EC.AB=DC,∴DC=4,=AB,BC=8,过A作AF⊥BC于F,过D作DG⊥BC于G,则∠AFB=∠AFE=∠DGC=90°,AF∥DG,∵AD∥BC,∴四边形AFGD是矩形,∴AD=GF=4,AF=DG,∵AB=CD,∴由勾股定理得:BF=CG=2,由勾股定理得:AF==2,∴梯形ABCD 的面积是×(4+8)×4=24.13.(1)∵D、E、F分别是△ABC各边的中点,∴DF∥BC,EF=AB,又∵AH是△ABC的高,∴HD=AB,∴HD=EF,∵DF≠HE,∴四边形DHEF为等腰梯形;(2)∵DF是△ABC的中位线,E是BC的中点,∴DF=BC=BE,又∵DF=HC,∴BE=HC,∴BE=(HE+EC),∴3BE=2HE+2EC=2HE+2BE,∴BE=2HE,∴H是BE的中点.14.(1)解:四边形ABEF是菱形,理由是:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE,∵AB∥EF,AD∥BC,∴四边形ABEF是平行四边形,∵AB=BE,∴平行四边形ABEF是菱形.(2)解:当∠B为60度数时,四边形AECD是等腰梯形,理由是:∵AD∥BC,AD≠CE,∴四边形AECD是梯形,∵∠B=60°,由(1)知AB=BE,∴△ABE是等边三角形,∴AB=AE,∵四边形ABCD是平行四边形,∴AB=CD=AE,∴梯形AECD是等腰梯形.15.∵EB=EC,∴∠EBC=∠ECB∵AD∥BC,∴∠EBC=∠AEB,∠ECB=∠DEC,∴∠AEB=∠DEC在△AEB和△DEC中,∠AEB=∠DEC,AE=DE,EB=EC,∴△AEB≌△DEC∴AB=DC,即ABCD是等腰梯形16.1)证明:过A作AM⊥BC,垂足为M,∵AD∥BC,∠DCB=90°,∴四边形AMCD是矩形,∵BC=2AD,∴AD=MC=BM,∴AM是线段BC的垂直平分线,∴AB=AC,又∵EP∥BC,∴∠AEP=∠ABC=∠ACB=∠APE,∴AE=AP,∴EB=PC,∵直线BE、PC相交于点A,∴EB不平行于PC,∴四边形EBCP是等腰梯形.(2)解:设AD=x,DC=y,由(1)得:AB=AC=10,又∵∠DCB=90°,∴x2+y2=102①,又∵S梯形ABCD=72,∴(x+2x)•y=72,∴(x+y)2=196,即x+y=14,x+y=﹣14(不合题意舍去),∴△ADC的周长为:x+y+AC=14+10=24.17.数量关系是:AE=DE.(2分)理由是:梯形ABCD是等腰梯形→AB=CD(5分)..18.梯形BCDE是等腰梯形.理由如下:∵AB=AC,∴∠ABC=∠ACB,∵CD⊥AC,BE⊥AB,∴∠ABE=∠ACD=90°,∴∠ABE+∠ABC=∠ACD+∠ACB,即∠CBE=∠BCD,又∵DE∥CB,∴梯形BCDE是等腰梯形(同一底边上的两个底角相等的梯形是等腰梯形).19.梯形CDEF是等腰梯形.(2分)∵ABCD是等腰梯形,∴∠C=∠D,(4分)∵EF∥DC,∴四边形CDEF是梯形,(6分)∵∠C=∠D,∴梯形CDEF是等腰梯形20.在△ABC中,∵AB=AC,∴∠ABC=∠ACB.∵BD、CE分别为∠ABC、∠ACB的角平分线,∴∠BCE=∠CBD,在△BEC和△CDB中,,∴△BEC≌△CDB(ASA).∴BE=CD.∴AE=AD.∴∠AED=∠ADE.∴∠AED=∠ABC.∴ED∥BC.又∵BE,CD不平行,21.∵E、F、G分别是AB、BC、AC的中点,根据三角形中位线定理,得EF=AC.EG∥BC,EF∥AC,∴四边形EFCG为平行四边形,∴EG=FC,又∵DF<FC,∴FD<EG.∴四边形EFDG是梯形.(3分)又∵AD⊥BC,G为AC边的中点,∴DG是Rt△ACD斜边的中线,∴DG=AC.∴EF=DG.∴四边形EFDG为等腰梯形22.∵AE∥BD∴∠1=∠3,∠2=∠E∵∠1=∠2∴∠3=∠E∴∠ADC=∠3+∠E=2∠E∵∠C=2∠E∴∠ADC=∠BCD=60°∴梯形ABCD是等腰梯形∴BC=AD=3∵∠2=30°,∠BCD=60°∴∠DBC=90°在Rt△DBC中,∵∠2=30°,BC=3∴CD=2BC=623.∵∠1=∠2,∴AM=BM.∵AB∥CD,∴∠DMA=∠1,∠CMB=∠2.∴∠DMA=∠CMB.∵DM=CM,∴△DMA≌△CMB.∴AD=BC.∴梯形ABCD为等腰梯形24.(1)四边形ABED是等腰梯形.又AD与BE不平行,所以四边形ABED是梯形,因为BC=BE,所以AD=BE,所以四边形ABED是等腰梯形;(2)因为∠D=60°,所以∠BCE=60°,所以△BCE是等边三角形.在Rt△BCF中,设BC=x,则BF=x,(x)2+()2=x2,x2=4,x=2,所以DE=DC+CE=3+2=5.过B作BH⊥DE于H(如答图),则BH=CF=,且BH也是平行四边形ABCD的高,所以S平行四边形ABCD=AB•BH=3.25.(1)AB=DE.理由如下:∵AD∥BC,AD=BE,∴四边形ABED是平行四边形,∴AB=DE;(2)梯形ABCD是等腰梯形.理由如下:∵梯形ABCD中,AD∥BC,∠B=∠C,∴梯形ABCD是等腰梯形(同一底边上的两个角相等的梯形是等腰梯形).26.∵DE∥AC,∴∠E=∠ACB,∵CA平分∠BCD,∴∠BCD=2∠ACD,∵AD∥BC,∴∠ACD=∠E,∵∠B=2∠E,∴∠BCD=∠B,∴梯形ABCD是等腰梯形,∴AB=DC.27.四边形BDEC是等腰梯形,理由是:∵BC∥DE,∴四边形BDEC是梯形,∵AB=AC,∴∠ABC=∠ACB,∵BC∥DE,∴∠D=∠ABC,∠E=∠ACB,∴∠D=∠E,∴梯形BDEC是等腰梯形28.四边形EBCF是等腰梯形.证明:在矩形ABCD中,AD∥BC,AD=BC,OD=OB=OA=OC,又∵E、F分别是OA、OD的中点,∴EF是△AOD的中位线,∴EF=AD,AD∥EF,OE=OF,∴BC∥EF,BC≠EF,∴四边形EBCF是梯形.又∵∠EOB=∠COF,∴△OBE≌△OCF(SAS),∴BE=CF.∴梯形EBCF是等腰梯形29.(1)要使四边形PQCD是平行四边形,则PD=CQ,∴3t=24﹣t,解得:t=6.(2)当AP+BQ=25时,PQ把梯形ABCD分成面积相等的两部分,即t+(26﹣3t)=25,解得:t=(3)如图,过点D作DE⊥BC,则CE=BC﹣AD=2cm.当CQ﹣PD=4时,四边形PQCD是等腰梯形.即3t﹣(24﹣t)=4.∴t=7.(4)存在,t1=2,t2=,t3=330.是.∵ABCD是正方形,∴AC⊥BD,BO=CO,∠ABO=∠ABE+∠EBO=45°,∠BCO=∠BCG+∠GCO=45°,∵CF⊥BE,∴∠BEC+∠GCO=90°,∵AC⊥BD,∴∠EBO+∠BEC=90°,∴∠EBO=∠GCO,∴∠ABE=∠BCG,又∠BAC=∠OBC=45°,AB=BC,∴△ABE≌△BGC,∴AE=BG,∴EO=GO,∠OEG=∠OAB=45°∴EG∥AB∴AE=BG等腰梯形的判定---11。
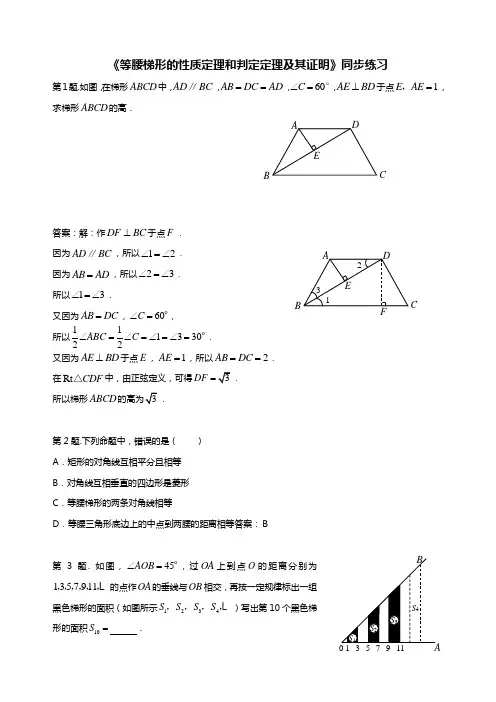
《等腰梯形的性质定理和判定定理及其证明》同步练习第1题.如图,在梯形ABCD 中,AD BC ∥,AB DC AD ==,60C ∠=°,AE BD ⊥于点1E AE =,,求梯形ABCD 的高.答案:解:作DF BC ⊥于点F . 因为AD BC ∥,所以12∠=∠. 因为AB AD =,所以23∠=∠. 所以13∠=∠.又因为AB DC =,60C ∠=,所以11133022ABC C ∠=∠=∠=∠=. 又因为AE BD ⊥于点E ,1AE =,所以2AB DC ==.在Rt CDF △中,由正弦定义,可得DF =. 所以梯形ABCD.第2题.下列命题中,错误的是( ) A .矩形的对角线互相平分且相等 B .对角线互相垂直的四边形是菱形 C .等腰梯形的两条对角线相等D .等腰三角形底边上的中点到两腰的距离相等答案:B第3题. 如图,45AOB ∠=,过OA 上到点O 的距离分别为1357911,,,,,,的点作OA 的垂线与OB 相交,再按一定规律标出一组黑色梯形的面积(如图所示1234S S S S ,,,,)写出第10个黑色梯形的面积10S = .BCBC答案:76第4题.用含30角的两块同样大小的直角三角板拼图形,下列四种图形:①平行四边形,②菱形,③矩形,④直角梯形.其中可以被拼成的图形是( )A .①②B .①③C .③④D .①②③答案:B第5题.顺次连接等腰梯形四边中点所得到的四边形是( ) A.等腰梯形B.直角梯形C.矩形D.菱形答案:D第6题.已知梯形的两底边长分别为6和8,一腰长为7,则另一腰长a 的取值范围是 .答案:5<a <9第7题.如图,在等腰梯形ABCD 中,AD BC ∥,60B ∠=,AD AB =.点E F ,分别在AD ,AB 上,AE BF =,DF 与CE 相交于P ,则DPE ∠=.答案:120第8题.如图,在等腰梯形ABCD 中,AD ∥BC ,AB=DC ,点E 是BC 边的中点,EM ⊥AB ,EN ⊥CD ,垂足分别为M 、N . 求证:EM =EN答案:因为AD ∥BC ,AB =DC ,所以B C ∠=∠……………………………2分 因为,,EM AB EN CD ⊥⊥所以90BME CNE ∠=∠=︒……………3分ENMDCBA在Rt △BME 和Rt △CNE 中, BME CNE B C BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩,所以Rt △BME ≌ Rt △CNE ………………………7分 所以EM =EN …………………………………8分第9题. 如图,在直角梯形ABCD 中,1cm 2cm AB CD AD CD AB AD ==∥,⊥,,,4cm CD =,则BC = cm .第10题. 如图,在平行四边形ABCD 中,点E F ,分别在AB CD ,上移动,且AE CF =,则四边形BFDE 不可能...是( ) A .矩形 B .菱形C .梯形D .平行四边形答案:C第11题. 如图,四边形ABCD 是矩形,F 是AD 上一点,E 是CB 延长线上一点,且四边形AECF 是等腰梯形.下列结论中不一定...正确的是( ) A.AE FC =B.AD BC = C.AEB CFD ∠=∠ D.BE AF =答案:D第12题.下列说法正确的是( ) A .有两个角为直角的四边形是矩形 B .矩形的对角线互相垂直C .等腰梯形的对角线相等D .对角线互相垂直的四边形是菱形答案:C第13题. 如图,将一张等腰直角三角形纸片沿中位线剪开可以拼成不同形状的四边形,请写出其中一种四边形的名称.BCDAA BCD F E答案:平行四边形、矩形、等腰梯形(三种中任选一种均给满分)第14题. 如图,将一张等腰直角三角形纸片沿中位线DE 剪开后,可以拼成的四边形是( )A .矩形或等腰梯形B .矩形或平行四边形C .平行四边形或等腰梯形D .矩形或等腰梯形或平行四边形 答案:D第15题.已知:如图,在等腰ABC △中,AB AC =,BD AC ⊥,CE AB ⊥, 垂足分别为点D ,E ,连接DE .求证:四边形BCDE 是等腰梯形.答案:证明:在等腰ABC △中,AB AC =,ABC ACB ∴∠=∠.CE AB ⊥,BD AC ⊥,90BEC CDB ∴∠=∠=.又BC CB =,BEC CDB ∴△≌△. 3分BE CD ∴=.AE AD ∴=.AED ADE ∴∠=∠.AED ABC ∴∠=∠.ED BC ∴∥. 5分 又BE CD ,不平行,∴四边形BCDE 是梯形.7分∴四边形BCDE 是等腰梯形.(理由:同一底上的两底角相等的梯形是等腰梯形,或两腰相等的梯形是等腰梯形) 8分第16题.如图,在正六边形ABCDEF 中,对角线AE 与BF 相交于点M ,BD 与CE 相交于点N . (1)观察图形,写出图中两个不同形状....的特殊四边形; (2)选择(1)中的一个结论加以证明.A DECBAD CB E答案:解:(1)矩形ABDE ,矩形BCEF ; 或菱形BNEM ;或直角梯形BDEM ,AENB 等. 4分(2)选择ABDE 是矩形. 证明:ABCDEF 是正六边形,120AFE FAB ∴==∠∠,30EAF ∴=∠,90EAB FAB FAE ∴=-=∠∠∠.5分同理可证90ABD BDE ==∠∠.∴四边形ABDE 是矩形.7分选择四边形BNEM 是菱形.证明:同理可证:90FBC ECB ==∠∠,90EAB ABD ==∠∠,BM NE ∴∥,BN ME ∥.∴四边形BNEM 是平行四边形.BC DE =,30CBD DEN ==∠∠,BNC END =∠∠,BCN EDN ∴△≌△. BN NE ∴=.∴四边形BNEM 是菱形.7分选择四边形BCEM 是直角梯形.证明:同理可证:BM CE ∥,90FBC =∠,又由BC 与ME 不平行, 得四边形BCEM 是直角梯形. 7分第17题.下列三角形纸片,能沿直线剪一刀得到等腰梯形的是( )剪,则打开后梯形的周长是(3cm70 A .80 B .C .D .A .(cm B .(cm C .22cm D .18cm 答案:A第19题. (内蒙呼和浩特课改,3分)如图在梯形ABCD 中,AD BC ∥,BC BD =,120A ∠=.则C ∠=度.答案:75第20题. 如图1,ABC △是直角三角形,如果用四张与ABC △全等的三角形纸片恰好拼成一个等腰梯形,如图2,那么在Rt ABC △中,ACAB的值是 .第21题.如图,在等腰梯形ABCD 中,AB CD ∥,对角线AC 平分602cm BAD B CD ∠∠==,,,则梯形ABCD 的面积为( )2cm A.B .6C.D .12答案:A第22题.如图,在梯形ABCD 中,AD BC ∥,对角线BD 平分ABC ∠,BAD ∠的平分线AE 交BC 于E F G ,,分别是AB AD ,的中点. (1)求证:EF EG =;(2)当AB 与EC 满足怎样的数量关系时,EG CD ∥?并说明理由.CAC图1图2BECDGA F答案:(1)证明:AD BC ∥DBC ADB ∴∠=∠又ABD DBC ∠=∠ABD ADB ∴∠=∠AB AD ∴=2分又12AF AB =,12AG AD =AF AG ∴=3分又BAE DAE ∠=∠,AE AE =AFE AGE ∴△≌△ EF EG ∴=5分 (2)当2AB EC=时,EG CD ∥6分2AB EC = 2AD EC ∴=12GD AD EC ∴==7分又GD EC ∥∴四边形GECD 是平行四边形EG CD ∴∥8分第23题. 如图,梯形ABCD 中,AD BC ∥,45B =∠,120D =∠,8cm AB =,则DC 的长为( )A B C . D .8cm 答案:A第24题.在等腰梯形ABCD 中,5A B D C A D B C ==∥,,71D C A B ==,,点P 从点A 出发,以3个单位/s 的速度沿AD DC →向终点C 运动,同时点Q 从点B 出发,以1个BECDGA FABCDABQ单位/s 的速度沿BA 向终点A 运动.在运动期间,当四边形PQBC 为平行四边形时,运动时间为( ) A .3s B .4s C .5s D .6s 答案:A第25题.如图,在等腰梯形ABCD 中,AB CD ∥,E F ,是边AB 上两点,且AE BF =,DE 与CF 相交于梯形ABCD 内一点O . (1)求证:OE OF =;(2)当EF CD =时,请你连接DF CE ,,判断四边形DCEF 是什么样的四边形,并证明你的结论.答案:(1)证明:梯形ABCD 为等腰梯形,AB CD ∥,∴AD BC =,A B ∠=∠.2分AE BF =,∴ADE BCF △≌△.3分 ∴DEA CFB ∠=∠.∴OE OF =.4分(2)当DC EF =时,四边形DCEF 是矩形. 5分证明:DC EF ∥且DC EF =.∴四边形DCEF 是平行四边形.6分 又由(1)得ADE BCF △≌△,∴CF DE =.7分 ∴四边形DCEF 是矩形.8分评分说明:判断四边形DCEF 为平行四边形,并说理正确的,得2分第26题. 如图,已知等腰梯形ABCD 中,AD BC ∥,110A =∠,则C =∠( ) A.90 B.80C.70D.60答案:CABCDOFEB FEA D CB第27题. 如图,梯形ABCD 中,AB ∥CD ,AD = CD ,E 、F 分别是AB 、BC 的中点,若∠1 = 35︒,则∠D =.答案:110︒第28题.如图,等腰梯形ABCD 中,AD BC ∥,点E 是AD 延长线上一点,DE BC =.(1)求证:E DBC ∠=∠;(2)判断ACE △的形状(不需要说明理由).答案:(1)AD BC ∵∥,BCD EDC ∠=∠∴. 1分B C D=∵,BCD EDC ∠=∠,CD DC =, B C D ED ∴△≌△. 3分 ED B∠=∠∴. 2分 另证:DE BC ∵∥,DE BC =, 2分 B C E ∴是平行四边形.2分 E DBC ∠=∠∴.2分 (2)ACE △是等腰三角形. 2分第29题.面积为l 个平方单位的正三角形,称为单位正三角形.下面图 中的每一个小三角形都是单位正三角形,三角形的顶点称为格点.在图1、2、3中分别画出一个平行四边形、梯形和对边都不平行的凸四边形,要求这三个图形的顶点在格点、面积都为l2个平方单位.DABCE答案:每画出一个(与顺序无关)正确的给l分,答案不唯一,下图供参考:第30题.我们学习了四边形和一些特殊的四边形,右图表示了在某种条件下它们之间的关系.如果①,②两个条件分别是:①两组对边分别平行;②有且只有一组对边平行.那么请你对标上的其他6个数字序号写出相对应的条件.答案:③——相邻两边垂直;④——相邻两边相等;⑤——相邻两边相等;⑥——相邻两边垂直;⑦——两腰相等;⑧——一条腰垂直于底边.。
等腰梯形性质练习题 姓名: 1.填空(1)在梯形ABCD 中,已知AD ∥BC ,∠B=50°,∠C=80°,AD=a ,BC=b ,,则DC= . (2)直角梯形的高为6cm ,有一个角是30°,则这个梯形的两腰分别是 和 . (3)等腰梯形 ABCD 中,AB ∥DC ,A C 平分∠DAB ,∠DAB=60°,若梯形周长为8cm ,则AD= .2.已知:如图,在等腰梯形ABCD 中,AB ∥CD ,AB >CD ,AD=BC ,BD 平分∠ABC ,∠A=60°,梯形周长是20cm ,求梯形的各边的长.3.下列命题中,真命题是( )A 、有一组对边平行但不相等的四边形是梯形B 、直角梯形中只有一个直角C 、等腰梯形的对角线相等且互相垂直D 、等腰梯形是轴对称图形,有两条对称轴4.在梯形ABCD 中,∠D =90°,AD =DC =4,AB =1,E 为AD 的中点,则点E 到BC 的距离为__________.5.已知等腰梯形的锐角等于60°它的两底分别为15cm 和49cm ,求它的腰长和面积. 6.已知,如图,梯形ABCD 中,AD ∥BC ,E 是AB 的中点,DE ⊥CE ,求证:AD+BC=DC .(延长DE 交CB 延长线于点F ,由全等可得结论)7.已知:如图,梯形ABCD 中,CD//AB ,∠=A 40 ,∠=B 70 . 求证:AD=AB —DC .8、梯形ABCD 中,AD ∥BC ,AB =CD =AD =1,∠B =60°,直线MN 为梯形ABCD 的对称轴,P 为MN 上一点,那么PC +PD 的最小值为______.等腰梯形判定练习 姓名:1.等腰梯形一底角60,上、下底分别为8,18,则它的腰长为_____,高为______,面积是_____.2.梯形两条对角线分别为15,20,高为12,则此梯形面积为_________. 3.已知:如图,在四边形ABCD 中,∠B=∠C ,AB 与CD 不平行,且AB=CD . 求证:四边形ABCD 是等腰梯形.4、已知,如图,在四边形ABCD 中,AB >DC ,∠1=∠2,AC=BD ,求证:四边形ABCD 是等腰梯形5.如图4.9-9,梯形ABCD 中,AB ∥CD ,AD=BC ,CE ⊥AB 于E ,若AC ⊥BD 于G . 求证:CE=21(AB+CD ).梯形中位线练习题1.已知梯形中位线长是5cm ,高是4cm ,则梯形的面积是 。
等腰梯形的性质和判定 同步练习一、看一看,选一选(每小题4分,共20分)1.等腰梯形ABCD 中,AB ∥DC ,AD=BC=8,AB=10,CD=6,则梯形ABCD 的面积是 ( )A 、1516 B 、516 C 、1532 D 、17162.对角线互相垂直平分且相等的四边形一定是( )。
A .正方形 B .菱形 C .矩形 D .等腰梯形 3、用两个全等的等腰三角形一定能拼出的图形是 (A )等腰梯形 (B)直角梯形(C )菱形 (D )矩形4、等腰梯形上底长2cm ,过它的一个端点引一腰的平行线与下底相交,所得三角形的周长为6cm ,则梯形的周长为 ( )A .12cmB .10cmC .8cmD .9cm5.四边形ABCD 中,AB ∥CD ,且AB 、CD 是关于x 的方程x 2-3mx +2m 2+m -2=0的两个实数根,则四边形ABCD 是A .矩形B .平行四边形C .梯形D .平行四边形或梯形二、想一想,填一填(每小题6分,共30分)6. 若等腰梯形的底角等于60°,它的两底分别为15cm 和29cm , 则它一腰的长为 ___cm.7.如图,在等腰梯形ABCD 中,AD ∥BC ,AC 、BD 相交于点O , 有如下四个结论:①AC =BD ;②梯形ABCD 是中心对称图形; ③∠ADB =∠DAC ;④△AOD ∽△COB. 请把正确..结论的序号填 写在横线上___________.8.等腰梯形上、下底之差等于一腰的长,那么腰与下底的夹角是__________.9.等腰梯形ABCD 中, AD ∥BC ,BD 平分∠ABC ,BD ⊥DC , 则等腰梯形的各角的度数为_________________.10.如图,梯形ABCD 中,BC AD //,1===AD CD AB ,︒=∠60B 直线MN 为梯形ABCD 的对称轴,P 为MN 上一点, 那么PD PC +的最小值。
等腰梯形证明题精选(初中数学)一、题目分析本文主要选取了几道与等腰梯形相关的证明题目,旨在提高初中数学学生的证明能力和思维逻辑能力。
以下是题目的详细分析和解答。
二、题目解答题目一:等腰梯形对角线垂直的证明题目描述:在平面直角坐标系中,有一个等腰梯形ABCD,其中AB∥CD,AD⊥AB。
设E是AB边上的一个点,连接CE,交BD于点F。
证明:AF⊥BF。
在平面直角坐标系中,有一个等腰梯形ABCD,其中AB∥CD,AD⊥AB。
设E是AB边上的一个点,连接CE,交BD于点F。
证明:AF⊥BF。
解答:首先,我们通过观察可以发现,等腰梯形ABCD可以用平面直角坐标系表示为四个顶点的坐标:A(0, 0),B(b, 0),C(a, h),D(d, h)。
其中,b、a、d、h是正实数。
我们可以根据等腰梯形的定义推导出以下两个关系式:1. AD⊥AB,即直线AD与直线AB垂直,可得直线AD的斜率为0,即:k1 = 0。
2. AB∥CD,即直线AB与直线CD平行,可得直线AB和直线CD的斜率相等,即:k2 = (h - 0) / (a - b) = h / (a - b)。
接下来,我们分别计算直线CE和直线BF的斜率。
设点E的坐标为E(x, 0),根据直线CE的斜率定义,可得直线CE的斜率为:k3 = (h - 0) / (a - x) = h / (a - x)。
设点F的坐标为F(f, y),根据直线BF的斜率定义,可得直线BF的斜率为:k4 = (h - y) / (f - d) = (h - y) / (f - d)。
根据直线垂直的性质,两条直线的斜率之积为-1,即:k1 * k4 = -1。
代入已知条件和计算结果,我们可以得到以下等式:0 * (h - y) / (f - d) = -1。
对上述等式进行变形,得到以下结果:h - y = 0。
即 h = y。
所以,AF⊥BF。
证毕。
题目二:等腰梯形对角线相等的证明题目描述:在平面直角坐标系中,有一个等腰梯形ABCD,其中AB∥CD,AD⊥AB,且AC = BD。
初中数学等腰梯形练习题
一、选择题
1. 等腰梯形的两腰相等,以下哪个选项是等腰梯形的性质?
A. 对角线相等
B. 对边平行
C. 对角线互相垂直
D. 对角线互相平分
2. 如果一个梯形的两底角相等,那么这个梯形是:
A. 等腰梯形
B. 直角梯形
C. 任意梯形
D. 不能确定
二、填空题
1. 在等腰梯形中,如果上底长为3cm,下底长为7cm,高为4cm,那么两腰的长度为____cm。
2. 等腰梯形的对角线相等,如果一条对角线的长度为10cm,那么另一条对角线的长度为____cm。
三、计算题
1. 已知等腰梯形的上底长为5cm,下底长为9cm,高为4cm,求两腰的长度。
2. 一个等腰梯形的对角线互相垂直,且一条对角线的长度为8cm,求另一条对角线的长度。
四、证明题
1. 证明:等腰梯形的对角线相等。
2. 证明:等腰梯形的两底角相等。
五、应用题
1. 一个等腰梯形的花坛,上底长为6m,下底长为10m,高为3m,求这个花坛的面积。
2. 一个等腰梯形的纸板,上底长为4cm,下底长为8cm,高为5cm,如果沿着高剪开,再将剪开的部分展开,求展开后的长方形的长和宽。
等腰梯形的性质(北京习题集)(教师版)一.选择题(共5小题)1.(2012秋•海陵区期末)顺次连接对角线互相垂直的等腰梯形四条边中点得到的四边形是( )A .平行四边形B .矩形C .菱形D .正方形2.(2012春•西城区期末)如图,在梯形ABCD 中,//AD BC ,AB CD =,2AD =,6BC =,60B ∠=︒,则AB 的长为( )A .3B .4C .5D .63.(2012•西城区模拟)如图,在等腰梯形ABCD 中,//AB CD ,3DC cm =,60A ∠=︒,BD 平分ABC ∠,则这个梯形的周长是( )A .21cmB .18cmC .15cmD .12cm4.(2011春•西城区期末)对角线相等且互相平分的四边形一定是( )A .等腰梯形B .矩形C .菱形D .平行四边形5.(2011春•北京校级期中)下列命题正确的是( )A .平行四边形的对角线相等B .矩形的对角线互相平分C .菱形的对角线相等且互相平分D .等腰梯形的一组对边相等且平行二.填空题(共7小题)6.(2013•东城区模拟)如图,在等腰梯形ABCD 中,//AD BC ,3AD =,5BC =,AC ,BD 相交于O 点,且60BOC ∠=︒,顺次连接等腰梯形各边中点所得四边形的周长是 .7.(2013春•北京校级期中)如图,等腰梯形ABCD 中,//AB DC ,BD 平分ABC ∠,60DAB ∠=︒,若梯形周长为8cm ,则AD = .8.(2012春•西城区校级期中)等腰梯形的下底是上底的3倍,高与上底相等,这个梯形的腰与下底所夹角的度数为 .9.(2012春•西城区期末)如图,在等腰梯形ABCD 中,//AD BC ,AB DC =,对角线AC ,BD 交于点O ,且90BOC ∠=︒.若12AD BC +=,则AC 的长为 .10.(2010秋•东城区期末)在等腰梯形ABCD 中,//AD BC ,4BC AD =,2AD =,45B ∠=︒.直角三角板含45︒角的顶点E 在边BC 上移动,一直角边始终经过点A ,斜边与CD 交于点F ,若ABE ∆是以AB 为腰的等腰三角形,则CF 的等于 .11.(2011春•西城区期末)正方形网格中, 每个小正方形的边长为 1 . 图 1 所示的矩形是由 4 个全等的直角梯形拼接而成的 (图 形的各顶点都在格点上;拼接时图形互不重叠, 不留空隙) ,如果用这 4 个直角梯形拼接成一个等腰梯形, 那么(1) 仿照图 1 ,在图 2 中画出一个拼接成的等腰梯形;(2) 这个拼接成的等腰梯形的周长为1222+.12.(2010春•西城区期末)如图,梯形ABCD 中,//AD BC ,AB CD =.//DE AB 交BC 于点E ,若60B ∠=︒,2AD =,4BC =,则DEC ∆的面积等于 .三.解答题(共3小题)13.(2014•房山区二模)阅读下列材料:我们定义:若一个四边形的一条对角线把四边形分成两个等腰三角形,则称这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如正方形就是和谐四边形.结合阅读材料,完成下列问题:(1)下列哪个四边形一定是和谐四边形A.平行四边形B.矩形C.菱形D.等腰梯形(2)如图,等腰Rt ABD∠=︒.若点C为平面上一点,AC为凸四边形ABCD的和谐线,且AB BC=,BAD∆中,90请直接写出ABC∠的度数.14.(2013春•昌平区期末)如图,梯形ABCD中,//⊥于点E,F∠=︒,AE BDC===,60AD BC,2AB AD DC是CD的中点,连接EF.(1)求证:四边形AEFD是平行四边形;(2)若点G是BC边上的一个动点,当点G在什么位置时,四边形DEGF是矩形?并求出这个矩形的周长;(3)在BC上能否找到另外一点G',使四边形DE G F'的周长与(2)中矩形DEGF的周长相等,请简述你的理由.15.(2013•昌平区二模)如图所示,等腰梯形ABCD中,//∠=︒.点M、N同CAB CD,15AD=,30AB=,20时以相同的速度分别从点A、点D开始在AB、DA上向点B、点A运动.(1)设ND的长为x,用x表示出点N到AB的距离;(2)当五边形BCDNM面积最小时,请判断AMN∆的形状.等腰梯形的性质(北京习题集)(教师版)参考答案与试题解析一.选择题(共5小题)1.(2012秋•海陵区期末)顺次连接对角线互相垂直的等腰梯形四条边中点得到的四边形是( )A .平行四边形B .矩形C .菱形D .正方形【分析】由等腰梯形ABCD ,得到AC BD =,根据三角形的中位线定理推出EH FG =,EF =,//EH FG ,即四边形是菱形,再推出90E ∠=︒,即可得出答案.【解答】解:等腰梯形ABCD ,//AD BC ,AC BD ∴=, E 为AD 的中点,H 为DC 的中点,//EH AC ∴,12EH AC =, 同理//FG AC ,12FG AC =, //EF DB ,12EF DB =, EH FG EF ∴==,//EH FG ,∴四边形EFGH 是菱形,AC DB ⊥,90AOD ∴∠=︒,//EH AC ,//FG AC ,90FEH HMO AOD ∴∠=∠=∠=︒,∴四边形EFGH 是正方形.故选:D .【点评】本题主要考查了等腰梯形的性质,平行四边形的判定,菱形的判定,正方形的判定等知识点,解此题的关键是证出(1)平行四边形(2)邻边相等(3)90E ∠=︒三个结论.2.(2012春•西城区期末)如图,在梯形ABCD 中,//AD BC ,AB CD =,2AD =,6BC =,60B ∠=︒,则AB 的长为( )A.3B.4C.5D.6【分析】由过点A作//=,AE CD,交BC于点E,由//AD BC,可得四边形ADCE是平行四边形,又由AB CD ∆是等边三角形,则可求得答案.∠=︒,易证得ABEB60【解答】解:过点A作//AE CD,交BC于点E,AD BC,//∴四边形ADCE是平行四边形,=,AE CD∴=,CE ADBE BC CE BC AD∴=-=-=-=,624=,AB CD∴=,AB AE60∠=︒,B∴∆是等边三角形,ABEAB BE∴==.4故选:B.【点评】此题考查了等腰梯形的性质、平行四边形的判定与性质以及等边三角形的判定与性质.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.3.(2012•西城区模拟)如图,在等腰梯形ABCD中,//∠,则这个∠=︒,BD平分ABCAAB CD,3DC cm=,60梯形的周长是()A.21cm B.18cm C.15cm D.12cm【分析】根据题意,可知60∠=︒,30BDC∠=︒,因此,ADBA ABC∠=∠=︒,90∠=∠=︒,即可推出30ABD DBC===,根据勾股定理,可知6AB=,便可推出梯形的周长.3CD BC AD【解答】解:等腰梯形ABCD中,//∠=︒,AAB CD,3DC cm=,60BC AD ∴=,60A ABC ∠=∠=︒, BD 平分ABC ∠,30ABD DBC ∴∠=∠=︒,30BDC ∴∠=︒,30ABD ∠=︒,60A ∠=︒,90ADB ∴∠=︒,3CD cm =,3CD BC AD ∴===,26AB AD ∴==,∴梯形ABCD 的周长633315AB BC CD DA cm =+++=+++=.故选:C .【点评】本题主要考查等腰梯形的性质、平行线的性质、解直角三角形、等腰三角形的性质,关键在于根据已知推出90ADB ∠=︒,CD BC AD ==.4.(2011春•西城区期末)对角线相等且互相平分的四边形一定是( )A .等腰梯形B .矩形C .菱形D .平行四边形【分析】根据平行四边形的判定与矩形的判定定理,即可求得答案.【解答】解:对角线互相平分的四边形是平行四边形,对角线相等的平行四边形是矩形,∴对角线相等且互相平分的四边形一定是矩形.故选:B .【点评】此题考查了平行四边形,矩形,菱形以及等腰梯形的判定定理.此题比较简单,解题的关键是熟记定理.5.(2011春•北京校级期中)下列命题正确的是( )A .平行四边形的对角线相等B .矩形的对角线互相平分C .菱形的对角线相等且互相平分D .等腰梯形的一组对边相等且平行【分析】根据平行四边形的性质判断A ;根据矩形的性质判断B ;根据菱形的性质判断C ;根据等腰梯形的等腰判断D 即可.【解答】解:A 、平行四边形的对角线只互相平分,故本选项错误; B 、矩形的对角线互相平分且相等,故本选项正确;C 、菱形的对角线互相平分且垂直,每一条对角线平分一组对角,故本选项错误;D 、等腰梯形的一组对边平行而另一组对边相等,故本选项错误;故选:B .【点评】本题主要考查对平行四边形的性质,矩形的性质,菱形的性质,等腰梯形的性质等知识点的理解和掌握,能熟练地运用性质进行判断是解此题的关键.二.填空题(共7小题)6.(2013•东城区模拟)如图,在等腰梯形ABCD 中,//AD BC ,3AD =,5BC =,AC ,BD 相交于O 点,且60BOC ∠=︒,顺次连接等腰梯形各边中点所得四边形的周长是 16 .【分析】根据等腰梯形对角线相等和中位线定理即可得出EF 、EH 、HG 、GF 的长度,从而可得出答案.【解答】解:在等腰梯形ABCD 中,AOB DOC ∆≅∆,故OB OC =,在BOC ∆中,60BOC ∠=︒,1(18060)602OBC OCB ∠=∠=︒-︒=︒, 则有5OB OC BC ===,同理3AO DO AD ===,则358AC BD ==+=,根据中位线定理,1842FG GH HE EF ====⨯=, 四边形的周长是4416⨯=,故答案为:16.【点评】本题考查等腰梯形的性质及中位线定理难度不大,学生要学会对等腰梯形的性质及梯形的中位线定理的理解及运用.7.(2013春•北京校级期中)如图,等腰梯形ABCD 中,//AB DC ,BD 平分ABC ∠,60DAB ∠=︒,若梯形周长为8cm ,则AD = 85cm .【分析】由梯形ABCD 是等腰梯形,于是得到AD BC =,60DAB ABC ∠=∠=︒,由于//AB DC ,得到CDB ABD ∠=∠,由BD 平分ABC ∠,得到30ABD CBD ∠=∠=︒,于是求得CDB CBD ∠=∠,90ADB ∠=︒,根据直角三角形的性质得到CD BC =,2AB AD =,于是得到结论.【解答】解:梯形ABCD 是等腰梯形,AD BC ∴=,60DAB ABC ∠=∠=︒,//AB DC ,CDB ABD ∴∠=∠, BD 平分ABC ∠,30ABD CBD ∴∠=∠=︒,CDB CBD ∴∠=∠,90ADB ∠=︒,CD BC ∴=,2AB AD =,梯形周长为8cm , 18855AD cm ∴=⨯=. 故答案为:85cm . 【点评】本题考查了等腰梯形的性质,直角三角形的性质,角的平分线的性质,熟练掌握等腰梯形的性质是解题的关键.8.(2012春•西城区校级期中)等腰梯形的下底是上底的3倍,高与上底相等,这个梯形的腰与下底所夹角的度数为 45︒ .【分析】分别过A ,B 作高AE ,BF ,根据已知得到DE AE AB ==,从而得到D ∠的度数.【解答】解:过点A 作AE DC ⊥于点E ,过点B 作BF BC ⊥于点F ,四边形ABCD 是等腰梯形,DE CF ∴=,又3CD AB =,DE CF EF AB ∴===,AE AB =,DE AE ∴=,45D ∴∠=︒.故答案为:45︒.【点评】此题主要考查等腰梯形的性质和等腰直角三角形的判定及性质,解答本题的关键是熟练掌握等腰梯形的性质.9.(2012春•西城区期末)如图,在等腰梯形ABCD 中,//AD BC ,AB DC =,对角线AC ,BD 交于点O ,且90BOC ∠=︒.若12AD BC +=,则AC 的长为 62 .【分析】首先过点D 作//DE AC ,交BC 的延长线于点E ,易得四边形ACED 是平行四边形,BDE ∆是等腰直角三角形,继而求得答案.【解答】解:过点D 作//DE AC ,交BC 的延长线于点E ,//AD BC ,90BOC ∠=︒,∴四边形ACED 是平行四边形,90BDE BOC ∠=∠=︒,CE AD ∴=,DE AC =,在等腰梯形ABCD 中,AB DC =,AC BD ∴=,DE BD ∴=,BDE ∴∆是等腰直角三角形,12BE BC CE AD BC =+=+=,设AC BD DE x ===,在Rt BDE ∆中,222BD DE BE +=,22212x x ∴+=,62AC BD ∴==.故答案为:62.【点评】此题考查了等腰梯形的性质、平行四边形的判定与性质以及等腰直角三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.10.(2010秋•东城区期末)在等腰梯形ABCD 中,//AD BC ,4BC AD =,2AD ,45B ∠=︒.直角三角板含45︒角的顶点E 在边BC 上移动,一直角边始终经过点A ,斜边与CD 交于点F ,若ABE ∆是以AB 为腰的等腰三角形,则CF 的等于 2或23 .【分析】首先理解题意,得出此题应该分两种情况进行分析,分别是AB AE =,AB BE =,从而得到最后答案.【解答】解:根据已知条件可得,()2cos 3AB BC AD B =-÷÷=.①当AB AE =时,如图,45B ∠=︒,45AEB ∠=︒,3AE AB ==,则在Rt ABE ∆中,223332BE =+=故4EC =2322.易得FEC ∆为等腰直角三角形, 故22(2)(2)2FC =+=.②当AB BE =时,45B BAE CEF ∠+∠=︒+∠,45B ∠=︒,CEF EAB ∴∠=∠,B C ∠=∠,ABE ECF ∴∆∆∽,AB BECE CF =, ∴3423CF =-,423CF ∴=;ABE FCE ∆∆∽, ∴AB EBFC CE =, ∴3423CF =-423CF =,故答案为:2或423-.【点评】此题主要考查了等腰梯形的性质,以及等腰直角三角形的性质,综合性较强.11.(2011春•西城区期末)正方形网格中, 每个小正方形的边长为 1 . 图 1 所示的矩形是由 4 个全等的直角梯形拼接而成的 (图 形的各顶点都在格点上;拼接时图形互不重叠, 不留空隙) ,如果用这 4 个直角梯形拼接成一个等腰梯形, 那么 (1) 仿照图 1 ,在图 2 中画出一个拼接成的等腰梯形; (2)这个拼接成的等腰梯形的周长为1222+.【分析】(1) 根据题意画出图形即可;(2) 求出AD 、AB 、CD 、BC 的长, 即可求出答案 . 【解答】解: (1)如图直角梯形AGHB 、GHRQ 、QRFE 、EFCD 组成等腰梯形ABCD .(2) 根据题意得到:5AG =,7BC =,22112AB CD ==+=,∴等腰梯形的周长是57221222++=+故答案为:1222+【点评】本题主要考查对等腰梯形的性质,直角梯形,勾股定理等知识点的理解和掌握,能正确画出图形是解此题的关键.12.(2010春•西城区期末)如图,梯形ABCD中,//AD BC,AB CD=.//DE AB交BC于点E,若60B∠=︒,2AD=,4BC=,则DEC∆的面积等于3.【分析】可证明四边形ABED是平行四边形,则DE AB=,从而得出DE CD=,根据有一个角是60︒的等腰三角形是等边三角形进而利用勾股定理求出三角形DEC的高,求出面积即可.【解答】解:过点D作DF EC⊥于点F,//AD BC,//DE AB,∴四边形ABED是平行四边形,DE AB∴=,AB DC=,DE DC∴=,//AB DE,60B∠=︒,60DEC∴∠=︒.又DE DC=,DEC∴∆是等边三角形,四边形ABED是平行四边形,2AD BE∴==,4BC=,2EC∴=,2DE EC CD∴===,1EF FC==,22213DF∴=-=,DEC∴∆的面积等于11233 22DF EC⨯⨯=⨯⨯=.故答案为:3.【点评】本题主要考查平行四边形的判定及等边三角形的判定和三角形面积求法等知识,熟练掌握等边三角形的判定定理是解题的关键.三.解答题(共3小题)13.(2014•房山区二模)阅读下列材料:我们定义:若一个四边形的一条对角线把四边形分成两个等腰三角形,则称这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如正方形就是和谐四边形.结合阅读材料,完成下列问题:(1)下列哪个四边形一定是和谐四边形CA.平行四边形B.矩形C.菱形D.等腰梯形(2)如图,等腰Rt ABD∠=︒.若点C为平面上一点,AC为凸四边形ABCD的和谐线,且AB BC=,BAD∆中,90请直接写出ABC∠的度数.【分析】(1)由和谐四边形的定义即可得到菱形是和谐四边形;(2)首先根据题意画出图形,然后由AC是四边形ABCD的和谐线,可以得出ACD∆是等腰三角形,从图1,图2,图3三种情况运用等边三角形的性质,正方形的性质和30︒的直角三角形性质就可以求出ABC∠的度数.【解答】解:(1)菱形的四条边相等,∴连接对角线能得到两个等腰三角形,∴菱形是和谐四边形;(2)解:AC是四边形ABCD的和谐线,∴∆是等腰三角形,ACD在等腰Rt ABD∆中,AB AD=,∴==,AB AD BC如图1,当AD AC=时,AB AC BC∠=∠∴==,ACD ADC∴∆是正三角形,ABC∴∠=︒.60ABC如图2,当AD CD=时,∴===.AB AD BC CD90BAD ∠=︒,∴四边形ABCD 是正方形,90ABC ∴∠=︒;如图3,当AC CD =时,过点C 作CE AD ⊥于E ,过点B 作BF CE ⊥于F , AC CD =.CE AD ⊥,12AE AD ∴=,ACE DCE ∠=∠. 90BAD AEF BFE ∠=∠=∠=︒,∴四边形ABFE 是矩形.BF AE ∴=.AB AD BC ==,12BF BC ∴=, 30BCF ∴∠=︒. AB BC =, ACB BAC ∴∠=∠. //AB CE , BAC ACE ∴∠=∠,1152ACB BAC BCF ∴∠=∠=∠=︒,150ABC ∴∠=︒,综上:ABC ∠的度数可能是:6090150︒︒︒.【点评】此题考查了等腰直角三角形的性质,等腰三角形的性质、矩形的性质、正方形的性质,菱形的性质,此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.14.(2013春•昌平区期末)如图,梯形ABCD 中,//AD BC ,2AB AD DC ===,60C ∠=︒,AE BD ⊥于点E ,F 是CD 的中点,连接EF .(1)求证:四边形AEFD 是平行四边形;(2)若点G 是BC 边上的一个动点,当点G 在什么位置时,四边形DEGF 是矩形?并求出这个矩形的周长; (3)在BC 上能否找到另外一点G ',使四边形DE G F '的周长与(2)中矩形DEGF 的周长相等,请简述你的理由.【分析】(1)由已知可得四边形ABCD 为等腰梯形,ABD ∆为等腰三角形,60C ∠=︒,可知120BAD ADC ∠=∠=︒,又AE BD ⊥,故1602EAD BAD ∠=∠=︒,BE DE =,在Rt ADE ∆中,30ADE ∠=︒,故90BDC ADC ADE ∠=∠-∠=︒,可证//AE DF ,而E 、F 两点为BD 、CD 边的中点,可证////EF BC AD ,故四边形AEFD 是平行四边形; (2)延长AE 交BC 于G ,可证G 点为BC 的中点,此时四边形DEGF 是矩形,解Rt DEF ∆,可求DE ,DF ,根据矩形的性质求周长;(3)当1CG CF '==时,△G EF '与DEF ∆关于直线EF 轴对称,可满足题意. 【解答】(1)证明:梯形ABCD 中,//AD BC ,2AB AD DC ===,∴四边形ABCD 为等腰梯形,60C ∠=︒,120BAD ADC ∴∠=∠=︒,又ABD ∆为等腰三角形,AE BD ⊥, 1602EAD BAD ∴∠=∠=︒,BE DE =,在Rt ADE ∆中,9030ADE EAD ∠=︒-∠=︒, 90BDC ADC ADE ∴∠=∠-∠=︒, //AE DF ∴,E 、F 两点为BD 、CD 边的中点,////EF BC AD ∴,∴四边形AEFD 是平行四边形;(2)解:延长AE 交BC 于G ,连接FG ,BE ED =,//AE CD ,AD BG GC ∴==,G ∴点为BC 的中点,//FG DE ∴,而90EDF ∠=︒,∴四边形DEGF 是矩形,在Rt DEF ∆中,3DE =,1DF =,∴矩形的周长223=+;(3)解:可以.当1CG CF '==时,△G EF '与DEF ∆关于直线EF 轴对称, DF FG =',DE EG =',则四边形DEG F '的周长223=+; 周长不变.【点评】本题考查了等腰梯形的性质,三角形中位线定理,直角三角形的性质,平行四边形,矩形的判断.关键是根据题意,推出特殊三角形.15.(2013•昌平区二模)如图所示,等腰梯形ABCD 中,//AB CD ,15AB =,20AD =,30C ∠=︒.点M 、N 同时以相同的速度分别从点A 、点D 开始在AB 、DA 上向点B 、点A 运动. (1)设ND 的长为x ,用x 表示出点N 到AB 的距离; (2)当五边形BCDNM 面积最小时,请判断AMN ∆的形状.【分析】(1)首先表示出AN 的长,进而得出PAN ∠的度数,利用1sin (20)2PN AN PAN x =∠=-得出即可;(2)首先得出12AMN S AM NP ∆=,进而得出其最值,利用AMN BCDNM S S S ∆=-五边形梯形,得出当10x =时,五边形BCDNM 面积最小,进而得出AMN ∆的形状.【解答】解:(1)过点N 作BA 的垂线NP ,交BA 的延长线于点P . 由已知得,AM x =,20AN x =-.四边形ABCD 是等腰梯形,//AB DC ,AD BC =, 30D C ∴∠=∠=︒. 30PAN D ∴∠=∠=︒.在Rt APN ∆中,1sin (20)2PN AN PAN x =∠=-.即点N 到AB 的距离为1(20)2x -.(2)根据(1)2111(20)5244AMN S AM NP x x x x ∆==-=-+. 104-<, ∴当10x =时,AMN S ∆有最大值.又AMN BCDNM S S S ∆=-五边形梯形,且S 梯形为定值,∴当10x =时,五边形BCDNM 面积最小.此时,10ND AM ==,10AN AD ND =-=,AM AN ∴=.∴当五边形BCDNM 面积最小时,AMN ∆为等腰三角形.【点评】此题主要考查了等腰梯形的性质以及二次函数最值问题以及等腰三角形的性质等知识,根据二次函数最值得出五边形BCDNM 面积最小时AN 、AM 的值是解题关键.。
等腰梯形的性质专项练习30题(有答案)1.如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AD=2,AB=6,∠B=60°,求下底BC的长.2.在等腰梯形ABCD中,AD∥BC,AB=CD=AD,AC⊥AB.求∠B的度数.3.如图,在等腰梯形ABCD中,AB∥DC,对角线AC平分∠BAD,∠B=60°,CD=3,求梯形中位线的长.4.如图在梯形ABCD中,AD∥BC,AB=AD=DC,AC⊥AB,将CB延长至点F,使BF=CD.求∠CAF的度数.5.如图,已知在梯形ABCD中,AD∥BC,AB=CD,AD=4,BC=8,∠C=60°,求AB的长.6.已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.7.如图,在等腰梯形△ABCD中,AB∥CD,AD=BC=CD,BD⊥AD.(1)求∠A的度数.(2)设AD=2cm,求梯形ABCD的面积.8.如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠B=60°.AE⊥BC于E;EF⊥CD于F,点F是CD的中点.求证:AD=BE.9.如图,在等腰梯形ABCD中,已知AD∥BC,AB=CD,AE⊥BC于E,∠B=60°,∠DAC=45°,,求梯形ABCD的周长?10.如图示,在等腰梯形ABCD中,AD∥BC,∠B=45°,中位线长为5cm,高为2cm,求梯形底边BC的长及梯形的面积.11.如图,在梯形ABCD中,AD∥BC,AB=DC=6cm,BD⊥CD于D,∠C=60°.(1)求∠DBC的度数;(2)求AD的长.12.如图,等腰梯形ABCD中,AB∥CD,AB=2AD,梯形周长为40,对角线BD平分∠ABC,求梯形的腰长及两底边的长.13.如图,在等腰梯形ABCD中,AD∥BC,AC平分∠BCD,已知AD=5cm,BC=9cm,求等腰梯形ABCD的周长.14.如图,在梯形ABCD中,AD∥BC,AB=DC,点E在BC的延长线上,DE=DB.求证:AD=CE.15.如图,等腰梯形ABCD中,AD∥BC,BD⊥DC,点E是BC边的中点,DE∥AB.(1)求∠BCD的度数;(2)若AB=4,求等腰梯形ABCD的面积.16.如图,在等腰梯形ABCD中,AB=CD,∠D=120°,AC平分∠BCD,梯形的中位线长为6,求AC的长及梯形的面积?17.如图,E是等腰梯形ABCD底边AB上的中点,求证:DE=CE.18.如图,在等腰梯形ABCD中,AB∥CD,AD=BC,E、F是AB上的两点且AE=BF,DF与CE相交于点O.问OE与OF相等吗?为什么?19.如图,在等腰梯形ABCD中,AD∥BC,∠A=2∠B,BC=3,AB=2.求AD的长.20.如图,等腰梯形ABCD中,AD∥BC,BD⊥CD,∠A=2∠C,BC=8cm,求腰DC的长.21.如图所示,在等腰梯形ABCD中,已知AD∥BC,AB=DC,∠ACB=42°,∠ACD=27°.(1)∠BAC=_________°;(2)如果BC=10cm,连接BD,求BD的长度.22.如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?23.如图,在梯形ABCD中,AB=DC=AD,AC=BC,求∠B的度数.24.如图,E是等腰梯形ABCD底边AB上的中点,DE和CE相等吗,为什么?25.如图,等腰梯形ABCD中,AD∥BC,AB=CD,两条对角线AC⊥BD,AE⊥BC.(1)求证:AE=(AD+BC);(2)若AC=10cm,求等腰梯形ABCD的面积.26.如图,已知在等腰梯形ABCD中,CD∥AB,AD=BC,四边形AEBC是平行四边形.求证:∠ABD=∠ABE.27.如图,等腰梯形ABCD中,AD∥BC,AB=CD,对角线BD平分∠ABC,且BD⊥DC,上底AD=3cm.(1)求∠ABC的度数;(2)求梯形ABCD的周长.28.已知等腰梯形ABCD中,AD∥BC,AB=CD,BD平分∠ABC,BD⊥CD,若梯形的周长为25cm,求梯形各边的长.29.如图,已知四边形ABCD是等腰梯形,AD∥BC,对角线AC⊥BD,延长BC至E点,使CE=AD,连接DE.(1)求∠ACE的度数;(2)若AD+BC=10cm,求△BDE的面积.30.如图所示:在等腰梯形ABCD中,AB∥DC,AD=DC=CB,∠ADC=120°.(1)试探讨线段AC与BC的位置关系;(2)若AD=4,求梯形ABCD的面积.参考答案:1.过点D作DE∥AB,则可得DE=AB=CD,又∵∠B=∠DEC=60°,∴△DEC为等边三角形,∴CE=AB=6cm,故可得BC=BE+EC=AD+EC=8cm.2.在等腰梯形ABCD中,∵AD∥BC,AB=CD,∴∠B=∠BCD.(1分)∵AD=CD,∴∠ACD=∠CAD.(1分)又∵AD∥BC,∴∠ACB=∠CAD.(1分)∴∠ACB=∠ACD.(1分)∵AC⊥AB,∴∠B+∠ACB=90°.(1分)∴∠B+∠B=90°.∴∠B=60°.3.∵四边形ABCD是等腰梯形,∠B=60°,∴∠BAD=∠B=60°,AD=BC,∵AC平分∠BAD,∴∠BAC=∠DAC=30°,∴∠ACB=90°,又∵AB∥DC,∴∠ACD=∠BAC,∴∠ACD=∠DAC,∴DC=AD=3,∴BC=AD=3,在Rt△ACB中,∵∠BAC=30°,∴AB=2BC=6,∴所求中位线的长是(AB+DC)=(6+3)=4.54.∵AD∥BC,∴∠DAC=∠ACB,∵AD=DC,∴∠DCA=∠DAC,∴∠ACD=∠ACB=∠DCB,∵AB=DC,∴∠ABC=∠DCB=2∠ACB,∵AC⊥AB,∴∠CAB=90°,∴∠ABC=60°,∵AB=BF,∴∠BAF=∠F,∵∠ABC=∠BAF+∠F,∴∠BAF=30°,∴∠CAF=∠CAB+∠BAF=90°+30°=120°.5.分别过点A,D作AE⊥BC,DF⊥BC.∵在梯形ABCD中,AD∥BC,AB=CD,AD=4,BC=8,∴AD=EF=4,BE=CF=(8﹣4)=2,∵∠C=60°,∴∠CDF=30°,∴CD=4,∵AB=CD,∴AB=4.6.如图,过点B作BE∥AC交DC的延长线于点E,∴∠EBD=∠CMD=90°,∵AB∥CD,∴四边形ACEB是平行四边形,∴AC=BE,CE=AB,∵AB=2,CD=4,∴DE=DC+CE=DC+AB=4+2=6,∵梯形ABCD中,AB∥CD,AD=BC,∴AC=BD,∴BD=BE,在Rt△BDE中,由勾股定理得,BD2+BE2=DE2,即BD2+BD2=62,解得BD=3.故答案为:3.7.1)解:∵AD=BC=DC,∴∠CDB=∠CBD,∵DC∥BA,∴∠CDB=∠DBA,∴∠CBA=2∠DBA,∵DC∥AB,AD=BC,∴∠A=∠ABC=2∠DBA,∵DB⊥AD,∴∠ADB=90°,∴∠A=×90°=60°,答:∠A=60°.(2)解:作DE⊥AB于E,∵∠A=60°,∠DEA=90°,∴∠ADE=30°,∴AE=AD=1cm,由勾股定理得:DE=cm,同理AB=2AC=4cm,∴梯形ABCD 的面积是(CD+AB)×DE=×(2cm+4cm)×cm=3cm2,答:梯形ABCD 的面积是cm28.连接ED.∵AD∥BC,AB=CD,∴∠B=∠C=60°,∵EF⊥CD,F是CD中点,∴ED=EC(3分)∴∠DEC=∠C=60°∴△ECD是等边三角形,(4分)∴∠B=∠DEC∴AB∥DE(5分)∴四边形ABED是平行四边形(6分)∴AD=BE(7分)9.∵AD∥BC,∠DAC=45°,∴∠ACB=45°∵AE⊥BC ,,∴,∵∠B=60°,∴BE=1,AB=2,∴DC=2,作DF⊥BC于点F,∴四边形AEFD是矩形,∴AE=DF,∵∠B=∠C,∠AEB=∠DFC=90°,∴△ABE≌△DCF(AAS),∴BE=FC=1,∴,∵AD∥BC,AE⊥BC,DF⊥BC,∴AE∥DF,∴四边形ADFE是平行四边形,∴,∴梯形ABCD的周长为:AD+DC+BC+AB=﹣1+2+2+2+﹣1=4+2.答:梯形ABCD的周长是4+2.10.取两腰AB,CD的中点分别为E和F,连接EF,根据梯形中位线定理得:EF=(AD+BC),∵EF=5cm,∴AD+BC=10cm,过A,D作出梯形的两条高AM和DN,∵梯形ABCD,∴AD∥BC,∴∠MAD=∠AMN=∠MND=90°,∴四边形AMND为矩形,∴AD=MN,又Rt△ABM和Rt△DCN中,AM=DN,AB=AC,∴Rt△ABM≌Rt△DCN,∴BM=CN,由∠AMB=90°,∠B=45°,得△ABM为等腰直角三角形,∴MB=AM=2cm,同理CN=DN=2cm,设AD=MN=xcm,则AD+BC=AD+BM+MN+NC=2x+4=10,解得:x=3,∴BC=2+x+2=7;∴梯形的面积S===10cm2.答:BC=7cm,梯形的面积10cm2.11.(1)∵BD⊥CD于D,∴∠BDC=90°,∵∠C=60°,∴∠DBC=180°﹣90°﹣60°=30°;(2)如图,过D作DE∥AB交BC于点E,∵AD∥BC,∴四边形ABED是平行四边形,∴AD=BE,AB=DE,∵AB=DC,∴DC=DE,∵∠C=60°,∴△CDE是等边三角形,∴CE=DC=6cm,在Rt△BCD中,∵∠DBC=30°,DC=6cm,∴BC=2DC=2×6=12cm,∴BE=BC﹣CE=12﹣6=6cm,∴AD的长为6cm.12.∵四边形ABCD是等腰梯形,AB∥DC,∴AD=BC,∠DBA=∠CDB,又BD平分∠ABC,∴∠CBD=∠DBA,∴∠CDB=∠CBD,∴CD=BC,又AB=2AD,AB+AD+CD+BC=40,∴2AD+AD+AD+AD=40,5AD=40,AD=8,∴CD=8,AB=16,即梯形腰长为8,两底边长为8和16,答:梯形的腰长是8,两底边的长分别是8,16 13.∵AD∥BC,∴∠DAC=∠ACB,∵AC平分∠BCD,∴∠DCA=∠ACB,∴∠DAC=∠DCA,∴AD=CD=AB=5cm,∴等腰梯形ABCD的周长是AB+BC+CD+AD=5cm+5cm+5cm+9cm=24cm,答:等腰梯形ABCD的周长是24cm.14.法一:在梯形ABCD中,∵AD∥BC,AB=AC,∴∠ABC=∠DCB(等腰梯形同一底上的内角相等),∠A+∠ABC=180°,又∵∠DCE+∠DCB=180°,∴∠A=∠DCE,∵DB=BE,∴∠DBC=∠E,∵∠ADB=∠DBC,∴∠ADB=∠E,在△ABD和△CDE 中,,∴△ABD≌△CDE(AAS),∴AD=CE;证法二:连接AC,在梯形ABCD中,∵AD∥BC,AB=AC,∴AC=BD(等腰梯形的对角线相等),∠ABC=∠DCB(等腰梯形同一底上的内角相等),在△ABC和△DCB 中,,∴△ABC≌△DCB(SAS),∴∠ACB=∠DBC,∵DB=BE,∴∠DBC=∠E,∴∠ACB=∠E,∴AC∥DE,又∵DE=BD,∴DE=AC,∴四边形ACED是平行四边形(一组对边平行的四边形是平行四边形),∴AD=CE.(平行四边形的对边相等).15.(1)∵梯形ABCD是等腰梯形,∴AB=CD,∵AD∥BC,DE∥AB,∴四边形ABED是平行四边形,∴AB=CD=DE,∵BD⊥DC,∴∠BDC=90°,∵点E是BC边的中点,∴BE=DE=CE,∴DE=DE=CE,即△CDE是等边三角形,∴∠BCD=60°;(2)过点D作DF⊥BC于点F,∵△CDE是等边三角形,AB=CD=4,∴DF=CD•sin60°=4×=2,∵AB=BE=CE=4,∴BC=2AB=8,∴S梯形ABCD =(AD6BC)•DF=×(4+8)×2=1216.∵四边形ABCD是等腰梯形,∠D=120°,∴∠B=∠BCD=60°,∵AC平分∠BCD,∴∠BCA=∠ACD=30°,则∠BAC=90°,又∠CAD=∠BCA,∴∠CAD=∠ACD,则AD=CD=AB ,在Rt △ABC 中,∵∠BCA=30°, ∴BC=2AB=2AD , ∵中位线长为6, ∴AD+BC=3AD=12, ∴AD=4,BC=2AD=8,在Rt △ABC中,由勾股定理,得,作AE ⊥BC 于E , 则,∴梯形的面积为,答:AC 的长是4,梯形的面积是12.17.∵等腰梯形ABCD , ∴BC=AD ,∠CBE=∠DAE . ∵E 是AB 上的中点, ∴BE=AE .∴△CBE ≌△DAE (SAS ). ∴DE=CE . 18.OE=OF . 理由:∵AE=BF ,∴AE+EF=BF+EF ,即AF=BE . ∵等腰梯形ABCD 中,AB ∥CD , ∴AD=CB ,∠A=∠B . ∴△ADF ≌△BCE . ∴∠DFE=∠CEF . ∴OE=OF19.过点A 作AE ⊥BC 于E ,过点D 作DF ⊥BC 于F ,则四边形AEFD 是矩形, 所以AD=EF ,BE=FC因为∠A=2∠B ,又∠BAD+∠B=180°,所以∠B=60° 在Rt △AEB 中,因为∠BAE=90°﹣60°=30°,AB=2, 所以BE=AB=所以AD=BC ﹣2BE=3﹣1×2=1.20.因为四边形ABCD 是等腰梯形,AD ∥BC , 所以∠A=∠ADC ,∠ADC+∠C=180°(2分)又∠A=2∠C ,则2∠C+∠C=180°,故∠C=60°(4分) 因为BD ⊥CD ,BC=8cm ,所以,∠DBC=180°﹣90°﹣60°=30°(6分)则DC=BC=4cm ,即为所求. 21.(1)∵∠ACB=42°,∠ACD=27°, ∴∠BCD=∠BCA+∠ACD=69°;(2)∵∠ABC=∠BAC=69°, ∴AC=BC=10cm ,又∵四边形ABCD 是等腰梯形, ∴BD=AC=10cm .22.∵四边形ABCD 是等腰梯形, ∴AB=DC ,∠A=∠D . ∵M 是AD 的中点, ∴AM=DM .在△ABM 和△DCM 中,,∴△ABM ≌△DCM (SAS ). ∴MB=MC23.∵四边形ABCD 是等腰梯形, ∴∠B=∠BCD . ∵AD ∥BC ,∴∠DAC=∠ACB , ∵AD=CD ,∴∠ACD=∠DAC , ∴∠ACB=∠DCA ,设∠ACD=x ,则得到∠DAC=∠ACB=x ,∠B=∠BAC=2x ,∴∠B+∠ACB+∠BAC=180°,即x+2x+2x=180°, 解得x=36°, ∴∠B=72°24.DE=CE .理由是:∵等腰梯形ABCD ,AB ∥CD , ∴∠A=∠B ,∵E 为AB 的中点, ∴AE=BE ,在△CBE 和△DAE 中,∴△CBE ≌△DAE (SAS ), ∴DE=CE .25.1)证明:过点D 作DF ∥AC ,交BC 的延长线于点F ,过点D 作DH ⊥BC 于点H , ∵AD ∥BC ,∴四边形ACFD 是平行四边形, ∴CF=AD ,DF=AC , ∵AC ⊥BD ,AE ⊥BC , ∴DH=AE ,DF ⊥BD , ∵AB=CD , ∴AC=BD , ∴BD=DF ,∴△BDF 是等腰直角三角形, ∴BH=FH ,∴DH=BF=(BC+CF)=(AD+BC),∴AE=(AD+BC);(2)解:∵AC=10cm,∴BD=DF=10cm,在Rt△BDF中,BF==10(cm),∴AD+BC=BF=10cm,∴AE=BF=5(cm),∴S梯形ABCD =(AD+BC)•AE=×10×5=50(cm2).26.∵四边形AEBC是平行四边形,AD=BC,∴AD=BC=AE,BD=AC=BE,在△AEB和△ADB中,,∴△AEB≌△ADB,∴∠ABD=∠ABE.27.(1)等腰梯形ABCD中,AD∥BC,AB=CD,∴∠C=∠ABC,∵BD平分∠ABC,∴∠C=∠ABC=2∠DBC,∵BD⊥DC,∴∠BDC=90°,∴3∠DBC=90°,∴∠DBC=30°,∴∠ABC=∠C=2∠DBC=60°;(2)∵AD∥BC,∴∠ADB=∠DBC,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABD=∠ADB,∴AB=AD=DC,∵AD=3cm,∴AB=DC=3cm,在Rt△BDC中,∠BDC=90°,∠DBC=30°,DC=3cm,∴BC=2DC=6cm,∴梯形ABCD的周长是AD+AB+BC+CD=3cm+3cm+6cm+3cm=15cm.28.∵在等腰梯形ABCD中,AB=CD,∴∠ABC=∠C,∵对角线BD平分∠ABC,∴∠DBC=∠ABC=∠C,∵AD∥BC,∴∠DBC=∠ADB,∴∠C=2∠DBC,∵BD⊥CD,∴∠DBC=30°,∴BC=2CD,∵梯形的周长=AD+AB+BC+CD=5AB=30cm,∴AB=AD=CD=6cm,BC=12cm29.(1)∵AD∥BC,CE=AD,∴四边形ACED为平行四边形∴DE∥AC,DE=AC∵四边形ABCD是等腰梯形,∴AC=BD,∴BD=DE,∴∠E=∠DBE,∵AC⊥BD,AC∥DE,∴DE⊥BD,∴∠BDE=90°,∴∠E=45°∵DE∥AC,∴∠E+∠ACE=180°,∴∠ACE=135°(2)∵AD=CE,∴BE=BC+CE=BC+AD=10cm,∴Rt△BDE中,由勾股定理得:BD2+DE2=BE2,又∵BD=DE,∴BD2=50,∴S△BDE =cm2.30.(1)线段AC与BC的位置关系是:AC⊥BC,理由是:∵等腰梯形ABCD,∠ADC=120°,∴∠DAB=∠CBA=60°,又由AD=DC,∠ADC=120°,∴∠DAC=30°,∴∠CAB=30°,∴∠ACB=90°,即AC⊥BC.(2)过C作CE∥AD交AB于E,∵DC∥AB,CE∥AD,AD=DC,∴四边形ADCE是菱形,∴AD=CE=4,又∠CBA=60°,△CBE为等边三角形,作CF⊥AB于F,∴,则梯形ABCD 的面积为cm2,答:梯形ABCD的面积是12cm2.等腰梯形的性质--- 11。