1.4.1正弦函数余弦函数的图像.ppt共25页文档
- 格式:ppt
- 大小:4.10 MB
- 文档页数:25








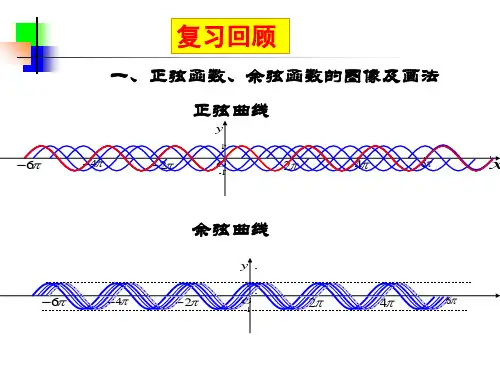


1.4.1 正弦函数、余弦函数的图象正弦函数、余弦函数的图象 函数y =sin xy =cos x图象图象画法 五点法五点法 关键 五点(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫3π2,-1,(2π,0)(0,1),⎝⎛⎭⎫π2,0, (π,-1),⎝⎛⎭⎫3π2,0,(2π,1)[点睛] “五点法”作图中的“五点”是指函数的最高点、最低点以及图象与坐标轴的交点.这是作正弦函数、余弦函数图象最常用的方法.[小试身手]1.判断下列命题是否正确.(正确的打“√”,错误的打“×”) (1)函数y =cos x 的图象与y 轴只有一个交点.( ) (2)将余弦曲线向右平移π2个单位就得到正弦曲线.( )(3)函数y =sin x ,x ∈⎣⎡⎦⎤π2,5π2的图象与函数y =cos x ,x ∈[0,2π]的图象的形状完全一致.( )答案:(1)√ (2)√ (3)√2.对于正弦函数y =sin x 的图象,下列说法错误的是( ) A .向左右无限伸展B .与y =cos x 的图象形状相同,只是位置不同C .与x 轴有无数个交点D .关于y 轴对称 答案:D3.函数y =-cos x ,x ∈[0,2π]的图象与y =cos x ,x ∈[0,2π]的图象( ) A .关于x 轴对称 B .关于原点对称 C .关于原点和x 轴对称 D .关于y 轴对称答案:A4.请补充完整下面用“五点法”作出y =-sin x (0≤x ≤2π)的图象时的列表.x 0π2①3π22π-sin x ②-10③0 ①________;②________;③________.答案:π0 1用“五点法”作简图[典例]用“五点法”作出下列函数的简图.(1)y=sin x-1,x∈[0,2π];(2)y=2+cos x,x∈[0,2π].[解](1)列表:x 0π2π3π22πsin x 010-10sin x-1-10-1-2-1 描点连线,如图所示.(2)列表:x 0π2π3π22πcos x 10-10 12+cos x 3212 3用五点法画函数y=A sin x+b(A≠0)或y=A cos x+b(A≠0)在[0,2π]上的简图的步骤如下(1)列表:x 0 π2 π 3π2 2π sin x (或cos x )y(2)描点:在平面直角坐标系中描出下列五个点:(0,y ),⎝⎛⎭⎫π2,y ,(π,y ),⎝⎛⎭⎫3π2,y ,(2π,y ),这里的y 是通过函数式计算得到的.(3)连线:用光滑的曲线将描出的五个点连接起来,不要用线段进行连接. [活学活用]作出函数y =-sin x (0≤x ≤2π)的简图. 解:列表:x 0 π2 π 3π2 2π sin x 0 1 0 -1 0 -sin x-11描点并用光滑的曲线连接起来,如图所示.正、余弦函数图象的简单应用[典例(1)sin x ≥12;(2)cos x ≤12.[解] [法一 函数图象法](1)作出正弦函数y =sin x ,x ∈[0,2π]的图象,如图所示,由图象可以得到满足条件的x 的集合为⎣⎡⎦⎤π6+2k π,5π6+2k π,k ∈Z.(2)作出余弦函数y =cos x ,x ∈[0,2π]的图象,如图所示,由图象可以得到满足条件的x的集合为⎣⎡⎦⎤π3+2k π,5π3+2k π,k ∈Z.[法二 三角函数线法](1)作直线y =12交单位圆于A ,B 两点,连接OA ,OB ,则OA 与OB围成的区域即为角α的终边的范围,故满足条件的角α的集合为⎩⎨⎧⎭⎬⎫α⎪⎪2k π+π6≤α≤2k π+56π,k ∈Z .(2)作直线x =12交单位圆于C ,D 两点,连接OC ,OD ,则OC 与OD围成的区域(图中阴影部分)即为角α终边的范围.故满足条件的角α的集合为⎩⎨⎧⎭⎬⎫α⎪⎪2k π+π3≤α≤2k π+5π3,k ∈Z .1.求解sin x >a (或cos x >a )的方法 (1)三角函数图象法.(2)三角函数线法(前面已讲解). 2.用三角函数图象解三角不等式的步骤(1)作出相应的正弦函数或余弦函数在[0,2π]上的图象; (2)写出适合不等式在区间[0,2π]上的解集; (3)根据公式一写出定义域内的解集. 根据函数图象解不等式:sin x >cos x ,x ∈[0,2π].解:画出函数y =sin x ,x ∈[0,2π],y =cos x ,x ∈[0,2π]的图象如图所示.观察图象可知,sin x >cos x ,x ∈[0,2π]的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪π4<x <5π4.层级一 学业水平达标1.用“五点法”画函数y =2-3sin x 的图象时,首先应描出五点的横坐标是( ) A .0,π4,π2,3π4,πB .0,π2,π,3π2,2πC .0,π,2π,3π,4πD .0,π6,π3,π2,2π3解析:选B 所描出的五点的横坐标与函数y =sin x 的五点的横坐标相同,即0,π2,π,3π2,2π,故选B. 2.下列函数图象相同的是( ) A .f (x )=sin x 与g (x )=sin(π+x ) B .f (x )=sin ⎝⎛⎭⎫x -π2与g (x )=sin ⎝⎛⎭⎫π2-x C .f (x )=sin x 与g (x )=sin(-x ) D .f (x )=sin(2π+x )与g (x )=sin x解析:选D A 、B 、C 中f (x )=-g (x ),D 中f (x )=g (x ). 3.以下对正弦函数y =sin x 的图象描述不正确的是( ) A .在x ∈[2k π,2k π+2π](k ∈Z)上的图象形状相同,只是位置不同 B .介于直线y =1与直线y =-1之间 C .关于x 轴对称 D .与y 轴仅有一个交点解析:选C 函数y =sin x 的图象关于原点中心对称,并不关于x 轴对称. 4.不等式cos x <0,x ∈[0,2π]的解集为( ) A .⎝⎛⎭⎫π2,3π2 B .⎣⎡⎦⎤π2,3π2 C .⎝⎛⎭⎫0,π2 D .⎝⎛⎭⎫π2,2π 解析:选A 由y =cos x 的图象知, 在[0,2π]内使cos x <0的x 的范围是⎝⎛⎭⎫π2,3π2. 5.函数y =ln cos x ⎝⎛⎭⎫-π2<x <π2的图象是( )解析:选A 首先y =ln cos x =ln cos(-x ),∴函数为偶函数,排除B 、D ,又∵-π2<x<π2时,cos x ∈(0,1], ∴y =ln x ≤0且图象左增右减,故选A. 6.方程sin x =lg x 的根的个数为________.解析:作出y =sin x 及y =lg x 的部分图象如图,由图可以看出两图象有3个交点,即方程有3个不同根.答案:37.函数y =2cos x -2的定义域是____________________________________. 解析:要使函数有意义,只需2cos x -2≥0, 即cos x ≥22.由余弦函数图象知(如图),所求定义域为⎣⎡⎦⎤-π4+2k π,π4+2k π,k ∈Z. 答案:⎣⎡⎦⎤-π4+2k π,π4+2k π,k ∈Z 8.y =1+sin x ,x ∈[0,2π]的图象与y =32的交点的个数是________.解析:由y =sin x 的图象向上平移1个单位,得y =1+sin x 的图象,故在[0,2π]上与y =32交点的个数是2个. 答案:29.用“五点法”作出函数y =1+2sin x ,x ∈[0,2π]的图象. 解:列表:x 0 π2 π 3π2 2π sin x 0 1 0 -1 0 1+2sin x131-11在直角坐标系中描出五点(0,1),⎝⎛⎭⎫π2,3,(π,1),⎝⎛⎭⎫3π2,-1,(2π,1),然后用光滑曲线顺次连接起来,就得到y =1+2sin x ,x ∈[0,2π]的图象.10.求函数y =log 21sin x-1的定义域. 解:为使函数有意义,需满足⎩⎪⎨⎪⎧log 21sin x -1≥0,sin x >0,即⎩⎪⎨⎪⎧sin x ≤12,sin x >0,由正弦函数图象或单位圆,如图所示.由图象知其定义域为:⎩⎨⎧⎭⎬⎫x ⎪⎪ 2k π<x ≤2k π+π6,k ∈Z ∪⎩⎨⎧⎭⎬⎫x ⎪⎪2k π+5π6≤x <2k π+π,k ∈Z层级二 应试能力达标1.用“五点法”作y =2sin 2x 的图象时,首先描出的五个点的横坐标是( ) A .0,π2,π,3π2,2πB .0,π4,π2,3π4,πC .0,π,2π,3π,4πD .0,π6,π3,π2,2π3解析:选B 由2x =0,π2,π,3π2,2π知五个点的横坐标是0,π4,π2,3π4,π.2.在同一平面直角坐标系内,函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象( )A .重合B .形状相同,位置不同C .关于y 轴对称D .形状不同,位置不同解析:选B 根据正弦曲线的作法过程,可知函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象位置不同,但形状相同.3.在[0,2π]内,不等式sin x <-32的解集是( ) A .(0,π) B .⎝⎛⎭⎫π3,4π3 C .⎝⎛⎭⎫4π3,5π3D .⎝⎛⎭⎫5π3,2π解析:选C 画出y =sin x ,x ∈[0,2π]的草图如下.因为sin π3=32,所以sin ⎝⎛⎭⎫π+π3=-32, sin ⎝⎛⎭⎫2π-π3=-32.即在[0,2π]内,满足sin x =-32的x =4π3或5π3.可知不等式sin x <-32的解集是⎝⎛⎭⎫4π3,5π3.故选C.4.方程|x |=cos x 在(-∞,+∞)内( ) A .没有根 B .有且仅有一个根 C .有且仅有两个根D .有无穷多个根解析:选C 求解方程|x |=cos x 在(-∞,+∞)内根的个数问题,可转化为求解函数f (x )=|x |和g (x )=cos x 在(-∞,+∞)内的交点个数问题.f (x )=|x |和g (x )=cos x 的图象如右图,显然有两交点,即原方程有且仅有两个根.5.函数y =2cos x ,x ∈[0,2π]的图象和直线y =2围成的一个封闭的平面图形的面积是________.解析:如图所示,将余弦函数的图象在x 轴下方的部分补到x 轴的上方,可得一个矩形,其面积为2π×2=4π.答案:4π6.当x ∈[-π,π]时,y =12x 与y =sin x 的图象交点的个数为________.解析:如图,有3个交点.答案:37.利用“五点法”作出函数y =sin ⎝⎛⎭⎫x -π2522x ππ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭,的图象. 解:列表如下:x π2 π 3π2 2π 5π2 x -π2 0 π2 π 3π2 2π sin ⎝⎛⎭⎫x -π2 01-1描点连线,如图所示.8.画出函数y =1+2cos 2x ,x ∈[0,π]的简图,并求使y ≥0成立的x 的取值范围. 解:按五个关键点列表:2x 0 π2 π 3π2 2π x 0 π4 π2 3π4 π cos 2x 1 0 -1 0 1 1+2cos 2x31-113描点并将它们用光滑的曲线连接起来,如图所示.令y =0,即1+2cos 2x =0,则cos 2x =-12.∵x ∈[0,π],∴2x ∈[0,2π]. 从而2x =2π3或4π3,∴x =π3或2π3.由图可知,使y ≥0成立的x 的取值范围是⎣⎡⎦⎤0,π3∪⎣⎡⎦⎤2π3,π.。