六方最密堆积

六方最密堆积的计算
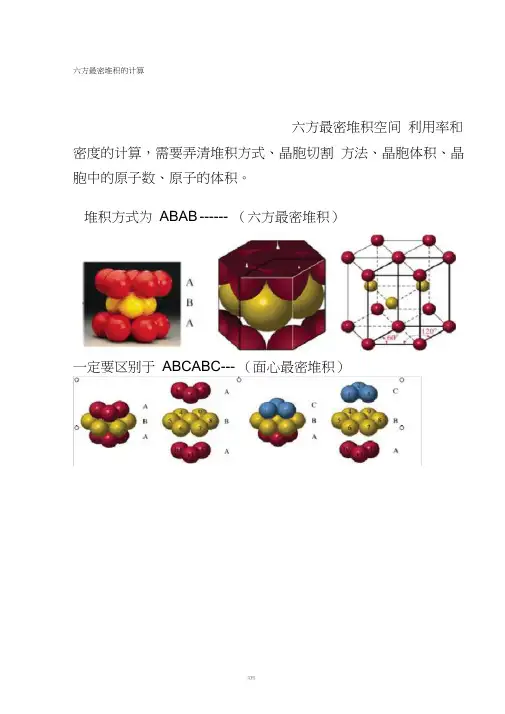
六方最密堆积空间利用率和密度的计算，需要弄清堆积方式、晶胞切割方法、晶胞体积、晶胞中的原子数、原子的体积。

堆积方式为ABAB ------ （六方最密堆积）
一定要区别于ABCABC--- （面心最密堆积）
面心立方密堆积密置层按三层一组相互错开，第四层正对着第一层的方式堆积而成。

配位数为12,晶胞所含原子数为4,金属原子空间利用率为74%。

÷ Ca t SL Pt l Pd J Cu, Ag等约50多种金属为面心立方密堆积
而学生感到困难的是六方最密堆积的晶胞体积，因为它的晶胞是平行六面体，其余的金属晶体晶胞是正六面体！
六方最密堆积计算的关键晶胞体积
文档
至此，你再求晶体空间利用率和晶体密度，障碍是不是消失了？。

六方最密堆积空间利用率和密度的计算六方最密堆积空间利用率和密度的计算，需要弄清堆积方式、晶胞切割方法、晶胞体积、晶胞中的原子数、原子的体积。

堆积方式为ABAB——（六方最密堆积）将密置层按二层相互错开第三层正对着第一层的方式堆积而成。

配位数为12,晶胞所含原子数为Z 金属原子空间利用率为74%。

*** Be, Mg, Sc, Ti, Zn T Cd笔金属廛壬屋壬玄方密境祀。

一定要区别于ABCABC---（面心最密堆积）面心立方密堆积密置层按三层一组相互错开，第四层正对着第一层的方式堆积而成。

配位数为12,晶胞所含原子数为4,金属原子空间利用率为74%o❖ Ca,礼Pt Pd, Cu, Ag等约50多种金属为面心立方密堆积。

而学生感到困难的是六方最密堆积的晶胞体积，因为它的晶胞是平行六面体，其余的金属晶体晶胞是正六面体!六方最密堆积计算的关键晶胞体积六右最密堆积皋木的位为蓝色格子六方审堆积腐他四点间的夹角均为60°sin 60"= 瞬昴砲的高U = 2h33先求S在镁型堆积中取出六方晶胞，平行六面体的底是平行四边形，各边长8=2“ 処予行四边形的面积,S —a-a sin 60。

= ——a 1再求H平行六面体的高=2个四面体的高， h = 2x 边长为a 的四面体高六方晶胞中,D4B0为正四面体，正四面体的高为c/2. a s 2rV6 2^6---- a = ------- a"三高” 一-即底面平行四边形^高、正四面体的高.晶16的高•【晶胞休积分解计算步费归纳】■"面、体.SH.求三态• 林态.得晶胸“面” 一平行四边形的面积，“体” 一-四面体.“胞”一平行六面体晶胸丿"三高” 一-即底面平行四边形^高、正四面体的高.晶16的高•。

六方最密堆积的空间利用率计算六方最密堆积，这个名字听上去就让人觉得神秘又复杂。

其实它简单得很，就像是在说如何把东西摆得更紧凑、更省地方，尤其是在我们生活中常常会碰到的问题。

想象一下，咱们去超市买水果，满满一车的苹果和橙子，要是把它们堆得乱七八糟，那真是让人抓狂。

可要是能找到一个聪明的办法，把这些水果堆得密密麻麻，既美观又省地方，那简直是太好了。

六方最密堆积，其实就像在讲一个“大侠”的故事。

这个“大侠”就是一个完美的堆积方式，能让相同形状的物体像拼图一样完美契合。

在这个堆积法里，物体之间的间隙几乎被降到了最低，空间利用率简直高得让人咋舌。

想象一下，如果把这些小球排成一排，可能会有不少空隙；但当你把它们一层层叠起来，形成一种六边形的结构，那些小空隙就能被填满，省下的空间可不是一星半点儿。

说到空间利用率，咱们常常感叹：“好东西不怕晚。

”六方最密堆积的概念就是在这儿发挥得淋漓尽致。

咱们在生活中，总是想尽办法地把东西装进一个小小的空间里，比如行李箱里，最后的结果总是“挤啊挤”的。

而这个“六方”堆积法，就好比是帮我们设计了一种超级行李箱，能把所有东西都放得严严实实，丝毫不浪费空间。

这样一来，去旅行的时候就能把喜欢的衣服、鞋子统统装进去了，再也不怕东西太多、装不下了。

六方堆积不仅仅是好看，更重要的是，它的原理就像生活中的一些哲理，教会我们如何合理安排、优化资源。

想想看，生活中总有许多小事情，我们也许能用更聪明的方式去处理。

比如，整理房间时，把常用的物品放在最容易拿到的地方，而那些不常用的放在角落里。

就像六方堆积一样，利用每一寸空间，让生活变得更加有序。

这个理论在科学上也得到了很好的验证。

研究者们通过反复实验，发现六方最密堆积的空间利用率可以达到约74%。

听起来是不是很厉害？意思就是说，在一个空间里，能有74%的部分被实际占用，剩下的只是微不足道的空隙。

想想看，要是我们在家里也能做到这个程度，那绝对是“无敌于天下”的状态了。

六方最密堆积计算六方最密堆积，也称为六方堆积或者立方堆积，是指以六个等边三角形构成的一个六面体为单元，通过相互堆叠而形成的一种堆积结构。

六方最密堆积是一种最常见的堆积现象，广泛应用于颗粒物理学、材料科学以及工程实践中。

本文将对六方最密堆积进行详细的计算。

首先，我们需要明确的是：六方最密堆积的结构是由等边三角形组成的六边形密堆积，我们需要计算的是每个等边三角形的面积和六边形的边长。

而面积和边长的计算又涉及到三角函数和几何图形的计算。

1.等边三角形的面积计算：三角形面积=(a^2*√3)/4其中，^表示乘方运算，√表示开根号。

2.六边形的边长计算：六边形边长=2*a3.六边形的面积计算：六边形的面积可以通过等边三角形的面积的计算结果得出。

在六方最密堆积中，六边形的面积等于等边三角形的面积的六倍，即：六边形面积=6*三角形面积以上是对六方最密堆积的基本计算公式。

接下来，我们将以一个实例来演示六方最密堆积的计算过程。

假设等边三角形的边长a为2 cm，那么我们可以通过上述公式进行如下计算：1. 三角形面积= (2^2 * √3) / 4 = (√3) cm^22. 六边形边长 = 2 * a = 4 cm3. 六边形面积 = 6 * 三角形面积= 6 * (√3) cm^2因此，当等边三角形的边长为2 cm时，六方最密堆积的六边形面积为6 * (√3) cm^2，六边形的边长为4 cm。

最后，需要注意的是，在实际计算中，我们需要根据具体的问题来确定等边三角形的边长a，进而得出六边形的面积和边长。

同时，我们还可以通过该结构的堆积密度、颗粒运动方式等参数进行更多的相关计算和分析。

综上所述，我们对六方最密堆积的计算过程进行了详细的阐述，并以一个实例进行了演示。

希望本文对您对六方最密堆积的理解有所帮助。

金属晶体的三种密堆积方式金属晶体的三种密堆积方式中，原子排列的密堆积方式是指原子在三维空间中紧密排列，以使得晶体的空间利用率达到最大。

密堆积方式可以有效影响金属的密度、强度、硬度等物理性质，因此在材料科学和固体物理中具有重要意义。

通常，金属晶体的密堆积方式主要分为以下三种：面心立方堆积（FCC）、六方最密堆积（HCP）和体心立方堆积（BCC）。

一、面心立方堆积（FCC）面心立方堆积（Face-Centered Cubic, FCC）是一种常见的密堆积方式，其中每个立方体的面上都有一个原子，且每个顶点上也有一个原子。

FCC结构可以看作是由许多面心立方单元重复堆积而成，其代表性金属包括铜（Cu）、铝（Al）、银（Ag）和金（Au）等。

1. 结构特点：在FCC结构中，每个原子都有12个最近邻原子，即配位数为12。

该结构单胞中包含4个原子（8个顶点上的原子分别与相邻单元共享，6个面的原子与邻近单元共享），堆积因子达到0.74，即约74%的空间被原子占据，属于最密堆积结构。

2. 性质：FCC结构由于其紧密的堆积方式，具有较高的塑性和延展性。

因此，FCC金属在室温下一般较易发生滑移，从而产生延展变形。

例如，铜和铝具有良好的延展性，易于加工成型。

3. 堆积方式：在面心立方堆积中，原子在平面上形成紧密的六边形排列，层间顺序为ABCABC 的排列模式。

这意味着每三层后结构重复，形成周期性排列。

4. 应用：FCC结构的金属由于其良好的延展性和抗冲击性，常用于制造电线、金属薄膜和结构材料等。

二、六方最密堆积（HCP）六方最密堆积（Hexagonal Close-Packed, HCP）是一种与面心立方相似的密堆积方式，但其晶体结构为六方柱体，且具有不同的堆积顺序。

HCP结构的代表性金属包括镁（Mg）、钛（Ti）、锌（Zn）和钴（Co）等。

1. 结构特点：在HCP结构中，原子的配位数同样为12，说明其紧密度与FCC相似。

六方最密堆积空间利用率和密度的计算计算六方最密堆积的空间利用率和密度需要考虑以下几个因素：物体的形状、大小和堆积规则。

首先，物体的形状对六方最密堆积的计算有重要的影响。

在最理想的情况下，物体的形状应该是一个正六面体，这样才能够确保最大程度地填充空间。

然而，现实情况中，物体的形状可能会有所不同，这就需要根据实际情况进行调整。

例如，对于长方体物体，可以尽量使其较长的边与堆积方向保持一致，以减少堆积空间的浪费。

其次，物体的大小也会对堆积的空间利用率和密度产生影响。

如果物体过大，它们之间的间距就会增大，导致空间的浪费。

因此，在进行六方最密堆积时，我们需要根据物体的大小选择合适的间距，以保证最大程度地填充空间。

同时，可以考虑将不同大小的物体进行分组堆积，使得不同组之间的间距最小化，进一步提高堆积的密度。

最后，堆积规则也是影响六方最密堆积的重要因素。

堆积规则可以包括物体的旋转和翻转。

通常情况下，允许物体进行旋转和翻转可以提高堆积的密度。

然而，这也会增加堆积过程的复杂性和计算难度。

因此，在实际应用中，需要平衡好堆积密度和堆积的可行性。

为了计算六方最密堆积的空间利用率和密度，可以采用以下步骤：1.确定物体的形状和大小。

如果物体是正六面体，则可以采用标准的堆积规则。

如果物体的形状不同，则需要调整堆积规则以适应不同的形状。

2.确定堆积的方向。

六方最密堆积可以分为三个不同的方向：x轴方向、y轴方向和z轴方向。

根据需要，选择合适的堆积方向。

3.计算堆积的间距。

根据物体的大小和形状，确定合适的间距。

通常情况下，间距应该尽量小，以保证最大程度地填充空间。

4.进行堆积计算。

根据选择的堆积规则和堆积方向，对所有的物体进行堆积计算，将它们尽量填充到空间中。

5.计算空间利用率和密度。

空间利用率可以通过计算已占用空间和总空间的比值得到。

堆积的密度可以通过计算已堆积物体的体积和堆积空间的比值得到。

需要注意的是，六方最密堆积的计算是一个复杂的问题，会受到实际应用中的各种因素的影响，如堆积规则的限制、堆积中的空隙等。

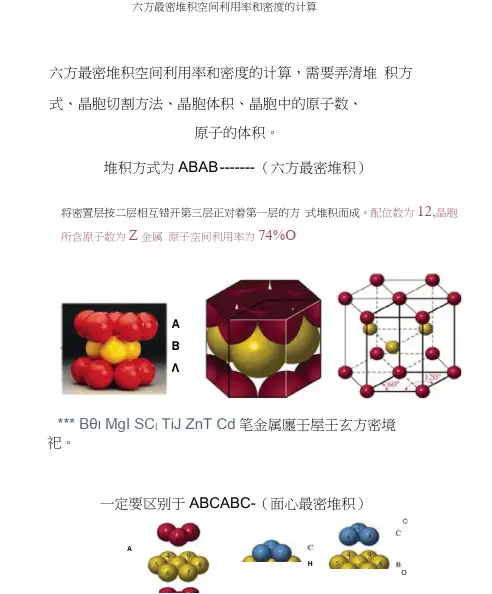
六方最密堆积空间利用率和密度的计算六方最密堆积空间利用率和密度的计算，需要弄清堆积方式、晶胞切割方法、晶胞体积、晶胞中的原子数、原子的体积。

堆积方式为ABAB ------- （六方最密堆积）将密置层按二层相互错开第三层正对着第一层的方式堆积而成。

配位数为12,晶胞所含原子数为Z金属原子空间利用率为74%OABΛ*** Bθι MgI SC l TiJ ZnT Cd笔金属廛壬屋壬玄方密境祀。

一定要区别于ABCABC-（面心最密堆积）AHO面心立方密堆积密置层按三层一组相互错开，第四层正对着第一层的方式堆积而成。

配位数为12,晶胞所含原子数为4,金属原子空间利用率为74%o Array* CaI SL Pt Pd, CUl Ag等约50多种金属为面心立方密堆积o而学生感到困难的是六方最密堆积的晶胞体积，因为它的晶胞是平行六面体，其余的金属晶体晶胞是正I 六面体！六方最密堆积计算的矢键晶胞体积六右最密堆积皋木的位为蓝色格子U六力晶胞中的閱球位貨六方％f堆积腐Sfe四点间的夹角均为60o Sin 60”二瞬昴砲的高U = Nh六方晶胞中Q4B0为正四面体，正四面体的高在镁型堆积中取出六方晶胞，平行六面体的底是平行四边形‘各边长a=2ιs 処予行四边形的面积， S —CI-Cl Sin 60 ° 二—R 再求H平行六面体的高=2个四面体的高，h = 2x 边长为α的四面体高=2 ×A a O 喩胞二SXh 先求S√6 2√6■…a = ------ a【晶胞休积分解计算步费归纳】■”面、体.SH.求三IS •知％・得晶胸"“面"一平行四边形的面积，“体”一・四面体• “胞”一平行六面体晶Iia 丿”三高” 一■即底面平行四边形A高、正四面体的高•晶IS的高•。