解三角形的实际应用举例
- 格式:docx
- 大小:131.99 KB
- 文档页数:4



解三角形应用举例一、测量距离问题例1(1)如图,A,B两点在河的同侧,且A,B两点均不可到达,要测出A,B 的距离,测量者可以在河岸边选定两点C,D,若测得CD=32km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,则A,B两点间的距离为km.答案6 4解析∵∠ADC=∠ADB+∠CDB=60°,∠ACD=60°,∴∠DAC=60°,∴AC=DC=32km.在△BCD中,∠DBC=180°-∠CDB-∠ACD-∠ACB=45°,由正弦定理,得BC=DCsin∠DBC·sin∠BDC=32sin 45°·sin 30°=64(km).在△ABC中,由余弦定理,得AB2=AC2+BC2-2AC·BCcos 45°=34+38-2×32×64×22=38.∴AB=64km.∴A,B两点间的距离为64km.(2)如图,为了测量两座山峰上P,Q两点之间的距离,选择山坡上一段长度为300 3 m且和P,Q两点在同一平面内的路段AB的两个端点作为观测点,现测得∠PAB=90°,∠PAQ=∠PBA=∠PBQ=60°,则P,Q两点间的距离为m.答案900解析由已知,得∠QAB=∠PAB-∠PAQ=30°.又∠PBA=∠PBQ=60°,∴∠AQB=30°,∴AB=BQ.又PB为公共边,∴△PAB≌△PQB,∴PQ =PA.在Rt△PAB中,AP=AB·tan 60°=900(m),故PQ=900 m,∴P,Q两点间的距离为900 m.二、测量高度问题例2如图所示,为测量一树的高度,在地面上选取A,B两点,从A,B两点分别测得树尖的仰角为30°,45°,且A,B 两点间的距离为60 m,则树的高度为m.答案30+30 3解析在△PAB中,∠PAB=30°,∠APB =15°,AB=60 m,sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=22×32-22×12=6-2 4,由正弦定理得PB sin 30°=AB sin 15°, 所以PB =12×606-24=30(6+2), 所以树的高度为PB ·sin 45°=30(6+2)×22=(30+303)(m ). 三、测量角度问题例3 已知岛A 南偏西38°方向,距岛A 3海里的B 处有一艘缉私艇.岛A 处的一艘走私船正以10海里/小时的速度向岛北偏西22°方向行驶,问缉私艇朝何方向以多大速度行驶,恰好用0.5小时能截住该走私船?⎝⎛⎭⎫参考数据:sin 38°≈5314,sin 22°≈3314 解 如图,设缉私艇在C 处截住走私船,D 为岛A 正南方向上一点,缉私艇的速度为x 海里/小时,结合题意知BC =0.5x ,AC =5,∠BAC =180°-38°-22°=120°.由余弦定理可得BC 2=AB 2+AC 2-2AB ·ACcos 120°,所以BC 2=49,所以BC =0.5x =7, 解得x =14.又由正弦定理得sin ∠ABC =AC ·sin ∠BAC BC=5×327=5314, 所以∠ABC =38°,又∠BAD =38°,所以BC ∥AD ,故缉私艇以14海里/小时的速度向正北方向行驶,恰好用0.5小时截住该走私船. 素养提升 数学抽象是指舍去事物的一切物理属性,得到数学研究对象的思维过程,主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并且用数学符号或数学术语予以表征.从实际问题中抽象出距离、高度、角度等数学问题,然后利用正弦定理、余弦定理求解,很好地体现了数学抽象的数学素养.。

利用三角形全等解决实际问题三角形全等是几何学中的一个重要概念,它具有广泛的应用。
通过运用三角形全等,我们可以解决实际生活和工作中的很多问题。
本文将介绍三角形全等的定义与性质,并通过几个实例来说明如何利用三角形全等解决实际问题。
三角形全等定义与性质在几何学中,三角形全等是指两个三角形的对应边和对应角完全相等。
当两个三角形的三个边和三个角分别相等时,我们可以得出这两个三角形全等的结论。
换句话说,如果两个三角形的三个边长度和三个夹角大小分别相等,那么这两个三角形就是全等的。
利用三角形全等解决实际问题的实例例1:测量高楼的高度假设我们在测量一座高楼的高度时,无法直接测量,但我们可以通过测量影子的长度来获得一些有用的信息。
为了解决这个问题,我们可以利用三角形全等的原理。
首先,选择一棵垂直于地面的直杆,使得直杆的长度和影子的长度成等比例。
然后,测量直杆的长度和它的投影长度,以及高楼的投影长度。
由于直杆和高楼的投影都是等比例关系,而直杆和影子之间的三角形是全等的,我们可以通过设置一个方程组来解决问题,从而计算出高楼的高度。
例2:求解行走距离假设我们需要从A点到B点行走,但由于某些原因,我们只能从A 点看到B点的某一侧,不直接看到B点。
为了确定行走的距离,我们可以利用三角形全等原理。
首先,从A点出发,设想一条虚拟的直线使其与B点相连。
然后,选择一个合适的地方设立一个测量点C,使得C点能够和B点连成一条直线。
测量AC的长度和∠C的角度。
由于三角形ABC与实际的三角形ABD是全等的,我们可以通过计算得到BD的长度,进而确定行走的距离。
总结通过本文的介绍,我们了解了三角形全等的定义与性质,并且通过两个实际问题的解决,展示了如何利用三角形全等来解决实际问题。
三角形全等在几何学中发挥着重要的作用,通过合理运用三角形全等的原理,我们可以解决许多实际问题,提升工作和生活的效率。
虽然本文只提供了两个实例,但是通过进一步的学习和实践,我们可以应用三角形全等的原理解决更多的实际问题。



第3节 解三角形在实际生活中的应用
1、 小红为了测量某一树身的高度,他站在A 处看树梢,测得此时的仰角为45°,前进200m
到达B 处,测得此时的仰角为60°,小红身高1.8m,试计算树身的高度是多少米?
2、 为了测量河对岸A 、B 两点的距离,在河的这边测出CD 的长为2
3km ,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,求A ,B 两点间的距离。
3、(2009宁夏、海南)为了测量两山顶M ,N 间的距离,飞机沿水平方向A ,B 两点进行测量。
A ,B ,M ,N 在同一铅垂平面内(如图)飞机能够测量的数据有俯角和A ,B 间的距离。
请设计一个方案。
包括:(1)指出需要测量的数据(用字母表示,并在图中标出)(2)用文字和公式写出计算M ,N 间的距离的步骤。
4、已知海岛A 四周8海里内有暗礁。
今有一货轮由西向东航行,望见岛A 在北偏东75°,航行202海里后,望见此岛在北偏东30°。
如果货轮不改变航向继续前进,有无触礁的危险?
5、甲船在A 处发现乙船在方位角45°与A 相距10海里的C 处正以20海里/小时的速度向南偏东75°方向航行。
已知甲船的速度是203海里/小时,问:甲船沿什么方向航行,需多长时间才能与已船相遇?。

解直角三角形在实际生活中应用直角三角形是一种特殊的三角形,其中一个角为90度,另外两个角则是锐角或钝角。
直角三角形的重要性在于它具有很多实际应用价值。
本文将介绍一些直角三角形在实际生活中的应用。
一、测量高度和距离直角三角形的一条腿可以用作测量高度或距离的工具。
通过测量一个物体的顶部和底部的距离,同时测量观察点到底座的距离,我们可以利用直角三角形的性质计算出物体的高度。
例如,在建筑工地上,工人可以使用测量工具和直角三角形的原理来测量建筑物的高度。
二、解决倾斜和斜率问题直角三角形可以帮助我们解决倾斜和斜率问题。
在地质学和土木工程中,我们经常需要测量地面的倾斜度和斜率。
直角三角形可以帮助我们测量坡度的比例。
通过测量斜坡上某一段的水平距离和相应的垂直距离,我们可以计算出斜坡的斜率。
三、计算不可测量的距离在某些情况下,两个点之间的距离无法直接测量,例如跨越湖泊或河流的距离。
然而,利用直角三角形的性质,我们可以使用三角函数计算出这种不可测量距离。
通过观察两个点之间的角度和某一点到这两个点之间的距离,我们可以使用正切函数计算出这个不可测量的距离。
四、导航和定位直角三角形在导航和定位中也有广泛的应用。
例如,航海员可以使用天文观测和直角三角形的性质来确定船只的位置。
通过测量星体和地平线之间的角度,同时知道船只和地平线之间的距离,我们可以利用正弦和余弦函数计算出船只的位置。
五、解决工程问题在工程领域中,直角三角形常常用于解决一些复杂问题。
例如,自然灾害生态学家可以使用直角三角形的概念来设计保护森林免受火灾侵蚀。
通过构建直角三角形网格,他们可以最大程度地减少火势蔓延的可能性,保护森林资源。
六、解决影子和光线问题在摄影和照明设计领域,直角三角形可以帮助我们解决影子和光线的问题。
通过观察物体和光源之间的角度,并结合直角三角形的性质,我们可以计算出物体产生的影子的长度。
这对于照明设计师来说非常重要,以确保正确照亮目标物体。


专题12 解直角三角形在实际生活中的应用【专题综述】在现实生活中, 有许多和解直角三角形有关的实际问题,如航海航空、建桥修路、测量技术、图案设计等,解决这类问题其关键是把具体问题抽象成“直角三角形”模型,利用直角三角形的边角关系以及勾股定理来解决.【方法解读】一、航空问题例1:抢险队派一架直升飞机去A 、B 两个村庄抢险,飞机在距地面450米上空的P 点,测得A 村的俯角为30︒,B 村的俯角为60︒(如图).求A 、B 两个村庄间的距离.(结果精确到米,参考数据2 1.4143 1.732==,)【举一反三】(2016内蒙古巴彦淖尔市)如图,某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘正在南海巡航的渔政船前往救援,当飞机到达海面3000m 的高空C 处时,测得A 处渔政船的俯角为45°,测得B 处发生险情渔船的俯角为30°,此时渔政船和渔船的距离AB 是( )A .30003mB .3000(31)+mC .3000(31)-mD .15003m二、测量问题例2:如图所示,课外活动中,小明在离旗杆AB 10米的C 处,用测角仪测得旗杆顶部A 的仰角为40︒,已知测角仪器的高CD =1.5米,求旗杆AB 的高(精确到0.1米) .【举一反三】我侦察员在距敌方200米的地方发现敌人的一座建筑物,但不知其高度又不能靠近建筑物测量,机灵的侦察员食指竖直举在右眼前,闭上左眼,并将食指前后移动,使食指恰好将该建筑物遮住。
若此时眼睛到食指的距离约为40cm,食指的长约为8cm,你能根据上述条件计算出敌方建筑物的高度吗?请说出你的思路。
三、建桥问题例3:如图所示,A、B两地之间有一条河,原来从A地到B地需要经过DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.一直BC=11km,∠A=45°,∠B=37°.桥DC和AB平行,2 ,sin37°≈0.60,则现在从A地到达B地可比原来少走多少路程?(结果精确到0.1km.参考数据: 1.41cos37°≈0.80).【举一反三】黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).参考数据:sin76.1°≈0.97,cos76.1°≈0. 24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5.四、图案设计问题例4. “创意设计”公司员工小王不慎将墨水泼在一张设计图纸上,导致其中部分图形和数据看不清楚(如图所示).已知图纸上的图形是某建筑物横断面的示意图,它是以圆O的半径OC所在的直线为对称轴的轴对称图形,A是OD与圆O的交点.由于图纸中圆O的半径r的值已看不清楚,根据上述信息(图纸中i 是坡面CE的坡度),求r的值.1:0.75【举一反三】如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:(1)画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;(2)结合你的示意图,写出求电线杆高度的思路.【强化训练】1.如图,一位同学想利用树影测量树高(AB),他在某一时刻测得高为1m的竹竿影长为0.9m,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上(CD),他先测得留在墙上的影高(CD)为1.2m,又测得地面部分的影长(BC)为2.7m,他测得的树高应为多少米?2.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD. (参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).3.如图,在我市的上空一架飞机由A向B沿水平直线方向飞行,沿航线AB的正下方有两个景点水城明珠大剧院(记为点C),光岳楼(记为点D),飞机在A处时,测得景点C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了3千米到B处时,往后测得景点C的俯角为30°.而景点D恰好在飞机的正下方,求水城明珠大剧院与光岳楼之间的距离(最后结果精确到0.1千米)4.某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)5.在某飞机场东西方向的地面l上有一长为1km的飞机跑道MN(如图),在跑道MN的正西端14.5千米处有一观察站A.某时刻测得二架匀速直线降落的飞机位于点A的北偏西30°,且与点A相距15千米的B处;经过1分钟,又测得该飞机位于点A的北偏东60°,且与点A相距5万千米的C处.⑴该飞机航行的速度是多少千米/小时?(结果保留根号)⑵如果该飞机不改变航向继续航行,那么飞机能否降落在跑道MN之间?请说明理由。
解三角形正,余弦定理在现实生活中的应用解三角形的正弦定理和余弦定理在现实生活中有广泛的应用。
例如,测量距离、测量高度、航海模型、物理问题等都与这些定理有关。
以下是一些例子:
1. 测量距离
利用正弦定理和余弦定理可以测量出无法直接测量的距离。
假设你想知道两个建筑物之间的距离,但你不能直接测量它们之间的直线距离。
你可以站在其中一个建筑物旁边,用一个工具测量你与另一个建筑物之间的角度和高度差,然后使用正弦定理或余弦定理计算出两个建筑物之间的直线距离。
2. 测量高度
同样可以利用正弦定理和余弦定理测量出无法直接测量的高度。
假设你想知道一个树的高度,但你只能在地面附近测量树的影子长度。
你可以使用正弦定理或余弦定理计算出树的高度。
3. 航海模型
在航海中,可以利用正弦定理和余弦定理计算船只的位置。
假设你知道船只在某个时间点的位置和朝向,以及它的速度和方向,你可以使用正弦定理和余弦定理计算出船只在任何其他时间点的位置和朝向。
这对于导航非常重要。
4. 物理问题
在物理学中,正弦定理和余弦定理也有很多应用,例如在振
动、波动等问题中。
例如,当一个弹簧上放置一个小球时,小球会以一定的频率来回摆动。
通过测量小球的振幅、周期等参数,可以使用正弦定理和余弦定理计算出小球的运动轨迹和速度。
解三角形在生活中的应用一、前言解三角形是初中数学中的一个重要内容,它是指已知三角形中的某些元素(如两个角度和一个边长),求出其余未知元素的过程。
虽然这个知识点在我们的学生时代可能并没有什么实际用处,但实际上,在我们的日常生活中,解三角形却有着广泛的应用。
二、建筑工程建筑工程是解三角形最常见的应用之一。
在建筑设计和施工过程中,经常需要测量建筑物各部分之间的距离、高度、倾斜度等信息。
这些信息可以通过解三角形来计算得出。
例如,在设计一座桥梁时,需要测量桥梁两端之间的距离和高度差。
如果只是简单地使用测量工具来进行测量,得到的结果可能会存在误差。
而通过解三角形来计算,则可以得到更加精确的结果。
三、导航导航也是解三角形的应用之一。
在旅行或驾车过程中,我们通常会使用地图或导航软件来确定行进方向和距离。
而这些软件所依据的原理就是通过解三角形来计算出当前位置与目标位置之间的距离和方向。
例如,当我们使用导航软件时,它会根据我们当前的位置和目标位置的坐标来计算出两点之间的距离和方向。
这个计算过程就是通过解三角形来实现的。
四、天文学天文学也是解三角形的应用之一。
在观测天体时,需要测量其位置、距离、速度等信息。
而这些信息可以通过解三角形来计算得出。
例如,在观测恒星时,需要测量其视差和视差变化,以确定其距离和速度。
而这个计算过程就是通过解三角形来实现的。
五、摄影摄影也是解三角形的应用之一。
在拍摄照片时,需要考虑拍摄角度、焦距等因素。
而这些因素可以通过解三角形来计算得出。
例如,在拍摄远景风景照片时,需要选择合适的焦距和拍摄角度,以保证整张照片都能清晰地呈现在画面中。
而这个计算过程就是通过解三角形来实现的。
六、总结综上所述,解三角形在我们日常生活中有着广泛的应用。
从建筑工程到导航、天文学再到摄影,它都扮演着重要的角色。
因此,学好解三角形不仅可以帮助我们在学术上取得更好的成绩,还能够为我们的生活带来更多便利和乐趣。
解三角形的实际应用举例
【学习目标】
1.了解斜三角形在测量、工程、航海等实际问题中的应用;能选择正弦定理、
余弦定理解决与三角形有关的实际问题.
2.在解三角形的实际问题中,进一步体会数学建模的思想,掌握数学建模的
方法.
3.体会数学知识来源于实际生活,体会正弦定理、余弦定理在实际生活中的
广泛应用.
【学习重点】
熟练掌握正弦定理、余弦定理和面积公式,结合几何性质建模解决生活中的应用问题.
【学习难点】
数学建模的过程及解三角形的运算.
【课前预习案】
1.有关概念:
仰角与俯角:在视线和水平线所成的角中,视线在水平线的角叫仰角,在水平线的角叫俯角(如图 ).
方位角:从指北方向顺时针转到目标方向线的水平角,如B点的方位角为α(如图②)
2.方向角:相对于某一正方向的水平角(如图③)
(1)北偏东α°即由指北方向顺时针旋转α°到达目标方向.
a
(2)北偏西α°即由指北方向逆时针旋转α°到达目标方向.
(3)南偏西等其他方向角类似.
思考:方位角与方向角的区别
3. 坡度与坡角:坡面与水平面的夹角叫坡角,坡面与垂直高度 h 和水平宽度l 的比叫坡度.
1. 解三角形的一般思路
(1)读懂题意,理解问题的实际背景,理解题中的有关名词的含义,如坡度、仰角、俯角、方位角等.
(2)根据题意画出示意图,将实际问题抽象成解三角形模型,
(3)选择正弦定理、余弦定理等有关知识求解.
(4)将三角形的解还原为实际意义,检验解出的答案是否具有实际意义,对解进行取舍.
【课堂探究案】
解决实际测量问题的过程一般要充分认真理解题意,正确做出图形,把实际问题里的条件和所求转换成三角形中的已知和未知的边、角,通过建立数学模型来求解
探究一:测量地面上两个不能到达的地方之间的距离
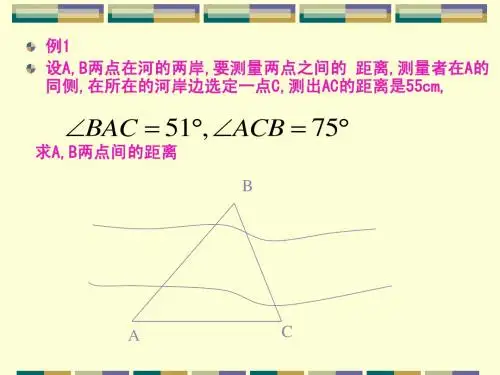
例1.如图,设A 、B 两点在河的两岸,要测量两点之间的距离,测量者在A 的同侧,在所在的河岸边选定一点C ,测出AC 的距离是42m ,∠BAC=45︒,∠ACB=︒75。
求A 、B 两点的距离.
变式1.为了开凿隧道,要测量隧道上D 、E 间的距离,为此在山的一侧选取适当点C ,如图,测得CA=400m ,CB=600m , ∠ACB=60°,又测得A 、B 两点到隧道口的距离AD=80m ,BE=40m(A 、D 、E 、B 在一条直线上),计算隧道DE 的长.
探究二:测量高度问题
例2、AB 是底部B 不可到达的一个建筑物,A 为建筑物的最高点,H 、G 、B 三点在同一条水平直线上。
在H 、G 两点用测角仪器测得A 的仰角分别是030ADE ∠=、045ACE ∠=、20CD m =,测角仪器的高是1h m =,求建筑物高度
AB。
变式1.如图,在山顶铁塔上B处测得地面上一点A的俯角0
60
α=,在塔底C处测得A处的俯角0
45
β=,已知铁塔的BC部分的高为40m,求山
高CD.
探究三:方位角问题
例3、如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧远处一山顶D在西偏北0
30的方向上,行驶82km
后到达B处,测得此山顶在西偏北0
75的方向上,仰角
为0
15,求此山的高度CD.
探究四:航海问题
例4、如图所示,在海岸A处,发现北偏东45°方向,距A为31
-)km的B处有一艘走私船.在A处北偏西75°方向,距A为2 km
的C处的缉私船奉命以103的速度追截走私船.此时
走私船正以10km/h的速度从B处向北偏东30°方向逃窜,则缉私船沿什么方向能最快追上走私船?并求出所需要的时间.
40 km
30 km
D
450
B
A
C
东西
北
【课后检测案】
1. 台风中心从A 地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B 在A 的正东40千米处,B 城市处于危险区内的时间为( )
A .0.5小时
B .1小时
C .1.5小时
D .2小时
2,。
在中,,的平分线把三
角形面积分成两部分,则( ) A B C D 3.如图,在斜度一定的山坡上的一点A 测得山顶上一建筑物顶端C 对于山坡的斜度为15︒,向山顶前进100m 后,又从点B 测得斜度为45︒,假设建筑物高50m ,设山对于地平面的斜度θ,则cos θ=.
ABC ∆:1:2A B =C CD 3:2cos A =131234。