湖南自主招生笔试真题笔试题目及答案

自主招生数学试题及答案一、选择题（每题5分，共20分）1. 若函数f(x) = x^2 - 4x + 3，求f(2)的值。

A. 1B. 3C. 5D. 7答案：B2. 已知等差数列{a_n}的首项a_1 = 3，公差d = 2，求a_5的值。

A. 13B. 15C. 17D. 19答案：A3. 计算定积分∫(0到1) x^2 dx的值。

A. 1/3B. 1/2C. 2/3D. 1答案：B4. 设A = {1, 2, 3}，B = {3, 4, 5}，求A∩B的值。

A. {1, 2}B. {3}C. {4, 5}D. 空集答案：B二、填空题（每题5分，共20分）5. 已知函数f(x) = 2x - 1，求f(-1)的值。

答案：-36. 计算等比数列1, 2, 4, ...的第5项。

答案：167. 已知圆的半径为5，求圆的面积。

答案：25π8. 已知向量a = (3, 4)，向量b = (-4, 3)，求向量a与向量b的点积。

答案：-7三、解答题（共60分）9. 已知函数f(x) = x^3 - 6x^2 + 11x - 6，求f(x)的导数。

答案：f'(x) = 3x^2 - 12x + 1110. 已知直线l1: y = 2x + 1和直线l2: y = -x + 3，求两直线的交点坐标。

答案：交点坐标为(1, 3)11. 已知圆心在原点，半径为5的圆，求圆的方程。

答案：x^2 + y^2 = 2512. 已知函数f(x) = x^2 - 6x + 8，求函数的最小值。

答案：函数的最小值为2，当x = 3时取得。

长郡中学20XX年高一实验班选拔考试试卷注意：(1) 试卷共有三大题16小题，满分120分，考试时间80分钟.(2) 请把解答写在答题卷的对应题次上, 做在试题卷上无效.一、选择题（本题有6小题，每小题5分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子)(A) 直线y = –x上(B) 抛物线y =x2上(C) 直线y = x上(D) 双曲线xy = 1上2．以等速度行驶的城际列车，若将速度提高25%，则相同距离的行车时间可节省k%，那么k的值是( )(A) 35 (B) 30 (C) 25 (D) 203．若－1＜a＜0，则a,a,a,(A)(C) 1a1a31a一定是( ) 最小，a3最大(B) 最小，a最大(D) a最小，a 最大 1a最小，a最大4．如图，将△ADE绕正方形ABCD的顶点A顺时针旋转90°，得△ABF，连结EF交AB于H，则下列结论错误的是（）(A) AE⊥AF （B）EF：AF =2：1(C) AF= FH²FE （D）FB ：FC = HB ：EC5．在△ABC中，点D，E分别在AB，AC上，且CD与BE相交于点F，已知△BDF的面积为10，△BCF的面积为20，△CEF的面积为16，则四边形区域ADFE的面积等于（）(A) 22 (B) 24 (D) 36 (D)446．某医院）（A）30 （B）35 （C）56 （D）448二、填空题（本题有6个小题，每小题5分，共30分）7．若4sinA – 4sinAcosA + cosA = 0, 则tanA. 222 第4题146424296.doc 第1页8．在某海防观测站的正东方向12海浬处有A、B两艘船相会之后，A船以每小时12海浬的速度往南航行，B船则以每小时3海浬的速度向北漂流. 则经过小时后，观测站及A、B两船恰成一个直角三角形.9．如右图，在坐标平面上，沿着两条坐标轴摆着三个相同的长方形，其长、宽分别为4、2，则通过A,B,C三点的拋物线对应的函数关系式是.10．桌面上有大小两颗球，相互靠在一起。

湖南单独招生统一考试数学试卷（满分90分，考试时间90分钟）一、选择题：（本题共20小题，每小题3分，共60分．）1.设为实数，若，则的取值范围是A．B．C．D．2.复数z＝的共轭复数是A．2+i B．2－iC．－1+iD．－1－i 3.已知双曲线的两条渐近线方程是，则双曲线的离心率为（）A．B．C．D．4.设，且，则A．B．C．D．5.由等式x 4+a 1x 3+a 2x 2+a 3x+a 4=（x+1）4+b 1（x+1）3+b 2（x+1）2+b 3（x+1）+b 4。

定义映射f:（a 1，a 2，a 3，a 4）→（b 1，b 2，b 3，b 4），则f（4，3，2，1）等于（）A、（1，2，3，4）B、（0，3，4，0）C、（－1，0，2，－2）D、（0，－3，4，－1）6.设x 、y 满足约束条件：⎪⎩⎪⎨⎧≥≤≤+01y xy y x 则y x z +=2的最大值为（）A．1B．2C．3D．47．如图，I 是全集，M、P、S 是I 的3个子集，则阴影部分所表示的集合是（）A．()SP M Ｂ．()SP MＣ．()S C I P M Ｄ．()SC P M I8．函数()|2|f x x =-的定义域为（）A．1,3⎡⎫+∞⎪⎢⎣⎭B．()1,22,3⎡⎫+∞⎪⎢⎣⎭C．1,23⎡⎫⎪⎢⎣⎭D．(2,)+∞9．已知{}n a 为等差数列，且7a －24a ＝－1,3a ＝0,则公差d＝（）A．－2B．－12C．12D．210.设..(),(),log (log ),a b c ===050433434443则（）A．c b a <<B．a b c<<C．c a b<<D．a c b<<11.sin1050°的值为（）A、22B、32C、−12D、1212.双曲线x 2a 2−y 2b 2=1的实轴长为10，焦距为26，则双曲线的渐渐近线方程为（）A、y =±135x B、y =±125x C、y =±512xD、y =±513x13.方程y =x 2−4x +4所对应曲线的图形是（）174.若角α的终边经过点(4，-3)，则cos2α的值为（A ）A、725B、−1625C、−725D、162514、函数12--=x x y 的图像是()A .开口向上，顶点坐标为）（45,21-的一条抛物线；B .开口向下，顶点坐标为）（45,21-的一条抛物线；C .开口向上，顶点坐标为（45,21-的一条抛物线；D .开口向下，顶点坐标为）（45,21-的一条抛物线；15.动点M 在y 轴上，当它与两定点E(4，10)、F(-2，1)在同一条直线上时，点M 的坐标是（）A、(1，6)B、(1，5)C、(0，4)D、(0，3)16.“2019k 2−1=1”是“k=1”的（）A、充分不必要条件B、必要不充分条件C、充分且必要条件D、既不充分也不必要条件17.某旅游景点有个人票和团队票两种售票方式，其中个人票每人80元，团队票（30人以上含30人）打七折.按照购票费用最少原则，建立实际游览人数x 与购票费用y （元）的函数关系，以下正确的是（）A、y =80x ，0≤x ＜24，x ∈N 1344，24≤x ≤30，x ∈N 56x ，x ＞30，x ∈NB、y =80x ，0≤x ＜21，x ∈N1680，21≤x ≤30，x ∈N56x ，x ＞30，x ∈NC、y =80x ，0≤x ＜24，x ∈N1920，24≤x ≤30，x ∈N56x ，x ＞30，x ∈ND、y =80x ，0≤x ＜21，x ∈N 2400，21≤x ≤30，x ∈N 56x ，x ＞30，x ∈N18、设2a＝5b＝m，且1a ＋1b ＝3，则m 等于()A、310B．10C．20D．10019、已知f(12x－1)＝2x＋3，f(m)＝8，则m 等于()A．14B、-14C、32D．－3220、函数y＝lg x＋lg(5－2x)的定义域是()A．)25,0[B．⎦⎤⎢⎣⎡250，C．)251[，D．⎥⎦⎤⎢⎣⎡251，二、填空题（共10小题，每小题3分；共计30分）1、已知A(1，1)、B(3，2)、C(5，3)，若AB CA l =，则λ为_____.2、双曲线2212516y x -=的两条渐近线方程为_______________.3、设集合A＝{－1,1,-2}，B＝{a＋2，a2＋4}，A∩B＝{-2}，则实数a＝_____.4、已知集合}42<<=x x A ｛，B=}0)3)(1{<--x x x （,则B A =_____.（用区间表示）5、已知集合}32|{2≥-=x x x P ,}42|{<<=x x Q ,则=Q P _____.（用区间表示）6、设集合{}xx x M ==2，{}0lg ≤=x x N ，则=N M _____.（用区间表示）7、已知f(x5)＝lg x，则f(2)＝_____.8、3-2，213，5log 2三个数中最大的数是_____.9、16log 01.0lg 2+的值是_____.10、如图，在半径为1的◎0上顺次取点A，B，C，D，E，连接AB，AE，OB，OC，OD，OE.若∠BAE=.∠COD=70°，则c 与的长度之和为__(结果保留π)三、大题：(满分30分)1、在△ABC 中，已知4,5b c ==，A 为钝角，且4sin 5A =，求A、2、判断函数32(+-=x x f ）在),(+∞-∞上是减函数.3、在等差数列}{n a 中，40,31131=+=a a a （1）求公差d 及通项公式（2）求它的前13项的和参考答案：一、选择题：1-5题答案:CDBCD6-10题答案:BCBBC11-15题答案:CBAAC16-20题答案:BBAAC1.设为实数，若，则的取值范围是A．B．C．D．【答案】C【解析】画出不等式组对应的可行域得，又满足，解得。

湖南高一自主招生考试试卷一、语文（共100分）（一）文言文阅读（20分）阅读下列文言文，回答1-5题。

（文言文材料）1. 请解释文中划线词语的意思。

（4分）2. 请概括文中人物的主要行为或思想。

（4分）3. 请分析文中所反映的时代背景。

（4分）4. 请根据文中内容，谈谈你对文中人物的看法。

（4分）5. 请翻译文中划线句子。

（4分）（二）现代文阅读（30分）阅读下列现代文，回答6-10题。

（现代文材料）6. 请概括文章的中心思想。

（6分）7. 请分析文章中的主要人物形象。

（6分）8. 请指出文章中运用了哪些修辞手法，并分析其作用。

（6分）9. 请谈谈你对文章主题的理解。

（6分）10. 请根据文章内容，写一篇200字左右的感想。

（6分）（三）作文（50分）11. 根据以下材料，写一篇不少于800字的议论文。

（50分）（作文材料）二、数学（共100分）（一）选择题（20分）1. 以下哪个选项是正确的数学命题？（5分）A. 对于任意实数x，x² ≥ 0B. 直线与平面相交，交点一定只有一个C. 所有三角形的内角和都是180°D. 所有圆的周长都是2πr2-10. 其他选择题（每题2分）（二）填空题（20分）11. 解方程：\( x^2 - 5x + 6 = 0 \)。

（5分）12. 已知函数\( f(x) = 2x - 3 \)，求\( f(-1) \)。

（5分）13. 求圆的面积，已知半径为4。

（5分）14. 计算等差数列的前10项和，首项为3，公差为2。

（5分）（三）解答题（60分）15. 解不等式：\( |x - 3| < 2 \)。

（10分）16. 证明：如果一个三角形的两边之和大于第三边，那么这个三角形是存在的。

（10分）17. 已知函数\( y = x^3 - 3x^2 + 2 \)，求其导数，并讨论其单调性。

（15分）18. 解析几何题：已知椭圆\( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \)，其中\( a > b > 0 \)，求椭圆的焦点坐标。

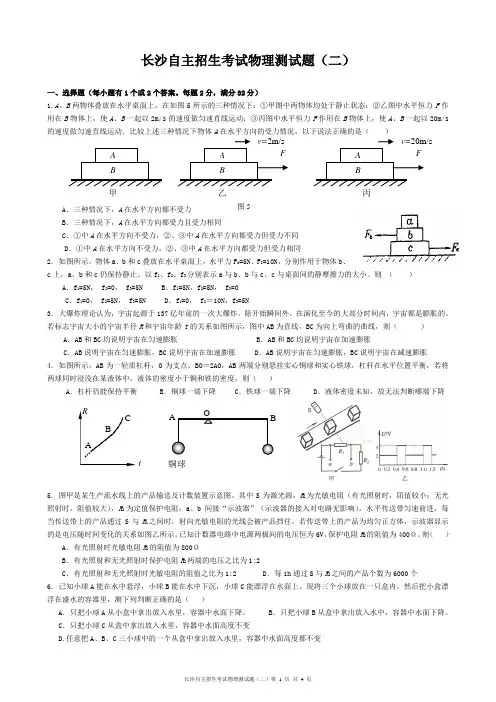
长沙自主招生考试物理测试题（二）一、选择题（每小题有1个或2个答案。

每题2分，满分32分）1.A 、B 两物体叠放在水平桌面上，在如图5所示的三种情况下：①甲图中两物体均处于静止状态；②乙图中水平恒力F 作用在B 物体上，使A 、B 一起以2m/s 的速度做匀速直线运动；③丙图中水平恒力F 作用在B 物体上，使A 、B 一起以20m/sA B ．三种情况下，A 在水平方向都受力且受力相同C ．①中A 在水平方向不受力，②、③中A 在水平方向都受力但受力不同D ．①中A 在水平方向不受力，②、③中A 在水平方向都受力但受力相同2. 如图所示，物体a 、b 和c 叠放在水平桌面上，水平力F b =5N 、F C =10N ，分别作用于物体b 、c 上，a 、b 和c 仍保持静止。

以f 1、f 2、f 3分别表示a 与b 、b 与c 、c 与桌面间的静摩擦力的大小。

则 （ ） A ．f 1=5N ， f 2=0， f 3=5N B ．f 1=5N ，f 2=5N ， f 3=0C ．f 1=0， f 2=5N ， f 3=5ND ．f 1=0， f 2＝10N ，f 3=5N3. 大爆炸理论认为，宇宙起源于137亿年前的一次大爆炸。

除开始瞬间外，在演化至今的大部分时间内，宇宙都是膨胀的。

若标志宇宙大小的宇宙半径R 和宇宙年龄t 的关系如图所示，图中AB 为直线，BC 为向上弯曲的曲线，则（ ）A ．AB 和BC 均说明宇宙在匀速膨胀 B ．AB 和BC 均说明宇宙在加速膨胀C ．AB 说明宇宙在匀速膨胀，BC 说明宇宙在加速膨胀D ．AB 说明宇宙在匀速膨胀，BC 说明宇宙在减速膨胀 4. 如图所示，AB 为一轻质杠杆，O 为支点，BO ＝2AO ，AB 两端分别悬挂实心铜球和实心铁球，杠杆在水平位置平衡，若将两球同时浸没在某液体中，液体的密度小于铜和铁的密度，则（ ）A ．杠杆仍能保持平衡B ．铜球一端下降C ．铁球一端下降D ．液体密度未知，故无法判断哪端下降5. 图甲是某生产流水线上的产品输送及计数装置示意图。

2023年湖南省长沙市普通高校对口单招数学自考真题(含答案)一、单选题(10题)1.若不等式|ax+2|＜6的解集是{x|-1＜x＜2}，则实数a等于（）A.8B.2C.-4D.-82.不等式-2x2+x+3<0的解集是（）A.{x|x＜-1}B.{x|x＞3/2}C.{x|-1＜x＜3/2}D.{x|x<-1或x＞3/2}3.设a＞b,c＞d则（）A.ac＞bdB.a+c＞b+cC.a+d＞b+cD.ad＞be4.用列举法表示小于2的自然数正确的是A.{1,0}B.{1,2}C.{1}D.{-1，1,0}5.已知集合，则等于（）A.B.C.D.6.以点P(2,0)，Q(0,4)为直径的两个端点的圆的方程是（)A.(x-l)2+(y-2)2=5B.(x-1)2+y2=5C.(x+1)2+y2=25D.(x+1)2+y=57.A.B.C.8.从200个零件中抽测了其中40个零件的长度，下列说法正确的是（）A.总体是200个零件B.个体是每一个零件C.样本是40个零件D.总体是200个零件的长度9.如图所示的程序框图中，输出的a的值是（）A.2B.1/2C.-1/2D.-110.A.B.C.二、填空题(10题)11.12.(x+2)6的展开式中x3的系数为。

13.不等式(x-4)(x + 5)>0的解集是。

14.执行如图所示的程序框图，若输入的k=11，则输出的S=_______.15.在△ABC中，AB=，A=75°，B=45°，则AC=__________.16.等差数列的前n项和_____.17.18.19.在ABC中，A=45°，b=4，c=，那么a=_____.20.三、计算题(5题)21.求焦点x轴上，实半轴长为4,且离心率为3/2的双曲线方程.22.在等差数列{a n}中，前n项和为S n ,且S4 =-62，S6=-75,求等差数列{an}的通项公式a n.23.甲、乙两人进行投篮训练，己知甲投球命中的概率是1/2，乙投球命中的概率是3/5,且两人投球命中与否相互之间没有影响.(1) 若两人各投球1次，求恰有1人命中的概率;(2) 若两人各投球2次，求这4次投球中至少有1次命中的概率.24.已知函数f(x)的定义域为{x|x≠0 },且满足.(1) 求函数f(x)的解析式;(2) 判断函数f(x)的奇偶性，并简单说明理由.25.从含有2件次品的7件产品中，任取2件产品，求以下事件的概率.(1)恰有2件次品的概率P1;(2)恰有1件次品的概率P2 .四、简答题(10题)26.证明：函数是奇函数27.如图：在长方体从中，E，F分别为和AB和中点。

单招考试题库及答案湖南一、单项选择题（每题2分，共20分）1. 湖南的省会城市是哪里？A. 长沙B. 株洲C. 湘潭D. 衡阳答案：A2. 湖南省的简称是什么？A. 湘B. 赣C. 鄂D. 渝答案：A3. 以下哪座山位于湖南省？A. 泰山B. 华山C. 衡山D. 黄山答案：C4. 湖南省的面积大约是多少平方千米？A. 20万B. 21万C. 22万D. 23万5. 湖南省的省花是什么？A. 牡丹B. 杜鹃C. 荷花D. 菊花答案：B6. 以下哪位历史人物不是湖南人？A. 毛泽东B. 刘少奇C. 曾国藩D. 邓小平答案：D7. 湖南省的省树是什么？A. 松树B. 银杏C. 樟树D. 柳树答案：C8. 湖南省的省鸟是什么？A. 燕子B. 麻雀C. 杜鹃D. 鹰答案：C9. 以下哪条河流不流经湖南省？B. 沅江C. 赣江D. 资江答案：C10. 湖南省的省会城市长沙，以下哪个景点不属于长沙？A. 岳麓山B. 橘子洲C. 爱晚亭D. 黄鹤楼答案：D二、多项选择题（每题3分，共15分）1. 以下哪些是湖南省的著名旅游景点？A. 张家界B. 凤凰古城C. 岳阳楼D. 武陵源答案：ABCD2. 湖南省的哪些城市是历史文化名城？A. 长沙B. 岳阳C. 衡阳D. 常德答案：AB3. 湖南省的哪些特色美食享誉全国？A. 臭豆腐B. 剁椒鱼头C. 糖油粑粑D. 湖南米粉答案：ABCD4. 以下哪些是湖南省的著名高校？A. 湖南大学B. 中南大学C. 国防科技大学D. 湖南师范大学答案：ABCD5. 湖南省有哪些著名的非物质文化遗产？A. 湘绣B. 花鼓戏C. 皮影戏D. 侗族大歌答案：ABC三、判断题（每题2分，共10分）1. 湖南省位于中国中南部，东临江西，西接重庆，南毗广东，北与湖北交界。

（错误）答案：错误2. 湖南省的气候属于亚热带湿润气候，四季分明。

（正确）答案：正确3. 湖南省的方言主要是湘语，属于汉藏语系汉语族。

2007年湖南省长沙一中自主招生考试数学试卷一、填空题1．设a为的小数部分，b为的小数部分，则的整数部分为_________．2．下列两个方程组与有相同的解，则m+n=_________．3．如图,在Rt△ABC中,∠C=90°,∠B=60°，∠A的平分线AD交BC于D,则=_________．4．已知a是方程x2﹣2002x+1=0的根，则=_________．5．A、B是平面内两个不同的定点，在此平面内找点C，使△ABC为等腰直角三角形，则这样的点C有_________个．6．某工程队要招聘甲乙两种工种的工人150名，甲乙两种工种工人的月工资分别是600元和1000元，现要求乙种工种的人数不少于甲种工种人数的两倍，问甲乙两种工种的人数各聘_________时可使得每月所付工资最少，最小值是_________．7．已知，则分式=_________．8．如图，D、E分别是△ABC的边AC、AB边上的点，BD、CE相交于点O，若S△COD=3,S△BDE=4，S△OBC=5，那么S四边形ADOE=_________．9．三边长为整数且最长边是11的三角形共有_________个．10．已知方程：x3+4x2﹣11x﹣30=0的两个根的和等于1，则这个方程的三个根分别是_________．11．若函数当a≤x≤b时的最小值为2a,最大值为2b，求a、b的值．12．函数,其中a为任意实数,则该函数的图象在x轴上截得的最短线段的长度为_________．二、解答题（共8小题，满分0分）13．已知关于x的方程x2﹣（2m﹣3)x+m﹣4=O的二根为a1、a2，且满足﹣3＜a1＜﹣2，a2＞0．求m的取值范围．14．在△ABC中，AD⊥BC于点D，∠BAC=45°，BD=3,DC=2，求△ABC的面积．15．一个三角形的三边长分别为a、a、b,另一个三角形的三边长分别为a、b、b，其中a＞b，若两个三角形的最小内角相等，则=_________．16．求方程组的实数解．17．如图,在半径为r的⊙O中，AB为直径,C为的中点，D为的三分之一分点,且的长等于两倍的的长，连接AD并延长交⊙O的切线CE于点E（C为切点),求AE的长．18．如图，△ABC是锐角三角形，以BC为直径作⊙O，AD是⊙O的切线，从AB上一点E作AB的垂线交AC的延长线于F，若．求证：AD=AE．19．如图,在正方形ABCD中，DC的中点为E，F为CE的中点，求证:∠DAE=∠BAF．20．如图，四边形ABCD是正方形，E为BF上一点，四边形AEFC恰好是一个菱形，求∠EAB的度数．2007年湖南省长沙一中自主招生考试数学试卷参考答案与试题解析一、填空题1．设a为的小数部分,b为的小数部分，则的整数部分为5．考点: 估算无理数的大小．分析：根据无理数的取值范围表示a、b，再代入所求算式计算,估计结果的整数部分．解答：解：∵1＜＜2,1＜＜2，∴a=﹣1，b=﹣1，∴===(﹣+﹣1)（+）=+2+1，∵≈1。

湖南单招试题及答案一、单项选择题（每题2分，共20分）1. 以下哪个选项是湖南省的简称？A. 湘B. 鄂C. 赣D. 粤答案：A2. 湖南省的省会城市是？A. 长沙B. 武汉C. 广州D. 南昌答案：A3. 湖南省的地理位置是？A. 华东地区B. 华南地区C. 西南地区D. 华北地区答案：C4. 湖南省境内最大的湖泊是？A. 洞庭湖B. 鄱阳湖C. 太湖D. 洪泽湖5. 湖南省的面积大约是多少？A. 21万平方公里B. 36万平方公里C. 55万平方公里D. 70万平方公里答案：A6. 湖南省的气候类型是？A. 亚热带季风气候B. 温带季风气候C. 热带季风气候D. 寒带气候答案：A7. 湖南省的著名景点张家界属于哪种类型的地貌？A. 喀斯特地貌B. 丹霞地貌C. 火山地貌D. 冰川地貌答案：A8. 湖南省的人口数量大约是多少？A. 6000万B. 7000万C. 8000万D. 9000万答案：B9. 湖南省的著名小吃臭豆腐起源于哪个城市？B. 岳阳C. 株洲D. 衡阳答案：A10. 湖南省的著名历史人物毛泽东的故居位于？A. 韶山B. 湘潭C. 常德D. 益阳答案：A二、多项选择题（每题3分，共15分）1. 以下哪些是湖南省的著名景点？A. 张家界B. 岳麓书院C. 橘子洲头D. 岳阳楼答案：ABCD2. 湖南省的哪些城市属于历史文化名城？A. 长沙B. 岳阳C. 常德D. 衡阳答案：ABCD3. 湖南省的哪些地方是国家级自然保护区？A. 洞庭湖B. 武陵源D. 东江湖答案：BCD三、填空题（每题2分，共10分）1. 湖南省的简称是________。

答案：湘2. 湖南省的省会城市是________。

答案：长沙3. 湖南省境内最大的湖泊是________。

答案：洞庭湖4. 湖南省的气候类型是________。

答案：亚热带季风气候5. 湖南省的著名景点张家界属于________地貌。

答案：喀斯特地貌四、简答题（每题5分，共10分）1. 简要介绍湖南省的地理位置和地形特点。

2015年湖南省常德市桃源一中自主招生数学试卷一、选择题1．不等式的解集是（）A．﹣＜x≤2 B．﹣3＜x≤2 C．x≥2 D．x＜﹣32．一个质地均匀的正方体骰子的六个面上分别刻有 1 到6 的点数，将骰子抛掷两次，掷第一次，将朝上一面的点数记为x，掷第二次，将朝上一面的点数记为y，则点（x，y）落在直线y=﹣x+5 上的概率为（）A．B．C．D．3．如图所示，在正方形铁皮中，剪下一个圆和一个扇形，使余料尽量少．用圆做圆锥的底面，用扇形做圆锥的侧面，正好围成一个圆锥，若圆的半径为r，扇形的半径为R，那么（）A．R=2r B．R=r C．R=3r D．R=4r4．如图所示，在边长为 a 的正方形中，剪去一个边长为 b 的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b 的恒等式为（）2 2 2 2 2 2A．（a﹣b）﹣2ab+b=a B．（a+b）=a +2ab+b 2 22C．a﹣b=（a+b）（a﹣b）D． a +ab=a（a+b）5．若直线x+2y=2m 与直线2x+y=2m+3 （m 为常数）的交点在第四象限，则整数m 的值为（）A．﹣3，﹣2，﹣1，0 B．﹣2，﹣1，0，1 C．﹣1，0，1，2 D．0，1，2，3二、填空题（每小题4分，共24分）6．定义新运算：a⊕b=，则函数y=3⊕x的图象大致是．7．|π﹣3.14|+sin30°+3.14﹣8=．8．函数y=的自变量x的取值范围是．9．将边长为a的正三角形各边三等分，以这六个分点为顶点构成一个正六边形，则这个正六边形的面积为．10．如图，AB是⊙O的直径，C，D为⊙0上的两点，若∠CDB=30°，则∠ABC的度数为，cos∠ABC=．211．已知实数x，y满足x+3x+y﹣3=0，则x+y的最大值为．12．古希腊数学家把数1，3，6，10，15，21，⋯叫做三角形数，它有一定的规律．若把第一个数记为a1，第二数记为a2，⋯，第n个数记为a n．计算a2﹣a1，a3﹣a2，a4﹣a3，⋯，由此推算a10﹣a9=，a2012=．三．解答题：（共52分）13．先化简：÷﹣，然后在0，1，2，3中选一个你认为合格的a值，代入求值．2﹣x+p+1=0有两个实数根x1，x2． 1012?桃源县校级自主招生）关于x的一元二次议程x（1）求p的取值范围．（2）[1+x1（1﹣x2）][1+x2（1﹣x1）]=9，求p的值．15．某服装厂批发应夏季T恤衫，其单价y（元）与批发数量x（件）（x为正整数）之间的函数关系如图所示，（1）直接写出y 与x 的函数关系式；（2）一个批发商一次购进250 件T 恤衫，所花的钱数是多少元？（其他费用不计）；（3）若每件T 恤衫的成本价是20 元，当100＜x≤400 件，（x 为正整数）时，求服装厂所获利润w（元）与x（件）之间的函数关系式，并求一次批发多少件时所获利润最大，最大利润是多少？216．如图，抛物线y=ax +c（a＞0）经过梯形ABCD 的四个顶点，梯形的底A D 在x 轴上，A 点到原点的距离为2，梯形的高为3，C 点到y 轴的距离为1，（1）求抛物线的解析式；（2）点M 为y 轴上的任意一点，求点M 到A，B 两点的距离之和的最小值及此时点M 的坐标；（3）在第（2）的结论下，抛物线上的P 的使S△P AD=S△ABM 成立，求点P 的坐标．1012?桃源县校级自主招生）如图所示，四边形OABC 是矩形，点A、C 的坐标分别为（3，0），（0，1），点D 是线段B C 上的动点（与端点B、C 不重合），过点 D 作直线y=﹣+b 交折线OAB 于点E．记△ODE 的面积为S．（1）当点 E 在线段O A 上时，求S 与b 的函数关系式；并求出 b 的范围；（2）当点 E 在线段A B 上时，求S 与b 的函数关系式；并求出 b 的范围；（3）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形OA1B1C1，试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化？若不变，求出该重叠部分的面积；若改变，请说明理由．2015年湖南省常德市桃源一中自主招生数学试卷参考答案与试题解析一、选择题1．不等式的解集是（）A．﹣＜x≤2 B．﹣3＜x≤2 C．x≥2 D．x＜﹣3考点：解一元一次不等式组．分析：先解不等式组中的每一个不等式的解集，再利用求不等式组解集的口诀“大小小大中间找”来求不等式组的解集．解答：解：由①得：x＞﹣3，由②得：x≤2，所以不等式组的解集为﹣3＜x≤2．故选B．点评：解不等式组是考查学生的基本计算能力，求不等式组解集的时候，可先分别求出组成不等式组的各个不等式的解集，然后借助数轴或口诀求出所有解集的公共部分．2．一个质地均匀的正方体骰子的六个面上分别刻有 1 到6 的点数，将骰子抛掷两次，掷第一次，将朝上一面的点数记为x，掷第二次，将朝上一面的点数记为y，则点（x，y）落在直线y=﹣x+5 上的概率为（）A．B．C．D．考点：列表法与树状图法；一次函数图象上点的坐标特征．分析：列举出所有情况，看落在直线y=﹣x+5 上的情况占总情况的多少即可．解答：解：共有36 种情况，落在直线y=﹣x+5 上的情况有（1，4）（2，3）（3，2）（4，1）4 种情况，概率是，故选C．1 2 3 4 5 61 （1，1）（1，2）（1，3）（1，4）（1，5）（1，6）2 （2，1）（2，2）（2，3）（2，4）（2，5）（2，6）3 （3，1）（3，2）（3，3）（3，4）（3，5）（3，6）4 （4，1）（4，2）（4，3）（4，4）（4，5）（4，6）5 （5，1）（5，2）（5，3）（5，4）（5，5）（5，6）6 （6，1）（6，2）（6，3）（6，4）（6，5）（6，6）点评：如果一个事件有n 种可能，而且这些事件的可能性相同，其中事件 A 出现m种结果，那么事件A 的概率P（A ）= ，注意本题是放回实验．3．如图所示，在正方形铁皮中，剪下一个圆和一个扇形，使余料尽量少．用圆做圆锥的底面，用扇形做圆锥的侧面，正好围成一个圆锥，若圆的半径为r，扇形的半径为R，那么（）A．R=2r B．R=r C．R=3r D．R=4r考点：圆锥的计算；弧长的计算．专题：压轴题．分析：让扇形的弧长等于圆的周长即可．解答：解：根据扇形的弧长等于圆的周长，∴扇形弧长等于小圆的周长，即：=2πr，解得R=4r，故选D．点评：考查了扇形的弧长公式；圆的周长公式；用到的知识点为：圆锥的弧长等于底面周长．4．如图所示，在边长为 a 的正方形中，剪去一个边长为 b 的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b 的恒等式为（）2 2 2 2 2 2A．（a﹣b）﹣2ab+b=a B．（a+b）=a +2ab+b 2 22C． a ﹣b=（a+b）（a﹣b）D． a +ab=a（a+b）考点：平方差公式的几何背景．专题：计算题．分析：可分别在正方形和梯形中表示出阴影部分的面积，两式联立即可得到关于a、b 的恒等式．2 2解答：解：正方形中，S 阴影=a ﹣b；梯形中，S 阴影= （2a+2b）（a﹣b）=（a+b）（a﹣b）；2 2故所得恒等式为： a ﹣b=（a+b）（a﹣b）．故选：C．点评：此题主要考查的是平方差公式的几何表示，运用不同方法表示阴影部分面积是解题的关键．5．若直线x+2y=2m 与直线2x+y=2m+3 （m 为常数）的交点在第四象限，则整数m 的值为（）A．﹣3，﹣2，﹣1，0 B．﹣2，﹣1，0，1 C．﹣1，0，1，2 D．0，1，2，3考点：两条直线相交或平行问题．专题：计算题；压轴题．分析：由直线x+2y=2m与直线2x+y=2m+3（m为常数）的交点在第四象限，则交点坐标的符号为（+，﹣），解关于x、y的方程组，使x＞0，y＜0，即可求得m的值．解答：解：由题意得，解得，∵直线x+2y=2m与直线2x+y=2m+3（m为常数）的交点在第四象限，∴，解得：﹣3，又∵m的值为整数，∴m=﹣2，﹣1，0，1，故选B．点评：考查了平面直角坐标系中点的符号，是一道一次函数综合性的题目，是中档题．二、填空题（每小题4分，共24分）6．定义新运算：a⊕b=，则函数y=3⊕x的图象大致是．考点：一次函数的图象；反比例函数的图象．专题：新定义．分析：根据题意可得y=3⊕x=，再根据反比例函数的性质可得函数图象所在象限和形状，进而得到答案．解答：解：由题意得y=3⊕x=，当x≥3时，y=2；当x＜3且x≠0时，y=﹣，图象如图：，故答案为：点评：此题主要考查了反比例函数的图象性质和一次函数的图象性质，要掌握它们的性质才能灵活解题．7．|π﹣3.14|+sin30°+3.14﹣8=π．考点：实数的运算；特殊角的三角函数值．专题：计算题．分析：原式第一项利用绝对值的代数意义化简，第二项利用特殊角的三角函数值计算，最后一项利用负整数指数幂法则计算即可得到结果．解答：解：原式=π﹣3.14++3.14﹣=π，故答案为：π点评：此题考查了实数的运算，熟练掌握运算法则是解本题的关键．8．函数y=的自变量x的取值范围是x＜﹣1或x≥4．考点：函数自变量的取值范围．分析：根据被开方数为非负数和分母不能为0计算即可．2解答：解：由题意得，x﹣3x﹣4≥0，x+1≠0，解得，x＜﹣1或x≥4，故答案为：x＜﹣1或x≥4．点评：本题考查的是函数自变量的范围，一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数为非负数．9．将边长为a的正三角形各边三等分，以这六个分点为顶点构成一个正六边形，则这个正六边形的2面积为 a ．考点：正多边形和圆．分析：由于正三角形各边三等分，就把整个三角形平均分成9个小正三角形，以这六个分点为顶点构成一个正六边形正好相当于6个小正三角形的面积．解答：解：如图所示：∵新的正六边形有三个顶点在正三角形的三边上，且是三边的等分点，∴连接正三角形的顶点与它对边的中点，可以看出新的正六边形的面积是六个小正三角形的面积之和，∵边长为a的正三角形各边三等分，∴小正三角形的边长为a，2∴每个小正三角形的面积是×a×=a×a= a，2 2∴新的正六边形的面积= a×6=a；2故答案为： a．点评：此题考查了正三角形的性质、正三角形面积的计算方法；熟练掌握正三角形的性质，并能进行推理计算是解决问题的关键．10．如图，AB是⊙O的直径，C，D为⊙0上的两点，若∠CDB=30°，则∠ABC的度数为60°，cos∠ABC=．考点：圆周角定理；特殊角的三角函数值．分析：由于AB是⊙O的直径，由圆周角定理可知∠ACB=90°，则∠A和∠ABC互余，欲求∠ABC 需先求出∠A的度数，已知了同弧所对的圆周角∠CDB的度数，则∠A=∠CDB，由此得解．解答：解：连接AC，∵AB是⊙O的直径，∴∠ACB=90°，即∠A+∠ABC=90°；又∵∠A=∠CDB=30°，∴∠ABC=90°﹣∠A=60°，∴cos∠ABC=．故答案为：60°．点评：此题主要考查了圆周角定理及其推论，半圆（弧）和直径所对的圆周角是直角，同弧所对的圆周角相等，还考查了三角函数，掌握圆周角定理是解题的关键．211．已知实数x，y 满足x +3x+y ﹣3=0，则x+y 的最大值为 4 ．考点：二次函数的应用．专题：压轴题．2分析：将函数方程x+3x+y ﹣3=0 代入x+y，把x+y 表示成关于x 的函数，根据二次函数的性质求得最大值．2解答：解：由x+3x+y ﹣3=0 得2﹣3x+3，把y 代入x+y 得：y=﹣x2 2 2﹣3x+3=﹣x ﹣2x+3= ﹣（x+1）x+y=x ﹣x +4≤4，∴x+y 的最大值为4．故答案为：4．点评：本题考查了二次函数的性质及求最大值的方法，即完全平方式法．12．古希腊数学家把数1，3，6，10，15，21，⋯叫做三角形数，它有一定的规律．若把第一个数记为a1，第二数记为a2，⋯，第n 个数记为a n．计算a2﹣a1，a3﹣a2，a4﹣a3，⋯，由此推算a10﹣a9=10 ，a2012= 2025078 ．考点：规律型：数字的变化类．分析：先计算a2﹣a1=3﹣1=2；a3﹣a2=6﹣3=3；a4﹣a3=10﹣6=4，则a10﹣a9=10，a2=1+2 ，a3=1+2+3 ，a4=1+3+4 ，即第n 个三角形数等于 1 到n 的所有整数的和，然后计算n=2012 的a 的值．解答：解：∵a2﹣a1=3﹣1=2；a3﹣a2=6﹣3=3；a4﹣a3=10﹣6=4，∴a10﹣a9=10∵a2=1+2，a3=1+2+3 ，a4=1+2+3+4 ，⋯∴a2012=1+2+3+4+ ⋯+2012= =2025078．故答案为：10，2025078．点评：本题考查了规律型：数字的变化类，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况是解答此题的关键．三．解答题：（共52分）13．先化简：÷﹣，然后在0，1，2，3 中选一个你认为合格的a 值，代入求值．考点：分式的化简求值．分析：先根据分式混合运算的法则把原式进行化简，再选出合适的x 的值代入进行计算即可．解答：解：原式= ? +a=a+a=2a．当a=2 时，原式=4a．点评：本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．2﹣x+p+1=0 有两个实数根x1，x2． 1012?桃源县校级自主招生）关于x的一元二次议程x（1）求p 的取值范围．（2）[1+x 1（1﹣x2）] [1+x2（1﹣x1）] =9，求p 的值．考点：根的判别式；根与系数的关系．分析：（1）根据题意得出△≥0，求出即可；2（2）根据根与系数的关系得出x1+x2=1，x1?x2=p+1 ，整理后得出（1﹣x1?x2）+（x1+x2）（1﹣x1?x2）+x1?x2=9，代入求出即可．2解答：解：（1）△=（﹣1）﹣4（p+1）=﹣3﹣4p，当﹣3﹣4p≥0，即p≤﹣时，方程有两个实数根，即p 的取值范围是p≤﹣；（2）根据根与系数的关系得：x1+x2=1，x1?x2=p+1 ，∵[1+x1（1﹣x2）][1+x 2（1﹣x1）]=9，2∴（1﹣x1?x2）+（x1+x2）（1﹣x1?x2）+x1?x2=9，2∴[1﹣（p+1）]+1×[1﹣（p+1）]+（p+1）=9，解得：p±2，∵p≤﹣，∴p=﹣2 ．点评：本题考查了根与系数的关系，根的判别式的应用，能正确利用知识点进行计算是解此题的关键，题目比较典型．15．某服装厂批发应夏季T 恤衫，其单价y（元）与批发数量x（件）（x 为正整数）之间的函数关系如图所示，（1）直接写出y 与x 的函数关系式；（2）一个批发商一次购进250 件T 恤衫，所花的钱数是多少元？（其他费用不计）；（3）若每件T 恤衫的成本价是20 元，当100＜x≤400 件，（x 为正整数）时，求服装厂所获利润w（元）与x（件）之间的函数关系式，并求一次批发多少件时所获利润最大，最大利润是多少？考点：二次函数的应用．分析：（1）由题意设出一次函数的解析式，再根据点在直线上待定系数法求出函数解析式；（2）列出总利润的函数表达式，转化为求函数最值问题，最后求出最大利润；（3）根据利润=单件利润×批发数量，列出二次函数表达式，再运用二次函数性质解决最值问题．解答：解：（1）当0≤x＜100 时，y=60；当x≥100 时，设y=kx+b ，由图象可以看出过（100，60），（400，40），则，，∴y= ；（2）∵250＞100，∴当x=250 件时，y=﹣×250+ =50 元，∴批发商一次购进250 件T 恤衫，所花的钱数是：50×250=12500 元；2（3）W= （﹣x+﹣20）×x=﹣x+ x=﹣（x﹣350）2+ ，∴当一次性批发350 件时，所获利润最大，最大利润是元．点评：本题考查了待定系数法求函数关系式以及运用函数的性质解决问题，根据题意列出函数表达式是解决问题的关键．216．如图，抛物线y=ax +c（a＞0）经过梯形ABCD 的四个顶点，梯形的底A D 在x 轴上，A 点到原点的距离为2，梯形的高为3，C 点到y 轴的距离为1，（1）求抛物线的解析式；（2）点M 为y 轴上的任意一点，求点M 到A，B 两点的距离之和的最小值及此时点M 的坐标；（3）在第（2）的结论下，抛物线上的P 的使S△P AD=S△ABM 成立，求点P 的坐标．考点：二次函数综合题．2分析：（1）易知A（﹣2，0），C（1，﹣3），将A、C两点的坐标代入y=ax+c，利用待定系数法即可求出抛物线的解析式；（2）由于A、D关于抛物线对称轴即y轴对称，那么连接BD，BD与y轴的交点即为所求的M点，可先求出直线BD的解析式，即可得到M点的坐标；（3）设直线BC与y轴的交点为N，那么S△ABM=S 梯形AONB﹣S△BMN﹣S△AOM，由此可求出△ABM和△PAD的面积；在△PAD中，AD的长为定值，可根据其面积求出P点纵坐标的绝对值，然后代入抛物线的解析式中即可求出P点的坐标．解答：解：（1）由题意可得：A（﹣2，0），C（1，﹣3），2∵抛物线y=ax+c（a＞0）经过A、C两点，∴，解得，∴抛物线的解析式为：y=x 2﹣4；（2）由于A、D关于抛物线的对称轴（即y轴）对称，连接BD，则BD与y轴的交点即为M点；设直线BD的解析式为：y=kx+b（k≠0），∵B（﹣1，﹣3），D（2，0），∴，解得，∴直线BD的解析式为y=x﹣2，当x=0时，y=﹣2，∴点M的坐标是（0，﹣2）；（3）设BC与y轴的交点为N，则有N（0，﹣3），∵M（0，﹣2），B（﹣1，﹣3），∴MN=1，BN=1，ON=3，∴S△ABM=S梯形AONB﹣S△BMN﹣S△AOM=（1+2）×3﹣×1×1﹣×2×2=2，∴S△PAD=S△ABM=2．∵S△PAD=AD?|y P|=2，AD=4，∴|y P|=1．2当P点纵坐标为1时，x﹣4=1，解得x=±，∴P1（，1），P2（﹣，1）；2当P点纵坐标为﹣1时，x﹣4=﹣1，解得x=±，∴P3（，﹣1），P4（﹣，﹣1）；故存在符合条件的P点，且P点坐标为：P1（，1），P2（﹣，1），P3（，﹣1），P4（﹣，﹣1）．点评：此题是二次函数的综合题型，其中涉及到二次函数解析式的确定、函数图象交点及图形面积的求法，轴对称的性质等．当所求图形不规则时，一般要将不规则图形转换为几个规则图形面积的和差来求．1012?桃源县校级自主招生）如图所示，四边形OABC是矩形，点A、C的坐标分别为（3，0），（0，1），点D是线段BC上的动点（与端点B、C不重合），过点D作直线y=﹣+b交折线OAB于点E．记△ODE的面积为S．（1）当点E在线段OA上时，求S与b的函数关系式；并求出b的范围；（2）当点E在线段AB上时，求S与b的函数关系式；并求出b的范围；（3）当点E在线段OA上时，若矩形OABC关于直线DE的对称图形为四边形OA1B1C1，试探究OA1B1C1与矩形OABC的重叠部分的面积是否发生变化？若不变，求出该重叠部分的面积；若改变，请说明理由．考点：一次函数综合题．专题：压轴题．分析：（1）要表示出△ODE 的面积，要分两种情况讨论，①如果点 E 在OA 边上，只需求出这个三角形的底边OE 长（E 点横坐标）和高（ D 点纵坐标），代入三角形面积公式即可；（2）如果点E 在AB 边上，这时△ODE 的面积可用长方形OABC 的面积减去△OCD、△OAE 、△BDE 的面积；（3）重叠部分是一个平行四边形，由于这个平行四边形上下边上的高不变，因此决定重叠部分面积是否变化的因素就是看这个平行四边形落在OA 边上的线段长度是否变化．解答：解：（1）∵四边形OABC 是矩形，点 A 、C 的坐标分别为（3，0），（0，1），∴B（3，1），若直线经过点 A （3，0）时，则b=若直线经过点B（3，1）时，则b=若直线经过点C（0，1）时，则b=1①若直线与折线OAB 的交点在OA 上时，即1＜b≤，如图1，此时E（2b，0）∴S= OE ?CO= ×2b×1=b；（2）若直线与折线OAB 的交点在BA 上时，即＜b＜，如图2此时E（3，），D（2b﹣2，1），∴S=S 矩﹣（S△OCD+S△OAE+S△D BE）=3﹣[ （2b﹣2）×1+ ×（5﹣2b）?（﹣b）+ ×3（b﹣）]2= b﹣b，∴S= ；（3）如图3，设O1A 1 与CB 相交于点M ，OA 与C1B1 相交于点N，则矩形O1A1B1C1 与矩形OABC的重叠部分的面积即为四边形DNEM 的面积．由题意知，DM ∥NE，DN∥ME ，∴四边形DNEM 为平行四边形根据轴对称知，∠MED= ∠NED，又∠MDE= ∠NED，∴∠MED= ∠MDE ，∴MD=ME ，∴平行四边形DNEM 为菱形．过点 D 作DH ⊥OA，垂足为H，由题易知，D（2b﹣2，1），对于y=﹣+b，令y=0，得x=2b，则E（2b，0），∴DH=1，HE=2b﹣（2b﹣2）=2，设菱形DNEM的边长为a，2则在Rt△DHN中，由勾股定理知： a=（2﹣a）2 2 +1，∴a=，∴S四边形DNEM=NE?DH=．∴矩形OA1B1C1与矩形OABC的重叠部分的面积不发生变化，面积始终为．点评：本题是一个动态图形中的面积是否变化的问题，看一个图形的面积是否变化，关键是看决定这个面积的几个量是否变化，本题题型新颖，是个不可多得的好题，有利于培养学生的思维能力，但难度较大，具有明显的区分度．。