Chapter3-稳态扩散问题-16
- 格式:pdf
- 大小:345.39 KB
- 文档页数:16

一、扩散方程稳态扩散与非稳态扩散1.稳态扩散下的菲克第一定律(一定时间内,浓度不随时间变化dc/dt=0)单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量(扩散通量)与该面积处的浓度梯度成正比即J=-D(dc/dx)其中D:扩散系数,cm2/s,J:扩散通量,g/cm2·s ,式中负号表明扩散通量的方向与浓度梯度方向相反。
可见,只要存在浓度梯度,就会引起原子的扩散。
x轴上两单位面积1和2,间距dx,面上原子浓度为C1、C2则平面1到平面2上原子数n1=C1dx ,平面2到平面1上原子数n2=C2dx若原子平均跳动频率f, dt时间内跳离平面1的原子数为n1f·dt跳离平面2的原子数为n2fdt,但沿一个方向只有1/2的几率,则单位时间内两者的差值即扩散原子净流量。
令,则上式2.扩散系数的测定:其中一种方法可通过碳在γ-Fe中的扩散来测定纯Fe的空心园筒,心部通渗碳气氛,外部为脱碳气氛,在一定温度下经过一定时间后,碳原子从内壁渗入,外壁渗出达到平衡,则为稳态扩散单位时单位面积中碳流量:A:圆筒总面积,r及L:园筒半径及长度,q:通过圆筒的碳量则:即:则:q可通过炉内脱碳气体的增碳求得,再通过剥层法测出不同r处的碳含量,作出C-lnr曲线可求得D。
第一定律可用来处理扩散中浓度不因时间变化的问3.菲克第二定律:解决溶质浓度随时间变化的情况,即dc/dt≠0两个相距dx垂直x轴的平面组成的微体积,J1、J2为进入、流出两平面间的扩散通量,扩散中浓度变化为,则单元体积中溶质积累速率为(Fick第一定律)(Fick第一定律)(即第二个面的扩散通量为第一个面注入的溶质与在这一段距离内溶质浓度变化引起的扩散通量之和)若D不随浓度变化,则故:4.Fick第二定律的解:很复杂,只给出两个较简单但常见问题的解a. 无限大物体中的扩散设:1)两根无限长A、B合?金棒,各截面浓度均匀,浓度C2>C12)两合金棒对焊,扩散方向为x方向3)合金棒无限长,棒的两端浓度不受扩散影响4)扩散系数D是与浓度无关的常数根据上述条件可写出初始条件及边界条件初始条件:t=0时, x>0则C=C1,x<0, C=C2边界条件:t≥0时, x=∞,C=C1, x=-∞, C=C2令,代入则,则菲克第二定律为即(1)令代入式(1)则有(2)若代入(2)左边化简有而积分有(3)令,式(3)为由高斯误差积分:应用初始条件t=0时x>0, c=c1,x<0, c=c2,从式(4)求得(5)则可求得(6)将(5)和(6)代入(4)有:上式即为扩散偶经过时间t扩散之后,溶质浓度沿x方向的分布公式,其中为高斯误差函数,可用表查出:根据不同条件,无限大物体中扩散有不同情况(1)B金属棒初始浓度,则(2)扩散偶焊接面处溶质浓度c0,根据x=0时,,则,若B棒初始浓度,则。



三材料的扩散扩散是物质中原子(分子或离子)的迁移现象,是物质传输的一种方式。
扩散的本质是原子依靠热运动从一个位置迁移到另一个位置。
是固体中原子迁移的唯一方式。
研究扩散一般有两种方法:表象理论—根据所测量的参数描述物质传输的速率和数量等;(宏观)原子理论—扩散过程中原子是如何迁移的。
(微观)3.1 扩散的分类1. 根据有无浓度变化自扩散:原子经由自己元素的晶体点阵而迁移的扩散。
(如纯金属或固溶体的晶粒长大-无浓度变化)互扩散:原子通过进入对方元素晶体点阵而导致的扩散。
(有浓度变化)2. 根据扩散方向下坡扩散:原子由高浓度处向低浓度处进行的扩散。
上坡扩散:原子由低浓度处向高浓度处进行的扩散。
固态扩散的条件1、温度足够高;2、时间足够长;3、扩散原子能固溶;4、具有驱动力:5、化学位梯度。
菲克第一定律稳态扩散:扩散过程中各处的浓度及浓度梯度不随时间变化(əC/ət=0,əJ/əx=0)菲克第一定律:在稳态扩散过程中,扩散通量J与浓度梯度成正比J为扩散通量,表示单位时间内通过垂直于扩散方向x的单位面积的扩散物质质量,其单位为kg/(m2s)或kg/(cm2s)。
D为扩散系数,其单位为m2/s;ρ是扩散物质的质量浓度,其单位为kg/m3。
式中的负号表示物质从高浓度向低浓度扩散的现象,扩散的结果导致浓度梯度的减小,使成份趋于均匀。
菲克第二定律非稳态扩散——各处的浓度和浓度梯度随时间发生变化的扩散过程。
(əC/ət≠0, əJ/əx≠0)。
大多数扩散过程是非稳态扩散过程,某一点的浓度是随时间而变化的菲克第二定律:扩散过程中,扩散物质浓度随时间的变化率,与沿扩散方向上物质浓度梯度随扩散距离的变化率成正比。
3.2 置换式固溶体中的扩散---互扩散与柯肯达尔效应互扩散——柯肯达尔效应柯肯达尔最先发现互扩散,在α黄铜—铜扩散偶中,用钼丝作为标志,785℃下保温不同时间后,钼丝向黄铜内移动,移动量与保温时间的平方根成正比,Cu-黄铜分界面黄铜侧出现宏观疏孔。

一、扩散方程稳态扩散与非稳态扩散1.稳态扩散下的菲克第一定律(一定时间,浓度不随时间变化dc/dt=0)单位时间通过垂直于扩散方向的单位截面积的扩散物质流量(扩散通量)与该面积处的浓度梯度成正比即J=-D(dc/dx)其中D:扩散系数,cm2/s,J:扩散通量,g/cm2·s ,式中负号表明扩散通量的方向与浓度梯度方向相反。
可见,只要存在浓度梯度,就会引起原子的扩散。
x轴上两单位面积1和2,间距dx,面上原子浓度为C1、C2则平面1到平面2上原子数n1=C1dx ,平面2到平面1上原子数n2=C2dx若原子平均跳动频率f, dt时间跳离平面1的原子数为n1f·dt跳离平面2的原子数为n2fdt,但沿一个方向只有1/2的几率,则单位时间两者的差值即扩散原子净流量。
令,则上式2.扩散系数的测定:其中一种方法可通过碳在γ-Fe中的扩散来测定纯Fe的空心园筒,心部通渗碳气氛,外部为脱碳气氛,在一定温度下经过一定时间后,碳原子从壁渗入,外壁渗出达到平衡,则为稳态扩散单位时单位面积中碳流量:A:圆筒总面积,r及L:园筒半径及长度,q:通过圆筒的碳量则:即:则:q可通过炉脱碳气体的增碳求得,再通过剥层法测出不同r处的碳含量,作出C-lnr曲线可求得D。
第一定律可用来处理扩散中浓度不因时间变化的问3.菲克第二定律:解决溶质浓度随时间变化的情况,即dc/dt≠0两个相距dx垂直x轴的平面组成的微体积,J1、J2为进入、流出两平面间的扩散通量,扩散中浓度变化为,则单元体积中溶质积累速率为(Fick第一定律)(Fick第一定律)(即第二个面的扩散通量为第一个面注入的溶质与在这一段距离溶质浓度变化引起的扩散通量之和)若D不随浓度变化,则故:4.Fick第二定律的解:很复杂,只给出两个较简单但常见问题的解a. 无限大物体中的扩散设:1)两根无限长A、B合?金棒,各截面浓度均匀,浓度C2>C12)两合金棒对焊,扩散方向为x方向3)合金棒无限长,棒的两端浓度不受扩散影响4)扩散系数D是与浓度无关的常数根据上述条件可写出初始条件及边界条件初始条件:t=0时, x>0则C=C1,x<0, C=C2边界条件:t≥0时, x=∞,C=C1, x=-∞, C=C2令,代入则,则菲克第二定律为即(1)令代入式(1)则有(2)若代入(2)左边化简有而积分有(3)令,式(3)为由高斯误差积分:应用初始条件t=0时x>0, c=c1,x<0, c=c2,从式(4)求得(5)则可求得(6)将(5)和(6)代入(4)有:上式即为扩散偶经过时间t扩散之后,溶质浓度沿x方向的分布公式,其中为高斯误差函数,可用表查出:根据不同条件,无限大物体中扩散有不同情况(1)B金属棒初始浓度,则(2)扩散偶焊接面处溶质浓度c0,根据x=0时,,则,若B棒初始浓度,则。


稳态扩散规则是指在一定条件下,物质在介质中自由扩散的过程符合一定的规律和规则。
稳态扩散规则是物质传输领域的基础理论之一,对于理解及解决物质在空间中传输和扩散的过程具有重要的理论指导和应用价值。
本文将从稳态扩散规则的基本概念、适用条件、数学模型以及实际应用等方面进行详细阐述,以期帮助读者全面了解稳态扩散规则,并在实际工作中做出合理的应用。
一、稳态扩散规则的基本概念稳态扩散规则是描述物质在介质中自由扩散的一种规律,是描述扩散过程的基本理论。
在稳态扩散过程中,物质从高浓度区域传输到低浓度区域,直到达到均匀分布的状态。
稳态扩散规则认为扩散速率与浓度梯度成正比,扩散的总通量与浓度梯度成正比。
在不考虑外界因素扰动的情况下,稳态扩散规则可以有效描述物质在介质中的传输过程。
二、稳态扩散规则的适用条件稳态扩散规则适用于物质在均质介质中的自由扩散过程。
其中,均质介质是指介质的性质在空间上是均匀分布的,在这样的介质中,物质的扩散过程可以被理想化为观察微观尺度上的分子移动。
稳态扩散规则还适用于扩散过程中不考虑其它外部干扰的理想化情况,例如不考虑温度、压力、湍流等外部因素的影响。
三、稳态扩散规则的数学模型稳态扩散规则可以用数学模型进行描述。
经典的稳态扩散模型是菲克定律,它可以用数学方程表示为:\[J = -D \frac{dC}{dx}\]其中,J表示单位面积上的物质通量,D表示扩散系数,C表示浓度,x表示扩散方向。
菲克定律是描述稳态扩散规则的基本方程,它将扩散通量与浓度梯度联系起来,揭示了浓度梯度对于扩散通量的影响。
除了菲克定律外,还有一些扩散模型可以用于描述不同情况下的稳态扩散规则,例如对于非均质介质、非线性扩散等情况,可以采用不同的数学模型来描述。
四、稳态扩散规则的实际应用稳态扩散规则在实际应用中具有广泛的意义。
在环境保护领域,稳态扩散规则可以用于描述大气污染物在大气中的扩散过程,为评估和预测大气污染物的扩散范围提供理论依据。
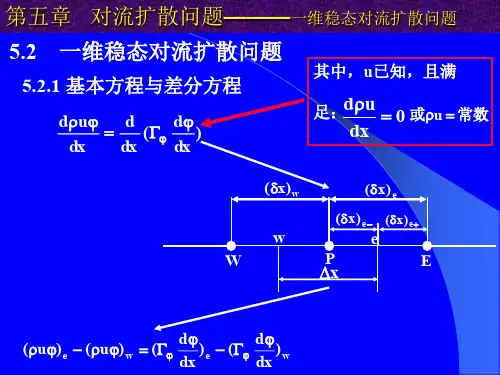



扩散方程稳态扩散与非稳态扩散1.稳态扩散下的菲克第一定律(一定时间内,浓度不随时间变化dc/dt=0)单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量(扩散通量)与该面积处的浓度梯度成正比即J=-D(dc/dx)其中D:扩散系数,cm2/s,J:扩散通量,g/cm2·s ,式中负号表明扩散通量的方向与浓度梯度方向相反。
可见,只要存在浓度梯度,就会引起原子的扩散。
x轴上两单位面积1和2,间距dx,面上原子浓度为C1、C2则平面1到平面2上原子数n1=C1dx ,平面2到平面1上原子数n2=C2dx 若原子平均跳动频率f, dt时间内跳离平面1的原子数为n1f·dt跳离平面2的原子数为n2fdt,但沿一个方向只有1/2的几率,则单位时间内两者的差值即扩散原子净流量。
令,则上式2.扩散系数的测定:其中一种方法可通过碳在γ-Fe中的扩散来测定纯Fe的空心园筒,心部通渗碳气氛,外部为脱碳气氛,在一定温度下经过一定时间后,碳原子从内壁渗入,外壁渗出达到平衡,则为稳态扩散单位时单位面积中碳流量:A:圆筒总面积,r及L:园筒半径及长度,q:通过圆筒的碳量则:即:则:q可通过炉内脱碳气体的增碳求得,再通过剥层法测出不同r处的碳含量,作出C-lnr曲线可求得D。
第一定律可用来处理扩散中浓度不因时间变化的问3.菲克第二定律:解决溶质浓度随时间变化的情况,即dc/dt≠0两个相距dx垂直x轴的平面组成的微体积,J1、J2为进入、流出两平面间的扩散通量,扩散中浓度变化为,则单元体积中溶质积累速率为(Fick第一定律)(Fick第一定律)(即第二个面的扩散通量为第一个面注入的溶质与在这一段距离内溶质浓度变化引起的扩散通量之和)若D不随浓度变化,则故:4.Fick第二定律的解:很复杂,只给出两个较简单但常见问题的解a. 无限大物体中的扩散设:1)两根无限长A、B合?金棒,各截面浓度均匀,浓度C2>C1 2)两合金棒对焊,扩散方向为x方向3)合金棒无限长,棒的两端浓度不受扩散影响4)扩散系数D是与浓度无关的常数根据上述条件可写出初始条件及边界条件初始条件:t=0时, x>0则C=C1,x<0, C=C2边界条件:t≥0时, x=∞,C=C1, x=-∞, C=C2令,代入则,则菲克第二定律为即(1)令代入式(1)则有(2)若代入(2)左边化简有而积分有(3)令,式(3)为由高斯误差积分:应用初始条件t=0时x>0, c=c1,x<0, c=c2,从式(4)求得(5)则可求得(6)将(5)和(6)代入(4)有:上式即为扩散偶经过时间t扩散之后,溶质浓度沿x方向的分布公式,其中为高斯误差函数,可用表查出:根据不同条件,无限大物体中扩散有不同情况(1)B金属棒初始浓度,则(2)扩散偶焊接面处溶质浓度c0,根据x=0时,,则,若B棒初始浓度,则。
一、扩散方程稳态扩散与非稳态扩散1.稳态扩散下的菲克第一定律(一定时间内,浓度不随时间变化dc/dt=0)单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量(扩散通量)与该面积处的浓度梯度成正比即J=-D(dc/dx)其中D:扩散系数,cm2/s,J:扩散通量,g/cm2·s ,式中负号表明扩散通量的方向与浓度梯度方向相反。
可见,只要存在浓度梯度,就会引起原子的扩散。
x轴上两单位面积1和2,间距dx,面上原子浓度为C1、C2则平面1到平面2上原子数n1=C1dx ,平面2到平面1上原子数n2=C2dx若原子平均跳动频率f, dt时间内跳离平面1的原子数为n1f·dt跳离平面2的原子数为n2fdt,但沿一个方向只有1/2的几率,则单位时间内两者的差值即扩散原子净流量。
令,则上式2.扩散系数的测定:其中一种方法可通过碳在γ-Fe中的扩散来测定纯Fe的空心园筒,心部通渗碳气氛,外部为脱碳气氛,在一定温度下经过一定时间后,碳原子从内壁渗入,外壁渗出达到平衡,则为稳态扩散单位时单位面积中碳流量:A:圆筒总面积,r及L:园筒半径及长度,q:通过圆筒的碳量则:即:则:q可通过炉内脱碳气体的增碳求得,再通过剥层法测出不同r处的碳含量,作出C-lnr曲线可求得D。
第一定律可用来处理扩散中浓度不因时间变化的问3.菲克第二定律:解决溶质浓度随时间变化的情况,即dc/dt≠0两个相距dx垂直x轴的平面组成的微体积,J1、J2为进入、流出两平面间的扩散通量,扩散中浓度变化为,则单元体积中溶质积累速率为(Fick第一定律)(Fick第一定律)(即第二个面的扩散通量为第一个面注入的溶质与在这一段距离内溶质浓度变化引起的扩散通量之和)若D不随浓度变化,则故:4.Fick第二定律的解:很复杂,只给出两个较简单但常见问题的解a. 无限大物体中的扩散设:1)两根无限长A、B合?金棒,各截面浓度均匀,浓度C2>C12)两合金棒对焊,扩散方向为x方向3)合金棒无限长,棒的两端浓度不受扩散影响4)扩散系数D是与浓度无关的常数根据上述条件可写出初始条件及边界条件初始条件:t=0时, x>0则C=C1,x<0, C=C2边界条件:t≥0时, x=∞,C=C1, x=-∞, C=C2令,代入则,则菲克第二定律为即(1)令代入式(1)则有(2)若代入(2)左边化简有而积分有(3)令,式(3)为由高斯误差积分:应用初始条件t=0时x>0, c=c1,x<0, c=c2,从式(4)求得(5)则可求得(6)将(5)和(6)代入(4)有:上式即为扩散偶经过时间t扩散之后,溶质浓度沿x方向的分布公式,其中为高斯误差函数,可用表查出:根据不同条件,无限大物体中扩散有不同情况(1)B金属棒初始浓度,则(2)扩散偶焊接面处溶质浓度c0,根据x=0时,,则,若B棒初始浓度,则。
稳态扩散和非稳态扩散是物理学和化学领域中常用的术语,用来描述物质在空间中的扩散行为。
稳态扩散是指物质在均匀介质中的扩散过程,而非稳态扩散则是指物质在非均匀介质中的扩散过程。
本文将通过对稳态扩散和非稳态扩散的名词解释,解析其物理意义、数学表达和实际应用,帮助读者更好地理解这两个概念。
一、稳态扩散的名词解释1.1 稳态扩散的物理意义稳态扩散是指当物质在均匀介质中的浓度分布达到稳定状态时的扩散过程。
在稳态扩散中,物质的浓度分布不再发生变化,达到了动态平衡状态。
这种扩散过程通常以弥散系数来描述,可以用弥散方程进行数学建模,是一种重要的物质传输过程。
1.2 弥散系数的数学表达在稳态扩散中,物质的弥散系数是一个重要的物理参数,用来描述物质在均匀介质中扩散的能力。
它通常用符号D表示,是一个与时间和空间无关的常数。
弥散系数与介质的性质、温度和压力等因素有关,不同的物质在不同的介质中有不同的弥散系数。
1.3 稳态扩散的实际应用稳态扩散在化学工程、环境科学和生物医学等领域有着广泛的应用。
在化学工程中,稳态扩散常用来描述气体或液体在反应器中的传质过程;在环境科学中,稳态扩散被用来研究大气、水体和土壤中的污染物传播行为;在生物医学中,稳态扩散可用于分子在细胞内的扩散和运输研究。
二、非稳态扩散的名词解释2.1 非稳态扩散的物理意义非稳态扩散是指当物质在非均匀介质中的浓度分布随时间和空间发生变化的扩散过程。
在非稳态扩散中,物质的浓度分布不断改变,未达到动态平衡状态,通常需要考虑时间和空间的变化。
2.2 非稳态扩散的数学表达在非稳态扩散中,物质的扩散过程通常需要考虑时间和空间的变化,所以需要使用偏微分方程进行描述。
这类方程常常包括时间导数和空间导数,需要通过适当的数值或解析方法进行求解,得到物质浓度随时间和空间的变化规律。
2.3 非稳态扩散的实际应用非稳态扩散在材料科学、地球科学和生物学等领域有着重要的应用价值。
在材料科学中,非稳态扩散常用来研究材料中的晶体生长和变形过程;在地球科学中,非稳态扩散被用来描述地表和地下水体中的渗透和溶质迁移过程;在生物学中,非稳态扩散可用于描述细胞内物质的输运和信号传导过程。
第七节 扩散问题的偏微分方程模型物质的扩散问题,在石油开采、环境污染、疾病流行、化学反应、新闻传播、煤矿瓦斯爆炸、农田墒情、水利工程、生态问题、房屋基建、神经传导、药物在人体内分布以及超导、液晶、燃烧等诸多自然科学与工程技术领域,十分普遍地存在着. 显然,对这些问题的研究是十分必要的,其中的数学含量极大. 事实上,凡与反应扩散有关的现象,大都能由线性或非线性抛物型偏微分方程作为数学模型来定量或定性地加以解决.MCM的试题来自实际,是“真问题⊕数学建模⊕计算机处理”的“三合一”准科研性质的一种竞赛,对上述这种有普遍意义和数学含量高,必须用计算机处理才能得到数值解的扩散问题,当然成为试题的重要来源,例如,AMCM-90A,就是这类试题;AMCM-90A要研究治疗帕金森症的多巴胺(dopamine )在人脑中的分布,此药液注射后在脑子里经历的是扩散衰减过程,可以由线性抛物型方程这一数学模型来刻划. AMCM-90A要研究单层住宅混凝土地板中的温度变化,也属扩散(热传导)问题,其数学模型与AMCM-90A一样,也是线性抛物型方程.本文交代扩散问题建模的思路以及如何推导出相应的抛物型方程,如何利用积分变换求解、如何确定方程与解的表达式中的参数等关键数学过程,且以AMCM-90A题为例,显示一个较细致的分析、建模、求解过程.§1 抛物型方程的导出设(,,,)u x y z t 是t 时刻点(,,)x y z 处一种物质的浓度. 任取一个闭曲面S ,它所围的区域是Ω,由于扩散,从t 到t t +∆时刻这段时间内,通过S 流入Ω的质量为2221(cos cos cos )dSd t ttSu u u M a b c t x y zαβγ+∆∂∂∂=++∂∂∂⎰⎰⎰. 由高斯公式得2222221222()d d d d t ttu u u M a b c x y z t x y z +∆Ω∂∂∂=++∂∂∂⎰⎰⎰⎰. (1) 其中,222,,a b c 分别是沿,,x y z 方向的扩散系数. 由于衰减(例如吸收、代谢等),Ω内的质量减少为22d d d d t ttM k u x y z t +∆Ω=⎰⎰⎰⎰, (2) 其中2k 是衰减系数.由物质不灭定律,在Ω内由于扩散与衰减的合作用,积存于Ω内的质量为12M M -.换一种角度看,Ω内由于深度之变化引起的质量增加为3[(,,,)(,,,)]d d d d d d d . (3)t ttM u x y z t t u x y z t x y zux y z t t Ω+∆Ω=+∆-∂=∂⎰⎰⎰⎰⎰⎰⎰显然312M M M =-,即2222222222d d d d ()d d d d .t ttt ttux y z t t u u u a b c k u x y z t x y z+∆Ω+∆Ω∂∂∂∂∂=++-∂∂∂⎰⎰⎰⎰⎰⎰⎰⎰由,,t t ∆Ω之任意性得2222222222u u u u a b c k u t x y z∂∂∂∂=++-∂∂∂∂ (4) 方程(4)是常系数线性抛物型方程,它就是有衰减的扩散过程的数学模型,对于具体问题,尚需与相应的定解条件(初始条件与边界条件等)匹配才能求得确定情况下的解.§2 Dirac 函数物理学家Dirac 为了物理模型之需要,硬是引入了一个当时颇遭微词的,使得数学与物理学传统密切关系出现裂痕的“怪”函数:0,0,() ()1.,0,x x x dx x δδ+∞-∞≠⎧==⎨∞=⎩⎰ (5)它的背景是清晰的,以一条无穷长的杆子为例,沿杆建立了一维坐标系,点的坐标为x ,杆的线密度是()x ρ,在(,]x -∞段,杆子质量为()m x ,则有d ()(), ()d ().d x m x x x x m x xρρ-∞==⎰. (6)设此无穷长的杆子总质量为1,质量集中在0x x =点,则应有001,,()0,,x x m x x x >⎧=⎨<⎩ 或写成 0()()m x H x x =-,其中()H x 为1,0,()0,0,x H x x >⎧=⎨<⎩ 如果沿用(6)中的算法,则在质量集中分布的这种情形有00,,(),0.x x x x ρ≠⎧=⎨∞=⎩且0()d ()xx x H x x ρ-∞=-⎰,于是得()d 1.x x ρ+∞-∞=⎰. (7)但是,从传统数学观点看,若一个函数除某点处处为零,则不论哪种意义下的积分,都必定为零,(7)式岂能成立!但是,δ函数对于物理学而言是如此之有用,以致物理学家正当地拒绝放弃它. 尽管当时数学家们大都嘲笑这种函数,但P.A.M.Dirac 及其追随者们在物理领域却收获颇丰,Dirac 于1933年获诺贝尔物理奖. 当然Dirac 也意识到()x δ不是一个通常的函数,至于找一种什么办法来阐明()x δ这一符号的合法性,那就是数学家的任务了. 1940年,法国数学家许瓦兹(L.Schwartz )严格证明了应用()x δ的正确性,把δ函数置于坚实的数学基础上;1950年,L. Schwartz 获数学界最高奖Fields 奖.δ函数的重要性质有:1)0()d 1x x x δ+∞-∞-=⎰. (8)2)00()()d ()x x f x x f x δ+∞-∞-=⎰. (9)其中()(,)f x C ∈-∞+∞,即0()x x δ-摘出了()f x 在0x x =的值.3)00()()dH x x x x dxδ-=-. (10)4)()x δ的导数是存在的,不过要到积分号下去理解:00()()(),x x f x dx f x δ+∞-∞''-=-⎰ (11)()()00()()(1)().n n n x x f x dx f x δ+∞-∞-=-⎰(12)事实上,由于0()x x δ-在,+∞-∞处为零,则形式地用分部积分公式000()()()()d ()()d ,x x f x x x f x xx x f x x δδδ+∞+∞-∞-∞+∞-∞'---'=-⎰⎰其中,()(,)nf x C ∈-∞+∞,于是有(11)与(12)公式.5)对于()(,)x C ϕ∈-∞+∞,有000()()()()x x x x x x ϕδϕδ-=-. (13)6)1()() (0)||bx x b b δδ=≠. (14)7)000000(,,)()()()x x y y z z x x y y z z δδδδ---=---. (15)8)付立叶变换00[()].i x y y e λδ--= (16)[()] 1.x δ= (17)11221122[()()][()][()].C x x C x x C x x C x x δδδδ-+-=-+- (18)9)拉普拉斯变换00[(),[() 1.x x x e x δδδ--== (19)11221122[()]()][()[()].C x x C x x C x x C x x δδδδ-+-=-+- (20) 从上面的定义与性质看出,Delta 函数()x δ与一般可微函数还是有重大区别的,我们说它是“广义函数. ”§3 Cauchy 问题的解设扩散源在点000(,,)x y z 处,则此扩散问题满足Cauchy 问题2222222222000, (21)(,,,0)()()(). (22)u u u u a b c k u tx y z u x y z M x x y y z z δδδ⎧∂∂∂∂=++-⎪∂∂∂∂⎨⎪=---⎩对(21)(22)进行付立叶变换,且令123ˆ(,,), (,)[(,,,)]ut u x y z t λλλλλ==, 由于222222123222ˆˆˆ[], [], [],u u u uu u x y zλλλ∂∂∂=-=-=-∂∂∂ 102030000()[(,,,0)][()][()][()] ,i x y z u x y z M x x y y z z Me λλλδδδ-++=---= 故得常微分方程Cauchy 问题1020302222222123()ˆ()0,ˆ(0,).i x y z du a b c k udtu Meλλλλλλλ-++⎧++++=⎪⎨⎪=⎩ 得唯一解2222222123102030()()ˆ(,)a b c k t i x y z ut Me λλλλλλλ-+++-++=. (23)对(23)求逆变换1-,由于2122214[]a xa eλ---=, 2110221240[]()i x e aa ex x λλ----=-, 故得12222000222ˆ(,,,)[]()()()exp 444u x y z t u x x y y z z k t a t b t c t -=⎧⎫---=----⎨⎬⎩⎭2222000222()()().444x x y y z z k t a t b t c t ⎧⎫---=----⎨⎬⎩⎭(24) 如果认为经过了相当长时间后,扩散已经终止,物质分布处于平衡状态,则方程(4)中的0ut∂=∂,于是有线性椭圆型方程的边值问题 22222222220, (,,)(,,)(,,).D u u u a b c k u x y z D xy z u x y z x y z ϕ∂⎧∂∂∂++-=∈⎪∂∂∂⎨⎪=⎩也可以用付立叶变换求解. 当然,根据实际情况,还可以考虑第二边条件(,,)Dux y z n ∂∂=ψ∂或第三边条件[](,,)D uu x y z nαβρ∂∂+=∂等,其中D ∂是区域D 的边界,n 是外法线方向,,αβ是实常数.§4 参数估计在Cauchy 问题(21)(22)的解(23)中,有四个未知的参数,,,a b c k ,它们分别是扩散与衰减过程中的扩散系数与衰减系数的算术平方根. 至于点源的质量与位置000,(,,)M x y z 是已知的.设观测取样为:11112222(,,,), (,,,),,(,,,),n n n n x y z m x y z m x y z m取样时刻为1t =(不然设00, t t t τ=是取样时间,则(21)变成2200t xx yy U t a U t b U =++2200zz t c U t k U -,对τ而言,取样时间为1,而方程形状与(21)一致),把在(,,)i i i x y z 点观测到的物质密度i m 与公式(24)都取对数,令1t =,则2222000222()()()ln (,,,1)ln []444x x y y z z u x y z abc k a b c ---=--+++. (25) 令222000222()()()111,,,,,,444x x y y z z X Y Z a b c αβγ---====-=-=-2ln ln abc k ε=--,则(25)写成 ln (,,,1)W u x y z X Y Z αβγε==+++,(26) 而我们已观测得(,,,)1,2,,i i i i X Y Z W i n =的数据,用三元回归分析方法求出,,,αβγε的估计值如下:ˆˆˆˆ()W X Y Z εαβγ=-++, (27)其中11111111, , , ,n n n nk i i i k k k k W W X X Y Y Z Z n n n n ========∑∑∑∑ˆˆˆ,,αβγ满足方程组 111213102122232031323330ˆˆˆ,,ˆˆˆ,,ˆˆˆ,.l l l l l l l l l l l l αβγαβγαβγ⎧++=⎪⎪++=⎨⎪++=⎪⎩ 其中10201130122211223311112131123211()(), ()(),()(),(), (), (),()(), ()(),()(), n nk k k k k k nk k k nn nk k k k k k nnk k k k k k nk k k l W X W W l Y Y W W l Z Z W W l X X l Y Y l Z Z l X X Y Y l X X Z Z l Y Y Z Z l ==========--=--=--=-=-=-=--=--=--∑∑∑∑∑∑∑∑∑1231133223, , .l l l l l ===由ˆˆˆ,,αβγ可求得222,,a b c 的估计值,即222111ˆˆˆ, , ˆa b cαβγ=-=-=-. 又由于 2ln k abc ε=+- (28) 由(27)式可得ˆε,再把ˆˆˆ,,a b c 代入(28)得 2ˆˆˆˆˆln kabc ε=+- (29)至此得到参数2222,,,a b c k 的估计值2222ˆˆˆˆ,,,a b c k ,把它们代入(24)分别替代2222,,,a b c k ,则得不含未知参数的解(,,,)u x y z t 的近似表达式.§5 竞赛试题分析AMCM-90A 不可用本文的思路与方法加以解决;该试题由东华盛顿大学数学系Yves Nievergelt 提供,要求研究药物在脑中的分布,题文称:“研究脑功能失调的人员欲测试新的药物的效果,例如治疗帕金森症往脑部注射多巴胺(Dopamine )的效果,为了精确估计药物影响到的脑部区域,它们必须估计注射后药物在脑内空间分布区域的大小和形状.“研究数据包括50个圆柱体组织样本的每个样本药物含量的测定值(如图6-1),每个圆柱体长0.76mm ,直径0.66mm ,这些互相平行的圆柱体样本的中心位于网格距为1m m ×0.76×m m ×1mm 的格点上,所以圆柱体互相间在底面上接触,侧面互不接触. 注射是在最高计数的那个圆柱体的中心附近进行的. 自然在圆柱体之间以及由圆柱体样本的覆盖的区域外也有药物.“试估计受到药物影响的区域中药物的分布. ”“一个单位表示一个闪烁微粒的计数,或多巴胺的4.753×10-18克分子量,例如表6-1指出位于后排当中那个圆柱体的含药量是28353个单位. ”后方垂直截面164442 1320 414 188 480 7022 14411 5158 352 2091 23027 28353 13138 681 789 21260 20921 11731 727 213 130337651715453前方垂直截面163 324 432 243166 712 1055 6098 1048 232 2137 15531 19742 4785 330 444 11431 14960 3182 301 29420611036 258188图6-1数学模型只是实际问题的近似,要建立数学模型,一般首先要对所研究的实际问题进行必要和允许的简化与假设,而且,不同的简化与假设,又可能导致不同的数学模型,例如[2]是抛物型方程模型,而[3]则是椭圆方程模型.假设:(1)注射前大脑中的多巴胺含量可以忽略不计.(2)大脑中多巴胺注射液经历着扩散与衰减的过程,且沿,,x y z 三个方向的扩散系数分别是常数,衰减使质量之减少与深度成正比.(3)注射点在后排中央那个圆柱中心,即注射点的坐标000(,,)x y z 已知,注射量有医疗记录可查,是已知的.(4)注射瞬间完成,可视为点源delta 函数. (5)取样也是瞬间完成,取样时间已知为1t =.(6)样本区域与整个大脑相比可以忽略,样本组织远离脑之边界,不受大脑边界面的影响.在以上假设之下,显然可以用本文前面讲过的思路来建模,于是得AMCM-90A 的数学模型为Cauchy 问题(21)(22),解的表达式为(24),且用三元回归分析来估出参数,,,a b c k ,于是可以求得任意位置任意时刻药物的深度.如果所给数据认为是在平衡状态测得的,药物注射进脑后,从高深度处向低深度处扩散,与扩散同时,一部分药物进入脑细胞被吸收固定,扩散系数与吸收系数都是常数,但过一段时间,所有药物都被脑细胞所固定,达到了平衡态. 在这种假设下,[3]给出了下述的分析、建模、求解过程.设(,,,)v x y z t 是t 时刻在(,,)x y z 点处游离的药物浓度,(,,,)w x y z t 是t 时刻(,,)x y z 点处吸收固定的药物浓度,(,,)u x y z 是达到平衡态时(,,)x y z 点处吸收固定的药物浓度. 又设游离药物在各方向上有相同的扩散系数k ,吸收系数为h ,于是有vk v hv t∂=∆-∂. (30)又whv t∂=∂,即吸收速度与游离的浓度成正比,代入(30)得 ()v k ww t h t t∂∂∂=∆-∂∂∂. (31) 对(31)关于t 从0到+∞积分得000t t t k v w w h+∞+∞+∞====∆-. (32)由于最后无游离药物,故(,,,)0v x y z +∞=,又开始时(0)t =无被吸收的药物,故(,,,0)0, (,,,0)0w x y z w x y z =∆=;平衡状态在t =+∞时达到,这时(,,)u x y z = (,,,)w x y z +∞,于是由(32)得(,,,0)ku u v x y z h-∆+=, (33)其中(,,,0)v x y z 是开始时的浓度分布,近似于注射点的点源脉冲函数. 把此注射点取为坐标原点(0,0,0),则(,,,0)(,,),v x y z L x y z L δ=是注射量,于是2k h σ⎛⎫= ⎪⎝⎭记2(,,)u u L x y z σδ-∆+=, (34)作付立叶变换得22222222ˆˆ(),ˆ,1()s u u L Lus σξησξη+++==+++ 再作反变换得u σ-=-, (35)其中C 是可计算常数.如果考虑各向不同性,设,,x y z 方向上扩散系数分别为222,,a b c ,注射点在000(,,)x y z ,则222222000222()()()u u u a b c u L x x y y z z x y z δδδ⎛⎫∂∂∂-+++=--- ⎪∂∂∂⎝⎭, 于是解为(,,)u x y z =exp 1⎧⎪-⎨⎪⎩,(36) (36)中的D 可计算常数.用前面类似的方法可以进行参数估计.在建模过程中,点源函数的使用显然与实况有差别;尤其是认为扩散系数与吸收系数都是常数,对于人脑这种有复杂结构的区域,这种假设与实际不会完全符合;夜间与白天(睡与醒)对这些系数有无影响?脑中各点这些系数是否有变?除时间位置应考虑外,可能还与药液浓度有关. 如此看来,脑内药液分布的数学模型很可能不是常系数线性偏微分方程,而是函数系数的线性微分方程甚至是非线性偏微分方程. 这时,其解不再能用封闭公式来表达,求解过程会变得极为复杂,所以也可以考虑是否试用其他数学模型来解,例如在平衡态的假设下,用回归分析方法建立药液的模拟分布(,,)u f x y z =.对一个实际问题,其数学模型未必唯一,各模型间孰优孰劣,没有一般的判别法,须经实践来检验.参 考 文 献[1]叶其孝,大学生数学建模竞赛辅导教材,湖南教育出版社,1993.[2]Christopher, R. Malone, Gian Pauletto, James, I. Zoellick, Distribution of Dopamine in the Brain, The Journal of Under graduate Mathematics, and its Applications, vol. 12(1991), Special Issue: The 1991 Mathematical Contest in Modeling, pp. 211-223.[3]孙晓东,荆秦,梁俊,脑中药物分布的数学模型,数学的实践与认识,1991年No. 4,63-69. [4]中国科学院数理统计组,常用数理统计方法,科学出版社,19784.。