下载文档原格式
Mm l{E考i1E：号：由白（在此卷上答题元效）2023年江西省高三教学质量监测卷理科数学说明：l.全卷满分150分．考试时间120分钟．2.会卷分为试题卷和答是是卡．答案妥求写在答题字上．不得在试卷上作o－否则不给分．一、选择题：本题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合A=(.r E R1x2<4l.B={.i:13’＜9｝.贝I]A.A门B=BB.A U B=(.r l O<.r<2fc.八门日＝A D.A U B=R2.已知主L数＝满足Cl+i>::=2-i(i为m：数单位）·则复数主的缺等于A俨’ B.�飞．在lo D.一23若O＜α＜π则子＜出以1”是W训”的A.充要条件c.必婆不充分条件 B.充分不必要条件D.既不充分也不必要条件4.在某校随机抽取了100名学生．调查他们课后完成作业的时间，根据调查结果绘栩如下频率分布直方图．根据此频率分布直方回．下y1J结论中正确的是组距o.sI.…0.4,.03, .....0.1，…O I 1.5 2 2.5 3 3.5 4 4.5 5完成作业时间／时A.估计该校有40%的学生在2小时｜人j元成i束后作业B.铀取的学生中有10人不能在4小时内完成以后作、I�.C.t自取学生课后完成作业时间的100个数据的中位数伍l丘1'111( 2.2. 5）内0.抽取学生课后完成作业时间的100个荣立据的众数一定（E f天fF-i l(2.2. 5）内5.已知抛物线x'=4y的焦点为f,,(i,M在抛物线上，H I M F l=3，贝11lJ. M到y铀的�li肉J-1A.48. 2/3 C.2J2 D. 36.函数刀。
＝sin2.r-/3cos 2.1寸l{.E隧I同［O.rr]Iλl的＇.）！，：点个败是A.28.3 c.4D.57. （［炎热的反天里．人们都喜欢在饮品里放冰块．如l 民I �主一个问脚杯．它的细11盹I 归是JE 王fr l %.容拇内有－定虫的水．扣在高脚杯l均放入一个球形冰块后．冰块没有开始融化前水面所在的平而价好经过冰块的球心。
基于毕达哥拉斯树的图像分割算法研究图像分割算法一直是计算机视觉领域中一个十分重要的研究方向。
毕达哥拉斯树（Pythagorean Tree）是一种自相似的图形，因此被很多学者用于图像分割领域。
本文将介绍基于毕达哥拉斯树的图像分割算法的研究进展。
一、毕达哥拉斯树的定义和应用毕达哥拉斯树是一种自相似的图形，也称作四分树（Quadtree）。
可以通过一个正方形递归地分割成4个相等的正方形，并在中心位置插入一个正方形。
这种简单的分形结构在计算机图形学、计算机视觉等领域都有广泛的应用。
在图像分割领域，毕达哥拉斯树被用于将一个图像分割成许多大小相等的矩形。
这种方法比传统的基于像素值或者区域增长的分割方法更加灵活，可以很好的适应不同的数据分布和图像特征。
二、基于毕达哥拉斯树的图像分割算法在毕达哥拉斯树上进行图像分割的基本流程如下：1、对于一幅给定的图像，将其转换为灰度图像，并在像素值较大的位置插入分割点。
例如，一幅显示了山地景色的图像，可以在山峰的顶端插入一个分割点，然后将图像分割成两部分。
2、对每个分割矩形计算特征值，例如均值、方差等。
3、通过选取一个合适的阈值，将特征值较大的矩形继续分割下去，已经达到一定的阈值的矩形则不再分割。
4、直到所有矩形都不能再分割为止，将每个矩形标记成前景或背景。
5、对标记矩形进行后处理，比如再次合并相邻的矩形，统一标记为前景或背景等。
三、基于毕达哥拉斯树的图像分割算法的优缺点毕达哥拉斯树分割算法常被用于大规模图像分割，因为它能够高效地处理大量的数据。
其优点主要有：1、算法非常可靠，对于许多种图像都能够得到很好的分割效果。
2、因为这种算法不依赖于传统的像素值分割方法，因此对图像的亮度、颜色、对比度等参数变化更具有鲁棒性。
但是它也有一些缺点：1、该算法依赖于插入分割点的位置，而选择不合适的位置可能导致分割结果不够准确。
2、由于算法本身的特点，它不能处理非矩形的图像。
四、总结毕达哥拉斯树是一种简单而有效的图形分割工具，在计算机视觉领域得到了广泛的应用。
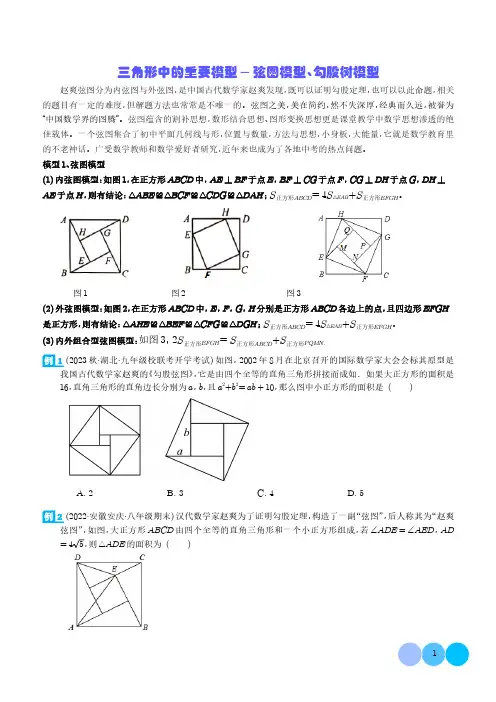
三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图，是中国古代数学家赵爽发现，既可以证明勾股定理，也可以以此命题，相关的题目有一定的难度，但解题方法也常常是不唯一的。
弦图之美，美在简约，然不失深厚，经典而久远，被誉为“中国数学界的图腾”。
弦图蕴含的割补思想，数形结合思想、图形变换思想更是课堂教学中数学思想渗透的绝佳载体。
一个弦图集合了初中平面几何线与形，位置与数量，方法与思想，小身板，大能量，它就是数学教育里的不老神话。
广受数学教师和数学爱好者研究，近年来也成为了各地中考的热点问题。
模型1、弦图模型(1)内弦图模型：如图1，在正方形ABCD中，AE⊥BF于点E，BF⊥CG于点F，CG⊥DH于点G，DH⊥AE于点H，则有结论：△ABE≌△BCF≌△CDG≌△DAH；S正方形ABCD =4S△EAB+S正方形EFGH。
图1图2图3(2)外弦图模型：如图2，在正方形ABCD中，E，F，G，H分别是正方形ABCD各边上的点，且四边形EFGH是正方形，则有结论：△AHE≌△BEF≌△CFG≌△DGH；S正方形ABCD =4S△EAB+S正方形EFGH。
(3)内外组合型弦图模型：如图3，2S正方形EFGH =S正方形ABCD+S正方形PQMN.1(2023秋·湖北·九年级校联考开学考试)如图，2002年8月在北京召开的国际数学家大会会标其原型是我国古代数学家赵爽的《勾股弦图》，它是由四个全等的直角三角形拼接而成如．如果大正方形的面积是16，直角三角形的直角边长分别为a，b，且a2+b2=ab+10，那么图中小正方形的面积是()A.2B.3C.4D.52(2022·安徽安庆·八年级期末)汉代数学家赵爽为了证明勾股定理，构造了一副“弦图”，后人称其为“赵爽弦图”，如图，大正方形ABCD由四个全等的直角三角形和一个小正方形组成，若∠ADE=∠AED，AD =45，则△ADE的面积为()A.24B.6C.25D.2103(2023·山西八年级期末)如图，图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的，若AC=6,BC=5，将四个直角三角形中的边长为6的直角边分别向外延长一倍，得到图2所示的“数学风车”，则这个风车的外围周长是()A.24B.52C.61D.764(2022·杭州九年级月考)我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”．如图是由弦图变化得到，它是用八个全等的直角三角形拼接而成，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3．若S1+S2+S3=12，则下列关于S1、S2、S3的说法正确的是()A.S1=2B.S2=3C.S3=6D.S1+S3=85(2023·广东·九年级专题练习)公元三世纪，我国汉代数学家赵爽在注解《周髀算经》题时给出了“赵爽弦图”．将两个“赵爽弦图”(如图1)中的两个正方形和八个直角三角形按图2方式摆放围成正方形MNPQ，记空隙处正方形ABCD，正方形EFGH的面积分别为S1，S2S1>S2，则下列四个判断：①S1+S2=14S四边形MNPQ②DG=2AF；③若∠EMH=30°，则S1=3S2；④若点A是线段GF的中点，则3S1=4S2，其中正确的序号是模型2. 勾股树模型6(2022·福建·八年级期末)如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，如果正方形A、B、C、D的边长分别为3，4，1，2．则最大的正方形E的面积是．7(2022·浙江·乐清市八年级期中)如图，在四边形ABCD中，∠B=∠D=90°，分别以AB，BC，CD，DA为一边向外作正方形甲、乙、丙、丁，若用S甲，S乙，S丙，S丁来表示它们的面积，那么下列结论正确的是()A.S 甲=S 丁B.S 乙=S 丙C.S 甲-S 乙=S 丁-S 丙D.S 甲+S 乙=S 丙+S 丁8(2022·河南八年级期末)如图，正方形ABCD 的边长为2，其面积标记为S 1，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S 2，⋯按照此规律继续下去，则S 9的值为()A.126B.127C.128D.1299(2023春·山东菏泽·八年级校考阶段练习)“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，如果第一个正方形面积为1，则第2023代勾股树中所有正方形的面积为．10(2023·浙江八年级期中)如图，以Rt △ABC 的三边为直径，分别向外作半圆，构成的两个月牙形面积分别为S 1、S 2，Rt △ABC 的面积S 3．若S 1=4，S 2=8，则S 3的值为．11(2022春·浙江温州·九年级校考开学考试)如图1，是数学家毕达哥拉斯根据勾股定理所画的“勾股树”．如图2，在Rt △ABC 中，∠BAC =90°，以其三边为边分别向外作正方形，延长EC ，DB 分别交GF ，AH 于点N ，K ，连接KN 交AG 于点M ，若S 1S 2=916，则tan ∠ACB 为()A.12B.23C.34D.51212(2023·贵州遵义·统考二模)如图1，毕达哥拉斯树，也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形．在图2中，∠ACB =90°，分别以Rt △ABC 的三条边为边向外作正方形，连接BE ，DG 、BE ，交AC 于点Q ，若∠BAC =30°，BC =2，则四边形EQGD 的面积是．13(2023秋·浙江·八年级专题练习)【背景阅读】勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了验证勾股定理，创制了一幅“弦图”(如图1)，后人称之为“赵爽弦图”，流传至今．【实践操作】(1)请叙述勾股定理；(2)验证勾股定理，人们已经找到了400多种方法，请从下列几种常见的验证方法中任选一种来验证该定理：(以下图形均满足验证勾股定理所需的条件)【探索发现】(3)如图4、5、6，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足S1+S2=S3的有个；(4)如图7所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案(图中阴影部分)的面积分别为S1、S2，直角三角形面积为S3，请判断S1、S2、S3的关系并说明理由．课后专项训练1(2022·云南九年级一模)如图是按照一定规律“生长”的“勾股树”：经观察可以发现：图(1)中共有3个正方形，图(2)在图(1)的基础上增加了4个正方形，图(3)在图(2)的基础上增加了8个正方形，⋯⋯，照此规律“生长”下去，图(6)应在图(5)的基础上增加的正方形的个数是()A.12B.32C.64D.1282(2022·浙江初三期中)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若图2中阴影部分的面积为2，且AB+AC=8，则BC的长为()图1图2A.42B.6C.254D.1323(2023·浙江·杭州八年级阶段练习)如图，Rt△ABC中，∠BAC=90°，分别以△ABC的三边为边作正方形ABDE，正方形BCFG，正方形ACHI，AI交CF于点J．三个正方形没有重叠的部分为阴影部分，设四边形BGFJ的面积为S1，四边形CHIJ的面积为S2，若S1-S2=12，S△ABC=4，则正方形BCFG的面积为()A.16B.18C.20D.224(2023春·湖北黄冈·八年级统考期中)“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则EF 的长为()A.9B.92C.32D.35(2022·四川成都·模拟预测)勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2．则图2中阴影部分面积等于()A.直角三角形的面积B.最大正方形的面积C.最大正方形与直角三角形的面积和D.较小两个正方形重叠部分的面积6(2023春·广东潮州·九年级校考期末)我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理，标志着中国古代的数学成就．如图所示的“弦图”，是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形．直角三角形的斜边长为13，一条直角边长为12，则小正方形ABCD 的面积的大小为()A.144B.100C.49D.257(2023春·湖北武汉·八年级统考期末)大约公元222年我国汉代数学家赵爽为《周髀算经》一书作序时介绍了“勾股圆方图”，亦称“赵爽弦图”，如图，四个全等的直角三角形拼成大正方形ABCD ，中空的部分是小正方形EFGH ，连接EG ，BD 相交于点O ，BD 与HC 相交于点P ，若GO =GP ，则直角三角形的边CG 与BG 之比是()A.12B.25C.2-1D.3-28(2023春·江苏泰州·七年级统考期末)大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了“勾股圆方图”，亦称“赵爽弦图”(如图1)．某数学兴趣小组类比“赵爽弦图”构造出图2：△ABC 为等边三角形，AD 、BE 、CF 围成的△DEF 也是等边三角形．已知点D 、E 、F 分别是BE 、CF 、AD 的中点，若△ABC 的面积为14，则△DEF 的面积是()A.1B.2C.3D.49(2023·河北石家庄·校考二模)如图1，毕达哥拉斯树，也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形．在图2中，∠ACB=90°，分别以Rt△ABC的三条边为边向外作正方形，连接BE，DG，BE交AC于点Q．若∠BAC=30°，BC=2，则四边形EQGD的面积是()B.23C.53+3D.3A.53+3210(2023·江苏扬州·统考中考真题)我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成．如图，直角三角形的直角边长为a、b，斜边长为c，若b-a=4，c=20，则每个直角三角形的面积为．11(2022秋·四川成都·八年级校考期中)“勾股图”有着悠久的历史，它曾引起很多人的兴趣．1955年希腊发行了以“勾股图”为背景的邮票(如图1)，欧几里得在《几何原本》中曾对该图做了深入研究．如图2，在△ABC中，∠ACB=90°，分别以△ABC的三条边为边向外作正方形，连接EB,CM,DG,CM分别与AB,BE相交于点P,Q．若∠ABE=30°，则DGQM的值为.12(2022春·安徽合肥·八年级合肥市第四十二中学校考期中)如图①，在Rt△ACB中∠ACB=90°，分别以AC、BC、AB为边，向形外作等边三角形，所得的等边三角形的面积分别为S1、S2、S3，请解答以下问题：(1)S1、S2、S3满足的数量关系是．(2)现将△ABF向上翻折，如图②，若阴影部分的S甲=6、S乙=5、S丙=4，则S△ACB=．13(2023·湖北孝感·统考三模)“勾股树”是以正方形一边为斜边向外作直角三角形，再以直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第五代勾股树中正方形的个数为．14(2022·山东临沂·统考二模)中国古代的数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位尤其是三国时期的数学家赵爽，不仅最早对勾股定理进行了证明，而且创制了“勾股圆方图”，开创了“以形证数”的思想方法．在图中，小正方形ABCD的面积为1，如果把它的各边分别延长一倍得到正方形A1B1C1D1(如图1)，则正方形的面积为；再把正方形A1B1C1D1的各边分别延长一倍得到正方形A2B2C2D2(如图2)，如此进行下去，得到的正方形A n B n C n D n的面积为(用含n的式子表示，n为正整数)．15(2023·浙江台州·八年级校考期中)如图1，是一个封闭的勾股水箱，其中Ⅰ，Ⅱ，Ⅲ部分是可盛水的正方形，且相互联通，已知∠ACB=90°，AC=6，BC=8，开始时Ⅲ刚好盛满水，而Ⅰ，Ⅱ无水．(1)如图2摆放时，Ⅰ刚好盛满水，而Ⅱ无水，则Ⅲ中有水部分的面积为；(2)如图3摆放时，水面刚好经过Ⅲ的中心O(正方形两条对角线的交点)，则Ⅱ中有水部分的面积为．16(2023·湖北黄冈·统考中考真题)如图，是我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形组成的一个大正方形．设图中AF=a，DF=b，连接AE,BE，若△ADE与△BEH的面积相等，则b2a2+a2b2=．17(2023·江苏徐州·统考二模)如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH．连接AC，若AG平分∠CAD，且正方形EFGH的面积为2，则正方形ABCD的面积为．18(2023·陕西渭南·统考二模)魏朝时期，刘徽利用下图通过“以盈补虚，出入相补”的方法，即“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”证明了勾股定理．如图，四边形ABCD、四边形BFGH和四边形AFMN都是正方形，BF交CD于E，若DE=2，CE=4，则BF的长为．19(2022·宁夏吴忠·统考一模)2002年8月，在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1)，且大正方形的面积是17，直角三角形的较短直角边为a，较长直角边为b．如果将四个全等的直角三角形按如图2的形式摆放，则图2中最大的正方形的面积为31．试求图1中小正方形的面积是为．20(2023·山东济宁·统考二模)勾股定理是人类最伟大的十个科学发现之一，西方国家称之为毕达哥拉斯定理．在我国古书《周髀算经》中就有“若勾三，股四，则弦五”的记载，我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”(如图1)，后人称之为“赵爽弦图”，流传至今．勾股定理内容为：如果直角三角形的两条直角边分别为a，b，斜边为c，那么a2+b2=c2．(1)如图2、3、4，以直角三角形的三边为边或直径，分别向外部作正方形、半圆、等边三角形，这三个图形中面积关系满足S1+S2=S3的有个；(2)如图5所示，分别以直角三角形三边为直径作半圆，设图中两个月形图案(图中阴影部分)的面积分别为S1，S2，直角三角形面积为S3，请判断S1，S2，S3的关系并证明；(3)如果以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程就可以得到如图6所示的“勾股树”．在如图7所示的“勾股树”的某部分图形中，设大正方形M的边长为定值m，四个小正方形A，B，C，D的边长分别为a，b，c，d，已知∠1=∠2=∠3=∠α，则当∠α变化时，回答下列问题：(结果可用含m的式子表示)①a2+b2+c2+d2=；②b与c的关系为，a与d的关系为．21(2022·湖南·八年级课时练习)如图①，美丽的弦图，蕴含着四个全等的直角三角形．(1)弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为a，较短的直角边为b，斜边长为c，结合图①，试验证勾股定理．(2)如图②，将这四个直角三角形紧密地拼接，形成飞镖状，已知外围轮廓(粗线)的周长24，OC=3，求该飞镖状图案的面积．(3)如图③，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1,S2,S3，若S1+S2+S3=40，求S2．22(2023·广东深圳·校联考三模)中华文明源远流长，如图①是汉代数学家赵爽在注解《周髀算经》时给出的图形，人们称之为赵爽弦图，被誉为中国数学界的图腾．2002年北京国际数学家大会依据赵爽弦图制作了会标，该图有4个全等的直角三角形围成几个大正方形和中间一个小正方形，巧妙的证明了勾股定理．问题发现：如图①，若直角三角形的直角边BC=3，斜边AB=5，则中间小正方形的边长CD=，连接BD，△ABD的面积为．知识迁移：如图②，P是正方形ABCD内一点，连接PA，PB，PC，当∠BPC=90°，BP=10时，△PAB的面积为．拓展延伸：如图③，已知∠MBN=90°，以点B为圆心，适当长为半径画弧，交射线BM，BN分别于A，C两点．(1)已知D为线段AB上一个动点，连接CD，过点B作BE⊥CD，垂足为点E；在CE上取一点F，使EF=BE；过点F作GF⊥CD交BC于点G，试判断三条线段BE，DE，GF之间的数量关系，并说明理由．(2)在(1)的条件下，若D为射线BM上一个动点，F为射线EC上一点；当AB=10，CF=2时，直接写出线段DE的长．三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图，是中国古代数学家赵爽发现，既可以证明勾股定理，也可以以此命题，相关的题目有一定的难度，但解题方法也常常是不唯一的。
18．2特殊的平行四边形18．2.1矩形第1课时矩形的性质1．理解并掌握矩形的性质定理及推论；(重点)2．会用矩形的性质定理及推论进行推导证明；(重点)3．会综合运用矩形的性质定理、推论以及特殊三角形的性质进行证明与计算．(难点)一、情境导入如图，用四段木条做一个平行四边形的活动木框，将其直立在地面上轻轻地推动点D，你会发现什么？可以发现，角的大小改变了，但不管如何，它仍然保持平行四边形的形状．我们若改变平行四边形的内角，使其一个内角恰好为直角，就得到一种特殊的平行四边形，也就是我们早已熟悉的长方形，即矩形，如图所示．二、合作探究探究点一：矩形的性质【类型一】运用矩形的性质求线段或角在矩形ABCD中，O是BC的中点，∠AOD＝90°，矩形ABCD的周长为24cm，则AB长为()A．1cm B．2cm C．2.5cm D．4cm解析：在矩形ABCD中，O是BC的中点，∠AOD＝90°.根据矩形的性质得到△ABO≌△OCD，则OA＝OD，∠DAO＝45°，所以∠BOA＝∠BAO＝45°，即BC＝2AB.由矩形ABCD的周长为24cm，得2AB ＋4AB＝24cm，解得AB＝4cm.故选D.方法总结：解题时矩形具有平行四边形的性质，又具有自己的特性，要注意运用矩形具备而一般平行四边形不具备的性质．【类型二】运用矩形的性质解决有关面积问题如图，矩形ABCD的对角线的交点为O，EF过点O且分别交AB，CD于点E，F，则图中阴影部分的面积是矩形ABCD 的面积的()A.15 B.14 C.13 D.310解析：∵在矩形ABCD中，AB∥CD，OB＝OD，∴∠ABO＝∠CDO.在△BOE和△DOF中，⎩⎪⎨⎪⎧∠ABO＝∠CDO，OB＝OD，∠BOE＝∠DOF，∴△BOE≌△DOF(ASA)，∴S△BOE＝S△DOF，∴S 阴影＝S △AOB ＝14S 矩形ABCD .故选B.方法总结：运用矩形的性质，通过证明全等三角形进行转化，将求不规则图形的面积转化为求简单图形面积是解题的关键．【类型三】 运用矩形的性质证明线段相等如图，在矩形ABCD 中，以顶点B 为圆心、边BC 长为半径作弧，交AD 边于点E ，连接BE ，过C 点作CF ⊥BE 于F .求证：BF ＝AE .解析：利用矩形的性质得出AD ∥BC ，∠A ＝90°，再利用全等三角形的判定得出△BFC ≌△EAB ，进而得出答案．证明：在矩形ABCD 中，AD ∥BC ，∠A ＝90°，∴∠AEB ＝∠FBC .∵CF ⊥BE ，∴∠BFC ＝∠A ＝90°.由作图可知，BC ＝BE .在△BFC 和△EAB 中，⎩⎪⎨⎪⎧∠A ＝∠CFB ，∠AEB ＝∠FBC ，EB ＝BC ，∴△BFC ≌△EAB (AAS)，∴BF ＝AE .方法总结：涉及与矩形性质有关的线段的证明，可运用题设条件结合三角形全等进行证明，一般是将两条线段转化到一对全等三角形中进行证明．【类型四】 运用矩形的性质证明角相等如图，在矩形ABCD 中，E 、F 分别是边BC 、AB 上的点，且EF ＝ED ，EF ⊥ED .求证：AE 平分∠BAD .解析：要证AE 平分∠BAD ，可转化为△ABE 为等腰直角三角形，得AB ＝BE .又AB ＝CD ，再将它们分别转化为两全等三角形的两对应边，根据全等三角形的判定和矩形的性质，即可求证．证明：∵四边形ABCD 是矩形，∴∠B ＝∠C ＝∠BAD ＝90°，AB ＝CD ，∴∠BEF ＋∠BFE ＝90°.∵EF ⊥ED ，∴∠BEF ＋∠CED ＝90°.∴∠BFE ＝∠CED ，∴∠BEF ＝∠EDC .在△EBF 与△DCE 中，⎩⎪⎨⎪⎧∠BFE ＝∠CED ，EF ＝ED ，∠BEF ＝∠EDC ，∴△EBF ≌△DCE (ASA)．∴BE ＝CD .∴BE ＝AB ，∴∠BAE ＝∠BEA ＝45°，∴∠EAD ＝45°，∴∠BAE ＝∠EAD ，∴AE 平分∠BAD .方法总结：矩形的问题可以转化到直角三角形或等腰三角形中去解决．探究点二：直角三角形斜边上的中线的性质如图，在△ABC 中，AD 是高，E 、F 分别是AB 、AC 的中点．(1)若AB ＝10，AC ＝8，求四边形AEDF 的周长；(2)求证：EF 垂直平分AD .解析：(1)根据“直角三角形斜边上的中线等于斜边的一半”可得DE ＝AE ＝12AB ，DF ＝AF ＝12AC ，再根据四边形的周长的公式计算即可得解；(2)根据“到线段两端点距离相等的点在线段的垂直平分线上”证明即可．(1)解：∵AD 是△ABC 的高，E 、F 分别是AB 、AC 的中点，∴DE ＝AE ＝12AB ＝12×10＝5，DF ＝AF ＝12AC ＝12×8＝4，∴四边形AEDF 的周长＝AE ＋DE ＋DF ＋AF ＝5＋5＋4＋4＝18；(2)证明：∵DE ＝AE ，DF ＝AF ，∴E 、F 在线段AD 的垂直平分线上，∴EF 垂直平分AD .方法总结：当已知条件含有线段的中点、直角三角形的条件时，可联想直角三角形斜边上的中线的性质进行求解．三、板书设计 1．矩形的性质矩形的四个角都是直角；矩形的对角线相等．2．直角三角形斜边上的中线的性质 直角三角形斜边上的中线等于斜边的一半．通过多媒体演示知识的探究过程，让学生在体验、实践的过程中有更直观地认识，扩大认知结构，发展能力，更好地理解平行四边形与矩形之间的从属关系和内在联系，使课堂教学真正落实到学生的发展上．17．1 勾股定理第1课时 勾股定理1．经历探索及验证勾股定理的过程，体会数形结合的思想；(重点) 2．掌握勾股定理，并运用它解决简单的计算题；(重点) 3．了解利用拼图验证勾股定理的方法．(难点) 一、情境导入如图所示的图形像一棵枝叶茂盛、姿态优美的树，这就是著名的毕达哥拉斯树，它由若干个图形组成，而每个图形的基本元素是三个正方形和一个直角三角形．各组图形大小不一，但形状一致，结构奇巧．你能说说其中的奥秘吗？二、合作探究探究点一：勾股定理【类型一】 直接运用勾股定理如图，在△ABC 中，∠ACB ＝90°，AB ＝13cm ，BC ＝5cm ，CD ⊥AB 于D ，求：(1)AC 的长；(2)S △ABC； (3)CD 的长． 解析：(1)由于在△ABC 中，∠ACB ＝90°，AB ＝13cm ，BC ＝5cm ，根据勾股定理即可求出AC 的长；(2)直接利用三角形的面积公式即可求出S △ABC ；(3)根据面积公式得到CD ·AB ＝BC ·AC 即可求出CD .解：(1)∵在△ABC 中，∠ACB ＝90°，AB ＝13cm ，BC ＝5cm ，∴AC ＝AB 2－BC 2＝12cm ；(2)S △ABC ＝12CB ·AC ＝12×5×12＝30(cm 2)；(3)∵S △ABC ＝12AC ·BC ＝12CD ·AB ，∴CD＝AC ·BC AB ＝6013cm. 方法总结：解答此类问题，一般是先利用勾股定理求出第三边，然后利用两种方法表示出同一个直角三角形的面积，然后根据面积相等得出一个方程，再解这个方程即可．【类型二】 分类讨论思想在勾股定理中的应用在△ABC 中，AB ＝15，AC ＝13，BC 边上的高AD ＝12，试求△ABC 的周长．解析：本题应分△ABC 为锐角三角形和钝角三角形两种情况进行讨论．解：此题应分两种情况说明：(1)当△ABC 为锐角三角形时，如图①所示．在Rt △ABD 中，BD ＝AB 2－AD 2＝152－122＝9.在Rt △ACD 中，CD ＝AC 2－AD 2＝132－122＝5，∴BC ＝5＋9＝14，∴△ABC 的周长为15＋13＋14＝42；(2)当△ABC 为钝角三角形时，如图②所示．在Rt △ABD 中，BD ＝AB 2－AD 2＝152－122＝9.在Rt △ACD 中，CD ＝AC 2－AD 2＝132－122＝5，∴BC ＝9－5＝4，∴△ABC 的周长为15＋13＋4＝32.∴当△ABC 为锐角三角形时，△ABC 的周长为42；当△ABC 为钝角三角形时，△ABC 的周长为32.方法总结：解题时要考虑全面，对于存在的可能情况，可作出相应的图形，判断是否符合题意．【类型三】 勾股定理的证明探索与研究： 方法1：如图：对任意的符合条件的直角三角形ABC 绕其顶点A 旋转90°得直角三角形AED ，所以∠BAE ＝90°，且四边形ACFD 是一个正方形，它的面积和四边形ABFE 的面积相等，而四边形ABFE 的面积等于Rt △BAE 和Rt △BFE 的面积之和．根据图示写出证明勾股定理的过程；方法2：如图：该图形是由任意的符合条件的两个全等的Rt △BEA 和Rt △ACD 拼成的，你能根据图示再写出一种证明勾股定理的方法吗？解析：方法1：根据四边形ABFE 面积等于Rt △BAE 和Rt △BFE 的面积之和进行解答；方法2：根据△ABC 和Rt △ACD 的面积之和等于Rt △ABD 和△BCD 的面积之和解答．解：方法1：S 正方形ACFD ＝S 四边形ABFE ＝S △BAE ＋S △BFE ，即b 2＝12c 2＋12(b ＋a )(b －a )，整理得2b 2＝c 2＋b 2－a 2，∴a 2＋b 2＝c 2；方法2：此图也可以看成Rt △BEA 绕其直角顶点E 顺时针旋转90°，再向下平移得到．∵S 四边形ABCD ＝S △ABC ＋S △ACD ，S 四边形ABCD ＝S △ABD ＋S △BCD ，∴S △ABC ＋S △ACD ＝S △ABD ＋S △BCD ，即12b 2＋12ab ＝12c 2＋12a (b －a )，整理得b 2＋ab ＝c 2＋a (b －a )，b 2＋ab ＝c 2＋ab －a 2，∴a2＋b 2＝c 2.方法总结：证明勾股定理时，用几个全等的直角三角形拼成一个规则的图形，然后利用大图形的面积等于几个小图形的面积和化简整理证明勾股定理．探究点二：勾股定理与图形的面积如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A 、B 、C 、D 的面积分别为2，5，1，2.则最大的正方形E 的面积是________．解析：根据勾股定理的几何意义，可得正方形A 、B 的面积和为S 1，正方形C 、D 的面积和为S 2，S 1＋S 2＝S 3，即S 3＝2＋5＋1＋2＝10.故答案为10.方法总结：能够发现正方形A 、B 、C 、D 的边长正好是两个直角三角形的四条直角边，根据勾股定理最终能够证明正方形A 、B 、C 、D 的面积和即是最大正方形的面积．三、板书设计 1．勾股定理如果直角三角形的两条直角边长分别为a ，b ，斜边长为c ，那么a 2＋b 2＝c 2.2．勾股定理的证明“赵爽弦图”、“刘徽青朱出入图”、“詹姆斯·加菲尔德拼图”、“毕达哥拉斯图”．3．勾股定理与图形的面积课堂教学中，要注意调动学生的积极性．让学生满怀激情地投入到学习中，提高课堂效率．勾股定理的验证既是本节课的重点，也是本节课的难点，为了突破这一难点，设计一些拼图活动，并自制精巧的课件让学生从形上感知，再层层设问，从面积(数)入手，师生共同探究突破本节课的难点．。
，勾股定理在西方被称为毕达哥拉斯定理，相传是古希腊数学家兼哲学家毕达哥拉斯（Pythagoras，公元前572?～公元前497?）于公元前550年首先发现的。
中国最早的一部数学著作——《周髀算经》里有关勾股定理的记载，比毕达哥拉斯要早了五百多年。
在稍后一点的《九章算术》一书中（约在公元50至100年间）勾股定理得到了更加规范的一般性表达。
中国古代的数学家们不仅很早就发现并应用勾股定理，而且很早就尝试对勾股定理作理论的证明。
最早对勾股定理进行证明的，是三国时期吴国的数学家赵爽。
赵爽创制了一幅“勾股圆方图”，用形数结合得到方法，给出了勾股定理的详细证明（右图）。
赵爽的这个证明可谓别具匠心，极富创新意识。
他用几何图形的截、割、拼、补来证明代数式之间的恒等关系，既具严密性，又具直观性，为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范。
以后的数学家大多继承了这一风格并且有发展，只是具体图形的分合移补略有不同而已。
例如稍后一点的刘徽在证明勾股定理时也是用以形证数的方法，中国古代数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位。
尤其是其中体现出来的“形数统一”的思想方法，更具有科学创新的重大意义。
在1876年一个周末的傍晚，在美国华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德。
他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨。
由于好奇心驱使伽菲尔德循声向两个小孩走去，想搞清楚两个小孩到底在干什么。
只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形。
于是伽菲尔德便问他们在干什么？只见那个小男孩头也不抬地说：“请问先生，如果直角三角形的两条直角边分别为3和4，那么斜边长为多少呢？”伽菲尔德答到：“是5呀。
”小男孩又问道：“如果两条直角边分别为5和7，那么这个直角三角形的斜边长又是多少？”伽菲尔德不加思索地回答到：“那斜边的平方一定等于5的平方加上7的平方。
毕达哥拉斯树★利用几何画板的测量、计算工具，验证勾股定理★利用各类几何图形证明勾股定理你知道毕达哥拉斯树吗？在古希腊数学家之中，毕达哥拉斯是最为人们所熟悉、出类拔萃的大数学家.毕达哥拉斯在西方首次证明了“毕达哥拉斯定理”.在当时的西方引起了轰动，并为此举行了一个“百牛大祭”以表庆贺.请你观察课件（附件06—1），使动态变静止，选取其中的一部分进行观察，毕达哥拉斯树应用的原理是问题一请你选择几何画板中的测量和计算功能验证勾股定理.操作（1）画一任意直角三角形（2）分别度量直角三角形三边长（3）计算a ²，b ²，c ²的值（4）拖动任一顶点改变直角三角形的形状，验证a ²+b ²=c ²问题二见课件（附件06—2）请你在下面给出的图形中适当选取一些图形来验证勾股定理a ²+b ²=c ²操作方法一、取边长为c 的正方形和四个直角三角形拼成一大正方形请你用其他方法也来拼一个。
问题一你知道伽菲尔德证法吗？这位美国第20任总统利用梯形证明了勾股定理a²+b²=c²，请你尝试一下，相信你一定行！问题二见课件（附件06—3）你能理解吗？结论：这个证明的关键是问题一你能利用圆的面积公式设计另一种图形来验明勾股定理吗？问题二1、公元前300年，古希腊数学家帕普斯证明了勾股定理的一个有趣的变形，他将直角三角形三边上的正方形改成平行四边形，请你根据以下的作图方法来画出图形作图方法：对于Rt△ABC，（1）分别以两直角边AB、AC为边，作两个平行四边形；（2）分别延长两个平行四边形中平行于直角边的两边，它们相交于点P；（3）作射线P A，与BC相交于点P，再截取RQ=P A；（4）以BC为一边作平行四边形，使另一组对边平行且等于RQ.结论:斜边上的平行四边形面积等于两条直角边上的平行四边形面积的和.2、你能尝试证明它是真命题吗？。
生活中的趣味数学智慧树知到课后章节答案2023年下石河子大学第一章测试1.海王星的发现 , 又一次成功地证明了以运动定律和万有引力定律为基础的牛顿宇宙力学模型的合理性（）.A:错 B:对答案:对2.蝴蝶效应是谁发现的( ).A:奥古斯丁·路易斯·柯西 B:爱德华·诺顿·洛伦茨 C:约瑟夫·拉格朗日 D:约翰·卡尔·弗里德里希·高斯答案:爱德华·诺顿·洛伦茨3.SI模型实际上是（）模型.A:Logistic 模型 B:Malthus模型 C:Volterra模型答案:Logistic 模型4.用A表示进食而摄取的能量，B表示基础代谢消耗的能量，R表示活动而消耗的能量，那么（）表示由于能量的摄入而增加的体重。
A: B: C:答案:5.SI模型实际上是Volterra模型模型（）.A:对 B:错答案:错6.SIR模型建立的是传染病有免疫性——病人治愈后即移出感染系统（）。
A:错 B:对答案:对7.SIR模型建立的是传染病无免疫性——病人治愈成为健康人，健康人可再次被感染（）。
A:对 B:错答案:错8.减肥最好的方法是节食（）。
A:错 B:对答案:错9.减肥最重要的措施有（）。
A:服用肥药 B:多吃营养品 C:增加运动量 D:控制饮食量答案:增加运动量;控制饮食量10.下列哪些现象可以看成蝴蝶效应（）。
A:厄尔尼诺现象 B:美国发生的股市风暴 C:1997年金融危机答案:厄尔尼诺现象;美国发生的股市风暴;1997年金融危机第二章测试1.简单图指的是没有环的图（）.A:对 B:错答案:错2.下列哪些选项中的图可以一笔画（）A:恰有两个奇度点的图 B:都是偶度点的连通图 C:恰有一个奇度点的图 D:恰有两个奇度点的连通图答案:都是偶度点的连通图;恰有两个奇度点的连通图3.无圈的图就是树（）A:对 B:错答案:错4.本节渡河问题中的摆渡人经过( )次渡河可以将狼羊菜顺利运过河去.A:6 B:5C:8 D:7 答案:75.用先深搜索算法可以找到一个连通图的生成树（）.A:对 B:错答案:对6.下列哪个选项是正确的（）A:树一定有完备匹配 B:图G的最大匹配指的是图G的边数最多的匹配 C:完全图一定有完备匹配 D:完全二分图一定有完备匹配答案:图G的最大匹配指的是图G的边数最多的匹配7.关于四色猜想下列说法正确的是（）A:任何一个图，都可以用四种颜色来着色，使得任何两个相邻的面着不同的颜色。
2023届高三第一次联考数学试题一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设全集为R ，集合{}{}230,1A xx x B x x =-<=≤∣∣，则()A B ⋂=R（ ）A.{01}xx <<∣ B.{13}x x <<∣ C.{03}xx <<∣ D.{3}x x >∣ 2.若复数17i1iz -=+，则（ ） A.5z =B.复数在复平面上对应的点在第二象限C.复数的实部与虚部之积为12-D.34i z =+3.62x⎛⎝的展开式中的常数项为（ ）A.60-B.60C.64D.1204.《九章算术.商功》中，将四个面都是直角三角形的四面体成为鳖臑.在鳖臑ABCD 中，AB ⊥平面BCD ，BC CD ⊥，且1,2,3AB BC CD ===，则四面体ABCD 外接球的表面积为（ ） A.143πB.7πC.13πD.14π 5.已知正实数,x y 满足144x y x y++=+，则x y +的最小值为（ ）2 B.2 C.2+ D.2+6.已知点()()4,0,0,4A B ，直线25:4l x =，动点P 到点A 的距离和它到直线l 的距离之比为4:5，则PB 的最大值是（ ）B.7C.D.7.已知函数()f x 的定义域为R ，且()()()112,2f x f x f x ++-=+为偶函数，若()00f =，1()111nk f k ==∑，则n 的值为（ ）A.107B.118C.109D.1108.已知向量,,a b c 满足1,20,2a a b c a c b =+=-=-，则向量c b -与a 夹角的最大值是（ ） A.12π B.6π C.4π D.3π二､多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.盒中装有大小相同的5小球（编号为1至5），其中黑球3个，白球2个.每次取一球（取后放回），则（ ）A.每次取到1号球的概率为15B.每次取到黑球的概率为25C.“第一次取到黑球”和“第二次取到白球”是相互独立事件D.“每次取到3号球”与“每次取到4号球”是对立事件 10.已知函数()[]f x x x =-，其中[]x 表示不大于x 的最大整数，如：][0.20, 1.22⎡⎤=-=-⎣⎦，则（ ） A.()f x 是增函数 B.()f x 是周期函数 C.()2f x 的值域为[)0,1 D.()2f x 是偶函数11.设抛物线2:4C x y =的焦点为F ，过点F 的直线与C 交于,A B 两点，C 的准线与y 轴交于点M ，O 为坐标原点，则（ ） A.线段AB 长度的最小值为4B.若线段AB 中点的横坐标为2，则直线AB 的斜率为1C.2AMB π∠>D.AMO BMO ∠∠= 12.已知函数()()ln ,e x xf xg x x x-==，若存在()120,,R x x ∞∈+∈，使得()()12f x g x k ==成立，则（ ）A.当0k >时，121x x +>B.当0k >时，21e 2e xx +<C.当0k <时，121x x +<D.当0k<时，21e k x x ⋅的最小值为1e-三､填空题：本题共4小题，每小题5分，共20分.13.函数sin 26y x π⎛⎫=+⎪⎝⎭的最小正周期为____________. 14.毕达哥拉斯树是由古希腊数学家毕达哥拉斯根据勾股定理画出来的一个可以无限重复的图形，因为重复数次后的形状好似一棵树，所以被成为毕达哥拉斯树，也叫“勾股树”.毕达哥拉斯树的生长方式如下：以边长为1的正方形的一边作为斜边，向外做等腰直角三角形，再以等腰直角三角形的两直角边为边向外作正方形，得到2个新的小正方形，实现了一次生长，再将这两个小正方形各按照上述方式生长，如此重复下去，设第n 次生长得到的小正方形的个数为n a ，则数列{}n a 的前n 项和n S =____________.15.已知正四棱柱11111,1,2ABCD A B C D AA AB -==，则直线1AA 与平面11B CD 所成角的正弦值为____________. 16.设直线()()():21330l a x a y a a +----=∈R 与圆222:(1)(0)C xy r r +-=>交于,A B 两点，当ABC 面积的最大值为2时，a 的值为____________.四､解答题：本题共6小题，共70分.解答应写出文字说明､证明过程或演算步骤.17.已知ABC 的内的,,A B C 的对边分別为,,a b c ，且()()3sin cos cos b A C c a B -=-.（1）求B ；（2）在①重心，②内心，③外心这三个条件中选择一个补充在下面问题中，并解决问题. 若5,3,a c O ==为ABC 的____________，求OAC 的面积. 注：如果选择多个条件分別解答，则按第一个解答计分. 18.已知数列{}n a 的各项均为正数，记n S 为{}n a 的前n 项和，111111,n n n n na a S S S S --==+（*N n ∈且2n ≥）. （1）求证：数列{}n S 是等差数列，并求{}n a 的通项公式：（2）当*N,2n n ∈≥时，求证：2222311111114n a a a +++<---. 19.如图，在四棱锥P ABCD -中，平面PAD ⊥平面,2,4,23ABCD PA AD BD AB ====，BD 是ADC ∠的平分线，且BD BC ⊥.（1）若点E 为棱PC 的中点，证明：BE ∥平面PAD ；（2）已知二面角P AB D --的大小为60，求平面PBD 和平面PCD 的夹角的余弦值. 20.随着时代的不断发展，社会对高素质人才的需求不断扩大，我国本科毕业生中考研人数也不断攀升，2020年的考研人数是341万人，2021年考研人数是377万人.某省统计了该省其中四所大学2022年的毕业生人数及考研人数（单位：千人），得到如下表格：A 大学B 大学C 大学D 大学2022年毕业人数x （千人）76542022年考研人数y （千人）0.5 0.4 0.3 0.2（1）已知y 与x 具有较强的线性相关关系，求yx 关于的线性回归方程ˆˆˆy bx a =+；（2）假设该省对选择考研的大学生每人发放0.5万元的补贴.（i ）若该省大学2022年皆业生人数为8千人，估计该省要发放补贴的总全额：（ii ）若A 大学的毕业生中小浙､小江选择考研的概率分別为,31p p -，该省对小浙､小江两人的考研补贴总金额的期望不超过0.75万元，求p 的取值范围.参考公式：()()()1122211,nniii ii i nniii i x x yy x ynxyb a y bx x x xnx ====---===---∑∑∑∑.21.已知双曲线2222:1(0,0)x y C a b a b-=>>的离心率为3，且点(在C 上. （1）求双曲线C 的方程：（2）试问：在双曲线C 的右支上是否存在一点P ，使得过点P 作圆221x y +=的两条切线，切点分别为,A B ，直线AB 与双曲线C 的两条渐近线分别交于点,M N，且MONS =求出点P ；若不存在，请说明理由. 22.已知函数()21ln ,2f x x x x ax a =--∈R . （1）当22e a =时，证明：()0f x ≤： （2）若函数()()()21e x Hx f x x ax x =--++在()0,∞+上单调递减，求a 的取值范围.数学参考答案一､单选题（共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）二､多选题（本大题共4小题，每小题5分共20分每小题列出的四个选项中有多个是符合题目要求的，全部选对得5分，部分选对得2分，有选错的得0分）三､填空题（本大题有4小题，单空每空4分，多空每空3分，共20分）13.π 14.122n +-15.6316.132a -±=四､解答题（本大题有6小题，共70分，解答应写出必要的文字说明，证明过程或演算步骤）17.解： （1）()()3sin cos cos bA C c aB -=-，()()sin 3sin cos sin sin cos BA C C AB ∴-=-，则()3sin sin sin sin cos A B B C A B =+-，即3sin sin sin sin cos A B A A B =-，sin 0,3sin cos 1A B B ≠∴+=，即有1sin 62B π⎛⎫+= ⎪⎝⎭，72,,6663B B ππππ⎛⎫+∈∴= ⎪⎝⎭（2）若选①O 为ABC 的重心，11153sin ;3324OACBACSS ac B ==⋅=若选②O 为ABC 的内心，2222cos 49,7,b a c ac B b =+-=∴=设内切圆半径为，则有()115324ABCa b c r S ++==， 则有32r =，此时17324aACS br ==；若选③O 为ABC 的外心，2222cos 49,7b a c ac B b =+-=∴=，设外接圆半径为R ，则2sin b R B =，解得73R =如图，23AOC π∠=，此时，21493sin 212OACS R AOC ∠== 18.解： （1）*11n n n n na n N S S S S --=∈且)2n ≥， 1,n n n a S S -∴=∴当2n≥时，11n n n n S S S S ---=(111n n n n n n S S S S S S ---∴=，又0n a >10n n S S ->，()112n n S S n -=≥，∴数列{}n S 111S a ==为首项，公差为1的等差数列，()111n S n n =+-⨯=，所以2n S n =.∴当2n≥时，1121n n n a S S n n n -=+-=-，又11a =满足上式，∴数列{}n a 的通项公式为21nan =-.另解： 当2n ≥时，221(1)21nn n a S S n n n -=-=--=-，当1n =时，11a =，满足上式， 所以{}n a 的通项公式为21nan =-.（2）当2n ≥时，221111114441n a n n n n ⎛⎫==- ⎪---⎝⎭， 故22211111111111111141223144n a a n n n ⎛⎫⎛⎫++=⨯-+-++-=⨯-< ⎪ ⎪---⎝⎭⎝⎭所以对*,2n N n ∈≥，都有222111114n a a ++<--. 19.解：（1）方法一：延长,CB DA 交于点F ，连接PF ， 在CDF 中，BD 是ADC ∠的平分线，且BD BC ⊥，∴点B 是CF 的中点， 又E 是PC 的中点， BE PF ∴∥，又PF ⊂平面,PAD BE ⊄平面PAD ， ∴直线BE ∥平面PAD .方法二：取CD 的中点为G ，连接GE ，E 为PC 的中点，GE PD ∴∥， 又PD ⊂平面,PAD GE ⊄平面PAD ， GE ∴∥平面PAD ，①又在四边形ABCD 中，2,4,23AD BD AB ===则90,60BAD BDA BDC ∠∠∠===， 又因为,BD BC G ⊥为CD 的中点， 所以60DBG BDA ∠∠==，所以AD BG ∥，可得BG ∥平面PAD ，② 由①②得平面BEG ∥平面PAD ， 又BE ⊂平面,BEG BE⊄平面PAD ，∴直线BE ∥平面PAD .（2）在ABD 中，2,4,23AD BD AB ===则90BAD ∠=，即BA AD ⊥，由已知得60,8BDC BDA CD ∠∠===， 又平面PAD ⊥平面,ABCD BA ⊂平面ABCD 所以BA ⊥平面PAD ，即BA PA ⊥，所以以PAD ∠为二面角P AB D --的平面角， 所以60PAD ∠=， 又2PA AD ==，所以PAD 为正三角形，取AD 的中点为O ，连OP ，则,OP AD OP ⊥⊥平面,ABCD 如图建立空间直角坐标系，则()()()()(1,0,0,1,23,0,5,43,0,1,0,0,3A B C D P --， 所以()()()1,0,3,2,23,0,4,43,0DP BD DC ==--=-， 设()()111222,,,,,m x y z n x y z ==分别为平面PBD 和平面PCD 的法向量，则00m DP m BD ⎧⋅=⎪⎨⋅=⎪⎩，即1111302230x z x ⎧+=⎪⎨--=⎪⎩，取11y =-，则()3,1,1m =--， 00n DP n DC ⎧⋅=⎪⎨⋅=⎪⎩，即2222304430x z x ⎧+=⎪⎨-+=⎪⎩，取21y =，则()3,1,1n =-，所以3cos ,5m n m n m n ⋅==⋅ 则平面PBD 和平面PCD 所成夹角的余弦值为35. 20.解：（1）由题意得45670.20.30.40.55.5,0.3544x y ++++++====，又4170.560.450.340.28.2i ii x y==⨯+⨯+⨯+⨯=∑4148.24 5.50.350.5i i i x y x y =∴-⋅=-⨯⨯=∑42222217654126ii x==+++=∑4222141264 5.55i i x x =∴-=-⨯=∑41422140.5ˆ0.1, 54i ii ii x yxybxx ==-∴===-∑∑ 所以ˆˆ0.350.1 5.50.2a y bx=-=-⨯=- 故得y 关于x 的线性回归方程为0.10.2y x =-.（2）（i ）将8x =代入0.10.20.180.20.6y x =-=⨯-=， 估计该省要发放补贴的总金额为0.610000.5300⨯⨯=（万元）（ii ）设小浙､小江两人中选择考研的人数为X ，则X 的所有可能值为0,1,2()()()20123352P X p p p p ==--=-+()()()()2113123661P X p p p p p p ==--+-=-+- ()()22313P X p p p p ==-=-()()()()222035266113241E X p p p p p p p ∴=⨯-++-+-⨯+-⨯=-()()50.50.5410.758E X p p =⨯-≤⇒≤ 1150311,1,338p p p ∴≤-≤∴≤≤∴≤≤故p 的取值范围为15,38⎡⎤⎢⎥⎣⎦. 21.解： （1）因为3c e a ==，所以222243c a a b ==+，即223a b =，又点(在双曲线2222:1(0,0)x yC a b a b-=>>图象上，所以22921a b -=，即229213b b-=，解得221,3b a ==， 所以双曲线22:13x C y -=.（2）由已知点,A B 在以OP 为直径的圆22220000224x y x y x y +⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭上， 又点,A B 在221x y +=上，则有方程组2222000022,2241,x y x y x y x y ⎧+⎛⎫⎛⎫-+-=⎪ ⎪ ⎪⎨⎝⎭⎝⎭⎪+=⎩解得直线AB 的方程为001x x y y +=， 设直线AB与渐近线,33y x y x ==-的交点分别为,M N ，由001,,3x x y y y x +=⎧⎪⎨=⎪⎩解得M ⎛⎫ ⎪，由001,,3x x y y y x +=⎧⎪⎨=-⎪⎩解得N ⎛⎫⎪，所以2200313MN x y ==-， 又点O 到直线AB的距离为d =则三角形MON的面积222200001113112233S MN d x y x y =⋅=⨯=--， 又因为220013x y -=，所以2001833S y ==+，由已知33S =203y =，即0y = 因为点P在双曲线右支上，解得0x =即点(P或(P . 22.解： （1）当22a e =时，()22211ln ln 1f x x x x x x x x e e ⎛⎫=--=-- ⎪⎝⎭， 要证()0f x ≤，即证21ln 10x x e --≤， 设()21ln 1,0g x x x x e =-->，令()2110g x x e =-='，解得2x e =， 所以()g x 在()20,e 上递增，在()2,e ∞+上递减，则()222max 21()ln 10g x g e e e e ==--⨯=， 所以()0gx ≤，即21ln 10x x e --≤成立， 所以()0f x ≤成立.（2）因为对任意的()0,x H x >在()0,∞+上单调递减，所以()0H x '≤恒成立， 即ln 1x xe x a x--≤在()0,∞+上恒成立， 解法一：令()ln 1(0)x xe x F x x x --=>，则()22ln x x e x F x x+='， 令()2ln x h x x e x =+，则()()2120x h x x x e x '=++>，所以()h x 在()0,∞+上为增函数，又因为()1122110,110e e e h e h e e e-⎛⎫=>=-=-< ⎪⎝⎭， 所以01,1x e ⎛⎫∃∈ ⎪⎝⎭，使得()00hx =，即0200ln 0x x e x +=， 当00x x <<时，()0hx <，可得()0F x '<，所以()F x 在()00,x 上单调递减； 当0x x >时，()0hx >，可得()0F x '>，所以()F x 在()0,x ∞+上单调递增， 所以()000min 00ln 1()x x e x F x F x x --==， 由0200ln 0x x e x +=，可得001ln 000000ln 111ln ln x x x x e e x x x x ⎛⎫=-== ⎪⎝⎭， ()()001,ln ,x t x xe t x t x ⎛⎫== ⎪⎝⎭令则又由()()10x t x x e =+>'，所以()t x 在()0,∞+上单调递增， 所以001ln x x =，可得00ln x x =-，所以001x e x =，即001x x e =，所以()0000min000ln 111()1x x e x x F x F x x x --+-====， 即得1a ≤. 解法二：先证()10x ex x ≥+≥， 设函数()1x h x e x =--，令()10x h x e ='-=，解得0x =， ()h x ∴在[)0,∞+上单调递增，()()00h x h ∴≥=，即1x e x ≥+成立. 设()ln (0)k x x x x =+>，()()110,k x k x x =+>∴'在()0,∞+上单调递增， ()1110,110k k e e ⎛⎫=-+<=> ⎪⎝⎭， ∴存在()00,x ∞∈+，使得00ln 0x x +=.今()ln 1(0)x xe x F x x x--=>， 则()tan ln ln 1ln 1ln 1ln 11x x x x e e x e x x x x F x x x x+----++--==≥=， 当ln 0x x +=时，即0x x =时，取等号.min ()1F x ∴=，即得1a ≤。
第一章测试1.古希腊世界人文和科学是统一的。
（）A:对B:错答案:A2.科学可以进行价值判断。
（）A:对B:错答案:B3.科学的使命是辅人律。
（）A:错B:对答案:B4.科技是指科学和技术。
（）A:错B:对答案:B5.爱因斯坦是物理学博士。
（）A:错B:对答案:A第二章测试1.数学奖有（）。
A:陈省身奖B:沃尔夫奖C:高斯奖D:邵逸夫奖E:菲尔兹奖答案:ABCDE2.莱茵德纸草书和莫斯科纸草书记载了古埃及关于数学方面的知识。
（）A:错B:对答案:B3.“欧几里得”的作者是毕达哥拉斯。
（）A:对B:错答案:B4.“周髀算经”是中国古代数学著作中最早的一部。
（）A:对B:错答案:A5.德国的哥廷根大学这一兴盛的数学中心，由于希特勒统治进行的政治迫害而衰落。
（）A:错B:对答案:B第三章测试1.“自然哲学之数学原理”的作者是牛顿。
（）A:错B:对答案:B2.麦克斯韦的电磁场理论把电、磁和光三个领域综合到一起了。
（）A:错B:对答案:B3.斐索是第一位测得光速的学者。
（）A:对B:错答案:B4.经典物理学到量子物理学的过渡中，X射线的研究起到了重要的作用。
（）A:错B:对答案:B5.安德逊发现宇宙射线，赫斯发现正电子。
（）A:错B:对答案:B第四章测试1.日用陶瓷主要原料，不包括（）。
A:纯碱B:石英砂C:莫来石D:粘土答案:AC2.普通陶瓷中的物相包括（）。
A:堇青石B:粘土C:莫来石D:尖晶石E:气孔F:玻璃体答案:CEF3.钢与铁的差别在于（）。
A:微观结构不同B:主要化学成分不同C:含碳量不同D:颜色不同E:硬度不同答案:ACE4.陶器与瓷器的主要差别在于（）。
A:主晶相B:成型方法C:釉料D:致密度E:原料F:气孔率答案:ADF5.下列说法正确的是（）。
A:生铁含碳量一般在2.11%–4.3%，适合铸造但不能锻压B:熟铁是指用生铁精炼而成的比较纯的铁，含碳量在0.02%以下质地很软，塑性好。
C:钢是合金的一种D:生铁质地柔软，不具有脆性。
