高中选修物理3-3第八章气体第二节教案

精品文档第八章气体的性质1、气体的等温变化玻意耳定律【教学目标】1. 知道什么是等温变化；2.知道玻意耳定律是实验定律；掌握玻意耳定律的内容和公式；知道定律的适用条件；3.理解气体等温变化的p-V 图象的物理意义；4.知道用分子动理论对玻意耳定律的定性解释；5.会用玻意耳定律计算有关的问题。

【重点难点】1. 通过实验使学生知道并掌握一定质量的气体在等温变化时压强与体积的关系，理解p-V 图象的物理意义，知道玻意耳定律的适用条件；2．“状态”和“过程”分不清，造成抓不住头绪，不同过程间混淆不清的毛病，这是难点。

【教学用具】橡皮膜（或气球皮）、直径为5cm 左右两端开口的透明塑料筒（长约25cm 左右）、与筒径匹配的自制活塞、20cmiX 6cm薄木板一块。

【教学过程】（一）引入新课1. 吹气球比赛：准备两个空矿泉水瓶，两瓶内装有气球，气球口和矿泉水瓶口重合并固定，瓶A 事先扎了小孔，瓶B 完好无损。

师：现在请两个同学来进行一场吹气球比赛，看看谁能把气球吹得更大。

活动进行……问：请参加比赛的同学说说看，在瓶子力吹气球时有什么不同的感觉呢？——关键词：吃力困难问：请同学分析一下，为什么B瓶中气球比A瓶中的更难以吹鼓起来呢？一一A瓶漏气、B瓶中不漏气师：可以利用身边资源进行验证一下，看看你的猜测是不是正确的。

――引导学生将A、B两瓶盖上盖子后压入水中，A瓶进了水，B瓶没有进水。

说明A瓶漏气。

——向全体同学展示两瓶的验证结果，明确A 瓶漏气，故A 瓶内气球更容易吹起来。

总结性问题1：现在请同学们根据已有的知识解释一下，为什么在密闭的瓶子中更难将气球吹鼓呢?―― 引导学生回答: 密闭瓶子中本身装有有一定量气体，当瓶中气球胀大时，瓶中气体被压缩，瓶中气体压强变大，使得吹大气球更加困难。

而漏气的瓶中的气体由于和外界连通，气压始终等于外界大气压，故吹起气球就和平时无异。

总结性问题2：这个比赛告诉我们，对于质量一定的气体，其压强跟什么因素有关呢？――体积2. 复原乒乓球：师：被踩扁的乒乓球，有什么办法将它复原吗？――将球泡在热水中。

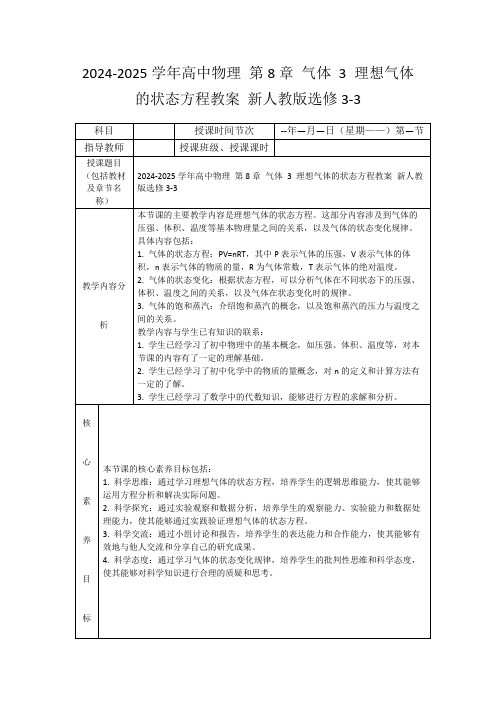
气体的等容变化和等压变化课时教学设计的变化，变到压强P2、温度T2的另一种状态，则有21P P ＝21T T 或者 11T P ＝22T P .(3)适用条件： ①气体的质量一定 ②气体的体积不变③压强不太大，温度不太低教学过程及方法环节二 合作释疑 环节三 点拨拓展过程设计二次备课例1．一定质量的气体保持体积不变，在0℃时压强为p 0，在27℃时压强为p ，则当气体从27℃升高到28℃时，增加的压强为A.1/273 p 0B.1/273pC.1/300p 0D.1/300p（4）.等容过程及P-T 图像 (1)等容过程：一定质量的气体在体积保持不变时所发生的状态变化过程.(2)P-T 图像上的等容线①P-T 图中的等容线是一条延长线通过原点的倾斜直线.②斜率K ＝T P＝C(恒量)与气体体积有关.体积越大，斜率越小.如图所示，4条等容线的关系为V1＞V2＞V3＞V4.例2. 一定质量的理想气体的P —t 图象，如图8.2—4所示，在状态A 到状态B 的过程中，体积：A.一定不变B.一定减小C.一定增加D.不能判定怎样变化 二、盖·吕萨克定律(1)内容：一定质量的气体，在压强保持不变时，体积和热力学温度成正比. (2)公式设一定质量的某种气体，由体积V1、温度T1的状态，保持压强不变，变化到体积V2、温度T2的另一种状态，则有 11T V ＝22T V 或者 21V V图8.2—4＝21T T .(3)适用条件 ①气体的质量一定 ②气体的压强不变 ③压强不太大，温度不太低 （4）.等压过程及V-T 图像(1)等压过程：一定质量的气体在压强保持不变时所发生的状态变化过程(2)V-T 图像上的等压线①V-T 图像中的等压线是一条延长线通过原点的倾斜直线②斜率K ＝T V＝C(恒量)与气体压强有关，压强越大，斜率越小.如图13.2-3所示P1＞P2＞P3＞P4.例题例3 、书本第25页例题（略）例4 如下图所示，在球形容器内充有一定质量的理想气体，当大气压强是760mmHg ，气体温度是27℃时，从接在容器下端U 形管水银压强计可以确定气体的压强是mmHg.如果大气压强保持不变，而气体的温度升高到47℃时，气体的压强将变为mmHg ，压强计左侧管内水银面D 将 (填“上升”或“下降”)mmHg(假设压强计细管的容积很小，球形容器的热膨也很小都可以不考虑).解析 题目中“假设压强计细管的容积很小，球形容器的热膨胀也很小都可以不考虑”是一个隐含条件，说明球形容器内气体发生的是等容变化过程，可利用查理定律求解.解答 在压强计左管中取与右管上端水银面等高的液片为研究对象，由压强平衡得 P0＝P1+Ph1 ∴P1＝P0-Ph1＝600mmHg. 以球形容器内封闭气体为研究对象，气体作等容变化，根据查理定律有11T P ＝22T P . ∴ P2＝12T T P1＝300320×600mmHg ＝640mmHg由于外界大气压不变，而P2＞P1,故水银面将下降.设温度升高后，水银面高度差为h2,则 P2＝P0-Ph2 Ph2＝P0-P2＝120mmHg.h2＝120mm,则水银面D 下降高度 L ＝21Δh ＝21(h1-h2)＝21(160-120)mm)＝20mm.教学过程及方环节四 当堂检测二次备课“当堂检测”：1．如图，是一定质量的气体从状态A 经B 到状态C 的V —T 图象，由图象可知（ ） A ．P A ＞P BB ．PC ＜P B C ．P A ＞P CD ．P C ＞P B2．如图是一定质量的气体从状态A 经B 到状态C 的P —T 图象，由图象可知（ ） A ．V A ＝V BB ．V B ＝V CVOTAB CPOTA B C北师版三年级数学上册月考卷（3\4）姓名：分数：一、 填一填，我能行。

理想气体的状态方程课时教学设计一、理想气体问题：以下是一定质量的空气在温度不变时，体积随常压和非常压变化的实验数据：压强（p）（atm）空气体积V（L）pV值( 1×1.013×105PaL)1 100 200 500 10001.0000.9730/1001.0100/2001.3400/5001.9920/10001.0000.97301.01001.34001.9920问题分析：（1）从表中发现了什么规律？在压强不太大的情况下，实验结果跟实验定律——玻意耳定律基本吻合，而在压强较大时，玻意耳定律则完全不适用了。

（2）为什么在压强较大时，玻意耳定律不成立呢？如果温度太低，查理定律是否也不成立呢？○1分子本身有体积，但在气体状态下分子的体积相对于分子间的空隙很小，可以忽略不计。

○2分子间有相互作用的引力和斥力，但分子力相对于分子的弹性碰撞时的冲力很小，也可以忽略。

○3一定质量的气体，在温度不变时，如果压强不太大，气体分子自身体积可忽略，玻意耳定律成立，但在压强足够大时，气体体积足够小而分子本身不能压缩，分子体积显然不能忽略，这样，玻意耳定律也就不成立了。

○4一定质量的气体，在体积不变时，如果温度足够低，分子动能非常小，与碰撞时的冲力相比，分子间分子力不能忽略，因此查理定律亦不成立了。

总结规律：设想有这样的气体，气体分子本身体积完全可以忽略，分子间的作用力完全等于零，也就是说，气体严格遵守实验定律。

这样的气体就叫做理想气体。

a.实际的气体，在温度不太低、压强不太大时，可以近似为理想气体。

b.理想气体是一个理想化模型，实际气体在压强不太大、温度不太低的情况下可以看作是理想气体． 二、理想气体的状态方程情景设置：理想气体状态方程是根据气体实验定律推导得到的。

如图所示，一定质量的理想气体由状态1（T 1、p 1、v 1）变化到状态2（T 2、p 2、v 2），各状态参量变化有什么样的变化呢？我们可以假设先让气体由状态1（T 1、p 1、v 1）经等温变化到状态c （T 1、p c 、v 2），再经过等容变化到状态2（T 2、p 2、v 2）。

第2节气体的等容变化和等压变化1.查理定律：一定质量的某种气体，在体积不变的情况下，压强p 与热力学温度T 成正比，即p T＝C 。

2．盖－吕萨克定律：一定质量的某种气体，在压强不变的情况下，其体积V 与热力学温度T 成正比，即V T＝C 。

3．玻意耳定律、查理定律、盖－吕萨克定律的适用条件均为一定质量的某种气体。

一、气体的等容变化 1．等容变化一定质量的某种气体，在体积不变时，压强随温度的变化。

2．查理定律 (1)内容：一定质量的某种气体，在体积不变的情况下，压强p 与热力学温度T 成正比。

(2)表达式：p T ＝C 或p 1T 1＝p 2T 2。

(3)适用条件：①气体的质量不变；②气体的体积不变。

3．等容线一定质量的气体，在体积不变时，其p ­T 图像是一条过原点的直线，这条直线叫做等容线。

二、气体的等压变化 1．等压变化一定质量的某种气体，在压强不变时，体积随温度的变化。

2．盖－吕萨克定律 (1)内容：一定质量的某种气体，在压强不变的情况下，体积V 与热力学温度T 成正比。

(2)表达式：V ＝CT 或V T ＝C 或V 1T 1＝V 2T 2。

(3)适用条件：①气体的质量不变；②气体的压强不变。

3．等压线一定质量的气体，在压强不变时，其V ­T 图像是一条过原点的直线，这条直线叫做等压线。

1．自主思考——判一判(1)气体的温度升高，气体体积一定增大。

(×)(2)一定质量的气体，在压强不变时体积与温度成正比。

(×)(3)一定质量的某种气体，在压强不变时，其V ­T 图像是过原点的直线。

(√) (4)一定质量的气体在体积不变的情况下，气体的压强与摄氏温度成正比。

(×) (5)pV ＝C 、p T ＝C 、V T＝C ，三个公式中的常数C 是同一个值。

(×) 2．合作探究——议一议(1)某登山运动员在一次攀登珠穆朗玛峰的过程中，在接近山顶时他裸露在手腕上的防水手表的表盘玻璃突然爆裂了，而手表没有受到任何撞击，你知道其中的原因吗？提示：手表表壳可以看成一个密闭容器，出厂时封闭着一定质量的气体，登山过程中气体发生等容变化，因为高山山顶附近的压强比山脚处小很多，内外压力差超过表盘玻璃的承受限度，便会发生爆裂。

高三物理选修3-3第八章气体第二节气体的等容变化和等压变化导学案【教学目标】1．知道什么是等容变化，知道查理定律的内容和公式。

2．了解等容变化的p-T图线及其物理意义3．知道什么是等圧过程，知道盖—吕萨克定律的内容和公式。

4．了解等圧変化的V-T图线及其物理意义。

【教学重点】1．对查理定律及盖·吕萨克定律的理解，以及应用定律求解有关问题。

2．理解等容变化的P-T图象和等压变化的V-T图象的物理意义。

【教学难点】采用“控制变量法”研究气体状态参量之间的关系。

【自主学习】一、气体的等容变化1．一定质量的某种气体，在体积不变时，压强随温度的变化叫做等容变化；在压强不变时，体积随温度的变化叫做等圧変化。

2．法国科学家查理在分析了实验事实后发现，一定质量的气体在体积不变时，各种气体的压强与温度之间都有线性关系，我们把它叫做。

从图甲可以看出，在等容过程中，压强P与摄氏温度t是一次函数关系，不是简单的正比例关系。

但是，如果把图甲中直线AB延长至与横轴相交，把交点当做坐标原点。

建立新的坐标系（如图乙所示），那么这时的压强与温度的关系就是正比例关系了。

图乙坐标原点的意义为。

可以证明，当气体的压强不太大，温度不太低时，坐标原点代表的温度就是。

所以说，在p-T图像中，一定质量的气体的等容线是线。

在P—t图象中一定质量的气体的等容线是线。

3．查理定律可以表述为：一定质量的某种气体，在体积不变的情况下，压强p与热力学温度T 成正比，即p∝T。

写成等式的形式就是p=CT或pT =C或p1T1=p2T24．一定质量的某种气体在不同体积下的几条等容线如图所示，其体积的大小关系是。

不同等容线的斜率与气体的体积成反比，斜率越大表示气体的体积越小。

二、气体的等压变化1．可以用实验研究一定质量的某种气体在压强不变的情况下其体积V 与热力学温度T的关系。

在V-T图像中，等压线是一条过原点的直线，如图所示。

2．法国科学家盖—吕萨克首先发现了这一线性关系，我们把它叫做盖—吕萨克定律：一定质量的某种气体，在压强不变的情况下，体积V 与热力学温度T成比，即V=CT或VT =C或V1T1=V2T23．在V-T图象中一定质量的某种气体的等压线是线。