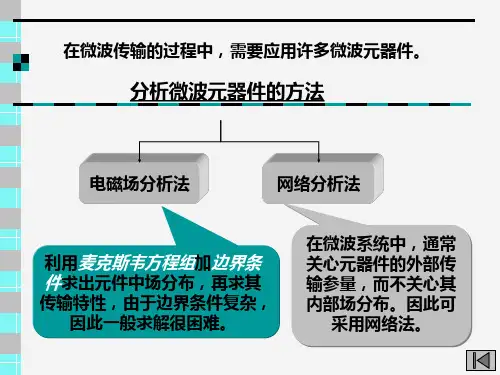
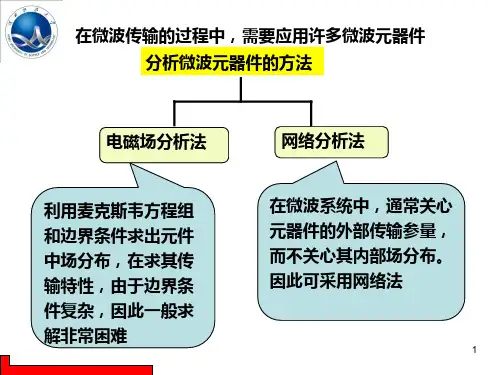
微波网络基础低频电路中，线路的尺寸与工作波长相比很小，从麦克斯韦方程组可推出在两根或多根导线周围存在的电磁场所满足的准静态解，进而引入电路理论中的基尔霍夫电压和电流定律，以及阻抗的概念等等。
低频电路技术一般来说不能直接应用于微波电路。
为了用电路这种简单而直观的概念来分析微波问题，需要把电路理论中电路和网络的概念加以推广，构建出微波电路和系统的等效电路模型和分析方法，即微波网络方法。
微波网络分析的基本过程：首先用场分析和麦克斯韦方程组处理一些基础性的标准问题，包括各种规则导行系统的等效电路，以及导行系统接头过渡的不连续性的等效电路，从而建立起等效微波网络。
定义描述微波网络工作特性的各种微波网络参数，并用于微波网络的分析。
对于TEM 导行系统（如同轴线、带状线），有明确的电压和电流的概念。
正导体相对于负导体的电压为:⎰-+⋅=l d E U，积分路径从正导体到负导体，由于两根导体之间的横向场具有静电场的性质，上式定义的电压是唯一的，且与积分路径的形状无关。
由安培定律可得在正导体上的总电流为：⎰+⋅=C l d H I，其中+C 积分回路为包围正导体的任意闭合路径。
对于非TEM 导行系统（如波导），可定义等效电压、等效电流和等效阻抗的概念，通常考虑如下思路：● 电压和电流仅对特定的波导模式定义，且定义电压与横向电场成正比，电流与横向磁场成正比。
● 为了按类似于电路理论中的电压和电流的方式使用，等效电压和等效电流的乘积应当等于该模式的功率流。
● 单一行波的电压和电流之比应等于该传输线的特性阻抗。
例题：求矩形波导TE 10模的等效电压和电流。
矩形波导TE 10模的横向场分量和功率流，以及TE 10模的等效传输线模型分别列在下表中由入射功率相等可得：*+++--++--++*++++==⇒⎪⎪⎭⎪⎪⎬⎫======21210221102214214C C A Z A ab P A I A I C AU A U C I U Z Aab P TE TE ⎪⎪⎩⎪⎪⎨⎧==⇒⎪⎪⎭⎪⎪⎬⎫===*21221021100212110abZ C ab C Z Z C C C C Z ab TE TE TE 所以等效电压和电流为：zj z j e A ab e A ab U ββ--++=22 zj TE z j TE e A ab Z e A ab Z I ββ--+-=21211010 电压和电流写成入射波和反射波之和：)()()(z U z U z U r i +=)]()([1)()()(0z U z U Z z I z I z I r i r i -=+= 归一化电压：0)()(~Z z U z U i i =（归一化入射波电压），0)()(~Z z U z U r r =（归一化反射波电压） 所以：)](~)(~[)(0z U z U Z z U r i +=， )](~)(~[1)(0z U z U Z z I r i -=)]()([21)()(~000z I Z Z z U Z z U z U i i +==，)]()([21)()(~000z I Z Z z U Z z U z U r r -== 反射系数：)()()()]()([21)]()([21)()()()()(~)(~00000z Z z Z Z z Z z I Z Z z U z I Z Z z U z U z U Z z U Z z U z U z U i i i i r i r i r Γ=+-=+-=== 传输的平均功率：[]⎪⎭⎫ ⎝⎛-==*22)(~)(~21)()(Re 21z U z U z I z U P r i L研究微波网络需先确定网络的参考面，随参考面选取不同，网络参数也随之改变。
