达朗贝尔原理习题解答~14293
- 格式:doc
- 大小:224.00 KB
- 文档页数:4





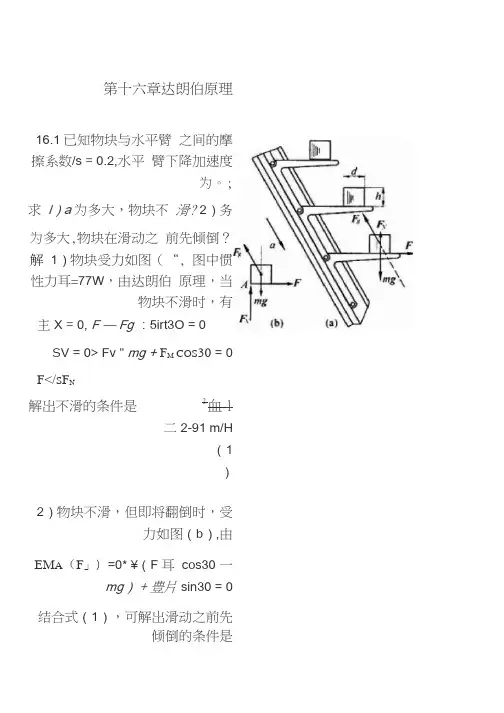
第十六章达朗伯原理16.1已知物块与水平臂之间的摩擦系数/s = 0.2,水平臂下降加速度为。
; 求l)a为多大,物块不滑? 2)务为多大,物块在滑动之前先倾倒?解1)物块受力如图(“, 图中惯性力耳=77W,由达朗伯原理,当物块不滑时,有主X = 0, F —Fg:5irt3O = 0SV = 0> Fv " mg + F M COS30 = 0 F</S F N解岀不滑的条件是2血l二2-91 m/H(1)2)物块不滑,但即将翻倒时,受力如图(b),由EM A(F」)=0* ¥(F耳cos30 一mg)+ 豊片 sin30 = 0结合式(1),可解岀滑动之前先倾倒的条件是h、1 孑鼻泾E6.2已知曲柄OC = rM匀角速度如转动;连杆召C = I端连有质量为櫛的物A ;求杆AB所受的力。
解设杆长AB =趴则物A 的运动方程为j : = b + r cos 爷 + I cos®cos® 1 — -y ^2 sin 2 卩j- = 6 + r cos 护 + I1 r2 . 2-2 7 s,n由达朗伯原理 SX = 0, mg - F - F* = 0得 AH 杆的力 F = 7ti[g + nw 2( cc^<p * y CQS 2^P )], 式中 ip — (Ait16.3已知 半径为『的圆轮对轴O 的转动惯量为丿*轮上 作用有恒力偶矩M 、轮缘上的销子C 推动质量为丹的滑槽ABD 沿水平滑道运动,滑道处摩擦系数为/ ■其余各处光滑;求 圆轮的转动微分方程。
解如图冷),圜盘角加速度为盘=花滑槽的运动方程和加 速度为J" = r COS 护, X = _ F (护2 8S 卩 + 0 审口爭)圆轮受力如图(b ),图中惯性力偶距皿0 =北=宛•由达朗伯原式中 cosB 二 J 1 -尹 sin* <p物块受力如图(b ),图中惯性力F 厂w(b)题16.3图乞Mo(F) = 0, A4 —- F.\r sin^j = 0得出J<p + F\r或1呻=M (1) 滑槽受力如图c、图中惯性力F f=豳,由达朗伯原理至X ~ 0* —P\ Fg l (F[ + F?) —0SY = 0, Fyp + F\i2 ~wg = 0 也及Fl =fFy;i, F2= JV池、Fy 二F、r 可得Fyj = Fv — ~ r>^ + fmg将式(2)代入式(1),得轮子的运动微分方程(J + mr~ sin2c:)G: + mr^ cos誓対口炉•炉'+ 6nijr sine? = M16.4已知物E质量m\ - 2 000 kg,物B质量酬2 =kg,物B下绳子拉力F r - 3 kN,不计滑轮的质量;求物E的加速度◎和绳FD的张力F HJC 解设物E*物B加速度如图*则a fl= 2a ;轮0和物E系统的受力.图中F曲=叱购=2叫;设轮O半径为厂2 .由达朗怕原理得SM Q( F) = 0, F( r;+ F测2「^1^2 什焜前2 =() ⑴轮C和物E系统的受力图中件=^2g, F;= Fi°设轮C半径为n,由达朗伯原理EM C(F)二0,_ *Fi厂I - F H Z I = 0SY = 0,F\ + F FD - mig - Eg = 0 (2) 由式(1)、(2)和其它各式,懈出一2丹七2如厂瞬“④讹/ni] +FfD^lg +-Wj-- = 10+21 kN16.5已知车重心为G,加速度为血’以及尺寸6f e t h ;求前后轮的压力;又,“为多大,方可使前后轮压力相等匸解设车质量为砒、受力如图,图中Fg = ma, P = mg 由达朗伯原理EM B(F) —0, (b+ c)F\x - 6P + hF K= 0SM A(F)= 0, -(b +CF.w + cP + = 0題込.4图4/2816.6已知曲杆线密度为宀圆弧半径为尸,以匀角速度绕轴O 转动,不计璽力,图(&)*求任意載面B处对AB段的约束反力。

第7章 达朗贝尔原理达朗贝尔原理是法国科学家达朗贝尔于1743年提出的,是分析力学的两个基本原理之一。
该原理揭示,对动力系统加入惯性力后,惯性力与外力构成平衡,因而提供一种用静力平衡方法处理动力学问题的普遍方法——动静法。
§7.1 质点系的达朗贝尔原理7.1.1 惯性力与质点的达朗贝尔原理1、质点达朗贝尔原理如图7.1所示,质量为m 的质点沿曲线轨道运动,受主动力F 和约束力N F 作用,由牛顿第二定律有N m +=F F a即0N m +-=F Fa 引入惯性力I m =-F a (7-1)则有0N I ++=F F F (7-2)这就是质点的达朗贝尔原理:作用在质点上的所有主动力、约束力和惯性力组成平衡力系。
这样,我们完全可以采用静力学的方法和技巧,求解动力学问题。
顺便指出,达朗贝尔原理作为分析力学的基本原理之一是不需要推导证明的。
这里由牛顿第二定律导出,可以说明它与牛顿力学在数学上的等价性。
问题7-1 如图所示,重为G 的小球用细绳悬挂,试求AC 绳断瞬时AB 绳的张力。
答 研究小球,加惯性力I F ,受力如图所示,由质点达朗贝尔原理,有0I T ++=F G F由力三角形有cos T F G =θ可见,加上惯性力,采用静力学中三力平衡的几何法求解决,直观简便。
2、惯性力的概念质点的惯性力I F 可以想象为:当质点加速运动时外部物质世界作用在质点上的一个场图7.1 质点达朗贝尔原理IF 问题7-1图力,其大小等于质点的质量与其加速度的乘积,方向与质点加速度方向相反。
惯性力与万有引力是完全等效的。
惯性力与参考系相关,如图7.2(a)所示,小球在旋转水平圆台上沿光滑直槽运动。
在地面惯性参考系观察,小球运动的绝对轨迹为螺旋线,见图7.2(b),在水平面内受滑槽侧壁对它的作用力N F 作用,加速度如图所示;从转动圆台非惯性参考系观察,小球的运动轨迹沿槽直线,在半径方向,受牵连法向惯性力2()nnIe Ie F mr ω=F 作用,小球沿直槽加速向外运动。


6-2. 图示系统由匀质圆盘与匀质细杆铰接而成。
已知:圆盘半径为 r 、质量为M ,杆长为L 、质量为 m 。
在图示位置杆的角速度为ω、角加速度为ε,圆盘的角速度、角加速度均为零,试求系统惯性力系向定轴O 简化的主矢与主矩。
解:∵圆盘作平动,相当一质点作用在A 点。
εττ⋅+==∑)2/(ML mL a m F Cii gR2)2/(ω⋅+==∑ML mL a m F nCii ngRεε⋅+==)31(2200ML mL J Mg6-3. 图示系统位于铅直面内,由鼓轮C 与重物A 组成。
已知鼓轮质量为m ,小半径为r ,大半径R = 2r ,对过C 且垂直于鼓轮平面的轴的回转半径ρ = 1.5r ,重物A 质量为2m 。
试求(1)鼓轮中心C 的加速度;(2)AB 段绳与DE 段绳的张力。
解:设鼓轮的角加速度为α, 在系统上加惯性力如图(a )所示,则其惯性力分别为:αmr F C =I ;αr m F A ⋅=2Iααρα222I 5.1mr m J M C C ===∑=0)(F DM;0)2(I I I =+-++C A C M r mg F F mg g g r a C 2145.132=+==α∑=0y F ;02I I =--+-mg mg F F F A C DE ;mg mr mg F DE 21593=-=α取重物A 为研究对象,受力如图(b )所示,∑=0yF;02I =-+mg F F A AB ;mg mg mr mg F AB 2134)2141(222=-=-=αa AM I gI A(b )6-4. 重力的大小为100N 的平板置于水平面上,其间的摩擦因数f = 0.20,板上有一重力的大小为300N ,半径为20cm 的均质圆柱。
圆柱与板之间无相对滑动,滚动摩阻可略去不计。
若平板上作用一水平力F = 200N ,如图所示。
求平板的加速度以及圆柱相对于平板滚动的角加速度。

第十一章 达朗贝尔原理一. 重点概括1 质点系的达朗贝尔原理在质点系运动的任一瞬时,作用于每一质点上的主动力、约束力和该质点的惯性力在形式上构成一平衡力系。
上式表明,作用在质点系上的外力系和虚加的惯性力系组成平衡力系——质点系的达朗贝尔原理。
用达朗贝尔原理求解非自由质点系动力学问题(已知运动求力或已知力求运动)的方法称为质点系的动静法。
对于空间力系,由这两个矢量式总共可写出6个投影方程;对于平面力系,由这两个矢量式总共可写出3个投影方程。
2 刚体惯性力简化(1) 惯性力系的主矢(2) 惯性力系的主矩I Ni =++i i F F F Ci i i m a m a F F -=-==∑∑)(I IR )(I I i O O F M M ∑=0I e =+∑∑iiF F 0)()(I e=+∑∑iOiOF M FM惯性力系的主矢与刚体的运动形式无关;惯性力系的主矩与刚体的运动形式有关。
3 几种刚体的惯性力(1)平移刚体主矢主矩刚体平移时,惯性力系简化为通过刚体质心的合力。
(2)定轴转动刚体主矢主矢等于刚体质量与质心加速度大小的乘积,方向与质心加速度方向相反。
对转轴的主矩主矩等于刚体对转动轴的转动惯量与角加速度的乘积,方向与角加速度方向相反。
(3)平面运动刚体(具有质量对称面的情形)IR ()i i m ∑F a =- () i C Cm m ∑a a =-=-I 0C M =)(n t R R IR C C C m m F a a a +=-=-αz z J M -=I主矢主矢大小等于刚体质量与质心加速度大小的乘积,方向与质心加速度方向相反。
主矩主矩小等于刚体对通过质心的转动轴的转动惯量与角加速度的乘积,方向与角加速度方向相反。
二. 常见问题和对策常见问题:1.惯性力系出错,表现在方向或大小出错,尤其主矩出错较多;2.质点系运动时,主动力系、约束反力系和惯性力系组成了形式上的平衡力系,切记不含质点之间的内力系(也不要画出内力系);3.质点系的运动参数之间联系出错。
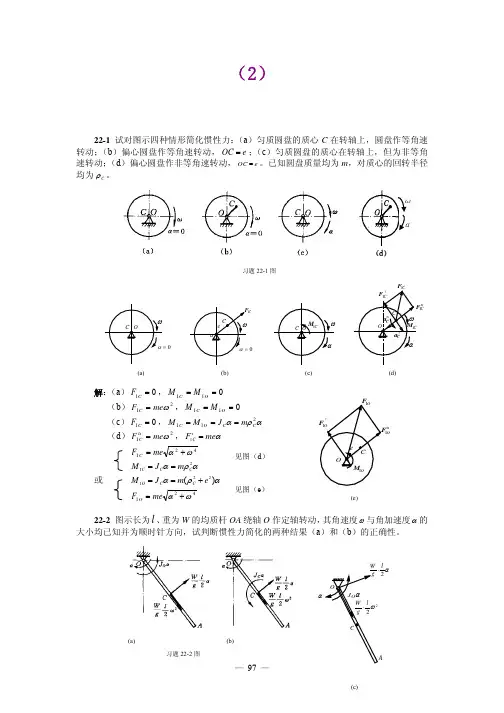
(a )习题11-1图第11章 达朗贝尔原理及其应用11-1 均质圆盘作定轴转动,其中图(a ),图(c )的转动角速度为常数,而图(b ),图(d )的角速度不为常量。
试对图示四种情形进行惯性力的简化。
解:设圆盘的质量为m ,半径为r ,则如习题11-1解图:(a )2I ωmr F =,0I =O M(b )2n I ωmr F =,αmr F =tI ,αα2I 23mr J M O O == (c )0I =F ,0I =O M (d )0I =F ,αα2I 21mr J M O O ==11-2矩形均质平板尺寸如图,质量27kg ,由两个销子 A 、B 悬挂。
若突然撤去销子B ,求在撤去的瞬时平板的角加 速度和销子A 的约束力。
解:如图(a ):设平板的质量为m ,长和宽分别为a 、b 。
αα375.3I =⋅=AC m Fααα5625.0])(121[222I =⋅++==AC m b a m J M A A∑=0)(F AM ;01.0I =-mg M A ;2rad/s 04.47=α ∑=0x F ;0sin I =-Ax F F θ;其中:6.053sin ==θN 26.956.004.47375.3=⨯⨯=Ax F∑=0y F ;0cos I =-+mg F F Ay θ;8.054sin ==θ习题11-2图习题11-1解图(a )(a )N 6.1378.004.47375.38.927=⨯⨯-⨯=Ay F11-3在均质直角构件ABC 中,AB 、BC 两部分的质量各为3.0kg ,用连杆AD 、DE 以及绳子AE 保持在图示位置。
若突然剪断绳子,求此瞬时连杆AD 、BE 所受的力。
连杆的质量忽略不计,已知l = 1.0m ,φ = 30º。
解:如图(a ):设AB 、BC 两部分的质量各为m = 3.0kg 。
直角构件ABC 作平移,其加速度为a = a A ,质心在O 处。
6-2. 图示系统由匀质圆盘与匀质细杆铰接而成。
已知:圆盘半径为 r 、质量为M ,杆长为L 、质量为 m 。
在图示位置杆的角速度为ω、角加速度为ε,圆盘的角速度、角加速度均为零,试求系统惯性力系向定轴O 简化的主矢与主矩。
解:∵圆盘作平动,相当一质点作用在A 点。
ετ
τ
⋅+==∑)2/(ML mL a m F Ci
i gR
2
)2/(ω⋅+==∑ML mL a m F n
Ci
i n
gR
ε
ε⋅+==)3
1(2
200
ML mL J M
g
6-3. 图示系统位于铅直面内,由鼓轮C 与重物A 组成。
已知鼓轮质量为m ,小半径为r ,大半径R = 2r ,对过C 且垂直于鼓轮平面的轴的回转半径ρ = 1.5r ,重物A 质量为2m 。
试求(1)鼓轮中心C 的加速度;(2)AB 段绳与DE 段绳的张力。
解:设鼓轮的角加速度为α, 在系统上加惯性力如图(a )所示,
则其惯性力分别为:
αmr F C =I ;αr m F A ⋅=2I
ααρα2
2
2
I 5.1mr m J M C C ===
∑=0)(F D
M
;
0)2(I I I =+-++C A C M r mg F F mg g g r a C 21
45
.132
=
+=
=α
∑
=0y F ;02I I =--+-mg mg F F F A C DE ;mg mr mg F DE 21
593=
-=α
取重物A 为研究对象,受力如图(b )所示,
∑=0y
F
;02I =-+mg F F A AB ;mg mg mr mg F AB 21
34)21
41(222=
-
=-=α
a A
M I g
I A
(b )
6-4. 重力的大小为100N 的平板置于水平面上,其间的摩擦因数f = 0.20,板上有一重力的大小为300N ,半径为20cm 的均质圆柱。
圆柱与板之间无相对滑动,滚动摩阻可略去不计。
若平板上作用一水平力F = 200N ,如图所示。
求平板的加速度以及圆柱相对于平板滚动的角加速度。
解:设平板的重力P 1 = 100 N ,加速度为a ;圆柱的重力P 2 = 300 N ,角加速度为α,
在平版上建立动系,则根据加速度合成定理可得:质心的加速度a O = a – αr ,或者
a O = a – αr ,
受力如图(a )。
a g P F 11I =;)(222I αr a g P a g P F O -==;αα2
2I 21r g
P J M O O ⋅==
∑=0)(F A
M ;0I 2I =-O M r F ;αα2
2221)(r g
P r r a g
P ⋅=
-;αr a 23=
∑=0x
F
;0f 2I 1I =---F F F F ;其中:N 80)(21N f =+=⋅=P P f F f F 080)(20021=---
-
αr a g
P a g P ;0)3(
12021=+
-a g
P g
P ;
2
m/s 88.5200
120==
g a ;2
rad/s 6.1932==
a r
α
6-5 图示匀质定滑轮装在铅直的无重悬臂梁上,用绳与滑块相接。
已知:轮半径r =1m, 重Q =20kN ,滑块重P =10kN ,梁长为2r ,斜面的倾角4/3tg =θ, 动摩擦系数1.0'
=f 。
若在轮O 上作用一常力偶矩m kN 10⋅=M 。
试用动静法求:(1)滑块B 上升的加速度;(2)支座A 处的反力。
解:(1)取滑块B 为研究对象,设其质量为m 1,加速度为a B ,则其惯性力为:B a m F 1I =,
受力如图(a )所示。
∑=0t
F
;0sin 1T I =+-+θg m F F F ;kN 8.0cos 1.01N ==⋅=θg m F f F
B B a m a m F 11T 8.68.06+=++=
取定滑轮O 为研究对象,设其质量为m 2,半径为r ,则其惯性力矩为:r
a r
m M B O 2
2I 2
1=,
受力如图(b )所示。
∑=0)(F O M ;0T I ='--r F M M O ;0108.61010=-
--B B a g
a g
;2
m/s 57.1=B a
kN 4.86.18.68.61T =+=+=B a m F
∑=0x F ;0cos T =-'Ox F F θ;kN 72.68.04.8=⨯=Ox F
∑=0y
F
;0sin 2T =-'-g m F F Oy θ;kN 04.25206.04.8=+⨯=Oy F
(2)取梁AO 为研究对象,设梁长为l ,受力如图(c )所示,
∑=0)(F A
M ;0='-l F M
Ox
A
;m kN 44.13227.6⋅=⨯=A
M
∑=0x F ;0=-'Ax Ox
F F ;kN 72.6=Ax F ∑=0y
F
;0='-Oy
Ay F F ;kN 04.25=Ay F
ϕ
ϕϕω
2sin )(sin cos 33
3
2
22
a b a b g
--=
/
2′
(a )
(b )
(c )
\。