雷达--地物回波系统分析

海面冰层冰层是非常复杂的介质。

观察者用许多不同的类别来描述冰层的特征。

而这些类别由冰层厚度、年代和形成过程决定[109]。

因此，人们不能用任何一种简单的方式来描述冰层的雷达回波，在这种意义上它和植被的散射类似。

从雷达观测的角度看，最重要的冰层类型是首年冰层（FY，1～2m厚），多年冰层（MY，大于2m厚），混合冰层（小于1m厚）。

与雪地相似，阳光融化和结冰温度之上的冰层所散射的微波，与正常结冰表层的散射相差很大。

在冬天，MY冰层的散射远大于FY冰层。

在夏天，MY冰层的σ0衰减到约等于FY 冰层的σ0。

图12.43[110]示出这种变化和典型的角度响应。

这些结果是在13.3GHz频率下测量得到的，但低至S波段频率，它们的结果也与此相似。

图12.44[91]示出不同冰层的σ0随频率的变化。

在海岸线上，与海岸紧紧相连的冰层位于海底之上，在这种情况下冰层可能是MY 类冰层。

灰色冰层是一种厚度小于FY类的冰层。

图12.43 当频率为13.9GHz时，海面冰层在夏季和冬季散射的比较（引自Gray等人[110]）第12章地物回波·460·图12.44 不同类型海面冰层σ0的频率响应举例（引自Kim[53]）Kim[53]提出一种理论来解释海面冰层σ0的大范围变化。

根据该理论和大量关于冰层特性的文献资料，图12.45[91]示出冬天FY和MY类冰层散射的变化范围。

很明显，较高频率在识别冰层类型上优于较低频率，并且当频率约低于5GHz时不能识别冰层的类型。

在L波段和更低的频率时，MY和FY类冰层的散射即使在冬天也相差无几。

这也意味着，较高频率的成像雷达在冬天（而非夏天）仅通过回波的强度就能轻易地区分冰层的类型。

这是前苏联和加拿大冰层监视系统的基础，其中前苏联采用Toros Ku波段侧视机载雷达（SLAR）[111]，加拿大采用改进型的X波段APS—94侧视机载雷达，最近加拿大采用STAR—1 X波段合成孔径雷达。

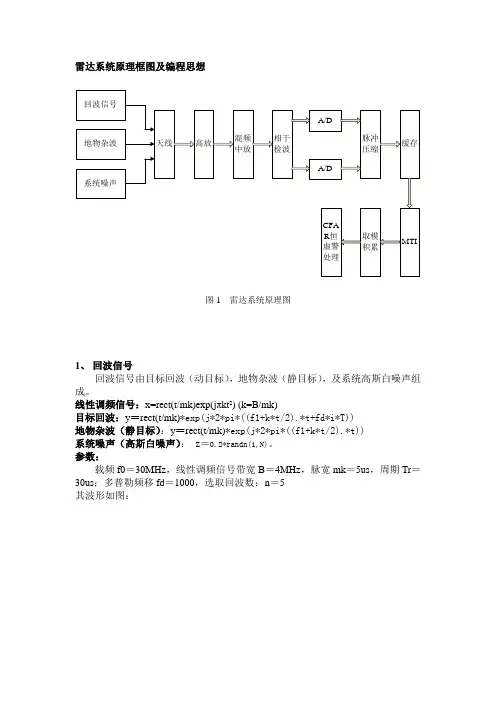
雷达系统原理框图及编程思想图1 雷达系统原理图1、回波信号回波信号由目标回波（动目标），地物杂波（静目标），及系统高斯白噪声组成。

线性调频信号：x=rect(t/mk)exp(jπkt²) (k=B/mk)目标回波：y＝rect(t/mk)*exp(j*2*pi*((f1+k*t/2).*t+fd*i*T))地物杂波（静目标）：y＝rect(t/mk)*exp(j*2*pi*((f1+k*t/2).*t))系统噪声（高斯白噪声）：z＝0.2*randn(1,N)。

参数：载频f0＝30MHz，线性调频信号带宽B＝4MHz，脉宽mk＝5us，周期Tr＝30us；多普勒频移fd＝1000，选取回波数：n＝5其波形如图：图2 回波2、高放高放采用50阶FIR滤波器，中心频率为30MHz，通带为20MHz。

高放后的波形图：图3 高放后时域频域图形3、混频＋中放混频的参考频率为20MHz中放采用50阶FIR滤波器，中心频率为10MHz，通带为4MHz。

图4 混频＋中放后时域频域图形4、相干检波参考源的时钟频率f0=10MHz;I 路：I=0.5*X*cos(Φ(t))；Q路：Q=0.5*X*sin(Φ(t))；原理图：中放之后的信号sin2πf0tcos2πf0t LDFLDFI路Q路波形图：图5 相位检波后I、Q两路时域图5、A/D转换采样频率为5MHz。

x0=(Vmax/2ª)*int{xi*2ª / Vmax };其中，a为AD位数图6 AD采样后后I、Q两路时域图6、脉冲压缩采用发射信号作为匹配滤波。

匹配滤波的脉冲响应：H(k)=X*(k)exp(-j2πkN), k=0,1,2…N线性调频信号：x(n)=rect(n/N)exp(jπkn²) (k=B/tao);图7 脉冲压缩时域图8、MTIMTI采用一次对消：y(n)=x(n)-x(n-1); n=1,2,3…N图8 MTI9、取模＋积累对20个回波信号取模并积累,此处是视频相参积累，y(n)= |∑x(n)| n=1,2, 3…N图9 取模加积累10、CFAR（恒虚警检测）恒虚警处理时利用的是前8后8的处理方法。

浅谈地物对气象雷达探测的影响及处理方法气象雷达是一种用于探测大气物理和化学特性的重要工具，可以实现对天气现象的实时监测和预报。

然而，雷达探测的精度受到大气中各种地物的干扰，因此需要对地物的影响进行分析并采取相应的处理方法。

地物对雷达探测的影响主要体现在以下几个方面：1. 反射效应地物表面反射雷达波，形成回波信号，干扰雷达探测。

不同地物的反射系数差异很大，例如水面和陆地的反射系数相差几十倍，这就是为什么雷达探测降水的可行性比探测大陆表面更高的原因。

2. 屏蔽效应地物会挡住探测波，使得雷达的覆盖范围受到限制。

例如，建筑物、山体等高物遮挡的范围就是雷达的盲区。

3. 多次反射干扰地物表面反射的信号还可能被其他地物反射，产生重复信号，干扰雷达探测结果。

这种现象称为多次反射干扰。

面对这些影响，可以采取以下措施：1. 选择合适的工作频段不同频段的雷达波对地物的反射系数有所差异，选择合适的工作频段能够有效减少地物反射对雷达探测的干扰。

2. 采用多波束探测和多角度扫描技术多波束探测和多角度扫描技术能够减少地物遮挡范围，提高雷达探测的覆盖范围。

其中，多波束天气雷达技术是现代天气雷达的重要发展方向，主要是用于降低地物对雷达探测的干扰。

3. 研究地物反射特性通过对地物反射特性的深入研究，有可能找到一些针对性的处理方法，例如通过计算地物的反射系数，恰当地调整雷达的反射系数来抵消地物反射干扰等。

总之，地物对雷达探测的干扰是必然的，但是通过科学合理的处理方法能够有效降低地物干扰对雷达探测的影响，提高雷达探测的精度和可靠性，为天气预报和防灾减灾提供有力技术支持。

衰落速率的计算计算多普勒频率是求衰减落速率〔Fading rate 〕最容易的方法。

为了在一个特定的多普勒频移范围内计算回波信号的幅度，必须将所有具有这些频移的信号相加。

这就需要了解散射面上的多普勒频移等值线〔等值多普勒频移〕。

对于每一种特殊形状的几何体都必须建立起这种多普勒频移等值线。

下面用一个沿地球外表水平运动的简单例子来说明。

它是普通巡航飞行飞机的一个典型实例。

假定飞机沿y 方向飞行，z 代表垂直方向，高度〔固定〕z = h 。

于是有v =1v vh y x z y x 111R -+=式中，1x ,1y ,1z 为单位矢量。

因而 h y x vy R v r 222++==•R v式中，v r 是相对速度。

等相对速度曲线也就是等多普勒频移曲线。

该曲线的方程为0222222=+--h v v v y x rr 这是双曲线方程。

零相对速度的极限曲线是一条垂直于速度矢量的直线。

图12.7示出这样一组等多普勒频移曲线。

只要把雷达式〔〕略加整理就可用来计算衰落回波的频谱。

这样，如果W r (f d )是频率f d 和f d +d f d 之间接收到的功率，那么雷达方程变为⎰π=积分区R A A G P f f W r t t d d r 402d )4(1d )(σ ⎰⎪⎪⎭⎫ ⎝⎛-π=d r t t df A R A G P f d d )4(d 402σ 〔〕图12.7 在地球平面做水平运动时的多普勒频移等值线 图12.8 计算复数衰落的几何关系图 〔引自Ulaby,Moore 和Fung [21]〕 上式的积分区是频率f d 和f d +d f d 间被雷达照射到的区域。

在此积分式中，f d 和f d +d f d 之间的面积元用沿着等值多普勒频移曲线的坐标和垂直于等值多普勒频移曲线的坐标来表示。

对每一种特定情况都必须建立这两个坐标。

图12.8示出水平传播的几何形状。

其中，坐标ξ 是等值多普勒频移曲线方向；η 是垂直方向。

浅谈地物对气象雷达探测的影响及处理方法1. 引言1.1 地物对气象雷达探测的影响地物对气象雷达探测的影响是气象雷达探测中不可忽视的因素之一。

在雷达探测过程中，地物会对雷达信号产生反射、遮挡和干扰等影响，进而影响雷达信号的接收和解译。

地物的影响主要表现在以下几个方面：地物反射对雷达探测的影响。

地物反射会导致雷达回波信号的变化和混叠，使得雷达图像中出现虚假回波或者信号叠加现象，从而影响对天气现象的准确探测和分析。

地物会对雷达回波产生遮挡效应。

高大的建筑物、山脉等地物会挡住部分雷达信号，导致雷达信号无法完全传播到目标区域，造成目标区域的天气信息缺失或变形。

地物还会对雷达回波产生干扰效应。

城市中的高楼大厦、高压线等地物会对雷达信号产生多次反射，形成干扰回波，影响雷达数据的准确性和可靠性。

地物对气象雷达探测的影响不可忽视，需要通过合理的处理方法和技术手段来降低其影响，提高雷达数据的质量和准确性。

1.2 地物对气象雷达探测的重要性地物对气象雷达探测的重要性在气象雷达技术中占据着重要的地位。

地物反射是影响雷达探测精度的一个重要因素，通过对地物的反射特性进行分析，可以更好地理解雷达回波的形成机制，提高对天气现象的监测和预测能力。

地物对雷达回波的遮挡效应和干扰效应也是需要重点关注的问题，只有充分了解地物对雷达探测的影响，才能有效地减少误差，提高数据的准确性和可靠性。

加强对地物影响的研究和处理，对于提高气象雷达探测的精度和效率至关重要。

随着技术手段的不断发展和完善，我们可以通过不断改进雷达探测算法、建设更多更密集的雷达站并提高监测覆盖范围，以及提高雷达站网络密度来进一步优化监测能力，实现更精准的气象监测和预测。

【已达到字数要求】2. 正文2.1 地物反射对雷达探测的影响地物反射对雷达探测的影响是气象雷达探测中重要的一环。

地物的特性会影响雷达波的传播和反射，从而对探测结果产生影响。

具体来说，地物的形状和表面特性会导致不同的反射效果，进而影响雷达探测的准确性和可靠性。

---------------------------------------------------------------最新资料推荐------------------------------------------------------1 / 3经典雷达资料-第12章 地 物 回 波第 12 章 地 物 回 波 Richard K. Moore 12.1 雷达地物回波用微分散射截面积或散射系数（单位面积的散射截面积）来描述， 而不用描述离散目 标的总散射截面积。

因为某一地面的总散射截面积是随照射区域而变化的， 而照射区域又取决于雷达的几何参数（脉冲宽度、 波束宽度等）。

的引入就是为了得到一个与这些参数无关的系数。

使用微分散射截面积意味着， 地物回波是由大量相位彼此独立的散射单元产生的。

这主要是由于各散射单元的距离差异所致， 尽管这个差别仅是总距离的很小一部分， 但却是波长的数倍。

并且， 功率的叠加可用于计算平均回波强度。

如果该条件不适用于一些特殊的地面目标， 那么微分散射截面积的概念对这些目标也就失去了意义。

例如， 高分辨力雷达可以分辨出小轿车的各部分， 则就不能正确地描述小轿车的光滑表面。

另一方面， 分辨力较差的雷达看到的是大型停车场上的很多小轿车， 这时测得的停车场的就是有效的。

假定在某一时刻某个雷达照射区域内有 n 个散射单元， 并且也满足上述条件， 因此功率可以相加，其雷达方程则变为式中， Ai为面积元； Pti,Gti,Ari是与 Ai相应的Pt,Gt,Ar值。

在等式右面分子中，括号内的因子是第 i 个单元的散射截面积增量，但此概念只适用于平均值。

于是，平均回波功率由下式给出：ntirGPP4 (式中，用来表示的平均值。

时，得到的形式为照射区（12.1）式中，Pr上面的一横表示平均值。

这种积分实际上并不正确，因为任何实际的独立散射中心都有一个最小尺寸。

然而，这种概念还是被广泛采用，并且只要照射面积大到足以包含许多这样的散射中心，这一概念就是可用的。

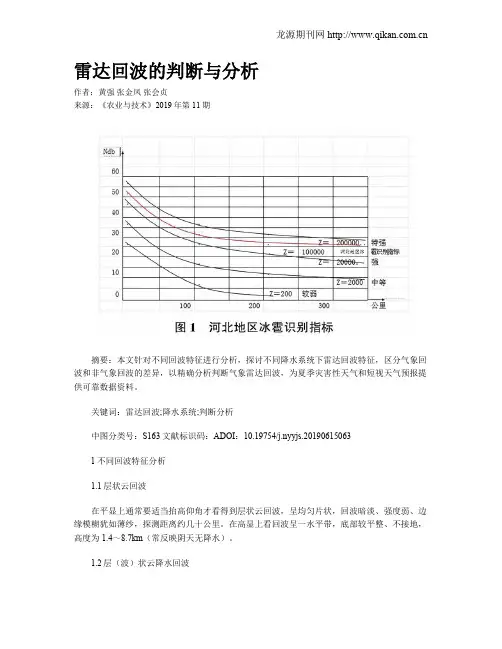
雷达回波的判断与分析作者：黄强张金凤张会贞来源：《农业与技术》2019年第11期摘要：本文针对不同回波特征进行分析，探讨不同降水系统下雷达回波特征，区分气象回波和非气象回波的差异，以精确分析判断气象雷达回波，为夏季灾害性天气和短视天气预报提供可靠数据资料。

关键词：雷达回波;降水系统;判断分析中图分类号：S163文献标识码：ADOI：10.19754/j.nyyjs.201906150631不同回波特征分析1.1层状云回波在平显上通常要适当抬高仰角才看得到层状云回波，呈均匀片状，回波暗淡、强度弱、边缘模糊犹如薄纱，探测距离约几十公里。

在高显上看回波呈一水平带，底部较平整、不接地，高度为1.4～8.7km（常反映阴天无降水）。

1.2层（波）状云降水回波在平显上，层（波）状云降水回波呈均匀片状，强度弱到中等，范围大，内部没有明显块体结构，边缘发毛，破碎模糊。

在高显上回波顶部平坦，且较均匀常看到0℃层300～1000m 的亮带，高度为3.6～8km（常反映大范围稳定性持续降水）。

1.3对流云回波在平显上回波呈小块状，有时零散孤立，有时排列成带状和不规则形状。

高显上常呈柱状、针状，底部不接地，强度为中等，高度为2.2～4.9km（为无降水）。

1.4阵雨回波在平显上回波呈孤立分散的小块单体或回波群，结构较松，边缘不清晰，单体水平尺度在10km以下，强度中等。

高显上回波呈针状顶部发毛，结构松散，回波高度在7～8km以下，回波底部接地（常反映短阵雨）。

1.5雷雨回波在平显上回波块体结识、肥大、紧密、轮廓清晰、边缘多折，单体水平尺度在10km以上，强度特强，很明亮。

在高显上呈柱状，低的仅5～6km，高的可达17～18km（常反映短暂雷雨）。

1.6雹云回波在平显上块体较大，结构紧密，发展急剧、多棱角、突起或小切口，移动迅速，强度特强，回波单块体范围小于10km。

在高显上强度最大值常出现在高于0℃等温线2～3km以上，云顶很高常在12～13km以上.通常呈针状接地的是阵雨回波，不接地的是对流云回波，平显上看单块体回波范围>10km、高显呈柱状，此回波可判定为雷雨回波。