北师大数学八年级上1.1.2勾股定理

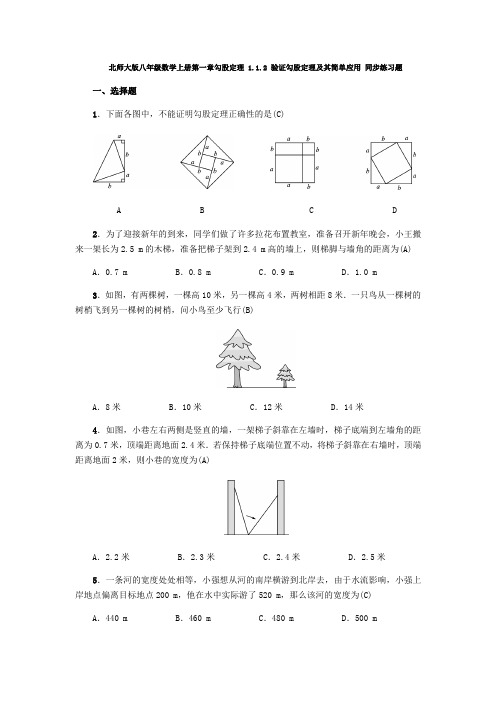
北师大版八年级数学上册第一章勾股定理 1.1.2 验证勾股定理及其简单应用同步练习题一、选择题1．下面各图中，不能证明勾股定理正确性的是(C)A B C D2．为了迎接新年的到来，同学们做了许多拉花布置教室，准备召开新年晚会，小王搬来一架长为2.5 m的木梯，准备把梯子架到2.4 m高的墙上，则梯脚与墙角的距离为(A)A．0.7 m B．0.8 m C．0.9 m D．1.0 m3．如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米．一只鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行(B)A．8米 B．10米 C．12米 D．14米4．如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米．若保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，则小巷的宽度为(A)A．2.2米 B．2.3米 C．2.4米 D．2.5米5．一条河的宽度处处相等，小强想从河的南岸横游到北岸去，由于水流影响，小强上岸地点偏离目标地点200 m，他在水中实际游了520 m，那么该河的宽度为(C)A．440 m B．460 m C．480 m D．500 m6．如图，在长方形纸片ABCD 中，已知AD ＝8，折叠纸片，使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且EF ＝3，则AB 的长为(D)A ．3B ．4C ．5D ．6 二、填空题7．如图，从电线杆离地面12 m 处向地面拉一条长为13 m 的钢缆，则地面钢缆固定点A 到电线杆底部B 的距离为5_m ．8．甲、乙两人同时从同一地点出发，甲往北偏东45°方向走了48米，乙往南偏东45°方向走了36米，这时两人相距60米．9．已知在△ABC 中，AB ＝17，AC ＝10，BC 边上的高AH ＝8，则BC 的长是21或9． 10．已知：如图，以Rt △ABC 的三边为斜边分别向外作等腰直角三角形．若斜边AB ＝3，则图中阴影部分的面积为92．11．一辆装满货物，宽为2.4米的卡车，欲通过如图所示的隧道(上方是一个半圆)，则卡车的外形高必须低于4.1米．12．如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC＝6，BC＝5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图2所示的“数学风车”，则这个风车的外围周长是76．三、解答题13．如图，在△ABC中，已知∠BAC＝90°，AD⊥BC于点D.试说明：BC2－AC2＝BD2＋AD2.解：在Rt△ABC中，BC2－AC2＝AB2，同理，在Rt△ABD中，BD2＋AD2＝AB2，所以BC2－AC2＝BD2＋AD2.14．如图是某宾馆的一段楼梯，楼梯高5 m，楼梯的最高点B与最低点A的距离是13 m，且楼梯宽度为2 m．若要给此段楼梯铺地毯，已知地毯单价为50元/m2，问铺完该楼梯表面至少需要多少钱？解：在Rt△ABC中，∠ACB＝90°，BC＝5 m，AB＝13 m，所以AC2＝AB2－BC2＝144.所以AC＝12 m.楼梯横向长度等价于AC 的长度，纵向长度等价于BC 的长度， 所以地毯的长度为12＋5＝17(m)， 地毯的面积为17×2＝34(m 2)．所以购买这种地毯至少需要50×34＝1 700(元)．15．如图，已知等腰三角形ABC 的底边BC ＝20 cm ，D 是腰AB 上一点，且CD ＝16 cm ，BD ＝12 cm.(1)求证：CD⊥AB；(2)求该三角形的腰的长度．解：(1)证明：在△BCD 中，因为BD 2＋CD 2＝122＋162＝400＝BC 2， 所以△BCD 是直角三角形，其中∠BDC＝90°.所以CD⊥AB. (2)设AB ＝AC ＝x cm ，则AD ＝(x －12)cm. 因为CD⊥AB，所以在△ACD 中，AD 2＋CD 2＝AC 2， 即(x －12)2＋162＝x 2， 解得x ＝503.所以该三角形的腰的长度为503cm. 16．如图，在Rt △ABC 中，∠A ＝90°，D 为斜边BC 的中点，DE ⊥DF ，求证：EF 2＝BE 2＋CF 2.证明：延长ED 到点G ，使DG ＝DE ，连接FG ，CG. 在△EDF 和△GDF 中， ⎩⎪⎨⎪⎧DF ＝DF ，∠EDF ＝∠FDG＝90°，DE ＝DG ，所以△EDF≌△GDF(SAS)． 所以EF ＝FG.因为D 为斜边BC 的中点，所以BD ＝DC. 在△BDE 和△CDG 中，⎩⎪⎨⎪⎧BD ＝DC ，∠BDE ＝∠CDG，DE ＝DG ，所以△BDE≌△CDG(SAS)． 所以BE ＝CG ，∠B ＝∠BCG. 所以AB∥CG.所以∠GCA＝180°－∠A＝180°－90°＝90°. 在Rt △FCG 中，由勾股定理，得 FG 2＝CF 2＋CG 2＝CF 2＋BE 2， 所以EF 2＝FG 2＝BE 2＋CF 2.17．如图，点C 在线段BD 上，AC ⊥BD ，CA ＝CD ，点E 在线段CA 上，且满足DE ＝AB ，连接DE 并延长交AB 于点F.(1)求证：DE⊥AB；(2)若已知BC ＝a ，AC ＝b ，AB ＝c ，设EF ＝x ，则△ABD 的面积用代数式可表示为S △ABD＝12c(c ＋x)，你能借助本题提供的图形，证明勾股定理？试一试吧．解：(1)证明：因为AC⊥BD， 所以BC 2＝AB 2－AC 2，EC 2＝DE 2－CD 2， ∠BAC ＋∠ABC＝180°－90°＝90°. 又因为DE ＝AB ，CA ＝CD ， 所以BC 2＝EC 2，即BC ＝EC. 所以△ABC≌△DEC(SSS)． 所以∠BAC＝∠EDC. 所以∠EDC＋∠ABC＝90°.所以∠DFB＝180°－(∠EDC＋∠ABC)＝90°， 即DE⊥AB. (2)由题意，知S △ABD ＝S △BCE ＋S △ACD ＋S △ABE ＝12a 2＋12b 2＋12cx.因为S △ABD ＝12c(c ＋x)，所以12a 2＋12b 2 ＋12cx ＝12c(c ＋x)．所以a 2＋b 2＝c 2.。

1.1.2 探索勾股定理1.掌握勾股定理,理解和利用拼图验证勾股定理的方法.2.能运用勾股定理解决一些简单的实际问题.通过拼图法验证勾股定理,使学生经历观察、猜测、验证的过程,进一步体会数形结合的思想.培养学生大胆探索,不怕失败的精神.【重点】经历勾股定理的验证过程,能利用勾股定理解决实际问题.【难点】用拼图法验证勾股定理.【教师准备】教材图1 - 4,1 - 5,1 - 6,1 - 7的图片.【学生准备】4个全等的直角三角形纸片.导入一:【提问】直角三角形的三边有怎样的关系?在研究直角三角形三边关系时,我们是通过测量、数格子的方法发现了勾股定理,那么,我们怎样用科学的方法去证明勾股定理的正确性呢?请跟我一起去探索吧!导入二:上节课我们用什么方法探索发现了勾股定理?学生思考(测量、数格子).一、勾股定理的验证思路一【师生活动】师:投影教材P4图1 - 4,分别以直角三角形的三条边的长度为边长向外作正方形,你能利用这个图说明勾股定理的正确性吗?你是如何做的?与同伴进行交流.生:割补法进行验证.师:出示教材P5图1 - 5和图1 - 6,想一想:小明是怎样对大正方形进行割补的?生:讨论交流.师总结:图1 -5是在大正方形的四周补上四个边长为a,b,c的直角三角形;图1 -6是把大正方形分割成四个边长为a,b,c的直角三角形和一个小正方形.图1 - 5采用的是“补〞的方法,而图1 - 6采用的是“割〞的方法,请同学们将所有三角形和正方形的面积用a,b,c的关系式表示出来.(1)动笔操作,独立完成.师:图1 - 5中正方形ABCD的面积是多少?你们有哪些方法求?与同伴进行交流. (2)分组讨论面积的不同表示方法.ab+c2两种方法.生:得出(a+b)2,4×12(3)板书学生讨论的结果.【提问】你能利用图1 - 5验证勾股定理吗?生:根据刚刚讨论的情况列出等式进行化简.师:化简之后能得到勾股定理吗?生:得到a2+b2=c2,即两直角边的平方和等于斜边的平方,验证了勾股定理.师:你能用图1 - 6也证明一下勾股定理吗?独立完成.师:(强调)割补法是几何证明中常用的方法,要注意这种方法的运用.思路二教师出示教材图1 - 4及“做一做〞,让学生观察图1 - 5和图1 - 6.【提问】小明是怎样拼的?你来试一试.(学生以小组为单位展开拼图尝试,同伴之间讨论、争辩、互相启发,将拼好的图形画下来)【思考】“做一做〞的三个问题.教师讲评验证勾股定理的方法.二、勾股定理的简单应用思路一：出示教材P5例题,教师分析并抽象出几何图形.【问题】(1)图中三角形的三边长是否满足AB2=AC2+BC2?(2)要想求敌方汽车的速度,应先求什么?你能利用勾股定理完成这道题吗?(学生独立完成,教师指名板演)出示教材P8图1 - 8.【提问】判断图中三角形的三边长是否满足a2+b2=c2.(学生以组为单位合作完成,分别计算出每个正方形的面积.独立完成,有困难的可以合作完成)思路二我方侦察员小王在距离东西向公路400 m处侦察,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400 m,10 s后,汽车与他相距500 m,你能帮小王计算敌方汽车的速度吗?〔解析〕 根据题意,可以画出右图,其中点A 表示小王所在位置,点C ,点B 表示两个时刻敌方汽车的位置.由于小王距离公路400 m,因此∠C 是直角,这样就可以由勾股定理来解决这个问题了.解:由勾股定理,可以得到AB 2=BC 2+AC 2,也就是5002=BC 2+4002,所以BC =300. 敌方汽车10 s 行驶了300 m,那么它1 h 行驶的距离为300×6×60=108000(m),即它行驶的速度为108 km/h .[知识拓展] 利用面积相等来验证勾股定理,关键是利用不同的方法表示图形的面积,一要注意局部面积和等于整体面积的思想,二要注意拼接时要做到不重不漏. 曾任美国总统的伽菲尔德在?新英格兰教育日志?上发表了他提出的一个勾股定理证明,如下图,这就是他拼出的图形.它的面积有两种表示方法,既可以表示为12(a +b )(a +b ),又可以表示为12(2ab +c 2),所以可得12(a +b )(a +b )=12(2ab +c 2),化简可得a 2+b 2=c 2.1.勾股定理的验证方法{测量法数格子法面积法2.在实际问题中,首先要找到直角三角形,然后再应用勾股定理解题. 1.以下选项中,不能用来证明勾股定理的是 ( )解析:A,B,C 都可以利用图形面积得出a ,b ,c 的关系,即可证明勾股定理,故A,B,C 选项不符合题意;D,不能利用图形面积证明勾股定理,故此选项正确.应选D .2.用四个边长均为a ,b ,c 的直角三角板,拼成如下图的图形,那么以下结论中正确的选项是 ( )A.c 2=a 2+b 2B.c 2=a 2+2ab +b 2C.c2=a2-2ab+b2D.c2=(a+b)2解析:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,ab×4+(b-a)2,整理得c2=a2+b2.里面的小四边形也为正方形,边长为b-a,那么有c2=12应选A.3.如下图,大正方形的面积是,另一种方法计算大正方形的面积是,两种结果相等,推得勾股定理是.ab+c2,即(a+b)2=4×解析:如下图,大正方形的面积是(a+b)2,另一种计算方法是4×121ab+c2,化简得a2+b2=c2.2ab+c2a2+b2=c2答案:(a+b)24×124.操作:剪假设干个大小形状完全相同的直角三角形,三边长分别记为a,b,c(如图(1)所示),分别用4张这样的直角三角形纸片拼成如图(2)(3)所示的形状,图(2)中的两个小正方形的面积S2,S3与图(3)中小正方形的面积S1有什么关系?你能得到a,b,c 之间有什么关系?解析:根据图形的形状得出面积关系,进一步证明勾股定理即可求解.解:分别用4张直角三角形纸片,拼成如图(2)(3)所示的形状,观察图(2)(3)可发现,图(2)中的两个小正方形的面积之和等于图(3)中的小正方形的面积,即S2+S3=S1,这个结论用关系式可表示为a2+b2=c2.1.1.21.勾股定理的验证.2.勾股定理的简单应用.一、教材作业【必做题】教材第6页随堂练习.【选做题】教材第7页习题1.2第3题.二、课后作业【根底稳固】1.我国古代数学家赵爽的?勾股圆方图?是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如下图).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a,b,那么(a-b)2的值是 ()A.1B.2C.12D.132.历史上对勾股定理的一种证法采用了如下图的图形,其中两个全等的直角三角形边AE,EB在一条直线上.证明中用到的面积相等的关系是()A.SΔEDA =SΔCEBB.SΔEDA+SΔCEB=SΔCDEC.S四边形CDAE =S四边形CDEBD.SΔEDA+SΔCDE+SΔCEB=S四边形ABCD3.北京召开的第24届国际数学家大会会标的图案如下图.(1)它可以看做是由四个边长分别为a,b,c的直角三角形拼成的,请从面积关系出发,写出一个关于a,b,c的等式.(要有过程)(2)请用四个这样的直角三角形再拼出另一个几何图形,也能验证(1)中所写的等式.(不用写出验证过程)(3)如果a2+b2=100,a+b=14,求此直角三角形的面积.【能力提升】4.勾股定理是几何中的一个重要定理.在我国古算书?周髀算经?中就有“假设勾三,股四,那么弦五〞的记载.如图(1)所示的是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图(2)是由图(1)放入矩形内得到的,∠BAC=90°,AB=6,AC=8,点D,E,F,G,H,I都在矩形KLMJ的边上,那么矩形KLMJ的面积为.5.在北京召开的国际数学家大会的会标如下图,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,假设大正方形的面积是13,小正方形的面积是1,直角三角形的较长直角边为a,较短直角边为b,那么a4+b4的值为()A.35B.43C.89D.976.据传当年毕达哥拉斯借助如下图的两个图验证了勾股定理,你能说说其中的道理吗?7.如下图,在平面内,把矩形ABCD 绕点B 按顺时针方向旋转90°得到矩形A'BC'D'.设AB =a ,BC =b ,BD =c.请利用该图验证勾股定理.【拓展探究】8.我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图〞,后人称其为“赵爽弦图〞(如图(1)所示).图(2)是由弦图变化得到的,它是用八个全等的直角三角形拼接而成的.记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为S 1,S 2,S 3.假设S 1+S 2+S 3=16,那么S 2的值是.9.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法〞给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图(1)或图(2)摆放时,都可以用“面积法〞来证明,下面是小聪利用图(1)证明勾股定理的过程.将两个全等的直角三角形按图(1)所示摆放,连接DC ,其中∠DAB =90°,求证a 2+b 2=c 2.证明:连接DB ,过点D 作BC 边上的高DF ,那么DF =EC =b-a. ∵S 四边形ADCB=S ΔACD+S ΔABC=12b 2+12ab ,又∵S 四边形ADCB =S ΔADB+S ΔDCB=12c 2+12a (b-a ),∴12b 2+12ab =12c 2+12a (b-a ),∴a 2+b 2=c 2.请参照上述证法,利用图(2)完成下面的验证过程.将两个全等的直角三角形按图(2)所示摆放,其中∠DAB =90°,连接BE. 验证a 2+b 2=c 2.证明:连接 , ∵S 五边形ACBED= , 又∵S 五边形ACBED= ,∴a 2+b 2=c 2. 【答案与解析】1.A(解析:根据勾股定理可得a 2+b 2=13,四个直角三角形的面积和是12ab ×4=13-1=12,即2ab =12,那么(a-b )2=a 2-2ab +b 2=13-12=1.应选A.) 2.D(解析:由S ΔEDA+S ΔCDE+S ΔCEB=S 四边形ABCD,可知12ab +12c 2+12ab =12(a +b )2,∴c 2+2ab =a 2+2ab +b 2,整理得a 2+b 2=c 2,∴证明中用到的面积相等的关系是S ΔEDA+S ΔCDE+S ΔCEB=S 四边形ABCD.应选D .)3.解:(1)大正方形的面积=4个三角形的面积+小正方形的面积,即c 2=4×12ab +(a-b )2=a 2+b 2. (2)如下图. (3)∵2ab =(a +b )2-(a 2+b 2)=196-100=96,∴ab =48,∴S =12ab =12×48=24.4.440(解析:如下图,延长AB 交KL 于P ,延长AC 交LM 于Q ,那么ΔABC ≌ΔPFB ≌ΔQCG ,∴PB =AC =8,CQ =AB =6,∵图(2)是由图(1)放入矩形内得到的,∴IP =8+6+8=22,DQ =6+8+6=20,∴矩形KLMJ 的面积=22×20=440.故答案为440.)5.D(解析:依题意有:a 2+b 2=大正方形的面积=13,2ab =四个直角三角形的面积和=13-1=12,ab =6,那么a 4+b 4=(a 2+b 2)2-2a 2b 2=(a 2+b 2)2-2(ab )2=132-2×62=169-72=97.应选D .)6.解:根据题意,第一个图形中间空白小正方形的面积是c 2;第二个图形中空白的两个小正方形的面积的和是a 2+b 2,∵它们的面积都等于边长为a +b 的正方形的面积-4个直角边分别为a ,b 的直角三角形的面积和,∴a 2+b 2=c 2,即在直角三角形中斜边的平方等于两直角边的平方和.7.解:连接D'D ,依题意,图中的四边形DAC'D'为直角梯形,ΔDBD'为等腰直角三角形,Rt ΔDAB 和Rt ΔBC'D'的形状和大小完全一样,设梯形DAC'D'的面积为S ,那么S =12(a +b )(a +b )=12(a 2+b 2)+ab ,又S =S Rt ΔDBD'+2S Rt ΔABD =12c 2+2×12ab =12c 2+ab ,∴12(a 2+b 2)+ab =12c 2+ab ,因此a 2+b 2=c 2.8.163(解析:∵八个直角三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形,∴CG =NG ,CF =DG =NF =GK ,∴S 1=(CG +DG )2=CG 2+DG 2+2CG ·DG =GF 2+2CG ·DG ,S 2=GF 2,S 3=(NG-NF )2=NG 2+NF 2-2NG ·NF ,∴S 1+S 2+S 3=GF 2+2CG ·DG +GF 2+NG 2+NF 2-2NG ·NF =3GF 2=16,∴GF 2=163,∴S 2=163.故答案为163.)9.证明:连接BD ,过点B 作DE 边上的高BF ,那么BF =b-a ,∵S 五边形ACBED =S ΔACB +S ΔABE +S ΔADE =12ab +12b 2+12ab ,又∵S 五边形ACBED =S ΔACB +S ΔABD +S ΔBDE =12ab +12c 2+12a (b-a ),∴12ab +12b 2+12ab =12ab +12c 2+12a (b-a ),∴a 2+b 2=c 2.在课堂教学中,始终注意了调动学生的积极性.兴趣是最好的老师,所以无论是引入、拼图,还是历史回忆,都注意去调动学生,让学生满怀激情地投入到活动中.勾股定理作为“千古第一定理〞,其魅力在于其历史价值和应用价值,因此充分挖掘了其内涵.特别是让学生事先进行调查,再在课堂上进行展示,这极大地调动了学生的积极性,既加深了对勾股定理文化的理解,又培养了学生收集、整理资料的能力.在教学过程中,过于让学生发散思维,而导致课堂秩序略有松散.勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,可以设计拼图活动,先让学生从形上感知,再层层设问,从面积(数)入手,师生共同探究,最后由学生独立探究,这样学生较容易突破本节课的难点.随堂练习(教材第6页)解:因为OM 2=MN 2+NO 2=302+402=502,所以OM =50 km .因为OQ 2=OP 2+PQ 2=502+1202=1302,所以OQ =130 km .所以该沿江高速公路的造价预计是(50+130)×5000=900000(万元).答:该沿江高速公路的造价预计是900000万元.习题1.2(教材第6页)1.解:因为42+32=52,所以旗杆折断之前的高为5+3=8(m).2.解:因为S 梯形=12(a +b )·(a +b )=12(a 2+2ab +b 2)=12a 2+ab +12b 2,S 梯形=12ab +12ab +12c 2=ab +12c 2,所以12a 2+ab +12b 2=ab +12c 2,所以a 2+b 2=c 2.(这个方法与本节探索的方法思路一样,都是构造一个图形,利用两种方法计算该图形的面积,从而得到a 2+b 2=c 2)3.解:箱子能放进储藏室,因为0.82+0.52<1.22.古诗中的数学题请你先欣赏下面一首诗:平平湖水清可鉴,面上半尺生红莲;出泥不染亭亭立,忽被强风吹一边;渔人观看忙向前,花离原位两尺远;能算诸君请解题,湖水如何知深浅?你能用所学的数学知识解决上述诗中的问题吗?〔解析〕 要解决诗中提出的问题,关键是将实际问题转化为数学问题,画出符合题意的图形,如下图.在Rt ΔBCD 中,由勾股定理建立方程求线段的长.解:如下图,AD 表示莲花的高度,CD 是水的深度,CB 是莲花吹倒后离原位的距离.设CD =x 尺,那么AD =BD =(x +12)尺. 在Rt ΔBCD 中,∠BCD =90°,由勾股定理得BD 2=CD 2+BC 2,即(x +12)2=22+x 2. 解得x =3.75.所以所求的湖水深度为3.75尺.[方法总结]建立数学模型是解决实际问题的常用方法.本例是利用莲花无风时与水面垂直构造直角三角形这一几何模型.在直角三角形中常用勾股定理建立方程求线段的长.。