K均值聚类分析(2020年整理).pptx

实验一 K均值聚类算法
一．实验平台
VC6.0
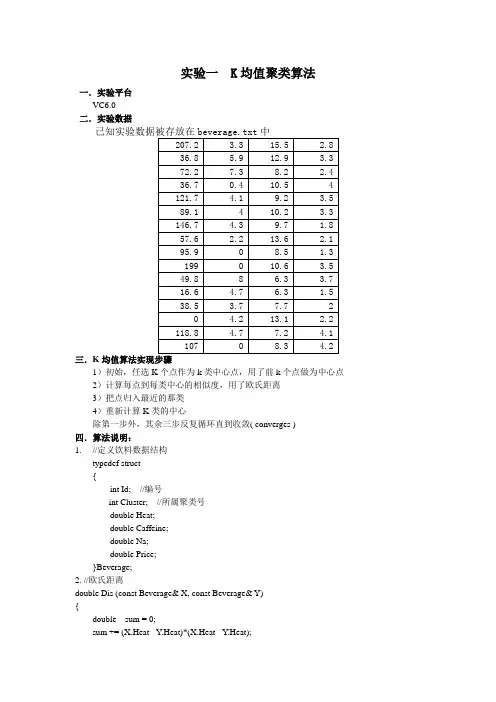
二．实验数据
三．K均值算法实现步骤
1）初始，任选K个点作为k类中心点，用了前k个点做为中心点2）计算每点到每类中心的相似度，用了欧氏距离
3）把点归入最近的那类
4）重新计算K类的中心
除第一步外，其余三步反复循环直到收敛( converges )
四．算法说明：
1. //定义饮料数据结构
typedef struct
{
int Id; //编号
int Cluster; //所属聚类号
double Heat;
double Caffeine;
double Na;
double Price;
}Beverage;
2. //欧氏距离------------------------
double Dis (const Beverage& X, const Beverage& Y)
{
double sum = 0;
sum += (X.Heat - Y.Heat)*(X.Heat - Y.Heat);
sum += (X.Caffeine - Y.Caffeine)*(X.Caffeine - Y.Caffeine);
sum += (X.Na - Y.Na)*(X.Na - Y.Na);
sum += (X.Price - Y.Price)*(X.Price - Y.Price);
return sqrt(sum);
}
五．结果
聚类后：
六．总结实验
使用前k个数据做为初始中心点，与实验结果还比较符合的。

1 案例题目：选取一组点（三维或二维），在空间内绘制出来，之后根据K 均值聚类，把这组点分为n 类。

此例中选取的三维空间内的点由均值分别为(0,0,0),(4,4,4),(-4,4,-4) ，3 0 0 0 0 0 30 0协方差分别为0 3 0，0 3 0 ，0 3 0 的150 个由mvnrnd 函数随机0 0 3 0 0 3 00 3生成。

2 原理运用与解析：2.1 聚类分析的基本思想聚类分析是根据“物以类聚” 的道理，对样本或指标进行分类的一种多元统计分析方法，它们讨论的对象是大量的样本，要求能合理地按各自的特性进行合理的分类。

对于所选定的属性或特征，每组内的模式都是相似的，而与其他组的模式差别大。

一类主要方法是根据各个待分类模式的属性或特征相似程度进行分类，相似的归为一类，由此将待分类的模式集分成若干个互不重叠的子集，另一类主要方法是定义适当的准则函数运用有关的数学工具进行分类。

由于在分类中不需要用训练样本进行学习和训练，故此类方法称为无监督分类。

聚类的目的是使得不同类别的个体之间的差别尽可能的大，而同类别的个体之间的差别尽可能的小。

聚类又被称为非监督分类，因为和分类学习相比，分类学习的对象或例子有类别标记，而要聚类的例子没有标记，需要由聚类分析算法来自动确定，即把所有样本作为未知样本进行聚类。

因此，分类问题和聚类问题根本不同点为：在分类问题中，知道训练样本例的分类属性值，而在聚类问题中，需要在训练样例中找到这个分类属性值。

聚类分析的基本思想是认为研究的样本或变量之间存在着程度不同的相似性（亲疏关系）。

研究样本或变量的亲疏程度的数量指标有两种：一种叫相似系数，性质越接近的样本或变量，它们的相似系数越接近 1 或-1 ，而彼此无关的变量或样本它们的相似系数越接近0，相似的为一类，不相似的为不同类。

另一种叫距离，它是将每一个样本看做p维空间的一个点，并用某种度量测量点与点之间的距离，距离较近的归为一类，距离较远的点应属于不同的类。

k均值聚类（k-means）机器学习中有两类的大问题，一个是分类，一个是聚类。

分类是根据一些给定的已知类别标号的样本，训练某种学习机器，使它能够对未知类别的样本进行分类。

这属于supervised learning （监督学习）。

而聚类指事先并不知道任何样本的类别标号，希望通过某种算法来把一组未知类别的样本划分成若干类别，这在机器学习中被称作unsupervised learning （无监督学习）。

在本文中，我们关注其中一个比较简单的聚类算法：k-means算法。

一、k-means 算法通常，人们根据样本间的某种距离或者相似性来定义聚类，即把相似的（或距离近的）样本聚为同一类，而把不相似的（或距离远的）样本归在其他类。

我们以一个二维的例子来说明下聚类的目的。

如下图左所示，假设我们的n个样本点分布在图中所示的二维空间。

从数据点的大致形状可以看出它们大致聚为三个cluster，其中两个紧凑一些，剩下那个松散一些。

我们的目的是为这些数据分组，以便能区分出属于不同的簇的数据，如果按照分组给它们标上不同的颜色，就是像下图右边的图那样：如果人可以看到像上图那样的数据分布，就可以轻松进行聚类。

但我们怎么教会计算机按照我们的思维去做同样的事情呢？这里就介绍个集简单和经典于一身的k-means算法。

k-means算法是一种很常见的聚类算法，它的基本思想是：通过迭代寻找k个聚类的一种划分方案，使得用这k个聚类的均值来代表相应各类样本时所得的总体误差最小。

k-means算法的基础是最小误差平方和准则。

其代价函数是：式中，生⑴表示第i个聚类的均值。

我们希望代价函数最小，直观的来说，各类内的样本越相似，其与该类均值间的误差平方越小，对所有类所得到的误差平方求和，即可验证分为k类时，各聚类是否是最优的。

上式的代价函数无法用解析的方法最小化，只能有迭代的方法。

k-means算法是将样本聚类成k个簇（cluster，其中卜是用户给定的，其求解过程非常直观简单，具体算法描述如下:1、随机选取k个聚类质心点2、重复下面过程直到收敛｛对于每一个样例i计算其应该属于的类:对于每一个类j重新计算该类的质心：£3二期=」｝/｝由「£隗1｛加=升卜图展示了对n个样本点进行K-means聚类的效果，这里k取2。

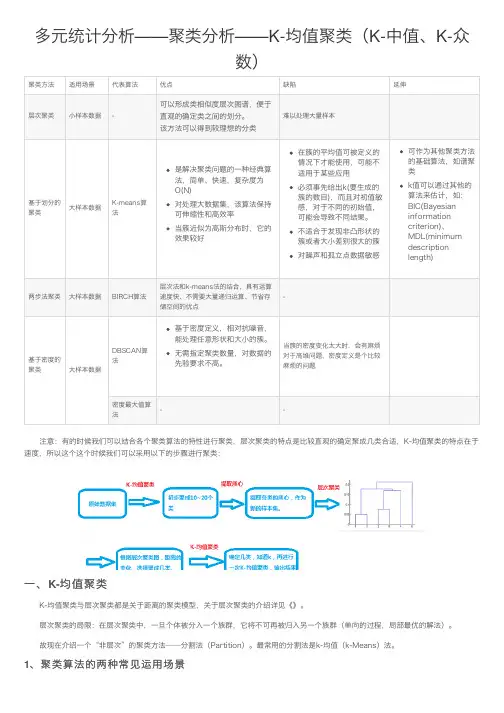
多元统计分析——聚类分析——K-均值聚类（K-中值、K-众数）注意：有的时候我们可以结合各个聚类算法的特性进⾏聚类，层次聚类的特点是⽐较直观的确定聚成⼏类合适，K-均值聚类的特点在于速度，所以这个这个时候我们可以采⽤以下的步骤进⾏聚类：⼀、K-均值聚类K-均值聚类与层次聚类都是关于距离的聚类模型，关于层次聚类的介绍详见《》。

层次聚类的局限：在层次聚类中，⼀旦个体被分⼊⼀个族群，它将不可再被归⼊另⼀个族群（单向的过程，局部最优的解法）。

故现在介绍⼀个“⾮层次”的聚类⽅法——分割法（Partition）。

最常⽤的分割法是k-均值（k-Means）法。

1、聚类算法的两种常见运⽤场景发现异常情况：如果不对数据进⾏任何形式的转换，只是经过中⼼标准化或级差标准化就进⾏快速聚类，会根据数据分布特征得到聚类结果。

这种聚类会将极端数据单独聚为⼏类。

这种⽅法适⽤于统计分析之前的异常值剔除，对异常⾏为的挖掘，⽐如监控银⾏账户是否有洗钱⾏为、监控POS机是有从事套现、监控某个终端是否是电话卡养卡客户等等。

将个案数据做划分：出于客户细分⽬的的聚类分析⼀般希望聚类结果为⼤致平均的⼏⼤类（原始数据尽量服从正态分布，这样聚类出来的簇的样本点个数⼤致接近），因此需要将数据进⾏转换，⽐如使⽤原始变量的百分位秩、Turkey正态评分、对数转换等等。

在这类分析中数据的具体数值并没有太多的意义，重要的是相对位置。

这种⽅法适⽤场景包括客户消费⾏为聚类、客户积分使⽤⾏为聚类等等。

以上两种场景的⼤致步骤如下：聚类算法不仅是建模的终点，更是重要的中间预处理过程，基于数据的预处理过程，聚类算法主要应⽤于以下领域：图像压缩：在使⽤聚类算法做图像压缩过程时，会先定义K个颜⾊数（例如128种颜⾊、256种颜⾊），颜⾊数就是聚类类别的数量；K均值聚类算法会把类似的颜⾊分别放在K个簇中，然后每个簇使⽤⼀种颜⾊来代替原始颜⾊，那么结果就是有多少个簇，就⽣成了由多少种颜⾊构成的图像，由此实现图像压缩。

聚类分析概述、k均值聚类算法KMeans处理数据及可视化⼀概述聚类分析⽬的将⼤量数据集中具有“相似”特征的数据点或样本划分为⼀个类别常见应⽤场景在没有做先验经验的背景下做的探索性分析样本量较⼤情况下的数据预处理⼯作将数值类的特征分成⼏个类别聚类分析能解决的问题包括数据集可以分为⼏类每个类别有多少样本量不同类别中各个变量的强弱关系如何不同类别的典型特征是什么k均值聚类算法 KMeans注意事项需要处理异常值如果建模的特征中，量纲差距⽐较⼤，需要做归⼀化/标准化创建KMeans对象建模n_cluster 聚类个数init='k-means++' 在选点的时候，找距离初始点⽐较远的点random_state 随机种⼦数kmeans.inertia_ 簇内误差平⽅和轮廓系数 metrics.silhouette_score()kmeans_model.cluster_centers_ 聚类中⼼点kmeans_bels_ 聚类之后的标签⼆案例1 数据准备import pandas as pddf = pd.read_csv('data.csv')# 使⽤最后两列作为分群依据x = df.iloc[:,3:].values2 创建 KMeans 模型，进⾏聚类【核⼼代码】# 导包from sklearn.cluster import KMeans# 模型创建kmeans_model = KMeans(n_clusters=5, init='k-means++', random_state= 11)# 进⾏聚类处理y_kmeans = kmeans_model.fit_predict(x)此时已经将数据分成了5类，将标签加⼊数据中3 聚类结果可视化# 导⼊可视化⼯具包import matplotlib.pyplot as plt%matplotlib inline# 颜⾊和标签列表colors_list = ['red', 'blue', 'green','yellow','pink']labels_list = ['Traditional','Normal','TA','Standard','Youth']# 需要将DataFrame转成ndarray,才能进⾏ x[y_kmeans==i,0]x = x.valuesfor i in range(5):plt.scatter(x[y_kmeans==i,0], x[y_kmeans== i,1], s=100,c=colors_list[i],label=labels_list[i])# 聚类中⼼点plt.scatter(kmeans_model.cluster_centers_[:,0],kmeans_model.cluster_centers_[:,1], s=300,c='black',label='Centroids') plt.legend()plt.xlabel('Annual Income (k$)')plt.ylabel('Spending Score (1-100)')plt.show()4 评估聚类个数# ⽤于盛放簇内误差平⽅和的列表distortion = []for i in range(1,11):kmeans = KMeans(n_clusters=i,init='k-means++', random_state=11)kmeans.fit(x)distortion.append(kmeans.inertia_)plt.plot(range(1,11), distortion)plt.title('The Elbow Method')plt.xlabel('Number of cluster')plt.ylabel('Distortion')plt.show()完成辣！附⼏个变量说明，便于复习================================================本⽂仅⽤于学习。

机器学习（⼆）——K-均值聚类（K-means）算法最近在看《机器学习实战》这本书，因为⾃⼰本⾝很想深⼊的了解机器学习算法，加之想学python，就在朋友的推荐之下选择了这本书进⾏学习，在写这篇⽂章之前对FCM有过⼀定的了解，所以对K均值算法有⼀种莫名的亲切感，⾔归正传，今天我和⼤家⼀起来学习K-均值聚类算法。

⼀ K-均值聚类（K-means）概述1. 聚类“类”指的是具有相似性的集合。

聚类是指将数据集划分为若⼲类，使得类内之间的数据最为相似，各类之间的数据相似度差别尽可能⼤。

聚类分析就是以相似性为基础，对数据集进⾏聚类划分，属于⽆监督学习。

2. ⽆监督学习和监督学习上⼀篇对KNN进⾏了验证，和KNN所不同，K-均值聚类属于⽆监督学习。

那么监督学习和⽆监督学习的区别在哪⼉呢？监督学习知道从对象（数据）中学习什么，⽽⽆监督学习⽆需知道所要搜寻的⽬标，它是根据算法得到数据的共同特征。

⽐如⽤分类和聚类来说，分类事先就知道所要得到的类别，⽽聚类则不⼀样，只是以相似度为基础，将对象分得不同的簇。

3. K-meansk-means算法是⼀种简单的迭代型聚类算法，采⽤距离作为相似性指标，从⽽发现给定数据集中的K个类，且每个类的中⼼是根据类中所有值的均值得到，每个类⽤聚类中⼼来描述。

对于给定的⼀个包含n个d维数据点的数据集X以及要分得的类别K,选取欧式距离作为相似度指标，聚类⽬标是使得各类的聚类平⽅和最⼩，即最⼩化：结合最⼩⼆乘法和拉格朗⽇原理，聚类中⼼为对应类别中各数据点的平均值，同时为了使得算法收敛，在迭代过程中，应使最终的聚类中⼼尽可能的不变。

4. 算法流程K-means是⼀个反复迭代的过程，算法分为四个步骤：1）选取数据空间中的K个对象作为初始中⼼，每个对象代表⼀个聚类中⼼；2）对于样本中的数据对象，根据它们与这些聚类中⼼的欧⽒距离，按距离最近的准则将它们分到距离它们最近的聚类中⼼（最相似）所对应的类；3）更新聚类中⼼：将每个类别中所有对象所对应的均值作为该类别的聚类中⼼，计算⽬标函数的值；4）判断聚类中⼼和⽬标函数的值是否发⽣改变，若不变，则输出结果，若改变，则返回2）。

课程实验聚类分析实验实验目的：加深对K 均值聚类分析算法的理解，掌握K 均值聚类分析分类器的设计方法。

实验内容：根据实验数据设计K均值聚类分析分类器，实验数据采用遥感彩色图像，以图像的所有象素为样本集，每一象素点的R、G、B值作为其特征向量。

1）选择合适的类别数K和初始聚类中心。

2）选择距离测度。

3）设计迭代中止条件，或人为设定迭代次数。

4）循环迭代结束时，各类的所有象素其R、G、B值用各类中心的R、G、B值表示，画出分类结果图。

5）分析不同初始聚类中心和迭代条件对分类效果的影响。

实验报告要求：上交电子版实验报告，实验报告内容包括问题求解思路，实验结果图表、实验结果分析以及实验源程序。

（采用Matlab或 C语言）问题求解思路：1)以下2个条件为可控制量：①选择合适的类别数K和初始聚类中心②设定迭代次数以K 均值聚类分析算法为基础运用MATLAB编写程序2）设定迭代次数，得出分析后的图片与原图片进行比较。

3）根据取值的不同分析不同初始聚类中心和迭代条件对分类效果的影响。

实验结果图表：（1）K值为6，迭代次数不同时实验结果如下（2）K值为7，迭代次数不同时实验结果如下实验代码：clearall;closeall;clc;a=imread('K:\model.bmp');R=a(:,:,1);G=a(:,:,2);B=a(:,:,3);r=reshape(R,50141,1);g=reshape(G,50141,1);b=reshape(B,50141,1);p=double([r,g,b]);z1=p(randi(50141,1),:);z2=p(randi(50141,1),:);z3=p(randi(50141,1),:);z4=p(randi(50141,1),:);z5=p(randi(50141,1),:);z6=p(randi(50141,1),:);zn=p(randi(50141,1),:); %n为K值d1=zeros(1,50141);d2=zeros(1,50141);d3=zeros(1,50141);d4=zeros(1,50141);d5=zeros(1,50141);d6=zeros(1,50141);dn=zeros(1,50141);%n为K值d=zeros(1,50141);fori=1:5%i:m m%为迭代次数m1=0;m2=0;m3=0;m4=0;m5=0;m6=0;mn=0;%n为K值for j=1:50141d1(j)=sqrt(dot((p(j,:)-z1),(p(j,:)-z1)));d2(j)=sqrt(dot((p(j,:)-z2),(p(j,:)-z2)));d3(j)=sqrt(dot((p(j,:)-z3),(p(j,:)-z3)));d4(j)=sqrt(dot((p(j,:)-z4),(p(j,:)-z4)));d5(j)=sqrt(dot((p(j,:)-z5),(p(j,:)-z5)));d6(j)=sqrt(dot((p(j,:)-z6),(p(j,:)-z6)));dn(j)=sqrt(dot((p(j,:)-zn),(p(j,:)-zn)));%n为K值endfor j=1:50141k=min([d1(j),d2(j),d3(j),d4(j),d5(j),d6(j)]); if d1(j)==kd(j)=1;elseif d2(j)==kd(j)=2;elseif d3(j)==kd(j)=3;elseif d4(j)==kd(j)=4;elseif d5(j)==kd(j)=5;elseif d6(j)==kd(j)=6;elseifdn(j)==kd(j)=n;%为K值endendz1=[0 0 0];z2=[0 0 0];z3=[0 0 0];z4=[0 0 0];z5=[0 0 0];z6=[0 0 0];zn=[0 0 0];%n为K值for j=1:50141if d(j)==1z1=z1+p(j,:);m1=m1+1;elseif d(j)==2z2=z2+p(j,:);m2=m2+1;elseif d(j)==3z3=z3+p(j,:);m3=m3+1;elseif d(j)==4z4=z4+p(j,:);m4=m4+1;elseif d(j)==5z5=z5+p(j,:);m5=m5+1;elseif d(j)==6z6=z6+p(j,:);m6=m6+1;elseif d(j)==nzn=zn+p(j,:);mn=mn+1; %n为K值endendz1=z1/m1;z2=z2/m2;z3=z3/m3;z4=z4/m4;z5=z5/m5;z6=z6/m6;zn=zn/mn;%n为K值endfor j=1:50141if d(j)==1p(j,:)=z1;elseif d(j)==2p(j,:)=z2;elseif d(j)==3p(j,:)=z3;elseif d(j)==4p(j,:)=z4;elseif d(j)==5p(j,:)=z5;elseif d(j)==6p(j,:)=z6;elseif d(j)==np(j,:)=zn;%n为K值endendp=uint8(p);r=p(:,1);g=p(:,2);b=p(:,3);R=reshape(r,247,203);G=reshape(g,247,203);B=reshape(b,247,203);a(:,:,1)=R;a(:,:,2)=G;a(:,:,3)=B;subplot(1,2,1);imshow(imread('F:\matlab2012_a\bin\模式识别\实验三\model.bmp'));title('原图片');subplot(1,2,2);imshow(a);title('图片（分析后K值为7，迭代5次)');。

k均值聚类法k均值聚类法是一种常见的无监督学习聚类方法。

其主要思想是将样本分成k类，使得同一类内样本之间的距离尽可能小，不同类之间的距离尽可能大。

本文将从以下几个方面分步骤阐述k均值聚类法。

一、算法流程1、初始化：随机选择k个样本作为主要质心。

2、分配样本：将所有样本分配到与它距离最近的质心中心。

3、移动质心：对于每个类别，重新计算该类别的质心中心。

4、重复操作2、3，直到稳定性达到预定值或迭代次数到达限度。

二、算法优缺点优点：1、易于实现。

2、速度较快，适用于大规模数据集。

3、可扩展性好，适用于多种数据类型和聚类目标。

缺点：1、对初值敏感。

质心的选择会影响聚类效果。

2、不一定能得到全局最优解。

很容易被局部最优解所卡住。

三、算法应用1、变化检测。

将多期遥感数据进行k均值聚类，以找到地表的变化现象。

2、图像分割。

将图像拆分成相似的区域，以便进一步处理。

3、市场细分。

将消费者分成相似的市场细分，以便为每个细分市场提供更好的产品或服务。

四、算法改进为了让k均值聚类法更加适用，也有学者提出了一些改进方法，例如：1、K-means++。

改进的质心初始化策略，可以使质心更加分散，从而获得更好的聚类效果。

2、MiniBatch K-means。

在随机中心和大规模数据集上进行k均值聚类，可以降低时间和计算成本。

3、Kernel k-means。

使用核技巧在非线性空间中进行聚类，可以获得更好的效果。

五、总结综上所述，k均值聚类法是一种简单而有效的聚类算法。

虽然在某些情况下会出现一些问题，但对于大多数聚类问题，它仍然是一种值得使用的方法。

此外，为了得到更好的聚类结果，我们也可以在实际应用中使用改进的方法。

K-均值聚类算法1. K-均值聚类算法的工作原理：K 均值算法（K-Means algorithm ）是最常用的聚类算法之一，属于划分聚类方法。

对于数据样本集 X={x1,x2,…,xn}，n 为样本数，设拟划分为 k 个聚类 V={v1,v2,…,vk }，cj 为 vj 的中心，j=1,2,…,k 。

k 均值算法将问题转化为组合优化问题：目标函数为),(minF 1j 1j i k ni j i y x d a ∑∑===；约束为：（1.1）αij ∈{0,1}；（1.2）1a 1ij =∑=kj ；（1.3）0a 1ij >∑=ni 。

其中，为样本与聚类中心的欧氏距离。

式（1.1）限制一数据样本属于或不属于某一聚类，二者必居其一；式（1.2）规定一数据样本只属于一个聚类；式（1.3）表明聚类非空。

K-means 聚类算法步骤：1）从数据集中随机选择 k 个样本作为初始聚类中心；2）将每个样本分配到与之最近的初始聚类中心；3）将所有样本分配到相应的聚类后，重新计算聚类中心 Cj ；4）循环执行第 2）步和第 3）步，直至聚类中心不再变化，算法终止。

2.K-means 聚类算法的一般步骤（1） 从 n 个数据对象任意选择 k 个对象作为初始聚类中心；（2） 根据每个聚类对象的均值（中心对象），计算每个对象与这些中心对象的距离；并根据最小距离重新对相应对象进行划分；（3） 重新计算每个（有变化）聚类的均值（中心对象）；（4） 循环（2）到（3）直到每个聚类不再发生变化为止。

3.K-均值聚类算法的总结K 均值算法原理简单、对大数据集计算速度很快，因此应用广泛。

但算法对初始聚类中心选择非常敏感。

此外，基于梯度下降和算法的贪心性，使得算法易于陷入局部极值而无法达到全局最优。

针对 k 均值算法易陷入局部最优的缺陷，许多研究将启发式规则引入算法，使聚类中心的移动产生扰动，取得理想效果。

本文提出将模拟退火算法与 k 均值算法相结合，以提高算法的全局寻优能力。