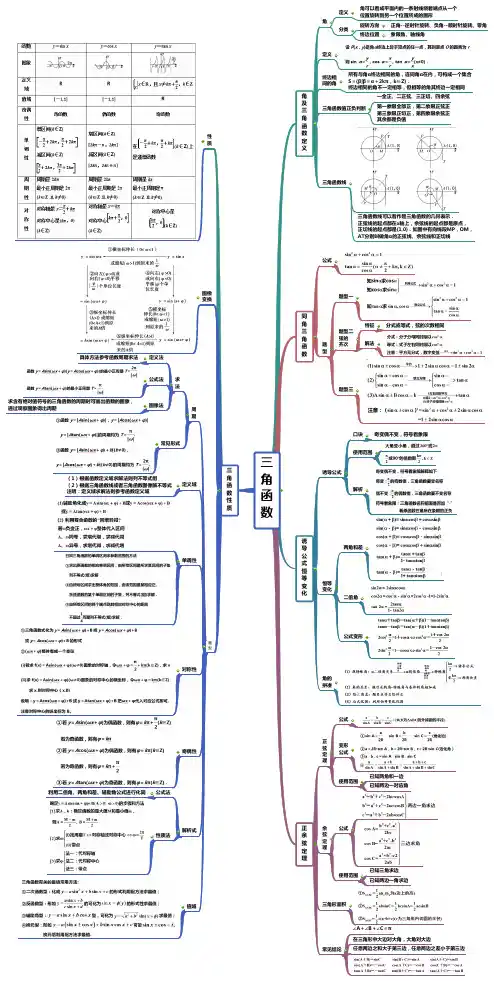
三角函数知识结构图
- 格式:doc
- 大小:57.50 KB
- 文档页数:2
所有与角α终边相同的角,连同角α在内,可构成一个集合特征
解法
分式或等式,弦的次数相同
奇变偶不变,符号看象限
求含有绝对值符号的三角函数的周期时可画出函数的图象,通过观察图象得出周期
(1)根据函数定义域求解法则列不等式组
(2)根据三角函数线或者三角函数图像解不等式公式法
利用二倍角、两角和差、辅助角公式进行化简
已知两角和一边已知两边一对应角
已知三角求边已知两边一角求边
A +∠
B +∠
C =π
在三角形中大边对大角,大角对大边。
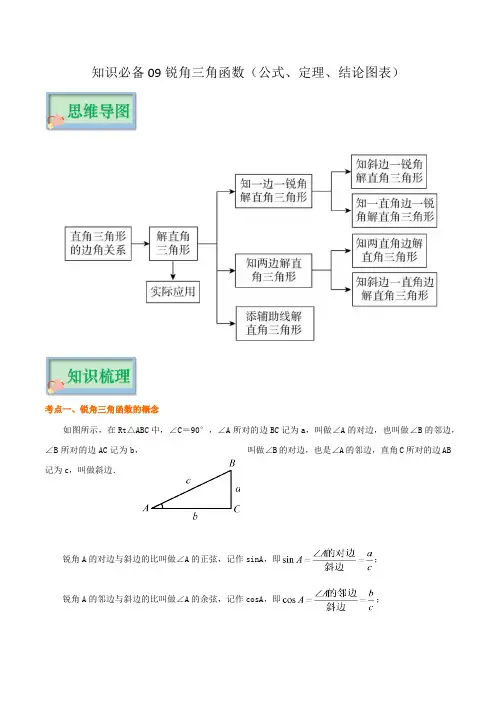
知识必备09锐角三角函数(公式、定理、结论图表)考点一、锐角三角函数的概念如图所示,在Rt△ABC中,∠C=90°,∠A所对的边BC记为a,叫做∠A的对边,也叫做∠B的邻边,∠B所对的边AC记为b,叫做∠B的对边,也是∠A的邻边,直角C所对的边AB记为c,叫做斜边. 锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即;锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即;锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即.同理;;.要点诠释: (1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化. (2)sinA,cosA,tanA分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin与∠A,cos与∠A,tan与∠A的乘积.书写时习惯上省略∠A的角的记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、常写成、、. (3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在. (4)由锐角三角函数的定义知:当角度在0°<∠A<90°之间变化时,,,tanA>0.典例1:(2022•扬州)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,若b2=ac,则sin A的值为 . .【分析】根据勾股定理和锐角三角函数的定义解答即可.【解答】解:在△ABC中,∠C=90°,∴c2=a2+b2,∵b2=ac,∴c2=a2+ac,等式两边同时除以ac得:=+1,令=x,则有=x+1,∴x2+x﹣1=0,解得:x1=,x2=(舍去),当x=时,x≠0,∴x=是原分式方程的解,∴sin A==.故答案为:.【点评】本题主要考查了锐角三角函数,熟练掌握勾股定理和锐角三角函数的定义是解答本题的关键.考点二、特殊角的三角函数值 利用三角函数的定义,可求出0°、30°、45°、60°、90°角的各三角函数值,归纳如下:要点诠释: (1)通过该表可以方便地知道0°、30°、45°、60°、90°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角. (2)仔细研究表中数值的规律会发现: 、、、、的值依次为0、、、、1,而、、、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:当角度在0°<∠A<90°之间变化时, ①正弦、正切值随锐角度数的增大(或减小)而增大(或减小) ②余弦值随锐角度数的增大(或减小)而减小(或增大).典例2:(2022•天津)tan45°的值等于( )A.2B.1C.D.【分析】根据特殊角的三角函数值,进行计算即可解答.【解答】解:tan45°的值等于1,故选:B.【点评】本题考查了特殊角的三角函数值,熟练掌握特殊角的三角函数值是解题的关键.考点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,; (2)平方关系:; (3)倒数关系:或; (4)商数关系:. 要点诠释: 锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.考点四、解直角三角形 在直角三角形中,由已知元素(直角除外)求未知元素的过程,叫做解直角三角形. 在直角三角形中,除直角外,一共有5个元素,即三条边和两个锐角. 设在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,则有: ①三边之间的关系:a2+b2=c2(勾股定理). ②锐角之间的关系:∠A+∠B=90°. ③边角之间的关系: ,,, ,,. ④,h 为斜边上的高.要点诠释: (1)直角三角形中有一个元素为定值(直角为90°),是已知的值. (2)这里讲的直角三角形的边角关系指的是等式,没有包括其他关系(如不等关系). (3)对这些式子的理解和记忆要结合图形,可以更加清楚、直观地理解.考点五、解直角三角形的常见类型及解法已知条件解法步骤两直角边(a ,b)由求∠A ,∠B=90°-∠A ,两边斜边,一直角边(如c,a)由求∠A ,∠B=90°-∠A ,锐角、邻边(如∠A ,b)∠B=90°-∠A ,,一直角边和一锐角锐角、对边(如∠A ,a)∠B=90°-∠A ,,Rt △ABC一边一角斜边、锐角(如c ,∠A)∠B=90°-∠A ,,要点诠释: 1.在遇到解直角三角形的实际问题时,最好是先画出一个直角三角形的草图,按题意标明哪些元素是已知的,哪些元素是未知的,然后按先确定锐角、再确定它的对边和邻边的顺序进行计算. 2.若题中无特殊说明,“解直角三角形”即要求出所有的未知元素,已知条件中至少有一个条件为边.典例3:(2022•丹东)如图,AB是⊙O的直径,点E在⊙O上,连接AE和BE,BC平分∠ABE交⊙O于点C,过点C作CD⊥BE,交BE的延长线于点D,连接CE.(1)请判断直线CD与⊙O的位置关系,并说明理由;(2)若sin∠ECD=,CE=5,求⊙O的半径.【分析】(1)结论:CD是⊙O的切线,证明OC⊥CD即可;(2)设OA=OC=r,设AE交OC于点J.证明四边形CDEJ是矩形,推出CD=EJ=4,CJ=DE=3,再利用勾股定理构建方程求解.【解答】解:(1)结论:CD是⊙O的切线.理由:连接OC.∵OC=OB,∴∠OCB=∠OBC,∵BC平分∠ABD,∴∠OBC=∠CBE,∴∠OCB=∠CBE,∴OC∥BD,∵CD⊥BD,∴CD⊥OC,∵OC是半径,∴CD是⊙O的切线;(2)设OA=OC=r,设AE交OC于点J.∵AB是直径,∴∠AEB=90°,∵OC⊥DC,CD⊥DB,∴∠D=∠DCJ=∠DEJ=90°,∴四边形CDEJ是矩形,∴∠CJE=90°,CD=EJ,CJ=DE,∴OC⊥AE,∴AJ=EJ,∵sin∠ECD==,CE=5,∴DE=3,CD=4,∴AJ=EJ=CD=4,CJ=DE=3,在Rt△AJO中,r2=(r﹣3)2+42,∴r=,∴⊙O的半径为.【点评】本题考查解直角三角形,切线的判定,垂径定理,矩形的判定和性质,勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型考点六、解直角三角形的应用解直角三角形的知识应用很广泛,关键是把实际问题转化为数学模型,善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键. 解这类问题的一般过程是: (1)弄清题中名词、术语的意义,如仰角、俯角、坡度、坡角、方向角等概念,然后根据题意画出几何图形,建立数学模型. (2)将已知条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形的问题. (3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形. (4)得出数学问题的答案并检验答案是否符合实际意义,得出实际问题的解. 拓展: 在用直角三角形知识解决实际问题时,经常会用到以下概念: (1)坡角:坡面与水平面的夹角叫做坡角,用字母表示. 坡度(坡比):坡面的铅直高度h和水平距离的比叫做坡度,用字母表示,则,如图,坡度通常写成=∶的形式. (2)仰角、俯角:视线与水平线所成的角中,视线中水平线上方的叫做仰角,在水平线下方的叫做俯角,如图. (3)方位角:从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角,如图①中,目标方向PA,PB,PC的方位角分别为是40°,135°,245°. (4)方向角:指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角,如图②中的目标方向线OA,OB,OC,OD的方向角分别表示北偏东30°,南偏东45°,南偏西80°,北偏西60°.特别如:东南方向指的是南偏东45°,东北方向指的是北偏东45°,西南方向指的是南偏西45°,西北方向指的是北偏西45°.要点诠释: 1.解直角三角形实际是用三角知识,通过数值计算,去求出图形中的某些边的长或角的大小,最好画出它的示意图. 2.非直接解直角三角形的问题,要观察图形特点,恰当引辅助线,使其转化为直角三角形或矩形来解.例如: 3.解直角三角形的应用题时,首先弄清题意(关键弄清其中名词术语的意义),然后正确画出示意图,进而根据条件选择合适的方法求解. 典例4:(2022•黑龙江)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,山高为( )米A.600﹣250B.600﹣250C.350+350D.500【分析】设EF=5x米,根据坡度的概念用x表示出BF,根据勾股定理求出x,根据正切的定义列出方程,解方程得到答案.【解答】解:设EF=5x米,∵斜坡BE的坡度为5:12,∴BF=12x米,由勾股定理得:(5x)2+(12x)2=(1300)2,解得:x=100,则EF=500米,BF=1200米,由题意可知,四边形DCFE为矩形,∴DC=EF=500米,DE=CF,在Rt△ADE中,tan∠AED=,则DE==AD,在Rt△ACB中,tan∠ABC=,∴=,解得:AD=600﹣750,∴山高AC=AD+DC=600﹣750+500=(600﹣250)米,故选:B.【点评】本题考查的是解直角三角形的应用—坡度坡角问题,掌握坡度是坡面的铅直高典例5:(2022•湖北)如图,有甲乙两座建筑物,从甲建筑物A点处测得乙建筑物D点的俯角α为45°,C 点的俯角β为58°,BC为两座建筑物的水平距离.已知乙建筑物的高度CD为6m,则甲建筑物的高度AB为 16 m.(sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果保留整数).【分析】过点D作DE⊥AB于点E,则BE=CD=6m,∠ADE=45°,∠ACB=58°,在Rt△ADE中,∠ADE=45°,设AE=xm,则DE=xm,BC=xm,AB=AE+BE=(6+x)m,在Rt△ABC中,tan∠ACB=tan58°=≈1.60,解得x=10,进而可得出答案.【解答】解:过点D作DE⊥AB于点E,如图.则BE=CD=6m,∠ADE=45°,∠ACB=58°,在Rt△ADE中,∠ADE=45°,设AE=xm,则DE=xm,∴BC=xm,AB=AE+BE=(6+x)m,在Rt△ABC中,tan∠ACB=tan58°=≈1.60,解得x=10,∴AB=16m.故答案为:16.【点评】本题考查解直角三角形的应用﹣仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键典例6:(2022•资阳)小明学了《解直角三角形》内容后,对一条东西走向的隧道AB进行实地测量.如图所示,他在地面上点C处测得隧道一端点A在他的北偏东15°方向上,他沿西北方向前进100米后到达点D,此时测得点A在他的东北方向上,端点B在他的北偏西60°方向上,(点A、B、C、D在同一平面内)(1)求点D与点A的距离;(2)求隧道AB的长度.(结果保留根号)【分析】(1)根据方位角图,易知∠ACD=60°,∠ADC=90°,解Rt△ADC即可求解;(2)过点D作DE⊥AB于点E.分别解Rt△ADE,Rt△BDE求出AE和BE,即可求出隧道AB的长.【解答】解;(1)由题意可知:∠ACD=15°+45°=60°,∠ADC=180°﹣45°﹣45°=90°,在Rt△ADC中,∴(米),答:点D与点A的距离为300米.(2)过点D作DE⊥AB于点E,∵AB是东西走向,∴∠ADE=45°,∠BDE=60°,在Rt△ADE中,∴(米),在Rt△BDE中,∴(米),∴(米),答:隧道AB的长为米.【点评】本题考查了解直角三角形的应用﹣方向角问题,掌握方向角的概念,掌握特殊角的三角函数值是解题的关键.考点七、解直角三角形相关的知识如图所示,在Rt△ABC中,∠C=90°,(1)三边之间的关系:;(2)两锐角之间的关系:∠A+∠B=90°;(3)边与角之间的关系:,,,.(4)如图,若直角三角形ABC中,CD⊥AB于点D,设CD=h,AD=q,DB=p,则由△CBD∽△ABC,得a2=pc;由△CAD∽△BAC,得b2=qc;由△ACD∽△CBD,得h2=pq;由△ACD∽△ABC或由△ABC面积,得ab=ch.(5)如图所示,若CD是直角三角形ABC中斜边上的中线,则①CD=AD=BD=AB;②点D是Rt△ABC的外心,外接圆半径R=AB.(6)如图所示,若r是直角三角形ABC的内切圆半径,则.直角三角形的面积:①如图所示,.(h为斜边上的高)②如图所示,.典例7:(2022•黄石)我国魏晋时期的数学家刘徽首创“割圆术”:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长l6=6R,则π≈=3.再利用圆的内接正十二边形来计算圆周率,则圆周率π约为( )A.12sin15°B.12cos15°C.12sin30°D.12cos30°【分析】利用圆内接正十二边形的性质求出A6A7=2A6M=2R×sin15°,再根据“圆周率等于圆周长与该圆直径的比”,即可解决问题.【解答】解:在正十二边形中,∠A6OM=360°÷24=15°,∴A6M=sin15°×OA6=R×sin15°,∵OA6=OA7,OM⊥A6A7,∴A6A7=2A6M=2R×sin15°,∴π≈=12sin15°,故选:A.【点评】本题主要考查了圆内接多边形的性质,解直角三角形等知识,读懂题意,计算出正十二边形的周长是解题的关键.。
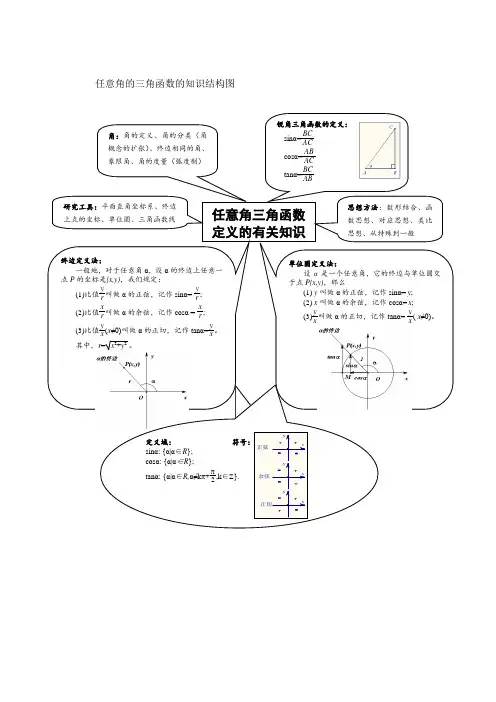
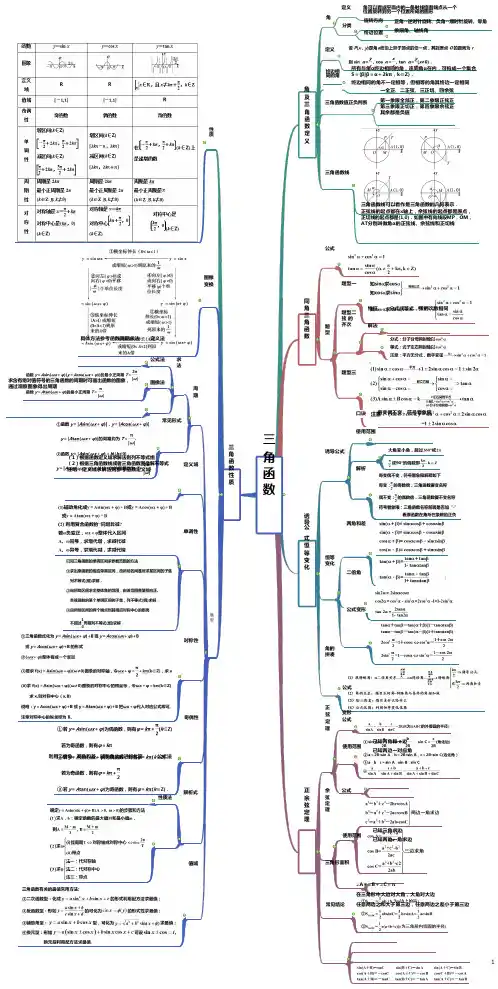
任意角三角函数
定义的有关知识
角:角的定义、角的分类(角概念的扩张)、终边相同的角、象限角、角的度量(弧度制)
锐角三角函数的定义:
sin α=BC AC
cos α=AB AC
tan α=BC AB
研究工具:平面直角坐标系、终边
上点的坐标、单位圆、三角函数线 思想方法:数形结合、函数思想、对应思想、类比思想、从特殊到一般
终边定义法:
一般地,对于任意角α,设α的终边上任意一点P 的坐标是(x,y),我们规定:
(1)比值 y r 叫做α的正弦,记作sin α= y r
;
(2)比值 x r 叫做α的余弦,记作cos α = x r ;
(3)比值 y x (x ≠0)叫做α的正切,记作tan α= y
x 。
其中,r =x 2+y 2 。
单位圆定义法:
设α是一个任意角,它的终边与单位圆交于点P(x,y),那么
(1) y 叫做α的正弦,记作sin α= y ; (2) x 叫做α的余弦,记作cos α= x ; (3) y x 叫做α的正切,记作tan α= y
x
( x ≠0)。
定义域: 符号:
sin α: {α|α∈R };
cos α: {α|α∈R };
tan α: {α|α∈R,α≠k π+π
2
,k ∈Z}.
任意角的三角函数的知识结构图
y x
y x
y x 正切
余弦+
+-
-
+
+----++正弦。
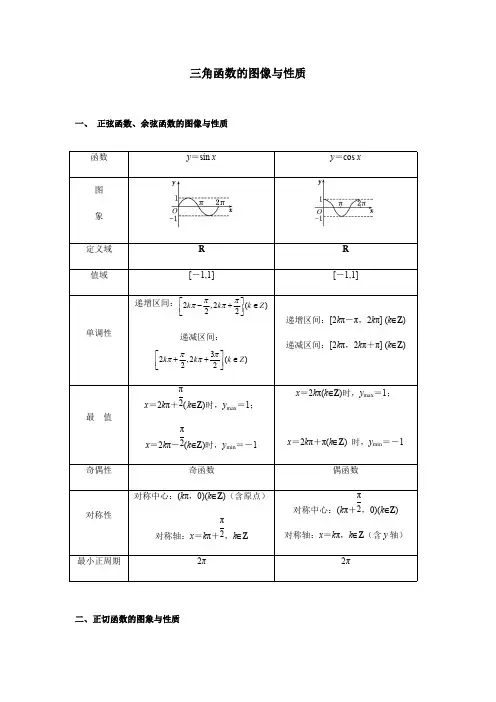
i ng si nt he i rb ei n ga re g三角函数的图像与性质一、 正弦函数、余弦函数的图像与性质二、正切函数的图象与性质函数y =sin x y =cos x图象定义域RR 值域[-1,1][-1,1]单调性递增区间:2,2()22k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦递减区间:32,2()22k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦递增区间:[2k π-π,2k π] (k ∈Z )递减区间:[2k π,2k π+π] (k ∈Z )最 值x =2k π+(k ∈Z )时,y max =1;π2x =2k π-(k ∈Z )时,y min =-1π2x =2k π(k ∈Z )时,y max =1;x =2k π+π(k ∈Z ) 时,y min =-1奇偶性奇函数偶函数对称性对称中心:(k π,0)(k ∈Z )(含原点)对称轴:x =k π+,k ∈Zπ2对称中心:(k π+,0)(k ∈Z )π2对称轴:x =k π,k ∈Z (含y 轴)最小正周期2π2π定义域{|,}2x x k k Z ππ≠+∈值域R单调性递增区间(,)()22k k k Z ππππ-+∈奇偶性奇函数对称性对称中心:(含原点)(,0)()2k k Z π∈最小正周期π三、三角函数图像的平移变换和伸缩变换1. 由的图象得到()的图象x y sin =)sin(ϕω+=x A y 0,0A ω>>xy sin =方法一:先平移后伸缩方法二:先伸缩后平移操作向左平移φ个单位横坐标变为原来的倍1ω结果)sin(ϕ+=x y xy ωsin =操作横坐标变为原来的倍1ω向左平移个单位ϕω结果)sin(ϕω+=x y 操作纵坐标变为原来的A 倍结果)sin(ϕω+=x A y 注意:平移变换或伸缩变换都是针对自变量x 而言的,因此在用这样的变换法作图象时一定要注意平移与伸缩的先后顺序,否则会出现错误。
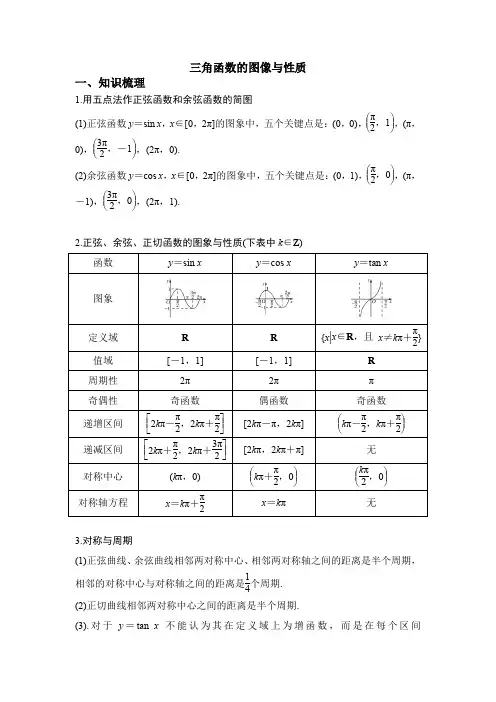
三角函数的图像与性质一、知识梳理1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),⎝ ⎛⎭⎪⎫π2,1,(π,0),⎝ ⎛⎭⎪⎫3π2,-1,(2π,0).(2)余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),⎝ ⎛⎭⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎫3π2,0,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k ∈Z )π3.对称与周期(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半个周期,相邻的对称中心与对称轴之间的距离是14个周期. (2)正切曲线相邻两对称中心之间的距离是半个周期.(3).对于y =tan x 不能认为其在定义域上为增函数,而是在每个区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )内为增函数.二、例题精讲 + 随堂练习1.判断下列结论正误(在括号内打“√”或“×”) (1)余弦函数y =cos x 的对称轴是y 轴.( ) (2)正切函数y =tan x 在定义域内是增函数.( ) (3)已知y =k sin x +1,x ∈R ,则y 的最大值为k +1.( ) (4)y =sin|x |是偶函数.( )解析 (1)余弦函数y =cos x 的对称轴有无穷多条,y 轴只是其中的一条. (2)正切函数y =tan x 在每一个区间⎝ ⎛⎭⎪⎫k π-π2,k π+π2(k ∈Z )上都是增函数,但在定义域内不是单调函数,故不是增函数.(3)当k >0时,y max =k +1;当k <0时,y max =-k +1. 答案 (1)× (2)× (3)× (4)√2.若函数y =2sin 2x -1的最小正周期为T ,最大值为A ,则( ) A.T =π,A =1 B.T =2π,A =1 C.T =π,A =2D.T =2π,A =2解析 最小正周期T =2π2=π,最大值A =2-1=1.故选A. 答案 A3.函数y =-tan ⎝ ⎛⎭⎪⎫2x -3π4的单调递减区间为________.解析 由-π2+k π<2x -3π4<π2+k π(k ∈Z ), 得π8+k π2<x <5π8+k π2(k ∈Z ),所以y =-tan ⎝ ⎛⎭⎪⎫2x -3π4的单调递减区间为⎝ ⎛⎭⎪⎫π8+k π2,5π8+k π2(k ∈Z ). 答案 ⎝ ⎛⎭⎪⎫π8+k π2,5π8+k π2(k ∈Z )4.(2017·全国Ⅱ卷)函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3的最小正周期为( )A.4πB.2πC.πD.π2解析 由题意T =2π2=π. 答案 C5.(2017·全国Ⅲ卷)函数f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+cos ⎝ ⎛⎭⎪⎫x -π6的最大值为( )A.65B.1C.35D.15解析 cos ⎝ ⎛⎭⎪⎫x -π6=cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫x +π3=sin ⎝ ⎛⎭⎪⎫x +π3,则f (x )=15sin ⎝ ⎛⎭⎪⎫x +π3+sin ⎝ ⎛⎭⎪⎫x +π3=65sin ⎝ ⎛⎭⎪⎫x +π3,函数的最大值为65. 答案 A6.(2018·江苏卷)已知函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫-π2<φ<π2 的图象关于直线x =π3对称,则φ的值是________.解析 由函数y =sin(2x +φ)⎝ ⎛⎭⎪⎫-π2<φ<π2的图象关于直线x =π3对称,得sin ⎝ ⎛⎭⎪⎫2π3+φ=±1.所以2π3+φ=π2+k π(k ∈Z ),所以φ=-π6+k π(k ∈Z ),又-π2<φ<π2,所以φ=-π6. 答案 -π6考点一 三角函数的定义域【例1】 (1)函数f (x )=-2tan ⎝ ⎛⎭⎪⎫2x +π6的定义域是( ) A.⎩⎨⎧⎭⎬⎫x |x ≠π6 B.⎩⎨⎧⎭⎬⎫x |x ≠-π12 C.⎩⎨⎧⎭⎬⎫x |x ≠k π+π6(k ∈Z ) D.⎩⎨⎧⎭⎬⎫x |x ≠k π2+π6(k ∈Z ) (2)不等式3+2cos x ≥0的解集是________.(3)函数f (x )=64-x 2+log 2(2sin x -1)的定义域是________. 解析 (1)由2x +π6≠k π+π2(k ∈Z ),得x ≠k π2+π6(k ∈Z ).(2)由3+2cos x ≥0,得cos x ≥-32,由余弦函数的图象,得在一个周期[-π,π]上,不等式cos x ≥-32的解集为⎩⎨⎧⎭⎬⎫x |-5π6≤x ≤56π,故原不等式的解集为⎩⎨⎧⎭⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z .(3)由题意,得⎩⎨⎧64-x 2≥0,①2sin x -1>0,②由①得-8≤x ≤8,由②得sin x >12,由正弦曲线得π6+2k π<x <56 π+2k π(k ∈Z ).所以不等式组的解集为⎝ ⎛⎭⎪⎫-116π,-76π∪⎝ ⎛⎭⎪⎫π6,56π∪⎝ ⎛⎦⎥⎤13π6,8. 答案 (1)D (2)⎩⎨⎧⎭⎬⎫x |-56π+2k π≤x ≤56π+2k π,k ∈Z (3)⎝ ⎛⎭⎪⎫-116π,-76π∪⎝ ⎛⎭⎪⎫π6,56π∪⎝ ⎛⎦⎥⎤13π6,8【训练1】 (1)函数y =sin x -cos x 的定义域为________. (2)函数y =lg(sin x )+cos x -12的定义域为______.解析 (1)要使函数有意义,必须使sin x -cos x ≥0.利用图象,在同一坐标系中画出[0,2π]上y =sin x 和y =cos x 的图象,如图所示.在[0,2π]上,满足sin x =cos x 的x 为π4,5π4再结合正弦、余弦函数的周期是2π,所以原函数的定义域为⎩⎨⎧⎭⎬⎫x |π4+2k π≤x ≤54π+2k π,k ∈Z .(2)要使函数有意义必须有⎩⎪⎨⎪⎧sin x >0,cos x -12≥0, 即⎩⎪⎨⎪⎧sin x >0,cos x ≥12,解得⎩⎪⎨⎪⎧2k π<x <π+2k π,-π3+2k π≤x ≤π3+2k π(k ∈Z ),所以2k π<x ≤π3+2k π(k ∈Z ),所以函数的定义域为⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3+2k π,k ∈Z .答案(1)⎩⎨⎧⎭⎬⎫x |π4+2k π≤x ≤54π+2k π,k ∈Z (2)⎩⎨⎧⎭⎬⎫x |2k π<x ≤π3+2k π,k ∈Z考点二 三角函数的值域与最值【例2】 (1)y =3sin ⎝ ⎛⎭⎪⎫2x -π6在区间⎣⎢⎡⎦⎥⎤0,π2上的值域是________.(2)(2017·全国Ⅱ卷)函数f (x )=sin 2x +3cos x -34⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0,π2的最大值是________. (3)函数y =sin x -cos x +sin x cos x 的值域为________.解析 (1)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,2x -π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-12,1,故3sin ⎝ ⎛⎭⎪⎫2x -π6∈⎣⎢⎡⎦⎥⎤-32,3,即y =3sin ⎝ ⎛⎭⎪⎫2x -π6的值域为⎣⎢⎡⎦⎥⎤-32,3. (2)由题意可得f (x )=-cos 2x +3cos x +14=-(cos x -32)2+1.∵x ∈⎣⎢⎡⎦⎥⎤0,π2,∴cos x ∈[0,1].∴当cos x =32,即x =π6时,f (x )max =1. (3)设t =sin x -cos x ,则t 2=sin 2x +cos 2x -2sin x cos x ,sin x cos x =1-t22,且-2≤t ≤2,所以y =-t 22+t +12=-12(t -1)2+1.当t =1时,y max =1;当t =-2时,y min =-12- 2 .所以函数的值域为⎣⎢⎡⎦⎥⎤-12-2,1. 答案 (1)⎣⎢⎡⎦⎥⎤-32,3 (2)1 (3)⎣⎢⎡⎦⎥⎤-12-2,1【训练2】 (1)函数f (x )=cos 2x +6cos ⎝ ⎛⎭⎪⎫π2-x 的最大值为( )A.4B.5C.6D.7(2)(2019·临沂模拟)已知函数f (x )=sin ⎝ ⎛⎭⎪⎫x +π6,其中x ∈⎣⎢⎡⎦⎥⎤-π3,a ,若f (x )的值域是⎣⎢⎡⎦⎥⎤-12,1,则实数a 的取值范围是________. 解析 (1)由f (x )=cos 2x +6cos ⎝ ⎛⎭⎪⎫π2-x =1-2sin 2x +6sin x =-2⎝ ⎛⎭⎪⎫sin x -322+112,又sin x ∈[-1,1],所以当sin x =1时函数的最大值为5.(2)由x ∈⎣⎢⎡⎦⎥⎤-π3,a ,知x +π6∈⎣⎢⎡⎦⎥⎤-π6,a +π6.因为x +π6∈⎣⎢⎡⎦⎥⎤-π6,π2时,f (x )的值域为⎣⎢⎡⎦⎥⎤-12,1,所以由函数的图象知π2≤a +π6≤7π6,所以π3≤a ≤π. 答案 (1)B(2)⎣⎢⎡⎦⎥⎤π3,π考点三 三角函数的单调性 角度1 求三角函数的单调区间【例3-1】 (1)函数f (x )=tan ⎝ ⎛⎭⎪⎫2x -π3的单调递增区间是( ) A.⎣⎢⎡⎦⎥⎤k π12-π12,k π2+5π12(k ∈Z ) B.⎝ ⎛⎭⎪⎫k π12-π12,k π2+5π12(k ∈Z )C.⎝ ⎛⎭⎪⎫k π+π6,k π+2π3(k ∈Z )D.⎝ ⎛⎭⎪⎫k π-π12,k π+5π12(k ∈Z ) (2)函数y =sin ⎝ ⎛⎭⎪⎫-2x +π3的单调递减区间为________. 解析 (1)由k π-π2<2x -π3<k π+π2(k ∈Z ),得k π2-π12<x <k π2+5π12(k ∈Z ),所以函数f (x )=tan ⎝ ⎛⎭⎪⎫2x -π3的单调递增区间为⎝ ⎛⎭⎪⎫k π2-π12,k π2+5π12(k ∈Z ).(2)y =-sin ⎝ ⎛⎭⎪⎫2x -π3,它的减区间是y =sin ⎝ ⎛⎭⎪⎫2x -π3的增区间.令2k π-π2≤2x -π3≤2k π+π2,k ∈Z ,得k π-π12≤x ≤k π+5π12,k ∈Z .故其单调递减区间为⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z . 答案 (1)B (2)⎣⎢⎡⎦⎥⎤k π-π12,k π+5π12,k ∈Z角度2 利用单调性比较大小【例3-2】 已知函数f (x )=2cos ⎝ ⎛⎭⎪⎫x +π6,设a =f ⎝ ⎛⎭⎪⎫π7,b =f ⎝ ⎛⎭⎪⎫π6,c =f ⎝ ⎛⎭⎪⎫π4,则a ,b ,c 的大小关系是( ) A.a >b >c B.a >c >b C.c >a >bD.b >a >c解析 令2k π≤x +π6≤2k π+π,k ∈Z ,解得2k π-π6≤x ≤2k π+5π6,k ∈Z ,∴函数f (x )=2cos ⎝ ⎛⎭⎪⎫x +π6在⎣⎢⎡⎦⎥⎤-π6,5π6上是减函数,∵-π6<π7<π6<π4<5π6, ∴f ⎝ ⎛⎭⎪⎫π7>f ⎝ ⎛⎭⎪⎫π6>f ⎝ ⎛⎭⎪⎫π4. 答案 A角度3 利用单调性求参数【例3-3】 (2018·全国Ⅱ卷)若f (x )=cos x -sin x 在[-a ,a ]是减函数,则a 的最大值是( ) A.π4B.π2C.3π4D.π解析 f (x )=cos x -sin x =2cos ⎝ ⎛⎭⎪⎫x +π4,由题意得a >0,故-a +π4<π4,因为f (x )=2cos ⎝ ⎛⎭⎪⎫x +π4在[-a ,a ]是减函数,所以⎩⎪⎨⎪⎧-a +π4≥0,a +π4≤π,a >0,解得0<a ≤π4,所以a 的最大值是π4.答案 A【训练3】 (1)设函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π3,x ∈⎣⎢⎡⎦⎥⎤-π2,π,则以下结论正确的是( )A.函数f (x )在⎣⎢⎡⎦⎥⎤-π2,0上单调递减B.函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上单调递增 C.函数f (x )在⎣⎢⎡⎦⎥⎤π2,5π6上单调递减 D.函数f (x )在⎣⎢⎡⎦⎥⎤5π6,π上单调递增(2)cos 23°,sin 68°,cos 97°的大小关系是________.(3)若函数f (x )=sin ωx (ω>0)在⎣⎢⎡⎦⎥⎤0,π3上单调递增,在区间⎣⎢⎡⎦⎥⎤π3,π2上单调递减,则ω=________.解析 (1)由x ∈⎣⎢⎡⎦⎥⎤-π2,0,得2x -π3∈⎣⎢⎡⎦⎥⎤-4π3,-π3,此时函数f (x )先减后增;由x ∈⎣⎢⎡⎦⎥⎤0,π2,得2x -π3∈⎣⎢⎡⎦⎥⎤-π3,2π3,此时函数f (x )先增后减;由x ∈⎣⎢⎡⎦⎥⎤π2,5π6,得2x -π3∈⎣⎢⎡⎦⎥⎤2π3,4π3,此时函数f (x )单调递减;由x ∈⎣⎢⎡⎦⎥⎤5π6,π,得2x -π3∈⎣⎢⎡⎦⎥⎤4π3,5π3,此时函数f (x )先减后增.(2)sin 68°=cos 22°,又y =cos x 在[0°,180°]上是减函数,∴sin 68°>cos 23°>cos 97°.(3)法一 由于函数f (x )=sin ωx (ω>0)的图象经过坐标原点,由已知并结合正弦函数的图象可知,π3为函数f (x )的14周期,故2πω=4π3,解得ω=32.法二 由题意,得f (x )max =f ⎝ ⎛⎭⎪⎫π3=sin π3ω=1.由已知并结合正弦函数图象可知,π3ω=π2+2k π(k ∈Z ),解得ω=32+6k (k ∈Z ),所以当k =0时,ω=32.答案 (1)C (2)sin 68°>cos 23°>cos 97° (3)32考点四 三角函数的周期性、奇偶性、对称性 角度1 三角函数奇偶性、周期性【例4-1】 (1)(2018·全国Ⅰ卷)已知函数f (x )=2cos 2x -sin 2x +2,则( ) A.f (x )的最小正周期为π,最大值为3 B.f (x )的最小正周期为π,最大值为4 C.f (x )的最小正周期为2π,最大值为3 D.f (x )的最小正周期为2π,最大值为4(2)(2019·杭州调研)设函数f (x )=sin ⎝ ⎛⎭⎪⎫12x +θ-3cos ⎝ ⎛⎭⎪⎫12x +θ⎝ ⎛⎭⎪⎫|θ|<π2的图象关于y 轴对称,则θ=( ) A.-π6 B.π6 C.-π3 D.π3解析 (1)易知f (x )=2cos 2x -sin 2x +2=3cos 2x +1=3cos 2x +12+1=32cos 2x +52,则f (x )的最小正周期为π,当2x =2k π,即x =k π(k ∈Z )时,f (x )取得最大值,最大值为4.(2)f (x )=sin ⎝ ⎛⎭⎪⎫12x +θ-3cos ⎝ ⎛⎭⎪⎫12x +θ=2sin ⎝ ⎛⎭⎪⎫12x +θ-π3, 由题意可得f (0)=2sin ⎝ ⎛⎭⎪⎫θ-π3=±2,即sin ⎝ ⎛⎭⎪⎫θ-π3=±1,∴θ-π3=π2+k π(k ∈Z ),∴θ=5π6+k π(k ∈Z ). ∵|θ|<π2,∴k =-1时,θ=-π6. 答案 (1)B (2)A角度2 三角函数图象的对称性【例4-2】 (1)已知函数f (x )=a sin x +cos x (a 为常数,x ∈R )的图象关于直线x =π6对称,则函数g (x )=sin x +a cos x 的图象( )A.关于点⎝ ⎛⎭⎪⎫π3,0对称B.关于点⎝ ⎛⎭⎪⎫2π3,0对称 C.关于直线x =π3对称 D.关于直线x =π6对称解析 (1)因为函数f (x )=a sin x +cos x (a 为常数,x ∈R )的图象关于直线x =π6对称,所以f (0)=f ⎝ ⎛⎭⎪⎫π3,所以1=32a +12,a =33,所以g (x )=sin x +33cos x =233sin ⎝ ⎛⎭⎪⎫x +π6,函数g (x )的对称轴方程为x +π6=k π+π2(k ∈Z ),即x =k π+π3(k ∈Z ),当k =0时,对称轴为直线x =π3,所以g (x )=sin x +a cos x 的图象关于直线x =π3对称. 规律方法 1.对于可化为f (x )=A sin(ωx +φ)形式的函数,如果求f (x )的对称轴,只需令ωx +φ=π2+k π(k ∈Z ),求x 即可;如果求f (x )的对称中心的横坐标,只需令ωx +φ=k π(k ∈Z ),求x 即可.2.对于可化为f (x )=A cos(ωx +φ)形式的函数,如果求f (x )的对称轴,只需令ωx +φ=k π(k ∈Z ),求x ;如果求f (x )的对称中心的横坐标,只需令ωx +φ=π2+k π(k ∈Z ),求x 即可.【训练4】 (1)(2018·全国Ⅲ卷)函数f (x )=tan x1+tan 2x的最小正周期为( )A.π4B.π2C.πD.2π(2)设函数f (x )=cos ⎝ ⎛⎭⎪⎫x +π3,则下列结论错误的是( )A.f (x )的一个周期为-2πB.y =f (x )的图象关于直线x =8π3对称 C.f (x +π)的一个零点为x =π6 D.f (x )在⎝ ⎛⎭⎪⎫π2,π单调递减解析 (1)f (x )的定义域为⎩⎨⎧⎭⎬⎫x |x ≠k π+π2,k ∈Z .f (x )=sin x cos x 1+⎝ ⎛⎭⎪⎫sin x cos x 2=sin x ·cos x =12sin 2x ,∴f (x )的最小正周期T =2π2=π.(2)A 项,因为f (x )的周期为2k π(k ∈Z 且k ≠0),所以f (x )的一个周期为-2π,A 项正确.B 项,因为f (x )图象的对称轴为直线x =k π-π3(k ∈Z ),当k =3时,直线x =8π3是其对称轴,B 项正确.C 项,f (x +π)=cos ⎝ ⎛⎭⎪⎫x +4π3,将x =π6代入得到f ⎝ ⎛⎭⎪⎫7π6=cos 3π2=0,所以x =π6是f (x+π)的一个零点,C 项正确.D 项,因为f (x )=cos ⎝ ⎛⎭⎪⎫x +π3的递减区间为⎣⎢⎡⎦⎥⎤2k π-π3,2k π+2π3 (k ∈Z ),递增区间为⎣⎢⎡⎦⎥⎤2k π+2π3,2k π+5π3 (k ∈Z ),所以⎝ ⎛⎭⎪⎫π2,2π3是减区间,⎣⎢⎡⎭⎪⎫2π3,π是增区间,D 项错误.答案 (1)C (2)D三、课后练习1.若对于任意x ∈R 都有f (x )+2f (-x )=3cos x -sin x ,则函数f (2x )图象的对称中心为( )A.⎝ ⎛⎭⎪⎫k π-π4,0(k ∈Z ) B.⎝ ⎛⎭⎪⎫k π-π8,0(k ∈Z ) C.⎝ ⎛⎭⎪⎫k π2-π4,0(k ∈Z ) D.⎝ ⎛⎭⎪⎫k π2-π8,0(k ∈Z ) 解析 因为f (x )+2f (-x )=3cos x -sin x ,所以f (-x )+2f (x )=3cos x +sin x .解得f (x )=cos x +sin x =2sin ⎝ ⎛⎭⎪⎫x +π4,所以f (2x )=2sin ⎝ ⎛⎭⎪⎫2x +π4. 令2x +π4=k π(k ∈Z ),得x =k π2-π8(k ∈Z ).所以f (2x )图象的对称中心为⎝ ⎛⎭⎪⎫k π2-π8,0(k ∈Z ). 答案 D2.(2017·天津卷)设函数f (x )=2sin(ωx +φ),x ∈R ,其中ω>0,|φ|<π.若f ⎝ ⎛⎭⎪⎫5π8=2,f ⎝ ⎛⎭⎪⎫11π8=0,且f (x )的最小正周期大于2π,则( ) A.ω=23,φ=π12 B.ω=23,φ=-11π12C.ω=13,φ=-11π24D.ω=13,φ=7π24解析 ∵f ⎝ ⎛⎭⎪⎫5π8=2,f ⎝ ⎛⎭⎪⎫11π8=0,且f (x )的最小正周期大于2π, ∴f (x )的最小正周期为4⎝ ⎛⎭⎪⎫11π8-5π8=3π, ∴ω=2π3π=23,∴f (x )=2sin ⎝ ⎛⎭⎪⎫23x +φ. ∴2sin ⎝ ⎛⎭⎪⎫23×5π8+φ=2,得φ=2k π+π12(k ∈Z ), 又|φ|<π,∴取k =0,得φ=π12.答案 A3.已知x 0=π3是函数f (x )=sin(2x +φ)的一个极大值点,则f (x )的单调递减区间是________.解析 因为x 0=π3是函数f (x )=sin(2x +φ)的一个极大值点,所以sin ⎝ ⎛⎭⎪⎫2×π3+φ=1,解得φ=2k π-π6(k ∈Z ). 不妨取φ=-π6,此时f (x )=sin ⎝ ⎛⎭⎪⎫2x -π6, 令2k π+π2≤2x -π6≤2k π+3π2(k ∈Z ),得f (x )的单调递减区间是⎣⎢⎡⎦⎥⎤k π+π3,k π+56π(k ∈Z ). 答案 ⎣⎢⎡⎦⎥⎤k π+π3,k π+56π(k ∈Z )4.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫π2-x sin x -3cos 2x +32. (1)求f (x )的最大值及取得最大值时x 的值;(2)若方程f (x )=23在(0,π)上的解为x 1,x 2,求cos(x 1-x 2)的值.解 (1)f (x )=cos x sin x -32(2cos 2x -1) =12sin 2x -32cos 2x =sin ⎝ ⎛⎭⎪⎫2x -π3. 当2x -π3=π2+2k π(k ∈Z ),即x =512π+k π(k ∈Z )时,函数f (x )取最大值,且最大值为1.(2)由(1)知,函数f (x )图象的对称轴为x =512π+k π(k ∈Z ),∴当x ∈(0,π)时,对称轴为x =512π.又方程f (x )=23在(0,π)上的解为x 1,x 2.∴x 1+x 2=56π,则x 1=56π-x 2,∴cos(x 1-x 2)=cos ⎝ ⎛⎭⎪⎫56π-2x 2=sin ⎝ ⎛⎭⎪⎫2x 2-π3, 又f (x 2)=sin ⎝ ⎛⎭⎪⎫2x 2-π3=23, 故cos(x 1-x 2)=23.5.已知函数f (x )=sin ⎝ ⎛⎭⎪⎫x -π6,若对任意的实数α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,都存在唯一的实数β∈[0,m ],使f (α)+f (β)=0,则实数m 的最小值是________.解析 因为α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,所以α-π6∈⎣⎢⎡⎦⎥⎤-π,-2π3,则f (α)=sin ⎝ ⎛⎭⎪⎫α-π6∈⎣⎢⎡⎦⎥⎤-32,0,因为对任意的实数α∈⎣⎢⎡⎦⎥⎤-5π6,-π2,都存在唯一的实数β∈[0,m ],使f (α)+f (β)=0,所以f (β)在[0,m ]上单调,且f (β)∈⎣⎢⎡⎦⎥⎤0,32,则sin ⎝ ⎛⎭⎪⎫β-π6∈⎣⎢⎡⎦⎥⎤0,32,则β-π6∈⎣⎢⎡⎦⎥⎤0,π3,所以β∈⎣⎢⎡⎦⎥⎤π6,π2,即实数m 的最小值是π2. 答案 π26.(2017·山东卷)函数y =3sin 2x +cos 2x 的最小正周期为( )A.π2B.2π3C.πD.2π解析 ∵y =2⎝ ⎛⎭⎪⎫32sin 2x +12cos 2x =2sin ⎝ ⎛⎭⎪⎫2x +π6, ∴T =2π2=π.答案 C7.(2019·石家庄检测)若⎝ ⎛⎭⎪⎫π8,0是函数f (x )=sin ωx +cos ωx 图象的一个对称中心,则ω的一个取值是( )A.2B.4C.6D.8解析 因为f (x )=sin ωx +cos ωx =2sin ⎝ ⎛⎭⎪⎫ωx +π4,由题意,知f ⎝ ⎛⎭⎪⎫π8=2sin ⎝ ⎛⎭⎪⎫ωπ8+π4=0,所以ωπ8+π4=k π(k ∈Z ),即ω=8k -2(k ∈Z ),当k =1时,ω=6.答案 C8.已知函数f (x )=2sin ωx (ω>0)在区间⎣⎢⎡⎦⎥⎤-π3,π4上的最小值是-2,则ω的最小值等于( ) A.23 B.32 C.2 D.3解析 ∵ω>0,-π3≤x ≤π4,∴-ωπ3≤ωx ≤ωπ4.由已知条件知-ωπ3≤-π2,∴ω≥32.答案 B9.(2019·湖南十四校联考)已知函数f (x )=2sin ωx -cos ωx (ω>0),若f (x )的两个零点x 1,x 2满足|x 1-x 2|min =2,则f (1)的值为( ) A.102 B.-102 C.2 D.-2解析 依题意可得函数的最小正周期为2πω=2|x 1-x 2|min =2×2=4,即ω=π2,所以f (1)=2sin π2-cos π2=2.答案 C10.(2018·北京卷)设函数f (x )=cos ⎝ ⎛⎭⎪⎫ωx -π6(ω>0).若f (x )≤f ⎝ ⎛⎭⎪⎫π4对任意的实数x 都成立,则ω的最小值为________.解析 由于对任意的实数都有f (x )≤f ⎝ ⎛⎭⎪⎫π4成立,故当x =π4时,函数f (x )有最大值,故f ⎝ ⎛⎭⎪⎫π4=1,πω4-π6=2k π(k ∈Z ),∴ω=8k +23(k ∈Z ).又ω>0,∴ωmin =23. 答案 2311.(2019·北京通州区质检)已知函数f (x )=sin ωx -cos ωx (ω>0)的最小正周期为π.(1)求函数y =f (x )图象的对称轴方程;(2)讨论函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的单调性. 解 (1)∵f (x )=sin ωx -cos ωx =2sin ⎝ ⎛⎭⎪⎫ωx -π4,且T =π, ∴ω=2,于是f (x )=2sin ⎝ ⎛⎭⎪⎫2x -π4. 令2x -π4=k π+π2(k ∈Z ),得x =k π2+3π8(k ∈Z ).即函数f (x )图象的对称轴方程为x =k π2+3π8(k ∈Z ).(2)令2k π-π2≤2x -π4≤2k π+π2(k ∈Z ),得函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π8,k π+3π8(k ∈Z ). 注意到x ∈⎣⎢⎡⎦⎥⎤0,π2,所以令k =0,得函数f (x )在⎣⎢⎡⎦⎥⎤0,π2上的单调递增区间为⎣⎢⎡⎦⎥⎤0,3π8; 同理,其单调递减区间为⎣⎢⎡⎦⎥⎤3π8,π2.。

三角函数知识点归纳 一、任意角与弧度制 1.任意角 (I)定义:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形. J 按旋转方向不同分为正角、负角、零角. (2)分类[按终边位置不同分为象限角和轴线角(3)终边相同的角:所有与角a 终边相同的角,连同角a 在内,可构成一个集合S={缈=a+ 2kιt, Λ∈Z!.(3)象限角与轴线角 今1(第一象限角)卜| 第二致限角阳2A"专VaV2痴 2⅛π<α<2⅛π+-g-,⅛∈z} +π,⅛∈ZT 第三敛限角)卜性"τrVaV2"+等"刃 第四象限角]{α∣2⅛π+^<α<2⅛π+2π,⅛∈z}2.弧度制的定义和公式 角a 的弧度数公式 IaI=%/表示弧长)角度与弧度的换算 ①1。
=念 rad ;② 1 rad=, 弧长公式 l=∖a ∖r 扇形面积公式S=»=如/ (1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad. 3.任意角的三角函数 一、定义:设α是一个任意角,它的终边与单位圆交于点P(x, y),那么Sina=y, cos α=x, tan α=^(x≠()).二、常用结论汇总——规律多一点(1)一个口诀:三角函数值在各象限的符号:一全正、二正弦、三正切、四余弦.(2)三角函数定义的推广:设点P(x, y)是角Q终边上任意一点且不与原点重合,r=∣OP∣,则• V X V,1八、sin a= , COSa=-, tanα=-(Xw0).r rχ∖ ,三、特殊角的三角函数:3.1 象限角及终边相同的角例1、若角。
是第二象限角,则辞()A.第一象限角B.第二象限角C.第一或第三象限角D.第二或第四象限角∩例2、一的终边在第三象限,则。
的终边可能在() 2A.第一、三象限B.第二、四象限C.第一、二象限或y轴非负半轴D.第三、四象限或y轴非正半轴3.2 三角函数的定义例1、已知角α的终边经过点P(一χ, — 6),且COSa=—/,则1;+%½= _________________ .1J SlIl (A IdIl (A例2、已知角α的终边经过点(3, -4),则Sin a+»^=.3.3 、三角函数符号的判定例1、已知Sina < 0旦cosa > 0,则a的终边落在()A.第一象限B.第二象限C.第三象限D.第四象限3.4 扇形面积问题1.已知一个扇形的弧长和半径都等于2,则这个扇形的面积为().A. 2B. 3C. 4D. 6二、同角三角函数的基本关系与诱导公式1 .同角三角函数的基本关系(1)平方关系:siMα+cos2α=l; (2)商数关系:tan α=黑吃.同角三角函数的基本关系式的几种变形(l)sin2α= 1 — cos2α=(l + cos «)(1 —cos a); cos2a= 1 - sin2a=(l ÷sin a)(l — sin a); (sin a±cos a)2 =l±2sin acos a.(2)sin a=tan acos a(a≠5+E, &WZ).2 .诱导公式“奇变偶不变,符号看象限”公式一:sin(a+2⅛π)=sin a, cos(a÷2hc)=cos a»la∏(6Z + <λkτf)= t∏∏OC其中公式二:sin(π+ct)= ~sin a> cos(π+cc)=~cos ct> Ian(Tr+a)=Ian a.公式三:sin(π~a)=sin a,cos(π-a) = — cos ct, ta∏(^-6Z)= —ta∏ OC ∙公式四:sin(-ct)=—sin a, cost—«)=cos a,t<l∏) = -13∏ CX .公式五:Sine-a) =cos a, COSe—a) =Sina 公式六:SinC+a)=cos a,CoSC+«) = -sin a.诱导公式可概括为〃∙]±a的各三角函数值的化简公式.口诀:奇变偶不变,符号看象限.其中的奇、偶是指方的奇数倍和偶数倍,变与不变是指函数名称的变化.若是奇数倍,则函数名称要变(正弦变余弦,余弦变正弦);若是偶数倍,则函数名称不变,符号看象限是指:把a看成锐角时,根据在哪个象限判断厚三曲函数值的符号,最后作为结果符号.8.方法与要点一个口诀I、诱导公式的记忆。

三角函数的图象一、知识回顾(一)熟悉.三角函数图象的特征:y =tanxy =cotx(二)三角函数图象的作法: 1.几何法(利用三角函数线)2. 描点法:五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).3. 利用图象变换作三角函数图象.三角函数的图象变换有振幅变换、周期变换和相位变换等,重点掌握函数y =Asin (ωx +φ)+B的作法.函数y =Asin (ωx +φ)的物理意义: 振幅|A|,周期2||T πω=,频率1||2fT ωπ==,相位;x ωϕ+初相ϕ(即当x =0时的相位).(当A >0,ω>0 时以上公式可去绝对值符号),y=cosxy=sinx-11-11o o y xy x(1)振幅变换或叫沿y 轴的伸缩变换.(用y/A 替换y )由y =sinx 的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y =Asinx 的图象.(2)周期变换或叫做沿x 轴的伸缩变换.(用ωx 替换x )由y =sinx 的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的1||ω倍,得到y =sin ω x 的图象.(3)相位变换或叫做左右平移.(用x +φ替换x )由y =sinx 的图象上所有的点向左(当φ>0)或向右(当φ<0)平行移动|φ|个单位,得到y =sin (x +φ)的图象.(4)上下平移(用y+(-b)替换y )由y =sinx 的图象上所有的点向上(当b >0)或向下(当b <0)平行移动|b |个单位,得到y =sinx +b 的图象.注意:由y =sinx 的图象利用图象变换作函数y =Asin (ωx +φ)+B (A >0,ω>0)(x ∈R )的图象,要特别注意:当周期变换和相位变换的先后顺序不同时,原图象延x 轴量伸缩量的区别。
二、基本训练1、为了得到函数)63sin(π+=x y 的图象,只需把函数x y 3sin =的图象 ( )A 、向左平移6π B 、向左平移18π C 、向右平移6π D 、向右平移18π 2、函数|2|sin 2)(π-=x x f 的部分图象是 ( )3、函数)cos (sin cos 2x x x y +=的图象一个对称中心的坐标是 ( )A 、)0,83(π B 、)1,83(π C 、)1,8(πD 、)1,8(--π 4、(00)函数y=-xcosx 的部分图象是OOO Ox x x xy y y y 2 2 22ADCB5、已知函数a x x x f -++-=1cos 4sin 4)(2,当]32,4[ππ-∈x 时)(x f =0恒有解,则a 的范围是______。

湘教版必修第二册三角恒等变换思维导图
三角函数恒等变换不但在三角函数式的化简、求值和证明三角恒等式中经常用到,而且.由于通过三角换元可将某些代数问题化归为三角问题;立体几何中的诸多位置关系以其交角来刻画,最后又以三角问题反映出来。
由于参数方程的建立,又可将解析几何中的曲线问题归结为三角问题.因此,三角恒等变换在整个高中数学中涉及面广.是常见的解题“工具”。
三角函数恒等变换在整个高中数学应用广泛,在掌握三角函数恒等变换之前,要在脑中有张“全局图”,是十分有必要的。
三角函数的基本关系式的总结。
所谓的平方关系,就是本质是勾股定理在三角函数里的另外表现。
三角函数的商关系,无非就是直角三角形各个边的比例关系。
三角函数的倒数关系,也是同样道理。
我们也可以用图四的关系图,更加直观理解他们的关系。
上图为三角函数恒等变换的思维导图。
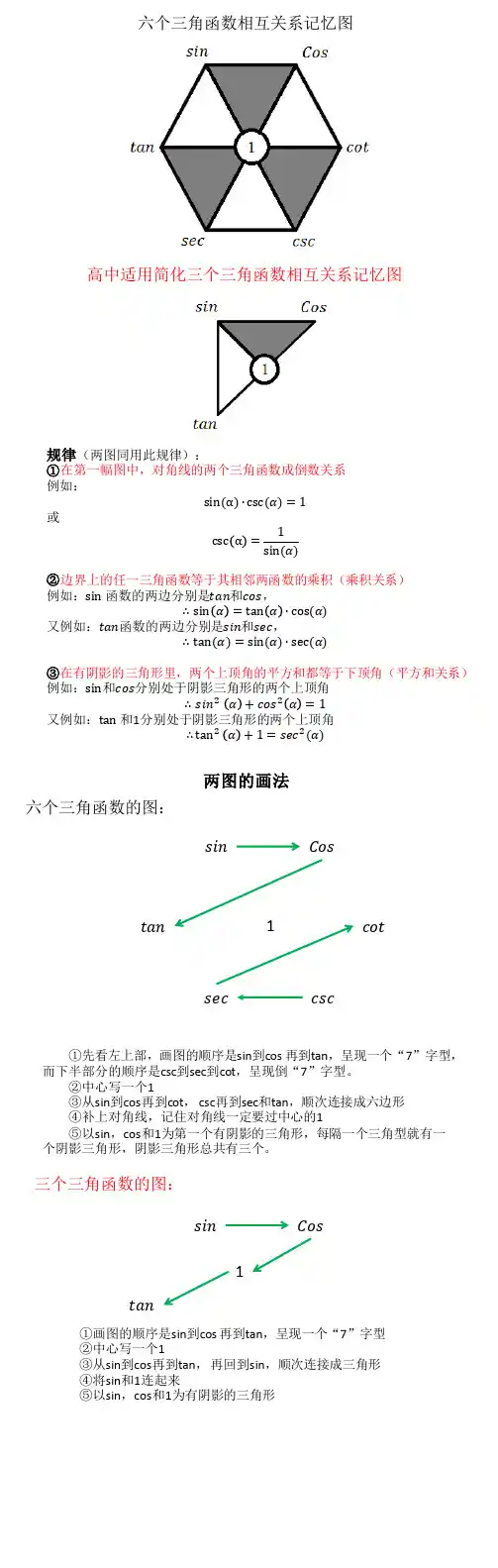
规律(两图同用此规律):①在第一幅图中,对角线的两个三角函数成倒数关系例如:sin(α)∙csc(α)=1或 csc α=1sin(α) ②边界上的任一三角函数等于其相邻两函数的乘积(乘积关系)例如:sin函数的两边分别是tan 和cos ,∴sin α=tan α∙cos(α)又例如:tan 函数的两边分别是sin 和sec ,∴tan(α)=sin(α)∙sec(α)③在有阴影的三角形里,两个上顶角的平方和都等于下顶角(平方和关系) 例如:sin 和cos 分别处于阴影三角形的两个上顶角∴sin 2α+cos 2α=1又例如:tan和1分别处于阴影三角形的两个上顶角∴tan 2α+1=sec 2(α)六个三角函数相互关系记忆图高中适用简化三个三角函数相互关系记忆图两图的画法六个三角函数的图:sin Costan cotcscsec ①先看左上部,画图的顺序是sin 到cos 再到tan ,呈现一个“7”字型,而下半部分的顺序是csc 到sec 到cot ,呈现倒“7”字型。
②中心写一个1③从sin 到cos 再到cot , csc 再到sec 和tan ,顺次连接成六边形④补上对角线,记住对角线一定要过中心的1⑤以sin ,cos 和1为第一个有阴影的三角形,每隔一个三角型就有一个阴影三角形,阴影三角形总共有三个。
1 三个三角函数的图:sin Costan1①画图的顺序是sin 到cos 再到tan ,呈现一个“7”字型②中心写一个1③从sin 到cos 再到tan , 再回到sin ,顺次连接成三角形④将sin 和1连起来⑤以sin ,cos 和1为有阴影的三角形。
三角函数的思维导图一:概述三角函数是数学中属于初等函数中的超越函数的函数。
它们的本质是任何角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的。
其定义域为整个实数域。
三角函数公式看似很多、很复杂,但只要掌握了三角函数的本质及内部规律,就会发现三角函数各个公式之间有强大的联系。
而掌握三角函数的内部规律及本质也是学好三角函数的关键所在。
下面是通过思维导图的方式,将这些内部规律和联系表现出现,方便学习者掌握三角函数。
图一为学习三角函数的主要分支。
我们从下列分支,一个一个分支开始学习。
图一二:角度与弧度制2.1我们知道,常见的度量方法有角度制与弧度制两种。
什么是角度制?所谓角度制,就是将圆周 360 等分,其中 1 份所对应的圆心角定义为 1 度,记作1°。
并将 1度的 1/60 定义为 1 分,记作 1';将 1 分的 1/60 定义为 1 秒,记作 1"。
换言之,1°=60',1'=60"。
图二是角度制的示意图。
2.2而弧度制则是根据圆心角、弧长、半径之间的数量关系而引入的。
当弧长等于半径时,弧所对应的圆心角为 1 弧度,记作 1rad。
正角度弧度数是一个正数,负角度弧度数是一个负数,零角度弧度数。
半径为r的圆的圆心角α所对的弧度长为l,那么角α的弧度数的绝对值是 | α | = l / r。
图二2.3角度制与弧度制的换算,数字表达式和图示表示如下所示。
2.4图四为角制和弧度制的思维导图。
图四角度制与弧度制数字表达式: 360 o = 2π rad 180 o = π rad1 o =(π / 180)rad ≈ 0.01745 rad 1 rad =(180 /π)o ≈ 57.30 o α 度的角 = α ·(π / 180)rad角度制与弧度制图示表示:三:三角函数基本属性3.1 三角函数的定义。
三角函数 1. 特殊锐角(0°,30°,45°,60°,90°)的三角函数值2.角度制与弧度制设扇形的弧长为l ,圆心角为a (rad ),半径为R ,面积为S 角a 的弧度数公式 2π×(a /360°)角度与弧度的换算①360°=2π rad ②1°=π/180rad③1 rad=180°/π=57° 18′≈57.3°弧长公式 l a R =扇形的面积公式 12s lR =3.诱导公式:(奇变偶不变,符号看象限)所谓奇偶指是整数k 的奇偶性(k ·π/2+a )所谓符号看象限是看原函数的象限(将a 看做锐角,k ·π/2+a 之和所在象限) 注:①:诱导公式应用原则:负化正、大化小,化到锐角为终了4. 三角函数的图像和性质:(其中z k ∈)①:三角函数x y sin = x y cos =x y tan = cot y x=函 数 图 象定义域 R R 2x k ππ≠+x k π≠值域 [-1,1][-1,1]RR周期 2π2πππ奇偶性 奇偶奇非奇非偶单 调 性 2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦2,222k k ππππ⎡⎤-+↑⎢⎥⎣⎦[]2,2k k πππ-↑ []2,2k k πππ+↓,22k k ππππ⎡⎤-+↑⎢⎥⎣⎦[],k k πππ+↓对 称 性 :2x k ππ=+对称轴对称中心:(,0)k π:x k π=对称轴:对称中心(+,0)2k ππ:对称中心(,0)2k π零值点 πk x =2ππ+=k xπk x =2ππ+=k x最 值 点2ππ+=k x ,1max=y2ππ-=k x ,1min-=yπk x 2=,1max =y ;2y k ππ=+,1min -=y②:函数)sin(ϕω+=x A y 的图像与性质:(1) 函数)sin(ϕω+=x A y 和)cos(ϕω+=x A y 的周期都是ωπ2=T(2) 函数)tan(ϕω+=x A y 和)cot(ϕω+=x A y 的周期都是ωπ=T5.三角函数尺度变换sin y x =经过变换变为sin y x ϖϕ=+A ()的步骤(先平移后伸缩): 1sin sin sin sin y x y x y x y x ϖϕϖϖϖϕϖϕ=−−−−−−−→=−−−−−→=+−−−−−−−→=+横坐标变为原来的倍向左或向右纵坐标不变平移个单位纵坐标变为原来的A 倍横坐标不变()A ()6.三角函数的对称变换:① )()(x f y x f y -=→=) 将)(x f y =图像绕y 轴翻折180°(整体翻折) (对三角函数来说:图像关于x 轴对称)② )()(x f y x f y -=→=将)(x f y =图像绕x 轴翻折180°(整体翻折) (对三角函数来说:图像关于y 轴对称)③ )()(x f y x f y =→= 将)(x f y =图像在y 轴右侧保留,并把右侧图像绕y 轴翻折到左侧(偶函数局部翻折)④ )()(x f y x f y =→=保留)(x f y =在x 轴上方图像,x 轴下方图像绕x 轴翻折上去(局部翻动)7.反三角函数的图像与性质:名称y=arsinx y=arccosx y=arctanx y=arccotx定义y=sinx((,))22xππ∈-的反函数,叫做反正弦函数y=cosx((0,))xπ∈的反函数,叫做反余弦函数y=tanx((,))22xππ∈-的反函数,叫做反正切函数y=cotx((0,))xπ∈的反函数,叫做反余切函数性质图像定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性[]1,1-增函数[]1,1-减函数(),-∞+∞增函数(),-∞+∞减函数奇偶性arcsin()arcsinθθ-=-arccos()arccosθπθ-=-arctan()arctanθθ-=-arccot()arccotθπθ-=-周期性非周期函数非周期函数非周期函数非周期函数7.三角函数公式:(1)倒数关系: (2)平方关系:tan cot 1sin csc 1cos sec 1αααααα⋅=⋅=⋅= 222222sin cos 11tan sec 1cot csc αααααα+=+=+=(3)三角和与差公式:sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ+=++=-++=- sin()sin cos cos sin cos()cos cos sin sin tan tan tan()1tan tan αβαβαβαβαβαβαβαβαβ-=--=+--=+(4)二倍角公式:()22222sin 22sin cos cos 2cos sin 2cos 112sin 2tan tan 21tan ααααααααααα==-=-=-=-升幂公式 22221cos 2sin 1cos 22sin 2(1cos 21cos 22cos cos 2αααααααα-⎫=⎪⎧-=⎪⎪⇒⎬⎨++=⎪⎩⎪=⎪⎭降幂公式) (5)三角函数的和差化积公式 (6)三角函数的积化和差公式sin sin 2sin cos22sin sin 2cos sin22cos cos 2cos cos22cos cos 2sin sin22αβαβαβαβαβαβαβαβαβαβαβαβ+-+=⋅+--=⋅+-+=⋅+--=-⋅ [][][][]1sin cos sin()sin()21cos sin sin()sin()21cos cos cos()cos()21sin sin cos()cos()2αβαβαβαβαβαβαβαβαβαβαβαβ⋅=++-⋅=+--⋅=++-⋅=-+-- 六边形记忆法:图形结构“上弦中切下割,左正右余中间1”;记忆方法“对角线上两个函数的积为1;阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方;任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。
第五章三角函数要点一:终边相同的角 1.终边相同的角凡是与α终边相同的角,都可以表示成360k α⋅︒+的形式. 要点诠释:(1)终边相同的前提是:原点,始边均相同;(2)终边相同的角不一定相等,但相等的角终边一定相同; (3)终边相同的角有无数多个,它们相差360︒的整数倍. 特例:终边在x 轴上的角集合{}|180k k Z αα=⋅︒∈,, 终边在y 轴上的角集合{}|18090k k Z αα=⋅︒+︒∈,, 终边在坐标轴上的角的集合{}|90k k Z αα=⋅︒∈,.在已知三角函数值的大小求角的大小时,通常先确定角的终边位置,然后再确定大小. 2.弧度和角度的换算(1)角度制与弧度制的互化:π弧度 180=,1801π=弧度,1弧度'180()5718π=≈(2)弧长公式:r l ||α=(α是圆心角的弧度数),扇形面积公式:2||2121r r l S α==. 要点诠释:(1)角有正负零角之分,它的弧度数也应该有正负零之分,如2ππ--,等等,一般地, 正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,角的正负主要由角的旋转方向来决定.(2)角α的弧度数的绝对值是:rl=α,其中,l 是圆心角所对的弧长,r 是半径. 要点二:任意角的三角函数的定义、三角函数的符号规律、特殊角的三角函数值、同角三角函数的关系式、诱导公式:1.三角函数定义:角α终边上任意一点P 为),(y x ,设r OP =||则:,cos ,sin r x r y ==ααxy =αtan 要点诠释:三角函数的值与点P 在终边上的位置无关,仅与角的大小有关.我们只需计算点到原点的距离22r x y =+那么22sin x y α=+,22cos x y α=+,tan yxα=. 2.三角函数符号规律:一全正,二正弦,三正切,四余弦(为正);要点诠释:口诀的含义是在第一象限各三角函数值为正;在第二象限正弦值为正,在第三象限正切值为正,在第四象限余弦值为正.α0 6π 4π 3π 2π π32π 2π sin α 0 21 22 23 1 0 -1 0 cos α 1 23 22 21 0 -1 0 1 tan α33 13不存在不存在22sin sin cos 1;tan cos ααααα+== 要点诠释:(1)这里“同角”有两层含义,一是“角相同”,二是对“任意”一个角(使得函数有意义的前提下)关系式都成立;(2)2sin α是2(sin )α的简写;(3)在应用平方关系时,常用到平方根,算术平方根和绝对值的概念,应注意“±”的选取. 5.诱导公式(奇变偶不变,符号看象限):sin(πα-)=sin α,cos(πα-)=-cos α,tan(πα-)=-tan α sin(πα+)=-sin α,cos(πα+)=-cos α,tan(πα+)=tan α sin(α-)=-sin α,cos(α-)=cos α,tan(α-)=-tan αsin(2πα-)=-sin α,cos(2πα-)=cos α,tan(2πα-)=-tan αsin(2k πα+)=sin α,cos(2k πα+)=cos α,tan(2k πα+)=tan α,()k Z ∈ sin(2πα-)=cos α,cos(2πα-)=sin α sin(2πα+)=cos α,cos(2πα+)=-sin α要点诠释:(1)要化的角的形式为α±⋅ 90k (k 为常整数); (2)记忆方法:“奇变偶不变,符号看象限”;(3)必须对一些特殊角的三角函数值熟记,做到“见角知值,见值知角”; (4)sin cos cos 444x x x πππ⎛⎫⎛⎫⎛⎫+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;cos sin 44x x ππ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭. 要点三:正弦函数、余弦函数和正切函数的图象与性质1.三角函数sin cos y x y x ==,的图象与性质: y=sinx y=cosx 定义域 (-∞,+∞) (-∞,+∞) 值域 [-1,1] [-1,1] 奇偶性奇函数偶函数单调性增区间[2,2],22k k k Z ππππ-+∈ 减区间3[2,2],22k k k Zππππ++∈ 增区间[]22k k k Zπππ-∈,减区间[]22k k k Zπππ+∈,周期性 最小正周期2T π=最小正周期2T π=最值 当2()2x k k Z ππ=-∈时,min 1y =-当2()2x k k Z ππ=+∈时,max 1y =当2()x k k Z ππ=+∈时,min 1y =- 当2()x k k Z π=∈时,max 1y = 对称性对称轴()2x k k Z ππ=+∈对称中心()0()k k Z π∈,对称轴()x k k Z π=∈ 对称中心(,0)()2k k Z ππ+∈y=cosx 的图象是由y=sinx 的图象左移2得到的. 2.三角函数tan y x =的图象与性质:y=tanx定义域 ,2x k k Z ππ≠+∈值域 R 奇偶性奇函数单调性 增区间(,),22k k k Z ππππ-+∈周期性 T π=最值 无最大值和最小值 对称性对称中心(,0)()2k k Z π∈ 要点四:函数sin()y A x ωϕ=+的图象与性质 用“五点法”作sin()y A x ωϕ=+的简图,主要是通过变量代换,设z x ωϕ=+,由z 取30,,,,222ππππ来求出相应的x ,通过列表,计算得出五点坐标,描点后得出图象. 要点诠释:用“五点法”作图的关键是点的选取,其中横坐标成等差数列,公差为4T. sin()y A x ωϕ=+2.sin()y A x ωϕ=+的性质 (1)三角函数的值域问题三角函数的值域问题,实质上大多是含有三角函数的复合函数的值域问题,常用方法有:化为代数函数的值域或化为关于sin (cos )x x 的二次函数式,再利用换元、配方等方法转化为二次函数在限定区间上的值域.(2)三角函数的单调性函数)0,0)(sin(>>+=ωϕωA x A y 的单调区间的确定,基本思想是把ϕω+x 看作一个整体,比如:由)(2222Z k k x k ∈+≤+≤-ππϕωππ解出x 的范围所得区间即为增区间,由)(23222Z k k x k ∈+≤+≤+ππϕωππ解出x 的范围,所得区间即为减区间; 要点诠释:(1)注意复合函数的解题思想;(2)比较三角函数值的大小,往往是利用奇偶性或周期性在转化为属于同一单调区间上的两个同名函数值,再利用单调性比较.3.确定sin()y A x ωϕ=+的解析式的步骤①首先确定振幅和周期,从而得到A ω,;②确定ϕ值时,往往以寻找“五点法”中第一个零点(,0)ϕω-作为突破口,要注意从图象的升降情况找准第一个零点的位置,同时要利用好最值点.要点五:正弦型函数sin()y A x ωϕ=+的图象变换方法 先平移后伸缩sin y x =的图象 sin()y x ϕ=+的图象sin()y x ωϕ=+的图象 sin()y A x ωϕ=+的图象的图象. 先伸缩后平移sin y x =的图象 sin y A x =的图象(01)(1)1()ωωω<<>−−−−−−−−−→横坐标伸长或缩短到原来的纵坐标不变 sin()y A x ω=的图象(0)(0)ϕϕϕω><−−−−−−−→向左或向右平移个单位sin()y A x ωϕ=+的图象的图象.要点六:两角和、差的正、余弦、正切公式()sin sin cos cos sin αβαβαβ±=±; ()cos cos cos sin sin αβαβαβ±=;ϕϕϕ<−−−−−−−→向左(>0)或向右(0)平移个单位长度()ωωω−−−−−−−−−→横坐标伸长(0<<1)或缩短(>1)1到原来的纵坐标不变()A A A >−−−−−−−−−→纵坐标伸长(1)或缩短(0<<1)为原来的倍横坐标不变(0)(0)k k k ><−−−−−−−→向上或向下平移个单位长度sin()y A x k ϕ=++(1)(01)A A A ><<−−−−−−−−−→纵坐标伸长或缩短为原来的倍(横坐标不变)(0)(0)k k k ><−−−−−−−→向上或向下平移个单位长度sin()y A x k ωϕ=++()tan tan tan 1tan tan αβαβαβ±±=.要点诠释:1.公式的适用条件(定义域) :公式①、②对任意实数α,β都成立,这表明①、②是R 上的恒等式;公式③中,∈,且R αβk (k Z)2±≠+∈、、παβαβπ2.正向用公式①、②,能把和差角()±αβ的弦函数表示成单角α,β的弦函数;反向用,能把右边结构复杂的展开式化简为和差角()±αβ 的弦函数.公式③正向用是用单角的正切值表示和差角()±αβ的正切值化简.要点七:二倍角公式1. 在两角和的三角函数公式βαβαβαβα=+++中,当T C S ,,时,就可得到二倍角的三角函数公式222,,S C T ααα:sin 22sin cos ααα=;2222cos 2cos sin 2cos 112sin ααααα=-=-=-;22tan tan 21tan ααα=-. 要点诠释:1.在公式22,S C αα中,角α没有限制,但公式2T αα中,只有当)(224Z k k k ∈+≠+≠ππαππα和时才成立;2. 余弦的二倍角公式有三种:ααα22sin cos 2cos -==1cos 22-α=α2sin 21-;解题对应根据不同函数名的需要,函数不同的形式,公式的双向应用分别起缩角升幂和扩角降幂的作用.3. 二倍角公式不仅限于2α和α的二倍的形式,其它如4α是2α的二倍,24αα是的二倍,332αα是的二倍等等,要熟悉这多种形式的两个角相对二倍关系,才能熟练地应用二倍角公式,这是灵活运用这些公式的关键.要点八:二倍角公式的推论升幂公式:21cos 22cos αα+=, 21cos 22sin αα-=降幂公式:ααα2sin 21cos sin =; 22cos 1sin 2αα-=;22cos 1cos 2αα+=.要点九:三角恒等变换的基本题型三角式的化简、求值、证明是三角恒等变换的基本题型: 1.三角函数式的化简(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等.(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数.2.三角函数的求值类型有三类(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角.3.三角等式的证明(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明.类型一:三角函数的概念例1. 已知角α的终边过点(,2)(0)a a a ≠,求α的三个三角函数值. 【思路点拨】分0,0a a ><两种情况求α的三个三角函数值. 【解析】因为过点(,2)(0)a a a ≠,所以5|r a =,,2x a y a ==.当250sin 55||5y a r a aα>====时,; 5cos 55x r aα===,2tan =α. 当250sin 5||5y a r a a α<====-时,5cos 55x r aα===--;2tan =α. 【总结升华】(1)当角α的终边上点的坐标以参数形式给出时,要根据问题的实际及解题的需要对参数进行分类讨论;(2)若角α已经给定,不论点选在α的终边上的什么位置,角α的三角函数值都是确定的;另一方面,如果角α终边上点坐标已经确定,那么根据三角函数定义,角α的三角函数值也是确定的.类型二:扇形的弧长与面积的计算例2.已知一半径为r 的扇形,它的周长等于所在圆的周长的一半,那么扇形的中心角是多少弧度?合多少度?扇形的面积是多少?【答案】2π- 65.44︒ 21(2)2r π-【解析】设扇形的圆心角是rad θ,因为扇形的弧长是θr ,所以扇形的周长是2.r r θ+ 依题意,得2,rr r θπ+=()2rad θπ∴=-180(2)ππ⎛⎫-⨯ ⎪⎝⎭≈1.14257.30⨯︒≈65.44,︒ 2211(2).22S r r θπ∴==-【总结升华】弧长和扇形面积的核心公式是圆周长公式2C r π=⋅和圆面积公式2122S r π=⋅⋅,当用圆心角的弧度数α代替2π时,即得到一般的弧长公式和扇形面积公式:211,.22l r S lr r αα=⋅==⋅类型三:同角三角函数的基本关系式 例3.已知1sin cos ,(0,),5A A A π+=∈,求tan A 的值. 【思路点拨】由题意知,12sin cos ,(0,),25A A A π=-∈所以A 为钝角,然后求出3cos 5α=-即可求得. 【解析】方法一:由51cos sin =+A A ,得(),251cos sin 2=+A A),,0(,2512cos sin π∈-=∴A A A .0cos sin ,0cos ,0sin ,2>-<>∴<<∴A A A A A ππ又().57cos sin ,2549cos sin 21cos sin 2=-∴=-=-A A A A A A 由,57cos sin 51cos sin ⎪⎪⎩⎪⎪⎨⎧=-=+A A A A 得,.53cos 54sin ⎪⎪⎩⎪⎪⎨⎧-==A A .34tan -=∴A方法二:由51cos sin =+A A 可得,sin 51cos 22⎪⎭⎫ ⎝⎛-=A A即,sin 51sin 122⎪⎭⎫⎝⎛-=-A A 整理得,012sin 5sin 252=--A A即,0)3sin 5)(4sin 5(=+-A A54sin =∴A 或53sin -=A ,由已知π<<A 0知53sin -=A 不合题意,舍去.1sin cos 5A A +=,两边平方得:12sin cos ,(0,),25A A A π=-∈(,)2A ππ∴∈,所以3cos 5A =- .34tan -=∴A【总结升华】同角三角函数基本关系是反映了各种三角函数之间的内在联系,为三角函数式的恒等变形提供了工具与方法.类型四:三角函数的诱导公式例4.已知sin(3π+θ)=13,求()()()cos cos(2)33cos cos 1sin cos sin 22πθθπππθπθθθπθ+-+--⎡⎤⎛⎫⎛⎫⎣⎦---+ ⎪ ⎪⎝⎭⎝⎭的值.【思路点拨】利用诱导公式,求出sin θ=-13.然后化简要求的式子,即可求得结果. 【答案】18【解析】 ∵sin(3π+θ)=-sin θ=13,∴sin θ=-13, ∴原式=()cos cos(2)3cos cos 1sin cos()cos 2θπθπθθθπθθ--+--⎛⎫---+ ⎪⎝⎭=21cos 1cos cos cos θθθθ++-+ =11cos θ++11cos θ-=221cos θ- =22sin θ=221()3-=18. 【总结升华】 诱导公式用角度和弧度制表示都成立,记忆方法可以概括为“奇变偶不变,符号看象限”,“变”与“不变”是相对于对偶关系的函数而言的,sin α与cos α对偶,“奇”、“偶”是对诱导公式中2k πα⋅+的整数k 来讲的,象限指2k πα⋅+中,将α看作锐角时,2k πα⋅+所在象限,如将3cos 2πα⎛⎫+⎪⎝⎭写成cos 32πα⎛⎫⋅+ ⎪⎝⎭,因为3是奇数,则“cos ”变为对偶函数符号“sin ”,又32πα+看作第四象限角,3cos 2πα⎛⎫+ ⎪⎝⎭为“+”,所以有3cos sin 2παα⎛⎫+= ⎪⎝⎭. 类型五:三角函数的图象和性质 例5. 函数ln cos 22y x x ππ⎛⎫=-<< ⎪⎝⎭的图象是( )【答案】A【解析】ln cos ()22y x x ππ=-<<是偶函数,可排除B 、D ,由cosx 的值域可以确定.因此本题应选A.例6.把函数y =cos2x +1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是( )【思路点拨】首先根据函数图象变换的公式,可得最终得到的图象对应的解析式为:y=cos (x+1),然后将曲线y=cos (x+1)的图象和余弦曲线y=cosx 进行对照,可得正确答案. 【解析】将函数y=cos2x+1的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到的图象对应的解析式为:y=cosx+1,再将y=cosx+1图象向左平移1个单位长度,再向下平移 1个单位长度,得到的图象对应的解析式为:y=cos (x+1),∵曲线y=cos (x+1)由余弦曲线y=cosx 左移一个单位而得,∴曲线y=cos (x+1)经过点1,02π⎛⎫- ⎪⎝⎭和31,02π⎛⎫- ⎪⎝⎭,且在区间31,122ππ⎛⎫-- ⎪⎝⎭上函数值小于0,由此可得,选项A 正确,故选A .例7.已知函数()sin(),f x x ωϕ=+其中0ω>,||2ϕ<(I )若coscos sinsin 0,44ππϕϕ3-=求ϕ的值; (Ⅱ)在(I )的条件下,若函数()f x 的图像的相邻两条对称轴之间的距离等于3π,求函数()f x 的解析式;并求最小正实数m ,使得函数()f x 的图像象左平移m 个单位所对应的函数是偶函数.【思路点拨】(1)把所给的式子化简,然后结合平方关系式得出tan ϕ,由0ω>,||2πϕ<,求出ϕ的值.(Ⅱ)由题意求得,23T π=,故3ω=,进一步求出()f x 的解析式. 【答案】(I )4π(Ⅱ)()sin(3)4f x x π=+ 12π【解析】 (I )由3coscos sin sin 044ππϕϕ-=,得22sin 022ϕϕ-=,得tan 1ϕ= 又||,24ππϕϕ<∴=.(Ⅱ)由(I )得,()sin()4f x x πω=+依题意,23T π= 又2,T πω=故3,()sin(3)4f x x πω=∴=+ 函数()f x 的图像向左平移m 个单位后所对应的函数为()sin 3()4g x x m π⎡⎤=++⎢⎥⎣⎦()g x 是偶函数当且仅当3()42m k k Z πππ+=+∈即()312k m k Z ππ=+∈ 从而,最小正实数12m π=【总结升华】本题考查了同角三角函数的基本关系式及函数sin()y A x ωϕ=+的性质,属中等难度题.类型六:正用公式例8.已知:41cos ,32sin -=β=α,求cos()αβ-的值. 【思路点拨】因为不知道角,αβ所在的象限,所以要对,αβ分别讨论求cos()αβ-的值.【解析】由已知可求得22515cos 1sin sin 1cos 34ααββ=-=±=-=±. 当α在第一象限而β在第二象限时,os()os cos sin sin c c αβαβαβ-=+51215)43=-+125152-=. 当α在第一象限而β在第三象限时,512152155cos())(43αβ+-=-+⋅=当α在第二象限而β在第二象限时, 512152155cos()()343412αβ+-=--+⋅=. 当α在第二象限而β在第三象限时,512152155cos()()(343412αβ-=--+⋅-=-. 【总结升华】分类的原则是:(1)分类中的每一部分是相互独立的;(2)一次分类按一个标准;(3)分类讨论要逐级进行.掌握分类的方法,领会其实质,对于加深基础知识的理解,提高分析问题、解决问题的能力是十分重要的.例9.已知παπ434<<,40πβ<<,53)4cos(=-απ,135)43sin(=+βπ,求sin()αβ+的值.【思路点拨】注意到)(2)4()43(βαπαπβπ++=--+,应把)43(),4(βπαπ+-看成整体,可以更好地使用已知条件.欲求sin()αβ+,只需求出)2cos(βαπ++-.【答案】5665【解析】∵ 042<-<-αππ, ∴54)4sin(-=-απ,∵ πβππ<+<4343, ∴1312)43cos(-=+βπ.∴)](2cos[)sin(βαπβα++-=+6556)54(135531312)]4sin()43sin()4cos()43[cos()]4()43cos[(=-⨯-⨯=-++-+-=--+-=απβπαπβπαπβπ【总结升华】(1)解题中应用了)(2)4()43(βαπαπβπ++=--+式子的变换,体现了灵活解决问题的能力,应着重体会,常见的变换技巧还有(),2()()βαβαααβαβ=+-=++-,2()()βαβαβ=+--, 2()αβαβα+=++等.(2)已知某一个(或两个)角的三角函数值,求另一个相关角的三角函数值,基本的解题策略是从“角的关系式”入手切入或突破.角的关系主要有互余(或互补)关系,和差(为特殊角)关系,倍半关系等.对于比较复杂的问题,则需要两种关系的混合运用.类型七:逆用公式 例10.求值:(1)001tan151tan15+-; (2)44(sin 23cos8sin 67cos98)(sin 730cos 730)''+-o o o o o o. 【思路点拨】 题目中涉及到的角并非特殊角,而从式子的结构出发应逆用和角公式等先化简再计算. (1)利用tan 451︒=将1tan15+︒视为tan 45tan15︒+︒,将1tan15-︒视为1tan 45tan15-︒︒,则式子恰为两角和的正切.【答案】(132)14- 【解析】(1)原式360tan )1545tan(15tan 45tan 115tan 45tan 0000000==+=-+=; (2)原式=44[sin 23cos8sin(9023)cos(908)](sin 730cos 730)''+-+-o o o o o o o o2222(sin 23cos8cos 23sin8)(sin 730cos 730)(sin 730cos 730)o o o o o o o o ''''=-+-22sin(238)(cos 730sin 730)o o o o ''=---11sin15cos15sin 3024=-︒︒=-︒=-.【总结升华】(1)把式中某函数作适当的转换之后,再逆用两角和(差)正(余)弦公式,二倍角公式等,即所谓“逆用公式”.(2)辅助角公式:22sin cos )a b a b αααϕ+++,其中角ϕ在公式变形过程中自然确定.例11. 求值:(1)cos36cos72︒︒;(2)πππ73cos 72cos 7cos【思路点拨】问题的特征是角存在倍角关系,且都是余弦的乘积.方法是分子分母(分母视为1)同乘以最小角的正弦.【答案】(1)1/4 (2)1/8 【解析】(1)原式=000000000sin 36cos36cos 721sin 72cos 721sin1441sin 362sin 364sin 364=⨯=⨯=; (2)原式=πππππππ74cos 72cos 7cos )74cos(72cos 7cos -=-24sin cos cos cos 7777sin7224sin cos cos 7772sin78sin 7...8sin718πππππππππππ=-=-==-=【总结升华】此种类型题比较特殊,特殊在:①余弦相乘;②后一个角是前一个角的2倍;③最大角的2倍与最小角的和与差是π.三个条件缺一不可.另外需要注意2的个数.应看到掌握了这些方法后可解决一类问题,若通过恰当的转化,转化成具有这种特征的结构,则可考虑采用这个方法.类型八:变用公式例12.在ABC ∆中,求值:tan tan tan tan tan tan 222222A B B C C A ++ 【答案】1【解析】∵A B C π++=,∴222+=-A B C π,∴tan tan()cot 2222A B C Cπ+=-= ∴原式=tan tan tan (tan tan )22222A B C A B++tan tan tan tan (1tan tan )222222tan tan tan cot (1tan tan )222222tan tan 1tan tan22221A B C A B A B A B C C A B A B A B +=+-=+⨯-=+-= 例13. 化简:(1)sin 50(13)︒︒;(2)222cos 12tan()sin ()44αππαα--+【思路点拨】(1)题中首先“化切为弦”,同时用好“50︒”和“40︒”的互余关系,注意逆用和角公式化简; (2)题初看有“化切为弦”,“降幂”等诸多想法,但首先应注意到2)4()4(παπαπ=++-这个关系.【答案】(1)1(2)1【解析】(1)原式003sin10sin50(1)cos10=+00cos103sin10sin 50+==000000sin 30cos10cos30sin102sin50cos10+⋅000000000sin 402cos40sin 402sin50cos10cos10sin80cos101cos10cos10=⋅==== (2)原式=2cos 22tan()sin [()]424απππαα---2cos 22sin()4cos ()4cos()4cos 22sin()cos()44cos 2cos 2cos 2sin(2)21απαπαπααππααααπαα=-⋅--=--==-=【总结升华】(1)三角变换所涉及的公式实际上正是研究了各种组合的角(如和差角,倍半角等)的三角函数与每一单角的三角函数关系.因而具体运用时,注意对问题所涉及的角度及角度关系进行观察.(2)三角变换中一般采用“降次”、“化弦”、“通分”的方法;在三角变换中经常用到降幂公式:21cos 2cos 2αα+=,21cos 2sin 2αα-=. 例14.已知32)sin(=+βα,51)sin(=-βα,求的值. 【思路点拨】 先分析所求式 sin tan sin cos cos sin tan cos sin cos αααβαββαββ==,分子、分母均为已知条件中和差角的展开式的项.【答案】137【解析】∵32sin cos cos sin )sin(=+=+βαβαβα, 51sin cos cos sin )sin(=-=-βαβαβα, 2tan()tan tan tan tan()αβαββαβ+--⋅+解得3013cos sin =βα, 307sin cos =βα, ∴tan sin cos 13tan cos sin 7ααββαβ==. 类型九:三角函数知识的综合应用 例15.函数2()6cos 33(0)2xf x x ωωω=->在一个周期内的图象如图所示,A 为图象的最高点,B 、C 为图象与x 轴的交点,且ABC ∆为正三角形.(Ⅰ)求ω的值及函数()f x 的值域;(Ⅱ)若083()f x =,且0102(,)33x ∈-,求0(1)f x +的值. 【答案】(Ⅰ)4π[3,3]-(Ⅱ)65【解析】(Ⅰ)由已知可得:2()6cos 33(0)2x f x x ωωω=-> =3cos ωx+)3sin(32sin 3πωω+=x x又由于正三角形ABC 的高为23,则BC=4 所以,函数482824)(πωωπ===⨯=,得,即的周期T x f所以,函数]32,32[)(-的值域为x f(Ⅱ)因为,由538)(0=x f (Ⅰ)有 ,538)34(sin 32)(00=+=ππx x f 54)34(sin 0=+ππx 即由x 0)2,2()34x (323100ππππ-∈+-∈),得,(所以,53)54(1)34(cos 20=-=+ππx 即 故=+)1(0x f =++)344(sin 320πππx ]4)34(sin[320πππ++x)22532254(324sin)34cos(4cos )34([sin 3200⨯+⨯=+++=ππππππx x567=【总结升华】本题主要考查三角函数的图像与性质同三角函数的关系、两角和的正(余)弦公式、二倍角公式等基础知识,考查运算能力,考查树形结合、转化等数学思想.。