第十一章-1相干光-2杨氏双缝干涉-劳埃德镜-教案
- 格式:docx
- 大小:327.00 KB
- 文档页数:7




§11-1 相干光
件及获得方法
2. 能分析杨氏双缝干涉条件、条纹分布规律和位置;理解劳埃德镜光干涉规律
三、教学过程:
引言:什么是光的干涉现象?
与机械波类似,光的干涉现象表现为在两束光的相遇区域形成稳定的、有强有弱的光强分布。
即在某些地方光振动始终加强(明条纹),在某些地方光振动始终减弱(暗条纹),从而出现明暗相间的干涉条纹图样。
光的干涉现象是波动过程的特征之一。
光的干涉:两束光的相遇区域形成稳定的、有强有弱的光强分布。
实际是满足一定条件的两列相干光波相遇叠加,在叠加区域某些点的光振动始终加强,某些点的光振动始终减弱,即在干涉区域内振动强度有稳定的空间分布。
干涉条纹:所形成的均匀分布的图样。
§11-1相干光
一、相干光:两束满足相干条件的光称为相干光
1、相干条件(Coherent Condition):
这两束光在相遇区域:①振动方向相同;
②振动频率相同;
③相相位同或相位差保持恒定
那么在两束光相遇的区域内就会产生干涉现象。
2、相干光的获得
(1)普通光源的发光机理
当原子中大量的原子(分子)受外来激励而处于激发状态。
处于激发状态的原子是不稳定的,它要自发地向低能级状态跃迁,并同时向外辐射电磁波。
当这种电磁波的波长在可见光范围内时,即为可见光。
原子的每一次跃迁时间很短(10-8 s )。
由于一次发光的持续时间极短,所以每个原子每一次发光只能发出频率一定、振动方向一定而长度有限的一个波列。
由于原子发光的无规则性,同一个原子先后发出的波列之间,以及不同原子发出的波列之间都没有固定的相位关系,且振动方向与频率也不尽相同,这就决定了两个独立的普通光源发出的光不是相干光,因而不能产生干涉现象。
(2)获得相干光源的两种方法
a.原理:
将同一光源上同一点或极小区域(可视为点光源)发出的一束光分成两束,让它们经过不同的传播路径后,再使它们相遇,这时,这一对由同一光束分出来的光的频率和振动方向相同,在相遇点的相位差也是恒定的,因而是相干光。
b 方法:
分波阵面法(Wavefront Spliting ):把光波的阵面分为两部分,例如:杨氏双缝干涉,双镜干涉,洛埃镜干涉。
分振幅法(Amplititude Spliting ):利用两个反射面产生两束反射光,例如:劈尖干涉,牛顿环,薄膜干涉。
§11-2杨氏双缝干涉 劳埃德镜
设法将同一束光分为两束。
下列分别是利用双缝、利用空气膜、利用肥皂膜、利用平面镜形成相干光源的示意图。
S b d a c 平面镜 肥皂
膜
空气膜
S S 1 S 2 平
行光 图1
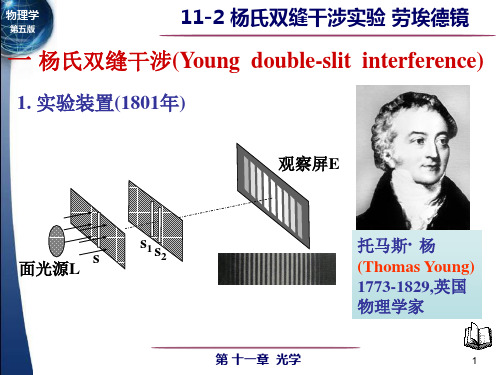
一、杨氏双缝干涉实验
图2 杨氏双缝干涉实验原理图
如图2所示,两个狭缝S 1、S 2长度方向彼此平行,单缝被照亮后相当于一线光源,发出以S 为轴的柱面波。
由于S 1、S 2关于S 对称放置,S 在S 1和S 2处激起的振动相同,从而可将S 1和S 2看作两个同相位的相干波源,它们发出的光波在屏上相遇后发生相干叠加,出现了明暗相间的平行条纹——干涉条纹。
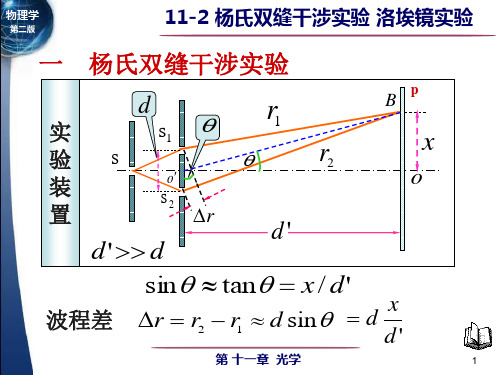
1、条纹的位置分布
S 1和S 2的间距为d,到光屏的距离为d ’。
考察屏上一点P ,设S 1P=r 1,S 2P=r 2,因一般情况下d<<d ’,x<< d ’,故两列光波到达相遇点P 处的波程差为
21sin 'x r r r d d d θ∆=-≈= 出现明纹和暗纹的条件是;0,1,2,'0,1,2,(21)2
k k x r d d k k λλ±⎧=⋯⎪∆==⎨=⋯±+⎪⎩加强减弱 式中k 称为干涉条纹的级次。
可得明纹暗纹的位置是:
';0,1,2,'1,2,(21)2k d k k d x d k k d λλ⎧±⎪=⋯⎪=⎨=⋯⎪±+⎪⎩
明纹暗纹
则相邻明纹和暗纹的间距
'd x d
λ∆= 上式说明,杨氏试验中相邻明纹或暗纹的间距与干涉条纹的级次无关,条纹呈等间距排列,如图3所示为双缝干涉条纹。
测出d ’和d 及相邻间距,即可求得入射光的波长,杨氏正式利用这一办法最先测量光波波长的;红光约为750nm ,紫光约为390nm 。
图3 双缝干涉
例1 在杨氏双缝实验中,欲使干涉条纹变宽,应作怎样的调整:
(A )增加双缝的间距,
(B )增加入射光的波长,
(C )减少双缝至光屏之间的距离,
(D )干涉级k 愈大时条纹愈宽。
解:由干涉条纹间距公式'd x d
λ∆=可知,应选(B ) d ’和d 确定后,波长较长的红光所产生的相邻条纹间距比波长较短的紫光为大,因此用白光进行双缝实验时,除中央明纹是白色外,其余各级明纹因各色光互相错开而形成由紫到红的彩色条纹,如图4所示。
图4白光双缝干涉
2. 明纹位置 由'k d x k d λ=±可知,k=0时,00x =。
零级明纹位于屏幕中央,只有一条。
k=1时,1'd x d λ=±。
1级明纹有两条,对称分布在屏幕中央两侧。
其它各级明纹都有两条,且对称分布,如图5所示。
图5.明纹分布 图6.暗纹分布
3. 暗纹位置
由'(21)
2k d x k d λ=±+可知,k=0时,0'2
d x d λ=±。
零级暗纹有两条,对称分布在屏幕中央两侧。
k=1时,13'2d x d λ=±。
1级暗纹有两条,对称分布在屏幕中央两侧。
其它各级暗纹都有两条,且对称分布,如图6所示。
例2 在杨氏双缝干涉实验中,用波长λ=589.3 nm 的纳灯作光源,屏幕距双缝的距离d’=800 mm ,问:(1)当双缝间距1mm 时,两相邻明条纹中心间距是多少? (2)假设双缝间距10 mm ,两相邻明条纹中心间距又是多少?
解:(1) d=1 mm 时 '0.47 mm d x d
λ∆== (2) d =10 mm 时 '0.047 mm d x d
λ∆== 但是0.047m 人的肉眼难以观测,所以试验中双缝间距不能太大。
例3 以单色光照射到相距为0.2 mm 的双缝上,双缝与屏幕的垂直距离为1 m.
(1)从第一级明纹到同侧的第四级明纹间的距离为7.5 mm ,求单色光的波长;
(2)若入射光的波长为600 nm,中央明纹中心距离最邻近的暗纹中心的距离是多少?
解:(1)',0,1,2,k d x k λk d =±=
()144141' Δd x x x k k d λ∴=-=
- ()
1441500 nm 'x d λd k k ∆==- (2)1''15 mm 2d x λ.d
∆== 二、劳埃德镜
半波损失 :光从光速较大的介质射向光速较小的介质时反射光的相位较之入射光的相位跃变了π,相当于反射光与入射光之间附加了半个波长的波程差,称为半波损失。
劳埃德镜实验不但显示了光的干涉现象,而且还显示了当光由光速较大(折射率较小)的介质射向光速较小(折射率较大)的介质时,反射光的相位发生了跃变。
从狭缝S 1发出的光,一部分直接射到屏幕上,另一部分掠射到反射角M 上,反射后到达屏幕上。
反射光可看成是由虚光源S 2发出的。
S 1和S 2构成一对相干光源。
图中阴影区域表示叠加的区域,在屏幕上可以观察到明暗相间的干涉条纹。
若把屏幕放到和镜面相接触的P 位置,此时从S 1和S 2发出的光到达接触点L 的路程相等,在L 处似乎应出现明纹,但是实验事实是,在接触处为一暗纹。
这表明,直接射到屏幕上的光与由镜面反射出来的光在L 处的相位相反,即相位差为π。
由于入射光的相位没有变化,只能是反射光的相位跃变了。
劳埃德镜干涉实验的特点:
1. 两束相干光由光源S 1 和虚光源S 2发出;
2. 两光源相位相同,可比作杨氏双缝干涉实验中的两个狭缝;
3. 只有虚光源有半波损失;
4. 重叠区形成条纹,条纹对两光源不对称。
例4、在双缝干涉实验中,单色光源S 到双缝S 1、S 2的距离相等,则观察到中央明纹在图中的O 处,若将单色光源向下移到图中的S ’位置,则【B 】
(A )中央明纹也向下移动,且条纹间距不变;
(B)中央明纹向上移动,且条纹间距不变;(C)中央明纹向下移动,且条纹间距变大;(D)中央明纹向上移动,且条纹间距变大。
作业7(单号交):标准化作业纸P21,下次课交。