形态学腐蚀膨胀

形态学运算中腐蚀，膨胀，开运算和闭运算：1. 腐蚀是一种消除边界点，使边界向内部收缩的过程。

可以用来消除小且无意义的物体。

2. 膨胀是将与物体接触的所有背景点合并到该物体中，使边界向外部扩张的过程。

可以用来填补物体中的空洞。

3. 先腐蚀后膨胀的过程称为开运算。

用来消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。

4. 先膨胀后腐蚀的过程称为闭运算。

用来填充物体内细小空洞、连接邻近物体、平滑其边界的同时并不明显改变其面积。

5. 通常，由于噪声的影响，图象在阈值化后所得到边界往往是很不平滑的，物体区域具有一些噪声孔，背景区域上散布着一些小的噪声物体。

连续的开和闭运算可以有效地改善这种情况。

有时需要经过多次腐蚀之后再加上相同次数的膨胀，才可以产生比较好的效果。

6. 腐蚀操作会去掉物体的边缘点，细小物体所有的点都会被认为是边缘点，因此会整个被删去。

再做膨胀时，留下来的大物体会变回原来的大小，而被删除的小物体则永远消失了。

7. 膨胀操作会使物体的边界向外扩张，如果物体内部存在小空洞的话，经过膨胀操作这些洞将被补上，因而不再是边界了。

再进行腐蚀操作时，外部边界将变回原来的样子，而这些内部空洞则永远消失了。

图像膨胀的Matlab实现：可以使用imdilate函数进行图像膨胀,imdilate函数需要两个基本输入参数，即待处理的输入图像和结构元素对象。

结构元素对象可以是strel函数返回的对象，也可以是一个自己定义的表示结构元素邻域的二进制矩阵。

此外，imdilate还可以接受两个可选参数：PADOPT(padopt) ——影响输出图片的大小、PACKOPT(packopt).——说明输入图像是否为打包的二值图像(二进制图像)。

举个实例如下：步骤1，首先创建一个包含矩形对象的二值图像矩阵。

>> BW=zeros(9,10);>> BW(4:6,4:7) =1BW =0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 1 1 1 1 0 0 00 0 0 1 1 1 1 0 0 00 0 0 1 1 1 1 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0步骤2，使用一个3×3的正方形结构元素对象对创建的图像进行膨胀。

像的形态学处理方法包括形态学处理是数字图像处理领域的重要技术之一，主要用于图像的形状、大小和结构的分析与变换。

以下是几种常见的形态学处理方法：1. 膨胀(Dilation)：膨胀操作可以扩大图像中明亮区域的像素值，从而增大目标物体的尺寸。

膨胀操作使用一个结构元素(strel)对图像进行滑动，当结构元素中的像素点与源图像中的像素点匹配时，将目标图像中对应位置设置为白色。

多次膨胀操作会导致目标物体变得更大。

2. 腐蚀(Erosion)：腐蚀操作与膨胀操作相反，它可以缩小图像中明亮区域的像素值，从而减小目标物体的尺寸。

腐蚀操作使用同样的结构元素(strel)对图像进行滑动，当结构元素中的所有像素点与源图像中的所有像素点匹配时，将目标图像中对应位置设置为白色。

多次腐蚀操作会导致目标物体变得更小。

3. 开运算(Opening)：开运算是先进行腐蚀操作，然后再进行膨胀操作。

开运算可以去除噪点、平滑图像边界，并保持图像中明亮区域的形态特征。

4. 闭运算(Closing)：闭运算是先进行膨胀操作，然后再进行腐蚀操作。

闭运算可以填充图像中的空洞、连接断裂的物体，并保持图像中较暗区域的形态特征。

5. 边缘检测：利用膨胀和腐蚀操作的差异来检测图像中的边缘。

常用的边缘检测算法有Sobel算法、Prewitt算法和Canny算法等。

6. 骨架化(Skeletonization)：骨架化是通过连续的腐蚀操作将物体细化到只有一个像素宽度的过程。

骨架化操作可以提取图像中物体的形状特征，并用于形状匹配、特征提取等应用。

7. 捕获区域(Region Filling)：捕获区域操作是通过连续的膨胀操作填充图像中的空洞，以便更好地分析和处理图像。

捕获区域操作可以应用于图像分割、目标识别等应用中。

除了上述方法，形态学处理还可以结合其他图像处理技术，如阈值化、滤波和边缘检测等，来进行更为复杂的操作和分析。

形态学处理方法在图像分析、目标识别、医学图像处理等领域有着广泛的应用和研究。

形态学运算中腐蚀，膨胀，开运算和闭运算(针对二值图而言)6.1腐蚀腐蚀是一种消除边界点，使边界向内部收缩的过程。

可以用来消除小且无意义的物体。

腐蚀的算法：用3x3的结构元素，扫描图像的每一个像素用结构元素与其覆盖的二值图像做“与”操作如果都为1,结果图像的该像素为1。

否则为0。

结果：使二值图像减小一圈把结构元素B平移a后得到Ba，若Ba包含于X，我们记下这个a点，所有满足上述条件的a点组成的集合称做X被B腐蚀(Erosion)的结果。

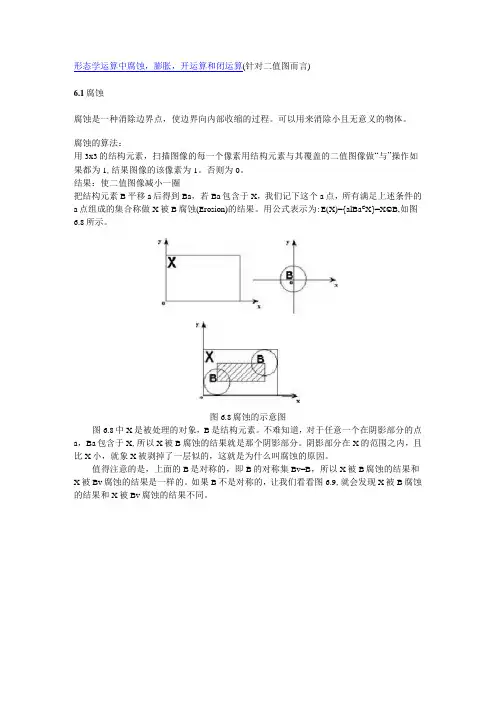
用公式表示为:E(X)={alBa C X}=X©B,如图6.8所示。

图6.8腐蚀的示意图图6.8中X是被处理的对象，B是结构元素。

不难知道，对于任意一个在阴影部分的点a，Ba包含于X,所以X被B腐蚀的结果就是那个阴影部分。

阴影部分在X的范围之内，且比X小，就象X被剥掉了一层似的，这就是为什么叫腐蚀的原因。

值得注意的是，上面的B是对称的，即B的对称集Bv=B，所以X被B腐蚀的结果和X被Bv腐蚀的结果是一样的。

如果B不是对称的，让我们看看图6.9,就会发现X被B腐蚀的结果和X被Bv腐蚀的结果不同。

y图6.9结构元素非对称时，腐蚀的结果不同图6.8和图6.9都是示意图，让我们来看看实际上是怎样进行腐蚀运算的。

在图6.10中，左边是被处理的图象X （二值图象，我们针对的是黑点），中间是结构元素B ，那个标有origin 的点是中心点，即当前处理元素的位置，我们在介绍模板操作时也有过类似的概念。

腐蚀的方法是，拿B 的中心点和X 上的点一个一个地对比，如果B 上的所有点都在X 的范围内，则该点保留，否则将该点去掉；右边是腐蚀后的结果。

可以看出，它仍在原来X 的范围内，且比X 包含的点要少，就象X 被腐蚀掉了一层。

o Q Q Q o & QO Qo Q o O oooo o o o o o 0- 0 O 0 o o •• • ■ Oo o oo o o 0 o o o o o 0 0 o o o ••o o o oo o o o ■ ■ o o 0 0 o o o ••o 0 0 oo o o 0 ■ • ♦ o QQ Q ■0 0 & o Q Q Q 0 0 * * 0 0 0 O 0 0 • ♦ ♦■ 0 Q Q ◎ 00o o ■ •0 0 o O ■ ■ ■ ■ *« O Q Qo o■ ■ ■ ■ Q Q c- O■ * ■ o GO O O O o o •o o ■ •• ■ o o o o O oO ■ ■ ■o 0o O O o O ♦<Q 0■••■ o a o o O o O o o 0 0 o 0oO o oooo\>o0 00o o o o 0 0 0'originFEX e 6图6.10腐蚀运算 图6.11为原图，图6.12为腐蚀后的结果图，能够很明显地看出腐蚀的效果。

形态学（膨胀、腐蚀、开运算和闭运算）形态学是数字图像处理中一类基础的图像处理方法，主要包括膨胀、腐蚀、开运算和闭运算。

膨胀运算是指将原图像中的对象进行膨胀，从而扩充其面积和增加其厚度的操作。

具体实现方法包括选定一个结构元素，在图像上滑动并进行覆盖操作。

该方法常被用于缩小空洞、连接断裂区域和增强图像边缘等处理，同时也可用于通常的形态学处理。

腐蚀运算则是指将原图像中的对象进行“腐蚀”，从而去除其周围的噪声和小细节。

具体实现方法和膨胀运算相似，同样需要选定一个结构元素，并在图像上滑动并进行覆盖操作。

不过需要特别注意的是，腐蚀运算会使图像缩小，因此需要对结果进行调整以避免造成图像的变形。

开运算和闭运算则是形态学处理中两个较为重要的操作。

开运算首先对原图像进行腐蚀操作，然后对处理后的图像进行膨胀，起到去除噪声和小细节、平滑增强边缘的作用。

而闭运算则是首先对原图像进行膨胀操作，然后再进行腐蚀，用于填充空洞、平滑边缘和连接断裂区域。

总之，形态学是数字图像处理中非常重要的一类方法，适用于去除噪声、连接区域、平滑边缘等各种实际问题的解决。

我们需要结合具体问题进行选用，并根据具体实现方法进行调整和优化，以达到最佳处理效果。

【二值形态学膨胀、腐蚀、开、闭运算opencv的深度解析】一、概念介绍1. 二值形态学在图像处理中，二值形态学是一种针对二值图像进行的形态学操作，主要包括膨胀、腐蚀、开、闭运算等。

2. 膨胀膨胀是二值形态学中的一种基本操作，它能够使目标区域扩张并填充内部的空洞，从而使目标变大。

3. 腐蚀腐蚀是二值形态学中的另一种基本操作，它能够使目标区域收缩并去除边缘细节，从而使目标变小。

4. 开运算开运算是先腐蚀后膨胀的组合操作，可以用来去除图像中的噪声和小的干扰目标。

5. 闭运算闭运算是先膨胀后腐蚀的组合操作，可以用来填补图像中的小孔和裂缝。

二、深入探讨1. 膨胀的原理和作用膨胀通过结构元素的滑动来扩张目标区域，可以使目标变大，填充空洞，连接断裂的目标，是图像处理中常用的操作之一。

2. 腐蚀的原理和作用腐蚀通过结构元素的滑动来收缩目标区域，可以使目标变小，去除边缘细节，分离接触的目标，也是图像处理中常用的操作之一。

3. 开闭运算的应用场景开运算通常用于去除图像中的小噪声和杂点，可以平滑目标轮廓，提高目标边缘的连通性；闭运算通常用于填补图像中的小孔和断裂，可以使目标更加完整，减少断裂和裂缝。

4. opencv中的二值形态学函数opencv提供了丰富的二值形态学函数，可以方便地进行膨胀、腐蚀、开、闭运算，如cv2.dilate()、cv2.erode()、cv2.morphologyEx()等，可以通过设置结构元素的形状和大小来调整操作效果。

5. 个人观点和理解对于二值形态学操作，我认为膨胀和腐蚀是其基础，而开闭运算则是在这两者基础上的进一步应用，能够更加精细地处理目标区域，去除干扰和噪声，提取有效信息。

在实际应用中，需要根据具体情况选择不同的操作和参数，以达到最佳的处理效果。

三、总结回顾通过本文的介绍和分析，我们深入理解了二值形态学中的膨胀、腐蚀、开、闭运算的原理和作用，以及在opencv中的应用方式。

我们也从个人观点出发，探讨了这些操作的实际意义和效果。

形态学处理膨胀和腐蚀好嘞，今天我们聊聊形态学处理里的膨胀和腐蚀。

这听起来像是高深的科学名词，其实它们在图像处理里就像是咱们生活中的调味品，能让你的图像变得更美味。

想象一下，你在厨房里做饭，光有盐和胡椒可不够，还得有些独特的香料来提升风味。

膨胀和腐蚀就是这样的小秘密。

咱们来说说膨胀。

这就像是给图像穿了一层华丽的衣服，真是让人眼前一亮。

你想想，图像上的小点点在这个过程中就像是被“喂胖”了一样，慢慢膨胀开来。

你瞧，原本那些稀稀拉拉的像素瞬间变得丰满起来，边缘变得更加圆润，整个图像看起来更饱满、更有活力。

是不是感觉就像看到朋友从一个青涩少年变成了一个风度翩翩的大叔，心里那个自豪啊，真想给他来个大拇指！这样处理过的图像，边缘更光滑，缺口也不见了，真是妙不可言。

不过，膨胀也有它的小麻烦。

就好比我们偶尔吃多了，肚子胀得不行。

有些细节可能就被淹没了，原本清晰的轮廓可能变得模糊不清。

想象一下，你在画画，结果一不小心把颜色泼到了旁边，哎，真是得不偿失。

要是这图像里的信息被淹没了，那可就麻烦了。

所以，咱们在使用膨胀的时候，要谨慎点，心里得有数，别让它把一切都搞得一团糟。

接下来就是腐蚀了，听起来是不是有点严肃？别担心，这可不是要让你的图像变得灰暗。

腐蚀其实就像是给图像减肥，帮助那些多余的部分去掉。

就像你秋天扫落叶，清理掉那些多余的杂草，留下干净整洁的花园。

经过腐蚀处理后，图像的细节会更加明显，原本杂乱的背景也会变得更加整洁，仿佛一下子清晰了不少。

这时候，边缘变得尖锐了，形状更加分明。

就像你用刀切蛋糕，切出的每一块都是那么整齐。

可是，腐蚀也是有它的短板哦。

减肥太过了，可能连必要的部分也一起减掉，最终图像看起来就像是被削减了好几块，失去了原有的风采。

这样一来，原本生动的画面瞬间变得干瘪，真是让人心疼。

咱们再说说这两者的结合，嘿，这可是魔法般的存在。

膨胀和腐蚀如果搭档起来，简直就像是一个完美的舞蹈组合。

先来个膨胀，让图像膨胀得更丰满，再进行腐蚀，修剪掉那些不必要的部分，最终呈现出的效果，简直就像是经过打磨的璀璨钻石，闪闪发光。

形态学处理简述膨胀和腐蚀的运算原理和适用场合下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!形态学处理：膨胀与腐蚀运算原理与适用场合1. 引言形态学处理是数字图像处理领域中的重要技术之一，其中膨胀与腐蚀是两种基础的形态学运算。

膨胀运算和腐蚀运算
膨胀运算和腐蚀运算是数字图像处理中常用的形态学图像处理技术。

它们是基于图像的形状和结构特征来操作，能够在图像中识别和增强物体的形态。

下面是膨胀运算和腐蚀运算的简要解释：
1. 膨胀运算是对图像进行扩张和增大的一种操作。

它的基本思想是利用一个结构元素在图像中滑动，当结构元素与原始图像上的像素重合时，取结构元素内最大的像素值作为该像素点的新像素值。

因此，膨胀运算可以使目标物体变得更加坚定、更加圆滑，同时可以去除孔洞和内部噪声，使物体形态更加清晰明了。

2. 腐蚀运算是一种对图像进行收缩和缩小的操作。

它的基本思想是利用结构元素在图像上滑动，当结构元素完全覆盖要处理的像素时，取结构元素内最小的像素值作为该像素点的新像素值。

因此，腐蚀运算可以使物体边缘变得更加精细和明显，同时可以消除细节和孤立的小物体，使边缘和形态更加清晰和明了。

总的来说，膨胀和腐蚀是图像处理中常用的两种基本形态学操作，常常配合使用，以达到更好的图像增强、物体分割、形态分析等目的。

1/ 1。

数学形态学运算——腐蚀、膨胀、开运算、闭运算腐蚀简单说：就是以结构B的原点为基点沿着将要被腐蚀的图像A中的所有点移动，如果此时结构B中的所有点（包括原点）被A包含，那么被B原点沿着的A中的该点就保留，否则，该点就被抛弃。

可以看出，执行完该腐蚀指令后，A中突出部分，以及外围至少减少了结构B的一半(假设B的原点为B的中心)。

膨胀简单说：就是以结构B的原点为基点沿着将要被膨胀前的图像A中的所有点移动，如果此时结构B中至少有一个点（包括原点）被A包含，那么被沿着的A中的该点及周围就被B扩充，扩充范围为B的整个区域。

可以看出，膨胀后，原A沿着边缘外围被扩充了B的一半(假设B的原点为B的中心)。

数学形态学操作可以分为二值形态学和灰度形态学，灰度形态学由二值形态学扩展而来。

数学形态学有2个基本的运算，即腐蚀和膨胀，而腐蚀和膨胀通过结合又形成了开运算和闭运算。

开运算就是先腐蚀再膨胀，闭运算就是先膨胀再腐蚀。

腐蚀粗略的说，腐蚀可以使目标区域范围“变小”，其实质造成图像的边界收缩，可以用来消除小且无意义的目标物。

式子表达为：该式子表示用结构B腐蚀A，需要注意的是B中需要定义一个原点，【而B的移动的过程与卷积核移动的过程一致，同卷积核与图像有重叠之后再计算一样】当B的原点平移到图像A的像元(x,y)时，如果B在（x,y）处，完全被包含在图像A重叠的区域，(也就是B中为1的元素位置上对应的A图像值全部也为1)则将输出图像对应的像元(x,y)赋值为1，否则赋值为0。

我们看一个演示图。

B依顺序在A上移动（和卷积核在图像上移动一样，然后在B的覆盖域上进行形态学运算），当其覆盖A的区域为[1,1;1,1]或者[1,0;1,1]时，（也就是B中‘1’是覆盖区域的子集）对应输出图像的位置才会为1。

膨胀粗略地说，膨胀会使目标区域范围“变大”，将于目标区域接触的背景点合并到该目标物中，使目标边界向外部扩张。

作用就是可以用来填补目标区域中某些空洞以及消除包含在目标区域中的小颗粒噪声。