R语言一元回归分析报告

R语言回归分析范文回归分析是一种利用已知自变量和因变量之间的关系，通过建立数学模型来预测未知值的统计分析方法。

在R语言中，回归分析可以通过多种函数和包来实现，如lm(函数和stats包。

首先，我们需要明确回归分析的目的和步骤。

回归分析主要用于探究自变量与因变量之间的相关性，并通过建立回归模型来预测未知值。

回归分析的步骤可以分为数据收集、数据预处理、模型建立、模型评估等。

在数据收集阶段，我们需要收集自变量和因变量的数据，并确保数据的质量和完整性。

在R语言中，可以使用read.csv(函数读取CSV格式的数据文件，并使用函数如head(和summary(来查看数据的前几行和描述统计信息。

在数据预处理阶段，我们需要对数据进行处理和清洗，以满足回归分析的假设条件。

常见的预处理方法包括缺失值处理、异常值处理和变量转换等。

在R语言中，可以使用函数如na.omit(来删除带有缺失值的观测，使用函数如boxplot(和hist(来检测异常值，使用函数如scale(和log(来进行变量的标准化和对数转换。

在模型建立阶段，我们需要选择适当的回归模型和估计方法，并拟合模型以得到回归系数和截距。

在R语言中，可以使用lm(函数来拟合线性回归模型，其中自变量和因变量的关系可以用公式形式表示，如lm(y ~x1 + x2)。

除了线性回归，R语言还提供其他类型的回归模型，如多项式回归、局部回归和广义线性模型等。

在模型评估阶段，我们需要对模型进行评估和诊断，以判断模型的拟合程度和稳健性。

常见的评估方法包括决定系数、残差分析和假设检验等。

在R语言中，可以使用summary(函数来查看模型的拟合统计和显著性检验，使用plot(函数绘制残差图以检测模型的合理性。

此外，在回归分析中还可以考虑模型的改进和优化。

例如，可以引入交互项和非线性项来拓展模型的灵活性，可以进行变量选择和模型比较来提高模型的解释力，还可以构建预测模型和模型调整来改善模型的预测和应用效果。

R语言回归模型项目分析报告论文摘要本文旨在介绍并分析一个使用R语言实现的回归模型项目。

该项目主要探究了自变量与因变量之间的关系，并利用R语言的回归模型进行了预测和估计。

本文将首先介绍项目背景和数据来源，接着阐述模型的构建和实现过程，最后对结果进行深入分析和讨论。

一、项目背景和数据来源本项目的目的是探究自变量X1、X2、X3等与因变量Y之间的关系。

为了实现这一目标，我们收集了来自某一领域的实际数据，数据涵盖了多个年份和多个地区的情况。

数据来源主要是公开可用的数据库和相关文献。

在数据处理过程中，我们对缺失值、异常值和重复值进行了适当处理，以保证数据的质量和可靠性。

二、模型构建和实现过程1、数据预处理在构建回归模型之前，我们对数据进行预处理。

我们检查并处理缺失值，采用插值或删除的方法进行处理；我们检测并处理异常值，以防止其对回归模型产生负面影响；我们进行数据规范化，将不同尺度的变量转化为同一尺度，以便于回归分析。

2、回归模型构建在数据预处理之后，我们利用R语言的线性回归函数lm()构建回归模型。

我们将自变量X1、X2、X3等引入模型中，然后通过交叉验证选择最佳的模型参数。

我们还使用了R-squared、调整R-squared、残差标准误差等指标对模型性能进行评价。

3、模型实现细节在构建回归模型的过程中，我们采用了逐步回归法（stepwise regression），以优化模型的性能。

逐步回归法是一种回归分析的优化算法，它通过逐步添加或删除自变量来寻找最佳的模型。

我们还使用了R语言的arima()函数进行时间序列分析，以探究时间序列数据的规律性。

三、结果深入分析和讨论1、结果展示通过R语言的回归模型分析，我们得到了因变量Y与自变量X1、X2、X3等之间的关系。

我们通过表格和图形的方式展示了回归分析的结果，其中包括模型的系数、标准误差、t值、p值等指标。

我们还提供了模型的预测值与实际值之间的比较图，以便于评估模型的性能。

数理统计上机报告上机实验题目：用R软件进行一元线性回归上机实验目的：1、进一步理解假设实验的基本思想，学会使用实验检验和进行统计推断。

2、学会利用R软件进行假设实验的方法。

一元线性回归基本理论、方法：基本理论：假设预测目标因变量为Y，影响它变化的一个自变量为X，因变量随自变量的增（减）方向的变化。

一元线性回归分析就是要依据一定数量的观察样本（Xi, Yi），i=1，2…，n，找出回归直线方程Y=a+b*X方法：对应于每一个Xi，根据回归直线方程可以计算出一个因变量估计值Yi。

回归方程估计值Yi 与实际观察值Yj之间的误差记作e-i=Yi-Yi。

显然，n个误差的总和越小，说明回归拟合的直线越能反映两变量间的平均变化线性关系。

据此，回归分析要使拟合所得直线的平均平方离差达到最小，据此，回归分析要使拟合所得直线的平均平方离差达到最小，简称最小二乘法将求出的a和b 代入式（1）就得到回归直线Yi=a+bXi 。

那么，只要给定Xi值，就可以用作因变量Yi的预测值。

（一）实验实例和数据资料：有甲、乙两个实验员，对同一实验的同一指标进行测定，两人测定的结果如试问：甲、乙两人的测定有无显著差异？取显著水平α=0.05.上机实验步骤：1（1）设置假设：H0：u1-u-2=0：H1：u1-u-2<0（2）确定自由度为n1+n2-2=14；显著性水平a=0.05 （3）计算样本均值样本标准差和合并方差统计量的观测值alpha<-0.05;n1<-8;n2<-8;x<-c(4.3,3.2,3.8,3.5,3.5,4.8,3.3,3.9);y<-c(3.7,4.1,3.8,3.8,4.6,3.9,2.8,4.4);var1<-var(x);xbar<-mean(x);var2<-var(y);ybar<-mean(y);Sw2<-((n1-1)*var1+(n2-1)*var2)/(n1+n2-2)t<-(xbar-ybar)/(sqrt(Sw2)*sqrt(1/n1+1/n2));tvalue<-qt(alpha,n1+n2-2)；（4）计算临界值：tvalue<-qt(alpha,n1+n2-2)（5）比较临界值和统计量的观测值，并作出统计推断实例计算结果及分析：alpha<-0.05;> n1<-8;> n2<-8;> x<-c(4.3,3.2,3.8,3.5,3.5,4.8,3.3,3.9);> y<-c(3.7,4.1,3.8,3.8,4.6,3.9,2.8,4.4);> var1<-var(x);> xbar<-mean(x);> var2<-var(y);> ybar<-mean(y);> Sw2<-((n1-1)*var1+(n2-1)*var2)/(n1+n2-2)> t<-(xbar-ybar)/(sqrt(Sw2)*sqrt(1/n1+1/n2));> var1[1] 0.2926786> xbar[1] 3.7875> var2[1] 0.29267862> ybar[1] 3.8875Sw2[1] 0.2926786> t[1] -0.3696873tvalue[1] -1.76131分析：t=-0.3696873>tvalue=-1.76131，所以接受假设H1即甲乙两人的测定无显著性差异。

数理统计上机报告上机实验题目: 用R软件进行回归分析上机实验目的:1 进一步理解回归分析的基本思想, 学会使用回归进行统计推理。

2 学会利用R软件进行回归分析的方法。

一元线性回归基本理论、方法:1 根据样本观察值对经济计量模型参数进行估计, 求的回归方程。

2 对回归方程、参数估计值进行显著性检验。

3 利用回归方程进行分析、评论及预测。

P430第十一题上机实验步骤:y<-c(2813,2705,11103,2590,2131,5181)x<-c(3.25,3.20,5.07,3.14,2.90,4.02)xbar<-mean(x)L11<-sum((x-xbar)^2)ybar<-mean(y)Lyy<-sum((y-ybar)^2)L1y<-sum((x-xbar)*(y-ybar))n<-length(x)beta_1<-L1y/L11beta_0<-ybar-xbar*beta_1sigma2_hat<-(Lyy-beta_1*L1y)/(n-2)sigma_hat<-sqrt(sigma2_hat)实例计算结果及分析:1> L11[1] 3.321333> Lyy[1] 59353704> L1y[1] 13836.19> beta_0[1] -10562.69> beta_1[1] 4165.854> sigma_hat[1] 654.6287>P=-10562.69+4165LP432 第十八题上机实验步骤:y<-c(64,60,71,61,54,77,81,93,93,51,76,96,77,93,95,54,168,99)X<-matrix(0, nrow = 18, ncol = 4)X[,1]<-rep(1,18)X[,2]<-c(0.4,0.4,3.1,0.6,4.7,1.7,9.4,10.1,11.6,12.6,10.9,23.1,23.1,21 .6,23.1,1.9,26.8,29.9)X[,3]<-c(53,23,19,34,24,65,44,31,29,58,37,46,50,44,56,36,58,51)X[,4]<-c(158,163,37,157,59,123,46,117,173,112,111,114,134,73,168,143, 202,124)beta<-solve(t(X)%*%X)%*%t(X)%*%yyhat<-X%*%betaytidle<-y-yhat23所求得的回归方程为123ˆ43.65 1.780.080.16y x x x =+-+。

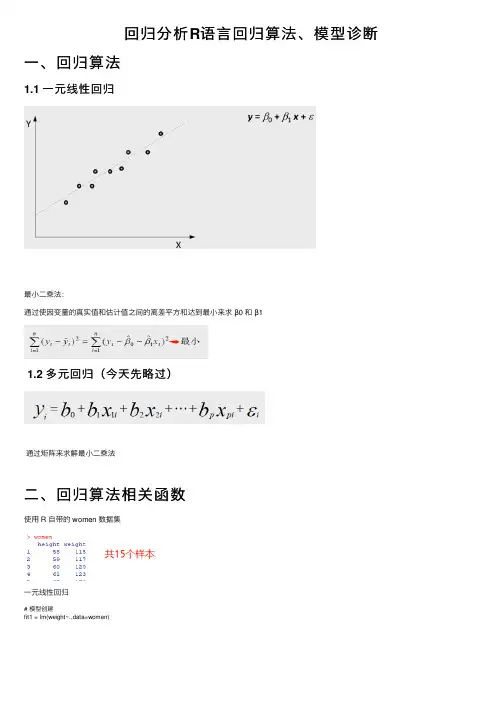
回归分析R语⾔回归算法、模型诊断⼀、回归算法1.1 ⼀元线性回归最⼩⼆乘法：通过使因变量的真实值和估计值之间的离差平⽅和达到最⼩来求β0 和β11.2 多元回归（今天先略过）通过矩阵来求解最⼩⼆乘法⼆、回归算法相关函数使⽤ R ⾃带的 women 数据集⼀元线性回归# 模型创建fit1 = lm(weight~.,data=women)# 查看拟合结果plot(women)abline(fit1)发现点有些弯曲，可能存在⼆次关系去除截距项的⽅法# 除去截距项fit2 = lm(weight~-1+height,data=women)⼀元⼆次回归# 模型创建fit3 = lm(weight~.+I(height^2),data=women)使⽤ summary 查看回归模型的信息summary(fit3)Tip：R⽅：（决定系数、拟合优度）拟合出来的结果解释了多少数据点中的信息（代表拟合程度，越接近1越好）：可以⽤来评估模型拟合的好不好F值：所有的参数是否为零（是否接受0假设），越⼩越拒绝0假设，检验模型整体指标的值模型诊断par(mfrow=c(2,2)) # par设置图⽚格式的函数（2*2的版式）plot(fit3)Tip：A ：检查整体的拟合情况B ：点越呈对⾓线分布，说明数据越呈正态分布C ：曲线波动越明显，越可能异⽅差D ：落在虚线外的点为异常值、离群值回归的预测函数lm.pred = predict(fit3, women)如需预测区间：interval ：给出相应的预测区间level：置信⽔平lm.pred = predict(fit3, women, interval="prediction", level=0.95)lm.pred三、模型选择指标：AIC信息准则即Akaike information criterion，⼜称⾚池信息量准则。

AIC = 2k - 2ln(L)⽅法：逐步回归（step）AIC 可以权衡所估计模型的复杂度和此模型拟合数据的优良性。

R软件一元线性回归分析合金钢强度与碳含量的数据序号碳含量/%合金钢强度/107pa1 0.10 42.02 0.11 43.03 0.12 45.04 0.13 45.05 0.14 45.06 0.15 47.57 0.16 49.08 0.17 53.09 0.18 50.010 0.20 55.011 0.21 55.012 0.23 60.0这里取碳含量为x是普通变量，取合金钢强度为y是随机变量使用R软件对以上数据绘出散点图程序如下：>x=matrix(c(0.1,42,0.11,43,0.12,45,0.13,45,0.14,45,0.15,47.5,0.16,49,0.17,53,0.18,50,0.2,55,0.21, 55,0.23,60),nrow=12,ncol=2,byrow=T,dimnames=list(1:12,c("C","E")))>outputcost=as.data.frame(x)>plot(outputcost$C,outputcost$E)0.100.120.140.160.180.200.224550556outputcost$Co u t p u t c o s t $E很显然这些点基本上（但并不精确地）落在一条直线上。

下面在之前数据录入的基础上做回归分析（程序接前文，下同）> lm.sol = lm(E~C,data = outputcost) >summary(lm.sol)得到以下结果：Call:lm(formula = E ~ C, data = outputcost)Residuals:Min 1Q Median 3Q Max -2.00449 -0.63600 -0.02401 0.71297 2.32451Coefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) 28.083 1.567 17.92 6.27e-09 *** C 132.899 9.606 13.84 7.59e-08 *** ---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 1.309 on 10 degrees of freedomMultiple R-squared: 0.9503, Adjusted R-squared: 0.9454 F-statistic: 191.4 on 1 and 10 DF, p-value: 7.585e-08由计算结果分析：常数项0∧β=28.083，变量（即碳含量）的系数1∧β=132.899 得到回归方程：∧y =28.083+132.899x由于回归模型建立使用的是最小二乘法 ,而最小二乘法只是一种单纯的数学方法 ,存在着一定的缺陷 ,即不论变量间有无相关关系或有无显著线性相关关系 ,用最小二乘法都可以找到一条直线去拟合变量间关系。

R语言数据分析回归研究案例：移民政策偏好是否有准确的刻板印象？数据重命名，重新编码，重组Group <chr> Count<dbl>Percent<dbl>6 476 56.00 5 179 21.062 60 7.063 54 6.354 46 5.41 1 27 3.18 0 8 0.94对Kirkegaard＆Bjerrekær2016的再分析确定用于本研究的32个国家的子集的总体准确性。

#降低样本的＃精确度GG_scatter(dk_fiscal, "mean_estimate", "dk_benefits_use",GG_scatter(dk_fiscal_sub, "mean_estimate", "dk_benefits_us e", case_names="Names")GG_scatter(dk_fiscal, "mean_estimate", "dk_fiscal", case_n ames="Names")#compare Muslim bias measures#can we make a bias measure that works without ratio scaleScore stereotype accuracy#add metric to main datad$stereotype_accuracy=indi_accuracy$pearson_rGG_save("figures/aggr_retest_stereotypes.png")GG_save("figures/aggregate_accuracy.png")GG_save("figures/aggregate_accuracy_no_SYR.png")Muslim bias in aggregate dataGG_save("figures/aggregate_muslim_bias.png")Immigrant preferences and stereotypesGG_save("figures/aggregate_muslim_bias_old_data.png") Immigrant preferences and stereotypesGG_save("figures/aggr_fiscal_net_opposition_no_SYR.png")GG_save("figures/aggr_stereotype_net_opposition.png")GG_save("figures/aggr_stereotype_net_opposition_no_SYR.pn g")lhs <chr>op<chr > rhs <chr> est <dbl> se <dbl> z <dbl> pvalue <dbl> net_opposition ~ mean_estimate_fiscal -4.4e-01 0.02303 -19.17 0.0e+00net_opposition~Muslim_frac 4.3e-02 0.05473 0.79 4.3e-01net_opposition~~net_opposition 6.9e-03 0.00175 3.94 8.3e-05dk_fiscal ~~ dk_fiscal 6.2e+03 0.00000 NA NAMuslim_frac~~Muslim_frac1.7e-01 0.0000NANAIndividual level modelsGG_scatter(example_muslim_bias, "Muslim", "resid", case_na mes="name")+#exclude Syria#distributiondescribe(d$Muslim_bias_r)%>%print()GG_save("figures/muslim_bias_dist.png")## `stat_bin()` using `bins = 30`. Pick better value with `GG_scatter(mediation_example, "Muslim", "resid", case_name s="name", repel_names=T)+scale_x_continuous("Muslim % in home country", labels=scal#stereotypes and preferencesmediation_model=plyr::ldply(seq_along_rows(d), function(rGG_denhist(mediation_model, "Muslim_resid_OLS", vline=medi an)## `stat_bin()` using `bins = 30`. Pick better value with `add to main datad$Muslim_preference=mediation_model$Muslim_resid_OLS Predictors of individual primary outcomes#party modelsrms::ols(stereotype_accuracy~party_vote, data=d)GG_group_means(d, "Muslim_bias_r", "party_vote")+ theme(axis.text.x=element_text(angle=-30, hjust=0))GG_group_means(d, "Muslim_preference", "party_vote")+#party agreement cors wtd.cors(d_parties)。

回归模型项目分析报告论文（附代码数据）摘要该项目包括评估一组变量与每加仑（MPG）英里之间的关系。

汽车趋势大体上是对这个具体问题的答案的本质感兴趣：* MPG的自动或手动变速箱更好吗？*量化自动和手动变速器之间的手脉差异。

我们在哪里证实传输不足以解释MPG的变化。

我们已经接受了这个项目的加速度，传输和重量作为解释汽油里程使用率的84％变化的变量。

分析表明，通过使用我们的最佳拟合模型来解释哪些变量解释了MPG 的大部分变化，我们可以看到手册允许我们以每加仑2.97多的速度驱动。

（A.1）1.探索性数据分析通过第一个简单的分析，我们通过箱形图可以看出，手动变速箱肯定有更高的mpg结果，提高了性能。

基于变速箱类型的汽油里程的平均值在下面的表格中给出，传输比自动传输产生更好的性能。

根据附录A.4，通过比较不同传输的两种方法，我们排除了零假设的0.05％的显着性。

第二个结论嵌入上面的图表使我们看到，其他变量可能会对汽油里程的使用有重要的作用，因此也应该考虑。

由于simplistisc模型显示传播只能解释MPG变异的35％（AppendiX A.2。

）我们将测试不同的模型，我们将在这个模型中减少这个变量的影响，以便能够回答，如果传输是唯一的变量要追究责任，或者如果其他变量的确与汽油里程的关系更强传输本身。

（i.e.MPG）。

### 2.模型测试（线性回归和多变量回归）从Anova分析中我们可以看出，仅仅接受变速箱作为与油耗相关的唯一变量的模型将是一个误解。

一个更完整的模型，其中的变量，如重量，加速度和传输被考虑，将呈现与燃油里程使用（即MPG）更强的关联。

一个F = 62.11告诉我们，如果零假设是真的，那么这个大的F比率的可能性小于0.1％的显着性是可能的，因此我们可以得出结论：模型2显然是一个比油耗更好的预测值仅考虑传输。

为了评估我们模型的整体拟合度，我们运行了另一个分析来检索调整的R平方，这使得我们可以推断出模型2，其中传输，加速度和重量被选择，如果我们需要，它解释了大约84％的变化预测汽油里程的使用情况。

⽤R语⾔做回归分析使⽤R做回归分析整体上是⽐较常规的⼀类数据分析内容，下⾯我们具体的了解⽤R语⾔做回归分析的过程。

⾸先，我们先构造⼀个分析的数据集x<-data.frame(y=c(102,115,124,135,148,156,162,176,183,195),var1=runif(10,min=1,max=50),var2=runif(10,min=100,max=200),var3=c(235,321,412,511,654,745,821,932,1020,1123))接下来，我们进⾏简单的⼀元回归分析，选择y作为因变量，var1作为⾃变量。

⼀元线性回归的简单原理：假设有关系y=c+bx+e,其中c+bx 是y随x变化的部分，e是随机误差。

可以很容易的⽤函数lm()求出回归参数b,c并作相应的假设检验。

model<-lm(y~var1,data=x)summary(model)Call:lm(formula = x$y ~ x$var1 + 1)Residuals:Min 1Q Median 3Q Max-47.630 -18.654 -3.089 21.889 52.326Coefficients:Estimate Std. Error t value Pr(>|t|)(Intercept) 168.4453 15.2812 11.023 1.96e-09 ***x$var1 -0.4947 0.4747 -1.042 0.311Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 30.98 on 18 degrees of freedomMultiple R-squared: 0.05692, Adjusted R-squared: 0.004525F-statistic: 1.086 on 1 and 18 DF, p-value: 0.3111从回归的结果来看，p值为0.311，变量var1不不显著，正常情况下p值⼩于0.05则认为有⾼的显著性⽔平。

data=read.table("clipboard",header=T)#在excel中选取数据，复制。

在R中读取数据apply(data,2,mean)#计算每个变量的平均值obs lnWAGE EDU WYEAR SCORE EDU_MO EDU_FA25.5000 2.5380 13.0200 12.6400 0.0574 11.5000 12.1000apply(data,2,sd) #求每个变量的标准偏差obs lnWAGE EDU WYEAR SCORE EDU_MO EDU_FA 14.5773797 0.4979632 2.0151467 3.5956890 0.8921353 3.1184114 4.7 734384cor(data)#求不同变量的相关系数可以看到wage和edu wyear score 有一定的相关关系plot(data)#求不同变量之间的分布图可以求出不同变量之间两两的散布图lm=lm(lnWAGE~EDU+WYEAR+SCORE+EDU_MO+EDU_FA,data=data)#对工资进行多元线性分析Summary(lm)#对结果进行分析可以看到各个自变量与因变量之间的线性关系并不显著，只有EDU变量达到了0.01的显著性水平，因此对模型进行修改，使用逐步回归法对模型进行修改。

lm2=step(lm,direction="forward")#使用向前逐步回归summary(lm2)可以看到，由于向前逐步回归的运算过程是逐个减少变量，从该方向进行回归使模型没有得到提升，方法对模型并没有很好的改进。

因此对模型进行修改，使用向前向后逐步回归。

lm3=step(lm,direction="both")#使用向前向后逐步回归Summary(lm3)从结果来看，该模型的自变量与因变量之间具有叫显著的线性关系，其中EDU变量达到了0.001的显著水平。

R软件一元线性回归分析合金钢强度与碳含量的数据序号碳含量/%合金钢强度/107pa10.10 42.020.11 43.030.12 45.040.13 45.050.14 45.060.15 47.570.16 49.080.17 53.090.18 50.0100.20 55.0110.21 55.0120.23 60.0这里取碳含量为x是普通变量，取合金钢强度为y是随机变量使用R软件对以上数据绘出散点图程序如下：>x=matrix(c(0.1,42,0.11,43,0.12,45,0.13,45,0.14,45,0.15,47.5,0.16,49,0.17,53,0.18,50,0.2,55,0.21, 55,0.23,60),nrow=12,ncol=2,byrow=T,dimnames=list(1:12,c("C","E")))>outputcost=as.data.frame(x)>plot(outputcost$C,outputcost$E)0.100.120.140.160.180.200.224550556outputcost$Co u t p u t c o s t $E很显然这些点基本上（但并不精确地）落在一条直线上。

下面在之前数据录入的基础上做回归分析（程序接前文，下同）> lm.sol = lm(E~C,data = outputcost)>summary(lm.sol)得到以下结果：Call:lm(formula = E ~ C, data = outputcost)Residuals: Min 1Q Median 3Q Max-2.00449 -0.63600 -0.02401 0.71297 2.32451Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 28.083 1.567 17.92 6.27e-09 ***C 132.899 9.606 13.84 7.59e-08 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 1.309 on 10 degrees of freedomMultiple R-squared: 0.9503, Adjusted R-squared: 0.9454 F-statistic: 191.4 on 1 and 10 DF, p-value: 7.585e-08由计算结果分析：常数项=28.083，变量（即碳含量）的系数=132.8990∧β1∧β得到回归方程：=28.083+132.899x∧y 由于回归模型建立使用的是最小二乘法 ,而最小二乘法只是一种单纯的数学方法 ,存在着一定的缺陷 ,即不论变量间有无相关关系或有无显著线性相关关系 ,用最小二乘法都可以找到一条直线去拟合变量间关系。

R实现⼀元线性回归（⼀）、数据的读⼊与变量间关系通过read.csv函数将整理好的数据读⼊到⼯作空间中，并将数据框中的数据存储为相应的变量名下---数学成绩赋值于math、物理成绩赋值于physics.然后绘制出两门成绩间的散点图以查看两者之间是否具有函数关系：data1 <-read.csv("C:/Users/MyPC/Desktop/管理统计学/管理统计-⼀元线性回归/six.csv",fileEncoding ="GBK")math <-data1[,2];physics <-data1[,3];plot(math,physics,main="散点图",xlab="数学成绩",ylab="物理成绩")（⼆）、图形的解释与关系的确定从散点图中可以看到，两门成绩间为线性关系，且为正相关---即同增同减. 于是利⽤函数cor()求出两门成绩的相关系数如下：cor(math,physics)## [1] 0.7847639（三）、⼀元线性模型的模拟及检验由散点图以及相关系数可知，可使⽤⼀元线性回归模型对所给数据进⾏拟合，并对未来的结果进⾏相应的预测.在拟合的模型基础上对拟合结果进⾏显著性检验，取αα=0.05. 函数代码及拟合结果如下：lm.fit <-lm(physics~math,data=data1)#⼀元线性拟合summary(lm.fit)#### Call:## lm(formula = physics ~ math, data = data1)#### Residuals:## Min 1Q Median 3Q Max## -10.326 -7.793 1.067 5.852 12.223#### Coefficients:## Estimate Std. Error t value Pr(>|t|)## (Intercept) 5.4221 15.0617 0.360 0.724227## math 0.9427 0.1990 4.738 0.000318 ***## ---## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1#### Residual standard error: 8.509 on 14 degrees of freedom## Multiple R-squared: 0.6159, Adjusted R-squared: 0.5884## F-statistic: 22.44 on 1 and 14 DF, p-value: 0.0003178从结果中可以得知：回归⽅程为:yy=0.9427xx+5.4221⼜因PP?vvvvvv vv vv<0.05,所以⾃变量数学成绩与因变量物理成绩有线性关系，且拟合情况良好.plot(residuals(lm.fit))（四）、预测与分析当给定数学成绩为80分时，估计物理成绩的95%的置信区间. 代码及结果如下： pre.point <-data.frame(math=80)predict(lm.fit,pre.point,interval="prediction",level=0.95)## fit lwr upr## 1 80.83471 61.89853 99.77088置信区间为：[61.89853,99.77088].（五）、回归直线与进⼀步的结果回归直线的拟合如下：代码及结果如下：plot(math,physics,main="⼀元线性回归",xlab="数学成绩",ylab="物理成绩") abline(lm.fit)使⽤ggplot2包进⾏进⼀步的分析---置信区间曲线图(取αα=0.05)：library(ggplot2)ggplot(data1,aes(math,physics),xlab("math"),ylab("physics"))+geom_sm ooth(method="lm",color="red",linetype=2)其中红⾊曲线是最佳拟合曲线，阴影带状就是每⼀个math（即数学成绩）对应的physics(即物理成绩)的95%置信区间.。

用R语言做回归分析标题：利用R语言进行回归分析，从数据准备到模型评估引言：回归分析是统计学中常用的一种方法，用于探索多个自变量与一个因变量之间的关系。

R语言是一种强大的统计分析工具，其中的回归分析函数可以帮助我们进行数据探索和建模。

本文将介绍如何使用R语言进行回归分析，从数据准备到模型评估，帮助读者更好地理解和应用回归分析方法。

一、数据准备回归分析的第一步是准备数据。

我们假设有一个数据集包含了多个自变量（如年龄、性别、教育水平等）和一个连续的因变量（如收入）。

在R语言中，我们可以使用read.csv(函数导入数据集，并使用head(函数查看数据的前几行，以了解数据的结构。

代码示例：data <- read.csv("data.csv")head(data)二、数据探索在进行回归分析之前，我们需要对数据进行探索，了解自变量与因变量之间的关系以及数据的分布情况。

在R语言中，可以使用summary(函数查看数据的统计摘要信息，使用cor(函数计算变量之间的相关系数矩阵，并使用scatterplotMatrix(函数绘制散点图矩阵。

代码示例：summary(data)cor(data)scatterplotMatrix(data)三、模型建立在完成数据的探索后，我们可以开始建立回归模型。

R语言中有多个函数可以进行回归分析，例如lm(函数用于建立线性回归模型，glm(函数用于建立广义线性模型等。

我们需要选择合适的模型，并根据自变量与因变量之间的关系来建立模型。

代码示例：summary(model)四、模型评估模型建立后，我们需要对模型进行评估，以确定其拟合效果和预测能力。

在R语言中，可以使用summary(函数查看模型的统计指标，例如R-squared、F-statistic和p-value等。

我们还可以使用plot(函数绘制模型的残差图，以判断模型是否满足回归分析的假设。

代码示例：summary(model)plot(model, which=1)五、模型改进在评估模型后，如果发现模型的拟合效果不理想，我们可以尝试改进模型。

R语⾔解读⼀元线性回归模型转载⾃：前⾔在我们的⽇常⽣活中，存在⼤量的具有相关性的事件，⽐如⼤⽓压和海拔⾼度，海拔越⾼⼤⽓压强越⼩；⼈的⾝⾼和体重，普遍来看越⾼的⼈体重也越重。

还有⼀些可能存在相关性的事件，⽐如知识⽔平越⾼的⼈，收⼊⽔平越⾼；市场化的国家经济越好，则货币越强势，反⽽全球经济危机，黄⾦等避险资产越⾛强。

如果我们要研究这些事件，找到不同变量之间的关系，我们就会⽤到回归分析。

⼀元线性回归分析是处理两个变量之间关系的最简单模型，是两个变量之间的线性相关关系。

让我们⼀起发现⽣活中的规律吧。

由于本⽂为⾮统计的专业⽂章，所以当出现与教课书不符的描述，请以教课书为准。

本⽂⼒求⽤简化的语⾔，来介绍⼀元线性回归的知识，同时配合R语⾔的实现。

⽬录1. ⼀元线性回归介绍2. 数据集和数学模型3. 回归参数估计4. 回归⽅程的显著性检验5. 残差分析和异常点检测6. 模型预测1. ⼀元线性回归介绍回归分析（Regression Analysis)是⽤来确定2个或2个以上变量间关系的⼀种统计分析⽅法。

如果回归分析中，只包括⼀个⾃变量X和⼀个因变量Y时，且它们的关系是线性的，那么这种回归分析称为⼀元线性回归分析。

回归分析属于统计学的基本模型，涉及统计学基础，就会有⼀⼤堆的名词和知识点需要介绍。

在回归分析中，变量有2类：因变量和⾃变量。

因变量通常是指实际问题中所关⼼的指标，⽤Y表⽰。

⽽⾃变量是影响因变量取值的⼀个变量，⽤X表⽰，如果有多个⾃变量则表⽰为X1, X2, …, Xn。

回归分析研究的主要步骤：1. 确定因变量Y 与⾃变量X1, X2, …, Xn 之间的定量关系表达式，即回归⽅程。

2. 对回归⽅程的置信度检查。

3. 判断⾃变量Xn(n=1,2,…,m)对因变量的影响。

4. 利⽤回归⽅程进⾏预测。

本⽂会根据回归分析的的主要步骤，进⾏结构梳理，介绍⼀元线性回归模型的使⽤⽅法。

2. 数据集和数学模型先让我们通过⼀个例⼦开始吧，⽤⼀组简单的数据来说明⼀元线性回归分析的数学模型的原理和公式。

数理统计上机报告姓名：班级：组别：成绩： .合作者：指导教师：实验日期： .上机实验题目：假设检验上机实验目的：1．进一步理解假设检验的基本思想，学会使用u检验、t检验、2 、F检验进行统计推断。

2．学会利用R进行假设检验的方法。

假设检验基本理论、方法：假设检验在数理统计中占有重要地位，它的推理方法与数学中通常使用的方法在表面上类似，但实际大不一样。

通常的数学推理都是演绎推理，即根据给定的条件，进行逻辑推理。

而统计方法则是归纳，从样本中的表现去推断总体的性质。

假设检验是推断统计中的一项重要内容，它与参数估计都是抽样分布的一种应用。

本章将通过使用R软件来进一步理解假设检验的思想，同时介绍如何使用R解决假设检验问题。

1122假设检验采用的思想方法是先假设结论成立，在此前提下进行推导和演算，并依据“小概率事件在一次试验中几乎不可能发生”这一实际推断原理．作出接受或拒绝原假设的结论。

假设检验的一般步骤如下：(1)提出原假设0H 和备择原假设1H ：(2)根据题设选择统计量；(3)根据实际问题选择显著水平性 ，确定拒绝域：(4)根据样本值计算出的统计量观察值是否落在拒绝域内，作出拒绝0H 或接受0H 的结论。

实验实例和数据资料：实验一：某型号玻璃纸的横向延伸率要求不低于65%，且其服从正态分布，现对一批该型号的玻璃纸测得100个数据如下：试问：该批玻璃纸的横向延伸率是否符合要求实验二：有一种新安眠剂，据说在一定剂量下能比某种旧安眠剂平均增加睡眠时间3h ，根据资料，用某种旧安眠剂时平均睡眠时间为，标准差为。

为了检验新安眠剂的这种说法是否正确，收集到一组使用新安眠剂的睡眠时间（以h 为单位）为：,,,,,,试问：这组数据是否能说明新安眠剂已达到新的疗效上机实验步骤：实验一：，分析原题可知，原假设为H0=65，备择假设为H1<65，单边假设检验，alpha=，单个正态总体，方差未知，对均值假设，t分布x<-c(rep,7),rep,8),rep,11),rep,9),rep,9),rep,12),rep,17),rep,14),rep,5), rep,3),rep,2),rep,0),rep,2),rep,0),rep,1))> length(x)[1] 100> ##rep()复制函数，（，7）为复制7次> xbar<-mean(x)> Sn<-sd(x)> n<-100> t<-(xbar-65)/(Sn/sqrt(n))> t[1]> alpha<> tt<-qt(alpha,n-1,=TRUE)> tt[1]实验二：分析原题可知，原假设为新药睡眠时间H0=，备择假设H1<标准差不变且已知为S=，取alpha=，方差未知判断期望的单个正态总体单边假设检验。