下载文档原格式
TSP 问题及LINGO 求解技巧巡回旅行商问题(Traveling Salesman Problem ，TSP)，也称为货郎担问题。
最早可以追溯到1759年Euler 提出的骑士旅行问题。
1948年，由美国兰德公司推动，TSP 成为近代组合优化领域的一个典型难题。
它已经被证明属于NP 难题。
用图论描述TSP ，给出一个图(,)G V E =，每边e E ∈上有非负权值()w e ,寻找G 的Hamilton 圈C ，使得C 的总权()()()W C w e e E C =∑∈最小. 几十年来，出现了很多近似优化算法。
如近邻法、贪心算法、最近插入法、最远插入法、模拟退火算法以及遗传算法。
这里我们介绍利用LINGO 软件进行求解的方法。
问题1设有一个售货员从10个城市中的某一个城市出发，去其它9个城市推销产品。
10个城市相互距离如下表。
要求每个城市到达一次仅一次后，回到原出发城市。
问他应如何选择旅行路线，使总路程最短。
我们采用线性规划的方法求解设城市之间距离用矩阵d 来表示，ij d 表示城市i 与城市j 之间的距离。
设0--1矩阵X 用来表示经过的各城市之间的路线。
设01,ij i j x i j i j ⎧=⎨⎩若城市不到城市若城市到城市且在前考虑每个城市后只有一个城市，则：11,nij j j ix =≠=∑1,,i n =… 考虑每个城市前只有一个城市，则：11,nij i i jx =≠=∑1,,j n =…； 但仅以上约束条件不能避免在一次遍历中产生多于一个互不连通回路。
为此我们引入额外变量i u (1,,i n =…），附加以下充分约束条件：1,i j ij u u nx n -+≤-1i j n <≠≤；该约束的解释：如i 与j 不会构成回路，若构成回路，有：1ij x =，1ji x =，则：1i j u u -≤-，1j i u u -≤-，从而有：02≤-，导致矛盾。
中国历届夏季奥运会获金牌数的变化与项目分布研究作者：李彪来源：《中国校外教育·综合(上旬)》2013年第07期通过对建国以来参加的历届夏季奥运会所取得金牌的数量及项目分布特征进行分析，旨在为我国竞技体育的可持续发展提供咨询。
研究表明：历届奥运会我国金牌数一直呈递增趋势，并已成为竞技体育强国；中国的夺金面正在变得全面；我国各项目金牌的贡献率有明显的分层现象，传统强项是主要支撑点；获得金牌项目各项群存在发展不平衡的特征；我国不同区域运动员获金牌数存在显著的区域差异，东部>中部>西部，男女运动员在金牌贡献率上的差距逐步缩小。
并对存在的问题提出建议。
夏季奥运会金牌项目分布中国中国与现代夏季奥运会有着长远的历史渊源，早在1894年第一届现代奥运会筹备时国际奥委会就向当时的清政府发出邀请，但由于清王朝对奥运会知之甚少，最终没有给予国际奥委会答复。
中国最早参加奥运会的运动员是刘长春，在1932年的洛杉矶奥运会上他在100米、200米预赛中位于小组第五、六名，未能取得决赛权。
随后，由于国力衰退，政府对竞技体育的漠视，中国体育一直没有在奥运会上有所突破[2]。
新中国成立后由于政治因素一直没有参加奥运会，1984年洛杉矶奥运会是新中国建国以来第一次参加奥运会就取得了金牌零的突破。
从此，中国竞技体育便走上了正轨，北京奥运会则到达了我国竞技体育的高峰，本文将对第23届至第30届夏季奥运会，中国代表团所获金牌数量及项目分布进行探讨。
1研究对象与方法运用文献资料法、数理统计法、逻辑分析法对1984年第23届奥运会至2012年第30届奥运会中国代表团所获得的金牌数进行分析。
2结果与分析2.1夏季奥运会中国军团金牌排名及数量体育界—个普遍认同的观点是金牌数量的多少反映各代表团的总体实力。
从图1可以看出，新中国自1984年参加奥运会以来在奖牌榜上的排名一直稳步上升。
第23届的洛杉矶奥运会，第一次参加奥运会的中国代表团派出225名运动员，取得了金牌榜第四名的好成绩，一雪“东亚病夫”的百年耻辱。
排球比赛中的赛事组织和赛程安排在排球比赛中，赛事组织和赛程安排起着至关重要的作用。
一个良好的赛事组织和赛程安排不仅能够提高比赛的公正性和竞争性，还能给参赛队伍和观众带来更好的赛事体验。
本文将从赛事组织和赛程安排两个方面来探讨排球比赛中的相关内容。
一、赛事组织在排球比赛中，赛事组织是为了确保比赛的顺利进行，保障比赛的公正和公平。
赛事组织包括赛事申请、参赛资格、裁判安排、场地准备等方面。
1. 赛事申请排球比赛通常由组织者或者相关机构发起，需要进行赛事申请。
赛事申请包括比赛的时间、地点、规模和级别等信息，组织者需要提前向相关部门或机构递交申请。
2. 参赛资格为了保证比赛的公平性，参赛队伍需要满足一定的参赛资格。
通常，参赛队伍需要提供相关的资质证明或者经过预选赛筛选出来。
比如，国际排联要求参加世界排球锦标赛的队伍必须符合一定的排名和资格要求。
3. 裁判安排排球比赛中，裁判的公正和中立至关重要。
赛事组织者需要安排合适和有经验的裁判，确保比赛的公平性。
裁判的选拔和培训需要经过严格的程序，以确保其技术和判罚水平达到要求。
4. 场地准备赛事组织者需要提前准备比赛场地，确保场地的平整、标准和安全。
场地的准备包括场地的画线、设备的摆放和检查以及必要的安全设施。
场地的准备需要严格按照排球比赛规则和标准进行。
二、赛程安排赛程安排是指为排球比赛确定具体的比赛时间和赛程安排，确保各项比赛按计划进行，并合理安排比赛的时间间隔和休息时间。
1. 比赛时间赛事组织者需要根据参赛队伍的数量和比赛规模，确定比赛的具体时间。
一般情况下，赛事组织者会提前和参赛队伍联系，商定比赛的具体时间。
2. 赛程规划赛程安排需要合理规划各个比赛项目的先后顺序和时间间隔。
通常，比赛项目会根据其重要性和参赛队伍数量进行排序，避免时间冲突和场地资源浪费。
赛程安排需要兼顾比赛的紧凑性和队伍的疲劳度，以确保比赛的质量和观赏性。
3. 休息时间赛程安排中需要合理安排休息时间，以让参赛队伍得到充分的休息和恢复。
运动会积分策划方案范文一、项目介绍运动会积分策划方案是为了在体育运动竞赛中进行综合评定和排名而制定的一套评分系统。
通过对各项赛事的积分计算和统计分析，可以全面客观地评估参赛队伍以及个人的综合实力和突出表现，从而得出最终的排名结果。
二、积分计算原则1. 统一标准：所有的赛事都将采用同一套积分计算标准，确保比赛的公平性和公正性。
2. 满分制：每个个人项目的满分均为100分，团体项目的满分为团体成员的总分之和。
3. 累计计分：在整个运动会期间，每个队伍和个人都可以累计积分，并在最后按照总分排名。
三、积分计算方式1. 个人项目积分计算个人项目的积分由该队伍或个人在每个项目中的表现和成绩来决定。
通过以下因素进行积分计算：（1）名次：根据参赛选手在比赛中的名次，第一名得到100分，依次比例递减。
（2）成绩：根据参赛选手在比赛中的成绩，按照一定的公式将成绩转化为分数，并加到总分中。
（3）个人表现：评委对参赛选手在比赛中的个人表现进行评分，并将分数加到总分中。
2. 团体项目积分计算团体项目的积分由该队伍在每个项目中的总成绩来决定。
通过以下因素进行积分计算：（1）名次：根据参赛队伍在比赛中的名次，第一名得到100分，依次比例递减。
（2）成绩：根据参赛队伍在比赛中的总成绩，按照一定的公式将成绩转化为分数，并加到总分中。
（3）团体表现：评委对参赛队伍在比赛中的团体表现进行评分，并将分数加到总分中。
3. 附加分为了激励参赛队伍和选手更好地发挥潜力，可以设置一些附加分项目，根据参赛队伍或个人在该项目中的表现给予额外的积分加成。
例如，设定最佳表现奖、最佳精神奖、最佳创意奖等。
四、积分统计和排名1. 积分记录为了方便统计和计算积分，需要建立一个专门的积分统计系统，对每个项目的积分进行记录和汇总。
可以使用电子计分板或者专门的计分软件进行统计和整理。
2. 排名规则根据每个队伍或个人的总分进行排名，得分最高的队伍或个人排名靠前。
如果总分相同，可以根据名次的数量、破纪录次数、附加分的数量等因素进行排序。
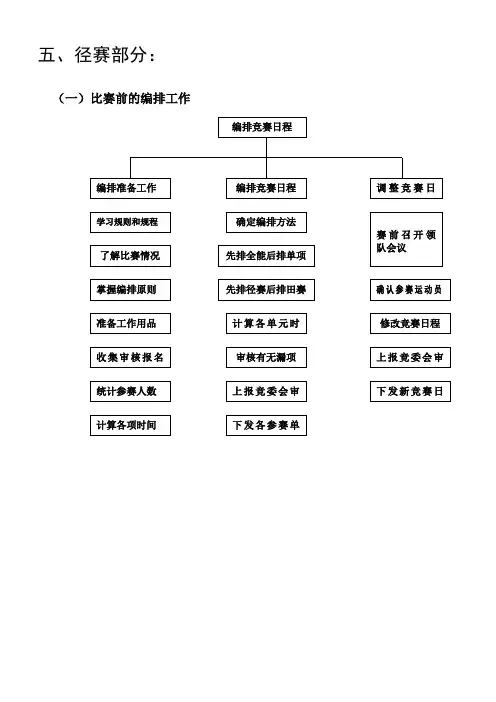
五、径赛部分：（一）比赛前的编排工作（二）学习编排竞赛日程的原则1．按照规则规定编排全能项目及注意各赛次之间的休息时间，应保证至少按最低标准留出休息时间。
2．按兼项的一般规律，尽量把相关项目分开编排，以减少兼项冲突。
性质相近的项目要注意先后顺序：一般先100米后200米、先5000米后10000米、先跳远后三级跳远等。
3．在时间允许情况下，尽量照顾到兼项之间的时间间隔，及格赛后隔1天再进行正式比赛。
4．不同组别的同一田赛项目，一般不连续安排在同一单元内进行。
5．不同组别的同一径赛项目，最好衔接进行，如男子100米和女子100米等，短距离径赛次如果少，最好安排一天结束。
6．为了节省摆栏时间，跨栏项目一般都安排在同一比赛单元的第一项，也可排在长距离比赛之后进行。
7．决赛和预计创纪录的项目等，应分配到各个比赛单元尽可能排在下午，并留出发奖时间。
8．同一时间内不要排两个田赛长投项目。
9．在举行竞走、长距离跑时，最好不要同时安排标枪等长投项目。
10．撑杆跳高要考虑阳光的照射方向和比赛时间比较长，最好安排上午进行。
11．在可能情况下，把比较精彩的决赛项目，排在开、闭幕式或观众较多的单元里。
田赛项目应防止一端过分集中，另一端空场冷落。
12．最后一个单元临近结束之前，可考虑安排一项长距离项目或适当减少项目，以便准备闭幕式，宣布团体成绩。
13．每一个单元的比赛，尽量安排使径赛和田赛同时结束。
（三）编印秩序册内容：1．封面：比赛名称、主办单位、批准单位、承办单位、赞助单位或祝贺单位。
2．如重大比赛可安排领导贺词、照片。
3．组委会及下属各委员会（处、组）人员名单。
4．技术代表、技术官员、仲裁委员会、裁判员名单。
5．竞赛规程、比赛补充通知、竞赛须知。
6．赛会活动日程安排。
7．竞赛日程。
8．各代表队名单。
9．各项运动员名单。
10．田径比赛各类人数统计表。
11．最新田径纪录、等级标准。
12．比赛和训练场地及有关设施平面图。
单循环比赛编排方法
单循环比赛编排方法是一种常用的比赛编排方法，适用于参赛队伍较少的比赛。
其编排方法如下：
1. 确定参赛队伍数量：假设参赛队伍数量为n。
2. 创建比赛日程表：创建一个n*n的方阵，用来表示各个队伍之间的比赛。
3. 安排首轮比赛：将编号为1到n的队伍按照某种规则（例如随机排列）分成两组，每组进行比赛。
4. 安排后续比赛：第一轮比赛结束后，胜者组成一个新的组别，负者组成一个新的组别。
每个组别的队伍按照某种规则互相比赛。
5. 进行比赛：根据比赛日程表上的对阵安排，进行比赛。
6. 更新比赛日程表：每场比赛结束后，更新比赛日程表上对应位置的比赛结果。
7. 比赛结束：当比赛日程表上的所有比赛都结束时，比赛结束。
需要注意的是，单循环比赛编排方法只适用于参赛队伍数量不超过16个的比赛。
如果参赛队伍数量较多，可以考虑采用其
他编排方法，例如混合比赛编排或积分循环编排。
比赛项目排序的研究
（马元陈三磊刘世家）
摘要：本论文研究了比赛中经常碰到的问题，即如何合理安排赛程，使得连续参加两项比赛的运动员人数达到最少，达到公平的目的。
通过对题目的分析并结合实际，提出合理假设，把参赛表转化为0-1矩阵，运用有关矩阵的知识，结合运筹学中图与网络分析原理，利用Matlab和WinQSB软件分析并计算出结果，最终给出合理的比赛项目顺序，并提出优化的建议和方案。
关键词： 0-1矩阵 WinQSB Matlab 图与网络分析 Hanmilton回路
一、问题的提出
在各种运动比赛中，为了使比赛公平、公正、合理的举行，一个基本要求是：在比赛项目排序过程中，尽可能使每个运动员不连续参加两项比赛，以便运动员恢复体力，发挥正常水平。
1．表1是某个小型运动会的比赛报名表。
有14个比赛项目，40名运动员参加比赛。
表中第1行表示14个比赛项目，第1列表示40名运动员，表中“＃”号位置表示运动员参加此项比赛。
建立此问题的数学模型，并且合理安排比赛项目顺序，使连续参加两项比赛的运动员人次尽可能的少；
2．说明上述算法的合理性；
3．对“问题2”的比赛排序结果，给出解决“运动员连续参加比赛”问题的建议及方案。
二、问题的分析
思路1：把表1看成是一个40*14的0-1矩阵，0表示运动员没有参加了这个项目，1表示参加，设此0-1矩阵为矩阵A，那么问题中安排合理的比赛顺序用数学语言表示为调整A的列向量使之成为矩阵B，若B满足一定的条件后，会使B中行向量连续出现1的次数最少，那么B就是最终要排出的比赛项目矩阵。
在这个过程中，我们使用了Hanmilton回路、Matlab 、WinQSB软件等来求解B。
三、模型的建立
1 模型假设：
（1）每个运动员都能按时参加比赛；
（2）天气情况良好，不出现因天气原因中断比赛项目；
（3）单纯比赛项目的早与迟不影响运动员的技能发挥；
（4）两项比赛不会同时进行；
（5）运动员在一夜休息后，体力可以得到充分恢复；
（6）比赛中不考虑个人因素（如裁判不公等）影响比赛的公平性。
2 符号说明
A:初始矩阵
B:最优矩阵
i :运动员序号（i=1,2,…m）
j: 项目序号 (j=1,2,…,n)
b j:第j个项目 (j=1,2,…,n)
p i:初始矩阵A的列向量
x ij:第i个运动员参加的第j项项目，x ij=1表示参加，x ij=0表示不参加。
w rs:第r项比赛项目对第s项的影响度(r,s=1,2…n)，即连续参加r项目和s项目的
运动员人数。
W：表示影响力矩阵，即任意两个项目连续进行，导致连续参加两个比赛项目的运动员人数的组合而形成的14*14矩阵,w rs为W矩阵的元素
3 模型的建立:
（1）把附录一变换为0-1矩阵A，如图附录二所示。
然后运用Matlab软件求出A矩阵的列矩阵A T
（2）求出影响力矩阵W
由符号说明，可知w rs=x r1* x s1+ x r2* x s2+ … + x rm* x sm由矩阵相关知识知W= A T *A,运用Matlab软件求得W矩阵如下
运动员人数例w12表示若项目一与项目二排在一起，共有两个人连续参加了项目一与项
目二，而w11表示项目一与项目一的重复人数，这与本题无关，不予考虑。
此时问题演
变成如何安排14个项目的顺序，使得连续参加比赛的运动员人数最少。
即对矩阵W=[b1,b2,b3,b4,b5,b6,b7,b8,b9,b10,b11,b12,b13,b14]的各列重新排序
四、模型的求解
（1）“旅行推销商”问题：一个推销商从n个城市v
1 v
2
v
n
中某一个城市出发，到其
他n-1个城市推销商品，每个城市都必须访问并只经过一次，最后回到出发点，那么如何安排他的旅行路线使其总距离最短。
我们发现，所求的问题与“旅行推销商”问题很相似，我们可以将此W矩阵问题看作为14个城市，现在就是要使连接这14个城市的路线最短，只不过“旅行推销商”问题是一个闭环的回路，项目排序问题是一条直线而已，如果我们运用Hamilton回路解法求出最优解，再在这个闭环回路中找出距离最长（即影响力最大的两个相临项目）的两个项目，从中把它割段，使闭环回路变成一条直线，便可得到我们所要的模型的解了
定义：[Hamilton回路]设b
1, b
2
, b
3
…b
n
是图G中的n个顶点，若有一条从某一
顶点b
j (1≤j≤n)出发，经过各节点一次且仅一次，最后返回出发点b
j
的回路，则称此
回路为Hamilton回路。
形成的圈称为H圈。
（2）Hamilton回路求解原理：
1,任取初始H圈：C0=v1 ,v2…v i,…v j…,v n, v1
2,对所有的i,j,1<i+1<j<n,若w(v i,v j)+w(v i+1,v j+1)< w(v i,v i+1)+w(v j, v j+1)
则在C0删去边(v i,v i+1)和(v j, v j+1)而加入边(v i,v j)和(v i+1,v j+1)，形成新的H 圈C，即：
C=v1,v2,…,v i ,v j ,v j-1 ,…,v i+1 ,v j+1 ,…v n ,v 1 3,对C重复步骤（2），直到条件不满足为止，最后得到的C即为所求。
（3）运用WinQSB软件可以进行对hamilton回路的求解。
运行WinQSB软件，调用子
程序Network Modeling,进入主界面后,选择Traveling Salesmen Problem,设置14个
项目。
采用三种近似方法：最近城市法（Nearest Neighbor Heuristic），两两交换法（Cheapest Insertion Heuristic），逐步包围法（Tow-way Exchange Improvement Heuristic）求得的最优项目顺序中连续参赛的运动员人数依次为9，6，4，因为前两种
方法的连续参赛运动员数目为9和6，大于第三种的4人，所以第三种方法优于前两种，则对于前两种方法不于考虑。
采用第三种方法求得的结果如下表：
从表中看出,从b14到b2，b8到b4,b9到b3,b5到b13，都有一人连续参加两项比赛。
所以断点处可以为四处任意一点，假设在b14到b2处断开，则比赛项目排序为b2,b6,b1,b8,b4,b9,b3,b11,b7,b5,b13,
b10,b12,b14。
按照此种排序，共有三人连续参加了两项比赛。
转换为网络图如下所示（粗线处为断开点）：
进一步简化图表为：
2 6 1 8 4
11 3 9
7
5
13 10 12 14。
