三角函数的图象和性质及三角恒等变换知识点归纳

简单的三角恒等变换xx年xx月xx日•三角函数基本概念•三角恒等变换的基本法则•三角恒等变换的应用目录•常见三角恒等变换技巧•三角恒等变换的注意事项•练习题与解答01三角函数基本概念$\sin x = \frac{y}{r}$正弦函数$\cos x = \frac{x}{r}$余弦函数$\tan x = \frac{y}{x}$正切函数三角函数的定义周期性$2k\pi, k\in Z$振幅$|\sin x| \leq 1, |\cos x| \leq 1$相位$\sin(x+2k\pi) = \sin x$；$\cos(x+2k\pi) = \cos x$；$\tan(x+k\pi) = \tan x$正弦函数$y=|\sin x|$，波动曲线余弦函数$y=|\cos x|$，波动曲线正切函数$y=\tan x$，曲线不连续，无界01020302三角恒等变换的基本法则和差角公式公式二$\cos(x+y)=\cos x\cos y-\sin x\sin y$应用用于解决角度和的问题，如求两角和的正弦、余弦等。

公式一$\sin(x+y)=\sin x\cos y+\cos x\sin y$$\sin x\cosy=\frac{1}{2}(\sin(x+y)+\sin(x-y))$积化和差公式公式一$\cos x\siny=\frac{1}{2}(\sin(x+y)-\sin(x-y))$公式二用于将两角和的正弦与余弦变换成和差角的形式，方便后续计算。

应用公式一$\sin\frac{x}{2}=\pm\frac{1}{\s qrt{2}}(\cos x+1)^{1/2}$公式二$\cos\frac{x}{2}=\pm\frac{1}{\sqrt{2}}(\cos x-1)^{1/2}$应用用于计算半角的角度，适用于解三角形等问题。

半角公式03三角恒等变换的应用利用三角函数解直角三角形，得到直角三角形的三个边长。

一、知识要点1、任意角三角函数的定义(1)单位圆定义法：在平面直角坐标系中，设α是一个任意角，它的终边与单位圆交于点P(x，y)，那么：①y叫做α的正弦，记作sinα，即sin α＝y；②x叫做α的余弦，记作cosα，即cos α＝x；③yx叫做α的正切，记作tanα，即tan α＝yx(x≠0)．对于确定的角α，上述三个值都是唯一确定的．故正弦、余弦、正切都是以角为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，统称为三角函数．(2)终边定义法：设角α终边上任意一点的坐标为(x，y)，它与原点的距离为r，则sin α＝yr，cos α＝xr，tan α＝y x.2、同角三角函数的基本关系式(1)平方关系：sin2α＋cos2α＝1.(2)商数关系：tan α＝sin αcos α(α≠kπ＋π2，k∈Z)．注意：同角三角函数的基本关系揭示了“同角不同名”的三角函数的运算规律，它的精髓在“同角”二字上，如sin22α＋cos22α＝1，sin 8αcos 8α＝tan 8α等都成立，理由是式子中的角为“同角”．(3)辅助角公式：a sinα＋b cosα＝a2＋b2sin(α＋φ)，其中cosφ＝aa2＋b2，sinφ＝ba2＋b2，或tanφ＝ba，φ角所在象限与点(a，b)所在象限一致．3、诱导公式（奇变偶不变，符号看象限）（1）公式一：sin(α＋2k π)＝sin α，cos(α＋2k π)＝cos α，tan(α＋2k π)＝tan α，其中k ∈Z. （2）公式二：sin(π＋α)＝ - sin α，cos(π＋α)＝- cos α，tan(π＋α)＝tan α. （3）公式三：sin(－α)＝- sin α，cos(－α)＝cos α，tan(－α)＝- tan α. （4）公式四：sin(π－α)＝sin α，cos(π－α)＝-cos α，tan(π－α)＝-tan α.（5）公式五：sin ⎝⎛⎭⎫π2－α＝cos α；cos ⎝⎛⎭⎫π2－α＝sin α. 以－α替代公式五中的α，可得公式六． （6）公式六：sin ⎝⎛⎭⎫π2＋α＝cos α；cos ⎝⎛⎭⎫π2＋α＝-sin α. 4、两角和与差公式(1)sin (α±β)＝sin αcos β±cos αsin β (2)cos (α±β)＝cos αcos β∓sin αsin β (3)tan (α±β)＝tan α±tan β1∓tan αtan β5、二倍角公式(1)sin2α＝2sin αcos α(2)cos2α＝cos 2α－sin 2α=2cos 2α－1=1－2sin 2α(3)tan2α＝2tan α1－tan 2α67、函数y ＝tan x 的性质与图象8、函数()sin y A x ωϕ=+的图象* 由函数y ＝sin x 的图象经过怎样的变换得到函数y ＝sin(ωx ＋φ)(ω>0)的图象？ y ＝sin x 的图象变换成y ＝sin(ωx ＋φ)(ω>0)的图象一般有两个途径： 途径一：先相位变换，再周期变换先将y ＝sin x 的图象向左(φ>0)或向右(φ<0)平移|φ|个单位长度，再将得到的图象上各点的横坐标变为原来的 1ω倍(纵坐标不变)，得y ＝sin(ωx ＋φ)的图象． 途径二：先周期变换，再相位变换先将y ＝sin x 的图象上各点的横坐标变为原来的1ω倍(纵坐标不变)，再将得到的图象向左(φ>0)或向右(φ<0)平移|φ|ω个单位长度，得y ＝sin(ωx ＋φ)的图象． * 函数y ＝A sin(ωx ＋φ)＋k (A >0，ω>0)的性质(1)y max ＝A ＋k ，y min ＝－A ＋k ；A ＝y max －y min 2，k ＝y max ＋y min2.(2)ω可由ω＝2πT确定，其中周期T 可观察图象获得．(3)由ωx 1＋φ＝0，ωx 2＋φ＝π2，ωx 3＋φ＝π，ωx 4＋φ＝32π，ωx 5＋φ＝2π中的一个确定φ的值．常考习题一、选择题1．设α角属于第二象限，且2cos2cosαα-=，则2α角属于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 2．02120sin 等于（ ）A ．23±B ．23C ．23-D ．21 3．已知4sin 5α=，并且α是第二象限的角，那么 tan α的值等于（ ） A.43- B.34- C.43 D.344．4tan 3cos 2sin 的值（ ）A.小于0B.大于0C.等于0D.不存在5．将函数sin()3y x π=-的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移3π个单位，得到的图象对应的解析式是（ ） A ．1sin 2y x = B ．1sin()22y x π=- C.1sin()26y x π=- D.sin(2)6y x π=-6．函数)652cos(3π-=x y 的最小正周期是（ ）A ．52π B ．25π C ．π2 D ．π5 7．在函数x y sin =、x y sin =、)322sin(π+=x y 、)322cos(π+=x y 中， 最小正周期为π的函数的个数为（ ） A ．1个 B ．2个 C ．3个 D ．4个二、填空题1．设θ分别是第二、三、四象限角，则点)cos ,(sin θθP 分别在第___、___、___象限．2．设扇形的周长为8cm ，面积为24cm ，则扇形的圆心角的弧度数是 。

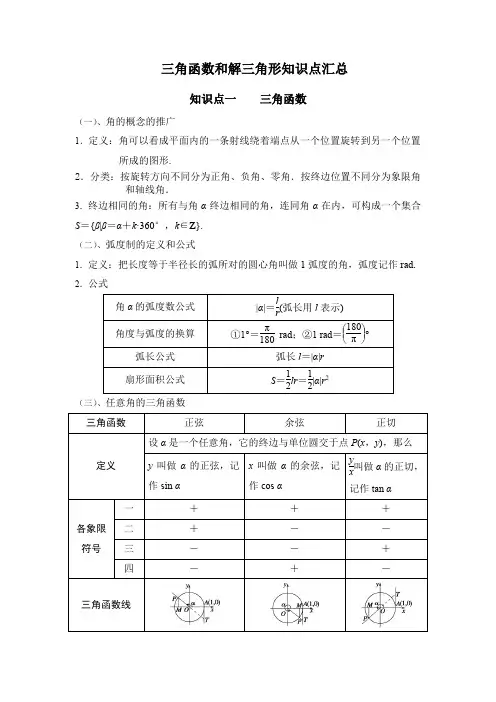
三角函数和解三角形知识点汇总知识点一三角函数（一）、角的概念的推广1．定义：角可以看成平面内的一条射线绕着端点从一个位置旋转到另一个位置所成的图形.2．分类：按旋转方向不同分为正角、负角、零角．按终边位置不同分为象限角和轴线角．3．终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S＝{β|β＝α＋k·360°，k∈Z}.（二）、弧度制的定义和公式1．定义：把长度等于半径长的弧所对的圆心角叫做1弧度的角，弧度记作rad. 2．公式（三）、任意角的三角函数（四）、同角三角函数的基本关系 1．平方关系：sin 2α＋cos 2α＝1. 2．商数关系：sin αcos α＝tan α.（五）、三角函数的诱导公式知识点二 三角函数的图像与性质（一）、用五点法作正弦函数和余弦函数的简图1．正弦函数y ＝sin x ，x ∈[0，2π]的图象中，五个关键点是：(0，0)，⎝ ⎛⎭⎪⎫π2，1，(π，0)，⎝ ⎛⎭⎪⎫3π2，－1，(2π，0).2．余弦函数y ＝cos x ，x ∈[0，2π]的图象中，五个关键点是：(0，1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫3π2，0，(2π，1).（二）、正弦、余弦、正切函数的图象与性质(下表中k ∈Z )知识点三函数y＝A sin(ωx＋φ)的图像及应用（一）、“五点法”作函数y＝A sin(ωx＋φ)(A>0，ω>0)的简图“五点法”作图的五点是在一个周期内的最高点、最低点及与x轴相交的三个点，作图时的一般步骤为：1．定点：如下表所示.2．作图：在坐标系中描出这五个关键点，用平滑的曲线顺次连接得到y＝A sin(ωx＋φ)在一个周期内的图象.3．扩展：将所得图象，按周期向两侧扩展可得y＝A sin(ωx＋φ)在R上的图象.（二）、函数y＝A sin(ωx＋φ)中各量的物理意义当函数y＝A sin(ωx＋φ)(A＞0，ω＞0)，x∈[0，＋∞) 表示一个振动量时，几个相关的概念如下表：（三）、函数y ＝sin x 的图象经变换得到y ＝A sin(ωx ＋φ)的图象的两种途径知识点四 三角恒等变换（一）、两角和与差的正弦、余弦和正切公式sin(α±β)＝sin αcos β±cos αsin β. cos(α∓β)＝cos αcos β±sin αsin β. tan(α±β)＝tan α±tan β1∓tan αtan β.（二）、二倍角的正弦、余弦、正切公式sin 2α＝2sin αcos α.cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α. tan 2α＝2tan α1－tan 2α.（三）、有关公式的逆用、变形等 1．tan α±tan β＝tan(α±β)(1∓tan αtan β). 2．cos 2α＝1＋cos 2α2， sin 2α＝1－cos 2α2. 3．1＋sin 2α＝(sin α＋cos α)2， 1－sin 2α＝(sin α－cos α)2，sin α±cos α＝2sin ⎝ ⎛⎭⎪⎫α±π4.（四）、函数f (α)＝a sin α＋b cos α(a ，b 为常数)，可以化为f (α)＝a 2＋b 2sin(α＋φ)⎝ ⎛⎭⎪⎫其中tan φ＝b a 或f (α)＝a 2＋b 2cos(α－φ)⎝ ⎛⎭⎪⎫其中tan φ＝a b .知识点五 解三角形（一）、正、余弦定理在△ABC 中，若角A ，B ，C 所对的边分别是a ，b ，c ，R 为△ABC 外接圆半径，则（二）、S△ABC＝12ab sin C＝12bc sin A＝12ac sin B＝abc4R＝12(a＋b＋c)·r(r是三角形内切圆的半径)，并可由此计算R，r.（三）、实际问题中的常用角1．仰角和俯角：在同一铅垂平面内的水平视线和目标视线的夹角，目标视线在水平视线上方叫仰角，目标视线在水平视线下方叫俯角(如图1).2．方位角：从某点的指北方向线起按顺时针转到目标方向线之间的水平夹角叫作方位角．如B点的方位角为α(如图2)．3．方向角：正北或正南方向线与目标方向线所成的锐角，如南偏东30°，北偏西45°等.4．坡度：坡面与水平面所成的二面角的正切值.。

三角函数专题一、核心知识点归纳：1、正弦函数、余弦函数和正切函数的图象与性质：sin y x =cos y x =tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k ∈Z 时，max 1y =; 当22x k ππ=-()k ∈Z 时，min 1y =-． 当()2x k k π=∈Z 时，max 1y =；当2x k ππ=+()k ∈Z 时，min 1y =-．既无最大值也无最小值周期性 2π2ππ奇偶性奇函数 偶函数奇函数单调性在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦()k ∈Z 上是增函数;在32,222k k ππππ⎡⎤++⎢⎥⎣⎦ ()k ∈Z 上是减函数．在[]()2,2k k k πππ-∈Z 上是增函数；在[]2,2k k πππ+ ()k ∈Z 上是减函数． 在,22k k ππππ⎛⎫-+ ⎪⎝⎭()k ∈Z 上是增函数．对称性对称中心()(),0k k π∈Z对称中心对称中心函 数 性 质2。

正、余弦定理：在ABC ∆中有: ①正弦定理：2sin sin sin a b cR A B C===（R 为ABC ∆外接圆半径) 2sin 2sin 2sin a R A b R B c R C =⎧⎪=⎨⎪=⎩⇒ sin 2sin 2sin 2a A Rb B Rc C R⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩注意变形应用 ②面积公式：111sin sin sin 222ABC S abs C ac B bc A ∆=== ③余弦定理： 2222222222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ⎧=+-⎪=+-⎨⎪=+-⎩ ⇒ 222222222cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ⎧+-=⎪⎪+-⎪=⎨⎪⎪+-=⎪⎩二、方法总结：1.三角函数恒等变形的基本策略。

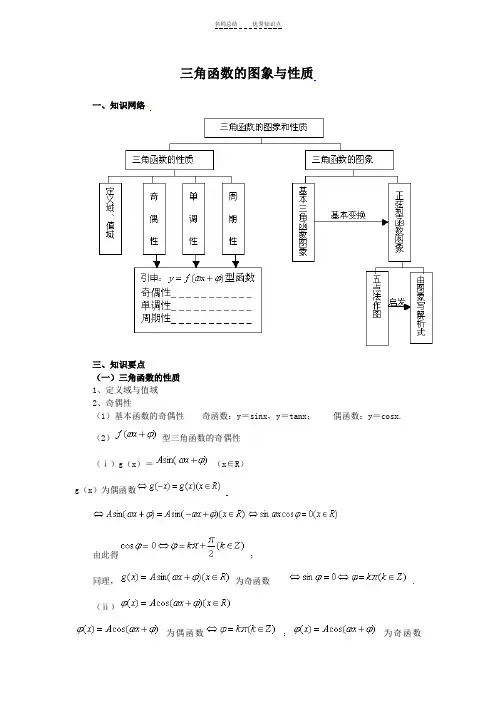
三角函数的图象与性质一、知识网络三、知识要点（一）三角函数的性质1、定义域与值域2、奇偶性（1）基本函数的奇偶性奇函数：y＝sinx，y＝tanx；偶函数：y＝cosx.（2）型三角函数的奇偶性（ⅰ）g（x）＝（x∈R）g（x）为偶函数由此得；同理，为奇函数 .（ⅱ）为偶函数；为奇函数.3、周期性（1）基本公式（ⅰ）基本三角函数的周期y＝sinx，y＝cosx的周期为；y＝tanx，y＝cotx的周期为 .（ⅱ）型三角函数的周期的周期为；的周期为 .（2）认知（ⅰ）型函数的周期的周期为；的周期为 .（ⅱ）的周期的周期为；的周期为 .均同它们不加绝对值时的周期相同，即对y＝的解析式施加绝对值后，该函数的周期不变.注意这一点与（ⅰ）的区别.（ⅱ）若函数为型两位函数之和，则探求周期适于“最小公倍数法”.（ⅲ）探求其它“杂”三角函数的周期，基本策略是试验――猜想――证明.（3）特殊情形研究（ⅰ）y＝tanx－cotx的最小正周期为；（ⅱ）的最小正周期为；（ⅲ）y＝sin4x＋cos4x的最小正周期为 .由此领悟“最小公倍数法”的适用类型，以防施错对象.4、单调性（1）基本三角函数的单调区间（族）依从三角函数图象识证“三部曲”：①选周期：在原点附近选取那个包含全部锐角，单调区间完整，并且最好关于原点对称的一个周期；②写特解：在所选周期内写出函数的增区间（或减区间）；③获通解：在②中所得特解区间两端加上有关函数的最小正周期的整数倍，即得这一函数的增区间族（或减区间族）循着上述三部曲，便可得出课本中规范的三角函数的单调区间族.揭示：上述“三部曲”也适合于寻求简单三角不等式的解集或探求三角函数的定义域.（2）y＝型三角函数的单调区间此类三角函数单调区间的寻求“三部曲”为①换元、分解：令u＝，将所给函数分解为内、外两层：y＝f（u），u＝；②套用公式：根据对复合函数单调性的认知，确定出f（u）的单调性，而后利用（1）中公式写出关于u的不等式；③还原、结论：将u＝代入②中u的不等式，解出x的取值范围，并用集合或区间形成结论.（二）三角函数的图象1、对称轴与对称中心（1）基本三角函数图象的对称性（ⅰ）正弦曲线y＝sinx的对称轴为；正弦曲线y＝sinx的对称中心为（，0） .（ⅱ）余弦曲线y＝cosx的对称轴为；余弦曲线y＝cosx的对称中心（ⅲ）正切曲线y＝tanx的对称中心为；正切曲线y＝tanx无对称轴.认知：①两弦函数的共性：x＝为两弦函数f（x）对称轴为最大值或最小值；（，0）为两弦函数f（x）对称中心＝0.②正切函数的个性：（，0）为正切函数f（x）的对称中心＝0或不存在.（2）型三角函数的对称性（服从上述认知）（ⅰ）对于g（x）＝或g（x）＝的图象x＝为g（x）对称轴为最值（最大值或最小值）；（，0）为两弦函数g（x）对称中心＝0.（ⅱ）对于g（x）＝的图象（，0）为两弦函数g（x）的对称中心＝0或不存在.2、基本变换（1）对称变换（2）振幅变换（纵向伸缩）（3）周期变换（横向伸缩）（4）相位变换（左右平移）（5）上、下平移3、y＝的图象（1）五点作图法（2）对于A，T，，的认知与寻求：①A：图像上最高点（或最低点）到平衡位置的距离；2A：图像上最高点与最低点在y轴上投影间的距离.②：图象的相邻对称轴（或对称中心）间的距离；：图象的对称轴与相邻对称中心间的距离.：由T＝得出. ③：解法一：运用“代点法”求解，以图象的最高点（或最低点）坐标代入为上策，若以图象与x轴交点坐标代入函数式求，则须注意检验，以防所得值为增根；解法二：逆用“五点作图法”的过程（参见经典例题）.四、经典例题例1、求下列函数的值域：（1）（2）（3）（4）（5）（6）分析：对于形如（1）（2）（3）的函数求值域，基本策略是（ⅰ）化归为的值域；（ⅱ）转化为sinx（或cosx）的二次函数；对于（4）（5）（6）之类含有绝对值的函数求值域，基本策略则是（ⅰ）在适当的条件下考察y2；（ⅱ）转化为分段函数来处理；（ⅲ）运用其周期性、奇偶性或函数图象对称性转化.解：（1）∵∴，即所求函数的值域为 .（2）由∴∴注意到这里x∈R，，∴∴所求函数的值域为[－1，1].（3）这里令sinx＋cosx＝t则有且由于是有∵∴因此，所求函数的值域为 .（4）注意到这里y>0，且∵∴即所求函数的值域为 .（5）注意到所给函数为偶函数，又当∴此时同理，当亦有 . ∴所求函数的值域为 .（6）令则易见f（x）为偶函数，且∴是f（x）的一个正周期. ①只需求出f（x）在一个周期上的取值范围.当x∈[0， ]时，又注意到，∴x＝为f（x）图象的一条对称轴②∴只需求出f（x）在[0， ]上的最大值.而在[0， ]上，递增. ③亦递增④∴由③④得f（x）在[0， ]上单调递增.∴即⑤于是由①、②、⑤得所求函数的值域为 .点评：解（1）（2）运用的是基本化归方法；解（3）运用的是求解关于sinx＋cosx 与sinxcosx的函数值域的特定方法；解（4）借助平方转化；解（5）（6）则是利用函数性质化繁为简，化暗为明.这一点在解（6）时表现得淋漓尽致.例2、求下列函数的周期：（1）；（2）；（3）；（4）；（5）分析：与求值域的情形相似，求三角函数的周期，首选是将所给函数化为＋k的形式，而后运用已知公式.对于含有绝对值的三角函数，在不能利用已有认知的情况下，设法转化为分段函数来处理.解：（1）＝＝∴所求最小正周期 .（2）＝＝＝∴所求周期 .（3）＝＝＝ .注意到的最小正周期为，故所求函数的周期为 .（4）注意到3sinx及-sinx的周期为2，又sinx≥0（或sinx<0）的解区间重复出现的最小正周期为2 . ∴所求函数的周期为2 .（5）注意到sin2x的最小正周期，又sinx≥0（或sinx<0）的解区间重复出现的最小正周期，这里的最小公倍数为 . ∴所求函数的周期 .点评：对于（5），令则由知，是f（x）的一个正周期.①又∴不是f（x）的最小正周期. ②于是由①②知，f（x）的最小正周期为 .在一般情况下，探求上述一类分段函数的周期，仅考虑各段函数的最小正周期的最小公倍数是不够的，还要考虑各分支中的条件区间重复出现的最小正周期.双方结合，方可能获得正确结果.请大家研究的最小正周期，并总结自己的有关感悟与经验.例3、已知函数的部分图象，（1）求的值；（2）求函数图象的对称轴方程和对称中心坐标.解：（1）令，则由题意得f（0）＝1∵∴注意到函数图象在所给长度为一个周期的区间的右端点横坐标为，故逆用“五点作图法”得：由此解得∴所求， .（2）由（1）得令，解得，∴函数f（x）图象的对称轴方程为；令解得，∴函数f（x）图象的对称中心坐标为 .点评：前事不忘，后事之师.回顾运用“五点作图法”作出所给三角函数在一个周期内图象的列表、描点过程，便可从中悟出所给函数图象上的五个关键点横坐标满足的等式：例4、（1）函数的单调递增区间为。

1. 任意角的三角函数的定义：设α是任意一个角，P (,)x y 是α的终边上的任意一点（异于原点），它与原点的距离是0r =>，那么sin ,cos y xr rαα==，()tan ,0yx xα=≠三角函数值只与角的大小有关，而与终边上点P 的位置无关。

2.三角函数在各象限的符号：（一全二正弦，三切四余弦）＋ ＋ － ＋ － ＋ － － － ＋ ＋ －sin α cos α tan α3. 同角三角函数的基本关系式：（1）平方关系：22221sin cos 1,1tan cos αααα+=+= （2）商数关系：sin tan cos ααα=（用于切化弦） ※平方关系一般为隐含条件，直接运用。

注意“1”的代换4.三角函数的诱导公式诱导公式（把角写成απ±2k 形式，利用口诀：奇变偶不变，符号看象限）Ⅰ）⎪⎩⎪⎨⎧=+=+=+x x k x x k x x k tan )2tan(cos )2cos(sin )2sin(πππ Ⅱ）⎪⎩⎪⎨⎧-=-=--=-x x x x x x tan )tan(cos )cos(sin )sin( Ⅲ） ⎪⎩⎪⎨⎧=+-=+-=+x x x x x x tan )tan(cos )cos(sin )sin(πππ Ⅳ）⎪⎩⎪⎨⎧-=--=-=-x x x x x x tan )tan(cos )cos(sin )sin(πππ Ⅴ）⎪⎪⎩⎪⎪⎨⎧=-=-ααπααπsin )2cos(cos )2sin( Ⅵ）⎪⎪⎩⎪⎪⎨⎧-=+=+ααπααπsin )2cos(cos )2sin(5.特殊角的三角函数值6.三角函数的图像及性质sin y x =cos y x = tan y x =图像定义域 R R,2x x k k Z ππ⎧⎫≠+∈⎨⎬⎩⎭值域[]1,1-[]1,1-R最值当22x k ππ=+()k Z ∈时，max 1y =；当22x k ππ=-()k Z ∈时，当()2x k k Z π=∈时，max 1y =；当2x k ππ=+()k Z ∈时，min 1y =-．既无最大值也无最小值度0 30 45 6090 120 135 150 180︒270360弧度0 6π 4π 3π 2π 23π 34π 56π π32π 2π sin α1222 32132 22121cos α132 221212- 22-32-1- 0 1tan α 0 331 3无3- 1-33-无7.函数sin()y A x ωϕ=+图象的画法： ①“五点法”――设X x ωϕ=+，令X ＝0，3,,,222ππππ求出相应的x 值，计算得出五点的坐标，描点后得出图象； ②图象变换法：这是作函数简图常用方法。

三角函数知识点总结1、任意角：正角： ；负角： ；零角： ；2、角α的顶点与 重合，角的始边与 重合，终边落在第几象限，则称α为第几象限角．第一象限角的集合为 第二象限角的集合为 第三象限角的集合为 第四象限角的集合为 终边在x 轴上的角的集合为 终边在y 轴上的角的集合为 终边在坐标轴上的角的集合为 3、与角α终边相同的角的集合为 4、已知α是第几象限角，确定()*n nα∈N 所在象限的方法：先把各象限均分n 等份，再从x 轴的正半轴的上方起，依次将各区域标上一、二、三、四，则α原来是第几象限对应的标号即为nα终边所落在的区域．5、 叫做1弧度．6、半径为r 的圆的圆心角α所对弧的长为l ，则角α的弧度数的绝对值是 ．7、弧度制与角度制的换算公式：8、若扇形的圆心角为()αα为弧度制，半径为r ，弧长为l ，周长为C ，面积为S ，则l= ．S=9、设α是一个任意大小的角，α的终边上任意一点P 的坐标是(),x y ，它与原点的距离是()0r r =>，则sin y r α=，cos x r α=，()tan 0yx xα=≠． 10、三角函数在各象限的符号：第一象限全为正，第二象限正弦为正，第三象限正切为正，第四象限余弦为正．11、三角函数线：sin α=MP ，cos α=OM ，tan α=AT ．12、同角三角函数的基本关系：(1) ;(2) ;(3) 13、三角函数的诱导公式：()()1sin 2sin k παα+=，()cos 2cos k παα+=，()()tan 2tan k k παα+=∈Z ． ()()2sin sin παα+=-，()cos cos παα+=-，()tan tan παα+=． ()()3sin sin αα-=-，()cos cos αα-=，()tan tan αα-=-．()()4sin sin παα-=，()cos cos παα-=-，()tan tan παα-=-．口诀：函数名称不变，符号看象限．()5sin cos 2παα⎛⎫-=⎪⎝⎭，cos sin 2παα⎛⎫-= ⎪⎝⎭． ()6sin cos 2παα⎛⎫+=⎪⎝⎭，cos sin 2παα⎛⎫+=- ⎪⎝⎭． 口诀：奇变偶不变，符号看象限． 重要公式⑴()cos cos cos sin sin αβαβαβ-=+；⑵()cos cos cos sin sin αβαβαβ+=-； ⑶()sin sin cos cos sin αβαβαβ-=-；⑷()sin sin cos cos sin αβαβαβ+=+； ⑸()tan tan tan 1tan tan αβαβαβ--=+（()()tan tan tan 1tan tan αβαβαβ-=-+）；⑹()tan tan tan 1tan tan αβαβαβ++=-（()()tan tan tan 1tan tan αβαβαβ+=+-）．二倍角的正弦、余弦和正切公式： ⑴sin 22sin cos ααα=．(2)2222cos2cos sin 2cos 112sin ααααα=-=-=-（2cos 21cos 2αα+=，21cos 2sin 2αα-=）．⑶22tan tan 21tan ααα=-．公式的变形：()βαβαβαtan tan 1)tan(tan tan •±=±，2cos 12cosαα+±=；αααααααsin cos 1cos 1sin cos 1cos 12tan -=+=+-±=辅助角公式()sin cos αααϕA +B =+，其中tan ϕB=A． 万能公式万能公式其实是二倍角公式的另外一种变形：2tan 12tan2sin 2ααα+=，2tan 12tan 1cos 22ααα+-=，2tan 12tan2tan 2ααα-=14、函数sin y x =的图象上所有点 得到函数()sin y x ωϕ=A +的图象．15.函数()()sin 0,0y x ωϕω=A +A >>的性质：①振幅：A ；②周期：2πωT =；③频率：12f ωπ==T ；④相位：x ωϕ+；⑤初相：ϕ． 函数()sin y x B ωϕ=A ++，当1x x =时，取得最小值为min y ；当2x x =时，取得最大值为max y ，则()max min 12y y A =-，()max min 12y y B =+，()21122x x x x T=-<．。