物理必修一匀变速直线运动专题

人教版高中物理必修一第2章专题匀变速直线运动推论的应用一、单项选择题（共5小题；共20分）1. 一个小球从斜面的顶端由静止开始匀加速沿斜面滑下，经过斜面中点时速度为3m/s，则小球到达斜面底端时的速度为A. 4m/sB. 5m/sC. 6m/sD. 3√2m/s2. 某质点由A经B到C做匀加速直线运动历时4s。

前2s和后2s位移分别为AB=8m和BC=12m，该质点的加速度大小及B点的瞬时速度的大小分别是A. 1m/s2；5m/sB. 2m/s2；5m/sC. 1m/s2；10m/sD. 2m/s2；10m/s3. 一个物体从静止开始做匀加速直线运动，它在第1s内与在第2s内位移之比为x1:x2，在走完第1m时与走完第2m时的速度之比为v1:v2，以下说法正确的是A. x1:x2=1:3，v1:v2=1:2B. x1:x2=1:3，v1:v2=1:√2C. x1:x2=1:4，v1:v2=1:2D. x1:x2=1:4，v1:v2=1:√24. 一小物体以一定的初速度自光滑斜面的底端a点上滑，最远可达b点，e为ab的中点。

已知物体由a到e的时间为t0，则它从e经b再返回e所需时间为A. t0B. (√2−1)t0C. 2(√2+1)t0D. (2√2+1)t05. 一物体做匀变速直线运动，在通过第一段位移x1的过程中，其速度变化量为Δv，紧接着通过第二段位移x2，速度变化量仍为Δv。

则关于物体的运动，下列说法正确的是A. 第一段位移x1一定大于第二段位移x2B. 两段运动所用时间一定不相等C. 物体运动的加速度为(Δv)2x2−x1D. 通过两段位移的平均速度为(x2+x1)Δvx2−x1二、双项选择题（共3小题；共12分）6. 如图所示，光滑斜面AD被分成三个长度相等的部分，即AB=BC=CD，一小物体从A点由静止开始下滑，下列结论中正确的是A. 物体到达各点的速率v B:v C:v D=1:2:3B. 物体在AB段和BC段的平均速度之比为(√2−1):1C. 物体通过 B 、 C 、 D 三点的速度满足 v C =√v B 2+vD 22D. 物体通过 B 、 C 、 D 三点的速度满足 v C =v B +v D27. 如图所示，物体自 O 点由静止开始做匀加速直线运动，A 、 B 、 C 、 D 为其运动轨迹上的四点，测得 AB =2 m ，BC =3 m ，且物体通过 AB 、 BC 、 CD 所用的时间相等，则下列说法正确的是A. 可以求出物体加速度的大小B. 可以求得 CD =4 mC. 可以求得 O 、 A 之间的距离为 1.125 mD. 可以求得 O 、 B 之间的距离为 12.5 m8. 如图所示，在水平面上固定着四个完全相同的木块，一颗子弹以水平速度 v 射入。

高中物理必修一第二章探究匀变速运动的规律近年高考考查的重点是匀变速直线运动的规律及 v-t 图像。

本章知识较多与牛顿运动定律、电场中带电粒子的运动等知识结合起来进行考察。

近年试题的内容与现实生活和生产实际的结合逐步密切。

专题一:自由落体运动◎ 知识梳理1．定义：物体从静止开始下落，并只受重力作用的运动。

2．规律：初速为 0 的匀加速运动，位移公式：h =1gt 2 ，速度公式：v=gt23 ．两个重要比值：相等时间内的位移比1 ：3 ：5-----，相等位移上的时间比1: ( 2 -1) : ( 3 - 2).....◎ 例题评析【例 1】建筑工人安装塔手架进行高空作业，有一名建筑工人由于不慎将抓在手中的一根长5m 的铁杆在竖直状态下脱落了，使其做自由落体运动，铁杆在下落过程中经过某一楼层面的时间为0.2s，试求铁杆下落时其下端到该楼层的高度？〔g＝10m/s2，不计楼层面的厚度〕【分析与解答】铁杆下落做自由落体运动，其运动经过下面某一楼面时间Δt=0.2s，这个Δt也就是杆的上端到达该楼层下落时间tA与杆的下端到达该楼层下落时间t B之差，设所求高度为h，那么由自由落体公式可得到：h =1gt 2 2 Bh + 5 =1gt 2 2 AtA－t B＝Δt解得h＝28.8mt 0t 0 落到地面的雨滴速度一般不超过 8m/s ，为什么它们之间有这么大的差异呢？【分析与解答】根据： s = 1gt22v t = gt可推出v t == 2 ⨯10 ⨯1.5 ⨯103 m / s = 1.732 ⨯102 m / s可见速度太大，不可能出现这种现象。

[点评]实际上雨滴在下落过程所受空气阻力和其速度是有关的,速度越大所受阻力也越大, 落到地面之前已做匀速运动.专题二:匀变速直线运动的规律 ◎ 知识梳理1.常用的匀变速运动的公式有:①v =v +at ②s=v t+at 2/2 ③v 2=v 2+2as-④ v =v 0 + v t2= v t / 2 S=(v 0+v t )t/2 ⑤ ∆s = aT 〔1〕说明：上述各式有 V 0，V t ，a ，s ，t 五个量，其中每式均含四个量，即缺少一个量，在 应用中可根据量和待求量选择适宜的公式求解。

匀变速直线运动题型归纳【题型一】匀变速直线运动的规律【例题】物体以一定的初速度从A 点冲上固定的光滑的斜面，到达斜面最高点C 时速度恰好为零，如图所示.已知物体运动到斜面长度3/4处的B 点时，所用时间为t ，求物体从B 运动到C 所用的时间.【解析】解法一：逆向思维法物体向上匀减速冲上斜面，相当于向下匀加速滑下斜面.故x BC ＝221BC at ，x AC ＝a (t ＋t BC )2/2，又x BC ＝x AC /4解得t BC ＝t解法二：比例法对于初速度为零的匀变速直线运动，在连续相等的时间内通过的位移之比为x 1∶x 2∶x 3∶…∶x n ＝1∶3∶5∶…∶(2n －1)现在x BC ∶x AB ＝1∶3通过x AB 的时间为t ，故通过x BC 的时间t BC ＝t解法三：利用相似三角形面积之比等于对应边平方比的方法，作出v-t图象，如图所示.S △AOC /S △BDC ＝CO 2/CD 2且S △AOC ＝4S △BDC ，OD ＝t ，OC ＝t ＋t BC所以4/1＝(t ＋t BC )2/2BC t ，解得t BC ＝t【练习】1、一物体以5 m/s 的初速度在光滑斜面上向上运动，其加速度大小为2 m/s 2，设斜面足够长，经过t 时间物体位移的大小为4 m 。

则时间t 可能为A ．1 sB ．3 sC ．4 s D.5＋412s2、一个物体从静止开始做匀加速直线运动，以T 为时间间隔，在第三个T 时间内位移为3m ，第三个T 时间末的瞬时速度为3m/s 则（ ）A. 物体在第一个T 时间的位移为0.6mB. 物体的加速度为2/1s m a =C. 时间间隔s T 1.2=D. 第一个T 时间末的瞬时速度为0.6m/s3、如图所示，一小滑块从斜面顶端A 由静止开始沿斜面向下做匀加速直线运动到达底端C ，已知AB ＝BC ，则下列说法正确的是A ．滑块到达B 、C 两点的速度大小之比为1∶ 2B ．滑块到达B 、C 两点的速度大小之比为1∶4C ．滑块通过AB 、BC 两段的时间之比为1∶ 2D ．滑块通过AB 、BC 两段的时间之比为1∶(2－1)4、小球每隔0.2s 从同一高度抛出，做初速为6m/s 的竖直上抛运动，设它们在空中不相碰．第一个小球在抛出点以上能遇到的小球数为（取g=10m/s 2 ）（ ）A ．三个B ．四个C ．五个D ．六个5、汽车以20m/s 的速度在平直公路上行驶，急刹车时的加速度大小为5m/s 2，则自驾驶员急踩刹车开始计时，2s 与5s 内汽车的位移之比为A.5∶4B.4∶5C.3∶4D.4∶3【题型二】运动学图像1、v-t 图例题：质点做直线运动的速度—时间图象如图所示，该质点（ ）A ．在第1秒末速度方向发生了改变B ．在第2秒末加速度方向发生了改变C ．在前2秒内发生的位移为零D ．第3秒末和第5秒末的位置相同练习1：一枚火箭由地面竖直向上发射，其v-t 图象如图所示，则（ ）A. 火箭在t 2～t 3时间内向下运动B ．火箭能上升的最大高度114t vC. 火箭上升阶段的平均速度大小为221v D.火箭运动过程中的最大加速度大小为32t v2：一个做直线运动的物体的t v -图象如图所示，由图象可知A ．0～1.5 s 内物体的加速度为2/4s m -， 1.5～3 s 内物体的加速度为4 m/s 2 B ．0～4 s 内物体的位移为12 mC ．3 s 末物体的运动方向发生变化D ．3 s 末物体回到出发点2、x-t 图例题：如图所示是甲、乙两物体从同一点出发的位移—时间(x -t )图象，由图象可以看出在0～ 4 s 这段时间内A ．甲、乙两物体始终同向运动B ．4 s 时甲、乙两物体之间的距离最大C ．甲的平均速度大于乙的平均速度D ．甲、乙两物体之间的最大距离为3 m练习：在平直公路上行驶的a 车和b 车，其位移—时间(x -t )图像分别为图中直线a 和曲线b ，已知b 车的加速度恒定且等于－2 m/s 2，t ＝3s 时，直线a 和曲线b 刚好相切，则A ．a 车做匀速运动且其速度为v a ＝83m/s B ．t ＝3 s 时a 车和b 车相遇但此时速度不等C ．t ＝1 s 时b 车的速度为10 m/sD ．t ＝0时a 车和b 车的距离x 0＝9 m3、t a 图像：例题：一物体由静止开始沿直线运动，其加速度随时间变化的规律如图所示。

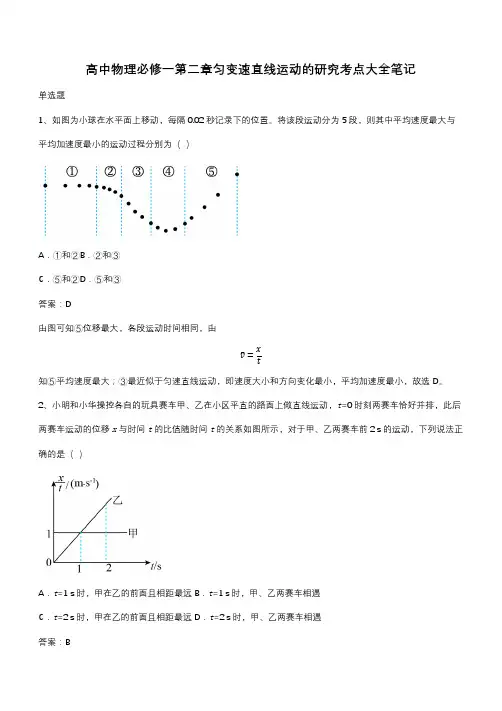
高中物理必修一第二章匀变速直线运动的研究考点大全笔记单选题1、如图为小球在水平面上移动，每隔0.02秒记录下的位置。

将该段运动分为5段，则其中平均速度最大与平均加速度最小的运动过程分别为（）A．①和②B．②和③C．⑤和②D．⑤和③答案：D由图可知⑤位移最大，各段运动时间相同，由v̅=x t知⑤平均速度最大；③最近似于匀速直线运动，即速度大小和方向变化最小，平均加速度最小，故选D。

2、小明和小华操控各自的玩具赛车甲、乙在小区平直的路面上做直线运动，t=0时刻两赛车恰好并排，此后两赛车运动的位移x与时间t的比值随时间t的关系如图所示，对于甲、乙两赛车前2 s的运动，下列说法正确的是（）A．t=1 s时，甲在乙的前面且相距最远B．t=1 s时，甲、乙两赛车相遇C．t=2 s时，甲在乙的前面且相距最远D．t=2 s时，甲、乙两赛车相遇答案：B甲赛车xt恒定不变，故做匀速直线运动，速度为v甲=1 m/s。

根据x=v0t+12at2可得x t=12at+v0可知乙赛车初速度为零，加速度为a=2 m/s2，故两质点在t=0.5 s时速度相等，此时两者相距最远；当两者相遇时v 甲t=12at2解得t=1s甲、乙相遇，此后乙的速度大于甲的速度，乙在甲的前面，ACD错误，B正确。

故选B。

3、某物理兴趣小组的同学们利用课堂上学到的物理知识，动手对自由落体运动的规律进行了实验研究，实验装置如图所示。

为了让实验效果更好，实验室提供以下几种小球，应选择哪种球会使得效果更好（）A．空心大铁球B．实心小铁球C．空心大木球D．实心小木球答案：B为了减小实验中空气阻力的影响，应该选密度大、体积小的实心小铁球做实验。

故选B。

4、一列火车正在做匀加速直线运动，从某时刻开始计时，第1分钟内，发现火车前进了180 m，第6分钟内，发现火车前进了360 m。

则火车的加速度为（）A．0.01 m/s2B．0.06 m/s2C．0.6 m/s2D．1.8 m/s2答案：A由相同时间内的位移差x6−x1=(6−1)aT2解得a=360−1805×(60)2m/s2=0.01m/s2故A正确，BCD错误。

高一物理必修一第二章匀变速直线运动整章基础练习题（实用）（带参考答案）高一物理必修一第二章匀变速直线运动整章基础练习题（实用）（带参考答案）高一物理第一章匀变速直线运动规律一、学习目标1、掌握匀变速直线运动的速度公式、位移公式及位移与速度关系的公式并会进行计算2、掌握匀变速直线运动的其它一些扩展公式，灵活运用各种公式解决实际问题二、学习过程（一）匀变速直线运动的基本规律1、速度公式：；2、位移公式：；3.初始速度、最终速度、加速度和位移之间的关系：；4、位移、时间、初速度、末速度间的关系式：。

问题1：如何解决单一过程的匀变速直线运动问题？例1：以36km/h的速度行驶的汽车开始下坡，在斜坡上以0.2m/s2的加速度直线匀速加速，30秒后到达坡底。

计算斜坡道路的长度和汽车到达斜坡底部时的速度。

练习1、一辆车以10m/s的速度匀速行驶，在距车站25m时开始制动，使车匀减速前进，到车站时恰好停下。

求：（1）车匀减速行驶时的加速度的大小；（2）车从制动到停下来经历的时间。

问题2：如何处理多个过程匀速直线运动的问题？例2、质点从静止开始做匀加速直线运动，经4s后速度达到20m/s，然后匀速运动了10s，接着经4s匀减速运动后静止。

要求：（1）质点在加速运动阶段的加速度是多大？（2）质点在16s末的速度为多大？（3）在整个过程中，粒子的位移是多少？练习2、一质点从静止开始以1m/s2的加速度匀加速运动，经5s后做匀速运动，最后2s的时间质点做匀减速运动直至静止时，整个过程中的颗粒位移为25m。

问：（1）粒子以匀速运动的速度有多快？（2）减速运动中粒子的加速度是多少？（3）粒子以恒定速度运动多长时间？1/24（二）匀速直线运动的特殊规律1、物体做匀变速直线运动，已知初速度v0、末速度vt、经历的时间为t，则这段时间内平均速度为：v=___________；中间时刻的即时速度为：vt/2=____________；二者的关系是：_______；中间位置的速度为：vs/2=_____________。

高中物理必修一【匀变速直线运动推论的应用】专题训练习题[基础达标练]1．做匀减速直线运动的物体经4 s后停止，若在第1 s内的位移是14 m，则最后1 s的位移是()A．3.5 m B．2 mC．1 m D．0 m解析：可以采用逆向思维，把物体的运动看作是初速度为0的匀加速直线运动，其在连续相等时间内的位移之比为1∶3∶5∶7，已知第4 s内的位移是14 m，所以第1 s内的位移是2 m，选项B正确。

答案：B2．物体从斜面顶端由静止开始下滑，经过斜面中点时速度为2 m/s，则物体到达斜面底端时速度为()A．3 m/s B．4 m/sC．6 m/s D．2 2 m/s解析：由v中＝v2＋v202得v＝2 2 m/s。

答案：D3．从静止开始做匀加速直线运动的物体，在第1 s内、第2 s内、第3 s内的平均速度之比为()A．1∶3∶5B．1∶4∶9C．1∶2∶3D．1∶2∶ 3解析：由于第1 s内、第2 s内、第3 s内的位移之比x1∶x2∶x3＝1∶3∶5，而平均速度v＝xt，三段时间都是1 s，故三段时间内的平均速度之比为1∶3∶5。

答案：A4．一个向正东方向做匀变速直线运动的物体，在第3 s内发生的位移为8 m，在第5 s内发生的位移为5 m，则关于物体运动加速度的描述正确的是()A．大小为3 m/s2，方向为正东方向B．大小为3 m/s2，方向为正西方向C．大小为1.5 m/s2，方向为正东方向D．大小为1.5 m/s2，方向为正西方向解析：设第3 s内、第5 s内位移分别为x3、x5，则x5－x3＝x5－x4＋x4－x3＝2aT2，得a＝－1.5 m/s2，负号表示加速度方向沿正西，故选项D正确。

答案：D5．(多选)一物体从斜面顶端由静止开始匀加速下滑，到达斜面中点用时1 s，速度为2 m/s，则下列说法正确的是()A．斜面长度为1 mB．斜面长度为2 mC．物体在斜面上运动的总时间为 2 sD．到达斜面底端时的速度为4 m/s解析：物体由静止运动到斜面中点的平均速度v＝v中2＝1 m/s，L2＝v t1＝1 m，L＝2 m，故A错，B对；由t1∶t2＝1∶(2－1)得t2＝(2－1)s，t＝t1＋t2＝ 2 s，故C对；由v＝at知，v底＝2 2 m/s，故D错。

高中物理必修一【匀变速直线运动的速度与时间的关系】专题训练习题[基础达标练]1．对于匀变速直线运动的速度与时间关系式v＝v0＋at，以下理解正确的是() A．v0是时间间隔t开始的速度，v是时间间隔t内的平均速度B．v一定大于v0C．at在时间间隔t内，可以是速度的增加量，也可以是速度的减少量，以初速度方向为正方向时，在匀加速直线运动中at为正值，在匀减速直线运动中at为负值D．a与匀变速直线运动的v－t图像的倾斜程度无关解析：v0、v都是瞬时速度，at是速度的变化量，A错误，C正确；在匀加速直线运动中v>v0，在匀减速直线运动中v<v0，B错误；在v－t图像中，v－t图像的斜率表示加速度，D错误。

答案：C2．如图所示为我国的“和谐号”列车，“和谐号”到某站时匀减速进站，停靠一段时间后又匀加速(同方向)出站。

在如图所示的四个v－t图像中，正确描述了“和谐号”运动情况的是()解析：进站速度均匀减小，出站速度均匀增大，故A、D错误；进站、出站的运动方向相同，故B正确，C错误。

答案：B3．一辆沿直线匀加速行驶的汽车，经过路旁的两根电线杆共用5 s时间，汽车的加速度为2 m/s2，它经过第二根电线杆时的速度是15 m/s，则汽车经过第一根电线杆的速度为()A．2 m/s B．10 m/sC．2.5 m/s D．5 m/s解析：汽车沿直线匀加速行驶，加速度为2 m/s2，经过第二根电线杆时的速度是15 m/s，用时5 s，根据速度与时间的关系式v＝v0＋at得v0＝v－at＝(15－2×5)m/s＝5 m/s，D正确。

答案：D4．(多选)2020年12月22日，我国新一代运载火箭“长征八号”在文昌航天发射场点火起飞。

假若某段时间内火箭速度的变化规律为v＝(8t＋16)m/s，由此可知这段时间内()A．火箭的初速度为8 m/sB．火箭的加速度为16 m/s2C．在3 s末，火箭的瞬时速度为40 m/sD．火箭做匀加速直线运动解析：在这段时间内，由速度的表达式可知，火箭的速度均匀增大，故火箭做匀加速直线运动，选项D正确；由匀变速直线运动的速度公式v＝v0＋at知，这段时间内火箭的初速度v0＝16 m/s，加速度a＝8 m/s2，选项A、B错误；将时间t ＝3 s代入得v3＝40 m/s，选项C正确。

追及和相遇问题当两个物体在同一条直线上运动时，由于两物体的运动情况不同，所以两物体之间的会不断发生变化，两物体间距越来越大或越来越小时，就会涉及追及、相遇或避免碰撞等问题．一．匀加速运动追匀速运动的情况（开始时v1< v2）：v1< v2时，两者距离变大；v1= v2时，两者距离最大；v1>v2时，两者距离变小，相遇时满足x1= x2+Δx，全程只相遇(即追上)一次。

【例1】一小汽车从静止开始以3m/s2的加速度行驶，恰有一自行车以6m/s的速度从车边匀速驶过．求：(1)小汽车从开动到追上自行车之前经过多长时间两者相距最远？此时距离是多少？(2)小汽车什么时候追上自行车，此时小汽车的速度是多少？二．匀速运动追匀加速运动的情况（开始时v1> v2）：v1> v2时，两者距离变小；v1= v2时，①若满足x1<x2+Δx，则永远追不上，此时两者距离最近；②若满足x1=x2+Δx，则恰能追上，全程只相遇一次；③若满足x1> x2+Δx，则后者撞上前者（或超越前者），此条件下理论上全程要相遇两次。

【例2】一个步行者以6m/s的最大速率跑步去追赶被红灯阻停的公共汽车，当他距离公共汽车25m时，绿灯亮了，汽车以1m/s2的加速度匀加速启动前进，问：人能否追上汽车？若能追上，则追车过程中人共跑了多少距离？若不能追上，人和车最近距离为多少？三．匀减速运动追匀速运动的情况（开始时v1> v2）：v1> v2时，两者距离变小；v1= v2时，①若满足x1<x2+Δx，则永远追不上，此时两者距离最近；②若满足x1=x2+Δx，则恰能追上，全程只相遇一次；③若满足x1> x2+Δx，则后者撞上前者（或超越前者），此条件下理论上全程要相遇两次。

【例3】汽车正以10m/s的速度在平直公路上前进，突然发现正前方有一辆自行车以4m/s 的速度做同方向的匀速直线运动，汽车立即关闭油门做加速度大小为6 m/s2的匀减速运动，汽车恰好不碰上自行车。

高中物理必修一第二章匀变速直线运动的研究重点归纳笔记单选题1、检测车在一段平直路段以10m/s的速度匀速行驶，某时刻检测车使用测距传感器测量该路段前方车辆的行驶情况。

计时开始时检测车距离前车100m，检测发现，10s后前车开始刹车做匀减速运动，16s后两车距离保持不变，两车之间的距离Δx随时间t的变化关系如图所示，则（）A．前车0~10s内的行驶速度为15m/sB．前车刹车的加速度大小为2.5m/sC．16s后两车距离为325mD．16s后前车停止行驶答案：BA．依题意，由运动学公式可知，0~10s内，有Δx=x前+100−10t由图像可知Δx=100+15t联立解得x前=25t则0~10s内前车行驶速度为25m/s，故A错误；BD．由图可知，16s后前后两车距离保持不变，则两车均以10m/s的速度匀速行驶，前车刹车的加速度大小为a=ΔvΔt=25−1016−10m/s2=2.5m/s2故B正确，D错误；C．16s后两车距离为Δx=250m+(25+10)2×(16−10)m−10×(16−10)m=295m故C错误。

故选B。

2、春节是我国的传统节日，以前人们常在过节时放烟花（如图甲所示）来表示庆祝，礼花弹在地面上从发射筒中沿竖直方向射出，到达最高点时炸开后，形成漂亮的球状礼花（如图乙所示）。

现有某烟花筒的结构如图丙所示，其工作原理为：点燃引线，引燃发射药燃烧发生爆炸，礼花弹获得一个初速度并同时点燃延期引线。

当礼花弹到最高点附近时，延期引线点燃礼花弹。

现假设某次放烟花中，礼花弹获得的初速度大小为35m/s，延期引线的燃烧速度为2cm/s，要求爆炸发生在超过礼花弹上升最大高度的96%。

忽略空气阻力的作用和烟花筒的长度，则延期引线的长度至少为（）A．7cm B．5.6cm C．6.86cm D．8.4cm答案：B设礼花弹上升的最大高度为h，假设当礼花弹上升至0.96h时刚好发生爆炸，且此时礼花弹的速度大小为v1，根据运动学规律有2gℎ=v022g(0.96ℎ)=v02−v12联立解得v1=7m/s所以延期引线燃烧的最短时间为t=v0−v1g=2.8s则延期引线的长度至少为l=vt=5.6cm故选B。

专题强化 匀变速直线运动的平均速度公式 v －t 图像看位移[学习目标] 1.理解平均速度公式，并能用平均速度公式解决相关问题(难点)。

2.会用v －t 图像求位移并判定直线运动位移的大小(重点)。

一、平均速度公式1．如图所示，一物体做匀变速直线运动，初速度为v 0，末速度为v ，这段时间中间时刻的瞬时速度为2t v ，试推导v ＝v 0＋v2＝2t v 。

________________________________________________________________________ ________________________________________________________________________ 2.v ＝v ＋v 02＝2t v 适合于所有的变速直线运动吗？________________________________________________________________________ ________________________________________________________________________1．匀变速直线运动的平均速度公式：v ＝2t v ＝v 0＋v2(1)匀变速直线运动中任意一段时间t 内的平均速度等于该段时间的中间时刻的瞬时速度，还等于该段时间初、末速度矢量和的一半。

(2)若同时涉及位移与时间而不涉及加速度，选用中间时刻瞬时速度公式及平均速度公式，即2t v ＝v 0＋v2，v ＝xt 。

2．三个平均速度公式的比较 v ＝xt 适用于任何运动；v ＝v 0＋v2及v ＝2t v 仅适用于匀变速直线运动。

例1 测试中，我国国产大飞机C919的初速度v 0＝2 m/s,4 s 内位移为20 m ，求： (1)飞机4 s 内的平均速度大小； (2)飞机4 s 末的速度大小； (3)飞机2 s 末的速度大小。

必修一专题1 匀变速直线运动一．区分v 、△v 、a1. v ——速度；△v ——速度的变化量〔大小〕；a ——速度变化率〔快慢〕2. 加速度的定义式：tva ∆∆=，方向：总是与______的方向一致，但与v 的方向无必然联系 ①物体的速度方向改变，加速度方向不一定改变； ②物体的加速度方向改变，速度方向不一定改变； ③比拟加速度大小时，只看绝对值，不看正负号。

3. 加速度a 取决于tv∆∆这个比值，与v 、△v 无直接联系 ①v 大，a 不一定大；v 小，a 也不一定小 ②速度变化量△v 大，加速度a 也不一定大③加速度不断减小，物体的速度不一定减小；加速度不断增大，物体的速度不一定增大 4. “同加异减〞a 、v 方向相同时做加速运动，方向相反时做减速运动 【根底】 1.(多项选择)由a=Δv Δt可知()A.a 与Δv 成正比B.物体加速度大小由Δv 决定C.a 的方向与Δv 方向相同D.Δv Δt叫速度变化率,就是加速度2.假设汽车的加速度方向与速度方向相反,当加速度增大时() A.汽车速度增加得越来越慢 B.汽车速度增加得越来越快 C.汽车速度减小得越来越快 D.汽车速度减小得越来越慢3.(多项选择)关于速度和加速度的关系,以下说法正确的选项是() A.物体的速度越大,加速度也越大B.物体速度的变化率为零时,加速度也为零C.物体速度的变化量越大,加速度越大D.物体的速度变化越快,加速度越大 4.(多项选择)以下说法正确的选项是() A.加速度为负值时,物体也可能做加速运动B.比拟加速度大小时,3 m/s 2比-5 m/s 2大 C.加速度逐渐变大,速度就逐渐变大D.在不同图像上,比拟物体的加速度时,要算出数值后再比拟 【提高】5.2021年6月17日，搭载着神舟十二号载人飞船的长征二号F 遥十二运载火箭在酒泉卫星发射中心点火升空。

关于火箭点火升空瞬间的速度和加速度的判断,以下说法正确的选项是()A.火箭的速度很小,但加速度可能较大B.火箭的速度很小,所以加速度也很小C.火箭的速度很大,所以加速度也很大D.火箭的速度很大,但加速度一定很小6.(多项选择)小球的初速度是v 1,经过一段时间后速度变为v 2,用Δv 表示Δt 时间内速度的变化量,为了在图中表示加速度a,我们以初速度v 1的箭头端为起点,以后来的速度v 2的箭头端为终点,作出一个新的箭头,表示速度的变化量Δv 。