河海大学《数学分析》习题16 三重积分的计算

三重积分计算方法
三重积分是数学中的一种重要的计算方法，用于计算三维空间中某个区域内的物理量。

它在物理学、工程学、计算机图形学等领域中具有广泛的应用。

三重积分可以理解为对一个三维区域进行体积的累加。

在直角坐标系下，三重积分可以表示为f(x, y, z)dV，其中f(x, y, z)为被积函数，dV表示微元体积。

计算三重积分的方法有多种，常见的方法包括直接计算法、柱坐标法和球坐标法。

直接计算法是最基本的计算方法，即将三重积分的积分区域分成小立方体，并对每个小立方体进行积分，然后将这些小立方体的积分结果相加。

这种方法适用于积分区域较简单的情况，但对于复杂的积分区域来说，计算量较大。

柱坐标法是一种将直角坐标系转换为柱坐标系进行计算的方法。

通过将积分区域转换为柱坐标系下的一个圆柱体，可以简化积分的计算过程。

这种方法尤其适用于具有旋转对称性的问题。

球坐标法是一种将直角坐标系转换为球坐标系进行计算的方法。

通过
将积分区域转换为球坐标系下的一个球体，可以进一步简化积分的计算过程。

这种方法尤其适用于具有球对称性的问题。

除了以上提到的方法外，还有其他一些积分变换方法，如椭球坐标法、柱坐标系下的旋转变换等，根据具体情况选择合适的方法进行计算。

需要注意的是，对于一些复杂的积分区域，可能需要将其分解为多个简单的子区域，然后对每个子区域进行积分。

此外，在实际计算中，还需要注意积分的顺序以及积分限的确定，以避免出现错误结果。

综上所述，三重积分是一种重要的计算方法，通过选择合适的计算方法和注意计算细节，可以有效地求解三维空间中的问题。

z z=1
解：先对 z 积分，将
向 xy 平面投影.
z= x2+y2
z= x2+y2
x2+y2=1
z=1
z=1
y
0
1
x
Dxy
D: x2+y2≤1
z z=1
z= x2+y2
y
0
1
x
Dxy
f(x,y,z)dxdydz

1 1d x1 1 xx 22d yx 1 2y2f(x,y,z)d z

其中 ={(x, y, z) | x2+y2+z2≤1, z≥0}.
解：x2+y2+z2=1 r=1
z
用 = 截 得 D()
而 0≤ ≤2 故
0
x
y
原积分
rc o s r2sid n rd d
*
02dr3cossindrd D()
x
0
dxdy02xycoxs(z)dz
y y y x
D


0 2d x0xd y0 2 xyco x sz)d (z
D
x
0

2
2 1
16 2
z
Dxz
y=y1(x, z) y=y2(x, z)
0
x
y

f(x,y,z)dxdydz

dxdzy2(x,z)f(x,y,z)dy

与三个坐标面所围闭区域.
解： D(x): 0≤ y ≤1–x, 0≤ z ≤ 1xy
z
1
0
x1
x:0≤x≤1
xdxdydz01xdxD(x

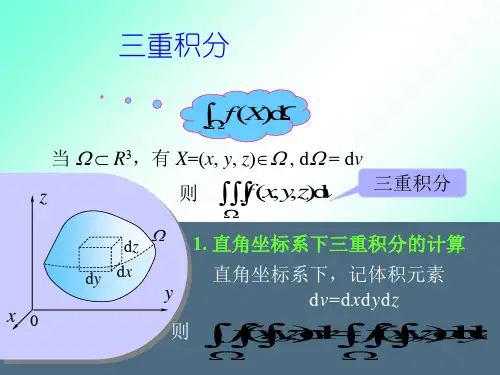
D xyyxyΩzxOD xy三重积分◆三重积分的物理意义：一个密度不均匀的空间物体，求其质量。

◆计算方法(一)直角坐标法①投影穿线法(先1后2法、先 z 后 xy 法)适用于无侧面，或者侧面为柱面的立体图形∭f (x ，y ，z )Ωdxdydz=∬dxdy D xy∫f (x ，y ，z )φ2(x ，y )φ1(x ，y )dz口诀： 后积先定限， 限内划条线。

先交写下限， 后交写上限。

释义：后面的积分，即dz 先进行限定，限定的上下限即位上表面和下表面的函数。

从投影面D xy 引出一条垂射线，方向向上。

第一次碰到Ω时，即下表面的函数写在下限的位置， 离开Ω时，即上表面的函数，写在上限的位置。

D zyΩzxOba②定限截面法、先2后1法、先 xy 后 z 法 适用于旋转体的立体图形∭f (x ，y ，z )Ωdxdydz=∫dz ba∬f (x ，y ，z )dxdy D z步骤：第一步：限内截个面，z =φ(x ，y )第二步：找出 z 的上下限。

做外层。

适用范围：{Ω边界曲面含有：x2+y2 f(x，y，z)含有：x2+y2方法同投影穿线法：第一步：投影，写出D xy的函数，φ1(x，y)≤z≤φ2(x，y)第二步：令{x=r cosθy=r sinθz=zα<θ<β，r1(θ)<r<r2(θ)则∭f(x，y，z)Ωdxdydz=∭f(r cosθ，r sinθ，z)Ωr dr=∫θdθβα∫r drr2(θ)r1(θ)∫f(r cosθ，r sinθ，z)φ2(r cosθ，r sinθ)φ1(r cosθ，r sinθ)dz上式积分是以常用次序，实际考题中，积分次序可以改变。

但注意上下限写法的规则：外层上下限不依赖内层，故最外层的上下限为常数，而内层是函数，其自变量为其外层积分的字母。

D xy yΩzx OyxDxyD xyyΩzxOD xyyΩzxOyxDxy令{x=r∙sinφ∙cosθy=r∙sinφ∙sinθz=r∙cosφα<θ<β，n<r<m则∭f(x，y，z)Ωdxdydz=∭f(r∙sinφ∙cosθ，r∙sinφ∙sinθ，r∙cosφ)Ωr2sinφdr=∫θdθβα∫φdφθ2θ1∫f(r cosθ，r sinθ，z)∙r2sinφr2(φ，θ)r1(φ，θ)dr极坐标的变换，上下限的写法：θ：一扇门xOz，绕着x轴转动，第一次碰到Ω时，记录θ1离开Ω时，记录θ2φ：一个与z轴的夹角为φ的圆锥喇叭，其逐渐扩大，第一次触及Ω时，记录φ1离开Ω时，记录φ2r：原点产生了爆炸源，冲击波看作球面，半径为r其第一次波及Ω时，记录r1离开Ω时，记录r2应用(1)体积V=∭Ωdv(2)总质量m=∭ρ(x，y，z)Ωdv (3)重心x=∭xρ(x，y，z)Ωdv∭ρ(x，y，z)Ωdv；y=∭yρ(x，y，z)Ωdv∭ρ(x，y，z)Ωdv；z=∭zρ(x，y，z)Ωdv∭ρ(x，y，z)Ωdv(4)转动惯量I x=∭(y2+z2)ρ(x，y，z)Ωdv；I y=∭(x2+z2)ρ(x，y，z)Ωdv；I z=∭(x2+y2)ρ(x，y，z)Ωdv。

dv r2 sin drd d
5
23
例3. 设由锥面
和球面
所围成 , 计算
提示:
I (x2 y2 z2 2 xy 2 yz 2 xz) dv
z 2
利用对称性
(x2 y2 z2 ) dv
4
oy
用球坐标
x
2 d
0
4 sin d
0
2r 4 d r 32 2
0
5
2
24
常数 常数
z 常数
圆柱面 半平面 平面
o
y
x
(x,
y,0)
13
如图所示, 在柱面坐标系中体积元素为
d v d dd z
z d
因此 f (x, y, z)dxdydz
z
d
dz
d d dz
o
其中 F(, , z) f ( cos , sin , z )
适用范围:
x
d
d
y
1) 积分域表面用柱面坐标表示时方程简单 ;
f (x, y, z) d v f (,, )V
2
二、三重积分的计算 1） 利用直角坐标计算三重积分
先假设连续函数 f (x, y, z) 0, 并将它看作某物体
的密度函数 , 通过计算该物体的质量引出下列各计算 方法:
方法1 . 投影法 (“先一后二”) 方法2. 截面法 (“先二后一”)
最后, 推广到一般可积函数的积分计算.
3
方法1. 投影法 (“先一后二” )
:
z1
( (
x, x,
y) y)
z D
z2
(x,
y)
z z2 (x, y)

Dz
其结果为 z 的函数 F ( z )； c2 (4)最后计算单积分 c F ( z )dz 即得三重积分值.
1
河海大学理学院《高等数学》
例 计算 I xdxdydz , 由三个坐标平面

z
及平面 x 2 y z 1 围成 .
1
例 计算三重积分 z dxdydz

0 i 1
其中dxdydz叫做直角坐标系中的体积元素.
河海大学理学院《高中将三重积分化为三次积分． z 闭区域 在 xoy 如图， z z ( x, y) z S 面上的投影为闭区域 D, S1 :z z1 ( x , y ), z S XY 型区域 S2 :z z2 ( x , y ), z z ( x, y) 过点 ( x, y ) D 作直线, o a D 从 z1 穿入，从 z2 穿出． ( x, y) y y ( x) b
河海大学理学院《高等数学》
f ( x , y , z )dz ]d . 1 D D 先一后二型 D : y1 ( x ) y y2 ( x ), a x b, 得 f ( x , y, z )dv

F ( x , y )d [ z ( x , y )
z2 ( x , y )
注意 这是平行于 z 轴且穿过闭区域 内部的直线与 闭区域 的边界曲面 S 相交不多于两点情形．
a dx y1 ( x ) dy z1 ( x , y )
b
y2 ( x )
z2 ( x , y )
f ( x , y , z )dz .
河海大学理学院《高等数学》
例 化三重积分 I f ( x , y , z )dxdydz

三重积分的定义和计算方法在多元微积分中，三重积分被用来计算三维空间中复杂曲面或体积的性质。

本文将介绍三重积分的定义和计算方法，以帮助读者更好地理解和应用这个概念。

一、定义三重积分是对一个三维空间区域内的函数进行积分。

类似于二重积分用来计算二维平面区域内的函数性质，三重积分将函数在三维空间内的性质展现出来。

它可以用于计算体积、质心、质量等相关问题。

二、直角坐标系下的三重积分计算在直角坐标系下，三重积分的计算可以通过以下步骤进行：1. 建立坐标系：确定一个适当的坐标系，常见的是笛卡尔坐标系(x, y, z)。

2. 划定积分区域：确定要求解的函数所在的空间区域，通常使用不等式或图形的方程来描述。

3. 分割积分区域：将积分区域划分为许多小立方体或长方体。

4. 选择积分方式：根据问题的要求选择适当的积分方式，常见的有直角坐标系下的直角坐标形式、柱坐标形式和球坐标形式。

5. 计算积分：根据所选择的积分方式，将函数进行变量替换并进行积分计算。

三、柱坐标系和球坐标系下的三重积分计算柱坐标系和球坐标系是常用的坐标系，它们在计算具有对称性的问题时非常有用。

1. 柱坐标系下的三重积分计算：柱坐标系中，用(r, θ, z)表示点的坐标。

三重积分的计算在柱坐标系下往往更加便捷，特别适用于具有圆柱对称性的问题。

2. 球坐标系下的三重积分计算：球坐标系中，用(ρ, φ, θ)表示点的坐标。

球坐标系下的三重积分计算常常用于具有球对称性的问题。

四、应用举例三重积分在物理学、工程学和计算机图形学等领域有着广泛的应用。

以下是一些常见的应用举例：1. 计算体积：通过三重积分可以计算具有复杂形状的立体体积。

2. 计算质心：对于有一定密度分布的物体，可以使用三重积分来计算其质心坐标。

3. 计算质量：类似地，通过三重积分可以计算具有复杂密度分布的物体的总质量。

4. 计算电荷分布：在电磁学中，可以利用三重积分来计算复杂电荷分布下的电势。

五、总结本文介绍了三重积分的定义和计算方法，包括在直角坐标系、柱坐标系和球坐标系下的计算。

规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
圆柱面；
z
为常数 半平面；
z 为常数 平 面．
柱面坐标与直角坐
o
标的关系为
y
x r cos ,
y
r
sin
,
x
z z.
柱面坐标变换的Jacobi行列式为
cos J ( x, y, z) sin
(r, , z)
0
r sin r cos
0
0 0 r, 1
f ( x, y, z)dxdydz
V
f (r cos , r sin , z)rdrddz.
V'
定理条件? 计算方法?
例2 计算I zdxdydz，其中V 是球面
V
x2 y2 z2 4与抛物面 x2 y2 3z
所围的立体.
V
2
d
4 d
a
cos r 4 sin 3dr000
2
4 0
sin
3
1 5
(
a5 cos5
0)d
a5. 10
解 2 采用柱面坐标
x2 y2 z2 z r, D : x2 y2 a2,
V : r z a, 0 r a, 0 2 ,
I
x r cos
解
由
y
r
sin
,
z z
知交线为
r2 z2 4
r2 3z
z 1, r 3,
V : r 2 z 4 r 2， 3 0 r 3,
0 2 .

三重积分的计算及重积分的应用三重积分是在三维空间中计算一些函数在一个有界区域内的体积的方法。

它是对二重积分的一种扩展，可以应用于多种问题中，包括物理、工程和数学等领域。

本文将从三重积分的计算方法开始，然后介绍一些三重积分的应用，以及如何解决这些应用问题。

一、三重积分的计算方法要计算三重积分，首先需要定义积分的坐标系和被积函数。

常用的坐标系有直角坐标系、柱坐标系和球坐标系。

选择合适的坐标系可以简化计算过程。

被积函数通常是一个连续函数或分段连续函数，也可以是具有一些特殊性质的函数，如奇函数或偶函数。

在直角坐标系中，三重积分的一般形式为∭f(x,y,z)dV，其中f(x,y,z)是被积函数，dV表示元体积元素。

元体积元素可以表示为dx dy dz，也可以写成其他坐标系对应的形式。

根据积分的定义，三重积分可以分解为对三个变量的依次积分。

具体方法为，先对z进行积分，然后再对y进行积分，最后对x进行积分。

以直角坐标系为例，三重积分可以表示为∭f(x,y,z)dxdydz。

其中，积分范围为对每个变量的积分范围进行限定。

对被积函数的积分范围的限定可以通过对空间区域的几何性质进行分析得到。

常见的限定方式有矩形区域和曲线边界。

根据具体问题，可以采用不同的方法来确定积分限定条件。

计算三重积分时，可以选择适当的计算工具，如数值积分、符号计算软件或计算机程序，并利用计算机进行数值计算。

三重积分在许多领域都有广泛的应用。

以下将介绍几个常见的应用以及解决这些应用问题的方法。

1.计算物体体积三重积分可以用于计算复杂形状的物体的体积。

通过将物体分解为无穷小的体积元素，然后对每个体积元素进行积分，最后将所有体积元素的积分结果相加，就可以得到整个物体的体积。

例如，计算一个以球面为上下界的圆锥体的体积。

首先可以选择球坐标系，然后确定积分限定条件，如半径和角度范围。

然后将球坐标系下的体积元素转换为直角坐标系下的体积元素进行积分。

最后将所有体积元素的积分结果相加，即可得到圆锥体的体积。

任取球体内一点
得锥面
对: 从0 积分，
对 : 从0 积分，扫遍球体
1. 为全球体
2. 为上半球体
3. 为下半球体
5. 为球体的第一、二卦限部分
6. 为空心球体
4. 为右半球体
三重积分的定义和计算
在直角坐标系下的体积元素
（计算时将三重积分化为三次积分）
第三节 三重积分的计算
一、三重积分的定义
二、利用直角坐标计算三重积分
三、利用柱面坐标计算三重积分
四、利用球面坐标计算三重积分
一、三重积分的定义
(1) 三重积分的存在性：
(2) 三重积分没有几何意义，但有物理意义.
性质１ (线性性质)
性质2 (对区域具有可加性)
性质3
性质4
则有
若在D上有
(3) 绝对可积性
若在D上有
则有
(2) 单调性
(1) 正性
性质5
（三重积分中值定理）
直角坐标系中将三重积分化为三次积分．
二、利用直角坐标计算三重积分 1、坐标面投影法
如图，
得
注意
这种方法称为坐标面投影法.
解
故 ：
解
如图，
解
如图,
2、坐标轴投影法(截面法)
坐标轴投影法(截面法)的一般步骤:
球面坐标下的体积元素
r
dr
d
x
z
y
0
d
rd
元素区域由六个坐标面围成：
rsin d
球面坐标下的体积元素
.
半平面 及+d ； 半径为r及r+dr的球面； 圆锥面及+d
r 2
sin drdd
dV

柱面坐标法
柱坐标系
将直角坐标系中的点表示为柱坐标形式，适用于具有圆柱对称性的三重积分。
积分顺序
通常按照先对半径进行积分，再对角度进行积分，最后对高度进行积分的顺序 进行计算。
球面坐标法
球坐标系
将直角坐标系中的点表示为球坐标形式 ，适用于具有球对称性的三重积分。
VS
积分顺序
通常按照先对半径进行积分，再对天顶角 进行积分，最后对方位角进行积分的顺序 进行计算。
计算质心坐标
质心坐标的定义
质心是物体质量的中心，其坐标可通过三重积分计算 得到。
质心坐标的计算公式
在直角坐标系下，质心坐标的计算公式为质量密度函 数对坐标的三重积分除以物体总质量。
质心坐标的应用
质心坐标在物理学、工程学等领域有广泛应用，如计 算物体的转动惯量、稳定性分析等。
计算转动惯量
转动惯量的定义
计算曲面面积
参数曲面面积的计算
对于由参数方程表示的曲面，可利用参数方 程求导得到曲面的法向量，进而计算曲面面 积。
显式曲面面积的计算
对于由显式方程表示的曲面，可利用偏导数求得曲 面的法向量，进而计算曲面面积。
隐式曲面面积的计算
对于由隐式方程表示的曲面，可利用隐函数 的求导法则求得曲面的法向量，进而计算曲 面面积。
02
三重积分的计算方法
先一后二法
投影法
将三重积分转化为二重积分，通过投 影确定积分区域。
截面法
通过截面确定被积函数在不同区间的 表达式，进而计算三重积分。
先二后一法
逆序法
将三重积分转化为累次积分，先对两 个变量进行积分，再对第三个变量进 行积分。
变量替换法
通过变量替换简化被积函数和积分区 域，进而计算三重积分。

三重积分的计算方法例题摘要：一、三重积分的概念及应用场景二、三重积分的计算方法1.重积分的计算2.重积分的换元法3.重积分的性质4.重积分的几何意义三、实例解析四、总结与拓展正文：一、三重积分的概念及应用场景三重积分是一种多元函数的积分形式，通常表示为对空间中一个几何体内部的属性进行积分。

它在物理学、工程学、经济学等领域具有广泛的应用。

三重积分的计算方法有多种，包括重积分、换元法等。

二、三重积分的计算方法1.重积分的计算重积分是指对一个空间函数在某个区域内的值进行积分。

求解重积分的过程通常包括以下步骤：确定被积函数、确定积分区域、选择积分顺序、进行积分计算。

2.重积分的换元法重积分的换元法是一种求解重积分的高效方法。

通过引入一个新的变量，将复杂的重积分问题转化为简单的一重积分问题。

换元法的关键在于选择合适的换元函数，使得积分过程变得简洁。

3.重积分的性质重积分具有线性、可交换、满足乘法公式等性质。

这些性质使得重积分在实际计算中具有很好的灵活性，可以简化计算过程。

4.重积分的几何意义重积分在几何上的意义是对一个立体图形的质量进行求解。

具体来说，重积分可以表示为空间曲线长度、曲面面积或体积的函数。

这为求解空间几何问题提供了理论依据。

三、实例解析以一个球体的体积为例，介绍三重积分的计算过程。

设球体的半径为R，球体的密度为ρ。

我们需要求解球体内部某一区域内质量的分布。

1.确定被积函数：球体内部的密度函数，即ρ(x, y, z)。

2.确定积分区域：球体内部，用球坐标系表示为x^2 + y^2 + z^2 <R^2。

3.选择积分顺序：先对z积分，再对y积分，最后对x积分。

4.进行积分计算：利用重积分公式，计算出球体内部的质量分布。

四、总结与拓展本文详细介绍了三重积分的计算方法，包括重积分、换元法等。

通过实际应用场景和实例解析，加深了对三重积分的理解。

在实际问题中，三重积分有着广泛的应用，掌握其计算方法有助于解决诸多实际问题。

) zdz
c
0 zdz dxdy
Dz
dxdy SDz
Dz
a2 (1
z2 c2
)
b2 (1
z2 c2
)
1 abc2.
4
2. 利用柱坐标计算三重积分
就称为点M 的柱坐标. 直角坐标与柱面坐标的关系:
坐标面分别为
圆柱面 半平面 平面
如图所示, 在柱面坐标系中体积元素为
f (x, y, z)dxdydz F (, , z)
z
ln( x x2
2
y
y
2
2
z z2
2
1
1)
d
z
I (x2 y 2 z 2 2 xy 2 yz 2 xz) dv
64 I
(x
y z)2 dv.
2r4 dr 0
5 1
(x y z ) dv 2 2 2
04 sin d
2 d 0
2
2
3. 设 由锥面 和球面 所围成 , 计算 提示: 利用对称性 用球坐标
1
2
(h
2 4
)
d
2
d
0
[(1
4h) ln(1
4h)
4h]
2
0
h
1
2
d
4
1
d
xd x2
yd
z y
2
,
3. 利用球坐标计算三重积分
就称为点M 的球坐标. 直角坐标与球面坐标的关系
坐标面分别为 球面
半平面 锥面
0 r
0 2 0
如图所示, 在球面坐标系中体积元素为
f (x, y, z)dxdydz F (r, ,)

三重积分的计算方法三重积分是多元函数积分的一种，它在物理、工程、数学等领域都有着广泛的应用。

在实际问题中，我们常常需要对三维空间中的函数进行积分，而三重积分就是用来描述这种情况的数学工具。

本文将介绍三重积分的计算方法，帮助读者更好地理解和掌握这一重要的数学工具。

首先，我们来看三重积分的定义。

对于空间中的函数f(x, y, z)，我们可以通过三重积分来求解其体积、质量、质心等物理量。

三重积分的计算方法主要有直角坐标系下的直角坐标法和柱面坐标法、球面坐标法，以及直角坐标系下的三重积分换元法等。

在直角坐标系下，三重积分的计算可以通过将积分区域分割成小立体体积，并对每个小立体体积进行积分来实现。

具体而言，我们可以将积分区域分割成若干个小立体体积，然后对每个小立体体积进行积分，最后将所有小立体体积的积分结果相加，即可得到整个积分区域的积分值。

而在柱面坐标法和球面坐标法中，我们可以通过变量替换的方法将三重积分转化为对应坐标系下的三个变量的积分，从而简化计算。

这种方法在处理对称性较强的积分区域时特别有效，能够大大减少计算量。

此外，三重积分换元法也是计算三重积分的重要方法之一。

当积分区域的形状较为复杂时，我们可以通过变量替换将其转化为一个简单的积分区域，从而简化计算。

这种方法在处理非直角坐标系下的积分问题时特别有用。

总的来说，三重积分的计算方法有很多种，我们可以根据具体情况选择合适的方法来进行计算。

在实际问题中，我们需要根据积分区域的形状、函数的性质等因素来选择合适的计算方法，以便更高效地求解三重积分。

在实际问题中，我们常常需要利用三重积分来求解物理、工程等领域的实际问题。

比如，我们可以利用三重积分来计算物体的质量、质心、重心等物理量，也可以用三重积分来描述电荷分布、密度分布等问题。

因此，掌握三重积分的计算方法对于理解和应用多元函数积分具有重要意义。

综上所述，本文介绍了三重积分的计算方法，包括直角坐标系下的直角坐标法和柱面坐标法、球面坐标法，以及三重积分换元法等。

适用范围：适用于积分区 域复杂的情况
步骤：选择适当的坐标系， 进行坐标变换
优点：简化计算过程，提 高计算效率
奇偶性法
定义：利用奇偶函数的性质简化三重积分的计算 适用范围：被积函数或其变量具有奇偶性时 步骤：判断奇偶性，选择合适的坐标系和积分顺序，简化计算 示例：计算三重积分时，利用奇偶性法可以简化计算过程
添加标题
三重积分的几何意义：三重积分可以理解为三维空间中一个函数与一个封闭曲面所围成 的区域的体积。
添加标题
三重积分的计算方法：三重积分可以通过累次积分的方法计算，即先对一个变量进行积 分，再对另一个变量进行积分，最后对第三个变量进行积分。
添加标题
三重积分的物理应用：三重积分在物理学中有广泛的应用，如计算物体的质量、质心、 转动惯量等物理量。
对于每个微元体，我们可以计算其上的函数值与微元体的体积的乘积，即 微元体的质量。
将所有微元体的质量相加，即可得到整个积分区域上的函数值与体积的乘 积，即三重积分的结果。
利用微元法计算三重积分时，需要注意每个微元体的形状和大小，以及函 数值在微元体上的变化情况。
三重积分的计算技 巧
坐标变换法
定义：将三重积分转化为 容易计算的形式
近似计算法
近似计算法：利用泰勒级数展开或数值积分方法，将三重积分转化为数值计算，适用于复 杂函数或高维空间的积分计算。
坐标变换法：通过坐标变换简化积分计算，适用于某些特殊函数或几何形状的积分计算。
分部积分法：将三重积分转化为多个一元或二元积分的和或差，适用于具有易于计算积分 的部分的三重积分计算。
计算三维物体的体积 计算三维物体的表面积 计算三维物体的质心 计算三维物体的转动惯量
在工程中的应用
计算复杂几何体 的质量、质心和 转动惯量

b
y2 ( x )
z2 ( x , y )
f ( x , y , z )dz .
注意
(1) 平行于 z 轴且穿过闭区域 内部的直线与闭 区域 的边界曲面 S 相交不多于两点情形．
( 2) 若平行于 z 轴且穿过闭区域 内部的直线与 闭区域 的边界曲面 S 相交多于两点时，把 分若干个小区域来讨论 ．


f ( x , y , z )dxdydz 为三次积分，
2 2
其中积分区域 为由曲面 z x 2 y
z 2 x
2
及
所围成的闭区域.
解
z x2 2 y2 由 , 2 z 2 x
得交线投影区域 x y 1,
1 x 1 2 2 故 ： 1 x y 1 x , 2 2 2 x 2y z 2 x
2
2
1 x 1 2 2 故 ： 1 x y 1 x , 2 2 2 x 2y z 2 x
因此， I
1 dx
1
1 x
2 2
1 x
dy
2 x
2
2 2
x 2 y
f ( x , y , z )dz .
例3
计算三重积分 z dxdydz 。
y b
2 2

z c
2 2
1 所成的空间闭区域.
解
: {( x , y , z ) | c z c ,
原式
x a
2 2

y b
2 2
1
z c
z
2 2
}
c
c
z dz dxdy ,

学法教法研究任水平,对公司、对社会也将是一件善事。

一是建立明晰的伦理道德责任。

从目前来看,各种类似“天津港的爆炸案”的案例已经不在少数,每天可能都在上演着,尽管造成这种事故的原因各式各样,有的是自然因素,有的是人为因素,但只要我们细细分析,大多与我们工程师的道德观念崩塌有着或多或少的关系,更有甚者,工程师没有履行职责,尤其是伦理责任没有到位而造成了巨大的损失。

二是建立责任评价和追究机制。

目前,我国的工程师主要是在公司、企业、政府担任一定的职责,在承担责任时往往都是单位,尤其是在追究道德层面的责任,由于责任不清晰,无法认定。

或者根本就没有单独制定这样的评价机制。

对工程师的约束就很少以至于没有,所以,建立公开、公正、公平的工程责任评价和追究机制是非常必要的,从制度机制层面明确工程活动主体的责任,对于社会、对企业或者工程师个人都是大有裨益的。

三是加强伦理教育,提升工程师伦理责任意识。

我们无论大学还是社会,对于工程师的伦理道德教育都不能放松,没有一定的伦理道德教育作为基础,想要工程师们的伦理责任有大幅的提高也是不可能的。

目前,我们的高校在人才培养上,可能注重工程专业技术的培训多,而对于工程师伦理责任的培养却是非常的少,重视程度还不是很够。

所以我们大学应该采取多种措施,加大对工程师伦理道德的培养。

当然,在现实社会中,工程伦理又是实践性和应用性很强的学科,必须结合工程的实际问题,培养出具有生态伦理价值观、思维观和执行力的工程技术人才。

通过以上结合天津港爆炸事件分析,对工程师的伦理责任有了更深层次的认识。

社会的进步和发展离不开工程建设活动,生态文明建设更离不开有效的工程活动,我们的工程师要切实树立增强伦理责任的理念,在工程的设计、施工中既要体现对企业、对公司的经济效益负责,又要体现出对社会、对环境的责任。

参考文献:[1]李世新.谈谈工程伦理学[J].哲学研究,2013(02).[2]张铁山.论阻碍工程师伦理责任发挥的因素及其对策[J].漯河职业技术学院学报,2012(01).[3]何放勋.论工程师的伦理责任[J].湖南工程学院学报,2012(04).[4]胡岩.对工程师伦理责任的探讨[J].中北大学学报(社会科学版),2012(04).三重积分的计算方法张辉李应岐陈春梅(火箭军工程大学理学院陕西西安710025)【摘要】介绍了计算直角坐标下三重积分的六种方法,给出相应的求解思路,并辅以典型例题,旨在使学生对三重积分的计算有更深的理解和掌握。