第三讲-刚体转动
- 格式:pdf
- 大小:877.92 KB
- 文档页数:27


第三讲 质心运动定理与刚体转动定律 2018.10.16多个质点构成的系统,假设系统的质量可以集中于一点,这个点即为质量中心,简称质心。
质心是质点系质量分布的平均位置,与重心不同的是,质心不一定要在有重力场的系统中。
值得注意的是,除非重力场是均匀的,否则同一物质系统的质心与重心通常不在同一假想点上。
一、质心运动定理设系统由n 个质点组成,各质点的质量分别为n m m m ⋅⋅⋅21、,位矢分别是n r r r ⋅⋅⋅21、,则此质点系质心的位置矢量C r 为n n n C m m m r m r m r m r +⋅⋅⋅+++⋅⋅⋅++=212211 因此,质心的加速度 nn n C m m m a m a m a m a +⋅⋅⋅+++⋅⋅⋅++=212211 设第i 个质点所受的外力为i F ,第j 个质点对第i 个质点所受的作用力为)(i j f ji ≠,则对每个质点应用牛顿第二定律有 11131211a m f f f F n =+⋅⋅⋅+++22232122a m f f f F n =+⋅⋅⋅+++••••••将n 个式子相加,并注意到质点间的相互作用力有ij ji f f -=,得n n n a m a m a m F F F +⋅⋅⋅++=+⋅⋅⋅++221121令F 21=+⋅⋅⋅++n F F F ,称为质点系所受到的合外力,m m m m n =+⋅⋅⋅++21,称为质点系的总质量,则C ma =F这表明,质点系所受的合外力等于质点系的总质量与其质心加速度的乘积,这就是质心运动定理。
二、质心运动守恒定理如果作用于质点系的合外力恒等于零,则质心将处于静止或匀速直线运动状态。
如果作用于质点系的所有外力在某轴上投影的代数和恒等于零,则质心在该轴的方向上将处于静止或匀速直线运动状态。
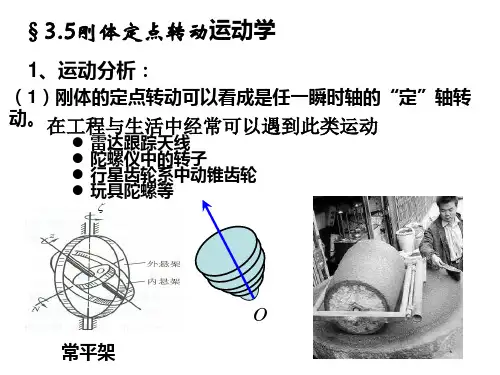
三、刚体的转动定律刚体是指在运动中和受力作用后,形状和大小不变,而且内部各点的相对位置不变的物体,是一种理想模型。

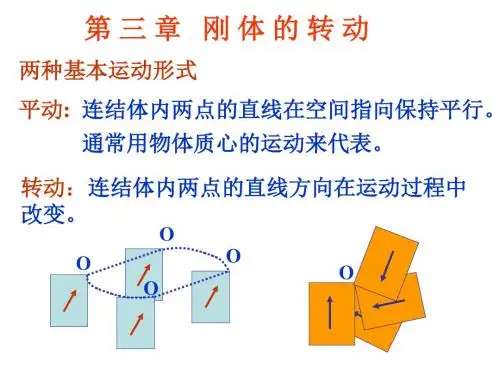

第三章 刚体的转动出发点:牛顿质点运动定律刚体的运动分为:平动,定轴转动,定点转动,平面平行运动,一般运动。
§3-1 刚体的平动,转动和定轴转动一 刚体的定义:在无论多大力作用下物体形状和大小均保持不变。
(理想模型)二 平动:在运动过程中,若刚体上任意一条直线在各个时刻的位置始终彼此平行,则这种运动叫做平动。
特征:1 平动时刚体中各质点的位移,速度,加速度相等。
2 动力学特征:将刚体看成是一个各质点间距离保持不变的质点组。
受力:内力和外力对每一个质元:满足牛顿运动定律+=Mi i 对刚体而言:∑(+fi )=∑Mi i⇒∑+∑=∑Mi i显然∑=0 ⇒∑=∑Mi I=∑Mi故:∑F ==M a即:刚体做平动时,其运动规律和一质点相当,该质点的质量与刚体的质量相等,所受的力等于刚体所受外力的矢量和。
三 转动和定轴转动定轴转动的运动学特征:用角位移、角速度、角加速度加以描述,且刚体中各质点的角位移 、角速度、角加速度相等。
ω=dt d θ, α=dtd ω对匀速、匀变速转动可参阅P210表4-2 角量与线量的关系:v=R ωa t=R αa n=ω2R更一般的形式:角速度矢量的定义:=ωγ⨯ , =dtd 显然,定轴转动的运动学问题与质点的圆周运动相同。
例:一飞轮在时间t 内转过角度θ=t b at 3+-c t 4,式中abc 都是常量。
求它的角加速度。
解: 飞轮上某点的角位置可用θ表示为θ=t b at 3+-c t 4,将此式对t 求导数,即得飞轮角速度的表达式为ω=(dtdt b at 3+-c t 4)=a+3b t 2-4c t 3角加速度是角速度对t 导数,因此得α =dt d ω=d td ( a+3b t 2-4c t 3)=6bt-12c t 2由此可见,飞轮作的是变加速转动。
§3-2 力距 刚体定轴转动定律一 力矩:设在转动平面内,=⨯是矢量,对绕固定轴转动,只有两种可能的方向,用正负即可表示,按代数求和(对多个力)。




第3章 刚体定轴转动和角动量守恒定律在前几章质点运动中,我们忽略了物体自身大小和形状,将物体视为质点,用质点的运动代替了整个物体的运动。
但是在实际物体运动中,不仅物体在大小和形状千差,而且运动又有平动和转动之别。
这时我们需要另一个突出主要特征,忽视其次要因素,既具有大小又具有形状的理想模型——刚体。
在受力的作用时,其形状和体积都不发生任何变化的物体,称做刚体。
本章将介绍刚体所遵从的力学规律,重点讨论刚体的定轴转动这种简单的情况。
由于刚体转动的基本概念和原理与前几章质点运动的基本概念和原理相似,因此我们将刚体转动与质点运动对比学习一会事半功倍。
§3-1 刚体定轴转动1. 刚体运动的形式刚体的运动可以分为平动、转动及平动与转动的叠加。
平动的定义为,在刚体在运动过程中,刚体中任意两点的连线始终平行。
如图5-1所示。
由于平动时刚体内各点的运动情况都是一样的,因此描述刚体平动只需要描写刚体内一点的运动,也就是说刚体的平动只要用其中一个点的运动就可以代表它整体的运动。
转动的定义为,刚体运动时,刚体中所有质点都绕同一条直线作圆周运动,这条直线称为转轴。
转轴可以是固定的,也可以是变化的。
若转轴固定,称为刚体定轴转动。
若转轴不固定,运动比较复杂。
刚体的一般运动可以看作是平动和转动的叠加。
平动在前几章已经研究过,本章我们主要研究定轴转动。
2. 刚体的定轴转动研究刚体绕定轴转动时,选与转轴垂直的圆周轨道所在平面为转动平面。
由于描述各质元运动的角量,如角位移、角速度和角加速度都是一样的,因此描述刚体运动时用角量较为方便。
因为刚体上各质元的半径不同,所以各质元的速度和加速度不相等。
角速度和角加速度一般情况下是矢量,由于刚体定轴转动时角速度和角加速度的方向沿转轴方向,因此可用带有“+、-”的标量表示角速度和角加速度。
这种方法我们并不陌生,质点作直线运动时我们也是用带有“+、-”的标量表示速度和加速度。
角速度的大小为 dtd θω= (3-1) 它的方向规定为沿转轴的方向,其指向由右手螺旋法则确定。
第三章 刚体的转动§3-1刚体运动一、刚体定义:物体内任意二点距离不变的物体称为刚体。
说明:⑴刚体是理想模型⑵刚体模型是为简化问题引进的。
二、刚体运动刚体运动:(1)平动:刚体内任一直线方位不变。
特点:各点运动状态一样,如:a 、v 等都相同,故可用一个点来代表刚体运动。
(2)转动:1)绕点转动2)绕轴转动:刚体中所有点都绕一直线作圆周运动说明:刚体的任何运动都可看作平动与转动的合成。
(如:乒乓球飞行等) 三、定轴转动(本章仅讨论此情况)定义:转轴固定时称为定轴转动。
转动特点:⑴刚体上各点的角位移θ∆相同(如:皮带轮),各点的ω、α相同。
⑵刚体上各点的)(ωr v =、)(2ωr a n =、()αr a t=一般情况下不同。
说明:⑴ω是矢量,方向可由右手螺旋法则确定。
⑵r v ⨯=ω§3-2 力矩 转动定律 转动惯量一、力矩1、外力F在垂直于轴的平面内定义:⑴力矩: F r M⨯= (3-1)⑵力矩 :大小:θsin Fr Fd M ==(θsin r d =,称为力臂);方向:沿(F r⨯)方向,它垂直于r 、F构成的平面即M 与轴平行。
注意:θ是r、F 间夹角。
2、外力F不在垂直于轴的平面内(垂直轴)平行轴)⊥+=F F F(// ∵ //F对转动无贡献∴ 对转动有贡献的仅是⊥F。
F 产生的力矩即⊥F的力矩,故上面的结果仍适用。
说明:F平行轴或经过轴时 0=M 。
二、转动定律0≠M 时,转动状态改变,即0≠α ,那么α与M的关系如何?这就是转动定律的内容。
推导:把刚体看成由许多质点组成的系统,这些质点在垂直于轴的平面内作圆周运动。
考虑第i 个质点: 质量:i m ∆到轴的距离:i r受力:外力:i F;内力:i f(设i F、i f 在垂直于转轴的平面内)在切线方向上由牛顿定律有:αi i t i it it r m a m f F ∆=∆=+ (3-2)即 αθϕi i i i i i r m f F ∆=+sin sin (3-3) (3-3)×i r : αθϕ2sin sin i i i i i i i i r m r f r F ∆=+⇒ (3-4) 每一个质点都有一个这样方程,所有质点对应方程求和之后,有αθϕ⎥⎦⎤⎢⎣⎡∆=+∑∑∑i i i i i i i i i i i r m r f r F 2sin sin (3-5)可证明0sin =∑iii i r F θ合内力矩。