下载文档原格式
统计学习题集答案第六版统计学习题集是一本经典的教材，对于学习统计学的人来说是必不可少的参考资料。
第六版的统计学习题集是该教材的最新版本，它涵盖了统计学的各个方面，从基础的概率论到高级的统计推断，都有详细的习题和解答。
在这篇文章中，我将为大家提供第六版统计学习题集的答案，希望能对大家的学习有所帮助。
首先，我们来看一下第一章的习题答案。
第一章主要介绍了统计学的基本概念和方法。
在习题中，会涉及到一些概率计算和统计推断的基本原理。
对于初学者来说，这些题目可能会有一定的难度。
但是只要掌握了基本的概率和统计知识，就能够轻松解答这些问题。
接下来，我们来看一下第二章的习题答案。
第二章主要介绍了统计学中的数据处理和描述性统计。
在习题中，会涉及到一些数据的整理和统计指标的计算。
对于初学者来说，这些题目可能需要一些实际的数据处理经验。
但是只要掌握了数据处理的基本方法，就能够很好地完成这些题目。
第三章是关于概率分布的习题。
在这一章中，会涉及到一些常见的概率分布，如二项分布、正态分布等。
对于初学者来说，这些题目可能需要一些概率计算的技巧。
但是只要掌握了概率分布的基本原理，就能够很好地解答这些题目。
第四章是关于参数估计的习题。
在这一章中，会涉及到一些参数的估计方法，如最大似然估计、贝叶斯估计等。
对于初学者来说，这些题目可能需要一些统计推断的知识。
但是只要掌握了参数估计的基本原理，就能够很好地解答这些题目。
第五章是关于假设检验的习题。
在这一章中，会涉及到一些假设检验的方法，如单样本t检验、方差分析等。
对于初学者来说，这些题目可能需要一些统计推断的技巧。
但是只要掌握了假设检验的基本原理，就能够很好地解答这些题目。
第六章是关于非参数统计的习题。
在这一章中，会涉及到一些非参数统计的方法，如秩和检验、K-S检验等。
对于初学者来说，这些题目可能需要一些非参数统计的知识。
但是只要掌握了非参数统计的基本原理，就能够很好地解答这些题目。
第七章是关于回归分析的习题。
参数估计试题及答案一、选择题（每题10分）1. 在统计学中，参数估计是指：a) 对总体参数进行估计b) 对样本参数进行估计c) 对总体与样本参数进行估计d) 对无限制的参数进行估计2. 下列哪个方法可以用于参数估计？a) 极大似然估计b) 最小二乘估计c) 贝叶斯估计d) 所有上述方法3. 哪个估计方法被广泛应用于正态分布的参数估计？a) 极大似然估计b) 最小二乘估计c) 方法一与二皆可d) 都不对4. 在参数估计中，抽样误差是指：a) 由于样本选择的随机性引起的误差b) 对总体参数的估计误差c) 由于参数估计方法的限制引起的误差d) 都对5. 当总体方差未知时，参数估计常常采用：a) Z检验b) T检验c) F检验d) 卡方检验二、判断题（每题10分）判断下列陈述的正误，并简要说明理由。
1. 在参数估计中，估计量的无偏性意味着样本均值等于总体均值。
2. 极大似然估计方法只适用于正态分布的参数估计。
3. 参数估计的置信区间给出了总体参数的准确范围。
4. 使用最小二乘法进行参数估计时，要求误差项满足正态分布假设。
5. 参数估计方法的选择应根据研究对象和研究目的来确定。
三、填空题（每题10分）1. 参数估计的基本思想是通过样本信息来推断总体的____________。
2. 参数估计的精度通常通过计算估计值的____________来衡量。
3. 极大似然估计方法的核心思想是选择使得样本观测出现的概率最____________的参数值。
4. 估计量的____________性是指估计值的抽样分布的中心与参数真值之间的偏离程度。
5. 参数估计的优良性包括无偏性、____________和一致性。
答案：一、选择题1. a2. d3. a4. a5. b二、判断题1. 正确。
估计量的无偏性意味着估计值的期望等于总体参数的真值。
2. 错误。
极大似然估计方法不仅限于正态分布，适用于各种分布的参数估计。
3. 错误。
第一章 先验分布与后验分布1.1 解：令120.1,0.2θθ==设A 为从产品中随机取出8个，有2个不合格，则22618()0.10.90.1488P A C θ== 22628()0.20.80.2936P A C θ== 从而有5418.03.02936.07.01488.07.01488.0)()|()()|()()|()|(2211111=⨯+⨯⨯=+=θπθθπθθπθθπA P A P A P A 4582.0)|(1)|(4582.03.02936.07.01488.03.02936.0)()|()()|()()|()|(122211222=-==⨯+⨯⨯=+=A A or A P A P A P A θπθπθπθθπθθπθθπ1.2 解：令121, 1.5λλ==设X 为一卷磁带上的缺陷数，则()XP λ∴3(3)3!e P X λλλ-==R 语言求：)4(/)exp(*)3(^gamma λλ-1122(3)(3)()(3)()0.0998P X P X P X λπλλπλ∴===+== 从而有111222(3)()(3)0.2457(3)(3)()(3)0.7543(3)P X X P X P X X P X λπλπλλπλπλ==========1.3 解：设A 为从产品中随机取出8个，有3个不合格，则3358()(1)P A C θθθ=-（1） 由题意知 ()1,01πθθ=<< 从而有.10,)1(504)|(504)6,4(/1)6,4(1)6,4()1()1()1()1()1()1()1()()|()()|()|(535311614531535315338533810<<-==-=--=--=--==⎰⎰⎰⎰--θθθθπθθθθθθθθθθθθθθθθθθθπθθπθθπA beta B R B d d d C C d A P A P A ：语言求（2）.10,)1(840)|(840)7,4(/1)7,4(1)7,4()1()1()1()1()1()1(2)1()1(2)1()()|()()|()|(636311714631636315338533810<<-==-=--=--=----==⎰⎰⎰⎰--θθθθπθθθθθθθθθθθθθθθθθθθθθπθθπθθπA beta B R B d d d C C d A P A P A ：语言求1.5 解：（1）由已知可得.5.125.11,110110/1)()|()()|()|(,2010,101)(5.125.111)|(2112211)|(12,2121,1)|(5.125.11201011111111<<===<<=<<=+<<-==+<<-=⎰⎰θθθθπθθπθθπθθπθθθθθθθθd d x p x p x x p x p x x x p ，，即，时，当（2）由已知可得.6.115.11,1010110/1)()|,,()()|,,(),,|(,2010,101)(6.115.111)|,,(,219.1121,214.1121,211.1121,217.1121215.11212112211)|,,(9.11,4.11,1.11,7.11,5.11,0.12,6,2,1,2121,1)|,,(6.115.112010621621621621621654321621<<===<<=<<=+<<-+<<-+<<-+<<-+<<-+<<-========+<<-=⎰⎰θθθθπθθπθθπθθπθθθθθθθθθθθθθθθθθθd d x x x p x x x p x x x x x x p x x x p x x x x x x i x x x x p i ，即，，时，当【原答案：由已知可得 ()1,0.50.5P x x θθθ=-<<+1(),102010πθθ=<< 11.611.51()0.0110m x d θ==⎰从而有()()()10,11.511.6()P x x m x θπθπθθ==<< 】1.6 证明：设随机变量()XP λ，λ的先验分布为(,)Ga αβ，其中,αβ为已知，则即得证！),(~),,|()()|,,(),,|(,0,)()(,!!)|,,(121)(121211112111βαλπλλπλλπλλαβλπλλλλβαβλααλλ++∑∑∝•∝>Γ=∑===+--+--=-=-==∏∏n x Ga x x x ex x x p x x x e x e x ex x x p ni i n n x n n ni in x ni i x n ni i ni ii【原答案： (),0!x e P x x λλλλ-=>1(),0()e ααβλβπλλλα--=>Γ 因此 11(1)()()()x x x P x e e e λαβλαβλπλλπλλλλ---+--+∝•∝= 所以 (,1)x Ga x λαβ++】 1.7 解：（1）由题意可知.1},max{,1)/(1)/(122)()|,,()()|,,(),,|(,10,1)(,,2,1,10,22)|,,(121},max{221},max{2121121212112122111<<∝===<<==<<<==⎰⎰∏∏⎰∏∏====θθθθθθθθθθπθθπθθπθθπθθθθn nx x nn x x nni in nni inn n n ni i nni inin x x d d x xd x x x p x x x p x x x n i x xx x x x p n n【原答案：由题意可知 ()1,01πθθ=<< 因此122()12(1)xxm x d x θθ=•=-⎰因此 2()()1(),1()1P x x x x m x x θπθπθθθ==<<- （实质是新解当n=1的情形）】（2） 由题意可知.1},max{,1)/(1)/(13232)()|,,()()|,,(),,|(,10,3)(,,2,1,10,22)|,,(12-21},max{2-22-21},max{2212211212121212122111<<∝=⨯⨯==<<==<<<==⎰⎰∏∏⎰∏∏====θθθθθθθθθθθθπθθπθθπθθθπθθθθn n x x n n x x nni in nni inn n n ni i nni inin x x d d x xd x x x p x x x p x x x n i x xx x x x p n n【原答案：由题意可知 1222()36xm x d x θθθ=•=⎰因此 ()()()1,01()P x x m x θπθπθθ==<<】 1.8 解：设A 为100个产品中3个不合格，则3397100()(1)P A C θθθ=-由题意可知 199(202)()(1),01(200)πθθθθΓ=-≤≤Γ 因此 3971994296()()()(1)(1)(1)A P A πθθπθθθθθθθ∝•∝--=- 由上可知)297,5(~)|(Be A θπ1.9 解：设X 为某集团中人的高度，则2(,5)XN θ∴25(,)10XNθ ∴2(176.53)5()p x θθ--=由题意可知 2(172.72)5.08()θπθ--=又由于X 是θ的充分统计量，从而有()()()()x x p x πθπθθπθ=∝•222(176.53)(172.72)(174.64)55.0821.26eeeθθθ------⨯∝•∝因此 (174.64,1.26)x N θ1.10 证明：设22(,),,N u u θσσ其中为已知又由于X 是θ的充分统计量，从而有()()()()x x p x πθπθθπθ=∝•222222251()()11252()11225252u x x u eeeσθθθσσσ+----+⨯--⨯+⨯∝∝因此 222251(,)112525u x xN σθσσ+++又由于21112525σ≤+ 所以 θ的后验标准差一定小于151.11 解：设X 为某人每天早上在车站等候公共汽车的时间，则(0,)X U θ.8,861)/(1192192)()|,,()()|,,(),,|(,4,192)(.81)|,,(8,8,5.3,2,1,0,1)|,,(768778774321321321433213213321>⨯====≥=>=====<<=⎰⎰⎰∞∞∞θθθθθθθθθθπθθπθθπθθθπθθθθθθd d d x x x p x x x p x x x x x x p x x x i x x x x p i ，时，当【原答案：设X 为某人每天早上在车站等候公共汽车的时间，则(0,)XU θ∴1(),0p x x θθθ=<<当8θ>时，31()p x θθ=43819211()8192m x d θθθ+∞==⎰从而有 7()()3()()128p x x m x θπθπθθ==, 计算错误】1.12 证明：由题意可知 1(),0,1,2,...,i np x x i n θθθ=<<=从而有 ()()()()x x p x πθπθθπθ∝•00111n n n ααααθθθθθ++++∝•∝ 因此 θ的后验分布仍是Pareto 分布。
参数估计习题与习题解答6.11．从一批电子元件中抽取8个进行寿命测试，得到如下数据(单位：h ）:1 050, 1 100， 1 130, 1 040， 1 250， 1 300， 1 200， 1 080试对这批元件的平均寿命以及分布的标准差给出矩估计。
解：样本均值 75.11438108011301101050=++++=x样本标准差 ∑=-=812)(71i i x x s []22)75.11431080()75.11431050(71-++-=0562.96= 因此,元件的平均寿命和寿命分布的标准差的矩估计分别为1143。
75和96.05622． 设总体),0(~θU X ，现从该总体中抽取容量为10的样本，样本值为0。
5,1.3,0。
6，1.7，2.2，1.2，0。
8,1。
5，2.0,1.6试对参数θ给出矩估计.解：由于E(X ）=2θ,即θ=2E(X ),而样本均值106.13.15.0+++=x =1.34，故θ的矩估计为68.22ˆ==x θ3． 设总体分布列如下,n x x ,1是样本，试求未知参数的矩估计.10,,3,2,)1()1()()2(,1,,2,1,0,1)()1(22<<=--==-===-θθθ k k k X P N N k Nk X P k ；（正整数）是未知参数 解：（1) 总体均值E （X )=21110-=-+++N N N ，解之可得N =2E （X )+1故N 的矩估计量12ˆ+=x N，其中x 为样本均值，若x 2不是整数，可取大于x 2的最小整数代替.2x（2) 总体均值E （X )==---+∞=∑222)1()1(k k k k θθ∑+∞=---222)1)(1(k k k k θθ，由于3222)1)(1(θθ=--∑+∞=-k k k k ,故有E(X ）θθθ2232=⨯=,即θ)(2X E =,从而参数的 θ 矩估计为.2ˆx=θ 4．设总体密度函数如下，n x x ,,1 是样本,试求未知参数的矩估计.0,,1),;()4(;0,10,);()3(;0,10,)1();()2(;0,0),(2);()1(12>>=><<=><<+=><<-=---θμθμθθθθθθθθθθθθθμθθx ex p x x x p x x x p x x x p x解：（1) 总体均值E （X ）==-⎰dx x x )(22θθθθθθθ31)(222=-⎰dx x x ，即即)(3X E =θ,故参数θ的矩估计为.3ˆx =θ(2)总体均值E(X ）=dx x x ⎰+1)1(θθ=21++θθ,所以1E(X)E(X)21--=θ，从而参数θ的矩估计.121ˆ--=x xθ （3)由E （X )=dx x x 11-⎰θθ=1+θθ可得2)(1)(⎪⎪⎭⎫ ⎝⎛-=X E X E θ，由此,参数θ的矩估计.1ˆ2⎪⎭⎫⎝⎛-=x x θ(4)先计算总体均值与方差E （X ）=dx ex x θμμθ--∞+⎰1=dt e t tθθ-∞+⎰01+dt e tθμθ-∞+⎰1=μθ+)(2X E =dx ex x θμμθ--∞+⎰12=dt e t tθθμ-∞+⎰+1)(02=dt e ttθθ-∞+⎰12+dt e t tθθμ-∞+⎰012+dt e tθθμ-∞+⎰12=.2222μμθθ++V a r(X )=22))(()(X E X E -=2θ由此可以推出)()(,)(X Var X E X Var -==μθ,从而参数μθ,的矩估计为.ˆ,ˆs x s -==μθ 5．设总体为)1,(μN ，先对该总体观测n 次,发现有k 次观测为正，使用频率替换方法求μ的矩估计。
参数估计习题及答案参数估计在统计学中是一个重要的概念，它涉及到根据样本数据来估计总体参数的过程。
下面，我将提供一些参数估计的习题以及相应的答案，以帮助学生更好地理解这一概念。
习题一：假设有一个班级的学生数学成绩，我们从这个班级中随机抽取了10名学生的成绩，得到样本均值 \(\bar{x} = 85\)，样本标准差 \(s = 10\)。
请估计总体均值 \(\mu\)。
答案：根据样本均值 \(\bar{x}\) 来估计总体均值 \(\mu\)，我们可以使用以下公式：\[ \hat{\mu} = \bar{x} \]因此，\(\hat{\mu} = 85\)。
习题二：在习题一中，如果我们想要估计总体方差 \(\sigma^2\)，我们应该如何操作？答案：总体方差 \(\sigma^2\) 通常使用样本方差 \(s^2\) 来估计，样本方差的计算公式为：\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]其中 \(n\) 是样本大小，\(x_i\) 是第 \(i\) 个观测值。
在这个例子中，\(n = 10\)，\(\bar{x} = 85\)，\(s = 10\)。
因此，我们可以使用以下公式来估计总体方差：\[ \hat{\sigma}^2 = s^2 = \frac{1}{10-1} \times 10^2 = 100 \]习题三：一个工厂生产的产品长度服从正态分布，样本均值为 \(\bar{x} =50\) 厘米，样本标准差为 \(s = 2\) 厘米。
如果我们知道总体均值\(\mu\) 为 \(50\) 厘米，我们如何估计总体标准差 \(\sigma\)？答案：根据已知的样本均值 \(\bar{x}\) 和样本标准差 \(s\)，我们可以使用以下公式来估计总体标准差 \(\sigma\)：\[ \hat{\sigma} = s \]因此，\(\hat{\sigma} = 2\) 厘米。
参数估计习题参考谜底之阿布丰王创作班级：姓名：学号：得分一、单项选择题：1.区间估计标明的是一个( B )（A）绝对可靠的范围（B）可能的范围（C）绝对不成靠的范围（D）不成能的范围2.甲乙是两个无偏估计量,如果甲估计量的方差小于乙估计量的方差,则称（ D ）（A）甲是充沛估计量（B）甲乙一样有效（C）乙比甲有效（D）甲比乙有效3.设总体服从正态分布,方差未知,在样本容量和置信度坚持不变的情形下,根据分歧的样本值获得总体均值的置信区间长度将（ D ）（A）增加（B）不变（C）减少（D）以上都对4.设容量为16人的简单随机样本,平均完成工作时间13分钟,总体服从正态分布且标准差为3分钟.若想对完成工作所需时间构造一个90%置信区间,则（ A ）5． 100(1-α)%是（ C ）6．参数估计的类型有（ D ）（A ）点估计和无偏估计（B ）无偏估计和区间估计（C ）点估计和有效估计（D ）点估计和区间估计7．在其他条件不变的情况下,提高抽样估计的可靠水平,其精度将 （C ）（A ）增加 （B ）不变 （C ）减少 （D ）以上都对 二、计算分析题1、是总体为无偏估计量.解 (I) 因为,所以2(,N nσμ,从而因为所以设总体X ~N （μ,σ2）,X 1,X 1,…,X n 是来自X 的一个样本.试确定常数c .解：由于X 1,X 2, X 3, X 4是来自均值为θ的指数分布总体的样本,其中θ未知,设有估计量（1）指出T 1,T 2, T 3哪几个是θ的无偏估计量； （2）在上述θ的无偏估计中指出哪一个较为有效.解：（1）由于X i 服从均值为θ的指数分布,所以E (X i )= θ, D (X i )= θ 2, i=1,2,3,4 由数学期望的性质2°,3°有即T 1,T 2是θ的无偏估计量（2）由方差的性质2°,3°并注意到X 1,X 2, X 3, X 4自力,知D (T 1)> D (T 2)所以T 2较为有效.4、设年末某储蓄所对某类储蓄存款户账号随机抽取100户的资料如下：（1）根据上述资料,计算这类储蓄账户的平均余额的无偏估计,并计算抽样平均误差；（2）试以95%的概率,估计该储蓄所存款户平均每户的存款余额的置信区间.解： 1.平均余额为：352元.（开口组的组距与相邻组相等）25、松江A、B两所年夜学某学期期末高等数学考试采纳同一套题目,Ａ校认为该校学生高数考试成果比Ｂ校学生成果高10分以上.为了验证这个说法,主管部份从A校随机抽取75人作为样本,测得其分数平均值为78.6分,标准差为8.2分；B校抽取了80个同学作为随机样本,测得分数平均值为73.8分,标准差为7.4分,试在99％的掌控下确定两校平均分之差的置信区间,根据此置信区间主管部份能够获得什么结论？解可以拒绝A校认为成果相差10分的观点.6、（江西财年夜2006研究生入学试题）某厂欲比力两条自动化蕃茄生产线甲和乙的优劣,分别从两条生产线上抽取12和17个样本,测得番茄酱的重量均值分别为10.6克和9.5克,对应的方差分别为2.4和4.7.假设这两条流水线灌装番茄酱的重量都服从正态分布,且方差相等,试计算甲乙均值差的95%的置信区间.（-0.4,2.6）7.随机地取某种炮弹9发做试验,得炮弹口速度的样本标准差为s=11(m/s).设炮口速度服从正态分布.求这种炮弹的炮口速度的标准差σ的置信度为的置信区间.解：σ的置信度为的置信区间为其中α=0.05, n=9查表知8、（英文改编题）为了解鸡肉三明治中脂肪的含量,抽取了20个样本获得的脂肪含量如下（单元：克）（1）计算总体鸡肉三明治中含有脂肪均值的95%置信区间.（2）为了进行（1）中的置信区间估计,还需要什么假设条件？（3）题目样本的数据满足（2）的假设条件吗？请说明理由.解：（1）小样本,总体方差未知,因此用t统计量来做区间估计：（2）假设总体服从正态分布（3）可以通过计算这组数据的峰度和偏度来判断,或者通过JB统计量来检验9、实验题.工厂对某批螺丝钉的长度进行抽检,从中抽出16个螺丝钉作为样本,丈量它们的长度后,并利用EXCEL软件中的“描述统计”获得的分析结果整理如下：平均标准误差中位数众数标准差方差峰度偏度区域最小值(1)请填出表中用序号标出的空格数值(2)请计算该批螺丝钉长度的95%置信区间.(1.0948,1.1177)。
参数估计公式最大似然估计贝叶斯估计矩估计参数估计是统计学中的一个重要问题，它的目标是通过已经观测到的样本数据来估计未知参数的值。
在参数估计中，最大似然估计、贝叶斯估计和矩估计是常用的方法。
下面将分别介绍这三种估计方法及其公式。
一、最大似然估计最大似然估计是一种常用的参数估计方法，它基于样本数据的观测结果，通过寻找参数值使得观测样本出现的概率最大化来估计未知参数的值。
最大似然估计的公式如下所示：$$\hat{\theta}_{MLE} = \arg \max_{\theta} P(X|\theta)$$其中，$\hat{\theta}_{MLE}$表示最大似然估计得到的参数值，$P(X|\theta)$表示给定参数$\theta$下观测样本$X$出现的概率。
二、贝叶斯估计贝叶斯估计是另一种常用的参数估计方法，它基于贝叶斯定理，通过在先验分布和观测数据的基础上更新参数的后验分布来进行参数估计。
贝叶斯估计的公式如下所示：$$P(\theta|X) = \frac{P(X|\theta)P(\theta)}{P(X)}$$其中，$P(\theta|X)$表示给定观测样本$X$后，参数$\theta$的后验分布；$P(X|\theta)$表示给定参数$\theta$下观测样本$X$出现的概率；$P(\theta)$表示参数$\theta$的先验分布；$P(X)$表示观测样本$X$的边缘概率。
三、矩估计矩估计是一种基于样本矩的无偏估计方法，它通过样本矩与理论矩之间的差异来估计未知参数的值。
矩估计的公式如下所示：$$\hat{\theta}_{MME} = g(\overline{X}_n)$$其中，$\hat{\theta}_{MME}$表示矩估计得到的参数值，$g(\cdot)$表示由样本矩计算得到参数的函数，$\overline{X}_n$表示样本的均值。
在实际应用中，最大似然估计常用于样本量较大、参数唯一可估情况下的参数估计；贝叶斯估计常用于样本量较小、先验分布已知情况下的参数估计；矩估计常用于样本量较大、参数个数较多时的参数估计。
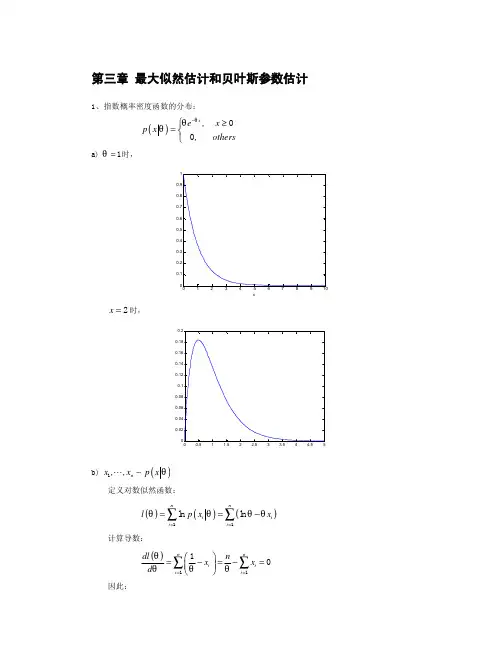
第一章 先验分布与后验分布1.1 解：令120.1,0.2θθ==设A 为从产品中随机取出8个，有2个不合格，则22618()0.10.90.1488P A C θ== 22628()0.20.80.2936P A C θ== 从而有5418.03.02936.07.01488.07.01488.0)()|()()|()()|()|(2211111=⨯+⨯⨯=+=θπθθπθθπθθπA P A P A P A 4582.0)|(1)|(4582.03.02936.07.01488.03.02936.0)()|()()|()()|()|(122211222=-==⨯+⨯⨯=+=A A or A P A P A P A θπθπθπθθπθθπθθπ1.2 解：令121, 1.5λλ==设X 为一卷磁带上的缺陷数，则()XP λ∴3(3)3!e P X λλλ-==R 语言求：)4(/)exp(*)3(^gamma λλ-1122(3)(3)()(3)()0.0998P X P X P X λπλλπλ∴===+== 从而有111222(3)()(3)0.2457(3)(3)()(3)0.7543(3)P X X P X P X X P X λπλπλλπλπλ==========1.3 解：设A 为从产品中随机取出8个，有3个不合格，则3358()(1)P A C θθθ=-（1） 由题意知 ()1,01πθθ=<< 从而有.10,)1(504)|(504)6,4(/1)6,4(1)6,4()1()1()1()1()1()1()1()()|()()|()|(535311614531535315338533810<<-==-=--=--=--==⎰⎰⎰⎰--θθθθπθθθθθθθθθθθθθθθθθθθπθθπθθπA beta B R B d d d C C d A P A P A ：语言求（2）.10,)1(840)|(840)7,4(/1)7,4(1)7,4()1()1()1()1()1()1(2)1()1(2)1()()|()()|()|(636311714631636315338533810<<-==-=--=--=----==⎰⎰⎰⎰--θθθθπθθθθθθθθθθθθθθθθθθθθθπθθπθθπA beta B R B d d d C C d A P A P A ：语言求1.5 解：（1）由已知可得.5.125.11,110110/1)()|()()|()|(,2010,101)(5.125.111)|(2112211)|(12,2121,1)|(5.125.11201011111111<<===<<=<<=+<<-==+<<-=⎰⎰θθθθπθθπθθπθθπθθθθθθθθd d x p x p x x p x p x x x p ，，即，时，当（2）由已知可得.6.115.11,1010110/1)()|,,()()|,,(),,|(,2010,101)(6.115.111)|,,(,219.1121,214.1121,211.1121,217.1121215.11212112211)|,,(9.11,4.11,1.11,7.11,5.11,0.12,6,2,1,2121,1)|,,(6.115.112010621621621621621654321621<<===<<=<<=+<<-+<<-+<<-+<<-+<<-+<<-========+<<-=⎰⎰θθθθπθθπθθπθθπθθθθθθθθθθθθθθθθθθd d x x x p x x x p x x x x x x p x x x p x x x x x x i x x x x p i ，即，，时，当【原答案：由已知可得 ()1,0.50.5P x x θθθ=-<<+1(),102010πθθ=<< 11.611.51()0.0110m x d θ==⎰从而有()()()10,11.511.6()P x x m x θπθπθθ==<< 】1.6 证明：设随机变量()XP λ，λ的先验分布为(,)Ga αβ，其中,αβ为已知，则即得证！),(~),,|()()|,,(),,|(,0,)()(,!!)|,,(121)(121211112111βαλπλλπλλπλλαβλπλλλλβαβλααλλ++∑∑∝•∝>Γ=∑===+--+--=-=-==∏∏n x Ga x x x ex x x p x x x e x e x ex x x p ni i n n x n n ni in x ni i x n ni i ni ii【原答案： (),0!x e P x x λλλλ-=>1(),0()e ααβλβπλλλα--=>Γ 因此 11(1)()()()x x x P x e e e λαβλαβλπλλπλλλλ---+--+∝•∝= 所以 (,1)x Ga x λαβ++】 1.7 解：（1）由题意可知.1},max{,1)/(1)/(122)()|,,()()|,,(),,|(,10,1)(,,2,1,10,22)|,,(121},max{221},max{2121121212112122111<<∝===<<==<<<==⎰⎰∏∏⎰∏∏====θθθθθθθθθθπθθπθθπθθπθθθθn nx x nn x x nni in nni inn n n ni i nni inin x x d d x xd x x x p x x x p x x x n i x xx x x x p n n【原答案：由题意可知 ()1,01πθθ=<< 因此122()12(1)xxm x d x θθ=•=-⎰因此 2()()1(),1()1P x x x x m x x θπθπθθθ==<<- （实质是新解当n=1的情形）】（2） 由题意可知.1},max{,1)/(1)/(13232)()|,,()()|,,(),,|(,10,3)(,,2,1,10,22)|,,(12-21},max{2-22-21},max{2212211212121212122111<<∝=⨯⨯==<<==<<<==⎰⎰∏∏⎰∏∏====θθθθθθθθθθθθπθθπθθπθθθπθθθθn n x x n n x x nni in nni inn n n ni i nni inin x x d d x xd x x x p x x x p x x x n i x xx x x x p n n【原答案：由题意可知 1222()36xm x d x θθθ=•=⎰因此 ()()()1,01()P x x m x θπθπθθ==<<】 1.8 解：设A 为100个产品中3个不合格，则3397100()(1)P A C θθθ=-由题意可知 199(202)()(1),01(200)πθθθθΓ=-≤≤Γ 因此 3971994296()()()(1)(1)(1)A P A πθθπθθθθθθθ∝•∝--=- 由上可知)297,5(~)|(Be A θπ1.9 解：设X 为某集团中人的高度，则2(,5)XN θ∴25(,)10XNθ ∴2(176.53)5()p x θθ--=由题意可知 2(172.72)5.08()θπθ--=又由于X 是θ的充分统计量，从而有()()()()x x p x πθπθθπθ=∝•222(176.53)(172.72)(174.64)55.0821.26eeeθθθ------⨯∝•∝因此 (174.64,1.26)x N θ1.10 证明：设22(,),,N u u θσσ其中为已知又由于X 是θ的充分统计量，从而有()()()()x x p x πθπθθπθ=∝•222222251()()11252()11225252u x x u eeeσθθθσσσ+----+⨯--⨯+⨯∝∝因此 222251(,)112525u x xN σθσσ+++又由于21112525σ≤+ 所以 θ的后验标准差一定小于151.11 解：设X 为某人每天早上在车站等候公共汽车的时间，则(0,)X U θ.8,861)/(1192192)()|,,()()|,,(),,|(,4,192)(.81)|,,(8,8,5.3,2,1,0,1)|,,(768778774321321321433213213321>⨯====≥=>=====<<=⎰⎰⎰∞∞∞θθθθθθθθθθπθθπθθπθθθπθθθθθθd d d x x x p x x x p x x x x x x p x x x i x x x x p i ，时，当【原答案：设X 为某人每天早上在车站等候公共汽车的时间，则(0,)XU θ∴1(),0p x x θθθ=<<当8θ>时，31()p x θθ=43819211()8192m x d θθθ+∞==⎰从而有 7()()3()()128p x x m x θπθπθθ==, 计算错误】1.12 证明：由题意可知 1(),0,1,2,...,i np x x i n θθθ=<<=从而有 ()()()()x x p x πθπθθπθ∝•00111n n n ααααθθθθθ++++∝•∝ 因此 θ的后验分布仍是Pareto 分布。
