感知高考刺金1

感知高考刺金336已知22252259x x a x a x c x x ++≤++≤++对任意x ∈R 恒成立，则a c += ．解：用两边夹逼的方法，令225259x x x x ++=++，解得2x =-故7447a a c ≤-+≤，即7c =所以()()22252712120x x ax ax a x a x ++≤++⇒-+-+≥对任意x ∈R 恒成立，所以 ()()()221013221810230a a a a a a ->>⎧⎧⎪⎪⇒⇒=⎨⎨∆=---≤-≤⎪⎪⎩⎩ 故172a c += 点评：这又是夹逼形式的好题，解法中让不等号两边同时取到，求出临界点的方法要注意.感知高考刺金337已知非零向量a 与向量 b 的夹角为钝角，2b =，当2t =-时，()b ta t -∈R 取最小值65，则()a b a -= ．解法一：由当2t =-时，()b ta t -∈R 取最小值65，可知本题是“神图”的应用，如图所示，设,a b θ=，则()635sin 25πθ-== 即4cos 5θ=- ()221425a b b a =--= 故()24825a b a a b a -=-=- 解法二：22222b ta b a bt a t -=-+当且仅当22a bt a ==-时，222364425b ta b a b a -=++= 所以22a b a =-且3644225a b a b +-=，得232225a b a =-=- 故()24825a b a a b a -=-=-感知高考刺金338已知椭圆()2211221110,0x y a b a b +=>>和双曲线()2222222210,0x y a b a b -=>>有相同的焦点，且椭圆与双曲线在第一象限的交点为P ，若2222OF OP OF =，则双曲线的离心率的取值范围是 ． 解：222222222cos ,OF OP OF OF OP OF OP OF =⇒= 2222222P P OF c x OF x a =⇒==> 故2222c e a =>感知高考刺金339已知函数()12x f x e x -=+-，()23g x x ax a =--+，若存在实数12,x x 使得()()120f x g x ==，且121x x -≤，则实数a 的取值范围是 ． 解：因为()f x 是增函数，且()10f =，故11x =，所以原条件等价于230x ax a --+=在区间[]0,2上有解，即231x a x +=+在[]0,2上有解 因为[]412,0,21y x x x =++-∈+的值域为[]2,3，所以实数a 的取值范围是[]2,3感知高考刺金340在ABC ∆中，1tan 3A =，4B π=，若椭圆E 以AB 为长轴，且过点C ，则椭圆E 的离心率是 ．解：如图，作CD AB ⊥于D ，则3t a n CD AD CD A==，BD CD =设()2,0B ，则44AB AD BD CD ==+=， 所以1OD CD ==，所以()1,1C设椭圆的方程为22221x y a b+=，将2a =与()1,1C 代入可得24b=，28 3c=故e=。

感知高考刺金711．设实数a 使得不等式2232x a x a a -+-≥对任意实数x 恒成立，则满足条件a 组成的集合是 。

解法一：设()232f x x a x a =-+-当0a ≥时，()53,22,23253,3a x a x a a f x x a x a x a x ⎧-+≤⎪⎪⎪=-+<≤⎨⎪⎪->⎪⎩所以()min 233a a f x f ⎛⎫== ⎪⎝⎭ 所以23a a ≤，解得103a ≤≤ 当0a <时，()253,32,3253,2a x a x a a f x x a x a x a x ⎧-+≤⎪⎪⎪=-<≤⎨⎪⎪->⎪⎩ 所以()min 233a a f x f ⎛⎫==- ⎪⎝⎭所以23a a ≤-，解得103a -≤< 综上，1133a -≤≤ 解法二：由齐次化思想，令()x at t =∈R ，则原不等式为22132a t a t a -+-≥ 转化为2132a t t ≤-+-对任意t ∈R 恒成立 易得()min121323t t -+-= 所以13a ≤，解得1133a -≤≤ 2．将号码为1,2,,9的九个小球放入一个袋中，这些小球仅号码不同，其余完全相同。

甲从袋中摸出一个球，其号码为a ，放回后，乙从此袋中再摸出一个球，其号码为b ，则使不等式2100a b -+>成立的事件发生的概率为 ．解：210b a <+列举法：1,2,3,4,5b =，1,2,,9a =，共45种6b =，3,4,,9a =，共7种7b =，5,,9a =，共5种8b =，7,8,9a =，共3种9b =，9a =，共1种 所以457531619981P ++++==⋅ 感知高考刺金721．双曲线22221x y a b-=的左右焦点分别为12,F F ，过1F 作圆222x y a +=的切线分别交双曲线的左、右支于,B C ，且2BC CF =，则双曲线的渐近线方程为 ．解：结合图形可得2224416cos 8b a c a c acα+-== 所以2232b c a c ac-= 即220b b a a ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭解得1b a所以渐近线方程为)1y x =± 2．将两个a 和两个b 共四个字母填入方格表的9个小方格中，每个小方格内至多填入1个字母，若使相同字母既不同行也不同列，则不同的填法共有 种．解：法一：使2个a 不同行不同列的填法有223318C A =（或94182⋅=）种 使2个b 不同行不同列的填法也18种其中不符合要求的有（1）2个a 方格中都填入b 有18种（2）2个a 方格中仅有1个填入b 有1294108C A =种 故共有21818108198--=种法二：先a 后b ，填a 有18种填法填b （两个b 记为12,b b ）分3种情况：（1）1b 所在行、列中不含a ，此时有1212C ⋅=（2）1b 所在行、列中含1个a ，此时有114312C C ⋅=（3）1b 所在行、列中含2个a ，此时有11248C C ⋅=所以在a 确定的情况下，b 的填法有2128112++=种 所以共有1811198⋅=种 感知高考刺金731．已知,a b 满足6a =，1b ≤，且932a b -≤，则a b 的取值范围是 ． 解：933232a ab b -≤⇒-≤，又1b ≤ 所以b OB =的终点B 既在圆22:1O x y +=内（含边界），又在圆()229:24C x y -+=内（含边界）， 6cos a b b θ=，所以转化为求OB 在a 方向上的投影的大小 由图可知1cos ,12b θ⎡⎤∈⎢⎥⎣⎦所以[]3,6a b ∈2．某人有5把钥匙，其中有1把是办公室的钥匙，但他忘了是哪一把，于是他便将5把钥匙逐一不重复试开，则恰好第三次打开抽屉的概率是 ．解：既可以445515A A =，也可以243515A A = 评注：这题其实说明了买彩票不分先后，抽签不分先后。

感知高考刺金391题在平面直角坐标系xOy 中，,A B 为x 轴正半轴上两个动点，点P （异于原点）为y 轴上的定点，若以AB 为直径的圆与圆()2221x y +-=相外切，且APB ∠的大小为定值，则线段OP 的长为 ．解：设以AB 为直径的圆的圆心为(),0t ，半径为r则()(),0,,0A t r B t r -+1r + 而tan t r OPB OP +∠=，tan t r OPA OP-∠= ()222222tan tan 231t r t r r OP r OP OP OP APB OPB OPA t r t r OP t r OP r OP OP+--⋅⋅∠=∠-∠===+-+-+-+⋅ 因为APB ∠的大小为定值，故上式与r无关，则OP =tan APB ∠ 点评：这又是一个山高模型的好题。

感知高考刺金392题已知()()2131124f x ax x t x t =---≤≤+，若()()max min 14f x f x -≥对任意t ∈R 恒成立，则实数a 的取值范围是 ．解：()21324f x ax x =--与2y ax =的图象完全“全等”，即可以通过平移完全重合。

因为11t x t -≤≤+且t ∈R ，即用一个区间宽度为2的任意区间去截取函数图象，使得图象的最高点与最低点间的纵坐标之差大于14因此取纵坐标之差最小的状态为()()211f x ax x =-≤≤，此时()()max min 104f x f x a -=-≥ 故14a ≥ 点评：本题是考查了二次函数的本质，要充分理解“a 管开口”这句话的真正含义，不仅只管抛物线开口方向，还决定了开口的大小程度。

同类型关于“一只碗”的题还有很多，大家要注意，掌握好了，在选择填空题中可以秒杀。

但大题要注意书写，至少说清楚每个步骤后面的奥秘。

感知高考刺金393题已知点()3,4P 和圆()22:24C x y -+=，,A B 是圆C 上两个动点，且AB =，则()O P O A O B +（O 为坐标原点）的取值范围是 ．解：取AB 的中点为(),D x y ，则弦心距1CD ==，所以点D 的运动轨迹为()2221x y -+=，()268OP OA OB OP OD x y +==+由()2221cos 2,sin x y x y θθ-+=⇒=+=所以()()[]686cos 8sin 1210sin 122,22OP OA OB x y θθθϕ+=+=++=++∈点评：圆的问题，弦心距是必添的辅助线，千万不能忘记。

感知高考刺金题
在中，若，则的最小值为．
解：常规思路“切化弦”
感知高考刺金题
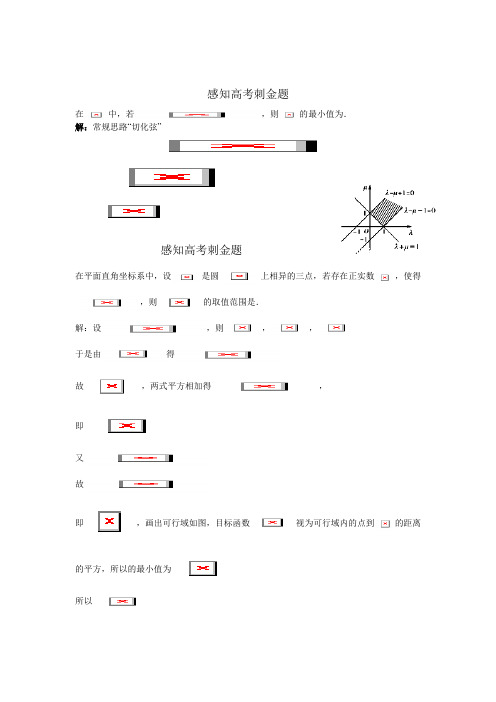
在平面直角坐标系中，设是圆上相异的三点，若存在正实数，使得
，则的取值范围是．
解：设，则，，
于是由得
故，两式平方相加得，
即
又
故
即，画出可行域如图，目标函数视为可行域内的点到的距离的平方，所以的最小值为
所以
感知高考刺金题
若对于满足的一切实数，不等式恒成立，则的取值范围为．
解：原不等式化为，∵，
∴或，
∴或
点评：本题常规的解法应该是将视为主元，将视为系数去解，但这个关于的不等式是三次不等式，不好处理，所以本题的解法是将不等式因式分解后先化简，在转为恒成立问题。

这个题目的解法也可以处理浙江省年高考题。

设，若时，均有，则．
本题有很多解法前面已经介绍过，这里用本题采用的方法再来处理一次。

解：将视为关于的二次不等式，即整理为
因为，故，
当
当时，，则，所以
即，即
当时，，则，所以
即，即
综上，
感知高考刺金题
如图，在平面直角坐标系中，椭圆被围于由条直线，所围成的。

感知高考刺金361题设x ∈R ,[]x 表示不超过x 的最大整数. 若存在实数t ,使得[]1t =,22t ⎡⎤=⎣⎦,…,n t n ⎡⎤=⎣⎦同时．．成立．．,则正整数n 的最大值是 ． 解：由[]1t =得12t ≤<由22t ⎡⎤=⎣⎦得223t ≤< 由44t ⎡⎤=⎣⎦得445t ≤<,所以22t ≤由33t ⎡⎤=⎣⎦得334t ≤<,所以56t ≤<由55t ⎡⎤=⎣⎦得556t ≤<与56t ≤<,故正整数n 的最大值是4感知高考刺金362题过点()1,1M -的直线l 交圆()22:11C x y -+=于点,A B ,O 为坐标原点,若在线段AB 上的Q 满足112MA MB MQ+=,则min OQ = ． 解：设()11,A x y ,()22,B x y ,(),Q m n ,直线():11l y k x =++则11MA +,21MB +,1MQ =+ 由112MA MB MQ+=得12112111x x m +=+++ 由()()221111x y y k x ⎧-+=⎪⎨=++⎪⎩得()()()2222122210k x k k x k +++-++= 所以21222221k k x x k +-+=-+,()212211k x x k +=-+ 所以421k m =-+ 所以()42111n m m ⎛⎫=-++ ⎪+⎝⎭整理得点(),Q m n 满足的轨迹方程为210m n --=所以min OQ感知高考刺金363题如图,已知点D 为ABC ∆的边BC 上一点,3BD DC =,()*n E n ∈N 为AC 边上一列点,满足()11324n n n n n E A a E B a E D +=-+,其中数列{}n a 满足0n a >,11a =,则{}n a 的通项公式为 ．解：由3BD DC =可得1344n n n E D E B E C =+ 又()11324n n n n n E A a E B a E D +=-+,且n n E C E A λ= 故()113132444n n n n n n E D E B a E B a E D λ+⎡⎤=+-+⎢⎥⎣⎦即()13131324164n n n n a E B a E D λλ+⎛⎫⎡⎤+=++ ⎪⎢⎥⎣⎦⎝⎭ 因为,n n E B E D 不共线,故()1310416313204n n a a λλ+⎧+=⎪⎪⎨⎪++=⎪⎩,两式相除消去λ得132n n a a +=+,又11a =,所以1231n n a -=⋅-感知高考刺金364题若点A 在圆C :22(1)(2)4x y -++=上运动,点B 在y 轴上运动,则对定点(3,2)P 而言,||PA PB +的最小值为 ．解法1：设11(,)A x y ,2(0,)B y ,则112(6,4)PA PB x y y +=-+-.若设||r PA PB =+,则由题意可得222112(6)(4)x y y r -++-=.即,点A 在以2(6,4)D y -为圆心,以r 为半径的圆D :2222(6)(4)x y y r -++-=上. 由圆C 与圆D 有公共点A可得2||5r CD +≥=≥,从而3r ≥.解法2：设11(,)A x y ,2(0,)B y ,则112(6,4)PA PB x y y +=-+-.从而,1||(63PA PB x x +=≥=-≥.解法3：由点A 在圆C 上可设(12cos ,22sin )A θθ+-+,(0,)B t ,则(2cos 5,2sin 6)PA PB t θθ+=-+-.故||(2cos 52cos 3PA PB θ+=≥=-≥. 解法4：设Q 为AB 的中点,则2PA PB PQ +=,过,,P Q A 作y 轴的垂线,垂足分别为',','P Q A .由于13|'||||'||||'|||22PP PQ QQ PQ AA PQ ≤+=+≤+, 因此33|||'|22PQ PP ≥-=,即||2||3PA PB PQ +=≥. 解法5：设'B 为点B 关于点P 的对称点,则|||'||'|PA PB PA PB B A +=-=.由于点'B 在直线6x =上,点A 在圆C :22(1)(2)4x y -++=上可得|'|523B A ≥-=.解法6：同解法5,设'A 为点A 关于点P 的对称点,则|||'||'|PA PB PB PA A B +=-=.由于点'A 在圆'C :22(5)(6)4x y -+-=上,点B 在y 轴上可得|'|523A B ≥-=感知高考刺金365题设实数,x y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩,则112u x y =+的取值范围为 ． 解：可行域如图所示,()1,2A ,()4,2B ,()3,1C ,所以14,12x y ≤≤≤≤设点(),P x y 是可行域内一动点, 目标函数112u x y=+既是关于x 的减函数,又是关于y 的减函数 所以当点P 与点C 重合时,此时x 取得最大值4,同时y 取得最大值2,此时u 取得最小值为1114222+=⋅ 对于每一个固定的y 的值,要使u 取得最大值,应使x 取得最小值,即点P 应位于线段AB 上,此时()5212x y y =-≤≤()()111152522252u y x y y y y y =+=+=--()12y ≤≤ 所以()max 54u y =,此时()1,2P 与点A 重合 综上所述,1524u ≤≤。

感知高考刺金1211．在ABC ∆中，若()4AB AC CB -⊥，则sin A 的最大值为。

解：()()()2204445AB AC CB AB ACCA AB AB AC AB AC =-=-+=+-()2245cos 45cos 45cos AB AC AB AC A AB AC AB AC A AB AC A =+-≥-=-即4cos 5A ≥，则3sin 5A ≤ 2．现有4人去旅游，旅游地点有A 、B 两个地方可以选择。

但4人都不知道去哪里玩，于是决定通过掷一枚质地均匀的骰子决定自己去哪里玩，掷出能被3整除的数时去A 地，掷出其他的则去B 地；（1）求这4个人中恰好有1个人去B 地的概率；（2）求这4个人中去A 地的人数大于去B 地的人数的概率。

解：依题意，这4个人中，每个人去A 地旅游的概率为13，去B 地的人数的概率为23设“这4个人中恰有k 人去A 地旅游”为事件()0,1,2,3,4i A i =∴()441233i ii i P A C -⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭（1）这4个人中恰有1人去A 地游戏的概率为()1311412323381P A C ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭（2）设“这4个人中去A 地的人数大于去B 地的人数”为事件B ，则34B A A =，314034441212133339P C C ⎛⎫⎛⎫⎛⎫⎛⎫=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭感知高考刺金1221．已知{}1234,,,A x x x x =，()212sin 14x B x R x π+⎧⎫=∈-=⎨⎬⎩⎭，且1234x x x x +++的最小值为。

解：sin4xy π=的周期为8，图象关于点()12,0中心对称，()1212y x =-图象也关于点()12,0中心对称，故要1234x x x x +++最小，在y 轴右侧最靠近y 轴的四个点123441248x x x x +++=⨯=2．将3个不相同的黑球和3个相同白球自左向右排成一排，如果满足：从任何一个位置（含这个位置）开始向右数，数到最末一个球，黑球的个数大于或等于白球的个数，就称这种排列为“有效排列”，则出现有效排列的概率为。

感知高考刺金221题已知以4T =为周期的函数())()11213x y f x x x ⎧≤⎪==⎨--<≤⎪⎩，其中0m >，若()3f x x =恰有5个实数解，则m 的取值范围是．解：当[]1,1x ∈-时，原函数式化为方程()22211y x y m +=≥，表示一个半椭圆，当[]1,3x ∈时，是两线段()112y x x =-<≤和()323y x x =-<≤组成的折线，再根据周期性画出大致图象如图所示。

由图象可知，当直线3x y =与第二个半椭圆()()222410y x y m-+=≥相交，而与第三个半椭圆()()222810y x y m -+=≥无交点时，方程()3f x x =恰有5个实数解，由方程组()()2223041x y y y x m ⎧=⎪⎪≥⎨⎪-+=⎪⎩消去y 得()22229172350m xm x m +-+=由0∆>，解得m >由方程组()()2223081x y y y x m ⎧=⎪⎪≥⎨⎪-+=⎪⎩消去y 得()2222911445670m x m x m +-+= 由0∆<，解得0m <m <<感知高考刺金222题（2015重庆理科第16题）若函数()12f x x x a =++-的最小值为5，则a = ________． 解法一：按照1,1a a <-≥-两类分类讨论，画出()12f x x x a =++-的折线图，图象最低点的纵坐标为5，求得6a =-或4a =解法二：由题意得125x x a ++-≥，从而1522x x a +-≥-设()()15,22x g x x a h x +=-=-()g x x a =-的图象是以(),0a 为顶点的开口向上的“V ”形图。

()1522x h x +=-的图象是以51,2⎛⎫- ⎪⎝⎭为顶点的开口向下（开口比()g x x a =-的图象开口大）的“V ”形图，且与x 轴交点的坐标为()()6,0,4,0-。

感知高考刺金336已知22252259x x a x a x c x x ++≤++≤++对任意x ∈R 恒成立,则a c += ．解：用两边夹逼的方法,令225259x x x x ++=++,解得2x =-故7447a a c ≤-+≤,即7c =所以()()22252712120x x ax ax a x a x ++≤++⇒-+-+≥对任意x ∈R 恒成立,所以 ()()()221013221810230a a a a a a ->>⎧⎧⎪⎪⇒⇒=⎨⎨∆=---≤-≤⎪⎪⎩⎩ 故172a c += 点评：这又是夹逼形式的好题,解法中让不等号两边同时取到,求出临界点的方法要注意。

感知高考刺金337已知非零向量a 与向量 b 的夹角为钝角,2b =,当2t =-时,()b ta t -∈R 取最小值65,则()a b a -= ．解法一：由当2t =-时,()b ta t -∈R 取最小值65,可知本题是“神图”的应用,如图所示,设,a b θ=,则()635sin 25πθ-== 即4cos 5θ=- ()221425a b b a =--= 故()24825a b a a b a -=-=- 解法二：22222b ta b a bt a t -=-+当且仅当22a bt a ==-时,222364425b ta b a b a -=++= 所以22a b a =-且3644225a b a b +-=,得232225a b a =-=- 故()24825a b a a b a -=-=-感知高考刺金338已知椭圆()2211221110,0x y a b a b +=>>和双曲线()2222222210,0x y a b a b -=>>有相同的焦点,且椭圆与双曲线在第一象限的交点为P ,若2222OF OP OF =,则双曲线的离心率的取值范围是 ． 解：222222222cos ,OF OP OF OF OP OF OP OF =⇒= 2222222P P OF c x OF x a =⇒==> 故2222c e a =>感知高考刺金339已知函数()12x f x e x -=+-,()23g x x ax a =--+,若存在实数12,x x 使得()()120f x g x ==,且121x x -≤,则实数a 的取值范围是 ． 解：因为()f x 是增函数,且()10f =,故11x =,所以原条件等价于230x ax a --+=在区间[]0,2上有解,即231x a x +=+在[]0,2上有解因为[]412,0,21y x x x =++-∈+的值域为[]2,3,所以实数a 的取值范围是[]2,3感知高考刺金340在ABC ∆中,1tan 3A =,4B π=,若椭圆E 以AB 为长轴,且过点C ,则椭圆E 的离心率是 ．解：如图,作CD AB ⊥于D ,则3tan CD AD CD A==,BD CD =设()2,0B ,则44AB AD BD CD ==+=, 所以1OD CD ==,所以()1,1C设椭圆的方程为22221x y a b+=,将2a =与()1,1C 代入可得24b=,28 3c=故e=。

感知高考刺金281题设对任意实数0x >，0y >．若不等式(2)x a x y ≤+恒成立，则实数a 的最小值为 ．解法一：1a x ≥=+t =，则()2112t g t t +=+ 令1t m +=，则()()2211423128412124t m g t t m m m+===≤==++-+- 故a解法二：待定系数法1111222k x x x kx y x y k k ⎛⎫⎛⎫=++=++ ⎪ ⎪⎝⎭⎝⎭与题中所给不等式(2)x a x y ≤+相比对，待定系数可得11:1:222k k⎛⎫+= ⎪⎝⎭解得k =()2x x y +⎝⎭故a感知高考刺金282题已知P 是双曲线221168x y -=右支上一点，12,F F 分别是双曲线的左、右焦点，O 为坐标原点，()10F P PM λλ=>，22PF PM PN PM PF μ⎛⎫ ⎪=+ ⎪⎝⎭， 20PN F N =．若22PF =，则ON = ．解：由22PF PM PN PM PF μ⎛⎫ ⎪=+ ⎪⎝⎭知PN 是2MPF ∠的角平分线 又20PN F N =，故延长2F N 交PM 于K ，则的角平分线又是高线，故2PF K ∆是等腰三角形，22PK PF ==因为22PF =，故110PF =，故112F K =注意到N 还是2F K 的中点，所以ON 是12F F K ∆的中位线，所以1162ON F K ==感知高考刺金283题设12a =，121n n a a +=+，21,*1nn n a b n a +=-∈-N ，则2015b = ． 解：这种特殊的递推关系，一旦没有思路，先做几项找找规律就是最好的办法。

算出123262,,,35a a a ===，1233,7,15,b b b ===找规律发现234123321,721,1521,b b b ==-==-==- 所以严格证明时就能想到办法，去证211n n n a b a ++=-是等比数列 111221221111212211n n n n n n n n n n a a a a b b a a a a ++++++--++===+++--，故12n n b +=，得21n n b =-，2015201521b =-点评：一般数列题中不常见的特殊递推关系或这为了应景而求有2015这样大数据出现时，题目往往有规律，例如周期数列或者能观察猜测出数列通项。

感知高考刺金231题设数列{}n a 满足121,2a a ==,且121max ,44n n n a a a ++⎧⎫⎨⎬⎩⎭=,则2015a = ． 解：找规律。

易知31ma x 2,14412a ⎧⎫⎨⎬⎩⎭==⨯,411max ,1244216a ⎧⎫⎨⎬⎩⎭==⨯,511max ,1164842a ⎧⎫⎨⎬⎩⎭==⨯,611max ,841416a ⎧⎫⎨⎬⎩⎭==⨯,71max 1,42148a ⎧⎫⎨⎬⎩⎭==⨯,……, 故数列{}n a 是周期为5的数列,所以2015518a a ==感知高考刺金232题设数列{}n a 满足191,7a a ==,且211221n n n n n a a a a a +++-+=+,则5a = ． 解：()()2221111211121111n n n n n n n n n n a a a a a a a a a a ++++++--+-+===-+++ 即()212111n n n a a a ++++=+令1n n b a =+,则221n n n b b b ++=,即数列{}n b 是等比数列,且192,8b b ==,故54b =,即53a =感知高考刺金233题 已知113k ≤<,函数()21x f x k =--的零点分别为()1212,x x x x <,函数()2121x k g x k =--+的零点分别为()3434,x x x x <,则()()4321x x x x -+-的最小值为 ． 解：()()()12122221021,21log 1,log 1x x x f x k k k x k x k =--=⇒=-=+⇒=-=+ ()3432421311312102,2log ,log 2121212121x x x k k k k k g x x x k k k k k ++++=--=⇒==⇒==+++++由（1）（2）得()()432122314log log 311k x x x x k k +⎛⎫-+-==- ⎪--⎝⎭ 因为113k ≤<,故()()43212log 3x x x x -+-≥感知高考刺金234题已知函数()()222147f x ax a x a =+-+-,其中*a ∈N ,设0x 为()f x 的一个零点,若0x ∈Z ,则符合条件的a 的值有 个．解：()()()()222722147022x f x ax a x a a x x +=+-+-=⇒=≠-+因为*a ∈N ,故()22712x x +≥+,解得()312x x -≤≤≠-由0x ∈Z 知,03,1,0,1x =--当03x =-时,1a =；当01x =-时,5a =；当00x =时,74a =（舍去）；当01x =时,1a = 综上,符合条件的1a =或5a =,有两个值。